1 Introduction

During the past decades, many researchers have dedicated much effort to develop nonlinear control approaches for dealing with the stability analysis and control design of nonlinear systems, such as adaptive backstepping control [1], sliding mode control [2, 3, 18], fault tolerant control [4], and so on. Especially, the backstepping-based adaptive control technique has become one of the most popular control approaches for a class of deterministic strict-feedback nonlinear systems. An adaptive backstepping design was proposed in [1] to obtain global stability for parametric strict-feedback systems with overparameterization, and was further developed for parameter uncertainty strict-feedback nonlinear systems [5–8]. Alternatively, approximation-based adaptive fuzzy control and adaptive neural network control approaches have been developed to control nonlinear systems with unknown nonlinear functions. Different from the classical adaptive backstepping control, the main idea of adaptive fuzzy control or adaptive neural control methodology is that fuzzy logic systems or neural networks are utilized to approximate unknown nonlinearities in system dynamics, and adaptive controllers are constructed by combining adaptive technique together with backstepping. By combining novel Lyapunov functions with neural networks or fuzzy logic systems, the adaptive backstepping design was extensively applied to control strict-feedback nonlinear systems with unknown functions [9–20, 37–40].

Unlike nonlinear strict-feedback systems, a pure-feedback system stands for a more general class of low-triangular systems that have no affine appearance of the state variables to be used as virtual control signals and an actual input. It is quite restrictive and difficult to find the explicit virtual control signals to stabilize the pure-feedback system based on backstepping technique. In practice, many control systems can be directly described by or transformed into non-affine structure, such as biochemical process, mechanical systems, Duffing oscillator, and so on [1]. Therefore, the study on stability analysis and controller synthesis for pure-feedback nonlinear systems is more important and meaningful both in theory and in practical applications [21–30]. By combining adaptive neural control and backstepping, in [21, 22], a class of pure-feedback systems was investigated, where the last equation of the controlled system is an affine nonlinear system to avoid the algebraic loop problem. In [23], an “ISS-modular” approach combined with the small-gain theorem was presented for adaptive neural control of completely non-affine pure-feedback systems. Afterwards, many researchers also considered some other types of nonlinear systems in non-affine structure [24–30].

Robust control of nonlinear time-delay systems is another important and challenging work in recent years. Time-delay appears commonly in various practical systems such as rolling mill systems, biological systems, metallurgical processing systems, and network systems [31–34]. Since time delays usually result in unsatisfactory performance and are frequently a source of instability, their presence must be taken into account in practical controller designs. There have been some reported studies that extended the backstepping-based adaptive neural control approach to nonlinear systems with time delays. By introducing a new Lyapunov–Krasovskii functional, an adaptive backstepping control scheme was presented in [35] for a class of nonlinear time-delay systems and applied to chemical reactor systems. Based on the Lyapunov–Razumikhin method, an adaptive stabilizing control scheme was presented in [36] for a class of strict-feedback nonlinear time-delay systems. By combining adaptive technique with neural networks or fuzzy logic systems, many interesting results have been reported in [30, 37–39] for uncertain nonlinear systems with unknown nonlinearities.

It is well known that large-scale systems, which are composed of interconnected subsystems, often exist in many practical systems, such as electric power systems, economic systems, aerospace systems, and multi-agent systems. Due to the complexity of the control synthesis and physical restrictions on information exchange among subsystems, it is common to design a decentralized controller to achieve an objective for the whole large-scale systems. The main characteristics of decentralized control are that it can alleviate computational burden and enhance robustness and reliability against interacting operation failures. Earlier research works on decentralized control were mainly concentrated on linear systems or nonlinear subsystems in which the uncertainties satisfy the matching conditions [41]. In Wen [42], proposed an adaptive backstepping decentralized control approach for a class of large-scale systems without satisfying the matching condition. Thereafter, backstepping-based adaptive decentralized control was extensively used to control uncertain interconnected large-scale nonlinear systems [43–45]. By combining the adaptive backstepping control technique with fuzzy logic systems or neural networks, much research work has focused on the control design of large-scale systems with unknown continuous nonlinear functions, for example, see [46–53] and the references therein. In [51, 52], the problem of approximation-based adaptive decentralized state-feedback control was investigated for non-affine nonlinear large-scale systems. However, in the aforementioned results [51, 52], the number of adaption laws depends on the number of the fuzzy rules bases. While the order of the considered systems increases, the number of adaptive parameters to be estimated will increase correspondingly. As a result, the online learning time could be very large. Thus, it is a meaningful issue to design an adaptive fuzzy controller containing fewer adaptive parameters for non-affine pure-feedback large-scale nonlinear time-delay systems.

Motivated by the above observations, the problem of adaptive fuzzy decentralized control is considered for a class of pure-feedback large-scale nonlinear interconnected systems with time-delay. In the controller design, fuzzy logic systems are used to approximate the unknown packaged nonlinearities and the backstepping technique is applied to design a controller. The presented controller guarantees that all the signals in the closed-loop system remain semi-globally uniformly ultimately bounded in mean square. The main contributions of this note lie in the following aspects: (1) a systemical approach is presented to control a class of pure-feedback nonlinear interconnected time-delay systems; (2) only one adaptive parameter needs to be estimated online for each subsystem. In this way, the computational burden is significantly alleviated, and thus the proposed control approach could be easily implemented in practical applications. Simulation results are provided to illustrate the effectiveness of the proposed control approach.

The remainder of this paper is organized as follows. The problem formulation and preliminaries are given in Sect. 2. An adaptive fuzzy decentralized control scheme is presented in Sect. 3. A simulation example is given in Sect. 4, followed by Sect. 5 which concludes the work.

2 Problem formulation and preliminaries

In this paper, we consider a class of interconnected large-scale nonlinear pure-feedback systems with \(N\) subsystems. The \(i\)th \((i=1,2,\ldots,N)\) subsystem is described by:

$$\left\{ \begin{array}{ll} \dot{x}_{i,j}=f_{i,j}\left( \bar{x}_{i,j},{x}_{i,j+1}\right) +h_{i,j}\left( \bar{y}_{\tau }\right),1\le j\le n_{i}-1, &{} \\ \dot{x}_{i,n{_{i}}}=f_{i,{n_{i}}}(\bar{x}_{i,n_{i}},u_{i})+h_{i,n_{i}}\left( \bar{y }_{\tau }\right), &{} \\ y_{i}=x_{i,1}, &{} \end{array} \right.$$
(1)

where \(\bar{x}_{i,j}=[x_{i,1},x_{i,2},\ldots,x_{i,j}]^{T},\,\bar{y}_{\tau }=[y_{\tau 1},y_{\tau 2},\ldots,\,y_{\tau N}]^{T}=[y_{1}(t-{\tau _{1}} ),y_{2}(t-{\tau _{2}}),\ldots,y_{N}(t-{\tau _{N}})]^{T}\), and \(\tau _{i}\) are unknown constant time delays in the \(i\)th subsystem and satisfies \(\tau _{i}\le \tau _{{\rm max}}\), which is a positive constant. \(x_{i}=[x_{i,1},x_{i,2}, \ldots ,x_{i,n_{i}}]^{T}\in R^{n_{i}},\,u_{i}\in R,\) and \(y_{i}\in R\) are the state, scalar control input, and scalar output of the \(i\)th nonlinear subsystem, respectively. \(f_{i,j}(\cdot ):R^{j+1}\rightarrow R,(j=1,2,\ldots ,n_{i})\) are unknown smooth nonlinear functions, \(h_{i,j}(\cdot ):R^{N}\rightarrow R\) \((j=1,2,\ldots ,n_{i})\) are unknown smooth interconnections between the \(i\)th subsystem and other subsystems, with \(f_{i,j}(0)=h_{i,j}(0)=0\).

Remark 1

The system (1) has been widely studied in the existing literature. For example, if the function \(f_{i,j}(\bar{x}_{i,j},{x} _{i,j+1})={x}_{i,j+1}\) and \(h_{i,j}(\cdot )=0\) for \(j=1,2,\ldots ,n_{i}-1\), the nonlinear system (1) becomes similar to the one investigated in [51]. Furthermore, if the function \(h_{i,j}(\cdot )=0\) for \(j=1,2,\ldots ,n_{i}\), it becomes the system investigated in [29].

Using the mean value theorem [54], \(f_{i,j}(\cdot)\) in (1 ) can be expressed as

$$\begin{aligned} f_{i,j}\left( \bar{x}_{i,j},x_{i,j+1}\right)&= f_{i,j}\left( \bar{x}_{i,j},x_{i,j+1}^{0}\right) +g_{ \mu _{i,j}}\left( x_{i,j+1}-x_{i,j+1}^{0}\right) , \nonumber \\ f_{i,n_{i}}\left( \bar{x}_{i,n_{i}},u_{i}\right)&= f_{i,n_{i}}\left( \bar{x} _{i,n_{i}},u_{i}^{0}\right) +g_{\mu _{i,n_{i}}}\left( u_{i}-u_{i}^{0}\right) , \end{aligned}$$
(2)

where \(g_{\mu _{i,j}}:=g_{i,j}(\bar{x}_{i,j},x_{\mu _{i,j}})=\frac{ \partial f_{i,j}(\bar{x}_{i,j},x_{i,j+1})}{\partial x_{i,j+1}} |_{x_{i,j+1}=x_{\mu _{i,j}}},\,x_{i,n_{i}+1}=u_{i},\,x_{\mu _{i,j}}=\mu _{i,j}x_{i,j+1}+(1-\mu _{i,j})x_{i,j+1}^{0},\,0<\mu _{i,j}<1,\, i=1,2,\ldots ,N,\,j=1,2,\ldots ,n_{i}\).

Furthermore, by substituting (2) into (1) and choosing \(x_{i,j+1}^{0}=0,u_{i}^{0}=0,\) it follows that

$$\left\{ \begin{array}{ll} \dot{x}_{i,j}=g_{\mu _{i,j}}x_{i,j+1}+f_{i,j}(\bar{x}_{i,j},0)+h_{i,j}(\bar{y }_{\tau }),1\le j\le n_{i}-1, &{} \\ \dot{x}_{i,n{_{i}}}=g_{\mu _{i,n_{i}}}u_{i}+f_{i,n_{i}}(\bar{x} _{i,n_{i}},0)+h_{i,n_{i}}(\bar{y}_{\tau }), &{} \\ y_{i}=x_{i,1}. &{} \end{array} \right.$$
(3)

Remark 2

Note that the terms \(g_{\mu _{i,j}}x_{i,j+1}^{0}\) and \(g_{\mu _{i,n_{i}}}u_{i}^{0}\) are removed in (3) by choosing \(x_{i,j+1}^{0}=u_{i}^{0}=0\), which simplifies the backstepping design procedure. If the values of all variables are not chosen in this way, then the similar results can also be obtained with minor changes on the virtual control signal \(\alpha _{i}\) and actual control input \(u\), see [30].

The control objective of this study is to design an adaptive fuzzy controller such that all the signals in the closed-loop system remain semi-globally uniformly ultimately bounded.

To facilitate the controller design, the following assumptions are imposed on the each subsystem.

Assumption 1

([23]) For \(1\le i \le N, 1\le j \le n_i\), function \(g_{\mu _{i,j}}\) is unknown, but its sign is known. And there exist unknown constants \(b_m\) and \(b_M\) such that

$$\begin{aligned} 0<b_m\le |g_{\mu _{i,j}}|\le b_M<\infty. \end{aligned}$$

Remark 3

Assumption 1 means \(g_{\mu _{i,j}}\) are either strictly positive or negative. Without loss of generality, it is assumed in this paper that \(0<b_m\le g_{\mu _{i,j}}\le b_M\). As shown later, the constants \(b_m\) and \(b_M\) are not required in the construction of the controllers. So, it is not necessary to know the true values of \(b_m\) and \(b_M\).

Assumption 2

([55]) For uncertain nonlinear functions \(h_{i,j}(\bar{y}_{\tau })\) in (1), there exist unknown smooth functions \(h_{i,j,l}(y_{\tau l})\) such that for \(1\le i \le N, 1\le j \le n_i\),

$$\begin{aligned} |h_{i,j}(\bar{y}_{\tau })|^2&\le \sum _{l=1}^N h^2_{i,j,l}(y_{\tau l}), \end{aligned}$$
(4)

where \(h_{i,j,l}(0)=0, l=1, 2, \ldots , N\).

Remark 4

Noting \(h_{i,j,l}(y_{\tau l})\) in Assumption 2 are smooth functions with \(h_{i,j,l}(0)=0\), so there exist unknown smooth functions \(\bar{h}_{i,j,l}(y_{\tau l})\) such that

$$\begin{aligned} |h_{i,j}(\bar{y}_{\tau })|^2\le \sum _{l=1}^N y_{\tau l}^2\bar{h} ^2_{i,j,l}(y_{\tau l}), \end{aligned}$$
(5)

In the proposed controller design procedure, fuzzy logic systems will be used to approximate nonlinear functions. In [56], the following lemma has been proved, which implies that fuzzy logic systems can be used as the nonlinear function approximators.

Lemma 1

([56]) Let \(f(x)\) be a continuous function defined on a compact set \(\Omega\). Then for any given constant \(\varepsilon > 0\), there exists a fuzzy logic system \(W^TS(x)\) such that

$$\begin{aligned} \sup _{x\in \Omega }\mid f(x)-W^TS(x)\mid \le \varepsilon. \end{aligned}$$

where \(W=[w_1, w_2,\ldots , w_N]^T\) is the ideal constant weight vector, \(S(x)=[s_1(x), \ldots , s_N(x)]^T/{\sum _{j=1}^Ns_j(x)}\) is the basis function vector, \(N > 1\) is the number of the fuzzy rules and \(s_i(x)\) are chosen as Gaussian functions, that is,

$$\begin{aligned} s_j(x)=\exp \left[ \frac{-(x-\mu _i)^T(x-\mu _i)}{\eta _i^2}\right], \quad i=1, 2, \ldots , N \end{aligned}$$

with \(\mu _i = [\mu _{i1},\mu _{i2}, \ldots ,\mu _{in}]^{T}\) being the center vector and \(\eta _i\) the width of the Gaussian function.

3 Adaptive fuzzy controller design

In this section, we will investigate adaptive fuzzy decentralized control by using the backstepping method combined with fuzzy approximation. The backstepping design procedure contains \(n\) steps. In the developed design procedure, for the \(i\)th subsystem, fuzzy logic systems \(W_{i,j}^{T}S(Z_{i,j})\) will be used to model the packaged unknown function \(\bar{f}_{i,j}(Z_{i,j})\) at step \(j\). Both virtual control signals and adaption laws will be constructed in the following forms:

$$\begin{aligned} \alpha _{i,j}(Z_{i,j}) =-k_{i,j}e_{i,j}-\frac{1}{2a_{i,j}^{2}}e_{i,j}\hat{ \theta _{i}}S_{i,j}^{T}(Z_{i,j})S_{i,j}(Z_{i,j}), \end{aligned}$$
(6)
$$\begin{aligned} \dot{\hat{\theta }}_{i} =\sum _{j=1}^{n_{i}}\frac{\lambda _{i}}{2a_{i,j}^{2}} e_{i,j}^{2}S_{i,j}^{T}(Z_{i,j})S_{i,j}(Z_{i,j})-\gamma _{i}\hat{\theta _{i}}, \end{aligned}$$
(7)

where \(i=1,2,\ldots ,N,\,j=1,2,\ldots ,n_{i},\,k_{i,j},\,a_{i,j},\, \lambda _{i},\) and \(\gamma _{i}\) are positive design parameters, \(Z_{i,1}=x_{i,1},\,Z_{i,j}=[\bar{x}_{i,j}^{T},\hat{\theta _{i}}]^{T},\, (j=2,\ldots ,n_{i})\) with \(\bar{x}_{i,j}=[x_{i,1},x_{i,2},\ldots ,\, x_{i,j}]^{T},\) and \(e_{i,j}\) satisfy the following variable transformation:

$$\begin{aligned} e_{i,j}=x_{i,j}-\alpha _{i,j-1} \end{aligned}$$
(8)

with \(\alpha _{i,0}=0\). \(\hat{\theta _{i}}\) is the estimation of an unknown constant \(\theta _{i}\) which will be specified as

$$\begin{aligned} \theta _{i}=\max \left\{ \frac{1}{b_{m}}\Vert W_{i,j}\Vert ^{2};\quad j=1,2,\ldots ,n_{i}\right\} , \end{aligned}$$
(9)

where \(b_{m}\) is defined in Assumption 1, and \(\Vert W_{i,j}\Vert\) denotes the norm of the ideal weight vector of fuzzy systems, which will be specified at the \(j\)th design step. Specifically, \(\alpha _{i,n_{i}}\) is the actual control input \(u_{i}\).

In the following, for simplicity, the time variable \(t\) and the state vector \(\bar{x}_{i,j}\) will be omitted from the corresponding functions and let \(S_{i,j}(Z_{i,j})=S_{i,j}\).

Step 1. Consider the first subsystem in (3) and use coordinate transformation \(e_{i,1}=x_{i,1}, e_{i,2}=x_{i,2}-\alpha _{i,1}\), we have

$$\begin{aligned} \dot{e}_{i,1}=g_{\mu _{i,1}}e_{i,2}+g_{\mu _{i,1}}\alpha _{i,1} +f_{i,j}(\bar{ x}_{i,j},0)+h_{i,1}(\bar{y}_{\tau }). \end{aligned}$$
(10)

Choose the Lyapunov function candidate as

$$\begin{aligned} V_{i,1}=\frac{1}{2}e_{i,1}^2. \end{aligned}$$
(11)

Then, the time derivative of \(V_{i,1}\) along (10) is

$$\begin{aligned} \dot{V}_{i,1}= e_{i,1}\left( g_{\mu _{i,1}}e_{i,2}+g_{\mu _{i,1}}\alpha _{i,1} +f_{i,1}(\bar{x}_{i,1},0)+h_{i,1}(\bar{y}_{\tau })\right). \end{aligned}$$
(12)

By employing (5) and Young’s inequality, we obtain

$$\begin{aligned} e_{i,1}h_{i,1}(\bar{y}_{\tau })&\le \frac{1}{2}e_{i,1}^2+\frac{1}{2} \sum _{l=1}^Ny_{\tau l}^2\bar{h}^2_{i,1,l}(y_{\tau l}). \end{aligned}$$
(13)

Substituting (13) into (12) gives

$$\begin{aligned} \dot{V}_{i,1}= e_{i,1}\left( g_{\mu _{i,1}}e_{i,2}+g_{\mu _{i,1}}\alpha _{i,1} +f_{i,1}(\bar{x}_{i,1},0)+\frac{1}{2}e_{i,1}\right) +\frac{1}{2} \sum _{l=1}^Ny_{\tau l}^2\bar{h}^2_{i,1,l}(y_{\tau l}). \end{aligned}$$
(14)

Step 2. According to (8), the time derivative of \(e_{i,2}\) is given by

$$\begin{aligned} \dot{e}_{i,2}=g_{\mu _{i,2}}e_{i,3}+g_{\mu _{i,2}}\alpha _{i,2}+f_{i,2}(\bar{ x}_{i,2},0)+h_{i,2}(\bar{y}_{\tau })-\dot{\alpha }_{i,1}, \end{aligned}$$

where

$$\begin{aligned} \dot{\alpha }_{i,1}=\frac{\partial \alpha _{i,1}}{\partial x_{i,1}}\left( f_{i,1}(\bar{x}_{i,2})+h_{i,1}(\bar{y}_{\tau })\right) +\frac{\partial \alpha _{i,1}}{\partial \hat{\theta _{i}}}\dot{\hat{\theta }}_{i}. \end{aligned}$$
(15)

Consider a Lyapunov function \(V_{i,2}=\frac{1}{2}e_{i,2}^{2}\). Its time derivation is given by

$$\begin{aligned} \dot{V}_{i,2}&= e_{i,2}\left( g_{\mu _{i,2}}e_{i,3}+g_{\mu _{i,2}}\alpha _{i,2}+f_{i,2}(\bar{x}_{i,2},0)+h_{i,2}(\bar{y}_{\tau })\right. \nonumber \\&\quad \left. -\,\frac{\partial \alpha _{i,1}}{\partial x_{i,1}}\left( f_{i,1}(\bar{ x}_{i,2})+h_{i,1}(\bar{y}_{\tau })\right) -\frac{\partial \alpha _{i,1}}{ \partial \hat{\theta _{i}}}\dot{\hat{\theta }}_{i}\right). \end{aligned}$$
(16)

Following the procedure similar to (13) results in

$$\begin{aligned} -e_{i,2}\frac{\partial \alpha _{i,1}}{\partial x_{i,1}}h_{i,1}(\bar{y}_{\tau }) \le \frac{1}{2}(\frac{\partial \alpha _{i,1}}{\partial x_{i,1}} )^{2}e_{i,2}^{2}+\frac{1}{2}\sum _{l=1}^{N}y_{\tau l}^{2}\bar{h} _{i,1,l}^{2}(y_{\tau l}), \end{aligned}$$
(17)
$$\begin{aligned} e_{i,2}h_{i,2}(\bar{y}_{\tau }) \le \frac{1}{2}e_{i,2}^{2}+\frac{1 }{2}\sum _{l=1}^{N}y_{\tau l}^{2}\bar{h}_{i,2,l}^{2}(y_{\tau l}). \end{aligned}$$
(18)

By combining (16) with (17) and (18) together, one has

$$\begin{aligned} \dot{V}_{i,2}&\le e_{i,2}\left( g_{\mu _{i,2}}e_{i,3}+g_{\mu _{i,2}}\alpha _{i,2}+f_{i,2}(\bar{x}_{i,2},0)-\frac{\partial \alpha _{i,1}}{\partial x_{i,1}}f_{i,1}(\bar{x}_{i,2})\right. \nonumber \\&\quad \left. +\,\frac{1}{2}(\frac{\partial \alpha _{i,1}}{\partial x_{i,1}} )^{2}e_{i,2}+\frac{1}{2}e_{i,2}-\frac{\partial \alpha _{i,1}}{\partial \hat{ \theta _{i}}}\dot{\hat{\theta }}_{i}\right) +\frac{1}{2}\sum _{k=1}^{2} \sum _{l=1}^{N}y_{\tau l}^{2}\bar{h}_{i,k,l}^{2}(y_{\tau l}). \end{aligned}$$
(19)

Step j \((3\le j\le n_{i}-1)\). From (3) and (8), the time derivative of \(e_{i,j}\) is given by

$$\begin{aligned} \dot{e}_{i,j}=g_{\mu _{i,j}}e_{i,j+1}+g_{\mu _{i,j}}\alpha _{i,j} +f_{i,j}(\bar{x}_{i,j},0) +h_{i,j}(\bar{y}_{\tau })-\dot{\alpha }_{i,j-1}, \end{aligned}$$
(20)

where

$$\begin{aligned} \dot{\alpha }_{i,j-1}=\sum _{k=1}^{j-1}\frac{\partial \alpha _{i,j-1}}{\partial x_{i,k}}\left( f_{i,k}(\bar{x}_{i, k+1})+h_{i,k}(\bar{y}_{\tau })\right) + \frac{\partial \alpha _{i,j-1}}{\partial \hat{\theta }_i}\dot{\hat{\theta }_i}. \end{aligned}$$
(21)

Next, choose a Lyapunov function \(V_{i,j}=\frac{1}{2}e_{i,j}^{2}\). Its time derivative is

$$\begin{aligned} \dot{V}_{i,j}&= e_{i,j}\left( g_{\mu _{i,j}}e_{i,j+1}+g_{\mu _{i,j}}\alpha _{i,j}+f_{i,j}(\bar{x}_{i,j},0)+h_{i,j}(\bar{y}_{\tau })-\sum _{k=1}^{j-1} \frac{\partial \alpha _{i,j-1}}{\partial x_{i,k}}\left( f_{i,k}(\bar{x}_{i,k+1})\right. \right. \nonumber \\&\qquad \left. \left. +h_{i,k}(\bar{y}_{\tau })\right) -\frac{\partial \alpha _{i,j-1}}{\partial \hat{\theta }_{i}}\dot{\hat{\theta }_{i}}\right). \end{aligned}$$
(22)

Furthermore, similar to the derivation process in (17) and (18), we have

$$\begin{aligned} -e_{i,j}\sum _{k=1}^{j-1}\frac{\partial \alpha _{i,j-1}}{\partial x_{i,k}} h_{i,k}(\bar{y}_{\tau }) \le \frac{1}{2}e_{i,j}^{2}\sum _{k=1}^{j-1}(\frac{ \partial \alpha _{i,j-1}}{\partial x_{i,k}})^{2}+\frac{1}{2} \sum _{k=1}^{j-1}\sum _{l=1}^{N}y_{\tau l}^{2}\bar{h}_{i,k,l}^{2}(y_{\tau l}), \end{aligned}$$
(23)
$$\begin{aligned} e_{i,j}h_{i,j}(\bar{y}_{\tau }) \le \frac{1}{2}e_{i,j}^{2}+\frac{1}{2} \sum _{l=1}^{N}y_{\tau l}^{2}\bar{h}_{i,j,l}^{2}(y_{\tau l}). \end{aligned}$$
(24)

Substituting (23) and (24) into (22) yields

$$\begin{aligned} \dot{V}_{i,j}&\le e_{i,j}\left( g_{\mu _{i,j}}e_{i,j+1}+g_{\mu _{i,j}}\alpha _{i,j}+f_{i,j}(\bar{x}_{i,j},0)-\sum _{k=1}^{j-1}\frac{\partial \alpha _{i,j-1}}{\partial x_{i,k}}f_{i,k}(\bar{x}_{i,k+1})+\frac{1}{2} e_{i,j}\right. \nonumber \\&\qquad \left. +\,\frac{1}{2}e_{i,j}\sum _{k=1}^{j-1}(\frac{\partial \alpha _{i,j-1}}{ \partial x_{i,k}})^{2}-\frac{\partial \alpha _{i,j-1}}{\partial \hat{\theta } _{i}}\dot{\hat{\theta }_{i}}\right) +\frac{1}{2}\sum _{k=1}^{j} \sum _{l=1}^{N}y_{\tau l}^{2}\bar{h}_{i,k,l}^{2}(y_{\tau l}). \end{aligned}$$
(25)

Step \(n_i\). Similar to (20), the following result can be obtained.

$$\begin{aligned} \dot{e}_{i,n_i}&= g_{\mu _{i,n_i}}u_i +f_{i,n_i}(\bar{x}_{i,n_i},0) +h_{i,n_i}(\bar{y}_{\tau })-\dot{\alpha }_{i,n_i-1}, \end{aligned}$$
(26)

where \(\dot{\alpha }_{i,n_i-1}\) is defined in (21) with \(j=n_i\).

Take a Lyapunov function as

$$\begin{aligned} V_{i,n_i}=\frac{1}{2}e_{i,n_i}^2+\frac{b_m}{2\lambda _i}\tilde{\theta }_i^2, \end{aligned}$$
(27)

where \(\tilde{\theta _i}=\theta _i-\hat{\theta _i}\) is the parameter error and \(\lambda _i\) is a positive design constant.

Furthermore, we can obtain

$$\begin{aligned} \dot{V}_{i,n_{i}}&= e_{i,n_{i}}\left( g_{\mu _{i,n_{i}}}u_{i}+f_{i,n_{i}}( \bar{x}_{i,n_{i}},0)+h_{i,n_{i}}(\bar{y}_{\tau })-\frac{\partial \alpha _{i,n_{i}-1}}{\partial \hat{\theta }_{i}}\dot{\hat{\theta }_{i}}\right. \nonumber \\&\quad \left. -\,\sum _{k=1}^{n_{i}-1}\frac{\partial \alpha _{i,n_{i}-1}}{\partial x_{i,k}}(f_{i,k}(\bar{x}_{i,k+1})+h_{i,k}(\bar{y}_{\tau }))\right) -\frac{ b_{m}}{\lambda _{i}}\tilde{\theta }_{i}\dot{\hat{\theta _{i}}}. \end{aligned}$$
(28)

Repeating the derivations similar to (23)–(25) results in

$$\begin{aligned} \dot{V}_{i,n_{i}}&\le e_{i,n_{i}}\left( g_{\mu _{i,n_{i}}}u_{i}+f_{i,n_{i}}(\bar{x}_{i,n_{i}},0)-\sum _{k=1}^{n_{i}-1}\frac{ \partial \alpha _{i,n_{i}-1}}{\partial x_{i,k}}f_{i,k}(\bar{x} _{i,k+1})\right. \nonumber \\&\quad \left. +\,\frac{1}{2}e_{i,n_{i}}\sum _{k=1}^{n_{i}-1}\left(\frac{\partial \alpha _{i,n_{i}-1}}{\partial x_{i,k}}\right)^{2}+\frac{1}{2}e_{i,n_{i}}-\frac{\partial \alpha _{i,n_{i}-1}}{\partial \hat{\theta }_{i}}\dot{\hat{\theta }_{i}}\right) \nonumber \\&\quad +\,\frac{1}{2}\sum _{k=1}^{n_{i}}\sum _{l=1}^{N}y_{\tau l}^{2}\bar{h} _{i,k,l}^{2}(y_{\tau l})-\frac{b_{m}}{\lambda _{i}}\tilde{\theta }_{i}\dot{ \hat{\theta _{i}}}. \end{aligned}$$
(29)

Now, consider the Lyapunov function for the whole system as

$$\begin{aligned} V=\sum _{i=1}^{N}\sum _{j=1}^{n_{i}}V_{i,j}+V_{Q}=\sum _{i=1}^{N}\left( \sum _{j=1}^{n_{i}}\frac{1}{2}e_{i,j}^{2}+\frac{b_{m}}{2\lambda _{i}}\tilde{ \theta }_{i}^{2}\right) +V_{Q}, \end{aligned}$$

where \(V_{Q}\) is used to compensate for the delay terms and defined as

$$\begin{aligned} V_{Q}=\frac{1}{2}\sum _{i=1}^{N}\sum _{j=1}^{n_{i}}\sum _{k=1}^{j} \sum _{l=1}^{N}e^{-(t-\tau _{l})}\int _{t-\tau _{l}}^{t}e^{s}y_{l}^{2}(s)\bar{h }_{i,k,l}^{2}(y_{l}(s))\hbox {d}s. \end{aligned}$$

Then, it follows from the results (14), (19), (25), and (29) that

$$\begin{aligned} \dot{V}&\le \sum _{i=1}^{N}e_{i,1}\left\{ g_{\mu _{i,1}}\alpha _{i,1}+f_{i,1}(\bar{x}_{i,1},0)+\frac{1}{2}e_{i,1}\right\} +\sum _{i=1}^{N}\sum _{j=2}^{n_{i}-1}e_{i,j}\left\{ g_{\mu _{i,j}}\alpha _{i,j}+g_{\mu _{i,j}}e_{i,j-1}\right. \nonumber \\&\quad \left. +\,f_{i,j}(\bar{x}_{i,j},0)-\sum _{k=1}^{j-1}\frac{\partial \alpha _{i,j-1}}{\partial x_{i,k}}f_{i,k}(\bar{x}_{i,k+1})+\frac{1}{2}e_{i,j}+\frac{ 1}{2}e_{i,j}\sum _{k=1}^{j-1}\left(\frac{\partial \alpha _{i,j-1}}{\partial x_{i,k} }\right)^{2}\right\} \nonumber \\&\quad +\,\sum _{i=1}^{N}e_{i,n_{i}}\left\{ g_{\mu _{i,n_{i}}}u_{i}+f_{i,n_{i}}(\bar{ x}_{i,n_{i}},0)-\sum _{k=1}^{n_{i}-1}\frac{\partial \alpha _{i,n_{i}-1}}{ \partial x_{i,k}}f_{i,k}(\bar{x}_{i,k+1})\right. \nonumber \\&\quad \left. +\,\frac{1}{2}e_{i,n_{i}}\sum _{k=1}^{n_{i}-1}\left(\frac{\partial \alpha _{i,n_{i}-1}}{\partial x_{i,k}}\right)^{2}+\frac{1}{2}e_{i,n_{i}}\right\} -\sum _{i=1}^{N}\frac{b_{m}}{\lambda _{i}}\tilde{\theta }_{i}\dot{\hat{\theta _{i}}}-\sum _{i=1}^{N}\sum _{j=2}^{n_{i}}e_{i,j}\frac{\partial \alpha _{i,j-1} }{\partial \hat{\theta }_{i}}\dot{\hat{\theta }_{i}} \nonumber \\&\quad +\,\frac{1}{2}\sum _{i=1}^{N}\sum _{j=1}^{n_{i}}\sum _{k=1}^{j} \sum _{l=1}^{N}e^{\tau _{l}}y_{l}^{2}\bar{h}_{i,k,l}^{2}(y_{l})-V_{Q}. \end{aligned}$$
(30)

By rearranging terms in the summation and using the definition of adaptive law in (7), we have

$$\begin{aligned}&\frac{1}{2}\sum _{i=1}^{N}\sum _{j=1}^{n_{i}}\sum _{k=1}^{j}\sum _{l=1}^{N}e^{ \tau _{l}}y_{l}^{2}\bar{h}_{i,k,l}^{2}(y_{l})=\frac{1}{2}\sum _{i=1}^{N} \sum _{l=1}^{N}\sum _{j=1}^{n_{l}}\sum _{k=1}^{j}e^{\tau _{i}}y_{i}^{2}\bar{h} _{l,k,i}^{2}(y_{i}), \end{aligned}$$
(31)
$$\begin{aligned}&-\sum _{i=1}^{N}\sum _{j=2}^{n_{i}}e_{i,j}\frac{\partial \alpha _{i,j-1}}{ \partial \hat{\theta }_{i}}\dot{\hat{\theta }_{i}} \nonumber \\&\quad =\sum _{i=1}^{N}\sum _{j=2}^{n_{i}}e_{i,j}\frac{\partial \alpha _{i,j-1}}{ \partial \hat{\theta }_{i}}\gamma _{i}\hat{\theta _{i}}-\sum _{i=1}^{N} \sum _{j=2}^{n_{i}}e_{i,j}\frac{\partial \alpha _{i,j-1}}{\partial \hat{\theta }_{i}}\sum _{k=1}^{j-1}\frac{\lambda _{i}}{2a_{i,k}^{2}} e_{i,k}^{2}S_{i,k}^{T}S_{i,k} \nonumber \\&\quad -\sum _{i=1}^{N}\sum _{j=2}^{n_{i}}e_{i,j}\frac{\partial \alpha _{i,j-1}}{\partial \hat{\theta }_{i}}\sum _{k=j}^{n_{i}}\frac{\lambda _{i}}{ 2a_{i,k}^{2}}e_{i,k}^{2}S_{i,k}^{T}S_{i,k} \nonumber \\&\quad \le \sum _{i=1}^{N}\sum _{j=2}^{n_{i}}e_{i,j}\frac{\partial \alpha _{i,j-1} }{\partial \hat{\theta }_{i}}\gamma _{i}\hat{\theta _{i}}-\sum _{i=1}^{N} \sum _{j=2}^{n_{i}}e_{i,j}\frac{\partial \alpha _{i,j-1}}{\partial \hat{\theta }_{i}}\sum _{k=1}^{j-1}\frac{\lambda _{i}}{2a_{i,k}^{2}} e_{i,k}^{2}S_{i,k}^{T}S_{i,k} \nonumber \\&\quad +\sum _{i=1}^{N}\sum _{j=2}^{n_{i}}\frac{\lambda _{i}}{2a_{i,j}^{2}} e_{i,j}^{2}S_{i,j}^{T}S_{i,j}\left(\sum _{k=2}^{j}|e_{i,k}\frac{\partial \alpha _{i,k-1}}{\partial \hat{\theta _{i}}}|\right). \end{aligned}$$
(32)

Taking (31) and (32) into account, we can rewrite (30) as

$$\begin{aligned} \dot{V}&\le -V_{Q}+\sum _{i=1}^{N}e_{i,1}\left( g_{\mu _{i,1}}\alpha _{i,1}+\bar{f}_{i,1}(Z_{i,1})\right) +\sum _{i=1}^{N}\sum _{j=2}^{n_{i}-1}e_{i,j}\left( g_{\mu _{i,j}}\alpha _{i,j}+ \bar{f}_{i,j}(Z_{i,j})\right) \nonumber \\&\quad +\,\sum _{i=1}^{N}e_{i,n_{i}}\left( g_{\mu _{i,n_{i}}}u_{i}+\bar{f} _{i,n_{i}}(Z_{i,n_{i}})\right) -\frac{1}{2}\sum _{i=1}^{N} \sum _{j=1}^{n_{i}}e_{i,j}^{2}-\sum _{i=1}^{N}\frac{b_{m}}{\lambda _{i}}\tilde{ \theta }_{i}\dot{\hat{\theta _{i}}}, \end{aligned}$$
(33)

where the functions \(\bar{f}_{i,j}(Z_{i,j}),\,i=1,2,\ldots ,N\), are defined as

$$\begin{aligned} \bar{f}_{i,1}(Z_{i,1})&= f_{i,1}(\bar{x}_{i,1},0)+e_{i,1}+\frac{y_{i}}{2} e^{\tau _{i}}\sum _{l=1}^{N}\sum _{s=1}^{n_{l}}\sum _{k=1}^{s}\bar{h} _{l,k,i}^{2}(y_{i}), \end{aligned}$$
(34)
$$\begin{aligned} \bar{f}_{i,j}(Z_{i,j})&= g_{\mu _{i,j}}e_{i,j-1}+f_{i,j}(\bar{x} _{i,j},0)-\sum _{k=1}^{j-1}\frac{\partial \alpha _{i,j-1}}{\partial x_{i,k}} f_{i,k}(\bar{x}_{i,k+1}) \nonumber \\&\quad +\,e_{i,j}+\frac{1}{2}e_{i,j}\sum _{k=1}^{j-1}\left( \frac{\partial \alpha _{i,j-1} }{\partial x_{i,k}}\right) ^{2}+\frac{\partial \alpha _{i,j-1}}{\partial \hat{\theta }_{i}}\gamma _{i}\hat{\theta _{i}} \nonumber \\&\quad -\,\frac{\partial \alpha _{i,j-1}}{\partial \hat{\theta }_{i}}\sum _{k=1}^{j-1} \frac{\lambda _{i}}{2a_{i,k}^{2}}e_{i,k}^{2}S_{i,k}^{T}S_{i,k} \nonumber \\&\quad +\,\frac{\lambda _{i}}{2a_{i,j}^{2}}e_{i,j}S_{i,j}^{T}S_{i,j}\left( \sum _{k=2}^{j}|e_{i,k}\frac{\partial \alpha _{i,k-1}}{\partial \hat{\theta _{i}}}|\right) ,j=2,\ldots ,n_{i}-1, \end{aligned}$$
(35)
$$\begin{aligned} \bar{f}_{i,n_{i}}(Z_{i,n_{i}})&= f_{i,n_{i}}\left( \bar{x}_{i,n_{i}},0\right) + \frac{1}{2}e_{i,n_{i}}\sum _{k=1}^{n_{i}-1}\left( \frac{\partial \alpha _{i,n_{i}-1} }{\partial x_{i,k}}\right) ^{2}-\sum _{k=1}^{n_{i}-1}\frac{\partial \alpha _{i,n_{i}-1}}{\partial x_{i,k}}f_{i,k}(\bar{x}_{i,k+1}) \nonumber \\&\quad +\,e_{i,n_{i}}+\frac{\partial \alpha _{i,n_{i}-1}}{\partial \hat{\theta }_{i}} \gamma _{i}\hat{\theta _{i}}-\frac{\partial \alpha _{i,n_{i}-1}}{\partial \hat{\theta }_{i}}\sum _{k=1}^{n_{i}-1}\frac{\lambda _{i}}{2a_{i,k}^{2}} e_{i,k}^{2}S_{i,k}^{T}S_{i,k} \nonumber \\&\quad +\,\frac{\lambda _{i}}{2a_{i,j}^{2}}e_{i,j}S_{i,j}^{T}S_{i,j}\left( \sum _{k=2}^{n_{i}}|e_{i,k}\frac{\partial \alpha _{i,k-1}}{\partial \hat{ \theta _{i}}}|\right). \end{aligned}$$
(36)

Since the functions \(f_{i,j},\,g_{\mu _{i,j}}\), and \(\bar{h}_{l,k,i}\) are unknown, \(\bar{f}_{i,j}(Z_{i,j}),\,i=1,2,\ldots ,N,\,j=1,2,\ldots ,n_{i}\), cannot be directly used to construct the virtual control signal \(\alpha _{i,j}\) and actual control signals \(u_{i}\). Then, according to Lemma 1, fuzzy logic system \(W_{i,j}^{T}S_{i,j}(Z_{i,j})\) is used to approximate \(\bar{f}_{i,j}(Z_{i,j})\), such that, for any given \(\varepsilon _{i,j}>0\),

$$\begin{aligned} \bar{f}_{i,j}(Z_{i,j})=W_{i,j}^{T}S_{i,j}(Z_{i,j})+\delta _{i,j}(Z_{i,j}), \end{aligned}$$
(37)

where \(\delta _{i,j}(Z_{i,j})\) denotes the approximation error and satisfies \(|\delta _{i,j}(Z_{i,j})|<\varepsilon _{i,j}\).

Furthermore, by Young’s inequality, one has

$$\begin{aligned} e_{i,j}\bar{f}_{i,j}(Z_{i,j})&= e_{i,j}\frac{W_{i,j}^T}{\Vert W_{i,j}\Vert } S_{i,j}\Vert W_{i,j}\Vert +e_{i,j}\delta _{i,j}(Z_{i,j}) \nonumber \\&\le \frac{1}{2a_{i,j}^2}e_{i,j}^2\Vert W_{i,j}\Vert ^2S^T_{i,j}S_{i,j} +\frac{1}{2} a_{i,j}^2+\frac{1}{2}e_{i,j}^2+\frac{1}{2}\varepsilon _{i,j}^2 \nonumber \\&\le \frac{b_m}{2a_{i,j}^2}e_{i,j}^2\theta _iS^T_{i,j}S_{i,j} +\frac{1}{2} a_{i,j}^2+\frac{1}{2}e_{i,j}^2+\frac{1}{2}\varepsilon _{i,j}^2, \end{aligned}$$
(38)

where \(i=1, 2, \ldots , N, j=1, 2, \ldots , n_i\) and \(\theta _i=\max \left\{ \frac{1}{b_m}\Vert W_{i,j}\Vert ^2; j=1, 2,\ldots ,n_i\right\}\).

Substituting (37) into (33) and using (38) results in

$$\begin{aligned} \dot{V}&\le \sum _{i=1}^{N}\sum _{j=1}^{n_{i}-1}e_{i,j}\left( g_{\mu _{i,j}}\alpha _{i,j}+\frac{b_{m}}{2a_{i,j}^{2}}e_{i,j}\theta _{i}S_{i,j}^{T}S_{i,j}\right) \nonumber \\&\quad +\,\sum _{i=1}^{N}e_{i,n_{i}}\left( g_{\mu _{i,n_{i}}}u_{i}+\frac{b_{m}}{ 2a_{i,n_{i}}^{2}}e_{i,n_{i}}\theta _{i}S_{i,n_{i}}^{T}S_{i,n_{i}}\right) \nonumber \\&\quad +\,\sum _{i=1}^{N}\sum _{j=1}^{n_{i}}\left( \frac{1}{2}a_{i,j}^{2}+\frac{1}{2} \varepsilon _{i,j}^{2}\right) -\sum _{i=1}^{N}\frac{b_{m}}{\lambda _{i}} \tilde{\theta }_{i}\dot{\hat{\theta _{i}}}-V_{Q}. \end{aligned}$$
(39)

Now, considering the virtual control signals \(\alpha _{i,j}\) in (6), the following inequality holds.

$$\begin{aligned} e_{i,j}g_{\mu _{i,j}}\alpha _{i,j}\le -k_{i,j}b_{m}e_{i,j}^{2}-\frac{b_{m}}{ 2a_{i,j}^{2}}e_{i,j}^{2}\hat{\theta _{i}}S_{i,j}^{T}S_{i,j},1\le i\le N,1\le j\le n_{i}. \end{aligned}$$
(40)

By taking (40) and adaptive law \(\dot{\hat{\theta }}_i\) in (7) into account, (39) can be rewritten as

$$\begin{aligned} \dot{V}&\le \sum _{i=1}^N\sum _{j=1}^{n_i-1}e_{i,j}\left( -k_{i,j}b_me_{i,j} + \frac{b_m}{2a_{i,j}^2}e_{i,j}\tilde{\theta }_iS^T_{i,j}S_{i,j} \right) \nonumber \\&\quad +\,\sum _{i=1}^Ne_{i,n_i}\left( -k_{i,n_i}e_{i,n_i} +\frac{b_m}{2a_{i,n_i}^2} e_{i,n_i}\tilde{\theta }_iS^T_{i,n_i}S_{i,n_i} \right) \nonumber \\&\quad -\,\sum _{i=1}^N\frac{b_m}{\lambda _i}\tilde{\theta }_i \left( \sum _{j=1}^{n_{i}}\frac{\lambda _i}{2a_{i,j}^2} e^2_{i,j}S^T_{i,j}S_{i,j} -\gamma _i\hat{\theta _i}\right) \nonumber \\&\quad +\,\sum _{i=1}^N\sum _{j=1}^{n_i}\left( \frac{1}{2}a_{i,j}^2 +\frac{1}{2} \varepsilon ^2_{i,j}\right) -V_Q \nonumber \\&\le -\sum _{i=1}^N\sum _{j=1}^{n_i}k_{i,j}b_me^2_{i,j}-V_Q +\sum _{i=1}^N \frac{\gamma _ib_m}{\lambda _i}\tilde{\theta }_i\hat{\theta _i} +\sum _{i=1}^N\sum _{j=1}^{n_i}\left( \frac{1}{2}a_{i,j}^2 +\frac{1}{2} \varepsilon ^2_{i,j}\right) \nonumber \\&\le -\sum _{i=1}^N\left( \sum _{j=1}^{n_i}k_{i,j}b_me^2_{i,j} +\frac{ \gamma _ib_m}{2\lambda _i}\tilde{\theta }^2_i\right) -V_Q +\sum _{i=1}^N\sum _{j=1}^{n_i}\left( \frac{1}{2}a_{i,j}^2 +\frac{1}{2} \varepsilon ^2_{i,j} +\frac{\gamma _ib_m}{2\lambda _i}\theta ^2_i\right) , \end{aligned}$$
(41)

where the inequality \(\tilde{\theta _i}\hat{\theta _i}\le -\frac{1}{2}\tilde{ \theta _i}^2+\frac{1}{2}\theta _i^2\) has been used in the above inequality.

Now, we are in the position to give our main result in the following theorem.

Theorem 1

Consider the large-scale pure-feedback nonlinear time-delay systems (1) with Assumptions 1–2. Suppose that for \(1\le i \le n\) the packaged unknown functions \(\bar{f}_{i,j}(Z_{i,j})\) can be well approximated by the fuzzy logic system \(W_{i,j}^TS_{i,j}(Z_{i,j})\) in the sense that the approximation errors \(\delta _{i,j}(Z_{i,j})\) is bounded. Then, for bounded initial conditions, the controller (6), and adaptive law (7) guarantee that all the signals in the closed-loop system remain bounded and the error signals \(e_{i,j}\) and \(\tilde{\theta }_i\) eventually converge to the compact set \(\Omega _{s}\) defined by

$$\begin{aligned} \Omega _{s}&= \left\{ \left. e_{i,j},\tilde{\theta }_i\right| |e_{i,j}|\le \sqrt{ 2\frac{\nu _0}{\gamma _0}}, |\tilde{\theta }_i|\le \sqrt{\frac{2\lambda _i}{b_m} \frac{\nu _0}{\gamma _0}}, 1\le i \le N, 1\le j\le n_i\right\}. \end{aligned}$$
(42)

Proof

Define

$$\begin{aligned} \gamma _{0}&= \min \{2k_{i,j}b_{m},\gamma _{i},1,i=1,2,\ldots ,N,j=1,2,\ldots ,n_{i}\}, \\ \nu _{0}&= \sum _{i=1}^{N}\sum _{j=1}^{n_{i}}\left( \frac{1}{2}a_{i,j}^{2}+\frac{1}{ 2}\varepsilon _{i,j}^{2}+\frac{\gamma _{i}b_{m}}{2\lambda _{i}}\theta _{i}^{2}\right). \end{aligned}$$

Then, one has

$$\begin{aligned} \dot{V}\le -\gamma _{0}V+\nu _{0},t\ge 0. \end{aligned}$$
(43)

Next, multiplying (43) by \(e^{\gamma _{0}t}\) and integrating it over \([0, t]\) gives

$$\begin{aligned} V(t)\le \left( V(0)-\frac{\nu _{0}}{\gamma _{0}}\right) e^{-\gamma _{0}t}+ \frac{\nu _{0}}{\gamma _{0}},\forall t>0, \end{aligned}$$
(44)

which means that

$$\begin{aligned} V(t)\le V(0)+\frac{\nu _{0}}{\gamma _{0}},\forall t>0. \end{aligned}$$
(45)

Therefore, from (45), \(e_{i,j}\) and \(\tilde{\theta }_{i}\) \((i=1,2,\ldots ,N,\,j=1,2,\ldots ,n_{i})\) are bounded. Since \(\theta _{i}\) are constants, \(\hat{\theta }_{i}\) are bounded. Consequently, \(\alpha _{i,j}\) are also bounded because \(e_{i,j}\) and \(\theta _{i,j}\) are bounded variables. Therefore, it can be concluded that \(x_{i,j}\) are bounded. This shows that all the signals in the closed-loop system are bounded.

Furthermore, it is easily verified from (44) that

$$\begin{aligned} V(t)\le \frac{\nu _0}{\gamma _0}, t\rightarrow +\infty. \end{aligned}$$
(46)

Therefore, the error signals \(e_{i,j}\) and \(\tilde{\theta }_i\) eventually converge to the compact set \(\Omega _{s}\) specified in (42), that is, all the signals in the closed-loop system are semi-globally uniformly ultimately bounded.

Remark 5

In this research, an adaptive fuzzy decentralized control scheme has been developed for a class of pure-feedback nonlinear large-scale systems with constant delays. Apparently, under some assumptions, the proposed method can also be extended to the case with time-varying delays [i.e. \(\tau _i=\tau _i(t)\)]. In this case, a common restriction to time delay is that there exists a constant \(\eta\) such that \(0<\dot{\tau }_i(t)<\eta <1\). Then with a minor change of the functions \(V_{Q}\), the similar result can be obtained by repeating the aforementioned procedure.

4 Simulation results

In this section, to illustrate the validity of the presented control scheme, consider the following interconnected pure-feedback nonlinear system with time-delay

$$\left\{ \begin{array}{ll} \dot{x}_{1,1}=(1+{x}_{1,1}^{2})x_{1,2}+x_{1,2}^{3}+y_{1}(t-\tau _{1})y_{2}^{2}(t-\tau _{2}), &{} \\ \dot{x}_{1,2}=(2+\sin (x_{1,1}x_{1,2}))u_{1}+\cos (0.5u_{1})+y_{1}^{3}(t-\tau _{1})y_{2}(t-\tau _{2}), &{} \\ y_{1}=x_{1,1}, &{} \\ \dot{x}_{2,1}=(2+\cos (x_{2,1}))x_{2,2}+0.25x_{2,2}^{5}+y_{1}(t-\tau _{1})\sin \left( y_{2}^{2}(t-\tau _{2})\right) , &{} \\ \dot{x}_{2,2}=(1+e^{-x_{2,1}x_{2,2}})u_{2}+0.3\sin (u_{2})+y_{2}(t-\tau _{2})\ln \left( 1+y_{1}^{2}(t-\tau _{1})\right) , &{} \\ y_{2}=x_{2,1}, &{} \end{array} \right.$$
(47)

where \(x_{1,1},x_{1,2},x_{2,1}\) and \(x_{2,2}\) denote the state variables, \(u_{1}\) and \(u_{2}\) are the system input signals. The non-affine functions are chosen as \(f_{1,1}(x_{1,2},x_{1,2}) =(1+{x} _{1,1}^{2})x_{1,2}+x_{1,2}^{3}, f_{1,2}(x_{1,1},x_{1,2},u_{1})=(2+\sin (x_{1,1}x_{1,2}))u_{1}+\cos (0.5u_{1}), f_{2,1}(x_{2,1},x_{2,2}) =(2+\cos (x_{2,1}))x_{2,2}+0.25x_{2,2}^{5}, f_{2,2}(x_{2,1},x_{2,2},u_{2}) =(1+e^{-x_{2,1}x_{2,2}})u_{2}+0.3\sin (u_{2})\) and the interconnected terms are in the following forms:

$$\begin{aligned} h_{11}(\bar{y}_{\tau })&= y_{1}(t-\tau _{1})y_{2}^{2}(t-\tau _{2}),h_{12}( \bar{y}_{\tau })=y_{1}^{3}(t-\tau _{1})y_{2}(t-\tau _{2}), \\ h_{21}(\bar{y}_{\tau })&= y_{1}(t-\tau _{1})\sin \left( y_{2}^{2}(t-\tau _{2})\right) , h_{22}(\bar{y}_{\tau }) =y_{2}(t-\tau _{2})\ln \left( 1+y_{1}^{2}(t-\tau _{1})\right). \end{aligned}$$

It can be seen that the system (47) is a non-affine pure-feedback interconnected system with time delay. In the simulation, choose the time-delays \(\tau _{1}=\tau _{2}=2\,{\rm s}\). Therefore, the upper bound \(\tau _{\max }=2\,{\rm s}\). The control objective is to design an adaptive fuzzy controller such that all the signals in the closed-loop system remain bounded. The fuzzy membership functions are chosen as follows:

$$\begin{aligned}\mu _{F_{i,j}^{1}}(x_{i,j})&= e^{-0.5*(x_{i,j}+9)^{2}}, \quad \mu _{F_{i,j}^{2}}(x_{i,j})=e^{-0.5*(x_{i,j}+7)^{2}} \nonumber \\ \mu _{F_{i,j}^{3}}(x_{i,j})&= e^{-0.5*(x_{i,j}+5)^{2}}, \quad \mu _{F_{i,j}^{4}}(x_{i,j})=e^{-0.5*(x_{i,j}+3)^{2}} \nonumber \\ \mu _{F_{i,j}^{5}}(x_{i,j})&= e^{-0.5*(x_{i,j}+1)^{2}}, \quad \mu _{F_{i,j}^{6}}(x_{i,j})=e^{-0.5*(x_{i,j}-0)^{2}} \nonumber \\ \mu _{F_{i,j}^{7}}(x_{i,j})&= e^{-0.5*(x_{i,j}-1)^{2}}, \quad \mu _{F_{i,j}^{8}}(x_{i,j})=e^{-0.5*(x_{i,j}-3)^{2}} \nonumber \\ \mu _{F_{i,j}^{9}}(x_{i,j})&= e^{-0.5*(x_{i,j}-5)^{2}}, \quad \mu _{F_{i,j}^{10}}(x_{i,j})=e^{-0.5*(x_{i,j}-7)^{2}} \nonumber \\ \mu _{F_{i,j}^{11}}(x_{i,j})&= e^{-0.5*(x_{i,j}-9)^{2}}. \end{aligned}$$
(48)

By using Theorem 1, the virtual control signals, actual controllers, and adaptive laws are chosen in the following forms:

$$\left\{ \begin{array}{ll} \alpha _{i,1}=-k_{i,1}e_{i,1}-\frac{1}{2a_{i,1}^{2}}e_{i,1}\hat{\theta _{i}} S_{i,1}^{T}(Z_{i,1})S_{i,1}(Z_{i,1}), &{} \\ u_{i}=-k_{i,2}e_{i,2}-\frac{1}{2a_{i,2}^{2}}e_{i,2}\hat{\theta _{i}} S_{i,2}^{T}(Z_{i,2})S_{i,2}(Z_{i,2}), &{} \\ \dot{\hat{\theta }}_{i}=\sum _{j=1}^{2}\frac{\lambda _{i}}{2a_{i,j}^{2}} e_{i,j}^{2}S_{i,j}^{T}(Z_{i,j})S_{i,j}(Z_{i,j})-\gamma _{i}\hat{\theta _{i}}, &{} \end{array} \right.$$

where \(e_{i,1}=x_{i,1},\,e_{i,2}=x_{i,2}-\alpha _{i,1},\,Z_{i,1}=[x_{i,1}],\,Z_{i,2}=[\bar{x}_{i,2},\hat{\theta }_{i}]^{T},\,i=1,2\). The simulation is run under the initial conditions \([x_{1,1}(0),x_{1,2}(0),x_{2,1}(0),x_{2,2}(0)]^{T}=[0.5,0.3,0.2,0.2]^{T}\) and \([\hat{\theta }_{1}(0),\hat{\theta }_{2}(0)]=[0,0]^{T}\). In the simulation, design parameters are taken as follows: \(k_{1,1}=k_{1,2}=9, k_{2,1}=k_{2,2}=5,\) \(a_{1,1}=a_{1,2}=a_{2,1}=a_{2,2}=1, \gamma _1=\gamma _2=1,\) and \(\lambda _1=\lambda _2=5\).

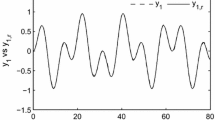
Figures 1, 2, 3 and 4 illustrate the simulation results. Figure 1 shows the state variables \(x_{1,1}\) and \(x_{1,2}\) of the first subsystems. Figure 2 shows the second subsystem state variables \(x_{2,1}\) and \(x_{2,2}\). Figure 3 shows the response curve of the adaptive parameters \(\hat{\theta }_{1}\) and \(\hat{\theta }_{2}\) and Fig. 4 displays the control input signals \(u_{1}\) and \(u_{2}\). Obviously, simulation results show that the controller works well and achieves the desired convergence performance.

Fig. 1
figure 1

The system state variables \(x_{1,1}\) and \(x_{1,2}\).

Full size image
Fig. 2
figure 2

The system state variables \(x_{2,1}\) and \(x_{2,2}\).

Full size image
Fig. 3
figure 3

The adaptive parameters \(\hat{\theta }_1\) and \(\hat{\theta }_2\).

Full size image
Fig. 4
figure 4

The system control signals \(u_{1}\) and \(u_{2}\).

Full size image

5 Conclusions

In this paper, an adaptive fuzzy decentralized control scheme has been presented for a class of pure-feedback large-scale nonlinear systems with time-delay. It has been shown that the proposed controller guarantees that all the signals in the closed-loop systems are semi-globally uniformly ultimately bounded in mean square. The main advantage of the proposed control scheme is that only one adaptive parameter need to be estimated online for each subsystem. Simulation results have been provided to show the effectiveness of the suggested approach.

Our future research will mainly focus on the problem of output-feedback control for pure-feedback nonlinear large-scale systems based on the result in this paper.