An SOS-Based Observer Design for Discrete-Time Polynomial Fuzzy Systems

Abstract

This paper investigates the polynomial fuzzy observer design for discrete-time uncertain polynomial systems. Three classes of discrete-time polynomial fuzzy systems are studied via a sum of squares (SOS) approach. A polynomial fuzzy system is a more general representation of the well-known Takagi–Sugeno (T–S) fuzzy system. The conditions in the proposed approach are derived in terms of SOS, which is the extension of the LMI method. Hence, the conditions obtained in this paper are more general than the corresponding LMI approaches for T–S fuzzy systems. All the design conditions in the proposed approach can be symbolically and numerically solved via the recently developed SOSTOOLS and a semidefinite-program solver, respectively. Numerical examples are provided to demonstrate the validity and applicability of the proposed SOS-based design approach.

1 Introduction

The fuzzy control [1–11] has emerged as one of the most active and fruitful areas for research in the application of fuzzy set theory since the idea was proposed by Zadeh in 1965 [12]. Takagi–Sugeno (T–S) models are nonlinear blending of linear models via membership functions which hold the convex-sum property [1]. Due to its exact representation of a nonlinear model in a compact subset of the domain of the state variables, T–S models [7–11] have been intensively studied. The T–S fuzzy control becomes more natural, simpler, and more effective to complement other nonlinear control methods [13] that require special and rather involved knowledge. The direct Lyapunov method has been usually employed to investigate the stability and stabilization of T–S models. This method often leads to conditions formulated in terms of linear matrix inequalities (LMIs) [9–11], which can be solved numerically and efficiently by LMI solvers. Though LMI approaches remain the most favorite tool of choice, not all the problems can be reformed to LMIs. It should be pointed that some nonlinear systems are not T–S fuzzy controlled via LMIs, but they can be controlled through polynomial fuzzy controllers via SOS approaches in this paper. This is a different approach from the existing LMI approaches. The polynomial fuzzy control was inspired in 2007 [14]. The paper uses polynomial fuzzy system to model and control the nonlinear systems via an SOS approach. The authors also study the SOS-based polynomial fuzzy observer design for three classes of continuous polynomial fuzzy systems: The polynomial matrices A _i and B _i are independent of the states x to be estimated (shortly name it as Class I) [15], [18], the polynomial matrices A _i are permitted to be dependent of the states x to be estimated (shortly name it as Class II) [16], [18], the polynomial matrices A _i and B _i are permitted to be dependent of the states x to be estimated (shortly name it as Class III) [17, 18]. And some extensive results have been obtained, e.g. another paper on relaxation for T–S systems’ stability analysis via SOS method is addressed in [19]. The SOS approach [14–19] presents that it is an extensive representation of LMIs. Obviously, the problems in them cannot be solved by interior point algorithms, e.g. by LMI solvers, but they can be solved via the recently developed SOSTOOLS [20] and an SDP solver [21].

Not all the states of a system are available in many practical applications, or the cost to measure some states is too high sometimes. Observer design methods were presented to deal with the problem, and observer-based control was developed following it. For fuzzy system, the authors [9] presented fuzzy observer designs for both continuous and discrete systems. Soon afterward, observer-based adaptive fuzzy sliding mode control method was developed in [2], observer-based adaptive fuzzy backstepping control method was obtained in [5] and [22], observer-based fuzzy adaptive control approach was proposed in [23], observer-based active fault-tolerant control problem was addressed in [24], an observer-based model reference adaptive iterative learning control strategy was proposed in [25], observer-based adaptive fuzzy output-feedback control problem was studied in [26], the observer-based non-quadratic H _∞ output-feedback stabilization problem was investigated in [27], and so on. However, for polynomial fuzzy systems, there are a few results. Polynomial fuzzy observer designs for continuous polynomial fuzzy systems were provided in [15–18] via a sum of squares (SOS) approach. Observer designs for discrete-time polynomial fuzzy systems have not been addressed in the literature. This motivates us to do this work. In this paper, we consider the observer design problem of the discrete-time polynomial fuzzy system with uncertainty under the SOS framework by exploiting the structure of the system. The main contribution of our paper lies in (1) The SOS-based observer designs for three classes of discrete-time polynomial fuzzy systems with uncertainty are provided in this paper for the first time. (2) The design of the observer is an extension to the discrete-time T–S fuzzy system. (3) The stability conditions given in this paper are more relaxed than the corresponding LMI approaches.

The rest of the paper is organized as follows: some foundational results for the later developments are recalled in Sect. 2. The SOS-based polynomial fuzzy controller and observer designs for Class I are presented in Sect. 3. The SOS-based polynomial fuzzy controller and observer designs for Class II are presented in Sect. 4. The SOS-based polynomial fuzzy controller and observer designs for Class III are presented in Sect. 5. Finally, a conclusion is given in Sect. 6.

2 Problem Formulation and Preliminaries

In this section, we recall the T–S fuzzy model, the fuzzy controller design, the polynomial fuzzy model, and the SOSTOOLS.

First of all, consider a class of nonlinear plant as follows:

$$ x(k + 1) = f(k,x(k),u(k)) $$

(1)

where f is a smooth nonlinear function such that $f\left( {0,0,0} \right) = 0.\,x(k) = [x_{1} (k),\,x_{2} (k), \ldots ,\,x_{n} (k)]^{T} \in {\mathbf{R}}^{n}$ is the system state vector, and the system input $u(k) = [u_{1} (k),\,u_{2} (k), \ldots ,\,u_{m} (k)]^{T} \in {\mathbf{R}}^{m}$.

The main feature of a T–S fuzzy model is the consequent of each IF–THEN rule is a linear system model and T–S fuzzy model can be regarded as a universal approximator of most general nonlinear system. Based on the sector nonlinearity method [9], we can represent the nonlinear system (1) with the following T–S fuzzy form:

Plant Rule i: IF $z_{1} (k)$ is $M_{i1} , \ldots ,z_{p} (k)$ is M _ip ,

THEN

$$ x(k + 1) = \tilde{A}_{i} x(k) + B_{i} u(k) $$

(2)

where $z_{j} (k)$ is the premise variable, M _ij is the fuzzy set associated with the ith model rule and the jth premise variable component, $\tilde{A}_{i} = A_{i} - \Delta A_{i}$, $A_{i} \in {\mathbf{R}}^{n \times n}$ and $B_{i} \in {\mathbf{R}}^{n \times m}$ are constant matrices, $\Delta A_{i} = E_{i} F_{i} (k)H_{i}$ is the uncertain matrix, where $F_{i} (k)$ is a real uncertain matrix function satisfying $F_{i}^{T} (k)F_{i} (k) \le I$, E _i and H _i are known real constant matrices, $i = 1,2, \ldots ,r,$ and r is the number of IF–THEN rules, $j = 1,2, \ldots ,p$. The defuzzification process of the model (2) can be represented as below:

$$ x(k + 1) = \frac{{\sum\nolimits_{i = 1}^{r} {\omega_{i} (z\,(k)(\tilde{A}_{i} x(k) + B_{i} u(k))} }}{{\sum\nolimits_{i = 1}^{r} {\omega_{i} (z(k))} }} $$

(3)

where it is assumed that $\omega_{i} (z(k)) = \prod\nolimits_{j = 1}^{p} {M_{ij} (z_{j} (k))}$, $\omega_{i} (z(k)) \ge 0,\,\;\sum\nolimits_{i = 1}^{r} {\omega_{i} (z(k))} > 0,\quad i = 1,2, \ldots ,r.$

The system (3) can be represented as below for brevity:

$$ x(k + 1) = \sum\limits_{i = 1}^{r} {h_{i} } (z(k))\{ \tilde{A}_{i} x(k) + B_{i} u(k)\} , $$

(4)

where $h_{i} (z(k)) = {{\omega_{i} (z(k))} \mathord{\left/ {\vphantom {{\omega_{i} (z(k))} {\varPi_{i = 1}^{r} \omega_{i} (z(k))}}} \right. \kern-0pt} {\varPi_{i = 1}^{r} \omega_{i} (z(k))}}, \, h_{i} (z(k)) \ge 0,$ $\sum\nolimits_{i = 1}^{r} {h_{i} (z(k))} = 1,\quad i = 1,2, \ldots ,r.$

The fuzzy controller for the nonlinear plant represented by (3) is designed to share the same IF parts with the plant as follows:

Control Rule i: IF $z_{1} (k)$ is $M_{i1} ,\, \ldots ,z_{p} (k)$ is M _ip , THEN

$$ u(k) = - K_{i} x(k) $$

(5)

where $K_{i} \in {\mathbf{R}}^{m \times n}$ is a constant matrix.

The defuzzification process of the model (5) can be represented as below:

$$ u(k) = \sum\limits_{i = 1}^{r} {h_{i} } (z(k))\{ - K_{i} x(k)\} . $$

(6)

The polynomial fuzzy system is a fuzzy model with a polynomial model consequence. Using the sector nonlinearity method, system (1) can be exactly represented with the following polynomial fuzzy model:

Plant Rule i: IF $z_{1} (k)$ is $M_{i1} ,\, \ldots ,z_{p} (k)$ is M _ip ,

THEN

$$ x(k + 1) = \tilde{A}_{i} (x(k))x(k) + B_{i} (x(k))u(k) $$

(7)

where $\tilde{A}_{i} (x(k)) = A_{i} (x(k)) + \Delta A_{i}$. $A_{i} (x(k)) \in {\mathbf{R}}^{n \times n}$ and $B_{i} (x(k)) \in {\mathbf{R}}^{n \times m}$ are polynomial matrices, $i = 1,2, \ldots ,r$, and r is the number of IF–THEN rules.

The defuzzification process of the model (7) can be represented as below:

$$ x(k + 1) = \sum\limits_{i = 1}^{r} {h_{i} } (z(k))\{ \tilde{A}_{i} (x(k))x(k) + B_{i} (x(k))u(k)\} . $$

(8)

For the convenience to the observer design, the following representation is introduced:

$$ x(k + 1) = \sum\limits_{i = 1}^{r} {h_{i} } (z(k))\{ \tilde{A}_{i} (m(k))x(k) + B_{i} (n(k))u(k)\} $$

(9)

where (9) reduces to (8) when $m(k) = n(k) = x(k)$.

Three types of polynomial observer-based control will be studied as below:

• (i) Class I: $m(k) = n(k) = \xi (k).$

• (ii) Class II: $m(k) = x(k)$ and $n(k) = \xi (k).$

• (iii) Class III: $m(k) = n(k) = x(k).$

$\xi (k)$ is a measurable vector that is assumed to be independent of the state x(k) to be estimated.

To stabilize the fuzzy system (8), a polynomial fuzzy controller will be designed as follows:

$$ u(k) = \sum\limits_{i = 1}^{r} {h_{i} } (z(k))\{ - K_{i} (x(k))x(k)\} $$

(10)

where $K_{i} (x(k)) \in {\mathbf{R}}^{m \times n}$ is a polynomial matrix in x(k), $i = 1,2, \ldots ,r$.

Definition 1 [20]

A multivariate polynomial p(x), $x \in {\mathbf{R}}^{n}$, is a SOS, if there exist polynomials $f_{1} (x), \ldots ,f_{m} (x)$ such that

$$ p(x) = \sum\limits_{i = 1}^{m} {f_{i}^{2} } (x). $$

(11)

Definition 2 [20]

The SOS condition (11) is equivalent to the existence of a positive semidefinite matrix Q, such that

$$ p(x) = Z^{T} (x)QZ(x), $$

(12)

where Z(x) is some properly chosen vector of monomials.

Before deriving the main results, one preliminary lemma is given in the following:

Lemma 1

Given matrices $P = P^{T}$, $E$ , and $H$.

$$ P - EF(k)H - H^{T} F^{T} (k)E^{T} > 0 $$

for all $F(k) \in R^{q \times p}$ satisfying $F^{T} (k)F(k) \le I$ if and only if there exists a scalar $\varepsilon > 0$ such that

$$ P - \varepsilon EE^{T} - \frac{1}{\varepsilon }H^{T} H > 0. $$

Proof

Using Lemma 2.4 in [28], the result can be derived easily.

In consideration of clear expression, we will drop the notation with respect to time k and variable z(k) in the following process about proof, e.g., h _i , ξ and x will be used to instead of $h_{i} (z(k)), \, \xi (k),$ and x(k), respectively.

3 Controller and Observer Design (Class I)

In industry control problems, not all the states of a system can be measured. The polynomial fuzzy observer design is proposed based on SOS conditions in this section.

Polynomial fuzzy observers are required to satisfy the following condition:

$$ \mathop {\lim }\limits_{t \to \infty } e = 0 $$

where $e = x - \hat{x}$, $\hat{x}$ denotes the state vector estimated by a polynomial fuzzy observer. In this part, we assume that $A_{i} (x(k))$ and $B_{i} (x(k))$ in (8) are measurable matrices. Under the assumption, we replace the polynomial fuzzy model (8) with

$$ x(k + 1) = \sum\limits_{i = 1}^{r} {h_{i} } (z(k))\{ \tilde{A}_{i} (\xi (k))x(k) + B_{i} (\xi (k))u(x(k))\} $$

(13)

where $\xi (k)$ is a measurable vector that could be outputs, time, both of them or others. And the output for the polynomial fuzzy model is defined as

$$ y(k) = Cx(k) $$

(14)

where $C \in {\mathbf{R}}^{q \times n}$ is a constant matrix.

Then the polynomial fuzzy observer is proposed:

$$ \begin{gathered} \hat{x}(k + 1) = \sum\limits_{i = 1}^{r} {h_{i} } (z(k))\{ A_{i} (\xi (k))\hat{x}(k) \hfill \\ \quad \quad \quad \quad + \,B_{i} (\xi (k))u(k) + L_{i} (\xi (k))(y - \hat{y})\} \hfill \\ \end{gathered} $$

(15)

$$ \hat{y}(k) = C\hat{x}(k) $$

(16)

where $L_{i} (\xi ) \in {\mathbf{R}}^{n \times q}$ is the polynomial observer gain. The following controller needs to be developed:

$$ u(k) = \sum\limits_{i = 1}^{r} {h_{i} } (z(k))\{ - K_{i} (\xi (k))\hat{x}(k)\} . $$

(17)

Theorem 1

The equilibrium of the overall control system consisting of (13)–(17) is asymptotically stable in the large and the steady error between the real state and the estimated state converges to zero if there exist polynomial matrices $M_{i} (\xi (k)) \in {\mathbf{R}}^{m \times n}$, $N_{i} (\xi (k)) \in {\mathbf{R}}^{n \times n}$ , a constant matrix $Q_{1} \in {\mathbf{R}}^{n \times n}$ , and a scalar $\varepsilon > 0$ satisfying the following conditions:

$$ \eta_{1}^{T} \left[ {\begin{array}{*{20}c} {X_{1ii} } & * & * \\ {X_{2ii} } & {X_{1ii} - \varepsilon \tilde{E}_{i} \tilde{E}_{i}^{T} } & * \\ {\tilde{H}_{i} Q} & 0 & {\varepsilon I} \\ \end{array} } \right]\eta_{1} \,{\text{is SOS}} $$

(18)

$$ \eta_{2}^{T} \left[ {\begin{array}{*{20}c} {2Q} & * & * & * \\ {X_{2ij} + X_{2ji} } & {X_{3ij} } & * & * \\ {\tilde{H}_{i} Q} & 0 & {\varepsilon I} & * \\ {\tilde{H}_{j} Q} & 0 & 0 & {\varepsilon I} \\ \end{array} } \right]\eta_{2} \,{\text{is SOS}},\,\,i < j $$

(19)

where

$$ X_{1ii} = \left[ {\begin{array}{*{20}c} {Q_{1} - r_{1i} I} & 0 \\ 0 & {Q_{1} - r_{2i} I} \\ \end{array} } \right],\quad Q = \left[ {\begin{array}{*{20}c} {Q_{1} } & 0 \\ 0 & {Q_{1} } \\ \end{array} } \right] $$

$X_{2ii} = \left[ {\begin{array}{*{20}c} {\varXi_{ii11} } & {\varXi_{ii12} } \\ 0 & {\varXi_{ii22} } \\ \end{array} } \right],\quad X_{2ij} = \left[ {\begin{array}{*{20}c} {\varXi_{ij11} } & {\varXi_{ij12} } \\ 0 & {\varXi_{ij22} } \\ \end{array} } \right]$ $\varXi_{ii12} = B_{i} (\xi (k))M_{i} (\xi (k)),\,\varXi_{ij12} = B_{i} (\xi (k))M_{j} (\xi (k))$

$$ \varXi_{ii22} = A_{i} (\xi (k))Q_{1} - N_{i} (\xi (k)) $$

$$ \varXi_{ij22} = A_{i} (\xi (k))Q_{1} - N_{i} (\xi (k)) $$

$$ \varXi_{ii11} = A_{i} (\xi (k))Q_{1} - B_{i} (\xi (k))M_{i} (\xi (k)) $$

$$ \varXi_{ij11} = A_{i} (\xi (k))Q_{1} - B_{i} (\xi (k))M_{j} (\xi (k)) $$

$$ X_{3ij} = 2Q - \varepsilon \tilde{E}_{i} \tilde{E}_{i}^{T} - \varepsilon \tilde{E}_{j} \tilde{E}_{j}^{T} $$

with $\tilde{E}_{i} = [E_{i}^{T} \;E_{i}^{T} ]^{T}$, $\tilde{H}_{i} = [H_{i} \;0]$, $i,\;j = 1,2, \cdots ,r$. $\eta_{1} \in {\mathbf{R}}^{4n + p}$ and $\eta_{2} \in {\mathbf{R}}^{4n + 2p}$ are vectors which are independent of x, r _1i and r _2i are nonnegative polynomial functions about $\xi (k)$ such that $r_{1i} > 0$ and $r_{2i} > 0$ for $\xi (k) \ne 0$ . Moreover, the gains can be obtained:

$$ K_{i} (\xi (k)) = M_{i} (\xi (k))Q_{1}^{ - 1} , \, L_{i} (\xi (k)) = N_{i} (\xi (k))Q_{1}^{ - 1} C^{ - } , $$

C ⁻ is the generalized inverse matrix of C.

Proof

First, the augmented system (20) consisting of (13–17) is obtained:

$$ \tilde{x}(k + 1) = \sum\limits_{i,j = 1}^{r} {h_{i} } (z(k))h_{j} (z(k))G_{ij} (\xi (k))\tilde{x}(k) $$

(20)

where

$$ \;\tilde{x}(k) = [x^{T} \;\;e^{T} ]^{T} ,\;G_{ij11} = \tilde{A}_{i} (\xi (k)) - B_{i} (\xi (k))F_{j} (\xi (k)) $$

$$ \begin{array}{*{20}c} {\;G_{ij21} = - \Delta A_{i} ,} & {G_{ij22} = A_{i} (\xi (k)) - L_{i} (\xi (k))C} \\ \end{array} $$

$$ \begin{array}{*{20}c} {G_{ij12} = B_{i} (\xi (k))F_{j} (\xi (k)),} & {G_{ij} (\xi (k)) = \left[ {\begin{array}{*{20}c} {G_{ij11} } & {G_{ij12} } \\ {G_{ij21} } & {G_{ij22} } \\ \end{array} } \right].} \\ \end{array} $$

Next, a candidate of a Lyapunov function is proposed:

$$ V(\tilde{x}(k)) = \tilde{x}^{T} (k)P\tilde{x}(k) $$

(21)

where $P = Q^{ - 1} > 0$. Then, if the following conditions are fixed, $\Delta V(\tilde{x}) < 0$ at $\tilde{x} \ne 0$.

$$ \left( {\sum\limits_{i,j = 1}^{r} {h_{i} h_{j} G_{ij}^{T} (\xi )} } \right)P\left( {\sum\limits_{i,j = 1}^{r} {h_{i} h_{j} G_{ij} (\xi )} } \right) - P < 0\; $$

(22)

Using Schur complement theorem and performing congruence transformation, the following inequality is obtained:

$$ \sum\limits_{i,j = 1}^{r} {h_{i} h_{j} } \left[ {\begin{array}{*{20}c} Q & * \\ {G_{ij} (\xi )Q} & Q \\ \end{array} } \right] > 0 $$

(23)

Due to

$$ \begin{gathered} \sum\limits_{i,j = 1}^{r} {h_{i} h_{j} } \left[ {\begin{array}{*{20}c} Q & * \\ {G_{ij} (\xi )Q} & Q \\ \end{array} } \right] \hfill \\ = \sum\limits_{i = 1}^{r} {h_{i}^{2} } \left[ {\begin{array}{*{20}c} Q & * \\ {G_{ii} (\xi )Q} & Q \\ \end{array} } \right] + \; \hfill \\ \;\;\;\sum\limits_{i \ne j}^{r} {h_{i} h_{j} } \left[ {\begin{array}{*{20}c} {2Q} & * \\ {(G_{ij} (\xi ) + G_{ji} (\xi ))Q} & {2Q} \\ \end{array} } \right] \hfill \\ \end{gathered} $$

(24)

if the conditions (18) and (19) hold, by Schur complement theorem and Lemma 1, the Eq. (24) > 0 could be obtained. The proof is completed.

Remark

If $\begin{array}{*{20}c} {A_{i} (\xi ),} & {B_{i} (\xi ),} & {L_{i} (\xi )} \\ \end{array}$ and $F_{i} (\xi )$ reduce to constant matrices in (13), (15), (17), they reduce to the T–S fuzzy model, the T–S fuzzy controller, and the T–S fuzzy observer, respectively. The SOS conditions in Theorem 1 reduce to the following LMIs:

$$ \left[ {\begin{array}{*{20}c} Q & * & * \\ {X_{2ii} } & {Q - \varepsilon \tilde{E}_{i} \tilde{E}_{i}^{T} } & * \\ {\tilde{H}_{i} Q} & 0 & {\varepsilon I} \\ \end{array} } \right] > 0 $$

(25)

$$ \left[ {\begin{array}{*{20}c} {2Q} & * & * & * \\ {X_{2ij} + X_{2ji} } & {X_{3ij} } & * & * \\ {\tilde{H}_{i} Q} & 0 & {\varepsilon I} & * \\ {\tilde{H}_{j} Q} & 0 & 0 & {\varepsilon I} \\ \end{array} } \right] \ge 0,\;i < j, $$

(26)

where

$$ Q = \left[ {\begin{array}{*{20}c} {Q_{1} } & 0 \\ 0 & {Q_{1} } \\ \end{array} } \right],\quad \,X_{2ij} = \left[ {\begin{array}{*{20}c} {A_{i} Q_{1} - B_{i} M_{j} } & {B_{i} M_{j} } \\ 0 & {A_{i} Q_{1} - N_{i} } \\ \end{array} } \right] $$

$$ X_{3ij} = 2Q - \varepsilon \tilde{E}_{i} \tilde{E}_{i}^{T} - \varepsilon \tilde{E}_{j} \tilde{E}_{j}^{T} ,\quad \,i,\;j = 1,2, \cdots ,r. $$

Therefore, Theorem 1 presents more general results.

3.1 Simulation Results I

Consider the following system:

$$ \left\{ {\begin{array}{*{20}c} {x_{1} (k + 1) = 0.5x_{1} (k) - \sin (k)x_{1} (k)\;\;\;\;\;\;\;} \\ {x_{2} (k + 1) = - x_{2}^{2} (k)x_{1} (k) + \sin (x_{2} (k))\;\;\;} \\ \end{array} } \right. $$

(27)

This nonlinear system has a polynomial term $- x_{2}^{2} (k)x_{1} (k)$ and a nonlinear term $\sin (x_{2} (k))$. Assume the range of x ₂(k), i.e. $x_{2} (k) \in [ - a,\;a]$, where a is a positive value. We can get the following fuzzy system using the sector nonlinearity [9]:

$$ \left\{ \begin{array}{l} x(k + 1) = \sum\limits_{i = 1}^{r} h_{i} (z(k))\{ \tilde{A}_{i} x(k) + B_{i} u(k)\} \\ y(k) = Cx(k) \end{array} \right. $$

(28)

where

$$ A_{1} = \left[ {\begin{array}{*{20}c} {0.5} & 0 \\ { - a^{2} } & 1 \\ \end{array} } \right],\,A_{2} = \left[ {\begin{array}{*{20}c} {0.5} & 0 \\ { - a^{2} } & { - 0.2172} \\ \end{array} } \right],\,B_{i} = \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right] $$

$$ A_{3} = \left[ {\begin{array}{*{20}c} {0.5} & 0 \\ 0 & 1 \\ \end{array} } \right],\,A_{4} = \left[ {\begin{array}{*{20}c} {0.5} & 0 \\ 0 & { - 0.2172} \\ \end{array} } \right],\,E_{i} = \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right] $$

$$ C = \left[ {\begin{array}{*{20}c} 0 & 1 \\ \end{array} } \right],\,H_{i} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right],\,i = 1, \ldots ,4. $$

$$ h_{1} (z(k)) = \frac{{x_{2}^{2} (k)}}{{a^{2} }}\frac{{\sin (x_{2} (k)) + 0.2172x_{2} (k)}}{{1.2172x_{2} (k)}} $$

$$ h_{2} (z(k)) = \frac{{x_{2}^{2} (k)}}{{a^{2} }}\frac{{x_{2} (k) - \sin (x_{2} (k))}}{{1.2172x_{2} (k)}} $$

$$ h_{3} (z(k)) = \frac{{a^{2} - x_{2}^{2} (k)}}{{a^{2} }}\frac{{\sin (x_{2} (k)) + 0.2172x_{2} (k)}}{{1.2172x_{2} (k)}} $$

$$ h_{4} (z(k)) = \frac{{a^{2} - x_{2}^{2} (k)}}{{a^{2} }}\frac{{x_{2} (k) - \sin (x_{2} (k))}}{{1.2172x_{2} (k)}}. $$

For a larger range $a \in [10^{ - 9} ,10^{9} ]$, the LMI conditions (25), (26) are infeasible. This also means that the obtained LMI-based T–S fuzzy controller design method for the nonlinear system is not valid. Conversely, the SOS design method based on the polynomial fuzzy systems realizes that the polynomial fuzzy controller stabilizes the system and the estimated states converge to the real states.

Assume that x ₂ is measurable and y = x ₂. The system (28) can be represented as the system (13) and (14), where

$$ A_{1} (y(k)) = \left[ {\begin{array}{*{20}c} {0.5} & 0 \\ { - y^{2} (k)} & 1 \\ \end{array} } \right]\quad E_{1} = E_{2} = \left[ {\begin{array}{*{20}c} 0 & 1 \\ \end{array} } \right]^{T} $$

$$ A_{2} (y(k)) = \left[ {\begin{array}{*{20}c} {0.5} & 0 \\ { - y^{2} (k)} & { - 0.2172} \\ \end{array} } \right]\quad C = \left[ {\begin{array}{*{20}c} 0 & 1 \\ \end{array} } \right] $$

$$ B_{1} (y(k)) = B_{2} (y(k)) = \left[ {\begin{array}{*{20}c} 0 & 1 \\ \end{array} } \right]^{T} \quad H_{1} = H_{2} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right] $$

$$ h_{1} (z(k)) = \frac{\sin (y(k)) + 0.2172y(k)}{1.2172y(k)} $$

$$ h_{2} (z(k)) = \frac{y(k) - \sin (y(k))}{1.2172y(k)}. $$

By solving the SOS conditions in Theorem 1, the feed back gains are given as below:

$$ K_{1} (y(k)) = \left[ {\begin{array}{*{20}c} {0.11e^{ - 2} - 0.18y^{2} (k)} & {0.48 + 0.32e^{ - 14} y^{2} (k)} \\ \end{array} } \right] $$

$$ L_{1} (y(k)) = \left[ {\begin{array}{*{20}c} {0.41e^{ - 15} + 0.20e^{ - 15} y^{2} (k)} \\ {0.91 + 0.72e^{ - 13} y^{2} (k)} \\ \end{array} } \right] $$

$$ K_{2} (y(k)) = \left[ {\begin{array}{*{20}c} { - 0.19e^{ - 3} - 0.89e^{ - 1} y^{2} (k)} & { - 0.10 - 0.94e^{ - 14} y^{2} (k)} \\ \end{array} } \right] $$

$$ L_{2} (y(k)) = \left[ {\begin{array}{*{20}c} {0.46e^{ - 15} + 0.22e^{ - 13} y^{2} (k)} \\ { - 0.18 + 0.30e^{ - 13} y^{2} (k)} \\ \end{array} } \right] $$

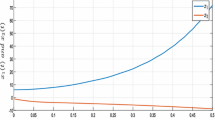
where e ^p means 10^p, p is an integer. Figure 1 shows the controlled system behavior for the initial condition $x(0) = [0.5\;\;0.5]^{T}$ and $\hat{x}(0) = [ - 0.5\;\;0.5]^{T}$. Figure 2 shows the control and estimation results by the polynomial fuzzy observer. It can be seen that the designed controller stabilizes the nonlinear system. The estimation error via the designed observer tends to zero.

Fig. 1

System response with the polynomial fuzzy observer

Fig. 2

Control and estimation results

4 Controller and Observer Design (Class II)

In the above section, an observer design for the polynomial fuzzy system (13) and (14) with the system matrix A _i and input matrix B _i are measurable. In this section, a more complicated class of nonlinear system is considered, i.e. the system matrix A _i depends on the state x. The following polynomial fuzzy system is considered:

$$ x(k + 1) = \sum\limits_{i = 1}^{r} {h_{i} } (z(k))\{ \tilde{A}_{i} (x(k))x(k) + B_{i} (\xi (k))u(k)\}$$

(29)

where $\xi (k)$ is a measurable vector that could be outputs, time, both of them or others. Then a polynomial fuzzy observer is proposed to estimate the states of (29):

$$ \begin{gathered} \hat{x}(k + 1) = \sum\limits_{i = 1}^{r} {h_{i} } (z(k))\{ A_{i} (\hat{x}(k))\hat{x}(k) + \hfill \\ \quad \quad \quad \quad B_{i} (\xi (k))u(k) + L_{i} (\hat{x}(k))(y - \hat{y})\} \hfill \\ \end{gathered} $$

(30)

where $L_{i} (\hat{x}(k)) \in {\mathbf{R}}^{n \times n}$ is the polynomial observer gain.

The following controller needs to be developed:

$$ u(k) = \sum\limits_{i = 1}^{r} {h_{i} } (z(k))\{ - K_{i} (\hat{x}(k))\hat{x}(k)\} $$

(31)

Theorem 2

The equilibrium of the overall control system consisting of (14), (16), and (29)–(31) is asymptotically stable in the large and the steady error between the real state and the estimated state converges to zero if there exist $Q_{1} \in {\mathbf{R}}^{n \times n}$ , and polynomial matrices $M_{i} (\hat{x}(k)) \in {\mathbf{R}}^{m \times n}$ , and $N_{i} (\hat{x}(k)) \in {\mathbf{R}}^{n \times n}$ satisfying the following conditions:

$$ \eta_{1}^{T} \left[ {\begin{array}{*{20}c} {X_{1ii} } & * & * \\ {X_{2ii} } & {X_{1ii} - \varepsilon \tilde{E}_{i} \tilde{E}_{i}^{T} } & * \\ {\tilde{H}_{i} Q} & 0 & {\varepsilon I} \\ \end{array} } \right]\eta_{1} \,is\,SOS $$

(32)

$$ \eta_{2}^{T} \left[ {\begin{array}{*{20}c} {2Q} & * & * & * \\ {X_{2ij} + X_{2ji} } & {X_{3ij} } & * & * \\ {\tilde{H}_{i} Q} & 0 & {\varepsilon I} & * \\ {\tilde{H}_{j} Q} & 0 & 0 & {\varepsilon I} \\ \end{array} } \right]\eta_{2} \,is \, SOS,\quad i < j $$

(33)

where

$$ X_{1ii} = \left[ {\begin{array}{*{20}c} {Q_{1} - r_{1i} I} & 0 \\ 0 & {Q_{1} - r_{2i} I} \\ \end{array} } \right],\quad \,Q = \left[ {\begin{array}{*{20}c} {Q_{1} } & 0 \\ 0 & {Q_{1} } \\ \end{array} } \right] $$

$$ X_{2ii} = \left[ {\begin{array}{*{20}c} {\varXi_{ii11} } & {\varXi_{ii12} } \\ 0 & {\varXi_{ii22} } \\ \end{array} } \right],\quad X_{2ij} = \left[ {\begin{array}{*{20}c} {\varXi_{ij11} } & {\varXi_{ij12} } \\ 0 & {\varXi_{ij22} } \\ \end{array} } \right] $$

$$ \varXi_{ii22} = \bar{A}_{i} (x(k),\hat{x}(k))Q_{1} - N_{i} (\hat{x}(k)) $$

$$ \varXi_{ij22} = \bar{A}_{i} (x(k),\hat{x}(k))Q_{1} - N_{i} (\hat{x}(k)) $$

$$ \varXi_{ii11} = A_{i} (\hat{x}(k))Q_{1} - B_{i} (\xi (k))M_{i} (\hat{x}(k)) $$

$$ \varXi_{ij11} = A_{i} (\hat{x}(k))Q_{1} - B_{i} (\xi (k))M_{j} (\hat{x}(k)) $$

$$ \bar{A}_{i} (x(k),\hat{x}(k))e = A_{i} (x(k))x(k) - A_{i} (\hat{x}(k))\hat{x}(k) $$

$$ \varXi_{ii12} = B_{i} (\xi (k))M_{i} (\hat{x}(k)),\;\varXi_{ij12} = B_{i} (\xi (k))M_{j} (\hat{x}(k)) $$

$$ X_{3ij} = 2Q - \varepsilon \tilde{E}_{i} \tilde{E}_{i}^{T} - \varepsilon \tilde{E}_{j} \tilde{E}_{j}^{T} $$

with $\tilde{E}_{i} = [E_{i}^{T} \;E_{i}^{T} ]^{T} ,$ $\tilde{H}_{i} = [H_{i} \;0].$ $\eta_{1} \in {\mathbf{R}}^{4n + p}$ and $\eta_{2} \in {\mathbf{R}}^{4n + 2p}$ are vectors which are independent of x. r _1i and r _2i are nonnegative polynomial functions about $\xi (k)$ such that $r_{1i} > 0$ and $r_{2i} > 0$ for $\xi (k) \ne 0$, $i, \, j = 1, \, 2, \, \ldots , \, r$ . Moreover, the gains can be obtained:

$$ K_{i} (\hat{x}(k)) = M_{i} (\hat{x}(k))Q_{1}^{ - 1} , \, L_{i} (\hat{x}(k)) = N_{i} (\hat{x}(k))Q_{1}^{ - 1} C^{ - } $$

C ⁻ is the generalized inverse matrix of C.

Proof

First, the augmented system (34) consisting of (14), (16), and (29)–(31) is obtained:

$$ \tilde{x}(k + 1) = \sum\limits_{i,j = 1}^{r} {h_{i} (z(k))h_{j} (z(k))G_{ij} (\xi (k),\hat{x}(k),x(k))\tilde{x}(k)} $$

(34)

where

$$ \tilde{x}(k) = [x^{T} \;\;e^{T} ]^{T} ,\quad G_{ij12} = B_{i} (\xi (k))F_{j} (\hat{x}(k)) $$

$$ G_{ij11} = \tilde{A}_{i} (x(k)) - B_{i} (\xi (k))F_{j} (\hat{x}(k)) $$

$$ G_{ij} (\xi (k),\hat{x}(k),x(k)) = \left[ {\begin{array}{*{20}c} {G_{ij11} } & {G_{ij12} } \\ { - \Delta A_{i} } & {G_{ij22} } \\ \end{array} } \right] $$

$$ G_{ij22} = \bar{A}_{i} (\hat{x}(k),x(k)) - L_{i} (\hat{x}(k))C. $$

Next, a candidate of a Lyapunov function is proposed:

$$ V(\tilde{x}(k)) = \tilde{x}^{T} (k)P\tilde{x}(k) $$

(35)

where $P = Q^{ - 1} > 0$. Then, if the following conditions are fixed, $\Delta V(\tilde{x}) < 0$ at $\tilde{x} \ne 0$,

$$ \left(\sum\limits_{i,j = 1}^{r} {h_{i} h_{j} } G_{ij}^{T} (\xi ,\hat{x},x)\right)P\left(\sum\limits_{i,j = 1}^{r} {h_{i} h_{j} } G_{ij} (\xi ,\hat{x},x)\right) - P < 0. $$

(36)

Following the similar lines of the proof of Theorem 1, the result can be easily derived.

4.1 Simulation Results II

Consider the following system:

$$ \left\{ {\begin{array}{*{20}l} {x_{1} (k + 1) = 0.1x_{2}^{2} (k)x_{1} (k) + 0.1x_{2} (k) - \sin (k)x_{1} (k)} \hfill \\ {x_{2} (k + 1) = 0.9x_{2}^{3} (k) + \sin (x_{1} (k)) + u(k)} \hfill \\ \end{array} } \right.. $$

(37)

This nonlinear system has polynomial terms $0.9x_{2}^{3} (k)$ and $0.1x_{2}^{2} (k)x_{1} (k)$. The premise variable vector z contains x ₂ to be estimated if a T–S fuzzy model is to be used in practical sense. The previous LMI conditions obtained cannot be applied to the system. Otherwise, x ₂ appears in the polynomial system matrix A _i , and it is not contained by the premise variable vector z in the polynomial fuzzy system.

Assume that x ₁ is measurable and y = x ₁. The system (37) can be represented as the system (29) and (14), where

$$ A_{1} (x_{2} (k)) = \left[ {\begin{array}{*{20}c} {0.1x_{2}^{2} (k)} & {0.1} \\ 1 & {0.900x_{2}^{2} (k)} \\ \end{array} } \right],\quad E_{i} = \left[ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right] $$

$$ A_{2} (x_{2} (k)) = \left[ {\begin{array}{*{20}c} {0.1x_{2}^{2} (k)} & {0.1} \\ { - 0.2172} & {0.900x_{2}^{2} (k)} \\ \end{array} } \right], \, B_{i} (y(k)) = \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right] $$

$$ h_{1} (z(k)) = \frac{\sin (y(k)) + 0.2172y(k)}{1.2172y(k)},\quad C = \left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right] $$

$$ h_{2} (z(k)) = \frac{y(k) - \sin (y(k))}{1.2172y(k)},\quad H_{i} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right], \, i = 1,2 $$

By solving the SOS conditions in Theorem 2, we have Q ₁, polynomial matrices $M_{i} (\hat{x}(k))$ and $N_{i} (\hat{x}(k))$. The polynomial feedback gains $F_{i} (\hat{x}(k))$ and $L_{i} (\hat{x}(k))$ could be obtained $F_{i} (\hat{x}(k)) = M_{i} (\hat{x}(k))Q_{1}^{ - 1} ,$ $L_{i} (\hat{x}(k))\, = N_{i} (\hat{x}(k))Q_{1}^{ - 1} C^{ - } ,$ where $i = 1,2$. In comparison with Fig. 3, which represents the system behavior for the initial condition $x(0) = [0.5\;\;1]^{T}$ and $\hat{x}(0) = [0.5\;\; - 1]^{T} ,$ Fig. 4 shows the controlled system behavior, which illustrates the efficiency of the designed fuzzy regulator and the fuzzy observer via SOS approach for the same initial condition. Figure 5 shows the control and estimation results by the designed polynomial fuzzy observer.

Fig. 3

System response without the input

Fig. 4

System response with the polynomial fuzzy observer

Fig. 5

Control and estimation results

5 Controller and Observer Design (Class III)

In this section, a more general class design is considered, i.e., both the system matrix A _i and the input matrix B _i are dependent on the state x. Consider the following polynomial fuzzy system:

$$ x(k + 1) = \sum\limits_{i = 1}^{r} {h_{i} } (z(k))\{ \tilde{A}_{i} (x(k))x(k) + B_{i} (x(k))u(k){\text{\} }} $$

(38)

Then a polynomial fuzzy observer is proposed to estimate the states of (38):

$$ \begin{gathered} \hat{x}(k + 1) = \sum\limits_{i = 1}^{r} {h_{i} } (z(k))\{ A_{i} (\hat{x}(k))\hat{x}(k) + \hfill \\ \quad \quad \quad \quad B_{i} (\hat{x}(k))u(k) + L_{i} (\hat{x}(k))(y - \hat{y})\} \hfill \\ \end{gathered} $$

(39)

where $L_{i} (\hat{x}(k)) \in {\mathbf{R}}^{n \times q}$ is the polynomial observer gain.

The following controller needs to be developed:

$$ u(k) = \sum\limits_{i = 1}^{r} {h_{i} } (z(k))\{ - K_{i} (\hat{x}(k))\hat{x}(k)\} $$

(40)

Theorem 3

The equilibrium of the overall control system consisting of (14), (16), and (38)–(40) is asymptotically stable in the large and the steady error between the real state and the estimated state converges to zero if there exist $Q_{1} \in {\mathbf{R}}^{n \times n}$, $Q_{2} \in {\mathbf{R}}^{n \times n} ,$ and polynomial matrices $M_{i} (\hat{x}(k)) \in {\mathbf{R}}^{m \times n}$ , and $N_{i} (\hat{x}(k)) \in {\mathbf{R}}^{n \times n}$ satisfying the following conditions:

$$ \eta_{1}^{T} \left[ {\begin{array}{*{20}c} {X_{1ii} } & * & * \\ {X_{2ii} } & {X_{1ii} - \varepsilon \tilde{E}_{i} \tilde{E}_{i}^{T} } & * \\ {\tilde{H}_{i} Q} & 0 & {\varepsilon I} \\ \end{array} } \right]\eta_{1} \,is \, SOS $$

(41)

$$ \eta_{2}^{T} \left[ {\begin{array}{*{20}c} {2Q} & * & * & * \\ {X_{2ij} + X_{2ji} } & {X_{3ij} } & * & * \\ {\tilde{H}_{i} Q} & 0 & {\varepsilon I} & * \\ {\tilde{H}_{j} Q} & 0 & 0 & {\varepsilon I} \\ \end{array} } \right]\eta_{2} \,is \, SOS,\quad i < j $$

(42)

where

$$ X_{1ii} = \left[ {\begin{array}{*{20}c} {Q_{1} - r_{1i} I} & 0 \\ 0 & {Q_{2} - r_{2i} I} \\ \end{array} } \right],\quad Q = \left[ {\begin{array}{*{20}c} {Q_{1} } & 0 \\ 0 & {Q_{2} } \\ \end{array} } \right] $$

$$ X_{2ii} = \left[ {\begin{array}{*{20}c} {\varXi_{ii11} } & {\varXi_{ii12} } \\ {\varXi_{ii21} } & {\varXi_{ii22} } \\ \end{array} } \right],\quad X_{2ij} = \left[ {\begin{array}{*{20}c} {\varXi_{ij11} } & {\varXi_{ij12} } \\ {\varXi_{ij21} } & {\varXi_{ij22} } \\ \end{array} } \right] $$

$$ \varXi_{ii22} = A_{i} (x(k))Q_{2} - N_{i} (\hat{x}(k)),{\kern 1pt} \quad \varXi_{ii12} = N_{i} (\hat{x}(k)) $$

$$ \varXi_{ij22} = A_{i} (x(k))Q_{2} - N_{i} (\hat{x}(k)),\quad \varXi_{ij12} = N_{i} (\hat{x}(k)) $$

$$ \varXi_{ii11} = A_{i} (\hat{x}(k))Q_{1} - B_{i} (\hat{x}(k))M_{i} (\hat{x}(k)) $$

$$ \varXi_{ij11} = A_{i} (\hat{x}(k))Q_{1} - B_{i} (\hat{x}(k))M_{j} (\hat{x}(k)) $$

$$ {\varXi}_{ij21} = (A_{i} (x(k)) - A_{i} ({\hat{x}}(k)))Q_{1} - {(B_{i} (x(k)) - B_{i} ({\hat{x}}(k)))M_{j} ({\hat{x}}(k))}. $$

$$ X_{3ij} = 2Q - \varepsilon \tilde{E}_{i} \tilde{E}_{i}^{T} - \varepsilon \tilde{E}_{j} \tilde{E}_{j}^{T} $$

with $\tilde{E}_{i} = [0\;E_{i}^{T} ]^{T}$, $\tilde{H}_{i} = [H_{i} \;H_{i} ]$. $\eta_{1} \in {\mathbf{R}}^{4n + p}$ and $\eta_{2} \in {\mathbf{R}}^{4n + 2p}$ are vectors which are independent of x. r _1i and r _2i are nonnegative polynomial functions about $\xi (k)$ such that $r_{1i} > 0$ and $r_{2i} > 0$ for $\xi (k) \ne 0$, $i,\;j = 1,\,2,\, \ldots ,\,r$ . Moreover, the gains can be obtained:

$$ K_{i} (\hat{x}(k)) = M_{i} (\hat{x}(k))Q_{1}^{ - 1} , \, L_{i} (\hat{x}(k)) = N_{i} (\hat{x}(k))Q_{1}^{ - 1} C^{ - } $$

C ⁻ is the generalized inverse matrix of C.

Proof

First, the augmented system (43) consisting of (14), (16), and (38)–(40) is obtained:

$$ \tilde{x}(k + 1) = \sum\limits_{i,j = 1}^{r} {h_{i} (z(k))h_{j} (z(k))} G_{ij} (\hat{x}(k),x(k))\tilde{x}(k) $$

(43)

where

$$ \tilde{x}(k) = [\hat{x}^{T} \;\;e^{T} ]^{T} ,\quad G_{ij} (\hat{x}(k),x(k)) = \left[ {\begin{array}{*{20}c} {G_{ij11} } & {G_{ij12} } \\ {G_{ij21} } & {G_{ij22} } \\ \end{array} } \right] $$

$$ G_{ij11} = A_{i} (\hat{x}(k)) - B_{i} (\hat{x}(k))F_{j} (\hat{x}(k)) $$

$$ G_{ij12} = L_{i} (\hat{x}(k))C,\quad G_{ij22} = \tilde{A}_{i} (x(k)) - L_{i} (\hat{x}(k))C $$

$$ \begin{gathered} G_{ij21} = \tilde{A}_{i} (x(k)) - A_{i} (\hat{x}(k)) - \hfill \\ \begin{array}{*{20}c} {} & {} & {(B_{i} (x(k)) - B_{i} (\hat{x}(k)))F_{j} (\hat{x}(k)).} \\ \end{array} \hfill \\ \end{gathered} $$

Next, a candidate of a Lyapunov function is proposed:

$$ V(\tilde{x}(k)) = \tilde{x}^{T} (k)P\tilde{x}(k) $$

(44)

where $P = Q^{ - 1} > 0$. Then, if the following conditions are fixed, $\Delta V(\tilde{x}) < 0$ at $\tilde{x} \ne 0$,

$$ \;\;\;\left( {\sum\limits_{i,j = 1}^{r} {h_{i} h_{j} } G_{ij}^{T} (\hat{x},x)} \right)P\left( {\sum\limits_{i,j = 1}^{r} {h_{i} h_{j} } G_{ij} (\hat{x},x)} \right) - P < 0 $$

(45)

Following the similar lines of the proof of Theorem 1, the result can be easily derived.

5.1 Simulation Results III

Consider the following system:

$$ \left\{ {\begin{array}{*{20}l} {x_{1} (k + 1) = f_{1} (k)} \hfill \\ {x_{2} (k + 1) = f_{2} (k)} \hfill \\ \end{array} } \right. $$

(46)

where

$$ f_{1} = 0.3x_{2}^{2} (k)x_{1} (k) + 0.1x_{2} (k) - 0.1\sin (k)(x_{1} (k) + x_{2} (k)) $$

$$ f_{2} = 0.5x_{2}^{3} (k) + \sin (x_{1} (k)) + (1 + x_{2}^{2} (k))u(k). $$

This nonlinear system has polynomial terms $0.5x_{2}^{3} (k)$, $0.3x_{2}^{2} (k)x_{1} (k)$, and $(1 + x_{2}^{2} (k))u(k)$. The SOS design method based on the polynomial fuzzy systems realizes that the polynomial fuzzy controller can stabilize the system and the estimated states converge to the real states. Assume that x ₁ is measurable and y = x ₁. The nonlinear system (46) can be represented as the system (14) and (38), where

$$ A_{1} (x(k)) = \left[ {\begin{array}{*{20}c} {0.3x_{2}^{2} (k)} & {0.1} \\ 1 & {x_{2} (k)} \\ \end{array} } \right],\quad E_{i} = \left[ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right] $$

$$ A_{2} (x(k)) = \left[ {\begin{array}{*{20}c} {0.3x_{2}^{2} (k)} & {0.1} \\ { - 0.2172} & {x_{2} (k)} \\ \end{array} } \right],B_{i} (y(k)) = \left[ {\begin{array}{*{20}c} 0 \\ {1 + x_{2}^{2} (k)} \\ \end{array} } \right] $$

$$ h_{1} (z(k)) = \frac{\sin (y(k)) + 0.2172y(k)}{1.2172y(k)},\quad H_{i} = \left[ {\begin{array}{*{20}c} {0.1} & {0.1} \\ \end{array} } \right] $$

$$ h_{2} (z(k)) = \frac{y(k) - \sin (y(k))}{1.2172y(k)},\quad C = \left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right], \, i = 1,2. $$

By solving the SOS conditions in Theorem 3, we could obtain Q ₁, Q ₂, polynomial matrices $M_{i} (\hat{x}(k))$ and $N_{i} (\hat{x}(k))$, the polynomial feedback gains $K_{i} (\hat{x}(k))$ and $L_{i} (\hat{x}(k))$. In comparison with Fig. 6, which represents the system behavior for the initial condition $x(0) = [0.5\;\;1]^{T}$ and $\hat{x}(0) = [ - 0.5\;\;0.5]^{T}$, Fig. 7 shows the controlled system behavior, which illustrates the efficiency of the designed fuzzy regulator and the fuzzy observer via SOS approach for the same initial condition. Figure 8 shows the control and estimation results by the designed polynomial fuzzy observer.

Fig. 6

System response without the input

Fig. 7

System response with the polynomial fuzzy observer

Fig. 8

Control and estimation results

6 Conclusions

In this paper, a SOS approach has been presented to design the polynomial fuzzy observer for the discrete polynomial fuzzy system. Three classes of discrete-time polynomial fuzzy systems have been studied: (1) the system matrices A _i and input matrices B _i are independent of the states x to be estimated; (2) the system matrices A _i are permitted to be dependent of the states x to be estimated; (3) the system matrices A _i and input matrices B _i are permitted to be dependent of the states x to be estimated. The parallel distributed compensation (PDC) has been employed to design polynomial fuzzy regulators and polynomial fuzzy observers. Numerical examples have been designed to demonstrate the utility of the proposed approach. Following these proposed approach, we can study the nonlinear control problems such as backstepping control, sliding mode control, and so on based on polynomial fuzzy observer further.