When solving counting problems, students often struggle with determining what they are trying to count (and thus what problem type they are trying to solve and, ultimately, what formula appropriately applies). There is a need to explore potential interventions to deepen students’ understanding of key distinctions between problem types and to differentiate meaningfully between such problems. In this paper, we investigate undergraduate students’ understanding of sets of outcomes in the context of elementary Python computer programming. We show that four straightforward program conditional statements seemed to reinforce important conceptual understandings of four canonical combinatorial problem types. We also suggest that the findings in this paper represent one example of a way in which a computational setting may facilitate mathematical learning.
In elementary combinatorics, there is a common set of distinctions between four fundamental types of counting problems. The two-by-two table, pictured in Table 1 below, is a component of most discrete mathematics or combinatorics textbooks (e.g., Martin 2001; Mazur 2010; Tucker 2002), and it offers general formulas for four basic problem types that involve arranging or selecting r objects from a set of n items (Tucker 2002). One axis represents whether or not elements can be repeated, and the other axis represents whether or not different orders of elements yield distinct outcomes (we will explain these formulas in subsequent sections of the paper). Having students understand these four problem types well enough to apply the formulas appropriately is a main goal of helping students count successfully. Indeed, a central aspect of being able to solve counting problems is understanding and having some conceptual grounding for these four basic types of counting problems and their corresponding formulas.
Table 1 Ways to arrange or select r objects from n items (Adapted from Tucker (2002))
We briefly offer canonical examples of these four problem types, which correspond to the problems in Table 2 below (note, we also elaborate more on these problem types in the “Results” section). In the upper left of the two-by-two grid, we have arrangement with unrestricted repetition problems, such as How many 2-character strings can be made from the numbers 1 through 5, where repetition of characters is allowed? Here repetition is allowed, so something like 22 is allowed, and order matters because a string such as 12 is considered different from 21. In the bottom left we have permutation problems, such as How many 2-character strings can be made from the numbers 1 through 5, where repetition of characters is not allowed? Here order matters, as we are counting strings of numbers, but the problem states that repetition is not allowed. Thus, we would count strings like both 12 and 21, but not 22. Note, a problem involving arranging all elements of a set (How many ways are there to arrange the numbers 1 through 5?) is a special case of this kind of problem. In the bottom right we have combination problems, such as How many 2-element subsets can be made from the numbers 1 through 5? Here order does not matter because we are counting subsets (and order is irrelevant in sets), and repetition again is not allowed. So, we would count {1,2} and {1,3}, but not {1,1} and also not both {1,2} and {2,1}. Finally, in the top right we have selection with repetition problems, where order does not matter but repetition is allowed. An example of such a problem is, How many non-decreasing 2-character sequences can be formed from the numbers 1 through 5, where repetition of characters is allowed? Here since repetition is allowed, we count outcomes like 11 and 22. However, because the sequences are non-decreasing, while we would count 12 and 23, we would not also count 21 and 31. We will explore these problems in detail subsequently in the paper. We note further that for each of these four problem types, there tend to be corresponding canonical types of outcomes – for example, permutations tend to count strings or sequences, while combinations tend to count subsets. Problem types thus articulate certain counting problems that satisfy certain constraints, and outcome types represent the actual outcomes that those problems tend to count. We have attempted to articulate this fact in these examples and in Table 2.
Table 2 Examples of Python code that will yield respective problem types
There is abundant evidence that students struggle to distinguish between these problem types (e.g., Annin and Lai 2010; Batanero et al. 1997; CadwalladerOlsker et al. 2012; Lockwood 2014a, b). Typically, this arises in differentiating between permutations and combinations (e.g., Lockwood 2014a), but deciding whether a problem involves selection with or without repetition can also be challenging for students (e.g., Batanero et al. 1997). Although some researchers have tried to find ways to help students understand these important distinctions (e.g., Lockwood et al. 2015; Reed and Lockwood 2018), there is still much to learn about how to help students meaningfully understand distinctions between these four fundamental types of problems.
In this paper, we report on an alternative useful way of distinguishing between the four problem types in Tables 1 and 2. This perspective emerged during a study in which we interviewed undergraduate students using Python programming as they solved combinatorics problems. In designing combinatorial tasks to have students code in Python, we used some simple constructs in Python (for loops and particular conditional statements) that reflected the respective distinctions in the two-by-two table. Table 2 shows counting problems that correspond to the four quadrants in Table 1. In Table 2, for each quadrant, we include a) a statement of a counting problem of that type, b) Python code that would enumerate all of the outcomes of the respective problems, and c) the set of outcomes that the given code would produce (including the total amount). Note the structural similarity between the four bits of code; we will subsequently elaborate on this figure in the “Additional Mathematical Discussion - Selection with Repetition and Completing the Two-by-Two Table” section. In addition, in Appendix 2 we elaborate details of how the Python code works for readers who may want more detail.
We make the case that when the students engaged in these tasks, they deepened their understanding of the distinction between these problem types (and, in particular, this came about by their attending to outcomes). We argue that the Python programming, the representations of each of the outcomes, and the formulas that were reflected in the code together offered an effective approach by which to enhance students’ combinatorial reasoning and activity.
Having students use such programming to solve counting problems is motivated by a desire to investigate a broader phenomenon of examining the role of computing in enriching students’ reasoning about and learning of mathematical concepts. In this paper, our goal is to highlight a potential pedagogical innovation that sheds light on our understanding of how students might reason about an important combinatorial idea (namely, the difference between fundamental types of counting problems) in a meaningful way. We hope that by considering this distinction in terms of basic programming tools, we offer a novel representation and way of understanding these fundamental counting formulas.
There is thus an overarching research question that we attempt to address in this study, which is, In what ways can computational activities inform and affect students’ reasoning about mathematical concepts? To address this question more specifically, we seek to answer the following research question in this paper: In what ways did certain programming structures and conditional statements enrich and deepen students’ reasoning about the nature of the outcomes of several fundamental types of counting problems? Note, we are careful not to claim causality (that is, we do not claim that computational activity caused students to reason more deeply about counting), nor do we make claims about whether those combinatorial understandings could or would have developed in a non-computational setting. However, we do explore the interaction between students’ computational activity and their combinatorial understandings, and our aim is to show ways in which the students’ combinatorial reasoning was enriched and deepened by their computational activity. To present results that answer this research question, we describe two pairs of undergraduate students’ work on combinatorial tasks in a computational environment.
Relevant Literature and Theoretical Perspectives on Combinatorial Thinking and Activity
In this section, we situate this study within the broader literature base, and we also articulate the theoretical perspectives that guided the design and implementation of this study. We first discuss literature on combinatorics, and then we describe how we are taking combinatorial thinking for the purposes of this paper. We address relevant literature and theory on computation in the “Relevant Literature and Theoretical Perspectives on Computational Activity” section.
Relevant Literature on Combinatorics
Attention to Fundamental Problem Types in the Literature
Distinctions between fundamental problem types has been a topic of interest since the inception of combinatorics education research. There is a long history in combinatorics education research of examining students’ reasoning about various types of problems. This began with work by Piaget and Inhelder (1975) and was continued by Fischbein and colleagues (such as Fischbein (1975), Fischbein et al. (1970), and Fischbein and Gazit (1988)), who focused on developmental stages and orders of difficulty for young students in solving basic problem types. These studies demonstrate that researchers have long valued such distinctions, although the particular attention on articulating stages of development and order of difficulty of problems is not our focus in this paper.
To our knowledge, and after searching the literature, there has been no research conducted on the teaching and learning of selection with repetition problems (the upper right quadrant of Tucker’s (2002) table shown in Table 1). This is perhaps not surprising, as such problems tend to require understanding of sophisticated ways of encoding outcomes and are typically reserved for more advanced settings than are typically studied in combinatorics education research. We discuss these problems further in the “Additional Mathematical Discussion - Selection with Repetition and Completing the Two-by-Two Table” section and Appendix 1, but we want to point out that there is not currently literature that explores student reasoning about such problems.
Student Difficulties with Four Fundamental Problem Types
As we have noted, researchers have demonstrated that students struggle to learn and distinguish between these fundamental problem types (e.g., Annin and Lai 2010; Batanero et al. 1997; CadwalladerOlsker et al. 2012). At the heart of this difficulty may be that students often apply formulas without understanding them – not that they willingly refuse to understand them, but they struggle to understand why formulas count specific outcomes. When this happens, counting can become a mysterious and often frustrating activity in which one must make an educated guess about which formula to use. This phenomenon is not unique to combinatorics, but it can be especially prevalent in counting, in which “each problem seems to be different” (Martin 2001, p. 1), and there is “no specific theory” for solving problems (Tucker 2002, p. 169). In particular, many researchers have cited that a common error and struggle for students is to determine whether a problem involves counting combinations or permutations. For instance, Batanero et al. (1997) cite “errors of order” as being one of the primary errors that students encounter (they specifically define this as follows: “This mistake consists of confusing the criteria of combinations and arrangements, that is, distinguishing the order of the elements when it is irrelevant, or, on the contrary, not considering the order when it is essential” (p. 191–192)). Annin and Lai (2010) also discuss difficulties that students have maneuvering issues of order in counting. Lockwood (2014a) previously showed examples of students not being sure of how to differentiate between when “order matters” and when it does not. Lockwood (2014a) reports that when solving a counting problem, an undergraduate student said “… I just kind of go off my gut for it, on the ones that don’t specifically say order matters or it doesn’t matter” (p. 33). This response is perhaps reflective of students’ approach to the distinction between permutations and combinations – they may not have concrete, reliable ways to differentiate between the two.
Similar phenomena occur when students have to distinguish between other kinds of problems. For example, Batanero et al. 1997 also articulated an error of repetition, in which “The pupil does not consider the possibility of repeating the elements when it is possible, or he/she repeats the elements when there is no possibility of doing so” (p. 192). This error highlights an interchange between the two problem types within the row of the table in Table 1 along the axis that determines whether or not order is allowed. This kind of error is representative of other ways in which students may confuse problem types or be unclear about whether or not elements in an outcome may be repeated.
Efforts to Allay these Difficulties
Several researchers have attempted to find productive and effective ways of helping students understand these four key problem types. Lockwood (2013, 2014a, b) has argued that one way to help with this issue and difficulty is to have students focus more explicitly on what outcomes they are trying to count. Lockwood contends that by focusing on the set of outcomes, students can reason about the nature of outcomes as a way to clarify what is being counted, thus helping to determine whether or not order or repetition matter. We explore this notion further in the “Characterizing Combinatorial Thinking and Activity for the Purposes of this Study” section.
There are also cases in which researchers have designed interventions to help students reflect on their own activity in order to develop formulas. For example, Lockwood et al. (2015) had undergraduate students engage in guided reinvention during a 10-session teaching experiment (see Steffe and Thompson 2000, for more detail on the teaching experiment methodology). They had the students solve problems of various kinds in a specific sequence in order to help the students develop formulas on their own (specifically formulas n!, nr, nPr, and nCr). The students successfully reinvented the formulas and demonstrated that they could use them effectively in most instances. In another case, Reed and Lockwood (2018) attempted to help undergraduate students understand basic types of counting problems by having them solve problems of various types (again those reflected by formulas n!, nr, nPr, and nCr), and then categorize those problems according to commonalities the students perceived.Footnote 1 Then, the researchers had the students articulate those commonalities and then come up with general formulas for how to solve the problems. Here again the students successfully developed formulas and were effectively able to articulate differences between problem types and their respective formulas. In each of these cases, the focus was on the formulas for arrangement with unrestricted repetition, arrangement without repetition, and selection without repetition, but not selection with repetition problems.
In summarizing this literature, we see that there has been a considerable focus on helping students understand basic problem types. Students struggle to differentiate between problem types, but there have been efforts to help them differentiate more successfully. Although some effective ways to facilitate students' reasoning about fundamental problem types exist, we consider the results in this paper as offering another, alternative way to enrich students’ thinking about and understanding of these important problem types. This approach we propose has the additional feature of incorporating computing, which, as we address in the “Relevant Literature and Theoretical Perspectives on Computational Activity” section, represents an increasingly desirable practice and perspective.
We now take a moment to characterize how we are taking combinatorial thinking for this study and to outline our theoretical perspective toward counting. Doing so will establish particular language and ideas that we will use throughout the paper, and it will also provide motivation for the computational aspect of the study described in this paper.
Characterizing Combinatorial Thinking and Activity for the Purposes of this Study
A Model of Students’ Combinatorial Thinking
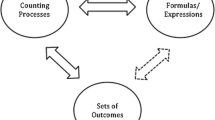
In this paper, we use Lockwood’s (2013) model to frame how we are taking students’ combinatorial thinking, which frames students’ combinatorial thinking in terms of three key components: Formulas/Expressions, Counting Processes, and Sets of Outcomes (Fig. 1). Formulas/Expressions are mathematical expressions that yield some numerical value. A formula or expression is what a student may write as “the answer” to a counting problem, such as 5·4·3·2·1, C(10,4), or n!. Counting Processes are the imagined or actual enumeration processes in which a student engages – that is, the steps or procedures that one completes when solving a counting problem. This could involve a procedure such as creating a case breakdown, applying the multiplication principle, or generating a systematic list. Sets of Outcomes are the sets of elements that are being counted in a combinatorial problem. The cardinality of the set of outcomes typically determines the answer to the problem.
Fig. 1
Lockwood’s model of students’ combinatorial thinking (Lockwood 2013)
We will explore these components in more detail throughout the paper, but we briefly exemplify them by discussing a particular counting problem that Lockwood (2013) used: “How many 3-letter ‘words’ are there using the letters A, B, and C (repetition of letters allowed)?” (p. 256). To see the relationship between counting processes and formulas/expressions, we follow Lockwood in noting that a certain process can elicit a particular formula or expression. For example, a counting process to solve the above problem would be iteratively to consider options for each position in the word and use multiplication. We could argue that there are three options for the first position, for any of those there are three options for the second position, and, similarly, for any of those there are three options for the third position. Because the number of options is independent at each stage (and will yield distinct outcomes), we can multiply the number of options at each stage together.Footnote 2 This process of considering options for each position yields a particular expression of 3·3·3. Similarly, given an expression like 3·3·3, one could interpret it as reflecting an underlying counting process.
Additionally, there is a relationship between a counting process and a set of outcomes, in that a certain process will generate particular outcomes of that process. Indeed, we use the term outcomes in the set of outcomes component because they are the result of (or outcome of) some particular counting process. Lockwood (2013) says the following of this relationship: “Counting processes may generate some set of outcomes, and conversely, a given set of outcomes may be enumerated (or its size may be determined) via some counting process” (p. 255). She also notes that, “In addition to generating a set of outcomes, a counting process can impose a structure onto a set of outcomes (and, in fact, different counting processes can result in different structures)” (p. 256). In the example of the 3-letter ‘words,’ the process of repeated multiplication will generate an alphabetical list of 3-character sequences consisting of As, Bs, and Cs. This demonstrates that there can be relationships between the components. These relationships describe ways in which a student may implicitly or explicitly coordinate more than one of these components.
Related to this model, we also adopt a set-oriented perspective (Lockwood 2014a), in which counting is viewed as inherently involving the determination of the cardinalities of sets of outcomes. Specifically, this set-oriented perspective toward counting is “a way of thinking about counting that involves attending to sets of outcomes as an intrinsic component of solving counting problems” (Lockwood 2014a, p. 31). Practically, adopting this perspective means that this is how we view students’ counting, and that we value activity in which students are generating, using, and reasoning about sets of outcomes. In designing this study, then, we prioritized developing tasks that would allow students to make explicit connections with their set of outcomes. For example, some of the tasks and follow up questions involved pointed questions about how the students’ outcomes (the outputs of the programs) would specifically be listed and structured – more details are given in the “Methods” section. These kind of prompts highlight our perspective that students’ reasoning about outcomes is an important part of their combinatorial thinking and, more specifically, such reasoning about outcomes might be an integral aspect of how they understand and distinguish between problem types.
Using Computing to Reinforce the Relationship between Counting Processes and Sets of Outcomes
Students understanding the relationship between counting processes and sets of outcomes entails understanding that a counting process they employ will generate a particular set of outcomes, which is organized and structured in some way. Research suggests that this is particularly important for students to develop. Lockwood has previously argued that being able to understand connections between sets of outcomes and counting processes is an essential aspect of successful counting (Lockwood 2013, 2014a; Lockwood et al. 2015), and this is related to the set-oriented perspective described previously. We propose that one way to reinforce the relationship between counting processes and outcomes is to have students explicitly articulate a counting process and then get feedback on what the output of that process is. One way to accomplish this is to leverage computational activities, allowing students to write computer programs to list sets of outcomes, and then have immediate feedback on the results of their process. The idea is that such activity can potentially strengthen the connection between counting processes and sets of outcomes, which can help students solve counting problems. By having to clearly articulate steps so that a computer program can understand them, and then seeing the output of the process in the form of sets of outcomes, the computational activity can help students better understand and strengthen the relationship between counting processes and sets of outcomes.
To summarize, then, prior research has suggested that it is desirable for students to connect and reinforce counting processes and sets of outcomes. One of the main premises of this study is that the computer (via simple Python programming) can be an effective way to help students articulate a process clearly and then get immediate feedback for how that process generates outcomes. This is why we are leveraging computing in this study. Before we elaborate the specific computational activity and how it relates to the four problem types in the two-by-two table (Table 1), we pause briefly to introduce literature on computational activity and describe how we are taking such activity in this study.
Relevant Literature and Theoretical Perspectives on Computational Activity
Computing and Computational Activity
The 2005 Joint Task Force for Computing Curricula report broadly defined computing by saying, “In a general way, we can define computing to mean any goal-oriented activity requiring, benefiting from, or creating computers” (p. 9), and we adopt this definition for this paper. Weintrop et al. (2016) developed a “taxonomy of practices focusing on the application of computational thinking to mathematics and science” (p. 128), shown in Fig. 2. We use this taxonomy of practices, especially the computational activities associated with Computational Problem Solving Practices (the third column in Fig. 2), to characterize computational activity in our study. Practically, for the results described in this paper, the students engaged in basic programming tasks in Python, and this primarily included preparing problems for computational solutions, programming, assessing different approaches/solutions to a problem, and troubleshooting and debugging.Footnote 3
Fig. 2
Computational thinking practices in mathematics and science taxonomy (Weintrop et al. 2016, p. 135)
We acknowledge that computation can be a broad term that entails activity that does not necessarily need to involve a machine as a computer. We still use it as a descriptor, but we clarify that in this paper we are specifically examining students’ work as they engaged in programming on a computer. Ultimately, we are interested in examining students’ observable activity of engaging with computing, and at times we use the terms computing, computational activity, and computation as descriptors of our students’ work.
Mathematics Education Research Involving Computing
There is a history of mathematics education researchers using computational environments to help students learn mathematics. Most notably, Papert (e.g., 1980, 1993) introduced the language LOGO that was explicitly designed to help young students reason about mathematical concepts. His legacy lives on today in the theory of constructionism (e.g., Harel and Papert 1991). More recently, there has been increased attention on investigating elements of computational thinking and activity within mathematics education in particular. This is seen, for example, in recent efforts to understand computing (e.g., Lockwood et al. 2019) and computational thinking (e.g., DiSessa 2018; Gadanidis et al. 2018; Hickmott et al. 2018; Kotsopoulos et al. 2017; Sinclair and Patterson 2018) within mathematics. There have also been recent studies that have continued to explore students’ experiences with programming in particular within mathematical contexts, both among children (e.g., DeJarnette 2019) and undergraduates (e.g., Buteau and Muller 2017). The field’s interest in computational thinking and activity within mathematics continues to grow, particularly as computers and programming become increasingly accessible and integrated into students’ everyday lives.
Of particular relevance to the study presented in this paper is previous work by Fenton and Dubinsky (1996), who developed the programming language ISETL in order to teach mathematical concepts. Fenton and Dubinsky also saw the potential value in using computers to reinforce mathematical ideas, and he specifically developed materials to teach discrete mathematics in an ISETL programming environment. There are similarities with our work and that of Fenton and Dubinsky, as we are both explicitly recognizing and seeking to leverage the overall connection between programming and the teaching and learning of mathematics (especially discrete mathematics). However, a main difference is in the nature of the programming language that we are using, which has implications for generalizability of our findings. Whereas Fenton and Dubinsky’s program put forth the development and use of a particular, new language in ISETL, we seek to use existing languages to reinforce combinatorial concepts. By using Python, which is a widely-used language, we are optimistic that tasks we develop or findings we observe may be broadly applicable to a variety of teachers and students. Even more, the loops and conditional statements we emphasize in the paper are commands that could work in any number of existing programming languages.
Methods
We report on data from two teaching experiments (Steffe and Thompson 2000) with two different pairs of students. These were conducted as part of a larger study in the United States that examined the role of computing in combinatorics. In this section we describe the participants, the data collection, and the data analysis.
Participants
For the data reported in this paper, we focus on interviews with two pairs of students who offered evidence of how they reasoned about the operations of != (“not equal”) and > (“greater than”) in Python, and how they connected those operations to their reasoning about basic problem types. Both pairs were recruited from vector calculus classes at a university in the US. In previous work in combinatorics education, we have had positive experiences with vector calculus students as a population, as they tend to be motivated and relatively mathematically mature while still being novice counters. They each participated in an individual 30-min selection interview in which they solved counting problems. We sought students who would not simply recall counting formulas or ideas, and we also wanted to recruit students who could engage with problems and articulate their thinking. We conducted selection interviews in order to determine this, and all four of the students described in this paper fit these criteria. All students were monetarily compensated for their time.
In the selection interviews, we asked students about their previous programming experience. In addition, we had several ways to try to determine students’ initial combinatorial experience. We first asked students what classes they had taken in high school and college to get a sense of their exposure to concepts in discrete mathematics (we asked specifically if they had taken probability, statistics, and computer science). Then, we showed students a list of several symbols, some of which might be associated with combinatoricsFootnote 4: nCr, , C(n,r), A × B, \( \left(\begin{array}{c}n\\ {}r\end{array}\right) \), n!, nPr, P(n,r) and \( \sum \limits_{1\le k\le 10}k \). We asked students if they had seen each symbol before and, if so, what they thought the symbol meant and what it did. This allowed us some insight into students’ familiarities with combinatorial formulas. Then, we had students solve several basic counting problems, which further let us see whether they were trying to recall formulas and how they were reasoning about these problems. Because we primarily wanted to see how students would reason about counting problems, we did not select students who referred regularly to certain problem types or who only seemed to be recalling formulas. If the selection interviews suggested that the students had little prior counting experience (had not seen the previous symbols and did not try to recall formulas in their combinatorial problem solving), we refer to them as novice counters.
Pair 1
Pair 1 consists of two female students whose pseudonyms are Charlotte and Diana. The selection interviews showed that they were novice counters – neither had taken courses involving counting, neither recognized any of common combinatorial symbols nCr, C(n,r) \( \left(\begin{array}{c}n\\ {}r\end{array}\right) \), nPr, or P(n,r) (they recognized n!, but only in a non-combinatorial setting as noted in the previous footnote), and their work on the problems suggested they were not recalling formulas. In addition, they both stated they had no programming experience in high school or in college. We paired them together because they had similar backgrounds and abilities, and they also had schedules that allowed them to meet together over the course of the term. Charlotte was a second-year student and Diana was a first-year student at the time of the interviews, and both students were majoring in chemistry with an interest in forensic science.
Pair 2
Pair 2 consists of two male students whose pseudonyms are CJ and Corey. The selection interviews showed that CJ was a novice counter – he had not taken courses involving counting, he did not recognize the combinatorial symbols (aside from n!, again in a non-combinatorial context), and in his work he did not indicate that he was recalling formulas. Corey had some moderate prior exposure to counting formulas, which he said he had seen in a pre-calculus course in high school. He did recognize some of the symbols, although he explained them vaguely as having to do with arranging objects. In spite of Corey’s occasional reference to past problems, his problem solving convinced us that he was thinking carefully about problems (not just applying formulas) and was adept at articulating his thinking, and we thought he would be a good fit to pair with CJ. CJ and Corey had more programming experience than did the Pair 1 students. They had each taken a programming course in high school, and Corey was enrolled in a MATLAB for engineers course during the time of the interviews, but they explicitly stated that they did not feel particularly comfortable with programming and did not consider themselves to be very familiar with programming. They, too, were paired together because they had similar backgrounds and abilities and schedules that aligned. CJ was a first-year civil engineering major, and Corey was a first-year mechanical engineering major.
Note that we decided to pair students with relatively similar backgrounds and abilities. Our rationale for this was that we wanted to examine relatively new phenomena (the role of computing in combinatorics), and we wanted to be able to do so without also needing to account for students having vastly different backgrounds. In future studies, we plan to examine these phenomena with different students with varying backgrounds.
Data Collection
The data collection for this study occurred during two paired teaching experiments (TEs). Steffe and Thompson (2000) say that a main purpose for such a methodology is “for researchers to experience, firsthand, students’ mathematical learning and reasoning” (p. 267). Steffe and Thompson specify that sessions of a TE (called a teaching episode), consists of a teaching agent, students, a witness, and a method of recording (p. 273). The teaching experiment methodology allows for a researcher to explore student reasoning over a period of time and to observe how they think about and learn particular mathematical concepts. Thus, during a TE, the interviewers formulate and test hypotheses about students’ thinking both within and across teaching episodes, and “teaching actions occur in a teaching experiment in the context of interacting with students” (p. 277). By taking the students through a sequence of tasks and regularly asking clarifying questions throughout the interviews, we were able to examine the students’ reasoning over time and in a variety of contexts.
During all of the TEs, the students sat together and worked at a computer (a large desktop in the interviewer’s office) in the programming environment PyCharm (JetBrains 2017). This environment allowed the students to type and edit code, and when they ran the code, the output would appear in an adjacent window. The students could then look at and reflect upon the output of their code. The students were given paper handouts with problem statements, and the tasks and prompts were also written in PyCharm, and the students used PyCharm to edit and run the Python code. We videotaped and audiotaped the interviews, and we also took a screen video recording of their work on the computer. This allowed us to view the students’ on-paper work and their interactions, as well as what they programmed and how they used the computer in real time. The students informally took turns typing, but we did not put formal constraints on who programmed on which problems.
The TEs involving Pairs 1 and 2 were conducted more or less concurrently during one academic spring term. Pair 1 met for a total of 16 hours, and Pair 2 met for a total of 12.5 hours.Footnote 5 Interviews with Pair 1 occurred, at times, several days before Pair 2, and so we had some time to adjust and prepare for Pair 2 interviews. However, our research team was generally progressing interview by interview and not making large adjustments between teaching experiments (such as adjustments we might make if we had engaged in an entire retrospective analysis of Pair 1’s TE before conducting Pair 2’s TE). This structure was largely due to practical reasons, as we needed to conduct both TEs in one term, and the term was not long enough to conduct them successively. We acknowledge that this lack of retrospective analysis between TEs may be a limitation of the study, but we also see value in having conducted multiple TEs.
Tasks
Over the course of the TEs, we gave the students a variety of counting tasks in which they were asked to use the computer to help determine the answers to counting problems. In many cases they solved or attempted to solve the problem first by hand, and then we would prompt them to code the solution to the problem. In other cases, they used the computer to solve the problem, and they regularly went back and forth between by-hand work and work on the computer. Generally, we had them engage in programming directly by writing and running code, and sometimes we had them evaluate excerpts or outputs of code. The students often used code from prior problems, sometimes copying and pasting previously used code and then editing or adjusting it. We frequently asked follow up questions or asked them to reflect on their thinking and activity. In this way, the TEs were relatively interactive. On the whole, in designing these tasks we chose counting problems that we thought (based on prior research or experience) would elicit certain combinatorial ideas. We have used some similar problems previously (e.g., Lockwood et al. 2015; Reed and Lockwood 2018), but never in a computational context. Thus, a broad design principle was to take tasks that we knew were effective in non-computational settings and then adjust them for a computational setting. Typically, this adjustment meant asking students to write code for a problem that would not just produce a numerical value, but that would actually create a complete list of the outcomes.
Figure 3 shows the first task we gave to all of the students. For the students who were not familiar with Python, we wanted to expose them to a program and let them see examples of the syntax. For these students, seeing the program gave some common syntax and language to talk about, and we instructed them how to run it. By engaging with this code, they could think more about what the program was doing and what the different components of the program and the syntax did.
For the purposes of this paper, we focus especially on the tasks involving the development of arrangements with unrestricted repetition, arrangement without repetition (permutations), and selection without repetition (combinations). In this section we provide examples of the kinds of tasks that we used to elicit particular ideas related to these problem types. These are not the only tasks we offered the students, and, in some cases, we investigated other combinatorial concepts with additional tasks. We are highlighting the tasks that are relevant to the results in this paper.
Arrangements with Unrestricted Repetition
For arrangement with unrestricted repetition tasks, we chose problems whose outcomes have elements that can be repeated (we further discuss this problem type in the “Outcomes as a Bridge between Code and Traditional Formulas” section). In the problems in Table 3, elements from a given set can be repeated, and we want to count different arrangements of different elements within an outcome as distinct (for example, the license plate 112ABC is different than 211ABC).
Table 3 Sample questions for arrangements with unrestricted repetition
For arrangement without repetition tasks, we chose problems whose outcomes have elements that cannot be repeated and the order of elements matters. Table 4 gives some examples of tasks we used. Note that in some cases we explicitly gave students code (we discuss particulars of the code further in the “Additional Mathematical Discussion - Selection with Repetition and Completing the Two-by-Two Table” section) because we wanted novice programmers to be able to examine (rather than create) code. Note that we began with arranging all objects and then later restricted to arranging some but not all of the objects.
Table 4 Sample tasks for arrangement without repetition
For selection without repetition tasks, we chose problems whose outcomes have elements that cannot be repeated, where the order of elements does not matter. Table 5 gives some examples of such tasks. Note that here, in some cases, we explicitly provided some code (which we will discuss further in the “Avenues for Future Research” section). As with the permutations, we did this because we wanted the students, as relatively novice programmers, to be able to make sense of and hopefully subsequently use this greater than operation.
Table 5 Sample questions for selection without repetition
As the interviews progressed, during the teaching experiments it was clear that the use of the != to and the > symbols, in conjunction with nested for loops, were reinforcing valuable combinatorial ideas for the students. We wanted to understand how these symbols and conditional statements potentially enriched students’ understandings of combinatorial problem types (and distinctions between problems such as permutations and combinations). Thus, in analyzing data for this paper, we attended particularly to episodes in which the students interacted with these particular conditional statements. To do this, we first reviewed transcripts, particularly episodes in which the students used, referred to, or reflected upon the != or > symbols in their code. We created documents with all of the instances from the transcripts involving the use of the != or > symbols, and we analyzed these documents using the qualitative analysis software MAXQDA 2018 (VERBI Software 2017). We specifically identified instances of two kinds of ways in which the students interacted with these conditional statements. First, we observed episodes when the students spoke explicitly about the conditional statements, such as explaining or reasoning about what they did. This often occurred when students were explaining their work or were evaluating given code. Second, we also observed instances when the students used the conditional statements in their combinatorial activity – that is, they incorporated != or > into their code as they solved a problem.
We reviewed the entire documents as a research team, and we found that we had episodes that illustrated student reasoning about the conditional statements (and their relationship to combinatorial problem types and outcomes) within each problem type. We also identified and analyzed instances in which students coordinated both types of conditional statements. Ultimately, we view this paper both as offering a theoretical, mathematical discussion and as sharing empirical findings. This is reflected in the results, as we provide both mathematical discussion of combinatorial ideas in a computational setting and evidence of student reasoning about those ideas in such a setting. In light of these goals, during analysis we decided to organize our findings according to problem types (as in Table 1), and we selected episodes that would best represent the students’ reasoning about conditional statements on these particular problem types. This analytical process allowed us to examine the students’ reasoning about the symbols within these conditional statements, and we sought to create a narrative (Auerbach and Silverstein 2003) about their reasoning about and use of those symbols. As the results will demonstrate, these symbols were related for the students, and the symbols seemed to provide an effective way for them to differentiate between the kinds of outcomes they were counting.
Results
We organize the results into the following parts. In the “Arrangement with Unrestricted Repetition Problems”, “Arrangement without Repetition Problems,” and “Selection Without Repetition Problems” sections, we describe the students’ work on the three respective problem types of arrangement with unrestricted repetition, arrangement without repetition, and selection without repetition. We first discuss the mathematical ideas involved in each of those problem types, and then we present the students’ work and their reasoning about the code. The goal in these sections is to demonstrate that the students developed solid understandings of each of these problem types in terms of the respective for loops and conditional statements they programmed in Python. Then, in the “Students’ Reasoning about both != and > Conditionals” section we briefly present data in which the students reasoned about and coordinated more than one type of conditional statements.
Arrangement with Unrestricted Repetition Problems
Arrangement with Unrestricted Repetition – Mathematical Discussion
In this problem type, we are counting arrangements of objects where order matters and where we are allowed to repeat elements. For example, such a problem may say “How many 3-character sequences can I make from the numbers 1, 2, 3, 4, 5, and 6, where repetition of numbers is allowed?” To answer this, we can consider the number of options we have for each of the three distinct spots. Because we can repeat elements, we have six options (the numbers 1 through 6) for what can go in each position. This counting process reflects an expression of 6·6·6 and yields 216 total outcomes. The general formula isnr, as we have n options for each of the r positions.
If we wanted to list the outcomes using Python code, we could use nested for loops as seen in Fig. 4. This code generates all of the outcomes as described above, as the nested for loops iterate through each item in the set Numbers, following an odometer strategy (English 1991) and producing a lexicographic list. The print statement within the nested loops prints the outcomes, and the Counter tracks the total number of outcomes and is printed at the end. Notice there are no additional restrictions or conditional statements within the for loops or the code. For an output of the code, enter the code into a Sage Math Cell (http://sagecell.sagemath.org/). For those who want more detail on the mechanics of how this code could produce outcomes, in Appendix 2 we have included a more detailed description of how the Python code works in generating outcomes to a given counting problem.
Fig. 4
Python code that prints ordered triples from the numbers 1–6, where elements can be repeated
We now present episodes involving both pairs of students that demonstrate their work on arrangement with unrestricted repetition problems.
Arrangement with Unrestricted Repetition – Student Work
We first describe Charlotte and Diana’s worked on the License Plate problem, which states, “A license plate consists of six characters. How many license plates consists of three numbers (from the digits 0 through 9), followed by 3 lower case letters (from the first 5 letters in the alphabet), where repetition of characters is allowed?” Charlotte first clarified what was being counted, asking, “And then when it says, where repetition of characters is allowed, that’s like – it could be 000AAA?,” which we confirmed. They then created the code in Fig. 5 by borrowing techniques from previous problems. When asked how the code might structure the list of outcomes, Diana responded with the explanation in the excerpt below.
Fig. 5
Charlotte and Diana’s code for the License Plate problem
Diana: Yeah. It’ll probably do – it’ll keep these – because these are the starting points. So, like the triple 0 and then it’ll probably go like 001, 002, 003, and include all those different combinations. And in terms of like a mathematical expression, I was thinking, maybe it might multiply the options by each other. So, like with our paper here – Since this is 0 –9, then there are ten options [refers to
Fig. 6
The students’ expression for the License Plate problem
Fig. 6]. And there’s ten options here, and there’s ten options here. It might do 10 times 10 times 10 times 5 times 5 times 5. Because there’s five options here.
Note that in her response, Diana (even if implicitly) allowed for repeats by listing the 000 and 001, etc. By leveraging the structure of the nested loops and the fact that they were repeatedly drawing from sets of Numbers and Letters, we infer that they were able to account for repetition being allowed.
We similarly asked Corey and CJ to write code that answered a refined version of the License Plate problem, where the digits were chosen from the numbers 0 through 5 rather than 0 through 9.Footnote 6 The students produced the code in Fig. 7 (and they later edited their code and realized they did not need multiple sets for numbers and letters).
Fig. 7
CJ and Corey’s initial code of their License Plate problem
We asked the students what they thought might happen when they ran the code in Fig. 7, and they had the following exchange (Corey initially misspoke and said there were five numbers, but they later addressed that and switched to six numbers).
Int. 1: So what do you think will happen? Tell me what you were doing.
Corey: So, for each it’s once again doing the same thing as it did here, but each array is just one character on the license plate. So, setting the first five characters like just the constant. The last character could be A, B, C, or D. And then that would just be for letters to A. And then it would go through again and it would get to letter to B. And then for letter to B it would have another five which would be A, B, C, D, E. So it should – the total number should be 5 times 5 times 5 times 5 times 5 times 5.
CJ: So you’re saying the first one will 000AAA. And then 000AAB? 000AAC.
The point here is that the students seemed to realize that their code was producing 6-character outputs where repetition was allowed – CJ noted that 000AAA, 000AAB, 000AAC would be the first three outcomes. After this conversation they ran the code and found that they were correct in their prediction.
Both pairs of students solved additional arrangement with unrestricted repetition problems in a similar way, including the Coin problem (Write a program to list (and determine the total number of) all possible outcomes of flipping a coin 7 times). Again, both pairs used nested for loops, arriving at the correct answer of 27. For example, CJ and Corey’s code for this problem is seen in Fig. 8, which was similar to the code Charlotte and Diana produced.
The purpose of presenting the examples in this section is to show that the students used nested for loops for problems involving arrangement, where repetition of elements was allowed. Further, both pairs used this same overall code structure to solve these problems.
As we move on to problems involving arrangement without repetition and selection without repetition in the following sections, we will contrast the structure of code used to solve those problems with code used to solve arrangement with repetition problems in this section. As we will see, by adding conditional statements after each for loop, the nested for loops can be tweaked relatively easily to account for arrangements without repetition (permutations) or selection without repetition (combinations).
Arrangement without Repetition Problems
Arrangement without Repetition – Mathematical Discussion
In this problem type, we solve problems in which order matters but repetition is not allowed, so we consider arrangements where elements of an outcome cannot be repeated. For example, such a problem may say “How many 3-character sequences can I make from the numbers 1, 2, 3, 4, 5, and 6, where repetition of numbers is not allowed?” To answer this, we can consider the number of options we have for each of the three distinct spots. Because we cannot repeat elements, we have six options (the numbers 1 through 6) for what can go in the first position, then for each of those we now have five options for what can go in the second position, and then for each of those we have four options for what can go in the third position. This counting process reflects an expression of 6·5·4, which yields 120 total outcomes. The general formula for arranging r objects from n objects is the product n· (n – 1) · (n – 2) ·…· (n – r + 1), so there is a total of r terms. This product can also efficiently be expressed as n!/(n – r)!, as a number of terms cancel.Footnote 7 These are called r-permutations (Tucker 2002), and they are often denoted as P(n,r).Footnote 8
To write Python code to list all of the outcomes and to determine the total number of outcomes, we note that we are considering available options for each position, so we can again use nested for loops. However, we also need to account for the fact that in this case we cannot repeat elements. Thus, we must incorporate a condition (in the form of a conditional if statement) that precludes the counting (and printing) of outcomes with repeated elements. To do this, we include a condition that specifies that the outcomes get counted and printed only if the number in each successive position is distinct from (not equal to) the numbers in the previous positions. As seen in Fig. 9, we incorporate this by using the “if j!= i” command, where, as we have noted, the symbol != means “not equal to.” Thus, the code in Fig. 9 generates all of the outcomes as described above. Again, the print statement within the nested loops prints the outcomes, and the Counter keeps track of the total number and is printed at the end. The conditional if statements with! = symbols make it so outcomes with repeated elements are not printed and do not contribute to the total – thus this code only counts those outcomes where elements are not repeated. Note we include both the k != i and k != j because we want no repetition throughout the sequence of numbers (if we only had k != j we might have an outcome like 121). Generally, if we are arranging r objects from a set of n distinct objects, we would have r nested loops and an original set of size n.
Fig. 9
Python code that prints arrangements of 3 numbers from the numbers 1–6
To write code that reflects the number of arrangements of n distinct objects, yielding an answer of n!, we would have n nested for loops where we include a conditional statement after each for loop to ensure that no elements repeat. Again, such a problem is a special case of P(n,r) problems.
Arrangement without Repetition – Student Work
We originally introduced the != symbol outside the context of permutations, and the students seemed to understand it as a way to account for ensuring certain elements would not be equal. We reintroduced the symbol in the context of permutations when we gave them the 5-People problem (Fig. 10). We included the code in the problem, and we asked them to make sense of it. Here we present Charlotte and Diana’s work on this problem, noting that CJ and Corey did similar work.
Fig. 10
The statement of the 5-people problem as given to the students
Diana: I think for sure that the statements have the exclamation point each time, that’s making it so that these values will not repeat, which makes sense when you have five people because you can’t just repeat a person.
Charlotte: Yeah, that makes sense. Yeah, kind of what she was saying, I think the code, yeah, just trying to figure out how many different arrangements each person can be in and then yeah, each of these exclamation points, like Diana said, is to make sure John isn’t sitting in two different seats at the same time.
Charlotte and Diana seemed to make sense of the != condition in terms of the context of the problem, with Charlotte viewing the != condition as ensuring that a person (for example, John) could not sit in two seats at the same time. In considering a solution to the problem, they realized that the answer was 5!, and we asked them about how that solution is reflected in the code. In the excerpt below, Charlotte reiterated her understanding of the != symbol, explaining that it eliminates options for each position. This demonstrates that by connecting the conditional statement in the code, the students were able both to eliminate a choice for the next position and reduce the number of options for the next position. In this way, the code served to connect the set of outcomes and counting process, in terms of Lockwood’s (2013) model.
Int. 1: Do you see the kind of factorial at all in the code? Like in the structure of the code or is that harder to see.
Charlotte: Yeah, in a way because with the P2 not equaling P1 then it eliminates one of the options, so then there’s only four. So, like, this first for loop you have five options, for this one it’s getting rid of one, so there’s only four. Then it gets rid of two, so there are three options, then it gets rid of three, so it’s two options. And then it gets rid of four, so there’s only one option.
Even though we illustrated their solutions to problem involving arranging all n elements of a set, the students also solved r-permutation problems, where they had to arrange r objects from n objects. In particular, Charlotte and Diana tended to edit their previous code that consisted of n for loops to only include r for loops. Charlotte recognized an r-permutation as being related to an n-permutation problem, saying, “It’s still the same type of problem, but we’re just limiting the amount that’s in the print.” CJ and Corey similarly reasoned about r-permutations, describing the purpose of the != symbol as “It would do 1, 1, 1 if we didn’t have the not equals to.” The point of these examples is to emphasize the role of the != symbol in their code.
Eventually, we asked both pairs of students about that formula for arranging n distinct objects (a special case of P(n,r)). Both pairs arrived at the formula of n!. We gave them the prompt that said, “How does your code in this worksheet reflect your answer in [the problem above]? In particular, what role does the != sign play in your mathematical formula? Charlotte and Diana’s response to this prompt suggests they understood how the conditional statement of their code related to their formula.
Charlotte: Right, I think it definitely comes across like, as a part of the factorial it’s, I wanna say, 5 times 4 times 3 times 2 times 1, the why it’s decreasing is because of that not equal to sign. So, you like can’t have the same letter or number multiple times.
Int. 1: Okay, great, is that what you’re thinking too Diana?
Diana: Yeah, and like, specifically like in the n formula […] Like, you’re subtracting like you’re subtracting a greater number each time by one because it’s going down to like the next lowest number or the next highest number. And that just shows that it’s not equal to itself like no object can be equal to itself in the string of whatever you’re building.
Particularly in Diana’s response, we see that the not equals to constraint in the code was related not just to the general formula she had found, but also to the outcomes that were being created. She included the != command because “no object can be equal to itself in the string of whatever you’re building.” This comment suggests to us that she understood how including the != condition in the code affected outcomes, and that it would only include outcomes with no repeated elements within them. Similarly, CJ and Corey made sense of the != condition in their formula for n!. They related it to a problem in which they were asked to arrange the letters in the word ROCKET.
CJ: So, it doesn’t account for all n of them all over again.
Corey: Because the way the code’s working is it’s just matching each one of the letters with another letter. So, if you didn’t have that not equals sign ROCKET, for example, would just print out R, R, R, R, R.
In subsequent work, both sets of students also found the formula for arranging r objects from n objects, and they similarly argued about the != not allowing for elements to be repeated.
In this section, we have demonstrated that both pairs of students made sense of the role of the! = conditional statement, and they contrasted code that included the != condition with the nested for loops that did not include !=. They seemed to understand the != condition in terms of outcomes and realized that including that condition in their code would not allow outcomes with repeated elements to be printed. They were able to do this both when arranging all n elements of a set or arranging r of n elements in a set.
Selection without Repetition Problems
Selection without Repetition – Mathematical Discussion
For selection without repetition problems, repetition is not allowed and order does not matter. Combinations count unordered selections (as opposed to arrangements) of r objects from n distinct objects. Said another way, combinations count sets rather than sequences. There are a couple of different ways to solve these problems. We briefly mention the most common solution method, and then we elaborate another approach that aligns nicely with a solution that involves coding.
The most common way to solve these problems is to focus on a relationship between combinations and permutations. We note that for any set of r distinct objects, there are r! ways to arrange the objects. Thus, we know there are r! times as many arrangements of r objects chosen from n objects as there are selections of r objects. Because we know (from above) that there are n!/(n- r)! arrangements of r objects from n objects, we can divide this value by r! to find the total number of combinations. Therefore, there are n!/((n – r)!r!) total selections (or combinations) of r objects from a set of n distinct objects. For example, when counting permutations of 3 numbers from the numbers 1–6, we could count 123, 132, 213, 231, 312, and 321 all as 6 distinct outcomes. For combinations, though, these each represent a single subset {1, 2, 3}, and we don’t want to distinguish between arrangements of those three numbers. Thus, a way to think about this is that for any subset of 3 numbers from 6 numbers, there are 3! = 6 arrangements of those numbers. Since we know there are 6!/3! total arrangements of 3 from 6 numbers, then to find the combinations in which order doesn’t matter we can divide that total by 3!. Hence, there are 6!/(3!3!) total subsets of 3 elements from the numbers 1 through 6. This highlights the notion of equivalence and emphasizes the fact that in a list of permutations there are r! equivalent arrangements of each set of r elements.
There is another way to think about generating and listing combinations. We could generate the following list of 3-element subsets from the numbers 1 to 6 by holding a first number constant, and then cycling through additional options where subsequent numbers must be strictly greater than previous numbers (Fig. 11). By writing the numbers in ascending order, we avoid repeating numbers and duplicating orderings.
Fig. 11
A list of 3-element subsets from the set of numbers 1 through 6
Notice that if we list in this way we can see a sum of sums: (4 + 3 + 2 + 1) + (3 + 2 + 1) + (2 + 1) + 1, or 10 + 6 + 3 + 1, for a total of 20. In terms of understanding the nature of what is being counted and comparing outcomes to other problem types, this is a useful way of thinking about combinations.
We note that if we tried to code the typical closed-form formula, it is inefficient for a computer to list all of the arrangements and then “divide out” (or not print) those elements that are equivalent. In coding this, then, we focus on the notion of listing sums of sums, which is the latter approach described above. Here we use the greater than sign (>) to help us list these sums of sums (note, we could equivalently use the < sign). We include a condition that specifies that the outcomes get printed only if the number in each successive position is greater than the number in the previous position. This prevents reordering elements and excludes duplicates of 123 (specifically, 132, 213, 231, 312, and 321) from being printed. As seen in Fig. 12, we incorporate this by using the if j > i condition, where the symbol > literally means that j must be numerically greater than i.Footnote 9 Thus, this code in Fig. 12 generates all of the outcomes as described above. Again, the print statement within the nested loops prints the outcomes, and the Counter keeps track of the total number and is printed at the end. The conditional if statements with > symbols make it so duplicate outcomes with re-ordered elements are not printed and do not contribute to the total.
Fig. 12
Python code that prints (unordered) selections of 3 numbers from the numbers 1–6
We note that we only employ this > technique if we are actually comparing numerical values, and so we intentionally encode our set of elements as numbers. Note, Python does allow for string comparisons, but it compares strings lexicographically according to ASCII characters, which is not something we would expect students to know or predict. Thus, in coding combinations using the > technique, we restrict to encoding strings as numbers and comparing numbers. We acknowledge that requiring encoding strings as numbers is a potential additional complication of a computational setting, which could be viewed as a limitation of this computational approach. The students in this study did not show difficulty in making connections between isomorphic problems, but we grant that this could be a difficulty for some students. However, we also point out that encoding outcomes is actually a very desirable and important combinatorial practice that we want to develop in students (e.g., Lockwood et al. 2015), as the combinatorial properties and relationships of sets of distinct objects are the same whether those objects are people, letters, numbers or something else. So, creating an isomorphism between a set of distinct objects and a set of numbers does not change the number of arrangements, and it is instructive for students to know this. We address this issue further in the "Conclusion, Discussion, and Avenues for Future Research" section.
Selection without Repetition – Student Work
The two pairs of students engaged in slightly different work on these problem types, but they made similar kinds of connections with the Python code. In this section, we describe both pairs’ approaches to combination problems and highlight connections they made between such problems and conditional statements in Python.
In solving problems involving combinations, Charlotte and Diana engaged in quite a bit of initial by-hand work before they coded, and they solved the problem by reasoning about equivalence. Charlotte and Diana seemed sure that they did not want to count outcomes in which the same elements were ordered as distinct, and they articulated the idea of “duplicates” to talk about such outcomes. In particular, they solved the 2-Book problem, which states Suppose you have 8 books and you want to take a pair of them with you on vacation. How many ways are there to do this? After reasoning about the problem and how they might code it for quite some time without being sure of how to proceed, the interviewer prompted them to try to consider the problem by hand. They then solved it by hand, arguing that they could have 8·7 total pairs of books and realizing that they could divide by 2 to account for duplicates (see the exchange below). Thus, they arrived at an answer of (8·7)/2 (Fig. 13), which is correct.
Charlotte: I would just say eight times seven.
Diana: Yes, but probably divided by two because there will be duplicates like with the marble scenario. With that you can take two books with eight options, then seven, then that goes to six if you divide that by two you get twenty-eight?
Charlotte: Yes.
Diana: I think there are twenty-eight ways to do it because it eliminates you taking Book A, and Book B; or Book B, and then A because it’s the same thing.
Fig. 13
Charlotte and Diana’s initial expression for the 2-Book problem
To connect this idea to the code, we introduced the idea of using “if j > i” by asking them to think about the code in Fig. 14 and to decide whether it would solve the problem (notably, we provided this code for them to evaluate).
The following exchange shows Charlotte and Diana interpreting this task. Notice that they made sense of the role of the j > i condition both in the code and in the printed outcomes. They returned to this idea of not wanting to count duplicates, and they made sense of the code in terms of that perspective.
Int. 1: Okay. Cool. Great. Now let’s try. What do you think that’s doing?
Diana: Yeah, it gets rid of the duplicates because it prevents it – j has to be bigger than i, if i is 1, then j can be anything above it, but then you can’t have it be flip-flopped.
Int. 1: Good. What do you mean flip-flopped?
Charlotte: You can’t have 2, 1; then j being 1 isn’t bigger than 2.
Int. 1: Mm-hmm. Okay. Great. So how do you think, what do you think the total will be, and how do you think the outcomes would be structured?
Charlotte: I feel it might be the 28 that we calculated. How it’s structured, it’ll do one paired with two through eight. Then two paired with three through eight. Then keep going three through, four through eight.
Int. 1: Great. What’s sort of expression would give you that total? Can you write it down, based on the code?
Diana: It seems it would be 7 plus 6 plus 5 plus 4 plus 3 plus 2 plus 1.
In this excerpt we see that both students were attuned to not wanting duplicates – outcomes of both 1,2 and 2,1. When asked how the outcomes were structured, they connected the 28 they had gotten to the ways in which 1 was paired with 2–8, 2 with 3–8, etc. In this way, they seemed able to relate the code to a sum of sums solution to this problem, in particular 7 + 6 + 5 + 4 + 3 + 2 + 1. This was tied closely to the set of outcomes they had found.
After they had solved the 2-Book problem, Charlotte and Diana solved the 3-Book problem (Suppose you have 8 books and you want to take three of them with you on vacation. Can you write code to list all of the ways you can choose your three books? What do you expect the structure of the list of outcomes to look like?). They extended their reasoning on the previous 2-book case to the 3 books, as seen in their correct code below (Fig. 15).
To summarize Diana and Charlotte’s work on these combination problems, they did not come up with the use of the conditional > statement on their own, but they were able to make sense of it when it was presented and were able to understand what it was doing in terms of the printed outcomes. They focused especially on “duplicates” and realized that using the > symbol would prevent duplicates they didn’t want from getting printed. Then, they demonstrated that they could extend this kind of reasoning as they coded additional problems.
Corey and CJ also worked on combination problems, and they began with the 2-Marbles problem (Suppose you have six different marbles in a bag. Write out all of the possible ways you could pick two marbles out of the bag, without replacement?). We initially encouraged them to do some by-hand listing on this problem, and in particular CJ came up with the list in Fig. 16. As he made his list, he said, “These are all the different ways you can pull marbles out. This is just 5 plus 4 plus 3 plus 2 plus 1,” and this sum is represented in the structure of his list. We note that it was particularly fortuitous for CJ to encode the marbles as the numbers 1 through 6, because it seemed to help attune him to the idea that having the second number greater than the first number eliminates duplicates.
The students then set out to try to code the outcomes of the problem. They came up with the code in Fig. 17, and we had the following exchange. In particular, we note that they were attuned to what the > conditional statement accomplished in their code. We conjecture that CJ was able to reason about this conditional statement in part because he had written the outcomes as strictly increasing pairs of numbers.
Corey: If i is not equal to j - This would be with replacement. If we can’t have 1, 2; and 2 1. I’m just writing it to help me think about how I could go about actually writing this out.
[…]
Int. 1: CJ, you observed something in there about the second column.
CJ: If it just goes through systematically the way a computer thinks, looking at the next one and then using it; then our second column always has to be bigger than our first column. If j is bigger than i then it won’t ever print 2 and then 1.
[…]
CJ: The i not equal to j that just makes it so it can’t be 1, 1; or 2, 2. If j was bigger than i, then print it. These are all the orders, it won’t ever do the same combination twice because it won’t choose 1 and 2; then 2 and 1.
In this excerpt CJ and Corey indicated that they were including the > condition because they wanted to produce a set of outcomes in which only one of 1,2 and 2,1 would be included. Also, they could think critically about the difference between the != and the > conditional statements and what each was doing in terms of their outcomes. We emphasize that the point of this example is that as they engaged in the activity of coding (and coming up with a way to have the computer generate strictly increasing pairs of numbers), CJ and Corey were very aware of the nature of the outcomes they were trying to count. That is, they were reasoning about the set of outcomes in order to inform their counting process. In contrast to Charlotte and Diana’s work, where their initial solution of (8·7)/2 reflected the more traditional approach to combinations (and the equivalence in the typical formula for combinations), we point out that listing combinations lexicographically was a natural thing for CJ to do. This suggests that the nested sum structure that our code reflects is not a contrived property that we imposed on students, but, at least in this case with CJ and Corey, it arose naturally.
CJ and Corey extended to the 3-Marbles problem (Suppose you have six different marbles in a bag. Write out all of the possible ways you could pick three marbles out of the bag, without replacement). They discussed adjusting their code from the 2-Marbles problem by adding another for loop and again focusing on using the > symbol. They had some discussion of whether or not they needed to include != as well, deciding that having “if j > i” also prevents j from equaling i, and they generated the following by-hand list (Fig. 18a) and code (Fig. 18b).
Fig. 18
a, b: CJ and Corey’s list and code for the 3-Marbles problem.
They then ran the code, and it produced 20 outcomes that aligned with their list. This episode highlights their continued use of the > sign to code these problems.
As an additional illustrative example of students’ work on these combination problems, Charlotte and Diana were working on the Lollipop problem (How many ways are there to give 3 identical lollipops to 8 different kids (if no kid can have more than 1 lollipop)?). The following exchange shows Charlotte and Diana reasoning about how to code the Lollipop problem. They had some basic loop structure written, but they were considering what conditional statements to include. This was important as they thought about whether they wanted to use a conditional statement involving != or >, and this indicates their understanding of what each symbol was doing.
Diana: Or, well – I think we need to fix our for loop – like edit it a little bit more, but it is numbers in the set, so it should arrange it correctly because we’re using that syntax that needs numbers. But you’re right. We do need like a – i is not equal to i, or whatever.
Charlotte: Yeah, but I don’t think we need the ‘greater than’ sign.
Diana: I think it could be useful, though. Because otherwise we’re gonna have to do ‘not equal to this, not equal to this, not equal to this.’ But if we use the ‘greater than’ sign, we just need to say, yeah, ‘k is greater than j,’ so, it doesn’t repeat itself.
Charlotte: But then the problem with that – because each slot is something different, so you could have 1, 2, 3, and 3, 2, 1. Because they’re completely different things. So –.
Diana: Could it though? Because if k needs to be greater than j, you couldn’t have 3, 2, 1. Because that would mean that k would be 1 and that’s less than 3.
Charlotte: Oh, right.
They then wanted some clarification about what it meant for the lollipops to be identical, and we clarified that there is no difference between, say, lollipop A and lollipop B. This led them to the conclusion that they did indeed want to use the greater than sign. As we see again, they realize what each condition is doing in terms of the outcomes they were trying to count.
Charlotte: Just like this part works [referring to the conditional statement].
Int. 1: Okay. Yeah.
Charlotte: Because, yeah, then it eliminates the factor of duplicates.
Int. 1: Okay. And can you say again, how that ‘greater than’ sign eliminates the duplicates like you said?
Diana: So, like it says that k is not able to be less than j, it always has to be greater than. So, and in the example of the 1, 2, 3, it’ll print 1, 2, 3, but then when it comes to printing 2, 3, 1, it won’t be able to do it because k can’t be 1 when these two are 2 and 3.
This example demonstrates that the students were wrestling with how to solve the Lollipop problem, and they were able to figure it out by attuning to the particular outcomes they were trying to count. This suggests that being able to distinguish between outcomes using! = and outcomes using < offered a useful perspective through which the students could reason about the nature of the outcomes. CJ and Corey also worked on the Lollipop problem, and they similarly reasoned about outcomes and the > symbol as they coded this problem.
Students’ Reasoning about both != and > Conditionals
We conclude the “Results” section with data in which the students solved a problem that involved coordinating two different types of problems. In particular, the Lollipop & Balloon problem states, How many ways are there to distribute 3 unique lollipops and 3 identical red balloons to 8 different kids (if no kid can have more than 1 object)? In this problem, students must code so they can account for unique lollipops (which involves permutations) and identical balloons (which involves combinations). The students had previously correctly coded a problem involving 3 identical lollipops and 3 identical balloons, and so they adjusted their code based on that problem. In the following exchange they discuss their approach to the problem, and they first came up with a mathematical solution (Fig. 19). We acknowledge that the fact that they solved the problem mathematically first limits suggests that the computation setting was not necessary for them to reason about the problem. However, as we demonstrate in this episode, the computational setting offered an additional perspective that enriched their understanding of outcomes and what they were counting.Footnote 10
Charlotte: Do you think that it’s going to be the exact same thing [referring to the question of 3 identical lollipops and 3 identical red balloons]?
Diana: I think it’s going to be a little bit different because I think that the three unique lollipops means that we’re getting rid of – or we’re accounting for the duplicates now. Like, we don’t have to get rid of them, or divide them out.
Charlotte: Okay. So, we can say 1, 2, 3 – Okay. So, we can still do – So, we’ll do these three because positions for the lollipops, and then we have the three different positions for the balloons. So, starting with the lollipops. Yes, you have the 8 times 7 times 6, and then you don’t divide it by anything.
Diana: Yeah. Because they’re unique. So, in an order like, 3, 2, 1, and you wanna count this different than like 1, 3, 2. Right?
Charlotte: Okay. But then for the balloons – So, you would do the 5 times 4 times 3, but then divide out the 6?
Diana: Yeah.
Charlotte: And then these are multiplied together?
Diana: That makes sense to me.
Fig. 19
Charlotte and Diana’s expression for the solution to the Lollipops Balloons problem
To solve the problem, they reasoned about a counting process by differentiating between the nature of the outcomes in permutations and combinations. They coded the answer to the problem (Fig. 20), and, as they describe in the following exchange, they thought about the difference between the > symbol and the != symbol. The underlined portion below demonstrates their reasoning about each symbol in terms of the kinds of outcomes they wanted to count – the greater than accounts for duplicates, and the not equal to makes sure elements do not repeat.
Diana: Well, we would have like j is not equal to i, right?
Charlotte: Yes.
Diana: Okay. If j is not equal to i – And then k is not equal to j, k is not equal to i?
Charlotte: Mm-hmm. All right.
Diana: Seems good.
Charlotte: Yeah. I think so. Yeah. I think that looks good.
Interviewer 1: Okay. So, yeah. Tell me what you did and why you think that will work out.
Charlotte: So, you kinda just changed – Instead of j happening to be greater than i, we just changed it to j not equal to i. Because the j being greater than i was accounting for duplicates, and so since we’re allowed to have duplicates this time, then we’ll just wanna make sure that you don’t get 1, 1, 1. That’s what the j not equal to i stands for.
Interviewer 1: And I know you said this before, but by duplicates, what do you mean?
Charlotte: So, with duplicates it will be like, 1, 2, 3 and 3, 2, 1.
Interviewer 1: Okay. Cool.
Diana: Yeah. And in this case, like they are counted as separate outcomes, so I guess, they’re no longer duplicates, but yeah, we keep calling them that because that’s what they were in the last problem.
Fig. 20
Charlotte and Diana’s code for the Lollipops Balloons problem
The students’ work on this problem that coordinates both != and > suggests that they understood how to coordinate those conditional statements and what each meant in terms of their outcomes. CJ and Corey solved the same problem by developing similar code, and they also articulated similar distinctions between the two conditionals.
Conclusion, Discussion, and Avenues for Future Research
In this section we briefly highlight a couple of key points of discussion. First, we discuss the importance of outcomes and summarize our results in terms of outcomes. In doing so, we discuss formulas and what we are learning about students’ formulas. Second, we provide additional mathematical discussion of a fourth problem type as it relates to code and the two-by-two table. This discussion will relate to avenues for future research, which we present in the “Avenues for Future Research” section.
Outcomes as a Bridge between Code and Traditional Formulas
In this paper, we have shown that students were able to reason about, understand, and use nested for loops and particular conditional statements within those for loops to computationally generate lists of outcomes for three main types of problems. In doing so, the students demonstrated that they could draw upon their experience with coding to make connections with what they were trying to count. Ultimately, we contend that the value in reasoning about the code, and the specific conditional statements, was in drawing attention to the outcomes being generated (in the sense of Lockwood 2013). That is, the symbols in the Python code seemed to enrich the students’ combinatorial reasoning by affording opportunities for the students to strengthen connections to the kinds of outcomes they were counting. Further, it seemed to facilitate productive discussions about the outcomes, especially whether repeats or duplicates counted as distinct. We argue that these kinds of discussions contributed to a more well-rounded understanding of these combinatorial problem types. Because of the demonstrated difficulty that students face in deciding what counting situation they are in (e.g., Annin and Lai 2010; Batanero et al. 1997; Lockwood 2013), we argue that the use of coding in this context offers an alternative and effective way in which to think about distinctions between these main problem types.
One point of discussion is that sometimes a common closed-form mathematical solution to a counting problem does not naturally translate to a listing procedure using programming commands. The clearest example of this is in coding solutions to combination problems. In our study, the students solved combination problems computationally by leveraging the “if j > i” constraint to ensure that no elements in an outcome were repeated. This naturally translated to coding sums of sums (sometimes of sums), which is a valid solution to combination problems. However, it does not represent the more commonly known formula for combinations, n!/((n - r)!r!) which involves the idea of equivalence and dividing out by duplicate outcomes. From a computational perspective, it would be very inefficient to code a solution that would reflect that particularly formula. That is, it is inefficient for a computer to list all of the arrangements and then “divide out,” or get rid of, those elements that are equivalent. By generating all permutations and then only printing or counting non-duplicated elements, the programmer (and the computer) would have to do considerable extra work.
In this study, the students managed to reason about both kinds of mathematical expressions for combinations. For example, Charlotte and Diana were able to make meaningful connections between the closed form of n!/((n - r)!r!) and their code. They understood the idea of “duplicates,” and they essentially thought about (and handled) duplicates in two different ways. In the code, they eliminated duplicates by coding constraints that did not allow the computer to print duplicates, and in the closed-form expression they divided out outcomes from permutations based on equivalence. An implication of this phenomenon is that this example of combinations might offer a useful opportunity to talk with students about efficiency and coding, particularly by demonstrating that some mathematical expressions do not correspond to efficient code. It also highlights why mathematical expressions and formulas might be valuable and demonstrates some limitations of a purely computational perspective.
More broadly, this suggests that there are some ideas that are fundamental to counting (such as notions of equivalence) that result in inefficient ways to program counting processes. A critic might say that there is then little value in examining computational approaches, but we maintain that computation has valuable perspectives to offer. In particular, the computational approach involving the “if j > i” condition focuses students on what they are trying to count, and they must clearly articulate the nature of the outcomes. It is important to identify ideas that are particularly valuable mathematically (such as equivalence) and highlight them in non-computational ways, just as it is important to emphasize ideas that are particularly valuable computationally (such as certain commands that distinguish between types of outcomes). For example, Diana’s quote below highlights the value of the coding process in helping to deepen her reason about what constitutes an outcome in a given situation.
Diana: I feel like it was also helpful to learn how to do them because then that helps me figure out how to translate a math problem on paper into code. But then also, it helps me see the structure of what it’s actually printing and if it’s gonna do 123, 124, it’s not gonna do 132. So, you know that that is not going to be an outcome.
Additional Mathematical Discussion – Selection with Repetition and Completing the Two-by-Two Table
We have already discussed the 2-by-2 Table shown in Table 1 (we display it again in Fig. 23), and we have described students’ work on three of those types of problems (arrangement with repetition, arrangement without repetition, and selection without repetition). In our study, we only had students look at these three problem types,Footnote 11 but we now briefly make an additional mathematical observation about selection with repetition problems. We save details of the mathematics for Appendix 1, but the point here is to highlight this fourth problem type for the sake of completion and to make useful mathematical connections. In these selection with repetition problems, we are selecting objects (so order does not matter), but we can repeat objects. An example of this type of problem is (adapted from Tucker 2002, p. 195): “Suppose I have 6 types of hot dogs, and I want to buy three hot dogs for lunch. In how many ways could I do this?” An equivalent way of framing this problem is, “How many strictly non-decreasing sequences of length three are there from a set of 6 distinct elements?” If we think about code like that in Fig. 22, then, we can see how the greater than or equal to symbols in the conditional if statements exactly correspond to this question of counting strictly non-decreasing sequences. Code that lists such sequences is in Fig. 21. The general formula (discussed in Appendix 1) to solve this kind of problem is C(n + r - 1,r).
With this fourth problem type in mind, we now summarize an important relationship between three natural conditional statements within nested for loops and the two-by-two table (Table 1 and Fig 23) we have discussed previously. For simplicity, we have presented examples of code involving two nested loops that print pairs of elements from a set of the numbers 1 through 5. Notice that it is natural to consider four cases that constrain relationships between elements in the set: a) those elements can be equal (with no additional restriction), b) the elements cannot be equal (!=), c) the elements can be related by strict inequality (>, with the second elements being strictly greater than the first), or d) the elements can be related by non-strict inequality (>=, with the second elements being greater than or equal to the first). These are four natural ways to relate elements in a set, and they are reflected in Fig. 22 below. We organize them so they correspond to the two-by-two table in Fig. 23.
Fig. 22
Code that yields appropriate outputs for the four respective problem types
In summary, these four ways of relating elements correspond nicely to the four common types of counting problems reflected in the two-by-two table (Tucker 2002). We contend that this is a potentially useful insight for researchers, teachers, and students who may be reasoning about and solving counting problems.
We acknowledge that these particular structures (nested for loops and conditional statements) are not the only or the best ways to program solutions to such problems. These problems may be more efficiently coded in other ways, such as recursion, and as n and r increase in size it is clear that needing to use r nested for loops becomes tedious and inefficient. However, the point here is that this code structure (nested for loops with four basic conditional if statements) involve very basic code with which students can interact, and they provide a clear point of contrast that emphasizes important differences in how they relate to four basic problem types. These relationships may allow for important connections to be made between counting processes (as represented by the code) and sets of outcomes (as represented by the output of the code), which Lockwood (2013) has posited is important in her model. We are not arguing that computing is the only kind of activity students should use to understand these ideas, nor are we proposing that this is necessarily better than other methods that have been suggested for deepening students’ understandings of counting problems. We do, however, hope we have made the case that there were some compelling and productive ways of thinking about these combinatorial concepts that seemed to emerge for the students within a computational setting.
Avenues for Future Research
In terms of future research, broadly these findings provide an existence proof that meaningful mathematical ideas can be introduced and reinforced in computational settings. Our case of combinatorics offers but one example of ways in which computational structures and representations connected synergistically with mathematical concepts. This suggests that there is more to study and learn related to the relationship between computational activity like programming and students’ mathematical reasoning and activity. There are opportunities in future studies to examine other ways in which computing might facilitate students’ mathematical reasoning, both within other combinatorial concepts, and in other mathematical domains as well. There is much more to be done to explore relationships between computational activity and mathematical thinking and learning, and the field would benefit from more exploration of ways in which computing and mathematics may complement each other. The students we worked with engaged in several computational thinking practices outlined by Weintrop et al. (2016), especially what they call Computational Problem Solving Practices (specifically programming, preparing problems for computational solutions, and troubleshooting and debugging). We see potential for other studies to explore how students might engage with and use other practices within Weintrop et al.’s taxonomy in a variety of mathematical domains.
More specifically in terms of combinatorics, it would be worthwhile to explore other potential ways of coding combinations in particular, and to consider whether recursive formulas or programs elicit similar productive student reasoning. We have had a narrow focus on for loops and conditional statements, but we see potential for additional computational structures that may provide insight about combinatorial concepts. Again, this might involve exploring additional practices that Weintrop et al. (2016) elaborate within their taxonomy of computational thinking practices.
Another clear direction for future research is to study student reasoning about selection with repetition problems. As noted previously, this has been an under-researched combinatorial structure, likely because it tends to be a more advanced topic. However, given the connection we described in this paper to other conditional statements in Python, there are potential opportunities to focus on students’ reasoning about such problems.
Notes
The students categorized them according to the problem types reflected in the first three quadrants of the two-by-two table – they were not given any selection with repetition problems.
This reflects the multiplication principle, which is a guiding principle that describes when it is appropriate to multiply in counting problems. See Tucker (2002), Lockwood et al. (2017), and Lockwood and Purdy (2019) for more details about the multiplication principle.
There are connections to the students’ activity to other parts of the taxonomy, including using computational models to understand a concept and constructing computational models, but we do not have space to detail how the students’ Python programming relates to these other practices.
We make a brief note about n!. Typically students recognize n! as the product of the positive integers from 1 to n, and they are exposed to this in calculus (especially Taylor series expansions). However, such exposure typically does not imply that they have a combinatorial interpretation of n factorial as the number of arrangements of n distinct elements (further insight about students’ reasoning about factorials can be found in Lockwood and Erickson 2017).
Specifically, Pair 1 met over 11 sessions that were each 60–90 min long over the course of 7 weeks. They met on TR of Weeks 1, 2, and 3, T of Week 4, TR of Week 5, and T of Weeks 6 and 7. Pair 2 meet over 9 sessions that were each 60–90 min long over the course of 4 weeks. They met MWF of Week 1, M of Week 2, MWF of Week 3, and WF of Week 4.
This change was made to reduce the number of outcomes, as PyCharm did not easily display all the outcomes in the original problem.
There is another useful interpretation of the quotient n!/(n-r)!, in which we consider arranging all n objects of the set. But, since we only care about the first r positions, for each arrangement of the first r positions, the arrangements of the remaining n-r positions all actually constitute equivalent outcomes (hence the division by (n-r)!). However, this interpretation is not relevant to this paper and we do not elaborate on it further.
Observe that another common counting formula, n!, is a special case of these r-permutations. P(n,n) = n! which is the number of arrangements of an entire set of n distinct objects.
Including j > i also subsumes the case in which j might be equal to i. Thus, we do not need to include both j != i and j > i, as the j > i includes these cases. Further including k > j this also accounts for k being greater than i, so it is not necessary to also include a command in which k > i as well. Including additional constraints like k > i or j != i would not be incorrect, but they are not necessary.
In addition, the mathematical solution they developed was not generated completely independently of any computational work. It emerged in a setting in which they had been working with the computer for multiple hours, and even if they did not directly draw on the computer in deriving this solution, we contend that both computational and noncomputational ideas and representations all contributed to a particular milieu in which the students were working.
As we have noted, there have been no studies that examine students’ reasoning about selection with repetition problems. We did not include such problems in our study because we were limited in scope of topics we could cover, and we made this mathematical connection to code after we had gathered our data.
In Python, the = sign is used to define a value rather than the familiar usage in mathematics, so Counter = Counter +1 is defining the new value of counter as one greater than the previous value of Counter.
References
Annin, S. A., & Lai, K. S. (2010). Common errors in counting problems. Mathematics Teacher, 103(6), 402–409.
Batanero, C., Navarro-Pelayo, V., & Godino, J. (1997). Effect of the implicit combinatorial model on combinatorial reasoning in secondary school pupils. Educational Studies in Mathematics, 32(2), 181–199.
Buteau, C., & Muller, E. (2017). Assessment in undergraduate programming-based mathematics courses. Digital Experiences in Mathematics Education, 3, 97–114. https://doi.org/10.1007/s40751-016-0026-4.
CadwalladerOlsker, T., Engelke, N., Annin, S., & Henning, A. (2012). Does a statement of whether order matters in counting problems affect students’ strategies? In the Electronic Proceedings of the 15thAnnual Meeting of the Research on Undergraduate Mathematics Education. Portland, OR: Portland State University.
DeJarnette, A. F. (2019). Students’ challenges with symbols and diagrams when using a programming environment in mathematics. Digital Experiences in Mathematics Education, 5, 36–58. https://doi.org/10.1007/s40751-018-0044-5.
DiSessa, A. A. (2018). Computational literacy and “the big picture” concerning computers in mathematics education. Mathematical Thinking and Learning, 20(1), 3–31. https://doi.org/10.1080/10986065.2018.1403544.
Fischbein, E., Pampu, I., & Manzat, I. (1970). Effects of age and instruction on combinatory ability in children. British Journal of Educational Psychology, 40, 261–270.
Gadanidis, G., Clements, E., & Yiu, C. (2018). Group theory, computational thinking, and young mathematicians. Mathematical Thinking and Learning, 20(1), 32–53. https://doi.org/10.1080/10986065.2018.1403542.
Hickmott, D., Prieto-Rodriguez, E., & Holmes, K. (2018). A scoping review of studies on computational thinking in K-12 mathematics classrooms. Digital Experiences in Mathematics Education, 4(1), 48–69. https://doi.org/10.1007/s4075-017-0038-8.
Kotsopoulos, D., Floyd, L., Khan, S., Kizito Namukasa, I., Somanath, S., Weber, J., & Yiu, C. (2017). A pedagogical framework for computational thinking. Digital Experiences in Mathematics Education, 3(2), 154–171. https://doi.org/10.1007/s40751-017-0031-2.
Lockwood, E. (2014b). Both answers make sense! Using the set of outcomes to reconcile differing answers in counting problems. Mathematics Teacher, 108(4), 296–301.
Lockwood, E., & Erickson, S. (2017). Undergraduate students’ initial conceptions of factorials. International Journal of Mathematical Education in Science and Technology, 48(4), 499–519. https://doi.org/10.1080/0020739X.2016.1259517.
Lockwood, E., & Purdy, B. (2019). Two undergraduate students’ reinvention of the multiplication principle. Journal for Research in Mathematics Education, 50(3), 225–267.
Lockwood, E., Swinyard, C. A., & Caughman, J. S. (2015). Patterns, sets of outcomes, and combinatorial justification: Two students’ reinvention of counting formulas. International Journal of Research in Undergraduate Mathematics Education, 1(1), 27–62. https://doi.org/10.1007/s40753-015-0001-2.
Lockwood, E., Reed, Z., & Caughman, J. S. (2017). An analysis of statements of the multiplication principle in combinatorics, discrete, and finite mathematics textbooks. International Journal of Research in Undergraduate Mathematics Education, 3(3), 381–416. https://doi.org/10.1007/s40753-016-0045-y.
Lockwood, E., Wasserman, N. H., & McGuffey, W. (2018). Classifying combinations: Do students distinguish between different categories of combination problems? International Journal of Research in Undergraduate Mathematics Education, 4(2), 305-322. https://doi.org/10.1007/s40753-018-0073-x.
Lockwood, E., DeJarnette, A. F., & Thomas, M. (2019). Computing as a mathematical disciplinary practice. Online first in Journal of Mathematical Behavior, 54.https://doi.org/10.1016/j.jmathb.2019.01.004.
Martin, G. E. (2001). The art of enumerative Combinatorics. New York: Springer.
Reed, Z., & Lockwood, E. (2018). Generalizing in combinatorics through categorization. In A. Weinberg, C. Rasmussen, J. Rabin, M. Wawro, & S. Brown (Eds.), Proceedings of the 21stannual conference on research in undergraduate mathematics education (pp. 311–325). San Diego: San Diego State University.
Sinclair, N., & Patterson, M. (2018). The dynamic geometrisation of computer programming. Mathematical Thinking and Learning, 20(1), 54–74. https://doi.org/10.1080/10986065.2018.1403541.
Steffe, L. P., & Thompson, P. W. (2000). Teaching experiment methodology: Underlying principles and essential elements. In R. Lesh & A. E. Kelly (Eds.), Research design in mathematics and science education (pp. 267–307). Mahwah: Lawrence Erlbaum Associates.
VERBI Software. (2017). MAXQDA 2018 [computer software]. Berlin: VERBI Software Available from https://www.maxqda.com. Accessed 24 Sept 2019
Weintrop, D., Beheshti, E., Horn, M., Orton, K., Jona, K., Trouille, L., & Wilensky, U. (2016). Defining computational thinking for mathematics and science classrooms. Journal of Science and Education Technology, 25, 127–147. https://doi.org/10.1007/s10956-015-0581-5.
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1
Here we provide a more detailed discussion of selection with repetition problems, which is a standard approach (e.g., Mazur 2010; Tucker 2002). The following question is an example of this type of problem (adapted from Tucker 2002, p. 195): “Suppose I have 6 types of hot dogs, and I want to buy three hot dogs for lunch. In how many ways could I do this?” One way to solve such a problem highlights a clever way to encode outcomes and make sense of the more general formula. If we consider an actual menu with 6 types of hot dogs and then consider placing xs on the menu to indicate which hot dogs we want to buy, we can end up with a menu like the one in Table 6. We listed out a few different possibilities in the first 6 rows of the menu.
Table 6 Representation of several outcomes of the Hot Dog problem
Notice that for each of the six rows in the menu, we could encode the outcomes as strings of three xs and five |s. For example, the entry in the first row, which represents three regular dogs, could be encoded as the string xxx | | | | |. The entry in the second row, which represents two regular dogs and a super dog, could be encoded as xx | x | | | |. The entry in the fifth row, which represents one super, one footlong, and one Dodger dog, is encoded as | x | x | | x |. In this way, counting the total number of outcomes is a matter of counting strings of length 8 that contain 3 xs and 5 bars. To count this, we can simply choose 3 of the 8 positions in which to place xs, and then the remaining positions must be bars (see Lockwood et al. 2018 for an extended discussion of interpreting such a situation as a combination problem). Thus, there are C(8,3) ways to buy 3 hot dogs from 6 types of hot dogs, where repetition is allowed. Note that more generally, if there are n types of objects, and we want to select r with repetition, there will be r xs and n – 1 bars (one fewer than the number of types). Thus the general formula to solve this kind of problem is C(n + r – 1,r).
An equivalent way to frame this question is to ask, “How many strictly non-decreasing sequences of length three are there from a set of 6 distinct elements?” Notice that these outcomes would be 111, 112, 113, 114, 115, 116, 122, 123, 124, 125, 126, 133, 134, 135, 136, 144, 145, 146, 155, 156, 166, 222, 223, 224, 225, 226, 233, 234, 235, 236, 244, 245, 246, 255, 256, 266, 333, 334, 335, 336, 344, 345, 346, 355, 356, 366, 444, 445, 446, 455, 456, 466, 555, 556, 566, 666. For any of these outcomes, though, they correspond to an arrangement of three xs and five bars, where the numbers in the 3-element sets represent in which categories the xs go. For example, 111 corresponds to xxx | | | | |, 223 corresponds to | x x | x | | |, and 366 corresponds to | | x | | | x x. This perspective of encoding outcomes offers another way to count these problems. If we think about code like that in Table 2, then, we can see how the greater than or equal to symbols in the conditional if statements exactly correspond to this question of counting strictly non-decreasing sequences. This code generates exactly the set of outcomes we listed above (in the same order).
Fig. 24
Code that counts selection with repetition problems
Here, we provide a more thorough discussion of the code presented in the lower left corner of the two-by-two table (Tucker 2002), and in particular in Table 2 of the body of the paper. That is, we will explain why the code in Fig. 25 counts arrangements with no repetition. This is intended to provide clarity for readers who are unfamiliar with programming or who are unfamiliar with Python syntax. The other programs used in this paper rely on the same concepts, although there may be more for loops and different additional conditional statements. In explaining the code, we will introduce for loops and conditional statements, which are important in framing the students’ work. For clarity, we have labeled the line numbers in the code.
Fig. 25
Code that counts arrangements with unrestricted repetition
The code begins by defining an ordered list, “Numbers = [1,2,3,4,5].” The list contains the integers 1, 2, 3, 4, and 5, and is ordered as written. The command in line (2), “Counter = 0,” creates a new integer variable, called Counter, that we will use to count the number of outcomes our code produces. Each time we produce a new outcome, we will increase the value of Counter by 1 (this occurs in Line (7)). Line (3) begins a for loop. The command “for i in Numbers:” will do a series of commands for each element in the set Numbers. In Python, indentation is an important element of specifying commands, and it helps to determine whether commands are nested. The series of commands is relayed in the instructions nested within the for loop, where instructions are considered nested within a loop while they are indented further (to the right) than the loop. The nesting ends when the program reaches a line that is not indented further to the right. In this case, lines (4) through (7) are nested within the for loop, and will be carried out for each i in Numbers, whereas line (8) is not nested within the for loops. Hence, the command “for i in Numbers:” will carry out the nested commands five times, once per element in Numbers in the order in which they appear (in this case, the numerical order 1, 2, 3, 4, and 5).
For each i in Numbers, the nested instructions will be carried out with i designated as a given value. For example, the first time lines (4) through (7) are carried out will be when the value of i is 1. Similarly, the command “for j in Numbers:” will carry out the instructions nested within it (lines (5) through (7)) for each value of j in Numbers. That is, lines (5) through (7) are carried out a total of 25 times (one time for each ordered pair (i,j), where both i and j are elements of Numbers).
For each value of i in Numbers and j in Numbers, the program will follow the command “if j != i:,” which we refer to as a conditional statement. That is, as long as the condition j != i is met, the program will follow the instructions nested within the conditional statement (lines (6) and (7)). If the condition is not met, then the program will skip over these instructions (in this case, as the remaining instructions are nested inside, the program will do nothing). Lines (6) and (7) accomplish two things: first, the ordered pair (i, j) is printed; and second, the value of Counter is increased by 1.Footnote 12 Hence, the program will follow the instructions to print (i,j) and to increment the counter for only those pairs (i, j) where j is not equal to i.
In sum, for each value in Numbers, the program will iterate through every value in Numbers, printing each pair of distinct numbers as well as keeping track of the total number of pairs that has been printed. Due to the conditional statement, these pairs are precisely those without repetition, showing we are counting and listing the desired outcomes. Line (8), “print(Counter),” prints the value of Counter after all previous instructions have been followed, giving the total number of arrangements of the numbers 1 through 5, where repetition is not allowed.
Lockwood, E., De Chenne, A. Enriching Students’ Combinatorial Reasoning through the Use of Loops and Conditional Statements in Python.
Int. J. Res. Undergrad. Math. Ed.6, 303–346 (2020). https://doi.org/10.1007/s40753-019-00108-2
