The integration of mathematics and computer programming arises naturally from the combination of efforts to foster greater integration of science, technology, engineering and mathematics (STEM) at all levels of instruction (DeCoito et al. 2016; Johnson 2012; Tai 2012), as well as policy recommendations for the use of technology in mathematics (NCTM 2000; CCSSM 2010). Although combined mathematics–computer programming instruction is atypical currently in middle and secondary grades, efforts persist to incorporate computing and computer programming into mathematics learning. Evidence of these efforts can be seen through federal initiatives, such as the US National Science Foundation’s STEM+C funding program, professional workshops on the nature of computational thinking (NRC 2010) and calls from the field (Grover and Pea 2013). Efforts to integrate mathematics and computer science foreshadow innovation in how students might learn about mathematics and computer programming in increasingly integrated ways. To prepare for this, there is a present need to consider carefully how students’ participation in computer programming tasks shapes their mathematical learning and, more specifically, their mathematical discourse.

Research using functional linguistics has documented how formal mathematical language has developed to its current level of abstraction and the difficulties that this formality can present for students (Halliday 1993; O’Halloran 2015; Schleppegrell 2007). From a multimodal perspective, which assumes that meaning is simultaneously created through spoken language, symbol systems and visual representations (Lemke 1998; O’Halloran 2015), each of these modes of communication presents challenges to students who must learn to communicate through the standard discourse of mathematics. With the integration of computer programming and mathematics – and the ways in which computer programming changes the nature of students’ mathematical work (Feurzeig and Papert 1968/2011) – it is important to consider how these challenges surface and are dealt with in such contexts.

O’Halloran (2015) has argued that, although language (both spoken and written) is often prioritized in the study of how meaning is made and communicated, modes of communication such as symbolism and images are often central to creating and sharing knowledge in mathematics. I adopt this perspective to consider ways in which students communicated mathematical ideas through the use of a computer programming environment and pose the following question: What challenges of communication through symbols and diagrams surfaced in students’ use of a computer programming environment to solve a mathematically oriented task, and how did students respond to these challenges? This work supports efforts towards integrated STEM learning and, specifically, the integration of mathematics and technology. By offering insight into how students’ use of a programming environment shapes their communication, this study can help researchers and educators anticipate, and respond to, students’ mathematical discourse in such settings.

A Review of Relevant Literature

In this section, I first describe how the increasing relevance of computer science and computational thinking helps to motivate the integration of mathematics and computer programming. Then, I briefly review existing literature on the use of computer programming environments in mathematics and introduce the notion of a visual programming environment. Finally, I introduce the framework guiding the present study, which is based on the multimodal nature (i.e. through language, symbols, and images) of mathematical communication.

Computational Thinking and its Applications to Mathematics

Computational thinking – a term which emerged in the discipline of computer science – has been characterized by a variety of actions such as “thinking recursively”, “using abstraction and decomposition when attacking a large complex task or designing a large complex system”, “using heuristic reasoning to discover a solution” and “making trade-offs between time and space and between processing power and storage capacity” (Wing 2006, pp. 33–34). In recent years, computational thinking has gained momentum from encompassing valued twenty-first-century skills and dispositions that can be applied across disciplines, including mathematics. Thus, while the purpose of the present study is not to document students’ use of computational thinking, a brief overview of research in this area is useful for contextualizing the research project, through which students used a computer programming environment to complete mathematical tasks in an after-school setting.

Arguments for the importance of computational thinking in K–12 settings have emerged alongside frameworks for what this practice may look like. For instance, Barr and Stephenson (2011) described computational thinking in terms of the capabilities students would need, the dispositions they would need to maintain and the classroom culture that would support such capabilities and dispositions. For example, not only should students learn to test and debug, but they also need persistence and a classroom climate accepting of failure. Based on observations of young students using a visual authoring environment, Brennan and Resnick (2012) offered a slightly different approach, enumerating a set of concrete concepts from computer science – such as loops and conditionals – and a set of practices – such as testing, debugging, and abstracting. From these studies, it is clear that students need some particular knowledge and dispositions to engage in computational thinking.

As the effort to characterize computational thinking across grade levels has been on-going, there have also been initiatives to integrate computation and computational thinking within existing STEM coursework (Weintrop et al. 2016). This effort has been supported by three central arguments: the knowledge and skills encompassed by computational thinking are applicable across STEM content areas; such integration is the best way to reach a wide range of students; it prepares students for the ways in which STEM disciplines are evolving (Jona et al. 2014; Weintrop et al. 2016).

Grover and Pea (2013) supported this argument for the applicability of computational thinking, claiming that, “the approach to problem solving generally described as [computational thinking] is a recognizable and crucial omission from the expertise that children are expected to develop through routine K–12 Science and Math education” (p. 40). Offering a complementary perspective, Baldwin et al. (2013) argued that, not only can principles of computer science be integrated into mathematics settings, but also mathematics content and practices should be more purposefully integrated into computer science courses.

The construct of computational thinking is important for understanding the role of computer programming, and computer environments, in the teaching and learning of mathematics. Across grade levels and settings, there is a movement to integrate technical disciplines, especially with respect to leveraging the affordances of computer science to solve problems in other disciplines such as mathematics.

Computer Programming Environments in Mathematics

Computer technologies for learning mathematics differ in the ways that students interact with the objects of those environments and, thereby, with the mathematical ideas they encounter through those environments. Computer programming environments are characterized by the feature that users can control what appears on the computer screen through symbolic inputs, entered according to the syntax of the environment. The earliest of these environments were those designed with the Logo programming language. Logo was meant to provide novice computer users with a language for expressing mathematical ideas (Papert 1980). Logo programming environments allowed for abstract mathematical ideas to be represented by concrete objects, and students controlled those objects through keyboard inputs.

Users of programming environments maintain symbolic control over their work by inputting commands, rather than directly manipulating objects on the screen (Healy and Hoyles 2001). Their syntax provides students with a language – less formal than abstract mathematical language – in which to talk about mathematical ideas (diSessa 2000; Eisenberg 1995; Hoyles and Sutherland 1989). In addition, these environments can support students to make connections between symbolic and visual representations of mathematical ideas (e.g. Clements and Battista 1989, 1990; Edwards 1991, 1997; Hoyles and Healy 1997; Hoyles and Noss 1992). But computer programming is itself part of a discipline with complex concepts and procedures, and it can be difficult for teaches toc ombine the teaching of programming with the teaching of mathematics (Benton et al. 2017). Many recent instances of teaching about computer programming occur outside of typical classroom settings and do not incorporate explicit mathematics related goals (Lye and Koh 2014). Thus, there is an on-going need to explore the relationship between learning programming and learning mathematics.

Since the popularity of Logo microworlds, students’ use of programming environments in mathematics has received relatively little attention in research and teaching, as dynamic geometry software became a more ubiquitous resource in mathematics classrooms (Sinclair 2014). However, as the construct of computational thinking has grown in prominence and utility, programming environments are re-emerging as popular educational resources (e.g. Higginson 2017; Lye and Koh 2014; Repenning 2012), and dynamic geometry environments have been re-envisioned as instances of visual programming languages (Sinclair and Patterson 2018). Additionally, there is a growing body of literature addressing the use of modern programming environments to support mathematical thinking and problem solving (e.g. Calder 2010; DeJarnette 2018a, b; Korkmaz 2016; Swanier et al. 2009; Smith and Neumann 2014). Part of the current popularity of computer programming in mathematics can be attributed to the relative ease of use of modern programming environments.

Scratch (http://scratch.mit.edu) and Etoys (www.squeakland.org) are examples of a class of visual programming environments, which provide a collection of blocks – known as code blocks – that can be put together like puzzle pieces to create a line of code. The purpose of a visual programming environment such as Scratch is that it provides syntactical support (Repenning 2012) through the menu of code blocks. Instead of learning a programming language (and its associated syntax), users can ‘piece together’ computer programs in a visual way. Code blocks are often color coded, and they represent commands through language that is closely related to informal spoken language. Even so, code blocks can be considered a form of symbolic representation in as much as they provide shorthand notation in reference to more complex ideas and procedures.

In this way, such environments incorporate a set of symbolic (through the use of code) and visual (through the activity produced by the code) representations. Although these modes of communication may be more intuitive than traditional mathematics (Feurzeig and Papert 1968/2011), they still require some degree of learning to use. Thus, this study seeks to examine some of the ways in which the challenges of symbolic and visual communication that have been documented in mathematics translate to a visual programming setting.

Multimodal Communication in Mathematics

A variety of perspectives have contributed to understanding how students engage in mathematical discourse in different settings (e.g. Adler and Ronda 2015; Forman et al. 1997; Morgan 2006; Sfard 2001; Zahner 2012). Mathematics, like any subject, requires the use of discipline-specific language with a technical vocabulary and grammar (Schleppegrell 2007), which facilitate the production of logical and coherent arguments (Halliday 1993). At the same time, these features create challenges for students, who must learn to speak and write in a way that is often decontextualized and disconnected from the use of language in everyday settings.

Much of the existing work on students’ mathematical discourse places a high priority on students’ and teachers’ spoken communication. For example, researchers have documented how students’ use of spoken, technical language in mathematics classrooms may differ from the language of formal, academic mathematics (Moschkovich 2007). In technology-rich settings, Anderson-Pence (2017) described how technology tools can mediate students’ spoken interactions around mathematics tasks. Attention to language is crucial, given that spoken interactions may be the most prominent mode through which teachers and students communicate in mathematical settings (Lemke 1988). However, given that mathematics is inherently multimodal – relying upon the use of spoken and written language, in addition to symbol systems and visual representations (Lemke 1998; O’Halloran 2015)Footnote 1 – there is a need to attend to the multiple modes through which meaning is constructed.

O’Halloran (2015), in particular, has suggested that language is often secondary to the use of symbols and images for creating and communicating meaning. Recognizing the situated nature of communication, and given my interest in how students’ created representations through their use of a visual programming environment, I adopt O’Halloran’s perspective and attend to the particular challenges of symbolic and visual communication. By highlighting some of the features of students’ use of symbols and images, there is opportunity to complement existing literature on the nature of students’ spoken interactions and expand existing frameworks for what constitutes mathematical discourse in technology rich settings.

Symbolic notation can be thought of in terms of its vocabulary (i.e. the meanings of specific symbols) and its grammar (i.e. the ways symbols are connected to communicate meaning). In the context of a visual programming environment, vocabulary would refer to the collection of code blocks, while grammar would encompass knowledge of how those blocks can be fitted together in meaningful ways. Symbolic notation in mathematics is a “designed” mode of communication (Halliday and Matthiessen 2014), in that conventional forms of use have been established to serve the functions of “encoding mathematical relations and deriving results to solve problems” (O’Halloran 2015, p. 69).

Efficiency is a primary feature of symbolic notation. Each symbol has a discipline-specific meaning and conventions such as spacing and the use of brackets encode meaning differently from typical written communication. Symbolic expressions are also dense in the information they convey (O’Halloran 1999, 2000, 2005). Related to the hierarchical nature of mathematical knowledge, understanding symbolic expressions often requires prior knowledge that is not made explicit (O’Halloran 2015). All of these features serve to create a level of abstraction that provides an efficient way to encode and solve problems, while also creating a potential barrier for students whose mathematical learning depends on mastering this mode of communication.

The use of visual representations such as graphs, tables and diagrams has been emphasized in mathematics education as a way for students to build connections between concepts and procedures (e.g. NCTM 2000). From an applied linguistics perspective, visual representations serve specific functions by connecting mathematical processes to the concrete, physical world (O’Halloran 1999) and by foregrounding key information and relationships without the additional detail embedded within symbolic notation or spoken language (O’Halloran 2015). Even as visual representations strip away some of the need for technical language and symbols, they present their own set of potential challenges to learners of mathematics.

As summarized by O’Halloran (2015), and similar to the use of symbolic notation, visual representations typically follow special conventions that are singular to the discipline; they tend to be dense in the amount of information they express, thus implicitly requiring prior knowledge of how they should be interpreted. The production of graphs and diagrams, especially in media with high production value (e.g. textbooks or professional websites), can decontextualize information and overstate the truth value of the relationships or processes represented in the image. Finally, visual representations frequently embed language or symbolic communication. For example, graphs require the labeling of axes, tables are sometimes populated with symbols and diagrams often use labels or keys to highlight central features. In many cases, this integration of visual representation with language or symbols can serve a purpose of making those connections more explicit to students, but it should not be taken for granted that they will always recognize the relationships between images and symbols.

In light of current efforts to establish a synergy in students’ knowledge related to mathematics and, respectively, computer science, computer programming suggests one potential source that may eventually serve students in doing mathematics. However, a question that is underdeveloped in existing literature is how students develop skill at communicating when interacting within an environment that merges the technical language of mathematics with the technical language of computer science.

This study represents an effort to acknowledge the potential value of the movement towards computational thinking, while also uncovering challenges that students may encounter when doing mathematics through the language of computer science. Documenting the challenges of such multimodal communication is not to suggest that these challenges should be avoided, but rather to help anticipate some of the ways in which teachers may respond to the needs of students.

Methods

The data for this study come from an after-school club designed to study the intersection of mathematical problem solving and computer programming for middle-grades students. The club ran for eight weeks during the fall term at a large suburban middle school in the United States, serving grades 7–8. This particular middle school has a large number of after-school clubs in which students can participate. After learning about the popularity of these clubs among students, I presented the idea to the school’s principal of an after-school club focused on programming and mathematics, and advertised the club at the school as an opportunity for students to learn some introductory coding skills and to use them to write computer programs in a mathematics setting.

Although I had no prior connection with the school, students and parents knew that the club was associated with a university research project. All students at the school had the opportunity to join the club; 29 students signed up: eighteen 7th-graders (12–13 years old) and eleven 8th-graders (13–14 years old). Some students who joined the club had had some exposure to coding through tasks with 3D printing and programming robots in a class offered at the school, although all students were at an introductory level of knowledge. All participants were enrolled in a mathematics class at the time of the club.

The after-school club met for 90 min, once per week, for eight weeks. I led each session and two graduate students helped facilitate. Students were introduced to Scratch, a visual programming environment, which they used for the duration of the club. In the first two weeks of the after-school club, I introduced students to some of the basic features of Scratch. Students learned to create an object and to make it move in different directions. They also practiced using basic logical relations, such as if–then statements and loops. Following this initial exposure to Scratch, students then spent the next six weeks working on a sequence of projects.

The projects included tasks such as creating visual representations to document the motion and speed of a moving object, designing a “function machine” that would create ordered pairs related through a mathematical function and creating a “number wizard” that would guess a number based on a sequence of questions posed to a user. In addition to the projects that students completed in Scratch, we conducted a weekly task from CS Unplugged (https://csunplugged.org/en), which is a program designed to foster the principles of computer science without using a computer. Students worked on tasks such as determining the most efficient way to sort a list and creating a map that would represent distances between nodes.

The projects that students completed required specific knowledge that they had learned in the first weeks of the club, but the projects also allowed students to explore other features of the Scratch environment. During weeks 3–8, when students worked primarily at their own pace, we began and closed each session by inviting several pairs of students to share the progress they had made or any new techniques they had learned. Intermittently during each session, I brought students together to introduce a particular technique or to respond to a common challenge that had surfaced. During times that students were working on their projects, the facilitators and I circulated the room and worked with individuals and small groups to answer questions and help debug.

Students worked in pairs throughout the club, with each pair of students sharing a single lap-top computer. The rationale for assigning students to work in pairs came from the novelty of Scratch and the potential challenge of learning to use it. Given that it was a new environment for most students, and all students were novice programmers, I expected that working with a partner would help overcome frustrations or the feeling of being “stuck” at any point in their work. I assigned students in same-gender pairs in order to reduce variation – as much as possible – in the gender dynamics that played into students’ interactions around the computer. I also tried to assign the student pairs according to grade level, although that was not always possible, so that students would know one another and have shared experiences in terms of their current classes and prior knowledge.

Students’ Use of Scratch to Represent Distance and Speed of Moving Objects

During weeks 3–4 of the club, students were tasked with using Scratch to program a car to drive around a track and then creating dynamic representations of the car’s speed and distance travelled as functions of time. With Scratch, users program objects through a collection of drag-and-drop code blocks that piece together to form lines of computer code.

The user interface of Scratch includes three primary components (Fig. 1), which are typical of visual programming environments: the left-most pane of the interface displays a back-drop, into which visual objects can be inserted; the middle pane includes a menu of blocks representing pieces of code that can be used to program the objects; the right pane is a workspace in which users can piece together the different code blocks to create short programs. In the example in Fig. 1, the backdrop represents a racetrack containing two cars and students have used the code blocks to compose a program making the red car drive continuously around the track.

Fig. 1
figure 1

The Scratch environment (the image across the bottom shows the full interface, while the pull-out images show the three components of the environment: the visual elements on the left, the menu of tile options in the center and the work space on the right)

Full size image

I provided students with a pre-made Scratch file with the racetrack back-drop on which a blue car was already programmed to drive around the track at a constant speed. I assigned students the two-part goal of (1) programming the red car so that it would be able to beat the blue car in a race around the track and (2) creating dynamic, visual representations of the distance the red car had travelled, and the speed at which it was traveling, at any given moment. The second part of the task was purposefully broad, as part of the intention of the project was to explore the degree to which students would translate their knowledge of mathematics to this after-school, computer-programming setting.

I provided each pair of students with a handout that described the task they were intended to achieve, as well as a set of questions to guide students’ reflection. However, I found that by mid-way through week 3 most students had disregarded the handout and were focused on the work they were engaged in at the computer. The task was projected at the front of the room for students to refer to periodically and the research team circulated the room to answer questions and press students for creative ideas.

At the beginning of the project, and throughout the two-week period, I reminded students of the common representations that are used in mathematics for representing speed and distance – graphs, tables, and symbolic representations – typically when students expressed feelings of being stuck or not knowing what types of representations to create. However, I most often saw that students created a range of novel representations and, in those cases, I pressed them to describe their motivation and process for creating such representations prior to suggesting alternative ideas.

Students’ knowledge of Scratch at this stage of the after-school club was at a novice level. They were familiar with the basic functionalities of Scratch, but they had not, for example, been given explicit instruction about how to create a graph. This was not problematic, in the context of the study, because its purpose was not to document to degree to which students could learn a taught procedure, but rather to examine the choices students would make in using the language of Scratch to create different representations. For the sake of supporting students to have productive experiences in the club, the research team gave fairly substantial help when students requested it and assisted students in executing ideas they suggested.

An important point about Scratch, particularly in contrast with more traditional mathematics technologies such as calculators or dynamic geometry environments, is that the built-in mathematical functionalities of Scratch are limited. The environment includes a pre-designed back-drop that mimics the look of a Cartesian plane. In the menu of code blocks, there are blocks to perform arithmetic operations on pairs of numbers; to compare numerical values; to manipulate the x- and y-co-ordinates, as well as the orientation, of objects on the screen.

But there is no built-in graphing function: to produce a graph, students would need to program an object to move through a sequence of corresponding x- and y-co-ordinates. Similarly, there is no built-in table feature. There is, however, a code block to create a list, which students would need to populate in order to maintain a current representation of the distance and speed of the car. One hypothesis of this study was that, rather than attempt to recreate traditional mathematical representations, students would make use of the capabilities of Scratch to create novel representations of the distance and speed of the car as it drove around the track. Moreover, the creation of these representations would depend, to some degree, upon how students had programmed their cars to move.

Participants and Data Collection

Data for this study came from weeks 3–4 of the club and I only included pairs of students for which both members of the pair were present for the two consecutive weeks. I excluded one pair from the analysis who completed the task primarily in conversation with the instructor. In all, four pairs of students were included in the analysis (Table 1).

Table 1 Pairs Included in the Analysis
Full size table

In total, students had approximately 75 min to work on the two parts of the car-driving project, spread across two weeks. Each computer was equipped with screen-capturing software that produced a video recording of all of the activity occurring on the computer monitor synched with an audio record of students’ conversations about the task. Following the data collection, I worked with two research assistants to segment the video recordings according to the phenomenon that students were discussing – speed or distance of the red car – according to the representation that was the topic of discussion. I produced transcripts of the relevant segments for the four pairs of students, transcribing students’ turns of speech and noting the ways in which students’ work on the computer screen was updated as they talked.

Data Analysis

I used an abbreviated version of O’Halloran’s (2015) framework for multimodal analysis of the mathematics register to code the transcripts according to symbolic and diagrammatic difficulties (see Table 2). Importantly, this list of challenges surfaced through analyses of traditional mathematics texts and communication (i.e. not through the use of programming environments). Thus, although this list served as a starting point, I did not assume that all of the challenges would surface in students’ work here, nor that they would surface in the same way. The challenges and descriptions served as phenomena to look for in the transcripts and videos of student work. The unit of analysis at this stage was a segment, or a section of transcript, in which students discussed a representation of speed or distance.

Table 2 Symbolic and diagrammatic difficulties of mathematical communication (from O’Halloran 2015)
Full size table

Following the coding of the transcripts, I aggregated them according to the themes that surfaced with regard to students’ challenges with communication and how they responded to those challenges. Because of the exploratory nature of this work, these themes highlight the most salient issues that I identified in students’ communication and provide a starting point for further research into the nature of students’ integrated mathematics–computer programming work.

Findings

Students’ work during the car-driving task yielded insights related to how challenges of symbolic communication and visual representations are situated within the context of a visual programming environment. There were several challenges that did not surface in students’ use of Scratch. Decontextualized knowledge was not a problem in either the use of symbolic or visual representations, because the task was contextualized through the use of Scratch and the physical motion of a car. Additionally, the use of visual representations did not present challenges related to special conventions, density of information, implicit reasoning, or recoding of uncertainty. Largely, these challenges did not surface because students had agency both in deciding which representations they would create and in determining the conventions they would follow.

The most prominent challenges that did surface in students’ work were related to the use of special symbols and grammatical strategies. I present the challenges related to symbolic and, respectively, diagrammatic representations in the following sections, as well as some of the ways that students addressed these communication challenges through their work.

Specialized Symbolic Meanings and New Grammatical Strategies

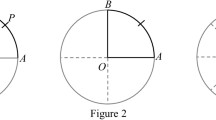
Visual programming environments are designed to translate complex programming languages into more intuitive collections of drag-and-drop blocks. While this design does help to overcome the burden of learning a programming language, drag-and-drop environments themselves incorporate structures and conventions for piecing together communication. The use of special symbols – or symbols that have discipline-specific meanings – became especially salient when the vocabulary of Scratch differed both from everyday and from more traditional mathematical language, such as in the case of variables. A variable, in the language of computer science, is a named storage location which stores user-determined values. In the excerpt below, Ashley and Rosie added a tile to their car-driving program to display a variable that they had created and labeled “speed” (see Fig. 2). Because they had not assigned a value to the variable, by default it took a constant value of 0, which it displayed as the car drove around the track.

Rosie: Um, oh, “show”. “Show variable”, click that.

Ashley: [Drags the “show variable” tile into the workspace and selects the variable “speed” from the drop-down menu.]

Rosie: Okay, ready? Play.

Ashley: [Runs the script. The car drives around the track, and the “speed” variable displays a value of 0.]

Rosie: Wait, what?

Ashley: But it says the speed is at zero.

Rosie: Oh no, that is definitely more than zero.

(Session 3, turns 3–9)

Fig. 2
figure 2

Ashley and Rosie’s first attempt to display the speed of the car

Full size image

As is illustrated in Fig. 2, Ashley and Rosie created a fairly sophisticated program to make the car drive, given their relative inexperience with Scratch. They used a “forever” loop to make the car move forward constantly and they used an “if–then” statement, along with color sensing commands, to adjust the orientation of the car any time it veered off the track and onto the grass. However, when they decided to use the “speed” variable to represent the speed of the car, they inserted a code block to display the variable without connecting its value to the motion of the car.

Ashley and Rosie, like some other students in the study, seemed to interpret that a variable with a given label would automatically display information that was consistent with the meaning of the label. This assumption was not unfounded, given that drag-and-drop blocks in Scratch are designed to mimic the informal language that would be used to discuss actions and features of an object. For example, blocks labeled “x position” and “y position” automatically display the position of an object within the co-ordinate grid, while a tile labeled “distance to” calculates the Euclidean distance from one object to another.

The challenge of variables came from the fact that, when students created variables, they also needed to assign values to them. Students were able to address this challenge in some cases by contextualizing their communication about variables through the programs that they were creating. In the following excerpt, Shannon had created a variable labeled “counter” meant to keep track of how far their car had moved, but the students did not know how to use the variable.

Kelly: How’d you make the red car counter?

Shannon: I just made a variable, said counter. Oh, wait a minute. I think I’ve got it. Change counter by one [dragging a “change counter by” tile into the workspace]. I think I have it.

(Session 3, turns 371–372)

Shannon seemed to know, based on the fact that she had just created the counter variable, that it did not yet encode any meaning. While studying the code that she had used to make the car drive around the track, she recognized that she could connect this variable to her existing script to give it meaning. Shannon and Kelly had previously created a control by which users could turn the car to the left or right by clicking the left or, respectively, right arrows.

To incorporate the counter variable, Shannon included a new command so that every time the left arrow key was pressed the counter increased by 1 (Fig. 3). As Kelly quickly noted, this construction effectively used the variable to count the number of left turns the car had made, rather than the number of steps it had moved. Still, Shannon’s work here was a first stage towards displaying understanding of the meaning of variable within the visual programming environment, by using it within the context of the program she was writing. In fact, many students eventually pursued similar strategies and used “counter” or “distance” variables set to increase in a 1–1 correspondence with the number of steps the car had moved.

Fig. 3
figure 3

Shannon and Kelly’s workspace, with scripts circled connecting the students’ use of the counter variable to the motion of the car

Full size image

Closely related to the specialized meanings of symbols within the Scratch environment was the challenge of the new grammatical strategies of the environment. This refers to the challenge students experienced not only of knowing what different code blocks meant, but also of knowing how they should be pieced together. Like any language, Scratch requires certain grammatical constructions in order to make meaning. Within Scratch, the shapes of blocks are meant to indicate where those blocks can fit. Long rectangular pieces are designed to be stand-alone pieces of code, which can be added to scripts and have other information embedded within them. However, there are also blocks that represent Boolean or numerical values, the state of an object (e.g. whether it is touching a certain color) or mathematical operations.

Students often struggled to translate what they wanted to do mathematically into the grammar of Scratch, as in the case of Melanie and Eleanor below. In this example, Melanie had found the “distance to” tile in the menu options for the red car (see Fig. 4) and the students wanted to use that tile to measure the distance from the red car to the finish line on the track.

Melanie: Now we can add in the drop-down menu “distance to” and then, Sprite one, I guess is what it’s called.

Eleanor: How does this [the “distance to” tile] get activated?

Melanie: Usually everything starts with the flag button.

Eleanor: This won’t attach to anything though.

Melanie: What?

Eleanor: This button doesn’t attach to anything.

Melanie: Because it goes […] You know how these have blanks? You have to put it into the blanks so it’s not already one of the blocks.

(Session 3, turns 131–137)

Fig. 4
figure 4

Melanie and Eleanor’s use of the “distance to” tile, which provided a menu to measure the distance from the car to several other objects on the screen

Full size image

Because the “distance to” tile represents a numerical value, it was designed to be embedded within another command requiring numerical input. Melanie and Eleanor wanted to use the tile to display the distance, but they did not know how to incorporate the tile within a string of commands. This unfamiliarity with the grammar of Scratch was a persistent challenge for students in their attempts to create representations of the speed and distance related to the motion of the car.

Embedding of Symbolic Terms within Visual Representations

The work of O’Halloran and others has documented the ways in which visual representations often incorporate symbolic or linguistic elements, such as the labeling of a diagram or the co-ordinates and units of a graph. The embedding of symbolic and linguistic elements within visual representations took a slightly different form in students’ use of Scratch and was closely related to challenges associated with symbolic communication. Before students had the opportunity to interpret visual representations, they needed to use the symbolic code to create the representations themselves. This challenge is exemplified particularly well through the case of Kyle and Allen, who spent most of their time over the two sessions working on creating a tabular display of the number of laps that each car had completed.

Kyle and Allen’s first technique for representing the distance their car had travelled, which they also applied to the computer-controlled car, was to construct a variable to calculate the number of laps the car had made around the track. Following that, they decided to create a tabular display of the number of laps each car had driven, using the “list” feature in Scratch. In Scratch, the “list” block stores a sequence of information that can be inputted manually or through an automated script. Lists can also be displayed on the screen and a list looks like a traditional table in as much as it is displayed as a column with several rows. Kyle and Allen created a list that they named “laps” and their process for populating the list revealed some of the challenges with the symbolic information that needed to be included within the visual representation.

The students’ first strategy was to create a script to add “1″ to the laps list every time their car touched yellow (i.e. crossed the finish line) (see Fig. 5). The representation they produced, also illustrated in Fig. 5, was a list called “laps” that stored a sequence of 1’s as the car drove around the track. Although the students did not make this point explicit, the car’s distance was encoded through the length of the list, which noted the car’s total number of laps around the track.

Fig. 5
figure 5

Kyle and Allen’s first attempt at creating a table to represent the car’s distances travelled

Full size image

Allen and Kyle expressed dissatisfaction with the display of the list and began modifying the display of information about the car’s distance. In their second iteration, the students changed their script so that each time the car crossed the finish line they added the text “red car laps” at the next open position in the list (see Fig. 6). After an initial test of the script, Allen added a final command at the end of the loop to delete the entire list. The effect of this construction was that the list was deleted each time the car went around the track, so that there was only ever one entry labeled “red car laps”. In their next iteration of the script, which began at the start of Session 4, Kyle and Allen replaced the text of “red car laps” with the value “laps + 1”, which was the length of the existing list. Again, because they were deleting the entire list with each iteration of the script, the list continually populated and deleted the value of “1” in the first entry. At this stage, Allen began to be more explicit about his interpretation of the list and what he wanted it to represent.

Allen: Okay so look at this. It says “one” then empty. Then “one”, then “one”, then “one”, then “one”. We need to make it add one even though it’s adding one.

Kyle: Just do “add laps” instead of “add laps plus one”. Delete all of laps. Move that out of there forever.

Allen: No, we need to do that or else it’ll keep on adding up and it’ll lag out.

(Session 4, turns 25–27)

Fig. 6
figure 6

Kyle and Allen’s second attempt at creating a table to represent the car’s distances travelled

Full size image

Eventually, Kyle and Allen produced a list that continually populated the value of “Laps + 1” (where “Laps” was a variable increasing by one each time the car touched the yellow finish line) at the top of the list. As is illustrated in Fig. 7, the total number of laps the car had travelled could be interpreted differently, depending on whether one looked at the top-most value of the list or whether one looked at the total length of the list. As Allen noted, the discrepancy surfaced because of the way they created their “Laps” variable – specifically, that the value of the variable increased every time the car touched the yellow finish line.

Allen: Well, dude, we need to do it, if touching color yellow then teleport away, because it might […] it’s so thick, because if it goes over it counts like two or three laps.

(Session 3, turn 305)

Because the car may have registered “touching” the finish line multiple times each time it crossed, the total number of laps according to the table entry was larger than the number of laps according to the length of the table. This recognition is significant not only because of its implications for the design of Allen and Kyle’s program, but also because it reveals Allen’s understanding of how the creation of the variable, the use of the variable to make a list and the eventual display of that list were interrelated and necessary for understanding the final product.

Fig. 7
figure 7

Kyle and Allen’s final attempt at creating a table to represent the cars’ distances travelled

Full size image

The challenge that Kyle and Allen encountered in embedding symbolic information for the creation of a visual representation was common across all pairs of students that participated in the Scratch club. The three other pairs of students in this study all discussed, and briefly attempted, the creation of tables and graphs to represent information about speed or distance, and none of the pairs made substantial progress in creating a graph.Footnote 2 The most productive way for students to overcome these challenges was to develop visual representations that were more straightforward and more tailored to the visual programming environment. Figure 8 illustrates two such examples, which are specific cases of fairly typical strategies that students employed. In the picture on the left of Fig. 8, Melanie and Eleanor programmed the two cars to draw pen trails as they moved around the route, keeping track of the cars’ paths and giving a rough estimate of the relative distance each car had travelled. In the picture on the right, Ashley and Rosie used text to display how much time had passed and they used features embedded within Scratch automatically to keep track of the time.

Fig. 8
figure 8

Two examples of how students simplified their visual representations, through the use of pen trails (left) and text (right)

Full size image

Discussion

The symbolic challenges that students encountered in their use of Scratch were primarily related to the special symbol meanings and new grammatical strategies of the Scratch language. The visual challenges that students encountered came from the embedding of symbolic and linguistic elements in visual representations, and these challenges were closely related to the symbolic challenges students experienced. They implicitly overcame several other challenges that have been documented as inherent to mathematics discourse by creating representations that were highly localized to the Scratch environment: There were few implied or special conventions required for interpreting the diagrams, as students made the information explicit in their creation; the density of visual information was substantially decreased compared with more traditional mathematical representations; the knowledge was contextualized to the specific task at hand. Finally, there was little implicit reasoning required to interpret the visual representations students created, because they were so closely connected to the concrete context that they represented.

In many ways, students’ work in this study confirmed the findings of prior research regarding the potential of computer programming environments to support students’ mathematical work (Clements and Battista 1989, 1990; diSessa 2000; Edwards 1991, 1997; Eisenberg 1995; Hoyles and Healy 1997; Hoyles and Noss 1992; Hoyles and Sutherland 1989). Students’ work was concretized in the context of representing the motion of a tangible object within the computer environment. The complexity and abstraction that is typical of traditional mathematical discourse was largely absent from students’ talk; instead, students’ use of Scratch allowed for expression and agency in determining what representations they would create and how they would create them. However, those decisions were constrained in some ways by the challenges that students encountered with interrelated modes of symbolic and visual communication.

The design of Scratch, and other environments like it, allows for more intuitive use, lowering the bar of entry for users to create and manipulate objects through computer code. With little or no programming experience, students in this study were able to move and control objects, as well as create various representations of that motion. However, the intuitive design of visual programming does not mean that there is nothing to learn, especially in cases where concepts and constructs are used differently in different disciplines. To learn to “speak” symbolic mathematical language, students need to learn the meanings of symbols, as well as how they are put together to form arguments (Schleppegrell 2007). To do mathematics that is integrated with computer programming, students need to translate between two related, but distinct, technical languages.

One could ask whether the challenges that students encountered were related to their knowledge of different mathematical representations (e.g. how a table should be created to purposefully represent information) or to their ability to translate that knowledge into the language of Scratch. Noss and Hoyles (1996) suggested that computers could serve as a ‘window’ into students’ understanding, by revealing difficulties that may be obscured through routine practice with standard representations and procedures. In a more typical paper-and-pencil environment, many students would likely have been able to draw a graph to represent a given context. But requiring students to communicate the creation of such a representation through the use of a novel language – even one that was designed to mimic intuitive, everyday language – revealed that students may have been missing some of the links between the multiple semiotic systems that make up the language of mathematics.

The question of whether students’ challenges originated in their understanding of the mathematics or their use of the technology risks losing a broader point about the nature of tasks that become possible through the use of a programming environment. In a more typical paper-and-pencil context, it would not be possible to create a dynamic representation corresponding to the action of an object in real time. Thus, even if a student were able to produce static visual representations, that knowledge would be of little use in modeling contexts that require more dynamic displays of information (English et al. 2016). The introduction of computer programming into mathematics and other STEM disciplines should not only support students’ learning but also help to re-envision what it means to engage in those disciplines (Baldwin et al. 2013; Barr and Stephenson 2011; Weintrop et al. 2016). Doing so requires further attention to how students can be supported in making connections among multiple semiotic systems.

The issue of which types of tasks become possible through the intersection of computer science and mathematics recalls the increasing prominence of computational thinking and computer science in K–12 education. Weintrop et al.’s (2016) taxonomy of computational thinking practices in mathematics and science offers one of the most comprehensive characterizations of how computational thinking is applied across STEM disciplines. Although this taxonomy describes some aspects of multimodal communication – including creating visualizations, communicating information about a system and programming – it was not intended to account explicitly for the nuances of communication in integrated settings. In addition to descriptions of the knowledge and competencies that students must develop to order to engage in computational thinking (Barr and Stephenson 2011; Brennan and Resnick 2012), it may be worthwhile for future work to attend to how applications of such thinking are communicated across other technical disciplines.

The difficulty of learning to use technology to do mathematics is not solely linked to programming environments. Studies of students’ use of computer algebra systems (CAS) have documented students’ struggles inputting or displaying information in such environments (Artigue 2002; Guin and Trouche 1998), while research findings on the use of dynamic geometry environments have shown that students do not always use the available tools correctly or to their fullest capacity (Jones 2002; Sinclair 2003). A key difference of the present study is that many of the technologies that have been previously researched “embody mathematics” in the sense that they employ mathematical models both at the level of user interface and in the underlying processes (Laborde 2007, p. 72). While visual programming environments such as Scratch certainly incorporate mathematical models for internal processing, they do not offer mathematically oriented user interfaces. Thus, the challenges that students experience arise from their ability to translate mathematical discourse to a new technical discourse, one with its own rules and conventions.

The findings of this research have implications for how teachers view students’ mathematical learning with technology. It is not uncommon for teachers to perceive technology as a ‘servant’, facilitating the work that students need to do while not changing the nature of that work (Goos et al. 2003; Smith et al. 2016). The introduction of a computer programming environment, one which is not designed with specific mathematical tasks or concepts in mind, upends such a perspective and requires a shift towards a more integrated approach to mathematics teaching and learning (Monaghan et al. 2016). There are efforts at various levels of instruction to pursue such initiatives (Baldwin et al. 2013; Barr and Stephenson 2011; Cetin and Dubinsky 2017), although there is no unified vision within the discipline of mathematics regarding the role either of computing or of computer programming (Lockwood et al. 2018). The role of the latter in school mathematics can be better understood as our knowledge of students’ use of mathematical discourse better incorporates the complexity of integrating other technical languages.