Tuning of the two degrees of freedom FOIMC based on the Smith predictor

Abstract

This paper proposes a novel two degrees of freedom (2-DOF) fractional order internal model controller (FOIMC) for the height control of a coupled tank system. Coupled tank systems find applications in the process control industries. The level control of the coupled tank system is a challenging problem in the control systems because of its nonlinearity and time delay involved. The level control of the coupled tank system has variable servo tracking and disturbance rejection requirements. 2-DOF controller achieves better servo tracking and disturbance rejection than a one degree of freedom (1-DOF) controller. The proposed servo tracking controller is designed using the Bode’s ideal loop transfer function and direct synthesis approach. The parameters of the Servo tracking controller are tuned using peak overshoot and settling time specifications. The disturbance rejection controller is designed analytically. A detailed study of the effect of the fractional order on the disturbance rejection property and stability. Robust stability of the proposed controller is analysed using $H_{\infty }$ norm of the uncertainty bound. Comparison of the simulation results of the proposed controller with the state of the art showed better performance of the proposed controller. Frequency domain analysis also indicates the superior performance of the proposed 2-DOF FOIMC.

1 Introduction

Coupled tank system comprises two or more than two similar or dissimilar tanks interconnected for the fluid flow and storage. The coupled tank system is used in the chemical industries, water treatment plants etc., and has nonlinear dynamics. The coupled tank has two modes of operation; interacting and noninteracting. In the interacting mode, two tanks are connected by a pipe. In the noninteracting mode, the two tanks are connected in a cascade. In the present work two similar cylindrical tanks are interconnected in the interacting mode. To design a controller for the level control of coupled tank system, a transfer function model is needed. Modelling and identification of the coupled tank system is discussed in [1, 2].

As processes are becoming complex day by day, a one degree of freedom (1-DOF) controller cannot satisfy two different performance specifications at a time. Hence Two degrees of freedom (2-DOF) controllers are designed to satisfy more than one performance specifications. A brief study of the relevant 2-DOF controllers is made. [3, 4] are some tutorial papers which discuss the different configurations of 2-DOF controllers available, and equivalent relationships among different 2-DOF configurations. The controllers used in the 2-DOF configuration can be a proportional integrator and differentiator (PID), internal model controller (IMC), fuzzy controllers etc. or a combination of them.

The controller parameters must be tuned and optimised for better performance of the closed loop system. Some tuning methods for the integer order 2-DOF controller are presented in [5,6,7]. While [5] proposed a gain margin based tuning, [6] proposed tuning based on the evolutionary techniques using integral error. [7] compared the tuning of 2-DOF controller parameters using two evolutionary algorithms. The coupled tank system in the present work has a first order plus delay time (FOPDT) model. To compensate for the time delay present in the system, Smith predictor based controllers are normally used. [8, 9] discuss the Smith predictor based controllers. 2-DOF controllers find many industry applications like power systems, magnetic levitation, and process control [10,11,12,13].

Fractional order controllers (FOC) are widely used from the last three decades, because of advantages like robustness to system gain variations, wider stability margins, near infinite gain margin, and more tunable parameters [14,15,16]. Fractional order operators like $s^{0.5}$, $s^{1.2}$ are part of the fractional order controller. IMC is a simple and stable model based controller [16]. Fractional order internal model controller (FOIMC) combines fractionality with IMC. FOPID with 2-DOF configuration is discussed in [17]. A new design method for the fractional order controller optimisation using frequency domain specifications is proposed in [18]. A DC motor position control case study is taken for implementation of the controller. [19] proposed a simple tuning method for fractional order controllers using Bode’s ideal open loop transfer function (OLTF). The proposed method uses rational functional approximation based pole placement. In [20], a FOIMC based 2-DOF is designed for the liquid level control system. The controller design uses frequency domain specifications for tuning the parameters. Application of the IMC based 2-DOF controller is given in [21]. Oustaloup recursive approximation is used in the controller tuning.

Along with excellent performance and stability, the controller designed should also have robustness to change in the system parameters and change in the set point. Robust stability can be analyzed analytically using the $H_{\infty }$ frequency norm [22]. A discrete time enhanced sliding mode controller is proposed for the fractional order system [23]. The disturbance rejection and robustness to parametric uncertainty of the proposed controller are proved. A discrete time model of the fractional actuator is obtained in [24]. The sliding mode controller developed for the actuator handles uncertainty and disturbance in the system. Two different tuning algorithms are proposed for FOIMC in [25]. They use IMC control structure and Smith predictor. The proposed controller has good robustness to modelling uncertainties. Bode’s integrals based FO-[PI] controller is designed using the frequency domain specifications in [26]. Robustness is analysed using the slope of the Nyquist diagram.

Different tuning methods, both analytical and soft computing based methods for the fractional order 2-DOF IMC are presented here. FOIMC with 2-DOF configuration is discussed in [27, 28]. Some works like [29,30,31,32] discuss the industrial applications of FOIMC based 2-DOF. Application of the IMC based 2-DOF controller is given in [33]. Some recent works discuss the soft computing based tuning of the 2-DOF fractional controllers [34,35,36,37]. [38] discussed 2-DOF FOIMC with analytical tuning of the controller parameters. Problems with the surveyed literature are high peak overshoot and long settling time in the step response, lack of robustness and higher control effort [39,40,41,42,43].

Motivation for the work and proposed method: Based on the previous discussion a need is felt to design a better 2-DOF controller, and a novel configuration for the 2-DOF FOIMC is proposed for the coupled tank system. The proposed controller combines the Smith predictor with two fractional order controllers to form a 2-DOF FOIMC. Bode’s ideal closed loop transfer function model is used as the reference and using direct synthesis method, the servo tracking controller is derived analytically. Since coupled tank system has slowly varying dynamics the servo tracking controller parameters are tuned using time domain specifications. Disturbance rejection controller is tuned by balancing disturbance rejection and servo tracking properties with stability. The results of the proposed work are compared with some recent state of the art literature on 2-DOF configuration (both fractional order and integer order 2-DOF controllers) [39,40,41,42,43]. In this work, simulations are done in the MATLAB/SIMULINK using the fractional order modeling and control (FOMCON) toolbox [44]. FOMCON tool box is used for the modelling and identification of fractional order systems and implementation of the fractional order controllers.

Novelty and main contributions:

• 1. Proposed a new configuration for the servo tracking controller.

• 2. Tuned the controllers analytically.

• 3. Designed both the servo tracking and disturbance rejection controllers as fractional order controllers.

• 4. Analysed the time domain and the frequency domain results.

• 5. Analysed the robustness of the controller to a change in the system gain and change in the operating point. Analysed robust stability of the proposed controller.

Organisation of the paper: The first section gives the introduction to the proposed work and surveys the literature. The second section states the problem and gives the preliminaries to the work. The third section gives the dynamics of the coupled tank system. The fourth section discusses the proposed methodology. The fifth section presents the results and discusses the findings. Finally, the sixth section concludes the results got.

2 Problem statement

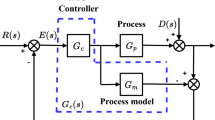
Design a 2-DOF controller based on the FOIMC; satisfying both the disturbance rejection and setpoint tracking requirements, using the Smith predictor to overcome problems with large time delays involved in the system. Of the available 2-DOF structures, the structure shown in Fig. 1 [4] is considered in this work. In Fig. 1$G_{c_{1}}$ is the servo tracking controller and $G_{c_{2}}$ is the disturbance rejection controller. R, U and Y are set point, controller output and system output, respectively.

Fig. 1

2-DOF configuration implemented

2.1 Basics of the fractional order control

Fractional calculus is a 300 year old area, but it’s applications became popular in the past three decades only. There are three definitions available for the fractional differentiation, Reimann-Liouville, Caputo, and Grunwald-Letnikov. Among these definitions, Caputo definition is used normally in the control and engineering applications. G-L definition is more amenable to digital implementation. The Caputo definition of the fractional order derivative is given by Eq. (1).

$$\begin{aligned} D^{\alpha }_{t}f(t)= \frac{1}{\varGamma (n-{\alpha })} \int _{0}^{t} \frac{f^{n}(\tau )}{(t-{\tau })^{{\alpha }-n+1}}d{\tau } \end{aligned}$$

(1)

In this definition, the function is first differentiated and then integrated. Fractional derivatives are nonlocal and are suitable to represent systems involving distributed parameters. The fractional controller is first developed by I. Podlubny [14]. Fractional power gives more flexibility to the integrator and the differentiator of the PID controller. Equation (2) represents a general form of the fractional PID controller.

$$\begin{aligned} C(s)=\Bigg ( K_{p}+\frac{K_{i}}{s^{\lambda }}+K_{d}s^{\mu } \Bigg ) \end{aligned}$$

(2)

where $K_{p}$, $K_{i}$, and $K_{d}$ are proportional, integral, and derivative gains respectively and $\lambda$ is the fractional power of the integrator and $\mu$ is the fractional power of the differentiator.

3 Coupled tank system

The coupled tank system in the interacting mode is taken as a case study and is shown in Fig. 2.

Fig. 2

Block diagram of the coupled tank system

In Fig. 2,

$Q_{1}$:

= Inlet flow rate

$Q_{12}$:

= Flow rate from tank 1 to tank 2

$Q_{d_{1}}$:

= Disturbance flow rate from tank 1

$Q_{d_{2}}$:

= Disturbance flow rate from tank 2

$h_{1}$:

= Variable height of the tank 1

$h_{2}$:

= Variable height of the tank 2

D:

= Diameter of each tank

A:

= Cross sectional area of each tank

The control objective is to regulate the height of the tank 2, by changing the inlet flow rate of the tank 1. The coupled tank system has nonlinear dynamics because of the valves. Table 1 shows the coupled tank system parameters.

Table 1 Parameters of the coupled tank system

Equations (3)–(4) represent the dynamics of the two tank system.

$$\begin{aligned} A\frac{dh_{1}}{dt}= & {} Q_{1}-Q_{12}V_{2}-Q_{d_{1}} \end{aligned}$$

(3)

$$\begin{aligned} A\frac{dh_{2}}{dt}= & {} Q_{12}V_{2}-Q_{d_{2}} \end{aligned}$$

(4)

The flow rate through the interconnecting solenoid valve B is,

$$\begin{aligned} Q_{12}= a_{12}sign(h_{1}-h_{2})\sqrt{2g|h_{1}-h_{2}|} \end{aligned}$$

(5)

Flow rates through the ball valves A and C are given by,

$$\begin{aligned} Q_{d_{1}}= & {} a_{d_{1}}\sqrt{2gh_{1}} \end{aligned}$$

(6)

$$\begin{aligned} Q_{d_{2}}= & {} a_{d_{2}}\sqrt{2gh_{2}} \end{aligned}$$

(7)

where

$a_{d_{1}}$:

= Coefficient of discharge for valve A

$a_{12}$:

= Coefficient of discharge for valve B

$a_{d_{2}}$:

= Coefficient of discharge for valve C

g:

= Acceleration due to the gravity ($98.4\, \hbox {gm/s}^{2}$)

$V_{2}$:

= Valve coefficient of valve B

d:

= Diameter of the interconnecting pipe between the tanks

In the operating mode considered ${h_{1}}\ge {h_{2}}$, hence Eq. (5) reduces to,

$$\begin{aligned} Q_{12}= a_{12}\sqrt{2g(h_{1}-h_{2})} \end{aligned}$$

(8)

Substituting (6)–(8) in (3), and (4)

$$\begin{aligned} A\frac{dh_{1}}{dt}= & {} Q_{1}-V_{2}(a_{12}\sqrt{2g(h_{1}-h_{2})})-a_{d_{1}}\sqrt{2gh_{1}} \end{aligned}$$

(9)

$$\begin{aligned} A\frac{dh_{2}}{dt}= & {} V_{2}(a_{12}\sqrt{2g(h_{1}-h_{2})})-a_{d_{2}}\sqrt{2gh_{2}} \end{aligned}$$

(10)

Linearising Eqs. (9)–(10), around the operating point $h_{1s}$, $h_{2s}$, $Q_{1s}$, using the Taylor series expansion,

$$\begin{aligned} A\frac{dh_{1}}{dt}= & {} Q_{1s}-V_{2}(a_{12}\sqrt{2g(h_{1s}-h_{2s})})-a_{d_{1}}\sqrt{2gh_{1s}}\nonumber \\&\quad +\,(Q_{1}-Q_{1s})+(h_{1}-h_{1s})\nonumber \\&\quad {\times }\,\Bigg [-V_{2}a_{12}\sqrt{2g}(1/2){(h_{1s}-h_{2s})^{-1/2}}\nonumber \\&\quad -\, a_{d_{1}}\sqrt{2g}(1/2){{h_{1s}}^{-1/2}}\Bigg ]\nonumber \\&\quad +\,(h_{2}-h_{2s})\nonumber \\&\quad {\times }\,\Bigg [-a_{12}\sqrt{2g}(1/2)V_{2}{(h_{1s}-h_{2s})^{-1/2}} \Bigg ] \end{aligned}$$

(11)

$$\begin{aligned} A\frac{dh_{2}}{dt}= & {} V_{2}(a_{12}\sqrt{2g(h_{1s}-h_{2s})})-a_{d_{2}}\sqrt{2gh_{2s}}\nonumber \\&\quad + \,(h_{1}-h_{1s})\nonumber \\&\quad {\times }\,\Bigg [a_{12}\sqrt{2g}(1/2)V_{2}{(h_{1s}-h_{2s})^{-1/2}}\Bigg ] \nonumber \\&\quad +\,(h_{2}-h_{2s})\nonumber \\&\quad {\times }\, \Bigg [V_{2}a_{12}\sqrt{2g}(-1/2){(h_{1s}-h_{2s})^{-1/2}}\Bigg ]\nonumber \\&\quad -\,(h_{2}-h_{2s})\Bigg [ a_{d_{2}}\sqrt{2g}(1/2){{h_{2s}}^{-1/2}}\Bigg ] \end{aligned}$$

(12)

At equilibrium, the following relations are obtained,

$$\begin{aligned}&Q_{1s}-(V_{2}a_{12}\sqrt{2g(h_{1s}-h_{2s})})-a_{d_{1}}\sqrt{2gh_{1s}}=0 \end{aligned}$$

(13)

$$\begin{aligned}&(V_{2}a_{12}\sqrt{2g(h_{1s}-h_{2s})})-a_{d_{2}}\sqrt{2gh_{2s}}=0 \end{aligned}$$

(14)

Also few constants are defined as,

$$\begin{aligned} K_{1}= & {} \frac{V_{2}a_{12}\sqrt{2g}{(h_{1s}-h_{2s})^{-1/2}}}{2A} \end{aligned}$$

(15)

$$\begin{aligned} K_{2}= & {} \frac{a_{d1}\sqrt{2g}{(h_{1s})^{-1/2}}}{2A} \end{aligned}$$

(16)

$$\begin{aligned} K_{3}= & {} \frac{a_{d2}\sqrt{2g}{(h_{2s})^{-1/2}}}{2A} \end{aligned}$$

(17)

$$\begin{aligned} {\tilde{h}}_{1}= & {} h_{1}-h_{1s} \end{aligned}$$

(18)

$$\begin{aligned} {\tilde{h}}_{2}= & {} h_{2}-h_{2s} \end{aligned}$$

(19)

$$\begin{aligned} {\tilde{Q}}_{1}= & {} Q_{1}-Q_{1s} \end{aligned}$$

(20)

Using Eqs. (13)–(20) in Eqs. (11)–(12),

$$\begin{aligned} \dot{\tilde{h}}_{1}= & {} -{\tilde{h}}_{1}(K_{1}+K_{2})-{\tilde{h}}_{2}K_{1}+({\tilde{Q}}_{1}/A) \end{aligned}$$

(21)

$$\begin{aligned} \dot{\tilde{h}}_{2}= & {} {\tilde{h}}_{1}K_{1}-{\tilde{h}}_{2}(K_{1}+K_{3}) \end{aligned}$$

(22)

Taking Laplace transforms on both the sides of Eqs. (21)–(22),

$$\begin{aligned} sH_{1}(s)= & {} -H_{1}(s)(K_{1}+K_{2})-H_{2}(s)K_{1}+({Q}_{1}(s)/A) \end{aligned}$$

(23)

$$\begin{aligned} sH_{2}(s)= & {} H_{1}(s)K_{1}-H_{2}(s)(K_{1}+K_{3}) \end{aligned}$$

(24)

By solving Eqs. (23)–(24), the transfer function,

$G(s)=H_{2}(s)/{Q}_{1}(s)$ is obtained as,

$$\begin{aligned} G(s)=\frac{K_{1}/A}{s^{2}+(2K_{1}+K_{2}+K_{3})s+{K_{1}}^{2}+K_{1}K_{3}+K_{2}K_{3}}\nonumber \\ \end{aligned}$$

(25)

In the present work, the operating region of the level control is selected as (5–15) cm. By substituting parameters of the system from Table 1 into Eq. (25), the analytical model of the system is obtained as,

$$\begin{aligned} G(s)= \frac{6{\times }10^{-5}}{s^{2}+0.0313s+0.236{\times }10^{-3}} \end{aligned}$$

(26)

Fig. 3

Open loop test results of the level control

But the experimental data from the laboratory setup shows that a FOPDT model is sufficient instead of the second order system. The transfer function of this problem is represented as, $h_{2}(s)/Q_{1}(s)$.

$$\begin{aligned} G(s)= \frac{h_{2}(s)}{Q_{1}(s)}= \frac{0.268e^{-10s}}{975s+1} \end{aligned}$$

(27)

Figure 3 shows the plot of open loop test results. Figure 3 is obtained by varying the inlet flow rate, from 50 LPH to 275 LPH in steps of 25 LPH and observing the steady state heights of the two tanks, $h_{1}$, $h_{2}$. Model Eq. (27) is obtained from the experimental data and is used in this work for the controller design. The modelling errors between two models Eqs. (26) and (27) are calculated. The mean absolute error (MAE) is obtained as 0.007135 and root mean squared error (RMSE) is obtained as 0.06954.

4 Methodology

Figure 4 shows the proposed configuration of FOIMC based on the Smith predictor with 2-DOF configuration. This is an improved structure from [39]. The transfer function of the system, G(s) in Fig. 4 is of FOPDT model given by Eq. (28), where T is time constant, K is gain and L is time delay.

Fig. 4

Proposed 2-DOF FOIMC configuration

$$\begin{aligned} G(s)= \frac{Ke^{-Ls}}{Ts+1} \end{aligned}$$

(28)

In Fig. 4,

$G_{m}(s)$:

= Model of the system

Q(s):

= FOIMC controller (disturbance rejection controller)

$G_{m0}(s)$:

= Model of the system without the time delay element

$G_{c}(s)$:

= Set point tracking controller

In the proposed configuration, R(s) is the set point, Y(s) is the output, U(s) is the controller output, and d(s) is the disturbance at the input side. Assuming that the accurate model of the system is available, following equations of the closed loop system with respect to set point tracking Eq. (29), and disturbance rejection Eq. (30) are obtained.

$$\begin{aligned} T_{yr}(s)= & {} \frac{G(s)G_{c}(s)}{1+G_{c}(s)G_{m0}(s)}(G_{m}(s){\approx }G(s)) \end{aligned}$$

(29)

$$\begin{aligned} T_{yd}(s)= & {} \frac{G(s)[1+G_{c}(s)G_{m0}(s)-G_{c}G_{m}(s)]}{[1+G_{c}(s)G_{m0}(s)][1+Q(s)G(s)]} \end{aligned}$$

(30)

From Eq. (29) it can be seen that in the set point tracking, the characteristic equation (denominator term) has no time delay element (neither G(s) nor $G_{m}(s)$). The disturbance rejection controller Q(s) is not appearing in the Eq. (29), so the set point tracking and disturbance rejection can be tuned independently. Hence the proposed configuration shown in Fig. 4, qualifies to be a 2-DOF controller. In the proposed configuration $G_{c}(s)$ is a FOIMC and the design is modified form of FOIMC presented in [43]. The design of both the controllers Q(s) and $G_{c}(s)$ is through analytical methods. To overcome the problems with longer time delays in the system, the configuration is based on the Smith predictor.

Servo controller design: Many of the 2-DOF controllers like [38], have common parameters in the two controllers (servo and disturbance controllers). In the proposed configuration the two controllers are dissimilar in structure. Most of the controller design methods use frequency domain specifications like gain margin, phase margin, gain crossover frequency etc., as the design will be direct and easy. In the proposed method two time domain specifications peak overshoot and settling time are used for the controller parameter tuning. The desired closed loop response of the system, with a fractional order feedback controller is the Bode’s closed loop transfer function $T_{new}(s)$ given by Eq. (31), which gives robustness to system gain variations (iso-damping property). Iso-damping property means even though the system gain varies; the phase of the system remains constant and therefore the step response is same over a range of system gain values. Hence if the model has some uncertainty or the system parameters (gain) change over time, it is taken care by the Bode’s open loop transfer function model.

$$\begin{aligned} T_{new}(s)= \Bigg (\frac{Y(s)}{R(s)}\Bigg )_{desired}=\frac{e^{-Ls}}{\tau _{c}s^{\gamma }+1} \end{aligned}$$

(31)

R(s):

= Set point of desired magnitude

Y(s):

= Output of the closed loop system

$\gamma$:

= Fractional order

$\tau _{c}$:

= Time constant

The set point tracking controller is obtained using the direct synthesis method, where desired reference closed loop transfer function and actual closed loop transfer function are compared, and the controller is synthesised. Substituting G(s) and $G_{m0}(s)$ in Eq. (29),

$$\begin{aligned} T_{yr}(s)= \frac{\Bigg (\frac{Ke^{-Ls}}{Ts+1}\Bigg )G_{c}(s)}{1+\Bigg (\frac{K}{Ts+1}\Bigg )G_{c}(s)} \end{aligned}$$

(32)

Equating the right hand sides of Eqs. (31) and (32) and solving for $G_{c}(s)$,

$$\begin{aligned} G_{c}(s)= K_{c}\Bigg (1+\frac{1}{T_{i}s}\Bigg )\Bigg (\frac{1}{s^{{\gamma }-1}}\Bigg ) \end{aligned}$$

(33)

Proportional gain constant $K_{c}= \frac{T}{K{\tau _{c}}}$

Integral gain constant $T_{i}=T$

Step responses are obtained using the Eq. (31) for different values of $\gamma$ [43]. By analysing the step responses the following relations are obtained among peak overshoot ($M_{p}$), fractional order ($\gamma$), settling time ($t_{s}$) and GCF ($\omega _{gc}$).

$$\begin{aligned}&M_{p}= 73.9(\gamma ^{2}-1.6739\gamma +0.6756) \end{aligned}$$

(34)

$$\begin{aligned}&t_{s}(2\%){\times }{\omega _{gc}}= \frac{0.7885\gamma -0.2693}{\gamma -0.8673}\qquad 1<\gamma <1.078 \end{aligned}$$

(35)

$$\begin{aligned}&t_{s}(2\%){\times }{\omega _{gc}}= \frac{3.003\gamma -2.981}{{\gamma }^{2}-2.012\gamma +1.056}\qquad 1.078<\gamma <1.486 \nonumber \\\end{aligned}$$

(36)

$$\begin{aligned}&t_{s}(5\%){\times }{\omega _{gc}}= \frac{0.812\gamma -0.2036}{\gamma -0.8007}\qquad 1<\gamma <1.15 \end{aligned}$$

(37)

$$\begin{aligned}&t_{s}(5\%){\times }{\omega _{gc}}= \frac{7.156\gamma -7.9}{{\gamma }^{2}-1.303\gamma +0.2578}\qquad 1.15<\gamma <1.5\nonumber \\ \end{aligned}$$

(38)

In the Eqs. (35–38) settling times with 2% and 5% tolerance band near steady state are shown. Among these four equations Eq. (35) is used because it gives peak overshoot less than 3%. In the controller transfer function $G_{c}(s)$ of Eq. (33) the unknown tunable parameters are $\tau _{c}$, $\gamma$. From the desired time domain specifications of $M_{p}$, $t_{s}$ and using Eqs. (34) and (35) $\omega _{gc}, \gamma$ are obtained. Using the relation $\tau _{c}=1/{\omega _{gc}}^{\gamma }$, finally $\tau _{c}$ is also obtained. The time domain design specifications selected for the design are, $M_{p}<3\%, t_{s}=1500$ s. From Eqs. (34)–(35), for the coupled tank system level control, the servo tracking controller parameters are obtained as,

$$\begin{aligned} \gamma= & {} 1.012 \nonumber \\ \omega _{gc}= & {} {2.43}\times {10^{-3}} \mathrm{rad/s} \nonumber \\ \tau _{c}= & {} 441.3 \mathrm{s}\nonumber \\ K_{c}= & {} 8.24\nonumber \\ G_{c}(s)= & {} 8.24\Bigg (1+\frac{1}{975s}\Bigg )\Bigg (\frac{1}{s^{0.012}}\Bigg ) \end{aligned}$$

(39)

Disturbance rejection controller design:

The design of Q(s) follows the design of any internal model controller [39].

$$\begin{aligned} G_{IMC}(s)= & {} \frac{F(s)}{G_{m0}(s)} \end{aligned}$$

(40)

$$\begin{aligned} F(s)= & {} \frac{1}{1+{\lambda }s^{\alpha }} \end{aligned}$$

(41)

F(s):

= Fractional filter

$\lambda$:

= Tunable parameter of IMC

$\alpha$:

= Fractional order

$$\begin{aligned} Q(s)= \frac{G_{IMC}(s)}{1-G_{IMC}(s)G_{m}(s)} \end{aligned}$$

(42)

Derivation of set point and disturbance rejection controllers assumes that a suitable model of the system is available. Using Eqs. (40) and (42),

$$\begin{aligned} G_{IMC}(s)= & {} \Bigg (\frac{Ts+1}{K}\Bigg )\Bigg (\frac{1}{1+{\lambda }s^{\alpha }} \Bigg ) \end{aligned}$$

(43)

$$\begin{aligned} Q(s)= & {} \frac{Ts+1}{K{\lambda }s^{\alpha }}= \frac{T}{K{\lambda }}s^{1-\alpha }+\frac{1}{K{\lambda }s^{\alpha }} \end{aligned}$$

(44)

When $0<\alpha <1$, Q(s) is a Fractional Integrator Fractional Differentiator (FIFD). When $1<\alpha <2$, Q(s) is a Fractional Integrator Fractional Integrator (FIFI). Selecting $\lambda$ between T/3 to T/2 ensures a balance between set point tracking and robustness to model uncertainty [16]. To select the proper value of the fractional order $\alpha$, a comparison of disturbance rejection property with different values of $\alpha$ is made and shown in Fig. 5. From which it is found that $\alpha$ value of 1.9 gives the best disturbance rejection property. The Bode plots of the sensitivity transfer function $T_{yd}(s)$ for different values of $\alpha$ are shown in Fig. 6. From Fig. 6 it is observed that corresponding to $\alpha$ value of 1.9, the Bode plot has the lowest magnitude plot in low frequency range, which gives good disturbance rejection. Hence the choice of $\alpha$ value of 1.9 is ideal. But such an extreme value of the fractional order near the stability margin is giving highly transient response in step response simulation. During the detailed simulation studies, it is found that the best value of $\alpha$ is near 1. To verify the effect of the fractional order $\alpha$ on the disturbance rejection controller Q(s), the Bode plots of Eq. (44), Q(s) are given as a function of alpha in Fig. 7. From Fig. 7 it is clear that the for values of $\alpha$ lower than 1, the controller is not rejecting the high frequency noise. Based on the above discussion, the disturbance rejection controller, Q(s) parameters are selected as,

$$\begin{aligned} \lambda= & {} 330\\ \alpha= & {} 1.1 \end{aligned}$$

Finally Q(s) is obtained from Eq. (44) as,

$$\begin{aligned} Q(s)= \frac{11.02s+0.011}{s^{1.1}} \end{aligned}$$

(45)

Fig. 5

Comparison of disturbance rejection with different fractional orders

Fig. 6

Comparison of Bode plots of sensitivity with different fractional orders

Fig. 7

Bode plots of disturbance rejection controller

4.1 Robust stability analysis

The designed controller has to perform reasonably well for a change in the operating point. The closed loop system is robustly stable, if the following equation is satisfied [22].

$$\begin{aligned} 20log_{10}(|T_{C}(j\omega )||G_{\varDelta }(j\omega )|)<0 dB \end{aligned}$$

(46)

Where $T_{C}(s)$ is the complementary sensitivity transfer function of the closed loop system given by,

$$\begin{aligned} T_{C}(s)= \frac{G(s)G_{c}(s)}{1+G_{c}(s)G_{m0}(s)}= \frac{e^{-Ls}}{\tau _{c}s^{\gamma }+1} \end{aligned}$$

(47)

Let the transfer function of the system at a different operating point be,

$$\begin{aligned} G_{1}(s)= \frac{K_{1}e^{-L_{1}s}}{T_{1}s+1}= \frac{-K_{1}L_{1}s+K_{1}}{T_{1}s+1} \end{aligned}$$

(48)

Uncertainty in the plant transfer function $G_{\varDelta }(s)$ is defined as,

$$\begin{aligned} G_{\varDelta }(s)= \frac{G_{1}(s)-G(s)}{G(s)} \end{aligned}$$

(49)

Substituting Eqs. (28) and (48) in Eq. (49), $G_{\varDelta }(s)$ is obtained as shown in Eq. (50).

$$\begin{aligned} \frac{(KLT_{1}-K_{1}L_{1}T)s^{2}+(K(L-T_{1})-K_{1}(L_{1}-T))s+K_{1}}{-KLT_{1}s^{2}+(KT_{1}-KL)s+K}\nonumber \\ \end{aligned}$$

(50)

In this work, the controller’s robustness is verified by operating it in an adjacent operating region of (16-30) cm. The transfer function of the new region is Eq. (51).

$$\begin{aligned} G_{1}(s)= \frac{0.3e^{-20s}}{1095s+1} \end{aligned}$$

(51)

$G_{\varDelta }(s)$ and $T_{C}$ are obtained as,

$$\begin{aligned} G_{\varDelta }(s)= & {} \frac{-2915.4s^{2}-4.28s+0.032}{-2934s^{2}+290.78s+0.268} \end{aligned}$$

(52)

$$\begin{aligned} T_{C}(s)= & {} \frac{-10s+1}{{441.3s^{1.012}}+1} \end{aligned}$$

(53)

The maximum value of $|T_{C}(j\omega )||G_{\varDelta }(j\omega )|$ is obtained as − 18.45 dB, hence Eq. (46) is satisfied. The closed loop system with the proposed 2-DOF FOIMC is robustly stable, when operated in the operating region (0–15) cm and it’s neighbouring region (16–30) cm only, i.e. the uncertainty in the setpoint should lie within (16–30) cm.

5 Simulation results

To compare the performance of the proposed controller, three recent state of the art 2-DOF controllers are designed for the coupled tank system. First one is a fractional filter and integer order PI controller proposed by Chekari [40].

$$\begin{aligned} C_{1}(s)= & {} 5+\frac{0.01}{s} \end{aligned}$$

(54)

$$\begin{aligned} C_{2}(s)= & {} \frac{s+1}{29s^{1.33}+1} \end{aligned}$$

(55)

Second one is fractional filter based FOIMC proposed by Jia [41].

$$\begin{aligned} C(s)= & {} \frac{975s+1}{0.181s^{1.0039}+10s} \end{aligned}$$

(56)

$$\begin{aligned} F(s)= & {} \frac{0.676s^{1.0039}+1}{0.02s^{1.0039}+1} \end{aligned}$$

(57)

Third one is an integer order IMC with 2-DOF Smith predictor proposed by Li [42].

$$\begin{aligned} G_{c}(s)= & {} 36.38+ \frac{0.037}{s} \end{aligned}$$

(58)

$$\begin{aligned} Q(s)= & {} \frac{200090s^{2}+5690s+3.73}{105625s^{2}+650s+1} \end{aligned}$$

(59)

Comparison of 1-DOF and 2-DOF results:

Before proceeding to the actual work, a comparison of the servo tracking and disturbance rejection properties of 1-DOF and 2-DOF controllers is made to stress the need of the 2-DOF controller. Consider the disturbance rejection controller Q(s) alone as 1-DOF disturbance rejection controller. Now R(s) is made zero and a step disturbance d(s) of 5 cm is given at the input side. Fig. 8 shows the comparison of the disturbance responses of 1-DOF and 2-DOF controllers (Y(s)/d(s) with set point $R(s)=0$). Both the controllers gave good disturbance rejection property.

Figure 9 compares the servo tracking performance of 1-DOF (Q(s)) and 2-DOF ($G_{c}$ with Q(s)) controllers. Figure 9 shows that the 1-DOF designed for disturbance rejection is not at all giving servo tracking ability, but 2-DOF showed better servo tracking than 1-DOF controller. Figure 10 shows the Bode plots of the closed loop system with 1-DOF and 2-DOF controllers. 2-DOF controller has higher bandwidth and more robustness compared to 1-DOF controller.

Fig. 8

Comparison of Disturbance rejection of 1-DOF and 2-DOF controllers

Fig. 9

Comparison of Servo tracking of 1-DOF and 2-DOF controllers

Fig. 10

Comparison of Bode plots of 1-DOF and 2-DOF FOIMC

Fig. 11

Step responses of the system with different controllers

Fig. 12

Regulatory responses of the system with different controllers

Fig. 13

Servo responses of the system with different controllers

Fig. 14

Robustness verification of the system with different controllers

The setpoint for the second tank height in the coupled tank system is chosen as 10 cm. Figure 11 shows the step responses of different controllers to a setpoint of 10 cm. Figure 11 also shows the control effort (in %) required by the controllers. From Fig. 11 it is observed that the proposed controller has the zero steady state error, zero peak overshoot, and least settling time. Also, the control effort is within the saturation limits and reached steady state quickly. The proposed controller gave less control effort when compared to other controllers. Figure 12 shows the regulatory responses to a disturbance of 5 cm at 5000 s. From Fig. 12, the disturbance rejection is faster than the remaining controllers. Figure 13 shows the servo responses with time varying step input of [5 15 10] cm at [0 5000 10,000] s. From Fig. 13 the proposed controller performed well with varying setpoint requirements. Whenever there is a change in the set point, there is a spike in the control effort to track that change quickly. Figure 14 shows the robustness verification of the controllers at a different operating point of 20 cm. The new transfer function given by Eq. (51) is used for verification of robustness to change in the set point. From Fig. 14 the proposed controller has less settling time and peak overshoot compared to other controllers when operated in a different operating region with different set point.

Table 2 Integral time domain indices

Table 3 Time domain performance specifications

Table 2 compares the integral performance indices of the controllers and Table 3 compares the time domain specifications of the step responses obtained with different controllers. From Table 2 it is observed that the proposed controller has least IAE, ITAE among all the controllers. The control energy indicated by the integral of control effort squared, is the lowest for the proposed controller. From Table 3, it can be seen that the proposed controller has least settling time, and peak overshoot. Also, the specifications of the controller design, $M_{p}<3\%$ and $t_{s}=1500$ s are met. Figure 15 shows the step responses of the system with different controllers when there is a + 20 % change in the system gain K. The proposed controller showed good robustness to change in the system gain. Similarly, Fig. 16 shows the step responses for a − 20 % change in the system gain. The proposed controller is best among all the controllers, whether it is a positive or negative change in the gain.

Fig. 15

Robustness to $+$ 20 % gain change

Fig. 16

Robustness to − 20 % gain change

Observations: 1. The design of the proposed controller is simple, effective, novel and robust.

• 2. Tutorial papers like [3–4] are useful in the design of the proposed controller.

• 3. Both the servo tracking and disturbance rejection controllers are of fractional order and tuned independently.

Frequency domain analysis:

Figure 17 shows the Bode plots of loop transfer functions of the system with different controllers. The proposed controller shows flat phase response throughout the entire frequency range. Figure 18 shows the Bode plots of loop transfer functions with different controllers at new set point 20 cm with new transfer function (Eq. 51). At the new setpoint also the proposed controller had good flat phase response. Figure 19 shows the Bode plots of the system with the proposed controller at two set points. The magnitude and phase plots of the controller are very close. This indicates the robustness property of the proposed controller. Figure 20 shows the Bode plots of the system with and without the proposed controller. The system with the proposed controller has flatter phase response than the uncontrolled system at low frequencies of the order $10^{-3}$ to $10^{-4}$ Hz. From the Fig. 20 it is observed that, at high frequencies of order kHz, the magnitude drops to − 30 dB, hence the proposed controller effectively rejects the high frequency noise.

Fig. 17

Bode plot of loop TF with different controllers

Fig. 18

Bode plots of open loop TF at a different set point

Fig. 19

Controller at two different set points

Fig. 20

Bode plots with and without proposed controller

6 Conclusion

In this work, a 2-DOF FOIMC is developed for the coupled tank system. Both the servo tracking and disturbance rejection controllers are of fractional order and are designed analytically for the FOPDT model of the coupled tank system. Simulation results indicate that the proposed controller has good servo tracking and disturbance rejection properties than the other controllers. The proposed controller gave settling time 44% less than Jia and 53.3% less than Chekari method and Li methods. Similarly, the peak overshoot of the step response with the proposed method is 20% less than Jia method and 8% less than Chekari method.

The proposed controller is also compared with a 1-DOF FOIMC and performance of the 2-DOF FOIMC is found to be better than the 1-DOF FOIMC. The system gain is varied by ± 20%, and the proposed controller showed better robustness to the change in the system gain. The controllers are operated in the neighbouring region of 16–30 cm and the proposed controller showed better set point tracking in a different operating region. Analytical proof of robust stability to a change in the set point is given. Comparison of the Bode plots indicated more flatter phase responses (isodamping property) with the proposed controller than the other controllers. Finally it can be concluded that the proposed 2-DOF FOIMC gives superior time domain and frequency domain performance compared to state of the art.