A novel tuning approach with SSR algorithm for non-minimum phase system

Abstract

Cascade control is extensively used in process industries. The enhanced performance of cascade control depends on the effective tuning. However, after encountering the non-minimum phase zeros in the system, the tuning of cascade control becomes complex. This work proposes a modified Bode’s ideal transfer function for tuning fractional filter. This modification is completed after consideration of non-minimum phase zeros in Bode’s ideal transfer function approach. This modified tuning approach elucidated the common pitfalls in the existing techniques. Here, the internal model control (IMC) context is utilized to construct the outer loop controller of the series cascade scheme after embedding the fractional filter and inverse response compensator. Moreover, a rudimentary structure of the IMC scheme is revealed for the inner loop controller design. The suggested way enhances the non-minimum phase system performance without compromising setpoint tracking and disturbance rejection. Additionally, the Riemann sheet principle is utilized for the stability analysis. Sensitivity analysis is carried out to adjudge the robustness. The search space reduction algorithm is employed to optimize the closed-loop response utilizing an objective function that minimizes the integral of square error. Two case studies are utilized for effectuating the benefits of the suggested control approach associated with state-of-the-art.

1 Introduction

Cascade control is a refined and prompt structure over a single feedback loop with a flow, level and pressure control loop to alleviate external disturbances [1]. This structure also deals with nonlinearities in the process elements. The cascaded control procedure involves two loops, where the consequence of the inner loop acts as an input for the outer loop. However, an improved version of the cascade control hinges on the worthwhile tuning of both loops, but the PID controller’s ubiquity lies up to fractional order [2].

Generally, a series cascade control configuration is adopted in process industries for load disturbance rejection due to fewer parameters being tuned [3]. More precisely, internal model control (IMC), a conventional tuning approach, is utilized for a cascade control scheme that deals with adaptability in tuning [4]. Successive tuning is carried out for the cascade control loop, where the inner loop is tuned and pursued by the outer loop.

Fractional-order controller has proven useful for tuning the standard industrial controllers. [5] sketched a fractional-filter-based IMC-PID controller for an integer system. [6] proposed a delayed version of Bode’s ideal transfer function approach; however, in their work, the delay time of the system was not accounted for. A novel control strategy was suggested after the accountability of fractional IMC filter instead of conventional control [7]. Further, a PID controller in the fractional IMC context was introduced after accountability of dead-time, and inverse response compensator [8]. Higher-order approximation and higher-order fractional filter were used for controller design in the IMC structure [9]. After utilizing Bode’s ideal transfer function notion in the IMC framework, the robust fractional-order controller design was explained [10]. Recently, [11] proposed a new tuning method accounting for the system’s time delay. A fractional IMC controller with a sequential tuning method is used in the cascade scheme [12]. [13] proposed a fractional filter for multi-loop systems. The authors have used the fractional IMC approach for two degrees of freedom in their work. Based on frequency domain analysis, cascade fractional PI control was utilized for linear positioning [14]. Enhanced tuning of series cascade scheme for integrating process was used [3]. However, encountering the non-minimum phase (NMP) zeros, the tuning of controller settings becomes more complex.

In chemical processes industries, specific processes demonstrate their preliminary outcome in a reverse direction. That is due to the presence of NMP zeros, which leads to restricted gain margin and bandwidth. To ameliorate the effects of NMP zeros, an inverse response compensator can be embedded with the fractional IMC controller. That predicts the preliminary opposite outcome and delivers a counteractive signal to eliminate inverse response behavior [12]. [8] proposed a fractional-order controller for the non-minimum phase with a dead-time system. In their method, the fractional-filter parameters are tuned via conventional Bode’s ideal transfer function approach, where the NMP zeros are not considered.

Furthermore, optimizing a fractional-filter-based controller is challenging due to its presence of extra parameters. [15] used the PSO algorithm for minimization of integral square error (ISE). In [16], a BAT algorithm for optimizing the fractional-filter-based controller parameters is utilized. Further, Tabu search-based algorithm is used in [17] to optimize fractional-filter-based controller parameters.

The above literature validates that cascade arrangement with the fractional filter and Smith predictors are available. Further, the tuning of fractional-filter parameters via Bode’s ideal transfer function and their delayed version is also present in the literature. Conversely, no method exists to describe the fractional filter’s tuning after utilizing Bode’s ideal transfer function with non-minimum phase zeros. For this reason, it is worth developing a novel tuning approach for fractional-filter parameters after consideration of non-minimum phase zero. This paper develops a unified theory for tuning fractional-filter parameters for a more general case of the process involving NMP zeros. The contributions of this paper are:

• This manuscript develops a fractional-filter tuning approach for non-minimum phase systems by accounting for the inverse response compensator in the IMC paradigm.

• Further, a metaheuristic-based algorithm, i.e., search space reduction algorithm (SSR), is used to optimize the suggested controller settings for Integral Square Error (ISE) minimization.

The proposed method offers more advantages, i.e., setpoint filter prevention, and both controllers are structured to resemble IMC. Since the inverse response compensator is embedded with the outer loop controller, it requires only two controllers. Further, the Riemann sheet principle is used to know the system’s stability. The robustness of the suggested controller is validated via sensitivity investigation [18]. After combining all the features, the proposed controller shows a superior closed-loop response compared with other literature controllers.

The rest of the work is arranged as follows: Sect. 2 presents theoretical development, Sect. 3 covers SSR algorithm, case studies are presented in Sect. 4, and finally, Sect. 5 describes conclusion of the work.

2 Theoretical development

2.1 Series cascade control in IMC context

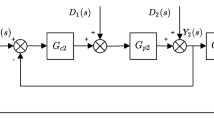
This manuscript deduces the inner loop with a stable pole and the outer loop with NMP zeros and a stable pole [19]. In series cascade control, the ill effect of the inner loop acts as input to the outer loop. In series cascade control, the outer loop results are posed through a manipulated variable and disturbances due to inner loop outcomes [1]. Figure 1 shows a series cascade scheme in the IMC framework after considering the inverse response compensator. Here, $K_{o}$, $K_{i}$ are the outer and inner loop controller transfer functions. $P_{o}$ and $P_{i}$ are the actual process and $\tilde{P}_{o}$, $\tilde{P}_{i}$ are model transfer functions of the outer and inner loop. $r_{1} (s)$, $d_{1} (s)$, $y_{1} (s)$ and $r_{2} (s)$, $d_{2} (s)$, $y_{2} (s)$ are the outer loop and inner loop input, disturbances, output [1]. The transfer function for the inner and outer loop is given as,

$$\begin{aligned} y_{2} (s)&= P_{i} (s)K_{i} (s)r_{2} +(1-P_{i} (s)K_{i} (s))d_{2}. \nonumber \\ y_{1} (s)&= P_{i} (s)K_{i} (s)P_{o} (s)( K_{o} (s)I_{o} (s) r_{1} (s)\nonumber \\&\quad +(1-P_{i} (s)K_{i} (s))) \nonumber \\&\quad (1-P_{i} (s)K_{i} (s)P_{o} (s)(K_{o} (s)I_{o} (s)d_{2}) \nonumber \\&\quad + ((1-P_{i} (s)G_{c_{2}} (s)P_{o} (s)K_{o} (s)I_{o} (s))d_{1} \end{aligned}$$

(1)

Fig. 1

Series cascade control in IMC paradigm

2.2 Bodes’ ideal transfer function

The idea of Bode’s ideal transfer function can be utilized for fractional-filter tuning [8]. It can be attributed as,

$$\begin{aligned} M(s) =\frac{1}{\delta s^{\alpha }}, \quad \alpha \in R, \end{aligned}$$

where $\delta$ and $\alpha$ are expressed as fractional-filter specifications. The Bode’s ideal transfer function unveils significant attributes, insensitive to gain deviations and steady phase margin. The fractional-filter parameters tuning expression is given [8],

$$\begin{aligned} \alpha =\frac{\pi - PM}{{\pi /2} } -1, \quad \delta =(\omega _{c} )^{-\alpha }. \end{aligned}$$

3 Design of controller

3.1 Proposed tuning expression

Bode’s ideal transfer function is modified to tune the fractional-filter parameters of the outer loop controller of series cascade control. After modification, the expression for tuning the fractional filter becomes,

$$\begin{aligned} \alpha =\frac{\frac{\pi }{2} -PM}{\frac{\pi }{2}} \quad \delta =\frac{\sqrt{1+\omega _{c} {}^{2} c^{2} } }{(\omega _{c} )^{\alpha +1}}. \end{aligned}$$

(2)

Procedure for adaptation

In this work, Bode’s ideal transfer function with NMP zero can be written as,

$$\begin{aligned} M'(s)=\frac{(1-cs)}{\delta s^{\alpha }}. \end{aligned}$$

(3)

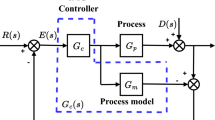
From Fig. 2, the conventional feedback controller is represented as,

$$\begin{aligned} K(s)=H_{r} (s)K_{c} \left( 1+\frac{1}{T_{I} s} +T_{D} s\right) , \end{aligned}$$

where $H_{r} (s)$ is the fractional–filter and the remaining part is the PID controller.

Fig. 2

Traditional control system

Three conditions to be fulfilled by the controller K(s) are as follows [6],

Condition 1: Phase margin conditions: $Arg(K(j\omega _{c} )$$P(j\omega _{c} ))=-\pi +PM$.

Condition 2: Gain cross-over frequency conditions $|K(j\omega _{c})$$P(j\omega _{c})|=1$.

Condition 3. Cancelation of the steady-state error.

When the $M'(s)$ is selected via Eq. (3), then the controller K(s) can satisfy the phase margin (PM) and gain cross-over frequency. Furthermore, PM and gain cross-over frequency can be calculated analytically via Eq. (12). However, if P(s) contains NMP zero and $M'(s)$ chosen via Eq. (3), then the controller K(s) can satisfy precisely the phase margin (PM) and gain cross-over frequency. This expression shows the uniqueness of the work. The following process is used to achieve the fractional-filter parameters $\delta , \alpha$.

• 1 Substituting $s=j\omega _{c}$ in Eq. (3), we have

  $$\begin{aligned} M'(j\omega _{c} )=\frac{(1\mathrm {-}cj\omega _{c} )}{\delta (j\omega _{c} )^{\alpha +1} }. \end{aligned}$$

  (4)

• 2 Now taking the argument on both sides of Eq. (4) and following condition 1, we get

  $$\begin{aligned} 2\pi \mathrm {-}\frac{\pi }{2} \mathrm {-}\frac{\alpha \pi }{2} =\mathrm {-}\pi +PM. \end{aligned}$$

  (5)

• 3 On simplifying Eq. (5), the expression of $\alpha$ can be written as,

  $$\begin{aligned} \alpha =\frac{\frac{\pi }{2} \mathrm {-}PM}{\frac{\pi }{2} }. \end{aligned}$$

  (6)

• 4 Additionally, taking the modulus of Eq. (4), we have

  $$\begin{aligned} |M'(j\omega _{c} )|=\frac{\sqrt{1+\omega _{c} {}^{2} c^{2} } }{\delta (\omega _{c} )^{\alpha +1}}. \end{aligned}$$

  (7)

• 5 Considering condition 2, Eq. (7) can be written as,

  $$\begin{aligned} 1=\frac{\sqrt{1+\omega _{c} {}^{2} c^{2} } }{\delta (\omega _{c} )^{\alpha +1} }. \end{aligned}$$

  (8)

• 6 Subsequently, On simplifying Eq. (8), the time constant $\delta$ is achieved as

  $$\begin{aligned} \delta =\frac{\sqrt{1+\omega _{c} {}^{2} c^{2} } }{(\omega _{c} )^{\alpha +1} }. \end{aligned}$$

  (9)

3.2 Controller design

In this section, a generalized controller is designed by utilizing the proposed tuning approach,

(a) Inner loop controller design: consider the first-order process model,

$$\begin{aligned} \tilde{P}_{i} (s)=\frac{k_{2} }{(Ts+1)}. \end{aligned}$$

Here, the system model is segregated into minimum phase part $\tilde{P}_{i}^{-} (s)=\frac{k_{2} }{Ts+1}$ and non-minimum phase part $P_{i}^{+} (s)=1$. Notably, the controller can be reported in the IMC paradigm as [19],

$$\begin{aligned} K_{i} (s)=\frac{f(s)}{P_{i}^{-} (s)}. \end{aligned}$$

Now utilize the IMC procedure for inner loop controller design,

$$\begin{aligned} K_{i} (s)=\frac{Ts+1}{k_{2} (\psi s+1)}. \end{aligned}$$

(10)

Here, $\psi$ is the tuning parameter, which can be tuned via maximum sensitivity$M_{s}$ [1].

$$\begin{aligned} \psi =\frac{\mathrm {-}1.508\mathrm {-}0.451M_{s} }{1.45M_{s} \mathrm {-}1.508} L'. \end{aligned}$$

where $L'$ depicts the time delay.

(b) Design of outer loop controller: An integrating process with NMP zero has been considered to construct the outer loop controller in the IMC paradigm with fractional filter and inverse response compensator. The control strategy is demonstrated in Fig. 3,

$$\begin{aligned} \tilde{P}_{o} (s)=\frac{k_{1} (1\mathrm {-}cs)}{s}. \end{aligned}$$

Since in series cascade control, the consequence of inner loop function act as an input to the outer loop. Thus, it can be written as,

$$\begin{aligned} P'(s)=H_{io} (s)P_{o} (s), \end{aligned}$$

(11)

where $H_{io}$ interprets the outcome of the inner loop given by,

$$\begin{aligned} H_{io} =\frac{K_{i} (s)P_{i}^{} (s)}{1+K_{i} (s)(P_{i} (s)-\tilde{P}_{i} (s))}. \end{aligned}$$

From Eq. (11), the overall controller transfer function becomes,

$$\begin{aligned} \tilde{P}'(s)=\frac{k_{i} (1\mathrm {-}cs)}{s(\psi s+1)}. \end{aligned}$$

(12)

Fig. 3

Controller with inverse response compensator in IMC paradigm

Fig. 4

Non-minimum phase version of Bode’s ideal transfer function

From Figure (3) and (4), the controller transfer function can be accomplished after utilization of equivalent system notion,

$$\begin{aligned} M'(s)=\frac{K_{o} (s)P'(s)}{1+K_{o} (s)I_{o} (s)}. \end{aligned}$$

(13)

After modifying Eq. (13), the generalized structure of the proposed controller becomes,

$$\begin{aligned} K_{o} (s)=\frac{M'(s)}{P'(s)\left[ 1\mathrm {-}M'(s)I_{o} (s)\right] } \end{aligned}$$

(14)

In this work, the inverse response compensator $I_{o} (s)=\eta sP'(s)$, $\eta \ge b$ is the indication that reaches the controller, so it appears to be from a typical system. The inverse response behavior and response compensator stipulate a corrective signal. This work utilizes $\eta =2b$ for the minimum mean square deviation of plant output from the desired setpoint. After substituting $I_{o} (s)$ (3) and (12) into (14), (14) can be modified as,

$$\begin{aligned} K_{o} (s)=\frac{s^{1-\alpha } }{\left[ \delta +2c^{2} s^{2-\alpha } -2cs^{1-\alpha } \right] }. \end{aligned}$$

(15)

Fig. 5

General procedure of proposed method

Figure 5 demonstrates the general procedure of proposed method after consideration of NMP zero. For further implementation, we can change the system with same tuning method.

4 Overview of search space reduction algorithm

Fig. 6

Structural outline of SSR algorithm

An innovative metaheuristic algorithm, i.e., search space reduction (SSR) algorithm, is described. In SSR, unlike other algorithms, the solution is updated randomly with reduced search space in each iteration [20]. Whereas in other algorithms, the solution updated for the next iteration depends on the current iteration solution. An artificial bee colony (ABC) optimization algorithm for FOPID tuning was proposed for cascade control arrangement [21], which results in premature convergence. The SSR algorithm promotes the exploration and exploitation capability of the algorithm by systematically reducing the search space in each. The flowchart of the SSR algorithm is demonstrated in Fig. 6. The implementation of the SSR algorithm has the following basic steps:

• 1. Search agents initialization randomly.

• 2. Calculating the objective function.

• 3. Outcome the paramount result accomplished so far.

• 4. Evaluate novel intermediate points for eliminating the search space.

• 5. Eliminating search space.

• 6. Producing novel search agents in the restructured search space.

Accomplishing the preliminary search range: Equation (16) interprets the upper bound (ub) and lower bound(lb) at $t'\!=\!\!1$,

$$\begin{aligned} m(t')=\frac{ub\mathrm {-}lb}{2}. \end{aligned}$$

(16)

Here, Eq. (16) observes that search agents are within limits. If Eq. (16) yield the search agents away from the original bounds ub, lb. It can be written as,

$$\begin{aligned} X'_{i} (t')=lb+(lb\mathrm {-}ub)\times rand_{o}. \quad if X'_{i} <lb \quad or X'_{i} >ub \end{aligned}$$

(17)

Calculating the midpoint: utilizing Eq. (18), the midpoint evaluation can be accomplished based on the paramount solution M.

$$\begin{aligned} mid_{o} (t')=mean(X'_{bestM} ). \end{aligned}$$

(18)

For an illustration, if the user selects $M=2$ the three universal paramount positions will be $X'_{gbest1}$, $X'_{gbest2}$, correspondingly,

$$\begin{aligned} mid_{o} (t')=\frac{X'_{best1} +X'_{best2} }{2}. \end{aligned}$$

Modifying the search range: According to Eq. (19), the search range $m'$ is reduced through the iterations,

$$\begin{aligned} m'(t)=m'(t'\mathrm {-}1)\times e^{({\mathrm {-}R_{f}\big /t'_{\max } )}}. \end{aligned}$$

(19)

Reformation of search agents: The resulting iteration is restructured nearby the intermediate point via updated search agent shown in Eqs. (20) and (21),

$$\begin{aligned}{} & {} X'_{i} (t')=mid'(t')+rand'\times m'(t''). \quad if \quad rand'>=0.5.\nonumber \\ \end{aligned}$$

(20)

$$\begin{aligned}{} & {} X'_{i} (t')=mid'(t)\mathrm {-}rand'\times m'(t'). \quad if \quad rand'<=0.5.\nonumber \\ \end{aligned}$$

(21)

Figure 7 establishes the recommended controller tuning process with the SSR algorithm. Here, the PI and PID controller parameters are indicated directly in the system parameters. The outcome of the filter parameters $\delta$, $\alpha$ is adapted through the SSR algorithm.

Fig. 7

FOIMC controller with SSR algorithm

5 Case studies

To assess the endorsed arrangement, two case studies are evaluated to determine the worth of recommended strategy for nominal and + 20% model mismatch.

5.1 Case Study 1

A higher-order system configuration transfer function is endorsed [22], given by

$$\begin{aligned} P(s)=\frac{0.5(1\mathrm {-}0.5s)e^{\mathrm {-}0.7s} }{s(0.5s+1)(0.4s+1)(0.1s+1)}. \end{aligned}$$

Since the delay time is minimal, we are considering it negligible. Afterward, a higher-order process is approximated as [22]

$$\begin{aligned} \tilde{P}_{o} (s)=\frac{(1-0.4699s)}{s},\tilde{P}_{i} (s)=\frac{0.5183}{1.1609s+1}. \end{aligned}$$

• a) The strategy of inner loop controller: The IMC paradigm (10) is used to evaluate the inner loop controller. As a result, we have

  $$\begin{aligned} K_{i} (s)=\frac{1.1609s+1}{0.5183(4s+1)}. \end{aligned}$$

  Now utilizing Eq. (12) to obtain the overall plant transfer function becomes,

  $$\begin{aligned} \tilde{P'}(s)=\frac{(1\mathrm {-}0.4699s)}{s(4s+1)} \end{aligned}$$

  (22)

• b) Outer loop controller design: After following the Eq. (15), the proposed controller transfer becomes,

  $$\begin{aligned} K_{o} (s)=\frac{s^{0.06} }{1.1+0.44s^{1.06} \mathrm {-}0.93s^{0.06} } \left( 1+\frac{0.25}{s} \right) , \end{aligned}$$

  (23)

where the fractional filter is$\frac{s^{0.06} }{1.1+0.44s^{1.06} \mathrm {-}0.93s^{0.06} }$ with $\delta =1.1$, $\alpha =0.94$, $\psi =4$ and $PM=65$.

Fig. 8

Closed-loop response of higher-order integrating process

Figure 8 demonstrates a comparative investigation among the suggested controller and two other controller structures [22, 23]. The disturbance of magnitude 0.15 at t = 50 is given to each control loop resulting from the suggested and two existing controllers. The essential settling time is less than existing controllers, which reveals the worth of the proposed technique. Figure 8a unveils that the suggested controller exhibits the minimum peak of overshoot and undershoot for the nominal case. The nominal case means the process transfer function does not account for process parameter variations. A related technique is assumed for the + 20% plant parameter variations. The consequential mismatch model is,

$$\begin{aligned} P'^{20} (s)=\frac{(1\mathrm {-}0.56s)}{1.20s(4.8s+1)}. \end{aligned}$$

The proposed controller depicts significant improvement even after + 20% mismatch, see Fig. 8b. The controller performance indices and transient response are listed in Table 1. Table 1 reveals less IAE, less ISE, less overshoot values for the suggested controller for the nominal case and a + 20% divergence case.

Table 1 Performance interpretation for higher-order system configuration

Stability Analysis:

The Riemann sheet is used for the stability investigation of fractional-order closed-loop response. Notably, the stability of the suggested fractional filter after accountability of the closed-loop system can be achieved via the notion of the fractional characteristic polynomial. Here, MATLAB FOMCON toolbox is used to determine the stability analysis [24]. The endorsed closed-loop setup of a fractional characteristic polynomial is given as,

$$\begin{aligned} f(s)=1+\delta s^{\alpha } +2c^{2} s^{2} \mathrm {-}2cs. \end{aligned}$$

The closed-loop setup of the fractional characteristic polynomial for the system is as reported,

$$\begin{aligned} f(s)=1+1.1s^{0.94} +0.44s^{2} \mathrm {-}0.93s. \end{aligned}$$

However, the analysis of roots of fractional order is problematic. Thus, we presented the mapping of a plane related to an equivalent specific polynomial. Select $\lambda =s^{\gamma }$. The related characteristic polynomial is,

$$\begin{aligned} f(\lambda ^{{1 \big / \gamma } } )=1+1.1\lambda ^{940} +0.44\lambda ^{2000} \mathrm {-}0.93\lambda ^{1000}. \end{aligned}$$

where $s^{0.001} =\lambda$. The graphical illustration of stability analysis is presented in Fig. 9. For the stability investigation, all the roots should lie outside of the principal surface of the Riemann sheet. The system reveals instability if roots are presented inside the principal sheet; however, it is clear from Fig. 9 that all the roots lie outside the principal sheet. Thus, confirming that the system is stable.

Fig. 9

Stability investigation of higher-order integrating process

Robustness analysis:

The robustness is tested effectively via sensitivity investigation under plant mismatch and input disturbances. This deviation disturbs the stability margin and robustness[8]. The sensitivity function is represented by,

$$\begin{aligned} S(s)=\frac{1}{1+P'(s)K_{o} (s)}. \end{aligned}$$

(24)

For the graphical illustration of robustness, substituting plant and controller transfer function value from Eq. (22), (23) into (24). The graphical description of the sensitivity function of the suggested controller and the other two controllers is given in Fig. 10a. The proposed controller has the least amplification for the frequency range $\omega >\omega _{cr}$. The disturbances with frequencies outside the frequency $\omega _{cr}$ are comparatively less improved in the suggested method than other controllers. Additionally, the minimum value $S_{\max }$ demonstrates improved stability margin for the proposed controller. That confirms the enhanced robustness of the proposed method as subject to input disturbances and process parameter variations. Figure 10b reveals that after a + 20% mismatch, the proposed controller shows a minimum jump compared to the existing controller.

Fig. 10

Robustness analysis of suggested method

Convergence: The objective function convergence is shown in Fig. 11. The actual universal paramount location has also been relocated from source for nearly the position to display the efficacy of the SSR algorithm.

More prominently, the achieved value of the controller setting has been optimized via the SSR algorithm. The assessment consequences illustrate that the suggested algorithm displays reasonable consideration and manipulation experiences. The parameters descriptions are listed in Table 2. Figure 12 exhibits a comparative study between the suggested controller structure and two other controller structures [22, 23] after utilizing the SSR algorithm. Figure 12a and b illustrates that after optimization the suggested method demonstrates good jump in results for nominal case and + 20% mismatch case.

Remark 1

For the same set of parameters, recommended procedure is compared with [23] and [22] since the system structure involves NMP zero which shows the inverse response behavior. In [23] and [22], higher-order model approximations and setpoint filters were used, but an essential component inverse response compensator was absent. No optimization algorithm has been used to obtain optimal controller settings. In this manuscript, an inverse response compensator is embedded with a fractional-filter-based IMC controller. More importantly, a modified tuning approach has been utilized to compensate for inverse response behavior. The avoidance of setpoint filters has also been revealed. The SSR algorithm has been used for all three controllers for fare comparison. After implementing the SSR algorithm, the suggested controller shows a good jump in results.

Fig. 11

Convergence curve of the objective function

Table 2 Parameters of SSR algorithms

Fig. 12

Closed-loop response via SSR algorithm

Fig. 13

Relative investigation of the suggested approach

5.2 Case study 2

An example of a boiler drum level is adopted, which shows inverse response behavior. For controlling drum level, the influence of the feed water is used. The boiler drum level transfer function has been endorsed [8],

$$\begin{aligned} \tilde{P}_{o} (s)=\frac{(1\mathrm {-}0.418s)}{s},\tilde{P}_{i} (s)=\frac{0.547}{1.06s+1}. \end{aligned}$$

• a) Inner loop controller design: After the utilization of the IMC scheme, the inner loop controller is designed via Eq. (10),

  $$\begin{aligned} K_{i} (s)=\frac{1.060s+1}{0.547(3.5s+1)}. \end{aligned}$$

  Now utilizing Eq. (12), the overall plant transfer function becomes,

  $$\begin{aligned} \tilde{P'}(s)=\frac{(1\mathrm {-}0.418s)}{s(3.5s+1)}. \end{aligned}$$

  (25)

• b) Outer loop controller design: After following Eq. (15), the proposed controller transfer becomes,

  $$\begin{aligned} K_{o} (s)=\frac{s^{0.23} }{1.2+0.34s^{1.23} \mathrm {-}0.83s^{0.23} } \left( 1+\frac{0.28}{s} \right) , \end{aligned}$$

  (26)

  where the fractional filter is $\frac{s^{0.23} }{1.2+0.34s^{1.23} -0.83s^{0.23} }$ with $\delta =1.2$, $\alpha =0.77$, $\psi =3.5$ and $PM=72$.

Table 3 Performance assessment and transient outcome for boiler drum level

Fig. 14

Stability investigation of boiler drum level

Fig. 15

Robustness analysis of proposed method

The step response for boiler drum level with an amplitude of 0.15 at t=20 s is demonstrated in Fig. 13a. It is demonstrated that initially the closed-loop response attains undershoot after that it shows the overshoot. In terms of boiler drum level, if the flow rate of clod feed water is increased by a step, the total volume of the boiling water and consequently liquid level will decrease for short period then it will start increasing. Further, the suggested method is compared with two existing methods [8] and [25]. Figure 13a illustrates that recommended controller has improved the outcome in the nominal case. After adaptability of the + 20% system parameter variation, the process transfer function becomes,

$$\begin{aligned} P'^{20} (s)=\frac{(1\mathrm {-}0.50s)}{1.2(4.2s+1)}. \end{aligned}$$

Figure 13b illustrates that after a + 20% mismatch, the suggested controller shows an adaptable outcome in contrast to the available controller. Table 3 displays less IAE, ISE and overshoot.

Fig. 16

Convergence graph of ISE objective function

Fig. 17

Comparative analysis of SSR algorithm

Stability Examination

This section is revealed the stability analysis of the boiler drum level. It is given as,

$$\begin{aligned} f(s)=1+1.2s^{0.77} +0.34s^{2} \mathrm {-}0.83s. \end{aligned}$$

Since the computation of roots of fractional-order characteristics becomes complex, we used mapping of the associated plane with a fractional characteristic polynomial. Select $\lambda =s^{\gamma }$ The linked characteristic polynomial is written as,

$$\begin{aligned} f(\lambda ^{{1 \big / \gamma }} )=1+1.2\lambda ^{770} +0.34\lambda ^{2000} \mathrm {-}0.83\lambda ^{1000}. \end{aligned}$$

where $s^{0.001} =\lambda$

Figure 14 shows the graphical illustration of the associated natural degree quasi-characteristic polynomial. The roots of the natural degree quasi-characteristic polynomial lie “greater” inside the principal sheet of the Riemann surface that implies the stability of the system.

Robustness analysis

The restricted attributes of the linear feedback scheme diverge with plant parameters deviations and input disturbances. This divergence upsets the stability margin and robustness. The robustness can be adeptly found via sensitivity analysis, for the graphical illustration of robustness substituting plant and controller transfer function value from Eqs. (25), (26) into (24). Figure 15 illustrates sensitivity analysis for nominal and + 20% mismatch cases. Figure 15a and b shows the existing controller’s relative robustness. The paramount absolute sensitivity is a better performance measure of robustness, while complimentary of sensitivity function shows stability margin. The recommended structure offers the minimum value of sensitivity function.

Convergence

More importantly, the accomplished value of the controller setting has been optimized via the SSR algorithm. Figure 16 shows the convergence graph. This algorithm explains the better significances of the residual algorithms in the literature. The illustration of the SSR algorithm displays reasonable consideration and manipulation. Figure 16 shows the convergence curve of the ISE objective function. Figure 16 displays that particle movement settles down after a particular iteration.

After optimizing the SSR algorithm, Fig. 17 shows a comparative investigation among the recommended controller arrangement and two other controller arrangements [8, 25]. Figure 17a and b illustrates that after optimizing the SSR, the algorithm suggested method, a good jump in results for nominal and + 20% mismatch cases are confirmed.

Remark 2

To examine the efficacy of the suggested method, a comparative investigation has been performed with [3] and [25]. In [8], a setpoint filter was used for overshoot compensation and optimization of controller setting was also absent. Further, in [25], inverse response compensator and controller setting optimization were lacking. In this manuscript, an inverse response compensator has been used and prevention of setpoint filter was also shown. The SSR optimization algorithm was implemented for all three controller settings for fare comparison.

6 Conclusion

In this manuscript, a novel tuning method is proposed that contributes to the combination of inverse response compensator and fractional filter to limit the undershoot and refine the overall consequence in non-minimum phase system. An improved version of Bode’s ideal transfer function approach is proposed for tuning of fractional-filter parameters. Further, to make the inner and outer loop controller design simple, the internal model control (IMC) paradigm is used for both the loops. No extra controller and setpoint filter are used for inverse response compensation and overshoot minimization. The optimal value of the controller setting is accomplished via the search space reduction (SSR) algorithm. The stability of the suggested controller is carried out via the Riemann surface. The robustness of the proposed controller structure is validated via sensitivity analysis. The recommended controller is implemented for two practical non-minimum phase systems and performs better than other controllers under nominal and mismatch conditions.