A new fractional order controller tuning method based on Bode’s ideal transfer function

Abstract

A new tuning method for Fractional Order Controllers (FOC) based on Bode’s ideal transfer function as a reference model is proposed in this paper. The proposed fractional order controller parameters are obtained by a simple tuning technique in two steps. In the first step, the open loop reference fractional integrator is designed according to the desired performances, and then approximated by a rational transfer function using Charef’s or Oustaloup’s approximation method. In the second step, a standard pole placement technique is used to align each pole of the plant transfer function with the nearest one of the Rational Function Approximation (RFA). The FOC transfer function is then obtained by gathering the remained poles and zeros of the RFA. The most innovative character of the proposed method is its simplicity and its remarkable performances in terms of robustness towards the variation of the static gain. Simulation of some illustrative examples confirms and validates the proposed method.

1 Introduction

In recent years, fractional calculus (FC) has become an important tool in many areas of science and engineering such as mathematical modeling, identification and control theory [1,2,3,4,5]. In control theory, the fractional calculus and its applications leads to fractional order controllers, e.g., CRONE control (French abbreviation for Commande Robuste d’Ordre Non Entier) [6, 7], Fractional PI$^\lambda$D$^\mu$ control [8,9,10] and Robust Fractional Adaptive Control [11,12,13].

Nowadays, tuning of fractional controllers becomes one of the most interesting topics for many researchers in the literature. Along these topics many tuning techniques were developed. Among them, optimization based tuning and reference model-based tuning where the open-loop is given by the so-called Bode’s ideal transfer function or fractional order integrator [14, 15], thanks to its best characteristic in terms of robustness ensured by its iso-damping property [16, 17]. In several of these methods authors have reported many acceptable results in numerous works and review articles.

Djouambi et al. [15] have proposed a simple technique to design fractional order controllers using the Bode’s ideal transfer function as a reference model of the open-loop transfer function. However, the author assumes that the process must be stable and not oscillatory. Therefore, in this paper, a generalization of the above method is proposed to the case where no assumption on the stability conditions is needed for any minimum phase systems.

The remainder of this paper is organized as follows. Section 2 presents a summary review of fractional order systems, fractional order integrator with their rational approximation. Section 3 presents the proposed tuning method to design a robust fractional order controllers. Simulation results are validated with illustrative examples in the Sect. 4. Finally, conclusion is given in Sect. 5.

2 Brief review of fractional calculus

A commonly used definition of the fractional integration is the Riemann–Liouville definition [11],

$$\begin{aligned} D^{-\alpha }f(t)=\frac{1}{\Gamma (\alpha )}\int ^{t}_{0}(t-\zeta )^{\alpha -1}f(\zeta )d(\zeta ) \end{aligned}$$

(1)

where $\Gamma (.)$ is the Gamma function and $\alpha$ is the fractional order integrator. Laplace transform is another useful tool for both the system analysis and the controller synthesis. The Laplace transform of Eq. (1), under zero initial conditions is,

$$\begin{aligned} L\left\{ D^{-\alpha }f(t)\right\} = s^{-\alpha }F(s) \end{aligned}$$

(2)

where F(s) is the Laplace transform of f(t).

A more general differential equation structure of fractional order systems can be expressed by,

$$\begin{aligned} \sum ^{N}_{i=1} a_i D^{\alpha _i}y(t) = \sum ^{M}_{j=1} b_j D^{\beta _j}u(t) \end{aligned}$$

(3)

where D is the derivative operator, $(\alpha _i, \beta _j ) \in R^2$ and $(a_i, b_j) \in R^2$.

2.1 Bode’s ideal transfer function

The well-known Bode’s ideal transfer function (BITF) or fractional order integrator is an irrational function given by [18],

$$\begin{aligned} \frac{1}{\left( \frac{s}{\omega _u}\right) ^\alpha } \end{aligned}$$

(4)

where $1<\alpha <2$ and $\omega _u$ is the unity gain crossover frequency.

The Bode plot of this function is characterized by a constant magnitude slope of $-\,20 \alpha$ and a constant phase of $-\,\alpha \pi /2$. The phase margin depends only on the fractional order $\alpha$ and is given by $\phi _m = \pi (1-\alpha /2)$.

The major advantage achieved through this structure is iso-damping, i.e. overshoot being independent of the system gain. Therefore, the use of the BITF as a reference model in control loop is one of the most promising applications of fractional calculus in control theory.

2.2 Charef’s approximation of fractional order integrator

In a given frequency band of interest $[\omega _l, \omega _h]$, Eq. (4) can be written as a Fractional Power Pole (FPP) form, given by [19],

$$\begin{aligned} L(s) \approx \frac{{L_0}}{\left( \frac{s}{\omega _c} +1\right) ^\alpha } \end{aligned}$$

(5)

with $1< \alpha < 2$.

where $\omega _c<< \omega$ for $\omega \in [\omega _l, \omega _h]$, such that $\omega _c = 0.1 \omega _l$ and ${L_0} = \left( \frac{\omega _u}{\omega _c} \right) ^\alpha$.

Using the so-called singularity function (Charef’s approximation method) presented in [19], Eq. 5) can be approximated by a rational function with a specified error y in dB in the frequency band of interest $[\omega _c, \omega _{max}]$ where $\omega _{max} = 10 \omega _h$,

$$\begin{aligned} L(s)=\,\approx \frac{{L_0}}{\left( \frac{s}{\omega _c} +1\right) ^\alpha } \approx {L_a(s)} \approx {L_0} \frac{\prod ^{N-1}_{i=0}\left( 1 + \frac{s}{z_i}\right) }{\prod ^{N}_{i=0}\left( 1 + \frac{s}{p_i}\right) } \end{aligned}$$

(6)

The poles and the zeros of (6) are given as,

$$\begin{aligned} p_{i}=p_0 (ab)^{i}\quad i=1,2,3,\ldots , N \end{aligned}$$

(7)

with $p_0 = \omega _c\sqrt{b}$, and

$$\begin{aligned} z_{i}=z_0 (ab)^{i}\quad i=1,2,3,\ldots , N-1 \end{aligned}$$

(8)

with $z_0 = a p_0$, where, $a=10^{\frac{y}{10(1-\alpha )}}$, $b=10^{\frac{y}{10\alpha }}$ and

$$\begin{aligned} N= Integer\; part\; of\ \left[ \frac{log(\frac{\omega _{max}}{p_{0}})}{log(ab)}\right] +1. \end{aligned}$$

(9)

3 The proposed fractional order controller structure

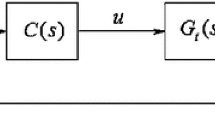
Let’s consider the unity feedback system represented in Fig. 1, where, C(s) is the fractional order controller and $G_p (s)$ is a minimum phase plant’s transfer function given by,

$$\begin{aligned} G_p (s) = K_0 \frac{\prod ^{m}_{i=0}\left( 1 + \frac{s}{z_i}\right) }{\prod ^{n}_{i=0}\left( 1 + \frac{s}{p_i}\right) } \end{aligned}$$

(10)

where $K_0$ is a constant and $m<n$. The open loop of the feedback control system Fig. 1 is given by,

$$\begin{aligned} G(s) = C(s) G_p (s) \end{aligned}$$

(11)

Fig. 1

Closed loop control system with Bode’s ideal transfer function

To ensure the iso-damping property for the control system, G(s) must be close to the Bode’s ideal transfer function (4) (see [2, 20]).

$$\begin{aligned} G(s) \approx \frac{1}{\left( \frac{s}{\omega _u}\right) ^\beta } \quad with\; 1<\beta <2 \end{aligned}$$

(12)

The proposed tuning method comprises two steps. In the first step, the open loop reference fractional integrator (12) must be approximated by a rational transfer function $G_a (s)$. Using the Charef’s approximation method, the approximation $G_a (s)$ can be given in the frequency band of interest $[\omega _c, \omega _{max}]$ by,

$$\begin{aligned} G(s)= & {} \frac{1}{\left( \frac{s}{\omega _u}\right) ^\beta } \approx \frac{K_1}{\left( \frac{s}{\omega _c} + 1\right) ^\beta } \\ \nonumber&\approx G_a (s) \approx K_1 \frac{\prod ^{N-1}_{i=0}\left( 1 + \frac{s}{z_i}\right) }{\prod ^{N}_{i=0}\left( 1 + \frac{s}{p_i}\right) } \end{aligned}$$

(13)

where N is given by (9), $(p_i, z_i) \in (R^+)^2$.

In the second step, a standard pole placement technique is used to align each pole of the plant transfer function (10) with the nearest one of the rational transfer function approximation (13). The obtained closed-loop feedback control system is illustrated in Fig. 2.

Fig. 2

Closed loop control system with pole placement algorithm

Hence, the open loop transfer function can be given by,

$$\begin{aligned} G_a(s) = C(s) \left( \frac{K G_p(s)}{1 + K G_p(s)}\right) = C(s) \times G^{'}_p(s) \end{aligned}$$

(14)

where, $G^{'}_p(s)$ represents the compensated plant transfer function.

The transfer function of the FOC system is then obtained by gathering the remained poles and zeros of the rational transfer function approximation.

$$\begin{aligned} C(s) = \left( \frac{1}{G^{'}_p(s)}\right) \times K_1 \frac{\prod ^{N-1}_{i=0}\left( 1 + \frac{s}{z_i}\right) }{\prod ^{N}_{i=0}\left( 1 + \frac{s}{p_i}\right) } = \frac{G_a(s)}{G^{'}_p(s)} \end{aligned}$$

(15)

So that, the zeros of $I_1$ will be compensated by some poles of $I_2$.

In the proposed design method, C(s) is supposed to be causal. This means that the relative degree $N_r$ between the denominator and the numerator of C(s) must be positive or equal zero. If C(s) is not causal, which corresponds to $N_r$ negative then, at least $N_r$ poles located outside the band $[\omega _c, \omega _max]$ can be added to C(s) to guarantee the causality. Thus, the controller C(s) will be given by,

$$\begin{aligned} C(s) = \left( \frac{K_1}{G^{'}_p(s)}\right) \times \frac{\prod ^{N-1}_{i=0}(1 + \frac{s}{z_i})}{\prod ^{N}_{i=0}\left( 1 + \frac{s}{p_i}\right) } \times \frac{1}{\prod ^{N_r}_{i=0}\left( 1 + \frac{s}{p_{ci}}\right) } \end{aligned}$$

(16)

where,

$$\begin{aligned} p_{ci} = p_0 (ab)^i, \ i = N+1,\dots N+N_r \end{aligned}$$

(17)

with $p_0 = \omega _c \sqrt{b}$.

4 Illustrative examples

In this section, we will give different simulation examples to illustrate the effectiveness of the proposed control strategy.

4.1 Example 1

As a first example, let’s consider the transfer function of the plant $G_p (s)$ given by [15],

$$\begin{aligned} G_p (s) = \frac{K_n \; (1 + s/50)}{s(1+s)(1+s/10)(1+s/100)} \end{aligned}$$

(18)

where $k_n = 1$ is the gain nominal value.

The specifications of the design are,

• Phase margin $= 62^{\circ }$;

• Unity gain crossover frequency $\omega _u = 5$ rad/s.

To achieve these specifications in a frequency range $[\omega _l, \omega _h ] = [0.1 \omega _u, 10 \omega _u] =$ [0.5 rad/s, 50 rad/s] around $\omega _u$.

According to the design specifications, the open loop transfer function (12) must be,

$$\begin{aligned} G(s) = \frac{1}{(s/5)^{1.3}} \end{aligned}$$

(19)

Using the Charef’s method discussed above, the open loop transfer function G(s) is approximated to, $G_a (s)$ can be decomposed as,

$$\begin{aligned} G_a (s) \approx \frac{1769.9\;(s+0.1456)(s+0.7543)(s+3.907)(s+20.24)(s+104.8)(s+542.9)}{(s+0.08891)(s+0.05)(s+0.4605)(s+2.385)(s+12.35)(s+63.99)(s+331.4)(s+1717)} \end{aligned}$$

(20)

$$\begin{aligned} G_a (s) = G_1 (s) \times G_2 (s) \end{aligned}$$

(21)

with,

$$\begin{aligned} G_1 (s) = \frac{1}{(s+0.05)(s+0.4605)(s+12.35)(s+63.99)} \end{aligned}$$

(22)

$$\begin{aligned} G_2 (s) = \frac{1769.9(s+0.1456)(s+0.7543)(s+3.907)(s+20.24)(s+104.8)(s+542.9)}{(s+0.08891)(s+2.385)(s+331.4)(s+1717)} \end{aligned}$$

(23)

and, where, $G_1 (s)$ arranges the poles of $G_a (s)$ that are close to the poles of the original process $G_p (s)$, and $G_2 (s)$ contains the remaining poles and zeros of the approximation $G_a (s)$.

Now, using the pole placement algorithm (state feedback $u=-\,Kx$), the process poles ($s=0$, $s=-\,1$, $s=-\,10$ and $s=-\,100$) are adjusted to be aligned respectively with the poles of the transfer function $G_1 (s)$ ($s=-\,0.05$, $s=-\,0.4605$, $s=-\,12.35$, and $s=-\,63.99$). Using MATLAB Control Toolbox then, the state feedback gain matrix K can obtained as,

$$\begin{aligned} K=[-\,34.1495\; -\,280.7289\; -\,594.8061\; 18.1961] \end{aligned}$$

(24)

Hence, the new obtained transfer function of the adjusted process $G^{'}_p(s)$ is given as,

$$\begin{aligned} \nonumber G^{'}_p(s)= & {} \frac{20\;(s+50)}{(s+0.05)(s+0.4605)(s+12.35)(s+63.99)}\\= & {} 20\; (s + 50)\; G_1 (s) \end{aligned}$$

(25)

As we can see, the poles of the adjusted process $G^{'}_p(s)$ in the Eq. (21) are now aligned and covered in the transfer function of $G_a (s)$ in the Eq. (20).

Thus, the controller transfer function C(s) can be obtained from Eq. (15) as,

$$\begin{aligned} C(s) = \frac{G_a (s)}{G^{'}_p(s)} = \frac{G_1 (s) \times G_2 (s)}{20\; (s+50) G_1 (s)} \end{aligned}$$

(26)

$$\begin{aligned} C(s) \approx \frac{1769.9(s+0.1456)(s+0.7543)(s+3.907)(s+20.24)(s+104.8)(s+542.9)}{20(s+50)(s+0.08891)(s+2.385)(s+331.4)(s+1717)} \end{aligned}$$

(27)

thus, From (22) we can see that C(s) is not causal with $N_r = 1$. Thus, at least one pole should be added to the transfer function C(s). Using (17) the additional pole is,

$$\begin{aligned} S_r = p_0 (ab)^9 = 8891. \end{aligned}$$

Finally, the proper controller transfer function is,

$$\begin{aligned} C(s) \approx \frac{1769.9(s+0.1456)(s+0.7543)(s+3.907)(s+20.24)(s+104.8)(s+542.9)}{20(s+50)(s+0.08891)(s+2.385)(s+331.4)(s+1717)(s+8891)} \end{aligned}$$

(28)

Figure 3 shows the Bode plots of the adjusted plant’s transfer function $G^{'}_p(s)$, the open loop transfer function $C(s) \times G^{'}_p(s)$ and the reference model $G_a (s)$. It can be seen that, in the given frequency band of interest [0.5, 50] rad/s, the phase curve of the open loop $C(s) \times G^{'}_p(s)$ overlaps the flat phase of the reference model $G_a (s)$ around the gain crossover frequency with a phase margin about $62^\circ$.

Fig. 3

Bode plot of the adjusted plant $G^{'}_p(s)$ (dash-dotted line), the open loop $C(s)\times G^{'}_p(s)$ (solid line) and the reference model $G_a (s)$ (dashed line)

In order to check the robustness of the control system, a variation of $\pm \, 50\%$ in the nominal plant gain $K_0$ is introduced $K_0 = {0.5,\; 1.0,\; 1.5}$. The step responses are illustrated in Fig. 4.

Fig. 4

Step responses of the plant with a variation in the nominal plant gain $K_0 = {0.5, 1.0, 1.5}$

This simulation result shows that the step responses are maintained in a constant overshoot (iso-damping property) in spite of the plant gain variations. From these observations, one can conclude that the designed controller, tuned by the proposed method, is robust against gain variations with an iso-damping property around the gain crossover frequency.

4.2 Example 2

To more illustrate the effectiveness of the proposed tuning method, let’s consider a pair of complex-conjugate poles system given by,

$$\begin{aligned} G_p (s) = \frac{k_n \; (s+2)}{s^2+2s+3} \end{aligned}$$

(29)

where, $k_n\ge 0$.

The specifications of the design are,

• Phase margin $= 55^\circ$;

• Unity gain crossover frequency $\omega _u = 3$ rad/s.

To achieve these specifications in a frequency range $[\omega _l, \omega _h] = [0.1\,\omega _u, 10\,\omega _u] =$[0.3 rad/s, 30 rad/s] around $\omega _u$.

According to the design specifications, the open loop transfer function (12) must be,

$$\begin{aligned} G(s) = \frac{1}{\left( \frac{s}{3}\right) ^{1.4}} \end{aligned}$$

(30)

Using the Charef’s method, G(s) is approximated to, $G_a (s)$ can be decomposed as,

$$\begin{aligned} G_a (s) \approx \frac{874.47(s+1948)(s+462)(s+109.6)(s+25.98)(s+6.161)(s+1.461)(s+0.3464)(s+0.08215)}{(s+4620)(s+1096)(s+259.8)(s+61.61)(s+14.61)(s+3.464)(s+0.0462)(s+0.03)(s+0.1948)(s+0.8215)} \end{aligned}$$

(31)

$$\begin{aligned} G_a (s) = G_1 (s) \times G_2 (s) \end{aligned}$$

(32)

with

$$\begin{aligned} G_1 (s) = \frac{1}{(s+0.1948)(s+0.8215)} \end{aligned}$$

(33)

$$\begin{aligned} G_2 (s) = \frac{874.47(s+1948)(s+462)(s+109.6)(s+25.98)(s+6.161)(s+1.461)(s+0.3464)(s+0.08215)}{(s+4620)(s+1096)(s+259.8)(s+61.61)(s+14.61)(s+3.464)(s+0.0462)(s+0.03)} \end{aligned}$$

(34)

and, Using the pole placement algorithm (state feedback $u = -Kx$). The transfer function $G^{'}_p(s)$ is given as,

$$\begin{aligned} \nonumber G^{'}_p(s)= & {} \frac{K (s+2)}{(s+0.1948)(s+0.8215)}\\= & {} K (s+2)\; G_1 (s) \end{aligned}$$

(35)

Thus, the controller transfer function for $K=1$.

$$\begin{aligned} C(s) = \frac{G_a (s)}{G^{'}_p(s)} = \frac{G_1 (s) \times G_2 (s)}{(s+2) \times G_1 (s)} \end{aligned}$$

(36)

Can be obtained as,

$$\begin{aligned} C(s) \approx \frac{874.47(s+1948)(s+462)(s+109.6)(s+25.98)(s+6.161)(s+1.461)(s+0.3464)(s+0.08215)}{(s+4620)(s+1096)(s+259.8)(s+61.61)(s+14.61)(s+3.464)(s+2)(s+0.0462)(s+0.03)} \end{aligned}$$

(37)

Figure 5 shows the Bode plots of the adjusted plant transfer function $G^{'}_p(s)$, the open loop $C(s)\times G^{'}_p(s)$ and the reference model $G_a (s)$.

Fig. 5

Bode plot of the adjusted plant $G^{'}_p(s)$, the open loop $C(s)\times G^{'}_p(s)$ and the reference model $G_a (s)$

From Fig. 5, one can see that, in the given frequency band of interest [0.3, 30] rad/s, the phase curve of the open loop $C(s)\times G^{'}_p(s)$ is flat around the gain crossover frequency and almost is about $55^\circ$. In order to check the robustness of the controlled system, a variation of $\pm \,50 \%$ in the nominal plant gain $K_0$ introduced $K_0 = \left\{ 0.5, 1.0, 1.5\right\}$. The step responses are illustrated in Fig. 6.

Fig. 6

Step responses of the plant with a variation in the nominal plant gain $K_0 = {0.5, 1.0, 1.5}$

From this figure it is clearly shown that the step responses are maintained in a constant overshoot (iso-damping property) in spite of the plant gain variations. From these observations, one can conclude that the designed controller, tuned by the proposed method, makes the unity feedback control system robust to gain variations with an iso-damping property around the gain crossover frequency.

4.3 Example 3

Let’s consider the transfer function of unstable plant $G_p (s)$ given by,

$$\begin{aligned} G_p (s) = \frac{k_n\; (s^2-1)}{s^2 (s^2-1)-1} \end{aligned}$$

(38)

where, $k_n\ge 0$.

The specifications of the design are,

• Phase margin $= 69^\circ$;

• Unity gain crossover frequency $\omega _u = 10$ rad/s.

To achieve these specifications in a frequency range $[\omega _l, \omega _h] = [0.1\,\omega _u, 10\,\omega _u] =$[1 rad/s, 100 rad/s] around $\omega _u$.

The plant poles are at $s=\pm \,1.272$ and $\pm \, j0.7862$. The system is clearly unstable.

In order to apply the proposed controller and according to the design specifications, the open loop transfer function $G(s)= C(s) \times G^{'}_p(s)$ must be,

$$\begin{aligned} G(s) = \frac{1}{(s/10)^{1.23}} \end{aligned}$$

(39)

The open loop transfer function G(s) is approximated to,

$$\begin{aligned} G_a (s) \approx \frac{11142(s+0.3318)(s+2.333)(s+16.4)(s+115.3)(s+810.6)}{(s+0.2119)(s+0.1)(s+1.49)(s+10.47)(s+73.62)(s+517.6)(s+3639)} \end{aligned}$$

(40)

$G_a (s)$ can be decomposed as,

$$\begin{aligned} G_a (s) = G_1 (s) \times G_2 (s) \end{aligned}$$

(41)

with

$$\begin{aligned} G_1 (s) = \frac{1}{(s+0.2119)(s+0.1)(s+1.49)(s+10.47)} \end{aligned}$$

(42)

and,

$$\begin{aligned}&G_2 (s)\nonumber \\&\quad = \frac{11142(s+0.3318)(s+2.333)(s+16.4)(s+115.3)(s+810.6)}{(s+73.62)(s+517.6)(s+3639)}\nonumber \\ \end{aligned}$$

(43)

Using the pole placement algorithm, the adjusted $G^{'}_p(s)$ of the original plant is,

$$\begin{aligned} \nonumber G^{'}_p(s)= & {} \frac{(s+1)(s-1)}{(s+0.2119)(s+0.1)(s+1.49)(s+10.47)}\\= & {} (s+1)(s-1)\times G_1 (s) \end{aligned}$$

(44)

Thus, the controller transfer function C(s) can be obtained from equation (15) as,

$$\begin{aligned} C(s) = \frac{G_a (s)}{G^{'}_p(s)} = \frac{G_1 (s) \times G_2 (s)}{(s+1)(s-1) G_1 (s)} \end{aligned}$$

(45)

thus,

$$\begin{aligned}&C(s)\nonumber \\&\quad \approx \frac{11142(s+0.3318)(s+2.333)(s+16.4)(s+115.3)(s+810.6)}{(s+1)(s-1)(s+73.62)(s+517.6)(s+3639)}\nonumber \\ \end{aligned}$$

(46)

Figure 7 shows the Bode plots of the adjusted plant’s $G^{'}_p(s)$, the open loop $C(s)\times G^{'}_p(s)$ and the reference model G(s).

Fig. 7

Bode plot of the adjusted plant $G^{'}_p(s)$, the open loop $C(s)\times G^{'}_p(s)$ and the reference model $G_a (s)$

From the phase Bode plot shown in Fig. 7, one can see that, in the given frequency band of interest [1, 100] rad/s, the phase curve of the open loop $C(s)\times G^{'}_p(s)$ overlaps the flat phase of the reference model $G_a (s)$ around the gain crossover frequency and is about $69^\circ$. In order to check the robustness of the controlled system, a variation of $\pm 50\%$ in the nominal plant gain $K_0$ is introduced $K_0 = {0.5, 1.0, 1.5}$. The step responses are illustrated in Fig. 8.

Fig. 8

Step responses of the plant with a variation in the nominal plant gain $K_0 = {0.5, 1.0, 1.5}$

This figure shows that the step responses are maintained in a constant overshoot (iso-damping property) in spite of the plant gain variations. From these observations, one can conclude that the proposed controller, tuned by the proposed method, stabilizes the unity feedback control system and makes it robust against gain variations with an iso-damping property around the gain crossover frequency.

4.4 Example 4

In order to compare the effectiveness of the proposed method with the classical PID and the CRONE controller [21], let’s consider the unity feedback control system of a DC motor whose transfer function $G_p (s)$ is given by,

$$\begin{aligned} G_p (s) = \frac{1}{\frac{s}{\omega _n}\left( 1 + \frac{s}{\omega _0}\right) } = \frac{1}{\frac{s}{16.98}\left( 1 + \frac{s}{50}\right) } \end{aligned}$$

(47)

The specifications of the design are,

• Phase margin $= 45^\circ$;

• Unity gain crossover frequency $\omega _u = 500$ rad/s.

To achieve these specifications in a frequency range $[\omega _l, \omega _h] = [0.1\omega _u, 10\omega _u] = [50 rad/s, 5000 rad/s]$ around $\omega _u$, the open loop transfer function (14) must be,

$$\begin{aligned} G(s) = \frac{1}{(s/500)^{1.5}} \end{aligned}$$

(48)

Thus, the controller transfer function $C_{FOC} (s)$ can be obtained as,

$$\begin{aligned} C_{FOC} (s) \approx \frac{3.4946\, 10^6 (s+14.75)(s+59.53)(s+240.3)(s+970.2)(s+3917)(s+1.581 \, 10^4 )(s+6.383\, 10^4 )}{849(s+6.844)(s+111.5)(s+450.3)(s+1818)(s+7339)(s+2.963\, 10^4 )(s+1.196\, 10^5 )} \end{aligned}$$

(49)

The transfer functions of the CRONE and classical PID controllers, tuned to achieve the same specifications, are given respectively by [21]:

$$\begin{aligned}&C_{CRONE} (s)\nonumber \\&\quad = C_0 \frac{(1{+}s/z_1)(1{+}s/z_2)(1{+}s/z_3)(1{+}s/z_4)(1{+}s/z_5)}{(1{+}s/p_1)(1{+}s/p_2)(1{+}s/p_3)(1{+}s/p_4)(1{+}s/p_5)} \end{aligned}$$

(50)

where, $C_0 = 4.84$; $z_1=0.5495$ rad/s; $z_2=2.747$ rad/s; $z_3=13.783$ rad/s; $z_4=68.692$ rad/s; $z_5=343.46$ rad/s; $p_1=1.9234$ rad/s; $p_2=6.144$ rad/s; $p_3=30.72$ rad/s; $p_4=153.6$ rad/s; $p_5=1202.1$ rad/s.

The PID controller is given by,

$$\begin{aligned} C_{PID} (s) = C^{'}_0 \frac{(1+s/z^{'}_1)(1+s/z^{'}_2)}{(1+s/p^{'}_1))(1+s/p^{'}_2))} \end{aligned}$$

(51)

where, $C^{'}_0=728.7$; $z^{'}_1=4.0824$ rad/s; $z^{'}_2=204.12$ rad/s; $p^{'}_1=0.6804$ rad/s; $p^{'}_2=1224.72$ rad/s.

Figure 9 shows the Bode plots of the adjusted plant’s transfer function $G^{'}_p(s)$ with the proposed controller $C_{FOC}(s)\times G^{'}_p(s)$ and the plant $G_p (s)$ with the CRONE and classical PID controllers.

Fig. 9

Phase Bode plot of the open loop transfer functions of the considered control system for each controller

From the phase Bode plot shown in Fig. 9, one can see that in the given frequency band of interest, the proposed controller gives best phase flatness around the gain crossover frequency and is about $45^\circ$.

In order to check the robustness of the controlled system with the three controllers, a variation in the nominal parameter $\omega _n$ is introduced, $\omega _n = {16.98/5, 16.98, 16.985\times 5}$. The step responses are illustrated in Figs. 10, 11 and Fig. 12 for each controller.

Fig. 10

Step responses of the unity feedback fractional order control system FOC, for different values of $\omega _n$

From the closed loop responses plot shown in Figs. 10, 11 and Fig. 12, for different values of plant parameter $\omega _n$ one can remark that the proposed controller $C_{FOC} (s)$ gives the best robustness results versus plant parameter variations.

4.5 Example 5

Another comparative example is a first order plus time delay (FOPTD) plant whose transfer function $G_p (s)$ is given as [22],

$$\begin{aligned} G_p (s)=\frac{k_n}{(0.4s+1)} e^{-0.01s} \end{aligned}$$

(52)

where the nominal value of the parameter $k_n=1$.

Three controllers are designed for the plant (52), namely:

• a classical PI controller $C_1 (s)$ designed in [22] based on analytical tuning method:

  $$\begin{aligned} C_1 (s)=2.46369+ \frac{33.06090}{s} \end{aligned}$$

  (53)

• a fractional order controller $C_2 (s)$ tuned as in [23] using analytical design method based fractional reference model:

  $$\begin{aligned} C_2 (s)=69.6041 \frac{1}{s} (\frac{1}{s^{0.5}} + 0.4s^{0.5} ) \end{aligned}$$

  (54)

• the proposed fractional controller $C_3 (s)$ tuned as discussed in Sect. 3: with state feedback gain matrix $K=[-\, 2.2390]$.

$$\begin{aligned} C_3 (s)= \frac{1778.3(s+1122)(s+281.8)(s+70.79)(s+17.78)(s+4.467)(s+1.122)(s+0.2818)}{(s+2239)(s+562.3)(s+141.3)(s+35.48)(s+8.913)(s+0.5623)(s+0.1413)(s+0.1)} \end{aligned}$$

(55)

The three controllers $C_1 (s)$, $C_2 (s)$, and $C_3 (s)$ are designed to satisfy the following specifications,

• Unity gain frequency ${\omega _{u}}=10$ rad/s;

• Phase margin $\phi _m = 45^{\circ }$.

Fig. 11

Step responses of the unity feedback CRONE control system, for different values of $\omega _n$

Fig. 12

Step responses of the unity feedback PID control system, for different values of $\omega _n$

In order to check the robustness of the control system with the three controllers, a variation in the nominal plant gain $k_n$ is introduced as ${k_n/5, k_n, 5k_n}$. The step responses are illustrated in Figs. 13,14 and 15 for each controller.

From Fig. 13, we see that the controller $C_1 (s)$ gives poor performance, while in Figs. 14 and 15, the controllers $C_2 (s)$ and $C_3 (s)$ ensure best results of iso-overshoot (iso-damping) property with a relative enhancement for $C_3 (s)$ controller.

Fig. 13

Step responses of the controlled system with $C_1 (s)$, for different values of the gain

Table 1 shows the performance comparison results of the controlled system using the Matlab command “StepInfo” with the three controllers. It appears that the designed controller is clearly the best one.

Fig. 14

Step responses of the controlled system with $C_2 (s)$, for different values of the gain

Fig. 15

Step responses of the controlled system with $C_3 (s)$, for different values of gain

5 Conclusion

In this paper, a new simple and useful tuning technique of fractional order controllers (FOC) has been proposed to achieve user-specified gain and phase margins using the so-called Bode’s ideal transfer function or fractional order integrator as a reference model. The basis of this method is to use a standard pole placement technique to align each pole of the plant transfer function with the nearest one given by the Rational Transfer Function Approximation (RTFA) of the fractional order integrator.

Table 1 Please write your table caption here

The set of the aligned poles are then removed from the RTFA. The transfer function of the FOC is then obtained by multiplying the remaining poles of the RTFA with the inverse of the zeros of the plant transfer function. This inverse imposes that the system must be a minimum phase. Simulations results show that the proposed method is simple, effective, can ensures the iso-damping property for the control system and can be investigated to cover processes that have complex-conjugate poles or unstable conditions.