1 Introduction

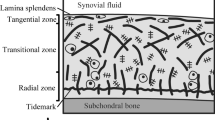
Cartilage is a connective, non-vascular, non-lymphatic, and cellular tissue that has a large amount of collagen in a proteoglycan (PG) matrix. Due to the strength of its extracellular matrix, this tissue can withstand mechanical stresses without permanent deformation. Moreover, its smooth surface and elasticity have slippery and shock-absorbing properties of joints [1,2,3]. Also, cartilage is involved in the development of long bones before and after birth.

The components of this tissue include cells (chondrocytes) and extracellular matrix (including fibrils and matrix substance) [4]. 70% to 80% of the weight of cartilage is water, the volume fraction of which varies according to the thickness of the tissue. In other words, the amount of proteoglycan and water increases and decreases in the direction of cartilage thickness from top to bottom, respectively. This results in nonlinear permeability through the tissue thickness [5, 6]. Approximately 60% to 70% of the dry weight of cartilage tissue contains collagen fibril [7, 8].

Osteoarthritis (OA) is a common disease characterized by the gradual degeneration of articular cartilage. In the early stages of OA, the amount of PGs on the cartilage surface decreases [9, 10], and at the same time changes occur in the collagen network [9,10,11]. These include significant changes in the orientation of surface collagen fibers [9, 12,13,14] and a decrease in collagen content [12]. As a result, these changes increase cartilage hydration through water uptake, which increases tissue permeability. These changes reduce the mechanical stiffness of cartilage and as a result weaken its mechanical function [9]. This may lead to further development of OA. As a result of OA in the composition and structure of tissue, the osmolality of the extracellular matrix also increases, which results in an increase in cell volume and thus a change in the biosynthetic properties of cartilage. Failure to treat damaged cartilage often leads to persistent pain and a negative impact on the quality of life because it makes human being susceptible to osteoarthritis in the long term.

Applied clinical procedures, such as osteochondral allografts and autografts allografts, do not create fully integrated tissues with the composition and mechanical strength similar to normal articular cartilage [15, 16]. Most of these methods do not have a long-term response and the patient suffers from secondary damage after a while. Therefore, to solve this problem, researchers have turned to tissue engineering and reconstructive medicine [17,18,19]. In tissue engineering, laboratory-made biological implants that can be adsorbed on bone are used. To achieve this objective, obtaining the mechanical properties of cartilage tissue is important, including shear and bulk moduli as well as its fiber-related properties.

Numerous structural models have been proposed in the last three decades; the nature of them derives from pro-elastic theory [20, 21]. Furthermore, different structural models for simulating cartilage behavior have been proposed in the framework of biphasic pro-elastic theories [22] and biphasic pro-viscoelastic [23, 24]. The orientation of collagen fibers during loading and its nonlinear tension–compression behavior increase the complexity of structural modeling for articular cartilage.

In previous studies, the nonlinear tension–compression behavior has been investigated using a fiber-reinforced model in which the mechanical stiffness of the material is affected by both a fiber network and anisotropic matrix [25, 26]. In fiber-reinforced models, the total stress is calculated as the sum of the matrix and fiber stresses. These structural models are divided into two groups: spring models and continuous models. In the finite element (FE) analyses of spring models, fibers are used as spring elements between element nodes limiting their direction in the direction of the element.

Some researchers have also employed the reverse engineering method to acquire the properties of articular cartilage materials coupled to finite element models with an optimization algorithm. For instance, Lee et al. [27, 28] developed various models in which the stiffness of the fibers was modeled using a linear spring parallel to a nonlinear spring with stiffness depending on the fiber strain. Folin and Zari utilized springs to model the fibers. They also determined Young's modulus and the permeability of hydrated water absorbent soft tissue through a finite element analysis coupled with an optimization algorithm [29]. Cao et al. [30] extracted only 3 parameters using a coupled finite element/optimization method to earn the properties of rat articular cartilage. Wilson et al. [31] and Garcia et al. [32] obtained the bovine articular cartilage material properties. They expressed the viscoelasticity of cartilage using a simple model consisting of a series of linear springs and dampers. They were capable of accurately obtaining Young's modulus and permeability. Lee et al. [27] obtained the mechanical properties of cartilage using a pro-elastic model reinforced with fibrils and based on the unconfined stress relaxation test. In this study, they used a spring system to display fibrils. Seifzadeh et al. [33] obtained the pro-viscoelastic properties of bovine cartilage using a coupled finite element/optimization method and the stress relaxation indentation test. In another study, Seifzadeh et al. [34] evaluated the constituent properties of native articular cartilage, tissue engineering and degeneration. The results of their work showed that for a given strain, the stiffness of the engineered cartilage was approximately one tenth of the native cartilage at 3 and 9 months.

Sasaki et al. [35] obtained shear and Young's moduli for bovine bone and bone collagen. They concluded that the process of stress relaxation in bone was controlled by the viscoelastic properties of the collagen matrix fiber. Toshia Liu et al. [36, 37] investigated the effect of structural anisotropy on the stress relaxation modulus of cortical bone. They presented an analytical expression for modeling experimental data of reduced relaxation. This is one of the analytical relaxation models proposed for cortical bone. In this expression, it was assumed that trabecular bone relaxation had two distinct stages related to short-term and long-term dynamics. They concluded that the parts related to short-term and long-term stress relaxation in the experimental formula were related to the bone collagen matrix and the higher-order structure, respectively, which were responsible for the anisotropic mechanical properties of this tissue. Leaks and Katz investigated the tissue matrix behavior of cortical bone. Deligiani et al. Goodes et al. and Virginia Coaglini et al. studied the viscoelastic behavior of trabecular bone [38,39,40,41].

Lan et al. [42] procured a 3D FE nonlinear model from magnetic resonance and tomography images of a total knee joint, consisting of bones, articular cartilage, ligaments, and meniscus. Men et al. [43] introduced a FE model to determine Young's modulus and Poisson's ratio of damaged articular cartilage.

Park et al. [44] investigated the dynamic modulus and compressive strain of bovine articular cartilage at the level of physiological compressive stress and loading frequencies. In this study, they obtained the functional characteristics of articular cartilage under loading. Recently, Snehal et al. [45], developed a comprehensive testing protocol for macro-scale mechanical characterization of knee articular cartilage with documented experimental repeatability. Jayed et al. [46] determined the anisotropic properties of articular cartilage under accelerated laboratory wear conditions. The results of their study demonstrated that wear in the transverse direction released about twice as many glycosaminoglycans (GAGs) than in the longitudinal direction.

Athanasiou et al. [47] determined the mechanical properties of articular cartilage in the femoral head and acetabulum of baboons, dogs, and cows and compared them with human hip cartilage. In situ creep and recovery indentation experiments were performed using an automated creep indentation apparatus. Based on this study’s data, the baboon represents the most appropriate animal model of normal human hip articular cartilage. In another study, Athanasiou et al. [48] examined the mechanical properties of the femoral head and acetabular cartilage. The results indicate that there are significant differences between these properties regionally in the acetabulum and femoral head and between the two anatomical structures. Specifically, it was found that cartilage in the superomedial aspect of the femoral head has a 41% larger aggregate modulus than its anatomically corresponding articulating surface in the acetabulum. Junyan Li et al. [49] examined the influence of size, clearance, cartilage properties, thickness, and hemiarthroplasty on the contact mechanics of the hip joint with biphasic layers. The modeling methods developed in their study provide a basic platform for biphasic simulation of the whole hip joint on which more sophisticated material models or other in-put parameters could be added in the future.

Harris et al. [50] predicted finite element of cartilage contact stresses in normal human hips. These results demonstrate the diversity and trends in cartilage contact stress in healthy hips during activities of daily living and provide a basis for future comparisons between normal and pathologic hips.

Soriano et al. [51] developed a method for performing the comparison of polycentric knee mechanisms and designing a stable and novel four-bar mechanism with a voluntary control configuration. They defined design parameters for the optimization of a stable knee mechanism with voluntary control. Ahmed et al. [52] obtained the equations governing elastic materials through thermos diffusion in the presence of thermal and diffusion processes. Dastjerdi et al. [53] studied the size- and time-dependent viscoelastic bending analysis of rotating spherical nanostructures made of functionally graded materials (FGMs). Agarwal et al. [54] reviewed various additive manufacturing (AM) techniques used to fabricate metallic orthopedic bone screws and summarized the characteristics, merits, and demerits of the prominent biomaterials explored to fabricate orthopedic bone screws until the twenty-first century.

One of the main goals of studies in the field of tissue engineering and medicine is to make biological implants with properties similar to living tissue. In addition to quasi-static tests, the need for dynamic tests with a frequency similar to biological loading on living tissue is inevitable to design and test such implants.

In the transition region, as the cartilage is loaded, between the moment the force is applied and the moment the tissue reaches equilibrium, the bulk and shear moduli change with time. Most previous studies have used spring elements to express the viscoelastic properties of the matrix. However, because of the nonlinear behavior of the matrix and its high deformation at high strains, this approach causes errors in the results.

In summary, in most previous studies that used optimization methods in order to determine optimized material parameters, it was difficult to determine the large number of material parameters required to model the behavior of cartilage, resulting in fairly simplified models that had a relatively low number of material parameters. Moreover, most commonly utilized optimization methodologies require good initial guesses to avoid local minima and convexity issues [29, 55]. The present work addressed these shortcomings by utilizing a coupled FE/optimization scheme to determine the 12 material parameters of a biphasic fiber-reinforced anisotropic porohyperviscoelastic model of human articular cartilage using a series of stress relaxation unconfined tests. Finite deformation, nonlinear permeability, strain stiffening, as well as the dispersion and reorientation of the fibers during loading were among the features of the present model. Since the model was highly nonlinear with a large number of unknown material parameters, the optimization design space had many local minima. In the used model, to consider the viscoelastic behavior of tissue, shear and bulk moduli were considered as a function of time. The stability of the mechanical behavior of the proposed model was scrutinized by considering the effects of various parameters on the tissue response in the unconfined stress relaxation test. The results demonstrated that the viscoelastic behavior of cartilage tissue was qualitatively similar to that of porous trabecular tissue, unlike dense cortical bone tissue in the stress relaxation test. To the best of the authors' knowledge, no research has been conducted yet to determine the properties of cartilage tissue using the present model and with the help of unconfined mechanical testing.

2 Materials and methods

2.1 Experimental method

Before the compression test, articular cartilage samples were prepared as cylindrical shapes that full thickness cylinders of 45–55 year old males (n = 3) femoral head of human articular cartilage were punched using a dermal punch, and removed from the underlying subchondral bone with a razor blade. Visual inspection is performed to make sure that disks were taken from the central, weight-bearing region of the femoral head of joints where the cartilage was shiny, smooth, and free of tissue degeneration. Cylindrical disks were cut from each core using a slicer with the thickness h and the radius R around 1 and 1.4 mm, respectively [27]. The specimens were kept in a Plexiglas chamber and sliced by razor blades. Fresh tissue specimens were equilibrated in phosphate-buffered saline, pH 7.4 for 1 h before performing the experiments.

An electromechanical material testing machine (Hounsfield 25KS, UK), with the top plate coupled to a 100 N capacity load cell, was applied to test Sample of articular cartilage of the head femur (n = 3) in unconfined compression between two impermeable, unlubricated plates (Fig. 1).

Fig. 1
figure 1

Articular cartilage sample under unconfined stress-relaxation test

Full size image

A pressure test was carried out at a speed of 0.5 mm/min under a 10-ramp as shown in Fig. 2, while in each ramp, samples were displaced around 0.03 mm and were then restarted. Briefly, 10 compressive displacement ramps were applied to each sample up to the 30% strain (Fig. 2), and their corresponding relaxation response was obtained as shown in Fig. 3.

Fig. 2
figure 2

Displacement–time diagram applied to the top plate of the device

Full size image
Fig. 3
figure 3

Reaction force–time diagram of measured unconfined compression response

Full size image

2.2 Finite element method

For simulation purposes, a fiber-reinforced porohyperviscoelastic model was chosen in the Abaqus2019. An anisotropic solid matrix with water-saturated pores was considered in this model. Both solid and liquid phases were considered incompressible. The fluid flow velocity through the articular cartilage matrix is called hydraulic permeability [56]. In the present study, changes in hydraulic permeability were calculated using Eq. (1).

$$ k = k_{0} \exp \left( {M\varepsilon } \right) $$
(1)

where \(\varepsilon\) is the dilatation of the bulk material, \(k_{0}\) is the initial permeability, and \(M\) is a constant coefficient. \(e\) is the void ratio at the given deformation, and the initial void ratio was assumed to be 4 (\(e_{0}\) = 4) [29]; ultimately, Eq. (1) [57] leads to Eq. (2) in the finite deformation as follows:

$$ k = k_{0} \exp \left( {M\frac{{e - e_{0} }}{{1 + e_{0} }}} \right) $$
(2)

2.2.1 Strain energy function

Using the theory of continuum mechanics for fiber-reinforced composites at finite strains [58], the strain energy function \(U\) = \(U\)(\(c\)\(\cdot \)A0\(\cdot \)B0) depends not only on the deformation gradient F but also on the directions of the fibers. In this regard, A0 = a0 \(\otimes\) a0 and B0 = b0 \(\otimes\) b0 are the structural tensors of the fibers in 2 directions and \(c\) is the Cauchy–Green deformation tensor [30, 59].

For two families of fibers, the strain energy function was expressed in terms of tensor \(c\) variables and fiber vectors a0 and b0. The vector F = a specifies the spatial orientation, and the amount of fiber elongation is equal to |a|. Holzapfel et al. [60], Gasser et al. [61], and Holzapfel et al. [62] proposed a structural model for modeling arterial layers with distributed collagen fiber directions according to Eq. (3) and Eq. (4):

$$ \begin{aligned} U = & C_{{10}} \left( {\bar{I}_{1} - 3} \right) + \frac{1}{D}\left[ {\frac{{\left( {J^{{{\text{el}}}} } \right)^{2} - 1}}{2} - \ln J^{{{\text{el}}}} } \right] \\ & + \frac{{k_{1} }}{{2k_{2} }}\sum\limits_{{\alpha = 1}}^{N} {\left[ {\exp \left( {k_{2} \bar{E}\alpha ^{2} } \right) - 1} \right]} \\ \end{aligned} $$
(3)
$$ \overline{E}\alpha = kappa\left( {\overline{I}_{1} - 3} \right) + \left( {1 - 3kappa} \right)\left( {\overline{I}_{{4\left( {\alpha \alpha } \right)}} - 1} \right) $$
(4)

where \(U\) is the strain energy per unit volume, \(C_{10}\),\( D\),\( k_{1}\),\( k_{2} \), and \(kappa\) are temperature-dependent material parameters, \(N\) is the number of fiber groups, \(\overline{I}_{1}\) is the first constant \(\overline{c}\), modified Cauchy–Green deformation tensor, \(J^{{{\text{el}}}}\) is the elastic volume ratio, and \(\overline{I}_{{4\left( {\alpha \alpha } \right)}}\) are quasi-constants of equations \(\overline{c}\) and Aα. Moreover, index \(\alpha\) refers to a different family of fibers. Stress is derived from the derivative of the strain energy function \(U\). It can be decomposed into deviatoric and hydrostatic components as follows Eq. (5) and Eq. (6) [27]:

$$ \begin{array}{*{20}c} {\tau^{D} \left( t \right) = \tau_{0}^{D} \left( t \right) + {\text{dev}}} \\ \end{array} \left[ {\mathop \int \limits_{0}^{\tau } \frac{{G\left( {\tau \prime } \right)}}{{G_{0} }}\overline{F}_{t}^{ - 1} \left( {t - t^{\prime}} \right)\tau_{0}^{D} \left( {t - t^{\prime}} \right)\overline{F}_{t}^{ - T} \left( {t - t\prime } \right){\text{d}}\tau \prime } \right] $$
(5)
$$ \tau^{H} \left( t \right) = \tau_{0}^{H} \left( t \right) + \mathop \int \limits_{0}^{\tau } \frac{{K\left( {\tau \prime } \right)}}{{K_{0} }}\tau_{0}^{H} \left( {t - t\prime } \right){\text{d}}\tau \prime $$
(6)

where dev (*) is the shear deformation of component (*). \(\overline{F}_{t} \left( {t - t^{\prime}} \right)\) is the deformation gradient from state \(t - t^{\prime} \) to state t. Equation (7) and Eq. (8) are relaxation shear and bulk moduli of viscoelasticity terms in the Prony series [63]:

$$ G\left( \tau \right) = G_{0} \left( {g_{\infty } + \mathop \sum \limits_{i = 1}^{N} g_{i} e^{{ - \frac{\tau }{{\tau_{i} }}}} } \right) $$
(7)
$$ K\left( \tau \right) = K_{0} \left( {\kappa_{\infty } + \mathop \sum \limits_{i = 1}^{N} \kappa_{i} e^{{ - \frac{\tau }{{\tau_{i} }}}} } \right) $$
(8)

where \(N\) is considered to be the number of terms in the Prony series, \(G_{0}\) and \(K_{0}\) are the shear and bulk moduli, respectively, and \(\kappa_{i}\) and \(g_{i}\) are the domain constants in the Prony series. \(g_{\infty }\) and \(\kappa_{\infty }\) are long-term bulk and shear moduli, respectively. The initial bulk moduli are computed from Eq. (9) [64]:

$$ K_{0} = \frac{2}{D} $$
(9)

Also, the following relations (Eq. (10) and Eq. (11) are established between \( G_{0}\), the initial shear modulus, the Poisson's ratio \(\nu\), and the initial Young's modulus \(E_{0}\)

$$ G_{0} = \frac{{E_{0} }}{{2\left( {1 + \nu } \right)}} $$
(10)
$$ G_{0} = 2C_{10} . $$
(11)

2.2.2 Simulation

To simulate the unconfined stress relaxation test in Abaqus, the biphasic porous CAX8PR element was employed in the symmetrical axis and deformable model (Fig. 4). To apply a uniform compressive force on the sample, a rigid plate was utilized and the boundary conditions were applied as follows: At z = h/2, a vertical displacement was applied varied with time and the surface was impermeable. At z = 0, the conditions were the same as z = h/2 except for the displacement, which was zero. At r = R, the surface was permeable.

Fig. 4
figure 4

Simulation meshing which was performed in Abaqus using symmetrical biphasic porous CAX8PR elements. In this meshing, the values of \(\beta_{1}\) and \(\beta_{2}\) are equal to 0.5 and 0.25, respectively

Full size image

2.2.3 Optimizations of main parameters

To obtain the material properties of cartilage, the coupled FE optimization method was applied through the optimization algorithm [33, 65,66,67,68,69,70,71,72]. In this study, the annealing optimization algorithm was used. The parameters related to the model were created at each time of the iteration in MATLAB R2017a and were sent to Abaqus as an input file. Using this file, the stress relaxation response in FE was calculated and its difference compared to the experimental response was calculated based on the specified objective function (Eq. (12)). This function was used as the objective function in the MATLAB optimization algorithm. The algorithm sent new values to the Abaqus input file as model parameters because of the received error. This process continued until the error between the responses obtained from the FE and the experimental observations became minimized. The objective function of the error between the simulated responses and the experimental observations was expressed using Eq. (12) [33] as follows:

$$ {\text{Er}}\left( {{\text{xopt}}} \right) = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {\frac{{\left[ {F^{{{\text{FEM}}}} \left( {{\text{xopt}}, t} \right)} \right]_{i} - \left[ {F^{{{\text{EXP}}}} \left( t \right)} \right]_{i} }}{{\left[ {F^{{{\text{EXP}}}} \left( t \right)} \right]_{i} }}} \right)^{2} $$
(12)

where \(F^{FEM}\) and \(F^{EXP}\) are the discrete relaxation force data for FE simulation and unconfined experiments, respectively, and n is the number of observed points.

3 Results

After converging the force–time curve of the simulated model in Abaqus with the experimental data (Fig. 5), the optimized parameters related to the proposed structural model were determined (Table 1).

Fig. 5
figure 5

Force–time response obtained using the finite element/optimization method fitted to the experimental data

Full size image
Table 1 Optimized parameters related to the proposed structural model
Full size table

Using the optimal values obtained in this study and considering the elastic equations relevant to the mechanical properties of the material, the values of the initial Young's modulus (\(E_{0}\)), initial shear modulus (\(G_{0}\)), aggregate modulus (HA), and Poisson's ratio (\(\nu\)) along with the obtained values in the reference [27, 29, 33, 47] are compared in Table 2.

Table 2 Comparison of the values obtained in this study with the ones reported by previous studies. HA: aggregate modulus, \(E_{0}\): initial Young's modulus, \(G_{0} :\) initial shear modulus and \(\nu\):Poisson's ratio
Full size table

By increasing and decreasing the parameters of the present model, their effects on the peak and relaxation of the force–time response were examined. Considering the viscoelastic behavior of cartilage [73, 74] and its division into flow-dependent and flow-independent behaviors [22, 75], the effects of the aforementioned parameters on the mechanism of these two behaviors were also analyzed. First, the parameters relevant to the hyperelastic properties of the used model were investigated. For this purpose, initially, the amount of \(C_{10}\) was increased and decreased by 20% as shown in Fig. 6.

Fig. 6
figure 6

Effect of changes in parameter \(C_{10}\) on the force obtained using the finite element/optimization method

Full size image

The effect of \(Kappa\), collagen fiber stiffness (\(k_{1}\)), relaxation time (\(\tau_{1}\)), normalized relaxation (\(g\)) changes on the force obtained using the finite element/optimization method is shown in Figs. 7, 8, 9, 10, respectively.

Fig. 7
figure 7

Effect of \(Kappa\) parameter changes on the force obtained using the finite element/optimization method

Full size image
Fig. 8
figure 8

Effect of the collagen fiber stiffness (\(k_{1}\)) changes on the predicted cartilage response using the finite element/optimization procedure

Full size image
Fig. 9
figure 9

Effect of changes of the parameter \(\tau_{1}\) on the cartilage response obtained using the finite element/optimization method

Full size image
Fig. 10
figure 10

Effect of changes in the \(g\) parameter on the force obtained from the finite element/optimization method

Full size image

In the sample under test, the total stress includes the sum of the stress stemming from the liquid pressure (i.e., pore pressure) and the stress of the solid matrix. The difference between the total applied stress to the tissue and the stress due to the increase in pore pressure is shown in Fig. 11.

Fig. 11
figure 11

Difference between the total applied stress to the tissue and the stress due to the increase in pore pressure

Full size image

The effect of changes in the parameter M on the force obtained from the finite element is shown in Fig. 12.

Fig. 12
figure 12

Effect of changes in the M parameter on the force obtained from the finite element/optimization method

Full size image

4 Discussion

Under large deformations, articular cartilage exhibits highly anisotropic and nonlinear elastic behavior due to the rearrangement of its microstructures. In recent decades, numerous constructive models have been proposed to simulate the structural and mechanical properties of cartilage tissue.

In this study, an anisotropic biphasic fiber-reinforced porohyperviscoelastic model was presented to predict the response of articular cartilage tissue in an unconfined stress relaxation test. This model considered cartilage as a porous matrix reinforced with collagen fibers and took into consideration the fiber reorientation during loading. Moreover, the intrinsic viscoelastic property of the cartilage matrix was included in this model. In the presented model, the lateral sides of the sample were free and permeable. If compressive forces were suddenly applied to the plates, the pore pressure in the center of the sample increased from its initial value after loading and became zero when it reached a maximum value. This was because as the liquid exited through the edges of the sample, most of the load was transferred to the center of the sample. This effect was also observed by Cryer [76] for the spherical sample under hydrostatic pressure.

Previous studies on cartilage have reported a wide range of Young's modulus. This difference in Young's modulus values can be due to differences in the sample’s ages, used models, test methods and conditions, loading rates and in some cases because of considering elastic behavior for matrix deformation. Thus, the material parameters in this study could not be directly compared with previous studies. However, a comparison is performed in Table 2.

Based on Eq. (9) and Eq. (10), the parameter \(C_{10}\) has a direct relationship with \(G_{0}\) and \(E_{0}\). Hence, increasing and decreasing the value of \(C_{10}\) had a direct impact on the peak point of the tissue response in each ramp (Fig. 6). Moreover, by increasing the value of \(C_{10}\), the slope of the stress relaxation diagram in the short-term region decreased and the resistance to deformation increased. It could be indicated that this behavior affected the flow-dependent viscoelastic mechanism of the tissue and diminished the velocity of the exiting water. By reducing this parameter, the slope of the stress relaxation diagram was raised and water was discharged faster. According to Fig. 6, increasing and decreasing the value of \(C_{10}\) directly affected the peak point of the force diagram in each ramp, so that by increasing and decreasing this parameter, the peak value increased and decreased, respectively. Also, by increasing the value of \(C_{10}\), the slope of the stress relaxation diagram lessened in the short term and the resistance to strain deformation increased. Changing this parameter also affected the mechanism which was dependent on the viscoelastic flow and corresponded to the fact that by increasing this parameter, the velocity of water leaving the tissue decreased. As it diminished, the slope of the stress relaxation diagram increased. This was consistent with the fact that tissue water was drained more rapidly. Examining some studies carried out in the past, such as the pro-elastic models proposed by [27] and [33], it was observed that the results of increasing the modulus of elasticity of the matrix and fibers were compatible with those of the present work.

In the present model, there was a scalar quantity that indicated the level of dispersion of fibers in the orientations of collagen fibers, generally in the range (0 ≤ \(Kappa\) ≤ 1/3). The larger the value of this parameter, the greater the dispersion of fibers. It was observed that the smaller the dispersion of the fibers, the larger the peak value per ramp. This was because of the better alignment of the fibers to withstand compression axially (tension laterally), and this happened in all ramps (Fig. 7).

Another parameter of the hyperelastic property was relevant to the stiffness of the fibers. This parameter was represented by \(k_{1}\). The resistance of the tissue to deformation and the peak of its response was directly proportional to the value of this parameter. Moreover, by decreasing this parameter, the short-term part of the stress relaxation diagram had a smoother slope and as a result, the water discharge rate was slower and vice versa. Based on Fig. 8, at larger stresses, the alignment of the fibers in tension (in the lateral direction) was increased. This led to more resistance of the tissue against lateral deformation. The effect of this parameter on the tissue response in higher ramps (higher strains) was more evident.

Although it is usually assumed that stress relaxation is independent of the elastic variable (initial stress) for most soft tissues [77], the effect of initial load on the magnitude of stress relaxation in some soft collagen tissues has been shown [78]. Contrary to the behavior of cortical bone tissue [38] and contrary to the hypotheses made by [39, 40], the results demonstrated that the viscoelastic behavior of spongy bone was nonlinear compared to the elastic variable (initial stress). Quaglini et al. [41] showed in a stress relaxation test performed on spongy bone, the larger the initial stress, the slower the rate of stress relaxation in the short term, and the smaller the stress on the equilibrium regime (long-term stress relaxation). Since the porosity of the spongy bone matrix was more than the cortical bone, these results could be attributed to its porous structure.

The results of the present study indicated that by decreasing and increasing 20% of \(\tau_{1}\), the stress relaxation rate became faster and slower, respectively. Also, in the first ramps where the initial stress was smaller, the stress relaxation rate was larger, and by increasing the initial stress, the stress relaxation rate was reduced (Fig. 9).

According to Fig. 10, there was a direct relationship between the \(g\) parameter and the force obtained using the finite element model. By increasing 10% in the value of the \(g\) parameter, the maximum force per ramp increased and reached equilibrium with a steeper slope. Also, by decreasing 10% in the value of the \(g\) parameter, the maximum force on each ramp decreased and reached equilibrium with a smaller slope.

In this study, by examining the finite element model during the stress relaxation test, it was observed that by applying a load on the sample and compressing it, initially, the force caused by the increase in liquid pressure in the pores had the largest share in bearing the applied load (total stress). During the test and over time, this value lessened, and the contribution of the solid matrix to the applied load (total stress) increased. The reason was that at the beginning, the water had not drained among the pores of the tissue, and gradually as the water drained, the pressure in the pores decreased. Figure 11 shows that the difference between the total stress applied to the tissue and the stress due to the increase in pore pressure at the initial ramps of the response was small. As time passed and the sample became more compressed, this difference became greater gradually. This figure shows that at the beginning of the experiment, the stress due to the increase in fluid pressure in the pores (pore pressure) had the largest share of the total applied stress. However, over time, because of the gradual discharge of liquid from the solid matrix, this share gradually decreased and was replaced with solid matrix stress.

According to the results of previous studies and because there is no specific value for the initial hydraulic permeability of various cartilages including humans, cattle, mice, and rabbits, the value of \(k_{0} =\) 2.8 × 10–15 \( {\text{m}}^{4} /{\text{Ns}}\) was considered [26, 29,30,31, 79, 80]. Moreover, the optimized value of M, which indicates the reduction in tissue permeability in compressive strain, was considered to be 20. As [27] has shown, a reduction in permeability can increase the amount of peak force and increase the relaxation time. However, it was observed that by changing the value of M, the value of the peak force did not change significantly. Moreover, a change in the value of M substantially changed the relaxation time in the last steps since the permeability of \(k\) in large compressions changed considerably (Fig. 12).

5 Conclusion

The 12 material parameters used to describe a biphasic fiber-reinforced anisotropic porohyperviscoelastic model of human articular cartilage were determined using an optimization scheme to calibrate a finite element model of a relatively simple stress relaxation unconfined test. To ensure convergence to a global minimum regardless of the quality of the initial guesses of the material properties, it was necessary to use a simulated annealing (SA) optimization algorithm. The effects of various parameters on the tissue response in the unconfined stress relaxation test were investigated to examine the stability of the mechanical behavior of the proposed model. The results demonstrated the robustness of the SA optimization algorithm to ensure convergence of a large number of material properties to a global minimum regardless of the quality of the initial guesses.

Also, the viscoelastic properties of the cartilage matrix, unlike previous studies used spring elements, were considered by utilizing the bulk and shear modulus of the tissue matrix as a function of time in the used structural model.

The model used in this research took into consideration the nonlinear properties of cartilage including finite deformation, nonlinear permeability, and strain stiffening, as well as the dispersion of fibers and their reorientation during loading in the simulation.

The viscoelastic behavior of cartilage tissue was compared with the porous tissue of similar tissues such as spongy bone tissue. The results indicated that the viscoelastic behavior of cartilage tissue was qualitatively similar to that of porous, spongy tissue in the stress relaxation test, unlike dense cortical bone tissue, and could be a way to estimate the porosity of engineered tissues by this experiment.

The cartilage tissue response was well predicted by the model employed in this study. The effects of the obtained structural model parameters on the cartilage stress relaxation response were investigated. It was seen that changing the \(C_{10}\), \(k_{1} ,\) and \(g\) parameters directly affected the peak force–time diagram. The values of the initial Young's modulus (\(E_{0}\)), initial shear modulus (\(G_{0}\)), aggregate modulus (HA), and Poisson's ratio (\(\nu\)) were calculated 0.63 \(\pm 0.065,\) 0.236 \(\pm 0.037,\) 1.27 \(\pm 0.66, \) and 0.35 \(\pm 0.09\), respectively.

It was observed that by applying a load on the sample and compressing it, initially, the force caused by the increase in liquid pressure in the pores had the largest share in bearing the applied load (total stress). During the test and over time, this value lessened, and the contribution of the solid matrix to the applied load (total stress) increased.

This study demonstrated how each of these parameters controlled part or parts of the cartilage transition response under the stress relaxation test. The shear and bulk moduli of the cartilage matrix were procured as a function of time, which could be used to predict the dynamic response of cartilage in the future.