1 Introduction

Articular cartilage, the connective tissue covering the surface of the subchondral bone in diarthrodial joints, plays a crucial role in shock absorption, load transmission and sustainability. As observed by researchers (Gao et al. 2015; Sophia Fox et al. 2009), articular cartilage suffers both dynamic and static loads, which may be up to ten times the bodyweight in daily living. Therefore, the biomechanical property of articular cartilage needs to be understood. This topic has attracted much attention, and many achievements have been made both experimentally and theoretically. As reported by Li et al. (2005), Responte et al. (2007) and Athanasiou et al. (2009), articular cartilage is a typical highly functional multiphase material that has some special features, i.e., high nonlinearity and viscocity. Based on the experimental observations, many constitutive models have been presented to simulate the biomechanical behaviors of articular cartilage (Armstrong et al. 1984; Ateshian 2017; Bursać et al. 1999; García and Cortés 2006; Huang et al. 2001; Kwan et al. 1990; Mow et al. 1980; Pierce et al. 2013; Seifzadeh et al. 2012; Soltz and Ateshian 2000a; Wilson et al. 2005). However, the existing research is mainly focused on describing the biomechanical responses under monotonic loading conditions, e.g., the monotonic stress-strain relationship and the creep and stress relaxation behavior.

It should be noted that articular cartilage suffers complicated cyclic loads in daily living (Barker and Seedhom 2001; Soltz and Ateshian 2000b). Since the mechanical fatigue caused by cyclic loading is assumed to be one of the major causes of osteoarthritis (Kurz et al. 2005), the cyclic deformation behavior of articular cartilage has also attracted attention. Barker and Seedhom (2001) experimentally studied the cyclic compressive deformation of articular cartilage from human cadaveric knee joints. Bellucci and Seedhom (2001) performed cyclic tensile tests of articular cartilage from the human knee to investigate the topographic and zonal variations in the fatigue behavior. Kerin et al. (2003) investigated the surface fissure propagation of articular cartilage of cow by cyclic loading tests in vitro. Gao et al. (2013) studied the depth-dependent strain fields of porcine articular cartilage under cyclic rolling load by an optimized digital image correlation technique.

However, the ratcheting behavior of articular cartilage was not investigated in the above-mentioned studies. Ratcheting is the inelastic strain accumulation under asymmetrical force/stress-controlled cyclic loading conditions, which may play an important role in assessing the wear property as well as fatigue life of the materials (Gao et al. 2015; Kang 2008; Kang and Wu 2011; Zhu et al. 2014a, b). The ratcheting behavior of metals (Kang 2008), polymeric materials (Chen and Hui 2005; Lu et al. 2016), composite materials (Ahmadzadeh and Varvanifarahani 2015; Guo et al. 2013) and biologic tissues (Kang and Wu 2011; Zhu et al. 2014b) was thus studied systematically. When the cartilage is subjected to cyclic loading, fatigue damage may occur in the cartilage joint because of accumulation of ratcheting strain (Gao et al. 2015). It is thus also important to investigate the ratcheting behavior of articular cartilage. Recently, Gao et al. (2015) carried out detailed experimental observations of the ratcheting behavior of articular cartilage under stress-controlled cyclic compressive loading conditions. In the experimental tests, the used material was the fresh articular cartilage of the knee joint from an 8-month-old pig. The dimensions of the experimental samples were approximately 5.5 mm long, 4.5 mm wide and 12 mm thick. To maintain the physiologic environment of cartilage, all samples were soaked in saline before the tests. An Electronic Universal Fatigue Testing System (EUF-1020) was used for all the tests. The experimental results showed that the ratcheting behavior of porcine articular cartilage depends strongly on the loading level and rate. Given that the ratcheting behavior of articular cartilage has not been considered by the previous constitutive models (Armstrong et al. 1984; Ateshian 2017; Bursać et al. 1999; García and Cortés 2006; Huang et al. 2001; Kwan et al. 1990; Mow et al. 1980; Pierce et al. 2013; Seifzadeh et al. 2012; Soltz and Ateshian 2000a; Wilson et al. 2005), a constitutive model for articular cartilage considering ratcheting is proposed in the present work. The current model is constructed in the framework of finite elasto-viscoplasticity theory by incorporating the logarithmic stress rate. According to experimental observations (Athanasiou et al. 2009; Li et al. 2005; Matzat et al. 2013; Responte et al. 2007), articular cartilage is a typical multiphase material composed of electrolytes, fluid, collagen fibers, proteoglycans, chondrocytes, etc. (as shown in Fig. 1). The fiber network mainly contributes strength and stiffness to the material. Therefore, in this work, articular cartilage is simply supposed to be composed of a fiber assembly (related to the collagen fibers) and a soft basis (related to the other components). Both parts contribute to the free energy and stress functions. The nonlinearity is considered as an exponential-type nonlinear elastic relation for the fiber assembly. Ratcheting is reflected by the viscoplasticity, the evolution rule of which is formulated from the Clausius-Duhem inequality by co-directionality hypotheses. The prediction ability of the presented model is finally validated by comparing the predictions with related experimental observations (Gao et al. 2015). It is shown that the ratcheting behavior as well as the cyclic stress-strain responses of articular cartilage is reasonably captured by the proposed model.

Fig. 1
figure 1

Microstructure of articular cartilage

Full size image

2 Proposed model

Based on the thermodynamic laws and logarithmic stress rate, an elasto-viscoplastic model to describe the ratcheting behavior of articular cartilage is presented in this section, which consists of three parts and is structured as follows:

In Sect. 2.1, some information on the kinematics and logarithmic stress rate are introduced; in Sect. 2.2, the free energy function is presented and the dissipative inequality derived; in Sect. 2.3, the stress functions and inelastic evolution equations are proposed.

2.1 Kinematics and logarithmic rate

In the present work, a constitutive model is developed in a rate type based on a finite elasto-plastic theory, the kinematics of which are as follows:

$$ {\mathbf{F}} = \frac{{\partial {\mathbf{x}}}}{{\partial {\mathbf{X}}}},\quad {\mathbf{L}} = \frac{{\partial {\dot{\mathbf{x}}}}}{{\partial {\mathbf{X}}}} = {\dot{\mathbf{F}}\mathbf{F}}^{ - 1} , $$
(1)
$$ {\mathbf{F}} = {\mathbf{VR}},\quad {\mathbf{R}}^{\text{T}} = {\mathbf{R}}^{ - 1} ,\quad {\mathbf{B}} = {\mathbf{V}}^{2} , $$
(2)
$$ {\mathbf{D}} = {\text{sym}}{\mathbf{L}},\quad {\mathbf{W}} = {\text{skw}}{\mathbf{L}}, $$
(3)
$$ {\mathbf{h}} = \ln {\mathbf{V}}, $$
(4)

where F and L are respectively the deformation gradient tensor and velocity tensor; x and X are respectively the spatial and related material vectors; R is an orthogonal rotation tensor; V and B are respectively the left stretch and left Cauchy-Green tensors; D (the symmetric part of L) and W (the skew part of L) are the stretching tensor and spin tensor, respectively; h is Hencky’s strain.

As reported by Bruhns et al. (1999) and Xiao et al. (1997a, b), only if the logarithmic stress rate is introduced are the constitutive models in rate type developed by hypo-elasticity self-consistent with the notion of elasticity. Besides, the logarithmic rate of Hencky’s strain h and the stretching tensor D are equal to each other, i.e.,

$$ \mathop {\mathbf{h}}\limits^{^\circ}{{}^{\log}} = \left({\ln \mathop {\mathbf{V}}\limits^{^\circ}} \right)^{\log} = {\mathbf{D}}, $$
(5)

with \( {\mathop {\mathbf{A}}\limits^{\circ}}{{}^{\log}} \), the logarithmic rate of an arbitrary symmetric second-order tensor A, defined as

$$ \mathop {\mathbf{A}}\limits^{^\circ} {{}^{\log}} = {\dot{\mathbf{A}}} + {\mathbf{A\varOmega}}^{\log} - {\varvec{\Omega}}^{\log} {\mathbf{A}}, $$
(6)

where \( {\varvec{\Omega}}^{\log } \) is the skew logarithmic spin, which is a function of the left stretch tensor B and the stretching tensor D. More details can be found in Bruhns et al. (1999) and Xiao et al. (1997a, b).

Furthermore, there is a time-dependent rotation \( {\mathbf{R}}^{\log } \), which can be used to define the logarithmic spin \( {\varvec{\Omega}}^{\log } \) as follows:

$$ {\dot{\mathbf{R}}}^{ \log } = {\varvec{\Omega}}^{ \log } {\mathbf{R}}^{ \log } , $$
(7)

with the initial condition \( \left( {{\mathbf{R}}^{ \log } } \right)_{t = 0} = {\mathbf{1}}. \)

According to Bruhns et al. (1999), we have

$$ {\mathbf{A}}:\mathop {\mathbf{A}}\limits^{^\circ} {{}^{\log}} = {\mathbf{A}}:{\dot{\mathbf{A}}}. $$
(8)
$$ \frac{\text{d}}{{{\text{d}}t}}\left({{\mathbf{Q}}^{\text{T}} {\mathbf{AQ}}} \right) = {\mathbf{Q}}^{\text{T}} \mathop {\mathbf{A}}\limits^{^\circ} {{}^{\log}} {\mathbf{Q}}. $$
(9)

where Q is an orthogonal tensor.

2.2 Free energy function and thermodynamic restrictions

As mentioned in Sect. 1, the articular cartilage is simply considered a typical composite material consisting of a fiber assembly and a soft basis.

Hence, the Kirchhoff stress tensor \( {\varvec{\uptau}} \) can be decomposed into two contributions, i.e.,

$$ {\varvec{\uptau}} = {\varvec{\uptau}}_{{}}^{\text{b}} + {\varvec{\uptau}}_{{}}^{\text{f}} , $$
(10)

where \( {\varvec{\uptau}}_{{}}^{\text{b}} \) and \( {\varvec{\uptau}}_{{}}^{\text{f}} \) are respectively the stress components associated with the basis and fiber assembly.

Suppose that the basis and fiber assembly have an identical deformation, indicating that

$$ {\mathbf{h}} = {\mathbf{h}}^{\text{b}} = {\mathbf{h}}^{\text{f}} . $$
(11)

For elasto-viscoplastic theory, Hencky’s strain h is further additively decomposed as:

$$ {\mathbf{h}}^{\text{b}} = {\mathbf{h}}^{{{\text{e}}\left( {\text{b}} \right)}} + {\mathbf{h}}^{{{\text{vp}}\left( {\text{b}} \right)}} ,\quad {\mathbf{h}}^{\text{f}} = {\mathbf{h}}^{{{\text{e}}\left( {\text{f}} \right)}} + {\mathbf{h}}^{{{\text{vp}}\left( {\text{f}} \right)}} , $$
(12)

where \( {\mathbf{h}}^{{{\text{e}}\left( {\text{b}} \right)}} \) and \( {\mathbf{h}}^{{{\text{e}}\left( {\text{f}} \right)}} \) are respectively the elastic strain tensors related to the basis and fiber assembly, and \( {\mathbf{h}}^{{{\text{vp}}\left( {\text{b}} \right)}} \) and \( {\mathbf{h}}^{{{\text{vp}}\left( {\text{f}} \right)}} \) represent the viscoplastic strain tensors related to the basis and fiber assembly, respectively.

According to Zhu et al. (2014a, 2016), in large deformation, Eqs. (11) and (12) can be directly replaced by

$$ {\mathbf{D}} = {\mathbf{D}}^{\text{b}} = {\mathbf{D}}_{{}}^{\text{f}} , $$
(13)
$$ {\mathbf{D}}^{\text{b}} = {\mathbf{D}}^{{{\text{e}}\left( {\text{b}} \right)}} + {\mathbf{D}}^{{{\text{vp}}\left( {\text{b}} \right)}} ,\quad {\mathbf{D}}^{\text{f}} = {\mathbf{D}}^{{{\text{e}}\left( {\text{f}} \right)}} + {\mathbf{D}}^{{{\text{vp}}\left( {\text{f}} \right)}} , $$
(14)

where \( {\mathbf{D}}^{{{\text{e}}\left( {\text{b}} \right)}} \), \( {\mathbf{D}}^{{{\text{e}}\left( {\text{f}} \right)}} \) and \( {\mathbf{D}}^{{{\text{vp}}\left( {\text{b}} \right)}} \) and \( {\mathbf{D}}^{{{\text{vp}}\left( {\text{f}} \right)}} \) represent the elastic stretching tensors and viscoplastic stretching tensors related to the basis and fiber assembly, respectively. In addition, it supposes

$$ {\mathbf{D}}^{{{\text{e}}\left({\text{b}} \right)}} = {\mathop {\mathbf{h}}\limits^{\circ}}{{}^{{\log({\text{e}}({\text{b}}))}}},\quad {\mathbf{D}}^{{{\text{e}}\left({\text{f}} \right)}} = {\mathop {\mathbf{h}}\limits^{\circ}}{{}^{{\log({\text{vp}}({\text{f}}))}}} . $$
(15)

Assuming plastic Hencky strains, \( {\mathbf{h}}^{{{\text{vp}}\left( {\text{b}} \right)}} \) and \( {\mathbf{h}}^{{{\text{vp}}\left( {\text{f}} \right)}} \) are strictly dissipated; the free energy ψ is hence supposed to be a function of the elastic Hencky strains \( {\mathbf{h}}^{{{\text{e}}\left( {\text{b}} \right)}} \) and \( {\mathbf{h}}^{{{\text{e}}\left( {\text{f}} \right)}} \), i.e.,

$$ \psi = \hat{\psi }\left( {{\mathbf{h}}^{{{\text{e}}\left( {\text{b}} \right)}} , \, {\mathbf{h}}^{{{\text{e}}\left( {\text{f}} \right)}} } \right). $$
(16)

Neglecting the coupling effect, ψ can be additively decomposed as

$$ \psi = \hat{\psi }^{\text{b}} \left( {{\mathbf{h}}^{{{\text{e}}\left( {\text{b}} \right)}} } \right) + \hat{\psi }^{\text{f}} \left( { \, {\mathbf{h}}^{{{\text{e}}\left( {\text{f}} \right)}} } \right), $$
(17)

where \( \hat{\psi }^{\text{b}} \) and \( \hat{\psi }^{\text{f}} \) represent the free energy function components associated with the contributions of the basis and fiber assembly, respectively.

Restricting to isothermal conditions, the dissipative inequality is given as

$$ {\varvec{\uptau}}:{\mathbf{D}} - \dot{\psi } \ge 0. $$
(18)

In view of Eq. (17), the time derivative of the free energy ψ is obtained as

$$ \dot{\psi } = \frac{{\partial \hat{\psi }^{\text{b}} }}{{\partial {\mathbf{h}}^{{{\text{e}}\left( {\text{b}} \right)}} }}:{\dot{\mathbf{h}}}^{{{\text{e}}\left( {\text{b}} \right)}} + \frac{{\partial \hat{\psi }_{{}}^{\text{f}} }}{{\partial {\mathbf{h}}_{{}}^{{{\text{e}}\left( {\text{f}} \right)}} }}:{\dot{\mathbf{h}}}_{{}}^{{{\text{e}}\left( {\text{f}} \right)}} . $$
(19)

According to Zhu et al. (2016), for initially isotropic elasticity, if ψ is a quadratic function of \( {\mathbf{h}}^{{{\text{e}}\left( {\text{b}} \right)}} \) and \( {\mathbf{h}}^{{{\text{e}}\left( {\text{f}} \right)}} \), Eq. (17) can be rewritten with Eqs. (7) and (12–15) as

$$ \dot{\psi } = \frac{{\partial \hat{\psi }^{\text{b}} }}{{\partial {\mathbf{h}}^{{{\text{e}}\left( {\text{b}} \right)}} }}:\left( {{\mathbf{D}} - {\mathbf{D}}^{{{\text{vp}}\left( {\text{b}} \right)}} } \right) + \frac{{\partial \hat{\psi }_{{}}^{\text{f}} }}{{\partial {\mathbf{h}}_{{}}^{{{\text{e}}\left( {\text{f}} \right)}} }}:\left( {{\mathbf{D}} - {\mathbf{D}}_{{}}^{{{\text{vp}}\left( {\text{f}} \right)}} } \right). $$
(20)

Hence, Eq. (18) is reformulated as

$$ \left( {{\varvec{\uptau}} - \frac{{\partial \hat{\psi }^{\text{b}} }}{{\partial {\mathbf{h}}^{{{\text{e}}\left( {\text{b}} \right)}} }} - \frac{{\partial \hat{\psi }_{{}}^{\text{f}} }}{{\partial {\mathbf{h}}_{{}}^{{{\text{e}}\left( {\text{f}} \right)}} }}} \right){:}{\mathbf{D}} + \frac{{\partial \hat{\psi }^{\text{b}} }}{{\partial {\mathbf{h}}^{{{\text{e}}\left( {\text{b}} \right)}} }}{:}{\mathbf{D}}^{{{\text{vp}}\left( {\text{b}} \right)}} + \frac{{\partial \hat{\psi }_{{}}^{\text{f}} }}{{\partial {\mathbf{h}}_{{}}^{{{\text{e}}\left( {\text{f}} \right)}} }}{:}{\mathbf{D}}_{{}}^{{{\text{vp}}\left( {\text{f}} \right)}} \ge 0. $$
(21)

It is reduced as

$$ {\varvec{\uptau}}^{\text{b}} :{\mathbf{D}}^{{{\text{vp}}\left( {\text{b}} \right)}} + {\varvec{\uptau}}_{{}}^{\text{f}} :{\mathbf{D}}_{{}}^{{{\text{vp}}\left( {\text{f}} \right)}} \ge 0. $$
(22)

with the following definitions

$$ {\varvec{\uptau}}^{\text{b}} = \frac{{\partial \hat{\psi }^{\text{b}} }}{{\partial {\mathbf{h}}^{{{\text{e}}\left( {\text{b}} \right)}} }}, \, {\varvec{\uptau}}_{{}}^{\text{f}} = \frac{{\partial \hat{\psi }_{{}}^{\text{f}} }}{{\partial {\mathbf{h}}_{{}}^{{{\text{e}}\left( {\text{f}} \right)}} }} $$
(23)

2.3 Constitutive equations

Commonly, a linear hypoelastic relationship can be assumed by adopting Hooker’s law. However, a highly nonlinear stress-strain response (generally J-shaped) of articular cartilage is observed according to the experimental research (Gao et al. 2015).

Such a nonlinearity is mainly caused by the fibers having different lengths and only undertaking loads after certain critical stress/strain. Therefore, a nonlinear elastic relationship for \( {\varvec{\uptau}}_{{}}^{\text{f}} \) is introduced in this work. The elastic relations related to \( {\varvec{\uptau}}_{{}}^{\text{b}} \) and \( {\varvec{\uptau}}_{{}}^{\text{f}} \) are respectively formulated as

$$ {\mathop {\varvec{\uptau}}\limits^{\circ}}{{}^{{\log({\text{b}})}}} = 2\mu_{{}}^{\text{b}} {\mathop {\mathbf{h}}\limits^{\circ}}{{}^{{\log({\text{e}}({\text{b}}))}}} + \lambda^{\text{b}} {\text{tr}}\left({\mathop {\mathbf{h}}\limits^{\circ}}{{}^{{\log({\text{e}}({\text{b}}))}}} \right){\mathbf{1}}={\mathbb{C}}_{{}}^{\text{b}} :{\mathbf{D}}^{{{\text{e}}\left({\text{b}} \right)}}, $$
(24a)

and

$$ {\mathop {\varvec{\uptau}}\limits^{\circ}}{{}^{{\log({\text{f}})}}} = 2\mu_{{}}^{\text{f}} {\mathop {\mathbf{h}}\limits^{\circ}}{{}^{{\log({\text{e}}({\text{f}}))}}} + \lambda^{\text{f}} {\text{tr}}\left({\mathop {\mathbf{h}}\limits^{\circ}}{{}^{{\log({\text{e}}({\text{f}}))}}} \right){\mathbf{1}}={\mathbb{C}}_{{}}^{\text{f}} :{\mathbf{D}}^{{{\text{e}}\left({\text{f}} \right)}}, $$
(24b)

where \( {\mathbb{C}}_{{}}^{\text{b}} \) and \( {\mathbb{C}}_{{}}^{\text{f}} \) are the fourth-order elastic tensors; \( \mu_{{}}^{i} = \frac{{E_{{}}^{i} }}{{2\left( {1 + \nu_{{}}^{i} } \right)}} \, \left( {i = {\text{b}},{\text{ f}}} \right) \) and \( \lambda_{{}}^{i} = \frac{{\nu_{{}}^{i} E_{{}}^{i} }}{{\left( {1 + \nu_{{}}^{i} } \right)\left( {1 - 2\nu_{{}}^{i} } \right)}} \, \left( {i = {\text{b, f}}} \right) \) are the Lamé constants (\( E_{{}}^{{{\text{b}},{\text{ f}}}} \) are the Young’s modulus and \( \nu_{{}}^{{{\text{b}},{\text{ f}}}} \) are the Poisson ratios); 1 is the second-order identity tensor. To describe the nonlinearity, \( E_{{}}^{\text{f}} \) is supposed to be evolved as

$$ E_{{}}^{\text{f}} = \beta \left( {\alpha + \bar{\tau }^{\text{f}} } \right), $$
(25)

where α and β are positive material parameters controlling the nonlinearity. \( \bar{\tau }^{\text{f}} = \sqrt {\frac{ 3}{ 2}} \left\| {{\varvec{\uptau}}^{\text{f}} } \right\| \) is the effective value of \( {\varvec{\uptau}}^{\text{f}} \). Considering a 1D problem, Eq. (24b) can be integrated as

$$ \tau^{\text{f}} = \alpha \left( {\exp \left( {\beta h^{\text{e}} } \right) - 1} \right), $$
(26)

where \( \tau^{\text{f}} \) and \( h^{\text{e}} \) are the axial Kirchhoff stress (related to the fiber assembly) and elastic Hencky strain, respectively.

The logarithmic form of Eq. (10) is further given as

$$ \mathop {\varvec{\uptau}}\limits^{^\circ} {{}^{\log}} = \mathop {\varvec{\uptau}}\limits^{^\circ} {{}^{{\log ({\text{b}}})}} + \mathop {\varvec{\uptau}}\limits^{^\circ} {{}^{{\log ({\text{f}}})}}, $$
(27)

Considering the co-directionality, corresponding to the classical notion of maximal dissipation, \( {\mathbf{D}}^{{{\text{vp}}\left( {\text{b}} \right)}} \) and \( {\mathbf{D}}^{{{\text{vp}}\left( {\text{f}} \right)}} \) are evolved as

$$ {\mathbf{D}}^{{{\text{vp}}\left( {\text{b}} \right)}} = \gamma^{\text{b}} {\varvec{\tau^{\prime}}}^{\text{b}} ,\quad {\mathbf{D}}^{{{\text{vp}}\left( {\text{f}} \right)}} = \gamma^{\text{f}} {\varvec{\tau^{\prime}}}^{\text{f}} , $$
(28)

where \( \gamma^{\text{b}} \) and \( \gamma^{\text{f}} \) are nonnegative coefficients controlling the evolution of ratcheting of material. It is readily obtained that the dissipative inequality given in Eq. (22) holds. Based on the experimental observations by Gao et al. (2015), the ratcheting strain rate of articular cartilage decreases with the loading cycle number. In addition, it was further found that the ratcheting strain evolution was mainly controlled by \( \gamma^{\text{f}} \). Therefore, \( \gamma^{\text{f}} \) is assumed to be evolved as

$$ \gamma^{\text{f}} = \gamma_{0}^{\text{f}} + \left( {\gamma_{\text{sat}}^{\text{f}} - \gamma_{0}^{\text{f}} } \right)\left( {1 - \exp \left( { - \rho p^{\text{f}} } \right)} \right), $$
(29)

where ρ is the positive material parameter controlling the evolution of \( \gamma^{\text{f}} \); \( \gamma_{0}^{\text{f}} \) and \( \gamma_{\text{sat}}^{\text{f}} \) are respectively the initial and saturated value of \( \gamma^{\text{f}} \); \( p^{\text{f}} \) is the accumulated plastic strain related to \( {\mathbf{D}}^{{{\text{vp}}\left( {\text{f}} \right)}} \), the rate of which is defined as

$$ \dot{p}^{\text{f}} = \sqrt {\frac{ 2}{ 3}} \left\| {{\mathbf{D}}^{{{\text{vp}}\left( {\text{f}} \right)}} } \right\|. $$
(30)

The proposed model is summarized in Table 1.

Table 1 Summary of the proposed model
Full size table

3 Results

In this section, the prediction ability of the proposed model to describe the ratcheting behavior of articular cartilage is validated by comparing the simulations with the related experimental data by Gao et al. (2015). Note that all the calculations are done by MATLAB, and an explicit integration algorithm is adopted in the numerical implementation of the proposed model for simplification. A brief description of the explicit stress integration algorithm is given in Appendix 2.

Three loading cases were investigated: (1) a compression-unloading test with a stress variation of 0.5 MPa and a stress rate of 0.1 MPa/s to study the stress-strain hysteresis loops and the ratcheting strain evolution; (2) compression-unloading test with varied stress variations and a stress rate of 0.1 MPa/s (load case A as listed in Table 2); (3) compression-unloading test with a stress variation of 0.5 MPa and varied stress rates (load case B as listed in Table 2).

Table 2 Load cases used in ratcheting tests of articular cartilage
Full size table

It should be noted that the applied stress and measured strain in the experiments are the engineering ones. To be consistent, the simulated Kirchhoff stress and Hencky strain are therefore converted into engineering stress and strain with the following equations:

$$ \varepsilon = \exp \left( h \right) - 1, $$
(31)

and

$$ \sigma = \frac{\tau }{{ 1 { + }\varepsilon }}, $$
(32)

where \( \varepsilon \) and h are the axial engineering and Hencky strains, respectively; σ and τ are axial engineering and Kirchhoff stresses, respectively.

According to Gao et al. (2013, 2015), the ratcheting strain ɛr is defined as

$$ \varepsilon_{r} = \frac{ 1}{ 2}\left( {\varepsilon_{\text{max} } + \varepsilon_{\text{min} } } \right), $$
(33)

where ɛmax and ɛmin are respectively the maximum and minimum axial strain in a loading cycle.

All the material parameters are determined by the method in Appendix 1 and listed in Table 3. In Table 3, \( \gamma^{\text{b}} \) is determined from the stress-strain curve in the first cycle of the compression-unloading test with a stress variation of 0.5 MPa and a stress rate of 0.1 MPa/s; \( \gamma_{0}^{\text{f}} \), \( \gamma_{\text{sat}}^{\text{f}} \) and ρ are determined from the ratcheting data of the same loading case.

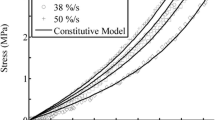
Table 3 Material parameters for articular cartilage in the proposed model
Full size table

Figure 2 gives the simulated and related experimental stress-strain response and ratcheting behavior of articular cartilage under compression-unloading conditions. It is seen that the proposed model can reasonably simulate the stress-strain hysteresis loops (Fig. 2a–c) and the two-stage (i.e., the ratcheting strain rate decreases rapidly in the initial stage and tends to a nearly constant value after certain cycles) ratcheting behavior (Fig. 2d). However, such good simulations are expected because the material parameters listed in Table 3 are obtained from fitting of the corresponding experimental data.

Fig. 2
figure 2

Experimental and simulated biomechanical behavior of articular cartilage under compression-unloading conditions

Full size image

The simulated and the related experimental ratcheting strain evolutions for the prescribed load cases A and case B are illustrated in Fig. 3. The figure implies that the proposed model can also capture the effect of the load level and rate on the ratcheting behavior of articular cartilage. Note that the ratcheting strains for load case A with a stress amplitude of 1.0 MPa and (Fig. 3a) load case B with a stress rate of 0.1 MPa/s (Fig. 3b) are under-predicted by the proposed model. This is because the ratcheting behavior of articular cartilage may depend not only on the accumulated plastic strain but also on the loading level and loading rate. However, there are not enough experimental data (only three tests for each load case) to achieve a more reasonable ratcheting strain evolution equation. In the present work, the ratcheting strain is assumed only to depend on the accumulated plastic strain for simplification (as shown in Eq. 29). Hence, there are deviations between the experimental and simulated ratcheting strains for some loading cases when adopting such a simple ratcheting strain evolution equation. In a future work, a modified ratcheting strain evolution equation will be proposed based on systematic experimental research on the effect of the loading level and rate on the ratcheting behavior of articular cartilage.

Fig. 3
figure 3

Experimental and simulated ratcheting behavior of articular cartilage in a load case A and b load case B

Full size image

4 Conclusions

This article seeks to propose a constitutive model to describe the ratcheting behavior of articular cartilage in the framework of finite elasto-viscoplastic theory by adopting the logarithmic stress rate. The constitutive equations are formulated based on the microstructure of articular cartilage. The predictive ability of the proposed model is validated by benchmarking the simulations with the related experimental data. The following conclusions can be drawn.

  1. 1.

    The proposed constitutive model is thermodynamically consistent.

  2. 2.

    Based on experimental observation, the articular cartilage is simplified as a composite that consists of a fiber assembly (related to the collagen fibers) and a soft basis (related to the other components). The free energy function and stress tensor are divided into two contributions accordingly.

  3. 3.

    The proposed model can reasonably describe the hysteresis loops and the dependence of the loading level and loading rate on the ratcheting behavior of articular cartilage under cyclic compression-unload conditions. However, there are large deviations between the experimental and simulated ratcheting strains for some loading cases because only a simple ratcheting strain evolution equation was adopted in the present work.