1 Introduction

The new kind of composites with smoothly varying material properties changing the volume fraction of constituents gradually along with one or more directions is called FGMs. In comparison with the traditional composite materials, FGMs exhibit not only superior features such as extremely high stiffness and strength combined with a very low density, resistance to chemicals, thermal and electrical insulation but also eliminate stress concentrations at the interfaces of composites [1, 2]. FGMs are regularly composed of two different kinds of structural components like ceramic and metal, and the volume fractions of these constituents change as a function of the certain dimensions of the structure to realize the desired functions. FGMs have a wide application range in modern technology including aerospace, medicine, defense, energy, optoelectronics, automotive, biotechnology, aviation, civil, and mechanical engineering [3,4,5,6,7,8,9,10].

Since the introduction of carbon nanotubes (CNTs) by Iijima [11], nanotechnology has become an important part of mankind as a result of the rapidly increasing use of nanosized structures in modern life as well as in defense technology for the miniaturization of information technology devices. Nanowires, nanotubes, nanobeams, nanomembranes, and nanoplates are some examples of nano-sized structures composed of nanomaterials with outstanding mechanical, chemical, electronic, electrical, and optical properties, and they have utilization in nano-/microelectromechanical systems (NEMS/MEMS), aerospace, biomedical and bioelectrical devices; some examples are photovoltaic cell, generators, micro-/nano-switches resonators, sensors, energy harvesting, transistors, and atomic force microscopy [12,13,14,15,16,17,18,19,20,21].

Nanostructures have ridiculously small dimensions that are comparable to the size of their material microstructure, and therefore, it becomes essential to study the size effect as the mechanical behaviors of nanostructures. Several approaches have been developed to capture the size influences as experimental, molecular dynamics simulations, and continuum mechanics. However, continuum mechanics is the most widely used method between these approaches because it is easy, cost-efficient, and effective. But the classical continuum mechanics cannot capture the size influence since the constitutive model of it does not include the material length parameters. Thus, a variety of size-dependent continuum mechanics approaches are established such as the surface elasticity theory, non-local elasticity theory, the modified couple stress theory, and strain gradient elasticity theory. Between these approaches, Eringen’s non-local elasticity theory contains only one scale parameter of small length for the definitions of the internal length scale of nanostructures and atomic forces, and hence, it has been widely employed [22,23,24].

Currently, the investigations on the mechanical behaviors of nanoplates composed of FGMs have attracted many researchers due to the increasing demand for applications of these structures in modern technology because of their superior properties. In various engineering practices, structural elements are exposed to dynamic loads, which can excite the structural vibrations and induce durability concerns or discomfort due to the resulting noise and vibration. Besides, if the vibration exceeds particular limits, breakage or failure may occur. Since FG nanoplates have been started to be used in micro-/nanoelectromechanical systems, such as the components in the form of shape-memory alloy thin films with a global thickness in micro- or nano-scale [25, 26], electrically actuated MEMS devices [27, 28], and atomic force microscopes [29], as well as medicines, gas sensors, energy storage, field emission, transportation of nano-cars and solar cells [30,31,32], the vibration analysis of nanoplates has been a vital task in their design for engineers and researchers for recent years. Gürses et al. [33] performed numerical computations using discrete singular convolution for the free vibration of nano-annular sector plates based on non-local continuum theory. The size-dependent free vibration of FG nanoplates is examined by Natarajan et al. [34] using the isogeometric-based finite element method. The three-dimensional non-local bending and vibration analyses of FG nanoplates are performed by Ansari et al. [35] using the variational differential quadrature method. Daneshmehr et al. [36] studied the free vibration of FG nanoplate using the generalized differential quadrature method. Nami and Janghorban [37] presented the free vibration of rectangular nanoplates with simply supported boundary conditions depending on refined plate theory with two variables employing strain gradient elasticity theory. Mechab et al. [38] examined the free vibration of FG nanoplate resting on Winkler–Pasternak elastic foundations based on refined plate theories with two variables including the effect of porosities. Phung-Van et al. [39] presented the size-dependent geometrically nonlinear transient analysis of FG nanoplates employing a solution procedure depending on isogeometric analysis combined with higher-order shear deformation theory. Arefi et al. [40] analyzed the free vibration of FG polymer composite nanoplates reinforced with graphene nanoplatelets resting on a Pasternak foundation applying a two-variable sinusoidal shear deformation theory adopting the non-local elasticity theory. Barati and Shahverdi [41] dealt with the semi-analytical nonlinear thermal vibration analysis of FG nanoplates modeled by four-variable refined plate theory. Zargaripoor et al. [42] examined the free vibration of FG nanoplate using the finite element method. Baretta et al. [43] studied the size-dependent elastostatic responses of axisymmetric annular nano-plates using a stress-driven non-local integral methodology of elasticity. Ruocco and Mallardo [44] considered the buckling and vibration of imperfect nanoplates via non-local Mindlin plate theory employing a coupling finite strip–finite element procedure. Sharifi et al. [45] dealt with the vibration of FG piezoelectric nanoplates based on the non-local strain gradient theory, analytically. Daikh et al. [46] analyzed the free vibration of rectangular FGM sandwich nanoplates with simply supported boundary conditions. Tran et al. [47] analyzed the bending and free vibration of FG nanoplates resting on elastic foundations utilizing a finite element model using four-unknown shear deformation theory integrated with the non-local theory. Zenkour et al. [48] examined the bending of simply supported FG nanoplate utilizing the non-local mixed variational formula. Liu et al. [49] studied the thermo-electro-mechanical free vibration of piezoelectric nanoplates based on the non-local theory and Kirchhoff theory. Malekzadeh and Shojaee [50] investigated the free vibration of nanoplates utilizing a refined plate theory joint with the non-local theory. Kiani [51] examined the features of in-plane and out-of-plane free vibrations of a conducting nanoplate subjected to the unidirectional in plane steady magnetic field utilizing different non-local shear deformable plate theories.

From the results of the search of open literature, it is observed that numerous studies are devoted to examine the mechanical behaviors of FG nanoplates. In most of these studies, numerical solution methods are employed, the number of studies based on the exact solution is quite limited, and in these studies, the exact solutions are developed for simple support boundary conditions, generally. Because the free vibration of the FG nanoplates has great importance in modern technology, it has become a necessity to derive a reliable exact solution for this behavior under different boundary conditions. Therefore, in the current study, an attempt is done to address this problem. For this aim, an exact analytical solution for the free vibration of nanoplates made of FGMs under four different boundary conditions is provided. The influence of the different parameters such as vibration mode, the aspect ratio, boundary conditions, power-law index, and non-local parameter on the natural frequencies of the FG nanoplate is discussed, in detail.

2 The formulation of the problem

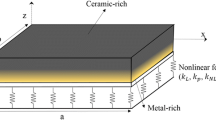
Figure 1 displays an FG nanoplate of length \(a\), width \(b\), and height \(h\). It is supposed that the top surface of the nanoplate \(\left( {z = + h/2} \right)\) is ceramic-rich and it is graded to the metal-rich one at the bottom surface \(\left( {z = - h/2} \right)\).

Fig. 1
figure 1

The geometry of FG nanoplate

Full size image

The material properties, \(P\), are supposed to grade across the thickness of FG nanoplate depending on the rule of the mixture as follows:

$$P\left( z \right) = P_{c} V_{c} + P_{m} V_{m}$$
(1)

where \(P_{c}\), \(P_{m}\), \(V_{c}\), and \(V_{m}\) represent the material properties and volume fractions of the ceramic and metal constituents, respectively.

The total volume fraction of constituents is as follows:

$$V_{m} + V_{c} = 1$$
(2)

The volume fraction of the ceramic constituent obeying the power-law distribution is as follows:

$$V_{c} = \left( {\frac{z}{h} + \frac{1}{2}} \right)^{k}$$
(3)

where \(k\) is a non-negative number and indicates the power-law index and \(z\) is the distance to the midplane of the nanoplate.

The efficient material properties of FG nanoplate could be expressed as:

$$E\left( z \right) = \left( {E_{c} - E_{m} } \right)V_{c} + E_{m}$$
(4a)
$$\rho \left( z \right) = \left( {\rho_{c} - \rho_{m} } \right)V_{c} + \rho_{m}$$
(4b)

where \(E\) and \(\rho\) are the Young’s modulus and the mass density of FG nanoplate, respectively.

Adopting Eringen’s [22, 23] non-local theory of elasticity, the influence of inter-atomic forces can be taken into account as the material parameters in the fundamental equation as follows:

$$\left( {1 - \tau^{2} L^{2} \nabla^{2} } \right)\sigma_{ij}^{NL} = \sigma_{ij}^{L} ;\quad \tau^{2} = \frac{\mu }{{L^{2} }} = \left( {\frac{{e_{0} a}}{L}} \right)^{2}$$
(5)

where superscripts (L, NL) denote the local and non-local, respectively, \(\mu = \left( {e_{0} a} \right)^{2}\) is the non-local parameter representing the small-scale influence, \(e_{0}\) is a physical parameter that has been identified by experimental results, and \(a\) and \(L\) are the internal and external characteristic lengths, respectively.

Non-local constitutive equations of FG nanoplate are as follows:

$$\left\{ \begin{gathered} \sigma_{x} \hfill \\ \sigma_{y} \hfill \\ \tau_{xy} \hfill \\ \tau_{yz} \hfill \\ \tau_{xz} \hfill \\ \end{gathered} \right\} - \mu \left( {\frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial y^{2} }}} \right)\left\{ \begin{gathered} \sigma_{x} \hfill \\ \sigma_{y} \hfill \\ \tau_{xy} \hfill \\ \tau_{yz} \hfill \\ \tau_{xz} \hfill \\ \end{gathered} \right\} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 & 0 & 0 \\ {Q_{12} } & {Q_{22} } & 0 & 0 & 0 \\ 0 & 0 & {Q_{44} } & 0 & 0 \\ 0 & 0 & 0 & {Q_{55} } & 0 \\ 0 & 0 & 0 & 0 & {Q_{66} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\gamma_{yz} } \\ {\gamma_{xz} } \\ {\gamma_{xy} } \\ \end{array} } \right\}$$
(6)

where \(\sigma_{x}\), \(\sigma_{y}\), \(\tau_{xy}\), \(\tau_{yz}\), \(\tau_{xz}\) and \(\varepsilon_{x}\), \(\varepsilon_{y}\), \(\gamma_{xy}\), \(\gamma_{yz}\), \(\gamma_{xz}\) are the components of stress and strain, respectively, and \(C_{ij}\) are the stiffness coefficients and described as follows:

$$Q_{11} = Q_{22} = \frac{E(z)}{{1 - \nu^{2} }},\quad Q_{12} = \frac{\nu \, E(z)}{{1 - \nu^{2} }},\quad Q_{44} = Q_{55} = Q_{66} = \frac{E(z)}{{2\left( {1 + \nu } \right)}}$$
(7)

Note that the transverse normal stress is negligible in comparison with in-plane stresses in x- and y-axes.

The displacements of FG nanoplate depending on the higher-order shear deformable plate theory are [7, 52, 53]:

$$\begin{gathered} u(x,y,z,t) = u_{0} (x,y,t) - z\frac{{\partial w_{b} }}{\partial x} - f\left( z \right)\frac{{\partial w_{s} }}{\partial x} \hfill \\ \hfill \\ v(x,y,z,t) = v_{0} (x,y,t) - z\frac{{\partial w_{b} }}{\partial y} - f\left( z \right)\frac{{\partial w_{s} }}{\partial y} \hfill \\ \hfill \\ w(x,y,z,t) = w_{b} (x,y,t) + w_{s} (x,y,t) \hfill \\ \end{gathered}$$
(8)

where \(u, \, v,{\text{ and }}w\) denote the displacements throughout \(x, \, y,{\text{ and }}z\) directions, respectively, and \(u_{0}\), \(v_{0}\), \(w_{b}\) and \(w_{s}\) are the unknowns as well as \(f(z)\) is the shape function and expressed as follows:

$$f(z) = z\left[ {1 + \frac{3\pi }{2}{\text{sech}} \left( \frac{1}{2} \right)^{2} } \right] - \frac{3\pi }{2}h\tanh \left( \frac{z}{h} \right)$$
(9)

The nonzero strains related to the displacement field are:

$$\begin{gathered} \left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\gamma_{xy} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } \\ {\varepsilon_{y}^{0} } \\ {\gamma_{xy}^{0} } \\ \end{array} } \right\} + z\left\{ {\begin{array}{*{20}c} {k_{x}^{b} } \\ {k_{y}^{b} } \\ {k_{xy}^{b} } \\ \end{array} } \right\} + f(z)\left\{ {\begin{array}{*{20}c} {k_{x}^{s} } \\ {k_{y}^{s} } \\ {k_{xy}^{s} } \\ \end{array} } \right\} \hfill \\ \hfill \\ \left\{ {\begin{array}{*{20}c} {\gamma_{yz} } \\ {\gamma_{xz} } \\ \end{array} } \right\} = g(z)\left\{ {\begin{array}{*{20}c} {\gamma_{yz}^{s} } \\ {\gamma_{xz}^{s} } \\ \end{array} } \right\} \hfill \\ \end{gathered}$$
(10)

where

$$\left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } \\ {\varepsilon_{y}^{0} } \\ {\gamma_{xy}^{0} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial u_{0} }}{\partial x}} \\ {\frac{{\partial v_{0} }}{\partial x}} \\ {\frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x}} \\ \end{array} } \right\},\quad \left\{ {\begin{array}{*{20}c} {k_{x}^{b} } \\ {k_{y}^{b} } \\ {k_{xy}^{b} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} { - \frac{{\partial^{2} w_{b} }}{{\partial x^{2} }}} \\ { - \frac{{\partial^{2} w_{b} }}{{\partial y^{2} }}} \\ { - 2\frac{{\partial^{2} w_{b} }}{\partial x\partial y}} \\ \end{array} } \right\},\quad \left\{ {\begin{array}{*{20}c} {k_{x}^{s} } \\ {k_{y}^{s} } \\ {k_{xy}^{s} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} { - \frac{{\partial^{2} w_{s} }}{{\partial x^{2} }}} \\ { - \frac{{\partial^{2} w_{s} }}{{\partial y^{2} }}} \\ { - 2\frac{{\partial^{2} w_{s} }}{\partial x\partial y}} \\ \end{array} } \right\},\quad \left\{ {\begin{array}{*{20}c} {\gamma_{yz}^{s} } \\ {\gamma_{xz}^{s} } \\ \end{array} } \right\} = g\left( z \right)\left\{ {\begin{array}{*{20}c} {\frac{{\partial w_{s} }}{\partial y}} \\ {\frac{{\partial w_{s} }}{\partial x}} \\ \end{array} } \right\}$$
(11a)

and then

$$g(z) = 1 - \frac{df(z)}{{dz}}$$

Utilizing Hamilton’s principle, the equations of motion could be found as follows:

$$0 = \int\limits_{{0}}^{t} {(\delta \, U - \delta \, K){\text{ d}}t}$$
(12)

where \(\delta \, U\) and \(\delta \, K\) are the variations strain and kinetic energies, respectively.

The variation of strain energy of FG nanoplate can be specified as follows:

$$\begin{aligned} & \delta \, U = \int\limits_{V} {\left[ {\sigma_{x} \delta \, \varepsilon_{x} + \sigma_{y} \delta \, \varepsilon_{y} + \tau_{xy} \delta \, \gamma_{xy} + \tau_{yz} \delta \, \gamma_{yz} + \tau_{xz} \delta \, \gamma_{xz} } \right]} {\text{ d}}V \\ & = \int\limits_{A} {\left[ {N_{x} \delta \, \varepsilon_{x}^{0} + N_{y} \delta \, \varepsilon_{y}^{0} + N_{xy} \delta \, \gamma_{xy}^{0} + M_{x}^{b} \delta \, k_{x}^{b} + M_{y}^{b} \delta \, k_{y}^{b} + M_{xy}^{b} \delta \, k_{xy}^{b} } \right.} \\ & \quad \left. { + M_{x}^{s} \delta \, k_{x}^{s} + M_{y}^{s} \delta \, k_{y}^{s} + M_{xy}^{s} \delta \, k_{xy}^{s} + S_{yz}^{s} \delta \, \gamma_{yz}^{s} + S_{xz}^{s} \delta \, \gamma_{xz}^{s} } \right]{\text{ d}}A = 0 \\ \end{aligned}$$
(13)

where \(A\) is the upper surface of FG nanoplate, and the stress resultants \(N\), \(M\), and \(S\) can be described as follows:

$$\left( {N_{i} ,M_{i}^{b} ,M_{i}^{s} } \right) = \int\limits_{ - h/2}^{h/2} {\left( {1,z,f} \right)\sigma_{i} {\text{d}}z} ,\,\,\,\left( {i = x,y,xy} \right)$$
(14a)
$$\left( {S_{xz}^{s} ,S_{yz}^{s} } \right) = \int\limits_{ - h/2}^{h/2} {g\left( {\tau_{xz} ,\tau_{yz} } \right){\text{d}}z}$$
(14b)

The variation of the kinetic energy of FG nanoplate can be specified as follows:

$$\begin{aligned} & \delta T = \int\limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\int\limits_{\Omega } {\left[ {\dot{u}\delta \, \dot{u} + \dot{v}\delta \, \dot{v} + \dot{w}\delta \, \dot{w}} \right] \, \rho (z) \, } } {\text{d}}\Omega \,{\text{d}}z \\ & \quad = \int\limits_{A} {\left\{ {I_{0} \left[ {\dot{u}_{0} \delta {\kern 1pt} \dot{u}_{0} + \dot{v}_{0} \delta {\kern 1pt} \dot{v}_{0} + \left( {\dot{w}_{b} + \dot{w}_{s} } \right)\left( {\delta {\kern 1pt} \dot{w}_{b} + \delta {\kern 1pt} \dot{w}_{s} } \right)} \right]} \right.} \\ & \quad - I_{1} \left( {\dot{u}_{0} \frac{{\partial \delta {\kern 1pt} \dot{w}_{b} }}{\partial x} + \frac{{\partial {\kern 1pt} \dot{w}_{b} }}{\partial x}\delta \, \dot{u}_{0} + \dot{v}_{0} \frac{{\partial \delta {\kern 1pt} \dot{w}_{b} }}{\partial y} + \frac{{\partial {\kern 1pt} \dot{w}_{b} }}{\partial y}\delta \, \dot{v}_{0} } \right) \\ & \quad - I_{2} \left( {\dot{u}_{0} \frac{{\partial \delta {\kern 1pt} \dot{w}_{s} }}{\partial x} + \frac{{\partial {\kern 1pt} \dot{w}_{s} }}{\partial x}\delta \, \dot{u}_{0} + \dot{v}_{0} \frac{{\partial \delta {\kern 1pt} \dot{w}_{s} }}{\partial y} + \frac{{\partial {\kern 1pt} \dot{w}_{s} }}{\partial y}\delta \, \dot{v}_{0} } \right) \\ & \quad + J_{1} \left( {\frac{{\partial \dot{w}_{b} }}{\partial x}\frac{{\partial \delta \, \dot{w}_{b} }}{\partial x} + \frac{{\partial \dot{w}_{b} }}{\partial y}\frac{{\partial \delta \, \dot{w}_{b} }}{\partial y}} \right) + K_{2} \left( {\frac{{\partial \dot{w}_{s} }}{\partial x}\frac{{\partial \delta \, \dot{w}_{s} }}{\partial x} + \frac{{\partial \dot{w}_{s} }}{\partial y}\frac{{\partial \delta \, \dot{w}_{s} }}{\partial y}} \right) \\ & \quad \left. { + J_{2} \left( {\frac{{\partial \dot{w}_{b} }}{\partial x}\frac{{\partial \delta \, \dot{w}_{s} }}{\partial x} + \frac{{\partial \dot{w}_{s} }}{\partial x}\frac{{\partial \delta \, \dot{w}_{b} }}{\partial x} + \frac{{\partial \dot{w}_{b} }}{\partial y}\frac{{\partial \delta \, \dot{w}_{s} }}{\partial y} + \frac{{\partial \dot{w}_{s} }}{\partial y}\frac{{\partial \delta \, \dot{w}_{b} }}{\partial y}} \right)} \right\}{\text{d}}A \\ \end{aligned}$$
(15)

where the dot superscript demonstrates differentiation concerning the variable of time \(t\), \(I_{i}\), \(J_{i}\), \(K_{i}\) terms define the mass moment of inertias of FG nanoplate as follows:

$$\left( {I_{0} ,I_{1} ,I_{2} } \right) = \int\limits_{ - h/2}^{h/2} {\left( {1,z,z^{2} } \right)\rho (z){\text{d}}z}$$
(16a)
$$\left( {J_{1} ,J_{2} ,K_{2} } \right) = \int\limits_{ - h/2}^{h/2} {\left( {f,z \, f,f^{2} } \right)\rho (z){\text{d}}z}$$
(16b)

Inserting Eqs. (13) and (15) in Eq. (12) and after some mathematical operations and simplification, the subsequent equations are found

$$\begin{aligned} & \delta u_{0} : \, \frac{{\partial N_{x} }}{\partial x} + \frac{{\partial N_{xy} }}{\partial y} = I_{0} \ddot{u}_{0} - I_{1} \frac{{\partial \ddot{w}_{b} }}{\partial x} - J_{1} \frac{{\partial \ddot{w}_{s} }}{\partial x} \\ & \delta v_{0} : \, \frac{{\partial N_{xy} }}{\partial x} + \frac{{\partial N_{y} }}{\partial y} = I_{01} \ddot{v}_{0} - I_{1} \frac{{\partial \ddot{w}_{b} }}{\partial y} - J_{1} \frac{{\partial \ddot{w}_{s} }}{\partial y} \\ & \delta w_{b} : \, \frac{{\partial^{2} M_{x}^{b} }}{{\partial x^{2} }} + 2\frac{{\partial^{2} M_{xy}^{b} }}{\partial x\partial y} + \frac{{\partial^{2} M_{y}^{b} }}{{\partial y^{2} }} \\ & \quad = I_{0} \left( {\ddot{w}_{b} + \ddot{w}_{s} } \right) + I_{1} \left( {\frac{{\partial \ddot{u}_{0} }}{\partial x} + \frac{{\partial \ddot{v}_{0} }}{\partial y}} \right) - I_{2} \nabla^{2} \ddot{w}_{b} - J_{2} \nabla^{2} \ddot{w}_{s} \\ & \delta w_{s} : \, \frac{{\partial^{2} M_{x}^{s} }}{{\partial x^{2} }} + 2\frac{{\partial^{2} M_{xy}^{s} }}{\partial x\partial y} + \frac{{\partial^{2} M_{y}^{s} }}{{\partial y^{2} }} + \frac{{\partial S_{xz}^{s} }}{\partial x} + \frac{{\partial S_{yz}^{s} }}{\partial y} \\ & \quad = I_{0} \left( {\ddot{w}_{b} + \ddot{w}_{s} } \right) + J_{1} \left( {\frac{{\partial \ddot{u}_{0} }}{\partial x} + \frac{{\partial \ddot{v}_{0} }}{\partial y}} \right) - J_{2} \nabla^{2} \ddot{w}_{b} - K_{2} \nabla^{2} \ddot{w}_{s} \\ \end{aligned}$$
(17)

Inserting Eqs. (6) and (11) in Eq. (14) and after some mathematical operations, the stress resultants concerning generalized displacements (\(u_{0}\),\(v_{0}\),\(w_{b}\),\(w_{s}\)) are as follows:

$$\begin{aligned} & \left\{ \begin{gathered} N \hfill \\ M^{b} \hfill \\ M^{s} \hfill \\ \end{gathered} \right\} - \mu \left( {\frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial y^{2} }}} \right)\left\{ \begin{gathered} N \hfill \\ M^{b} \hfill \\ M^{s} \hfill \\ \end{gathered} \right\} = \left[ {\begin{array}{*{20}c} A & B & {B^{s} } \\ B & D & {D^{s} } \\ {B^{s} } & {D^{s} } & {H^{s} } \\ \end{array} } \right]\left\{ \begin{gathered} \varepsilon \hfill \\ k^{b} \hfill \\ k^{s} \hfill \\ \end{gathered} \right\}, \\ & S - \mu \left( {\frac{{\partial^{2} S}}{{\partial x^{2} }} + \frac{{\partial^{2} S}}{{\partial y^{2} }}} \right) = A^{s} \gamma \\ \end{aligned}$$
(18)

where

$$N = \left\{ {N_{x} ,N_{y} ,N_{xy} } \right\}^{t} ,\quad M^{b} = \left\{ {M_{x}^{b} ,M_{y}^{b} ,M_{xy}^{b} } \right\}^{t} ,\quad M^{s} = \left\{ {M_{x}^{s} ,M_{y}^{s} ,M_{xy}^{s} } \right\}^{t}$$
(19a)
$$\varepsilon = \left\{ {\varepsilon_{x}^{0} ,\varepsilon_{y}^{0} ,\gamma_{xy}^{0} } \right\}^{t} ,\quad k^{b} = \left\{ {k_{x}^{b} ,k_{y}^{b} ,k_{xy}^{b} } \right\}^{t} ,\quad k^{s} = \left\{ {k_{x}^{s} ,k_{y}^{s} ,k_{xy}^{s} } \right\}^{t}$$
(19b)
$$A = \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & 0 \\ {A_{12} } & {A_{22} } & 0 \\ 0 & 0 & {A_{66} } \\ \end{array} } \right],\quad B = \left[ {\begin{array}{*{20}c} {B_{11} } & {B_{12} } & 0 \\ {B_{12} } & {B_{22} } & 0 \\ 0 & 0 & {B_{66} } \\ \end{array} } \right],\quad D = \left[ {\begin{array}{*{20}c} {D_{11} } & {D_{12} } & 0 \\ {D_{12} } & {D_{22} } & 0 \\ 0 & 0 & {D_{66} } \\ \end{array} } \right]$$
(19c)
$$B^{s} = \left[ {\begin{array}{*{20}c} {B_{11}^{s} } & {B_{12}^{s} } & 0 \\ {B_{12}^{s} } & {B_{22}^{s} } & 0 \\ 0 & 0 & {B_{66}^{s} } \\ \end{array} } \right],\quad D^{s} = \left[ {\begin{array}{*{20}c} {D_{11}^{s} } & {D_{12}^{s} } & 0 \\ {D_{12}^{s} } & {D_{22}^{s} } & 0 \\ 0 & 0 & {D_{66}^{s} } \\ \end{array} } \right],\quad H^{s} = \left[ {\begin{array}{*{20}c} {H_{11}^{s} } & {H_{12}^{s} } & 0 \\ {H_{12}^{s} } & {H_{22}^{s} } & 0 \\ 0 & 0 & {H_{66}^{s} } \\ \end{array} } \right]$$
(19d)
$$S = \left\{ {S_{xz}^{s} ,S_{yz}^{s} } \right\}^{t} ,\quad \gamma = \left\{ {\gamma_{xz}^{0} ,\gamma_{yz}^{0} } \right\}^{t} ,\quad A^{s} = \left[ {\begin{array}{*{20}c} {A_{44}^{s} } & 0 \\ 0 & {A_{55}^{s} } \\ \end{array} } \right]$$
(19e)

where \(A_{ij}\), \(B_{ij}\), \(D_{ij}\) are the material stiffness coefficients and defined as follows:

$$\left\{ {\begin{array}{*{20}c} {A_{11} } & {B_{11} } & {D_{11} } & {B_{11}^{s} } & {D_{11}^{s} } & {H_{11}^{s} } \\ {A_{12} } & {B_{12} } & {D_{12} } & {B_{12}^{s} } & {D_{12}^{s} } & {H_{12}^{s} } \\ {A_{66} } & {B_{66} } & {D_{66} } & {B_{66}^{s} } & {D_{66}^{s} } & {H_{66}^{s} } \\ \end{array} } \right\} = \int\limits_{ - h/2}^{h/2} {Q_{11} \left( {1,z,z^{2} ,f(z),z \, f(z),f^{2} (z)} \right)} \left\{ {\begin{array}{*{20}c} 1 \\ \nu \\ {\frac{1 - \nu }{2}} \\ \end{array} } \right\}{\text{d}}z$$
(20a)
$$\left( {A_{22} ,B_{22} ,D_{22} ,B_{22}^{s} ,D_{22}^{s} ,H_{22}^{s} } \right) = \left( {A_{11} ,B_{11} ,D_{11} ,B_{11}^{s} ,D_{11}^{s} ,H_{11}^{s} } \right)$$
(20b)
$$A_{44}^{s} = A_{55}^{s} = \int\limits_{ - h/2}^{h/2} {Q_{44} \left[ {g(z)} \right]^{2} {\text{d}}z}$$
(20c)

Inserting Eq. (18) in Eq. (17), the following equation is found:

$$\begin{aligned} & A_{11} \frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + A_{66} \frac{{\partial^{2} u0}}{{\partial y^{2} }} + \left( {A_{12} + A_{66} } \right)\frac{{\partial^{2} v}}{\partial x\partial y} - B_{11} \frac{{\partial^{3} w_{b} }}{{\partial x^{3} }} - \left( {B_{12} + 2B_{66} } \right)\frac{{\partial^{3} w_{b} }}{{\partial x\partial y^{2} }} \, \\ & \quad - B_{11}^{s} \frac{{\partial^{3} w_{s} }}{{\partial x^{3} }} - \left( {B_{12}^{s} + 2B_{66}^{s} } \right)\frac{{\partial^{3} w_{s} }}{{\partial x\partial y^{2} }} = \left( {1 - \mu \nabla^{2} } \right)\left[ {I_{0} \ddot{u}_{0} - I_{1} \frac{{\partial \ddot{w}_{b} }}{\partial x} - J_{1} \frac{{\partial \ddot{w}_{s} }}{\partial x}} \right], \\ \end{aligned}$$
(21a)
$$\begin{aligned} & \left( {A_{12} + A_{66} } \right)\frac{{\partial^{2} u_{0} }}{\partial x\partial y} + A_{66} \frac{{\partial^{2} v_{0} }}{{\partial x^{2} }} + A_{22} \frac{{\partial^{2} v_{0} }}{{\partial y^{2} }} - \left( {B_{12} + 2B_{66} } \right)\frac{{\partial^{3} w_{b} }}{{\partial x^{2} \partial y}} - B_{22} \frac{{\partial^{3} w_{b} }}{{\partial y^{3} }} \\ & \quad - B_{22}^{s} \frac{{\partial^{3} w_{s} }}{{\partial y^{3} }} - \left( {B_{12}^{s} + 2B_{66}^{s} } \right)\frac{{\partial^{3} w_{s} }}{{\partial x^{2} \partial y}} = \left( {1 - \mu \nabla^{2} } \right)\left[ {I_{0} \ddot{v}_{0} - I_{1} \frac{{\partial \ddot{w}_{b} }}{\partial y} - J_{1} \frac{{\partial \ddot{w}_{s} }}{\partial y}} \right] \\ \end{aligned}$$
(21b)
$$\begin{aligned} & B_{11} \frac{{\partial^{3} u_{0} }}{{\partial x^{3} }} + \left( {B_{12} + 2B_{66} } \right)\frac{{\partial^{3} u_{0} }}{{\partial x\partial y^{2} }} + \left( {B_{12} + 2B_{66} } \right)\frac{{\partial^{3} v_{0} }}{{\partial x^{2} \partial y}} + B_{22} \frac{{\partial^{3} v_{0} }}{{\partial y^{3} }} - D_{11} \frac{{\partial^{4} w_{b} }}{{\partial x^{4} }} \\ & \quad - 2\left( {D_{12} + 2D_{66} } \right)\frac{{\partial^{4} w_{b} }}{{\partial x^{2} \partial y^{2} }} - D_{22} \frac{{\partial^{4} w_{b} }}{{\partial y^{4} }} - D_{11}^{s} \frac{{\partial^{4} w_{s} }}{{\partial x^{4} }} - 2\left( {D_{12}^{s} + 2D_{66}^{s} } \right)\frac{{\partial^{4} w_{s} }}{{\partial x^{2} \partial y^{2} }} \\ & \quad - D_{22}^{s} \frac{{\partial^{4} w_{s} }}{{\partial y^{4} }} = \left( {1 - \mu \nabla^{2} } \right)\left[ {I_{0} \left( {\ddot{w}_{b} + \ddot{w}_{s} } \right) + I_{1} \left( {\frac{{\partial \ddot{u}_{0} }}{\partial x} + \frac{{\partial \ddot{v}_{0} }}{\partial y}} \right) - I_{2} \nabla^{2} \ddot{w}_{b} - J_{2} \nabla^{2} \ddot{w}_{s} } \right] \\ \end{aligned}$$
(21c)
$$\begin{aligned} & B_{11}^{s} \frac{{\partial^{3} u_{0} }}{{\partial x^{3} }} + \left( {B_{12}^{s} + 2B_{66}^{s} } \right)\frac{{\partial^{3} u_{0} }}{{\partial x\partial y^{2} }} + \left( {B_{12}^{s} + 2B_{66}^{s} } \right)\frac{{\partial^{3} v_{0} }}{{\partial x^{2} \partial y}} + B_{22}^{s} \frac{{\partial^{3} v_{0} }}{{\partial y^{3} }} - D_{11}^{s} \frac{{\partial^{4} w_{b} }}{{\partial x^{4} }} \\ & \quad - 2\left( {D_{12}^{s} + 2D_{66}^{s} } \right)\frac{{\partial^{4} w_{b} }}{{\partial x^{2} \partial y^{2} }} \, - D_{22}^{s} \frac{{\partial^{4} w_{b} }}{{\partial y^{4} }} - H_{11}^{s} \frac{{\partial^{4} w_{s} }}{{\partial x^{4} }} - 2\left( {H_{12}^{s} + 2H_{66}^{s} } \right)\frac{{\partial^{4} w_{s} }}{{\partial x^{2} \partial y^{2} }} \\ & \quad - H_{22}^{s} \frac{{\partial^{4} w_{s} }}{{\partial y^{4} }} + A_{55}^{s} \frac{{\partial^{2} w_{s} }}{{\partial x^{2} }} + A_{44}^{s} \frac{{\partial^{2} w_{s} }}{{\partial y^{2} }} \\ & = \left( {1 - \mu \nabla^{2} } \right)\left[ {I_{0} \left( {\ddot{w}_{b} + \ddot{w}_{s} } \right) + J_{1} \left( {\frac{{\partial \ddot{u}_{0} }}{\partial x} + \frac{{\partial \ddot{v}_{0} }}{\partial y}} \right) - J_{2} \nabla^{2} \ddot{w}_{b} - K_{2} \nabla^{2} \ddot{w}_{s} } \right] \\ \end{aligned}$$
(21d)

3 The solution of the problem

In the present part, solutions for the free vibration of FG nanoplate under four different boundary conditions are found.

The boundary conditions of a random edge are defined as follows:

Clamped (C) edge boundary conditions

$$u_{0} = v_{0} = w_{b} = w_{s} = \frac{{\partial w_{b} }}{\partial x} = \frac{{\partial w_{s} }}{\partial x} = 0\,\,\,{\text{at}}\,\,x = 0,a$$
(22a)
$$u_{0} = v_{0} = w_{b} = w_{s} = \frac{{\partial w_{b} }}{\partial y} = \frac{{\partial w_{s} }}{\partial y} = 0\,\,\,{\text{at}}\,\,y = 0,b$$
(22b)

Simply supported (S) edge boundary conditions

$$N_{x} = v_{0} = w_{b} = w_{s} = M_{x} = 0\quad {\text{at}}\quad x = 0,a$$
(23a)
$$u_{0} = N{}_{y} = w_{b} = w_{s} = M_{y} = 0\quad {\text{at}}\quad y = 0,b$$
(23b)

Free (F) edge boundary conditions

$$N_{x} = N_{xy} = \frac{{\partial M_{x} }}{\partial x} + 2\frac{{\partial M_{xy} }}{\partial y} = Q_{x} = M_{x} = 0\,\,\,{\text{at}}\,\,x = 0,a$$
(24a)
$$N_{xy} = N_{y} + 2\frac{{\partial M_{xy} }}{\partial y} + \frac{{\partial M_{y} }}{\partial y} = Q_{y} = M_{y} = 0\,\,\,{\text{at}}\,\,y = 0,b$$
(24b)

The subsequent appropriate expressions are utilized for the related boundary conditions

$$\left\{ {\begin{array}{*{20}c} {u_{0} } \\ {v_{0} } \\ {w_{b} } \\ {w_{s} } \\ \end{array} } \right\} = \left\{ \begin{gathered} U_{mn} \frac{{\partial X_{m} \left( x \right)}}{\partial x}Y_{n} \left( y \right){\text{e}}^{{{\text{i}}\omega t}} \hfill \\ V_{mn} X_{n} \left( x \right)\frac{{\partial Y_{n} \left( y \right)}}{\partial y}{\text{e}}^{{{\text{i}}\omega t}} \hfill \\ W_{bmn} X_{n} \left( x \right)Y_{n} \left( y \right){\text{e}}^{{{\text{i}}\omega t}} \hfill \\ W_{smn} X_{n} \left( x \right)Y_{n} \left( y \right){\text{e}}^{{{\text{i}}\omega t}} \hfill \\ \end{gathered} \right\}$$
(25)

where \(U_{mn}\), \(V_{mn}\), \(W_{bmn}\), and \(W_{smn}\) identify the random parameters and \(\omega = \omega_{mn}\) shows the eigenfrequency related to \(\left( {m,n} \right)^{{{\text{th}}}}\) eigenmode.

The following functions for \(X_{m} \left( x \right)\) and \(Y_{n} \left( y \right)\) which are suggested by Reddy [54, 55] are utilized to satisfy various boundary conditions in Eqs. (22)–(24) and signify the deflected surface of the nanoplate approximately:

SSSS

$$\begin{aligned} & X_{m} \left( x \right) = \sin \left( {\lambda x} \right),\,\,\lambda = \frac{m\pi }{a} \\ & Y_{n} \left( y \right) = \sin \left( {\beta y} \right),\,\,\beta = \frac{n\pi }{b} \\ \end{aligned}$$
(26)

CCCC

$$\begin{aligned} & X_{m} \left( x \right) = \left[ {\sin \left( {\lambda x} \right) - \sinh \left( {\lambda x} \right)} \right] - \left[ {\frac{{\sin \left( {\lambda a} \right) - \sinh \left( {\lambda a} \right)}}{{\cos \left( {\lambda a} \right) - \cosh \left( {\lambda a} \right)}}} \right]\left[ {\cos \left( {\lambda x} \right) - \cosh \left( {\lambda x} \right)} \right],\,\,\lambda = \frac{{\left( {m + 0.5} \right)\pi }}{a} \\ & Y_{n} \left( y \right) = \left[ {\sin \left( {\beta y} \right) - \sinh \left( {\beta y} \right)} \right] - \left[ {\frac{{\sin \left( {\beta b} \right) - \sinh \left( {\beta b} \right)}}{{\cos \left( {\beta b} \right) - \cosh \left( {\beta b} \right)}}} \right]\left[ {\cos \left( {\beta y} \right) - \cosh \left( {\beta y} \right)} \right],\,\,\beta = \frac{{\left( {n + 0.5} \right)\pi }}{b} \\ \end{aligned}$$
(27)

CSCS

$$\begin{aligned} & X_{m} \left( x \right) = \left[ {\sin \left( {\lambda x} \right) - \sinh \left( {\lambda x} \right)} \right] - \left[ {\frac{{\sin \left( {\lambda a} \right) + \sinh \left( {\lambda a} \right)}}{{\cos \left( {\lambda a} \right) + \cosh \left( {\lambda a} \right)}}} \right]\left[ {\cos \left( {\lambda x} \right) - \cosh \left( {\lambda x} \right)} \right],\,\lambda = \frac{{\left( {m + 0.25} \right)\pi }}{a} \\ & Y_{n} \left( y \right) = \left[ {\sin \left( {\beta y} \right) - \sinh \left( {\beta y} \right)} \right] - \left[ {\frac{{\sin \left( {\beta b} \right) + \sinh \left( {\beta b} \right)}}{{\cos \left( {\beta b} \right) + \cosh \left( {\beta b} \right)}}} \right]\left[ {\cos \left( {\beta y} \right) - \cosh \left( {\beta y} \right)} \right],\,\beta = \frac{{\left( {n + 0.25} \right)\pi }}{b} \\ \end{aligned}$$
(28)

FCFC

$$\begin{aligned} & X_{m} \left( x \right) = \left[ {\sin \left( {\lambda x} \right) - \sinh \left( {\lambda x} \right)} \right] - \left[ {\frac{{\sin \left( {\lambda a} \right) - \sinh \left( {\lambda a} \right)}}{{\cos \left( {\lambda a} \right) - \cosh \left( {\lambda a} \right)}}} \right]\left[ {\cos \left( {\lambda x} \right) - \cosh \left( {\lambda x} \right)} \right],\,\,\lambda = \frac{{\left( {m - 0.25} \right)\pi }}{a} \\ & Y_{n} \left( y \right) = \left[ {\sin \left( {\beta y} \right) - \sinh \left( {\beta y} \right)} \right] - \left[ {\frac{{\sin \left( {\beta b} \right) - \sinh \left( {\beta b} \right)}}{{\cos \left( {\beta b} \right) - \cosh \left( {\beta b} \right)}}} \right]\left[ {\cos \left( {\beta y} \right) - \cosh \left( {\beta y} \right)} \right],\,\,\beta = \frac{{\left( {n - 0.25} \right)\pi }}{b} \\ \end{aligned}$$
(29)

Substituting the expression (25) in Eqs. (21) and multiplying each eigenfunction with the corresponding equation and integrating throughout the solution domain, and after some mathematical operations, the following equation is found

$$\left( {\left[ {\begin{array}{*{20}c} {a{}_{11}} & {a{}_{12}} & {a{}_{13}} & {a{}_{14}} \\ {a{}_{21}} & {a{}_{22}} & {a{}_{23}} & {a{}_{24}} \\ {a{}_{31}} & {a{}_{32}} & {a{}_{33}} & {a{}_{34}} \\ {a{}_{41}} & {a{}_{42}} & {a{}_{43}} & {a{}_{44}} \\ \end{array} } \right] - \omega^{2} \left[ {\begin{array}{*{20}c} {m{}_{11}} & 0 & {m{}_{13}} & {m{}_{14}} \\ 0 & {m{}_{22}} & {m{}_{23}} & {m{}_{24}} \\ {m{}_{31}} & {m{}_{32}} & {m{}_{33}} & {m{}_{34}} \\ {m{}_{41}} & {m{}_{42}} & {m{}_{43}} & {m{}_{44}} \\ \end{array} } \right]} \right)\left\{ {\begin{array}{*{20}c} {U_{mn} } \\ {V_{mn} } \\ {W_{bmn} } \\ {W_{smn} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right\}$$
(30)

in which

$$\begin{aligned} & a_{11} = A_{11} \alpha_{12} + A_{66} \alpha_{8} ,\,\,a_{12} = \left( {A_{12} + A_{66} } \right)\alpha_{8} ,\,\,a_{13} = - B_{11} \alpha_{12} - \left( {B_{12} + 2B_{66} } \right)\alpha_{8} , \\ & a_{14} = - \left( {B_{12}^{s} + 2B_{66}^{s} } \right)\alpha_{8} - B_{11}^{s} \alpha_{12} ,\,\, \\ & a_{21} = \left( {A_{12} + A_{66} } \right)\alpha_{10} ,\,a_{22} = A_{22} \alpha_{4} + A_{66} \alpha_{10} ,a_{23} = - B_{22} \alpha_{4} - \left( {B_{12} + 2B_{66} } \right)\alpha_{10} , \\ & a_{24} = - \left( {B_{12}^{s} + 2B_{66} } \right)\alpha_{10} - B_{22}^{s} \alpha_{4} , \\ & a_{31} = B_{11} \alpha_{13} + \left( {B_{12} + 2B_{66} } \right)\alpha_{11} ,\,\,a_{32} = \left( {B_{12} + 2B_{66} } \right)\alpha_{11} + B_{22} \alpha_{5} ,\,\, \\ & a_{33} = - D_{11} \alpha_{13} - 2\left( {D_{12} + 2D_{66} } \right)\alpha_{11} - D_{22} \alpha_{5} ,\, \\ & a_{34} = - D_{11}^{s} \alpha_{13} - 2\left( {D_{12}^{s} + 2D_{66}^{s} } \right)\alpha_{11} - D_{66}^{s} \alpha_{5} , \\ & a_{41} = B_{11}^{s} \alpha_{13} + \left( {B_{12}^{s} + 2B_{66}^{s} } \right)\alpha_{11} ,\,\,a_{42} = \left( {B_{12}^{s} + 2B_{66}^{s} } \right)\alpha_{11} + B_{22}^{s} \alpha_{5} ,\,\, \\ & a_{43} = - D_{11}^{s} \alpha_{13} - 2\left( {D_{12}^{s} + 2D_{66}^{s} } \right)\alpha_{11} - D_{22}^{s} \alpha_{5} ,\, \\ & a_{44} = - H_{11}^{s} \alpha_{13} - 2\left( {H_{12}^{s} + 2H_{66}^{s} } \right)\alpha_{11} - H_{22}^{s} \alpha_{5} + A_{44}^{s} \alpha_{9} + A_{55}^{s} \alpha_{3} \\ \end{aligned}$$
(31)

and

$$\begin{aligned} & m_{11} = - I_{0} \left[ {\alpha_{6} - \mu \left( {\alpha_{12} + \alpha_{8} } \right)} \right],\,m_{12} = 0,\,\,m_{13} = I_{1} \left[ {\alpha_{6} - \mu \left( {\alpha_{12} + \alpha_{8} } \right)} \right],\, \\ & m_{14} = J_{1} \left[ {\alpha_{6} - \mu \left( {\alpha_{12} + \alpha_{8} } \right)} \right],\,\, \\ & m_{21} = 0,\,\,m_{22} = - I_{0} \left[ {\alpha_{2} - \mu \left( {\alpha_{10} + \alpha_{4} } \right)} \right],\, \\ & m_{23} = I_{1} \left[ {\alpha_{2} - \mu \left( {\alpha_{10} + \alpha_{4} } \right)} \right],\,\,m_{24} = J_{1} \left[ {\alpha_{2} - \mu \left( {\alpha_{10} + \alpha_{4} } \right)} \right], \\ & m_{31} = - I_{1} \left[ {\alpha_{9} - \mu \left( {\alpha_{13} + \alpha_{11} } \right)} \right],\,m_{32} = - I_{1} \left[ {\left( {\alpha_{3} - \mu \left( {\alpha_{11} + \alpha_{5} } \right)} \right)} \right], \\ & m_{33} = - I_{0} \left[ {\alpha_{1} - \mu \left( {\alpha_{9} + \alpha_{3} } \right)} \right] + I_{2} \left[ {\left( {\alpha_{9} + \alpha_{3} } \right) - \mu \left( {\alpha_{13} + \alpha_{5} + 2\alpha_{11} } \right)} \right], \\ & m_{34} = - I_{0} \left[ {\alpha_{1} - \mu \left( {\alpha_{9} + \alpha_{3} } \right)} \right] + J_{2} \left[ {\left( {\alpha_{9} + \alpha_{3} } \right) - \mu \left( {\alpha_{13} + \alpha_{5} + 2\alpha_{11} } \right)} \right], \\ & m_{41} = - J_{1} \left[ {\alpha_{9} - \mu \left( {\alpha_{13} + \alpha_{11} } \right)} \right],m_{42} = - J_{1} \left[ {\alpha_{3} - \mu \left( {\alpha_{11} + \alpha_{5} } \right)} \right], \\ & m_{43} = - I_{0} \left[ {\alpha_{1} - \mu \left( {\alpha_{9} + \alpha_{3} } \right)} \right] + J_{2} \left[ {\left( {\alpha_{9} + \alpha_{3} } \right) - \mu \left( {\alpha_{13} + \alpha_{5} + 2\alpha_{11} } \right)} \right], \\ & m_{44} = - I_{0} \left[ {\alpha_{1} - \mu \left( {\alpha_{9} + \alpha_{3} } \right)} \right] + K_{2} \left[ {\left( {\alpha_{9} + \alpha_{3} } \right) - \mu \left( {\alpha_{13} + \alpha_{5} + 2\alpha_{11} } \right)} \right] \\ \end{aligned}$$
(32)

with

$$\begin{aligned} & \left( {\alpha_{1} ,\alpha_{3} ,\alpha_{5} } \right) = \int\limits_{0}^{b} {\int\limits_{0}^{a} {\left( {X_{m} Y_{n} ,X_{m} Y_{n}^{{{\prime \prime }}} ,X_{m} Y_{n}^{{{\prime \prime \prime \prime }}} } \right)} } X_{m} Y_{n} {\text{d}}x{\text{d}}y \\ & \left( {\alpha_{2} ,\alpha_{4} ,\alpha_{10} } \right) = \int\limits_{0}^{b} {\int\limits_{0}^{a} {\left( {X_{m} Y_{n}^{{\prime }} ,X_{m} Y_{n}^{{{\prime \prime }}} ,X_{m}^{{{\prime \prime }}} Y_{n}^{{\prime }} } \right)} } X_{m} Y_{n}^{{\prime }} {\text{d}}x{\text{d}}y \\ & \left( {\alpha_{6} ,\alpha_{8} ,\alpha_{12} } \right) = \int\limits_{0}^{b} {\int\limits_{0}^{a} {\left( {X_{m}^{{\prime }} Y_{n} ,X_{m}^{{\prime }} Y_{n}^{{{\prime \prime }}} ,X_{m}^{{{\prime \prime \prime }}} Y_{n} } \right)} } X_{m}^{{\prime }} Y_{n} {\text{d}}x{\text{d}}y \\ & \left( {\alpha_{7} ,\alpha_{9} ,\alpha_{11} ,\alpha_{13} } \right) = \int\limits_{0}^{b} {\int\limits_{0}^{a} {\left( {X_{m}^{{\prime }} Y_{n}^{{\prime }} ,X_{m}^{{{\prime \prime }}} Y_{n} ,X_{m}^{{\prime }} Y_{n}^{{{\prime \prime }}} ,X_{m}^{{{\prime \prime \prime \prime }}} Y_{n} } \right)} } X_{m} Y_{n} {\text{d}}x{\text{d}}y \\ \end{aligned}$$
(33)

The nontrivial solution of the present problem is found equating the determinant of Eq. (30) to zero.

4 The numerical results and discussion

Herein numerous examples are given for validating the accuracy of the current solution procedure as well as the investigation of the natural frequencies of FG nanoplate considering four different cases of boundary conditions. For this aim, in Tables 1, 2 and 3 comparison studies are given to validate the accuracy of the present work. Then, detailed analyses are performed to study the influence of different parameters such as vibration mode, the aspect ratio, boundary conditions, power-law index, and non-local parameter on natural frequencies of the FG nanoplate in Tables 4, 5 and 6 and Fig. 2.

Table 1 The non-dimensional fundamental frequencies of FG nanoplate against the varying non-local parameter
Full size table
Table 2 The non-dimensional frequencies of the first four modes of FG nanoplate with SSSS edges against the varying non-local parameter and power-law index
Full size table
Table 3 The non-dimensional frequencies of the first four modes of FG nanoplate with CCCC edges against the varying non-local parameter and power-law index
Full size table
Table 4 The change in the non-dimensional frequencies of the first four modes of FG square nanoplates under different boundary conditions against the varying non-local parameter and power-law index
Full size table
Table 5 The change in the non-dimensional fundamental frequency of FG rectangular nanoplates under different boundary conditions against the varying non-local parameter and power-law index
Full size table
Table 6 The change in the frequency ratio of FG rectangular nanoplates under different boundary conditions against the non-local parameter
Full size table
Fig. 2
figure 2

The change in the non-dimensional fundamental frequencies of FG rectangular nanoplates under different boundary conditions against the varying aspect ratio

Full size image

In all numerical analyses, the free vibration analysis is performed considering that the top surface of the plate is Si3N4 (ceramic) and the bottom surface is SUS304 (metal). Young’s modulus, \(E\), and mass density, \(\rho\), are taken to be \(E_{{\text{c}}} = 348.43\,{\text{GPa}}\), \(\rho_{{\text{c}}} = 2370\,{\text{kg}}/{\text{m}}^{3}\) for Si3N4 and \(E_{{\text{m}}} = 201.01\,{\text{GPa}}\), \(\rho_{m} = 8166\,{\text{kg}}/{\text{m}}^{3}\) for SUS304. Besides, the non-dimensional natural frequency, \(\Omega\), and frequency ratio, \(F_{{\text{r}}}\), are expressed as follows:

$$\Omega _{i} = \omega _{i} h\sqrt {\frac{{\rho _{c} }}{{G_{c} }}} ,\,\,F_{{{\text{r}}_{i} }} = \frac{{\overline{\omega } _{{i_{{{\text{NL}}}} }} }}{{\overline{\omega } _{{i_{{\text{L}}} }} }}\,\,,\,\,i = 1,2,3,4$$

where \(\rho_{{\text{c}}}\) and \(G_{{\text{c}}}\) are the mass density and shear modulus of the ceramic constituent, respectively, \(\overline{\omega }_{{i_{{{\text{NL}}}} }}\) and \(\overline{\omega }_{{i_{{{\text{L}}}} }}\) are the non-local and local (\(\mu = 0\)) non-dimensional frequencies, respectively.

4.1 Comparison examples

Example 1

The non-dimensional fundamental natural frequencies, \(\Omega_{1}\), of FG square nanoplates versus the varying non-local parameter (\(\mu\)) are checked against the findings of Natarajan et al. [34] and Zargaripoor et al. [42], in Table 1. Here, fully simply supported (SSSS), fully clamped (CCCC) and SCSC edge conditions, \(a/b = 1\) and \(a/h = 10\), are considered.

Example 2

The non-dimensional frequencies, \(\Omega_{i}\), of the first four modes of FG square nanoplates versus varying non-local parameter (\(\mu\)) and power-law exponent (\(k\)) are checked against the findings of Natarajan et al. [34] and Zargaripoor et al. [42], in Table 2. Here, SSSS edge conditions \(a/b = 1\) and \(a/h = 10\) are considered.

Example 3

The non-dimensional frequencies, \(\Omega_{i}\), of the first four modes of FG square nanoplates versus varying non-local parameter (\(\mu\)) and power-law exponent (\(k\)) are checked against the findings of Natarajan et al. [34] and Zargaripoor et al. [42], in Table 2. Here, CCCC edge conditions \(a/b = 1\) and \(a/h = 10\) are considered.

Consequently, it is realized that the obtained results are coinciding with the existing ones.

4.2 Illustrative examples

Example 4

The influence of varying non-local parameter, \(\mu\), and power-law index, \(k\), on non-dimensional first four natural frequencies, \(\Omega_{i} \,\,(i = 1,2,3,4)\), of FG nanoplates under different boundary conditions is examined for square and rectangular plates in Tables 5 and 6, respectively. Here, \(a/h = 10\), \(a/b = 1\), and \(a/b = 2\) are considered. The findings revealed that the values of \(\Omega_{i}\) decrease with the increment of \(k\) since the percentage of metal phases that are weaker than ceramic phases become more prominent. The influence of the variation of \(k\) on the values of \(\Omega_{i}\) is independent of the variation of the non-local parameter, mode number, and edge conditions. Furthermore, the values of \(\Omega_{i}\) decrease with the increase in the \(\mu\). Note that the influence of the variation of \(\mu\) on the values of \(\Omega_{i}\) is changing according to the boundary conditions, as well as the influence of the variation of \(\mu\) on the values of \(\Omega_{i}\) increases with the increment of the number of the mode, while it is independent of the variation of the \(k\).

Example 5

The influence of varying non-local parameter, \(\mu\), on the frequency ratio, \(F_{{{\text{r}}i}} \,\,(i = 1,2,3,4)\), of FG rectangular nanoplates versus four distinct boundary conditions is examined in Table 6. Here, \(k = 2\), \(a/h = 10\), and \(a/b = 2\) are considered. The results revealed that the values of \(F_{{{\text{r}}i}}\) decrease with the increment of \(\mu\). Note that the influence of the variation of \(\mu\) on the values of is \(F_{{{\text{r}}i}}\) which is changing according to the boundary conditions, as well as the influence of the variation of \(\mu\) on the values of \(F_{{{\text{r}}i}}\) frequency ratio of FG nanoplates changes with the number of the mode.

Example 6

The influence of varying aspect ratio, \(a/b\) and non-local parameter, \(\mu \left( {{\text{nm}}^{2} } \right)\), on the non-dimensional fundamental frequencies, \(\Omega_{1}\), of FG rectangular nanoplates versus four distinct boundary conditions is examined in Fig. 2. Here, \(k = 5\), \(a/h = 10\) are considered. The results indicated that the values of \(\Omega_{1}\) increase with the increase in \(a/b\). Note that the influence of the variation of \(a/b\) on the values of \(\Omega_{1}\) is changing according to the boundary conditions, as well as the influence of the variation of \(a/b\) on the values of \(\Omega_{1}\) decreases with the increment of \(\mu\).

5 Conclusions

In the present study, an analytical solution for the free vibration of nanoplates made of FGMs under four different boundary conditions was provided. For this aim, a new refined plate theory with four variables based on the theory of non-local elasticity including the small-scale influence. Here, the number of unknowns and governing equations of the present model were reduced to four separating the vertical displacement into shear and bending components, and so the number of unknowns has become less than the other alternative theories. The influence of the different parameters such as vibration mode, the aspect ratio, boundary conditions, power-law index, and non-local parameter on the natural frequencies of the FG nanoplate is discussed, in detail.

In sum, the following results were obtained:

  • The non-dimensional natural frequencies reduce with the increment of the power-law index

  • The non-dimensional natural frequencies reduce with the increment of the non-local parameter

  • The influence of variation of the non-local parameter on non-dimensional natural frequencies increases with the increment of the mode number

  • The frequency ratio reduces with the increment of non-local parameter

  • The influence of non-local parameter on the frequency ratio changes with mode number

  • The values of non-dimensional fundamental natural frequency increase with the increase in aspect ratio.

  • The influence of aspect ratio on the non-dimensional fundamental natural frequency decreases with the increment of the non-local parameter

  • All said influence on non-dimensional natural frequencies changes depending on boundary conditions

Consequently, it is decided that considered factors have key influences on the natural frequencies of FG nanoplates. Furthermore, the proposed exact solution method not only satisfactorily handled the present problem and yielded successful results but also it supplied ease for the non-local vibration analysis of FG nanoplates. In the future studies, the presented solution procedure will be extended for mechanical behaviors of other types of structures composed of varied materials with macro-/micro-dimensions.