1 Introduction

Functionally graded materials (FGMs) are a new class of composite structures that are of great interest for engineering design and manufacture. FGMs have continuous variation of material properties in one or more directions. Typically, FGMs are made from a mixture of ceramics and metals with the variation of the volume fraction according to a power law through thickness [1, 2]. FGMs have received wide applications as structural components in modern industries such as mechanical, aerospace, nuclear reactors, and civil engineering.

In the process of FGMs fabrication, the existence of porosities and micro-voids inside the materials possibly occurs due to technical problems, especially at the ceramic zone. The impact of this failure has been the subject of much attention, as evidenced by the large number of studies on this subject. For porous plates and shells, Magnucka–Blandzi [3] studied the dynamic stability for a circular porous plate to determine the critical loads. The influence of unstable regions for the Mathieu equation was described. She [4, 5] also examined the nonlinear dynamic stability and axi-symmetrical deflection and buckling of circular porous plates. Belica and Magnucki [6, 7] investigated the dynamic stability of a porous cylindrical shell under different loading.

Wattanasakulpong and Ungbhakor [8] investigate linear and nonlinear vibration problems of FGMs beams having porosities. Wattanasakulpong et al. and Ebrahimi [9, 10] presented a work on porosities happening inside FGMs samples fabricated by a multi-step sequential infiltration technique. FGMs may possess a number of advantages such as high resistance to temperature gradients, significant reduction in residual and thermal stresses, and high wear resistance.

Composite structures on elastic foundations have wide applications in modern engineering and pose great technical problems in structural design. In the vast majority of the classical mechanics, plates on an elastic foundation are a simplified approach for two continuum media interacting together such as flexible structural elements in contact with a bearing soil, rubber, polymer or any deformable substrate material. The mechanical behaviour of elastic foundations was discussed by Winkler [11], whereas Pasternak [12] presented a two-parameter model, which considers the shear deformation between the springs over the one parameter model. The Winkler model can be considered a special case of Pasternak model by setting the shear modulus to zero. A review of literature shows that there are only a few studies on free vibration of rectangular and porous nano FGM plates based on the nonlocal plate shear deformation theory. It is well-known that classical Love–Kirchhoff theory of beam bending, also known as elementary theory of bending (CPT), disregards the effects of the shear deformation. The theory is suitable for slender plate and is not suitable for thick or deep, implying that the transverse shear strain is zero. Timoshenko and Reissner–Mindlin showed that the effect of transverse shear is much greater than that of rotatory inertia on the response of transverse vibration of prismatic bars and thick plate (FPT). In this theory, transverse shear strain distribution is assumed to be constant through the plates thickness and thus requires shear correction factor to appropriately represent the strain energy of deformation. In order to overcome the limitations of FPT, higher order shear deformation theories (HPT) involving higher order terms in Taylor’s expansions of the displacements in the thickness coordinate were developed by Reddy and several researchers [13–21]. A two-variable refined plate theory (RPT) using only two unknown functions was developed by Shimpi [22] for isotropic plates, and was extended by Shimpi and Patel [23, 24] to orthotropic plates. Recently, a two-variable RPT was developed by Kim et al. [25], El Meiche et al., Mechab et al. and Thai et al. [26–32].

Nanostructural elements are objects of intermediate size between molecular and microscopic structures such as nanobeams, nanomembranes and nanoplates. In recent years, these elements are commonly used in nanoelectromechanical (NEM) devices. Hence, accurate prediction of their vibrational behaviour becomes essential for engineering design and manufacture. The nonlocal elasticity theory is also used as proposed and developed by Eringen [33, 34], nonlocal theory of Eringen is based on this assumption that the stress at a point is considered as a function of the strain field at all neighbour points in the continuum body. The inter-atomic forces and atomic length scales directly come to the constitutive equations as material parameters. Importance of accurate prediction of nanostructures vibration characteristics has been discussed by Lu et al., eAghababaei and Reddy [35, 36]. Hence, many papers have been published on this topic, specially for analysing nonlocal plate models of bending, vibration and buckling [37–39], Malekzadeh and Shojaee [40] analysed the free vibration of nanoplates based on a nonlocal two-variable RPT.

This paper investigates the effect of porosities occurring inside FGMs during fabrication, the new model ψ(z) is employed for analysis the FGM nanoplates resting on Winkler–Pasternak elastic foundations based on two-variable RPT. The small-scale effects are introduced using the nonlocal elasticity theory with a new shear deformation function. The governing equations are obtained through the Hamilton’s principle. The effect of material property, porosities, various boundary conditions and elastic foundation stiffnesses on free vibration are presented. The present solutions are compared with those obtained by other researchers.

2 Mathematical formulations

2.1 Theory of nonlocal elasticity

This theory assumes that the stress state at a reference point \( X \) in the body is regarded to be dependent not only on the strain state at \( X \) but also in the strain states at all other points \( X^{\prime} \) of the body.

The most general form of the constitutive relation in the nonlocal elasticity type representation involves an integral over the entire region of interest. The integral contains a nonlocal kernel function, which describes the relative influences of the strains at various locations on the stress at a given location. For nonlocal linear elastic solids, the equations of motion have the form [33–35]

$$ t_{ij,j} + f_{i} = \rho {\textit{\"{u}}_{i}} $$
(1)

where \( \rho \) and \( f_{i} \) are, respectively, the mass density and the body (and/or applied) forces; \( u_{i} \) is the displacement vector; and \( t_{ij} \) is the stress tensor of the nonlocal elasticity defined by

$$ t_{ij} \left(X \right) = \int\limits_{V} {\alpha \left({\left| {X^{\prime} - X} \right|} \right)} \;\sigma_{ij} \left({X^{\prime}} \right)\;{\text{d}}v\left({X^{\prime}} \right) $$
(2)

in which \( X \) is a reference point in the body; \( \alpha \left({\left| {X^{\prime} - X} \right|} \right) \) is the nonlocal kernel function; and \( \sigma_{ij} \) is the local stress tensor of classical elasticity theory at any point \( X^{\prime} \) in the body and satisfies the constitutive relations

$$ \sigma_{ij} = Q_{ijkl} \varepsilon_{kl} $$
(3)
$$ \varepsilon_{kl} = \frac{1}{2}\left({u_{k,l} + u_{l,k}} \right) $$
(4)

for a general elastic material, in which \( Q_{ijkl} \) are the elastic modulus components with the symmetry properties \( Q_{ijkl} = Q_{jikl} = Q_{ijlk} = Q_{klij} \), and \( \varepsilon_{kl} \) is the strain tensor. It should be emphasized here that the boundary conditions involving tractions are based on the nonlocal stress tensor \( t_{ij} \) and not on the local stress tensor \( \sigma_{ij} \).

The properties of the nonlocal kernel \( \alpha \left({\left| {X^{\prime} - X} \right|} \right) \) have been discussed in detail by Eringen [33]. When \( \alpha \left({\left| X \right|} \right) \) takes on a Greens function of a linear differential operator \( {\mathcal{L}} \), i.e.

$$ {\mathcal{L}}\alpha \left({\left| {X^{\prime} - X} \right|} \right) = \delta \left({\left| {X^{\prime} - X} \right|} \right) $$
(5)

The nonlocal constitutive relation (2) is reduced to the differential equation

$$ {\mathcal{L}}t_{ij} = \sigma_{ij} $$
(6)

and the integro-partial differential Eq. (1) is correspondingly reduced to the partial differential equation

$$ \sigma_{ij} + {\mathcal{L}}\left({f_{i} - \rho {\textit{\"{u}}}} \right) = 0 $$
(7)

By matching the dispersion curves with lattice models, Eringen [33, 34] proposed a nonlocal model with the linear differential operator \( {\mathcal{L}} \) defined by

$$ {\mathcal{L}} = 1 - \mu^{2} \nabla^{2} $$
(8)

where \( \mu = e_{0} a \), (a) is an internal characteristic length (lattice parameter, granular size or molecular diameters) and \( e_{0} \) is a constant appropriate to each material for adjusting the model to match some reliable results from experiments or other theories. Therefore, according to Eqs. (3), (4), (6) and (8), the constitutive relations may be simplified to

$$ \left({1 - \mu^{2} \nabla^{2}} \right)\;t_{ij} = \left({1 - \left({e_{0} a} \right)^{2} \nabla^{2}} \right)\;t_{ij} = \sigma_{ij} = Q_{ijkl} \varepsilon_{kl} $$
(9)

For simplicity and to avoid solving integro-partial differential equations, the nonlocal elasticity model, defined by the relations (6)–(9), has been widely adopted in tackling various problems of linear elasticity and micro-/nanostructural mechanics.

For general boundary value problems, like a nonzero boundary force conditions, the method for the solution of the nonlocal plate theories will be more complicated than those of the local plate theories. It is known that the force boundary conditions for the nonlocal plate models are based on the nonlocal components \( N_{ij} \) and \( M_{ij} \) defined as

$$ N_{ij} = \int\limits_{{{{- h} \mathord{\left/{\vphantom {{- h} 2}} \right. \kern-0pt} 2}}}^{{{h \mathord{\left/{\vphantom {h 2}} \right. \kern-0pt} 2}}} {t_{ij} {\text{d}}z},\quad M_{ij} = \int\limits_{{{{- h} \mathord{\left/{\vphantom {{- h} 2}} \right. \kern-0pt} 2}}}^{{{h \mathord{\left/{\vphantom {h 2}} \right. \kern-0pt} 2}}} {zt_{ij} {\text{d}}z} $$
(10)

The global governing equations of the plate structures can be derived by integrating the equations of motion (1) through the thickness. By multiplying Eq. (1) by \( {\text{d}}z \), then integrating through the thickness and noting (10), we have

$$ N_{ij,j} + \int\limits_{{- \frac{h}{2}}}^{{\frac{h}{2}}} {f_{i} {\text{d}}z} = \int\limits_{{- \frac{h}{2}}}^{{\frac{h}{2}}} {\rho {\textit{\"{u}}_{i}} {\text{d}}z} $$
(11)

Furthermore, multiplying Eq. (1) by \( z{\text{d}}z \) followed by integrating through the thickness and noting (10), we have

$$ M_{ij,j} + \int\limits_{{- \frac{h}{2}}}^{{\frac{h}{2}}} {zf_{i} {\text{d}}z} = \int\limits_{{- \frac{h}{2}}}^{{\frac{h}{2}}} {\rho z {\textit{\"{u}}_{i}} {\text{d}}z} $$
(12)

By applying the linear differential operator (8) and the differential Eq. (6) to Eq. (10), we have

$$ \left({1 - \mu^{2} \nabla^{2}} \right)N_{ij} = N_{ij}^{L} \;{\text{and}}\;\left({1 - \mu^{2} \nabla^{2}} \right)M_{ij} = M_{ij}^{L} $$
(13)

where \( N_{ij}^{L} \) and \( M_{ij}^{L} \) are the local (classical) resultant forces and the local resultant moments defined by

$$ N_{ij}^{L} = \int\limits_{{{{- h} \mathord{\left/{\vphantom {{- h} 2}} \right. \kern-0pt} 2}}}^{{{h \mathord{\left/{\vphantom {h 2}} \right. \kern-0pt} 2}}} {t_{ij} {\text{d}}z},\quad M_{ij}^{L} = \int\limits_{{{{- h} \mathord{\left/{\vphantom {{- h} 2}} \right. \kern-0pt} 2}}}^{{{h \mathord{\left/{\vphantom {h 2}} \right. \kern-0pt} 2}}} {zt_{ij} {\text{d}}z} $$
(14)

Furthermore, by applying the operator to Eqs. (11) and (12), we obtain the general equations of motion for the nonlocal plate model as

$$ N_{ij,j} = - \left({1 - \mu^{2} \nabla^{2}} \right)\int\limits_{{- \frac{h}{2}}}^{{\frac{h}{2}}} {f_{i} dz} + \int\limits_{{- \frac{h}{2}}}^{{\frac{h}{2}}} {\rho {\textit{\"{u}}_{i}} {\text{d}}z} - \mu^{2} \int\limits_{{- \frac{h}{2}}}^{{\frac{h}{2}}} {\nabla^{2} \left({\rho {\textit{\"{u}}_{i}} {\text{d}}z} \right)} $$
(15a)

and

$$ M_{ij,j} + \int\limits_{{- \frac{h}{2}}}^{{\frac{h}{2}}} {zf_{i} {\text{d}}z} = \int\limits_{{- \frac{h}{2}}}^{{\frac{h}{2}}} {\rho z {\textit{\"{u}}_{i}} {\text{d}}z} - \mu^{2} \int\limits_{{- \frac{h}{2}}}^{{\frac{h}{2}}} {\nabla^{2} \left({\rho z {\textit{\"{u}}_{i}}} \right){\text{d}}z} $$
(15b)

The differential operator \( \nabla^{2} \) in (15a) and (15b) is the three-dimensional Laplace operator in general. For thin-plate models, it may be reduced to the two-dimensional Laplace operator by ignoring the differential component with respect to z, i.e. \( \nabla^{2} = \frac{{\partial^{2}}}{{\partial x^{2}}} + \frac{{\partial^{2}}}{{\partial y^{2}}} \). With this approximation, the equations of motion (15a) and (15b) become

$$ N_{ij,j}^{L} = - \left({1 - \mu^{2} \nabla^{2}} \right)\left({\int\limits_{{- \frac{h}{2}}}^{{\frac{h}{2}}} {f_{i} {\text{d}}z} + \int\limits_{{- \frac{h}{2}}}^{{\frac{h}{2}}} {\rho {\textit{\"{u}}_{i}} {\text{d}}z}} \right) $$
(16a)

and

$$ M_{ij,j}^{L} + \int\limits_{{- \frac{h}{2}}}^{{\frac{h}{2}}} {zf_{i}} {\text{d}}z = \left({1 - \mu^{2} \nabla^{2}} \right)\int\limits_{{- \frac{h}{2}}}^{{\frac{h}{2}}} {\left({\rho z {\textit{\"{u}}_{i}}} \right)} {\text{d}}z $$
(16b)

The nonlocal resultant force and moment tensors, \( N_{ij} \) and \( M_{ij} \), respectively, in (10) can be simplified as

$$ \begin{aligned} N_{ij} \left(X \right) & = \int\limits_{A} {\alpha \left({\left| {X^{\prime} - X} \right|} \right)} \;N_{ij}^{L} \left({X^{\prime}} \right)\;{\text{d}}S\left({X^{\prime}} \right) \\ M_{ij} \left(X \right) & = \int\limits_{A} {\alpha \left({\left| {X^{\prime} - X} \right|} \right)} \;M_{ij}^{L} \left({X^{\prime}} \right)\;{\text{d}}S\left({X^{\prime}} \right) \\ \end{aligned} $$
(17)

where the integrals are taken along the mid-plane s of the plate, \( N_{ij}^{L} \) and \( M_{ij}^{L} \) are given in (14). The two-dimensional nonlocal kernel \( \alpha \left({\left| {X^{\prime} - X} \right|} \right) \) in Eq. (17) can be defined to satisfy the relation (5), in which the differential operator is as given in Eq. (8) instead of a two-dimensional Laplace operator, i.e. \( L = 1 - \mu^{2} \left({\frac{{\partial^{2}}}{{\partial x^{2}}} + \frac{{\partial^{2}}}{{\partial y^{2}}}} \right) \).This approximation is acceptable for plates with very small thickness span ratios.

Generally used three and two-dimensional nonlocal kernel functions are given the following equations, respectively,

$$ \alpha \left({\left| X \right|} \right) = \frac{1}{{4\pi \ell^{2} \xi^{2} \left| X \right|}}{\text{e}}^{{- \frac{\left| X \right|}{\ell \xi}}} $$
(18)
$$ \alpha \left({\left| X \right|} \right) = \frac{1}{{2\pi \ell^{2} \xi^{2} \left| X \right|}}K_{0} \left({\frac{\left| X \right|}{\ell \xi}} \right) $$
(19)

where \( \xi = \frac{\mu}{\ell} \); \( K_{0} \) is the modified Bessel function and \( \ell \) is a characteristic length of the considered structure. For more examples of different boundary value problems based on the nonlocal elasticity models, refer to Eringen [32].

The nonlocal constitutive equations of an FGM nonlocal plate can be written as:

$$ \left\{{\begin{array}{*{20}c} {\sigma_{x}} \\ {\sigma_{y}} \\ {\tau_{xy}} \\ {\tau_{yz}} \\ {\tau_{xz}} \\ \end{array}} \right\} - \left({e_{0} \ell} \right)^{2} \left({\frac{{\partial^{2}}}{{\partial x^{2}}} + \frac{{\partial^{2}}}{{\partial y^{2}}}} \right)\left\{{\begin{array}{*{20}c} {\sigma_{x}} \\ {\sigma_{y}} \\ {\tau_{xy}} \\ {\tau_{yz}} \\ {\tau_{xz}} \\ \end{array}} \right\} = \left[{\begin{array}{*{20}c} {Q_{11} \left(z \right)} &\quad {Q_{12} \left(z \right)} &\quad 0 &\quad 0 &\quad 0 \\ {Q_{12} \left(z \right)} &\quad {Q_{22} \left(z \right)} &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad {Q_{66} \left(z \right)} &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad {Q_{44} \left(z \right)} &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad {Q_{55} \left(z \right)} \\ \end{array}} \right]\left\{{\begin{array}{*{20}c} {\varepsilon_{x}} \\ {\varepsilon_{y}} \\ {\gamma_{xy}} \\ {\gamma_{yz}} \\ {\gamma_{xz}} \\ \end{array}} \right\} $$
(20)

where (\( \sigma_{x} \), \( \sigma_{y} \), \( \tau_{xy} \), \( \tau_{yz} \), \( \tau_{yx} \)) and (\( \varepsilon_{x} \), \( \varepsilon_{y} \), \( \gamma_{xy} \), \( \gamma_{yz} \), \( \gamma_{yx} \)) are the stress and strain components, respectively. Where the elastic constants \( Q_{ij} \) in terms of Young’s modulus E and Poisson’s ratio \( \nu \) are:

$$ Q_{11} \left(z \right) = Q_{22} \left(z \right) = \frac{E\left(z \right)}{{1 - \nu^{2}}},\quad Q_{12} \left(z \right) = Q_{21} \left(z \right) = \frac{\nu E\left(z \right)}{{1 - \nu^{2}}},\quad Q_{44} \left(z \right) = Q_{55} \left(z \right) = Q_{66} \left(z \right) = G\left(z \right) = \frac{E\left(z \right)}{{2\left({1 + \nu} \right)}} $$
(21)

\( z \) is a distance parameter along the graded direction are such that \( {{- h} \mathord{\left/{\vphantom {{- h} 2}} \right. \kern-0pt} 2} \le z \le {h \mathord{\left/{\vphantom {h 2}} \right. \kern-0pt} 2} \)

2.2 Higher-order plate theory

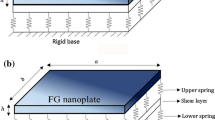
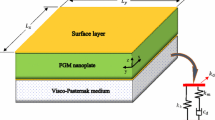
The high shear models considered in this paper are defined from a variational methodology and are then variationallly consistent. Consider a FGMs structure made of three isotropic layers of arbitrary thickness h, width (b 1) and length (a 1) as shown Fig. 1. The FGM nanoplate is supported at four edges defined in the \( ({x,y,z}) \) coordinate system with x- and y-axes located in the middle plane (z = 0) and its origin placed at the corner of the plate. It is assumed to be rested on a Winkler–Pasternak type elastic foundation with the Winkler stiffness of \( k_{\text{w}} \) and shear stiffness of \( k_{\text{p}} \).

Fig. 1
figure 1

Geometry of the functionally graded materials plate resting on elastic foundations

Full size image

Consider a FGM with a porosity volume fraction \( \alpha \left({\alpha < < 1} \right) \). The FGM is made from a mixture of a metal and a ceramic, while a core is made of an isotropic homogeneous material. The material properties of FGM are assumed to vary continuously through the plate thickness by a power law distribution as [8]:

$$ P\left(z \right) = P_{\text{m}} \left({V_{\text{m}} - \frac{\alpha}{2}} \right) + P_{\text{c}} \left({V_{\text{c}} - \frac{\alpha}{2}} \right) $$
(22a)

where \( P_{\text{m}} \), \( P_{\text{c}} \), \( V_{\text{m}} \) and \( V_{\text{c}} \) are the material properties and the volume fraction of the metal and ceramic, respectively, the compositions represent in relation to

$$ V_{\text{m}} + V_{\text{c}} = 1 $$
(22b)

The mathematical model, called a power law distribution, has been used widely in a number of research investigations, especially for the mechanical engineering field (Wattanasakulpong [8, 9], Mechab et al. [27, 28] and Navazi et al. [41]). The power law distribution based on the rule of mixture was introduced by Wakashima et al. [42] to define the effective material properties of FGMs. The volume fraction of ceramic (V c) can then be written as follows:

$$ V_{\text{c}} = \left({\frac{z}{h} + \frac{1}{2}} \right)^{p} $$
(23)

Hence, all properties of the FGMs with a porosity can be written as [8, 9]:

$$ P\left(z \right) = \left({P_{\text{c}} - P_{\text{m}}} \right)\left({\frac{z}{h} + \frac{1}{2}} \right)^{p} + P_{\text{m}} - \left({P_{\text{c}} + P_{\text{m}}} \right)\frac{\alpha}{2} $$
(24)

It is noted that the positive real number p \( ({0 \le p < \infty}) \) is the power law or volume fraction index, and z is the distance from the mid-plane of the FGM plate. The FGM plate becomes a fully ceramic when p is set to zero and fully metal for large value of (p).

Thus, the Young’s modulus (E) and material density (\( \rho \)) equations of the FGMs with a porosity can be expressed as [8, 9]:

$$ E\left(z \right) = \left({E_{\text{c}} - E_{\text{m}}} \right)\left({\frac{z}{h} + \frac{1}{2}} \right)^{p} + E_{\text{m}} - \left({E_{\text{c}} + E_{\text{m}}} \right)\frac{\alpha}{2} $$
(25a)
$$ \rho \left(z \right) = \left({\rho_{\text{c}} - \rho_{\text{m}}} \right)\left({\frac{z}{h} + \frac{1}{2}} \right)^{p} + \rho_{\text{m}} - \left({\rho_{\text{c}} + \rho_{\text{m}}} \right)\frac{\alpha}{2} $$
(25b)

However, Poisson’s ratio (\( \nu \)) is assumed to be constant. The material properties of FGMs plate without porosity can be obtained when \( \alpha \) is set to zero.

The displacements of a material point located at (x, y, z) in the plate may be written as:

$$ \begin{aligned} U(x,y,z) & = u_{0} (x,y) - z\frac{{\partial w_{0}}}{\partial x} + \psi \left(z \right)\theta_{x} \\ V(x,y,z) & = v_{0} (x,y) - z\frac{{\partial w_{0}}}{\partial y} + \psi \left(z \right)\theta_{y} \\ W(x,y,z) & = w_{0} (x,y) \\ \end{aligned} $$
(26a)

The shape function \( \psi \left(z \right) \) is to be specified a posteriori (see Zenkour [21]). It may be chosen such that

$$ \left. {\psi^{\prime} \left(z \right)} \right|_{{z = \pm \frac{h}{2}}} = 0,\;\int\limits_{{z = - \frac{h}{2}}}^{{z = \frac{h}{2}}} {\psi \left(z \right){\text{d}}z} = 0 $$
(26b)

where, \( U,V,W \) are displacements in the \( x,y,z \) directions, \( u_{0},v_{0} \) and \( w_{0} \) are mid-plane displacements, \( \theta_{x} \) and \( \theta_{y} \) rotations of the \( yz \) and \( xz \) planes due to bending, respectively. \( \psi (z) \) represents shape function determining the distribution of the transverse shear strains and stresses along the thickness.

The Love–Kirchhoff plate theory or classical plate theory (CPT) is a particular case of such an enriched kinematics based on the vanishing kinematics function \( \psi \left(z \right) = 0 \). The Reissner–Mindlin theory is simply obtained from the linear relationship [13, 14]:

$$ \psi \left(z \right) = z $$
(27a)

In this case, the shape factor \( \kappa \) is equal to unity, as suggested for instance in literature a \( \kappa \) factor close to 5/6 would be more relevant for the Reissner–Mindlin plate theory (FPT, first shear plate theory). The higher-order shear plates (HPT) models considered in this paper are the model of Reddy [18], the model of Touratier [43] and the present model.

  • Model of Reddy third plate theory (TPT) [18]

    $$ \psi \left( z \right) = z\left( {1 - \frac{{4z^{2} }}{{3h^{2} }}} \right) $$
    (27b)

  • Model of Touratier sinusoidal plate theory (SPT) [43]

    $$ \psi \left(z \right) = \frac{h}{\pi}{ \sin }\left({\pi \frac{z}{h}} \right) $$
    (27c)

  • The new shape function shear deformation plate theory presented in this work:

    $$ \psi \left(z \right) = z - \frac{{8z^{3}}}{{7 h^{2}}}{\text{e}}^{{\left({\frac{{z^{2}}}{{h^{2}}} - \frac{1}{4}} \right)}} $$
    (27d)

2.3 Present refined shear deformation theory

Unlike the other theories, the number of unknown functions involved in the new trigonometric shear deformation plate theory is only four, as against five in case of other shear deformation theories. The theory presented is variationally consistent, does not require shear correction factor, and gives rise to transverse shear stress variation such that the transverse shear stresses vary parabolically across the thickness satisfying shear stress free surface conditions.

2.3.1 Assumptions of the present plate theory

Assumptions of the present plate theory are as follows:

  1. (1)

    The displacements are small in comparison with the plate thickness and, therefore, strains involved are infinitesimal.

  2. (2)

    The transverse displacement W includes two components of bending \( w_{\text{b}} \), and shear \( w_{\text{s}} \). These components are functions of coordinates x, y only.

    $$ W(x,y,z) = w_{0} (x,y) = w_{\text{b}} (x,y) + w_{\text{s}} (x,y) $$
    (28)
  3. (3)

    The transverse normal stress \( \sigma_{z} \) is negligible in comparison with in-plane stresses \( \sigma_{x} \) and \( \sigma_{y} \).

  4. (4)

    The displacements U in x-direction and V in y-direction consist of extension, bending, and shear components.

    $$ U = u_{0} + u_{\text{b}} + u_{\text{s}},\quad V = v_{0} + v_{\text{b}} + v_{\text{s}} $$
    (29)

The bending components \( u_{\text{b}} \) and \( v_{\text{b}} \) are assumed to be similar to the displacements given by the CPT. Therefore, the expression for \( u_{\text{b}} \) and \( v_{\text{b}} \) can be given as

$$ u_{\text{b}} = z\frac{{\partial w_{0}}}{\partial x} = - z\frac{{\partial \left({w_{\text{b}} + w_{\text{s}}} \right)}}{\partial x},\quad v_{\text{b}} = - z\frac{{\partial w_{0}}}{\partial y} = - z\frac{{\partial \left({w_{\text{b}} + w_{\text{s}}} \right)}}{\partial y} $$
(30)

\( \theta_{x} \) and \( \theta_{y} \) rotations of the \( yz \) and \( xz \) due to shear displacement, and \( w_{0} \) includes two components of bending \( w_{\text{b}} \), and shear \( w_{\text{s}} \), the expression for \( \theta_{x} \) and \( \theta_{y} \) can be given as

$$ \theta_{x} = \frac{{\partial w_{\text{s}}}}{\partial x},\quad \theta_{y} = \frac{{\partial w_{\text{s}}}}{\partial y} $$
(31)

The shear components \( u_{\text{s}} \) and \( v_{\text{s}} \) give rise, in conjunction with \( w_{\text{s}} \), to the parabolic variations of shear strains \( \gamma_{xz} \), \( \gamma_{yz} \) and hence to shear stresses \( \tau_{xz} \), \( \tau_{yz} \) through the thickness of the plate in such a way that shear stresses \( \tau_{xz} \), \( \tau_{yz} \) are zero at the top and bottom faces of the plate. Consequently, the expression for \( u_{\text{s}} \) and \( v_{\text{s}} \) can be given as

$$ u_{\text{s}} = \psi (z)\frac{{\partial w_{\text{s}}}}{\partial x} = \psi (z)\theta_{x},\quad v_{\text{s}} = \psi (z)\frac{{\partial w_{\text{s}}}}{\partial y} = \psi (z)\theta_{y} $$
(32)

Substituting Eqs. (30), (31) and (32) into Eq. (26a), the displacement field resultants are given as

$$ \begin{aligned} U(x,y,z) & = u_{0} (x,y) - z\frac{{\partial w_{\text{b}}}}{\partial x} + \left({\psi \left(z \right) - z} \right)\frac{{\partial w_{\text{s}}}}{\partial x} \\ V(x,y,z) & = v_{0} (x,y) - z\frac{{\partial w_{\text{b}}}}{\partial y} + \left({\psi \left(z \right) - z} \right)\frac{{\partial w_{\text{s}}}}{\partial y} \\ W(x,y,z) & = w_{\text{b}} (x,y) + w_{\text{s}} (x,y) \\ \end{aligned} $$
(33)

with

$$ f(z) = \psi (z) - z $$
(34)

2.3.2 Kinematics and constitutive equations

The new shear deformation plate theory of the four variables (\( u_{0} \), \( v_{0} \), \( w_{\text{b}} \), \( w_{\text{s}} \)) can be given as [22–32]

$$ \begin{aligned} U(x,y,z) & = u_{0} (x,y) - z\frac{{\partial w_{\text{b}}}}{\partial x} + f\left(z \right)\frac{{\partial w_{\text{s}}}}{\partial x} \\ V(x,y,z) & = v_{0} (x,y) - z\frac{{\partial w_{\text{b}}}}{\partial y} + f\left(z \right)\frac{{\partial w_{\text{s}}}}{\partial y} \\ W(x,y,z) & = w_{\text{b}} (x,y) + w_{\text{s}} (x,y) \\ \end{aligned} $$
(35)

The strains associated with the displacements in Eq. (35) are:

$$ \left\{{\begin{array}{*{20}c} {\varepsilon_{xx}} \\ {\varepsilon_{yy}} \\ {\gamma_{xy}} \\ \end{array}} \right\} = \left\{{\begin{array}{*{20}c} {\varepsilon_{x}^{0}} \\ {\varepsilon_{y}^{0}} \\ {\gamma_{xy}^{0}} \\ \end{array}} \right\} + z\left\{{\begin{array}{*{20}c} {\kappa_{x}^{b}} \\ {\kappa_{y}^{b}} \\ {\kappa_{xy}^{b}} \\ \end{array}} \right\} + f\left(z \right)\left\{{\begin{array}{*{20}c} {\eta_{x}^{b}} \\ {\eta_{y}^{b}} \\ {\eta_{xy}^{b}} \\ \end{array}} \right\},\quad \varepsilon_{z} = 0,\left\{{\begin{array}{*{20}c} {\gamma_{xz}} \\ {\gamma_{yz}} \\ \end{array}} \right\} = g\left(z \right)\left\{{\begin{array}{*{20}c} {\gamma_{xy}^{s}} \\ {\gamma_{yz}^{s}} \\ \end{array}} \right\} $$
(36)

where

$$ \varepsilon_{x}^{0} = \frac{{\partial u_{0}}}{\partial x},\;\varepsilon_{y}^{0} = \frac{{\partial v_{0}}}{\partial y},\;\gamma_{xy}^{0} = \frac{{\partial u_{0}}}{\partial y} + \frac{{\partial v_{0}}}{\partial x},\;k_{x}^{b} = - \frac{{\partial^{2} w_{\text{b}}}}{{\partial x^{2}}},\;k_{y}^{b} = - \frac{{\partial^{2} w_{\text{b}}}}{{\partial y^{2}}},\;k_{xy}^{b} = - 2\frac{{\partial^{2} w_{\text{b}}}}{\partial x\partial y} $$
(37)
$$ k_{x}^{s} = \frac{{\partial^{2} w_{\text{s}}}}{{\partial x^{2}}},\;k_{y}^{s} = \frac{{\partial^{2} w_{\text{s}}}}{{\partial y^{2}}},\;k_{xy}^{s} = 2\frac{{\partial^{2} w_{\text{s}}}}{\partial x\partial y},\;\gamma_{yz}^{s} = \frac{{\partial w_{\text{s}}}}{\partial y},\;\gamma_{xz}^{s} = \frac{{\partial w_{\text{s}}}}{\partial x},\;\gamma_{yz}^{s} = \frac{{\partial w_{\text{s}}}}{\partial y},\;\gamma_{xz}^{s} = \frac{{\partial w_{\text{s}}}}{\partial x}, $$

The shape function must be chosen in such a way to satisfy the boundary conditions in the free edges \( z = \pm \frac{h}{2} \):

$$ f\left({- z} \right) = - f\left(z \right),\;\left. {g = \left({\frac{\partial f}{\partial z} + 1} \right)} \right|_{{- \frac{h}{2}}}^{{\frac{h}{2}}} = 0 $$
(38)

2.3.3 Governing equations

The governing equations of equilibrium can be derived by using the principle of virtual displacements. The principle of virtual work in the present case yields

$$ \begin{aligned} \left[{\int\limits_{- h/2}^{h/2} {\int_{S} {\left[{\sigma_{x} \delta \varepsilon_{x} + \sigma_{y} \delta \varepsilon_{y} + \tau_{xy} \delta \gamma_{xy} + \tau_{yz} \delta \gamma_{yz} + \tau_{xz} \delta \gamma_{xz}} \right]{\text{d}}S}} \;{\text{d}}z + \int_{\varOmega} {f_{\text{e}} \delta W\;{\text{d}}S}} \right. \hfill \\ \left. {- \int\limits_{- h/2}^{h/2} {\int_{S} {\rho \left[{ {\textit{\"{U}}}\delta U + {\textit{\"{V}}}\delta V + {\textit{\"{W}}}\delta W} \right]{\text{d}}S}} \;{\text{d}}z} \right]{\text{d}}t = 0 \hfill \\ \end{aligned} $$
(39)

where S is the top surface.

Substituting Eqs. (35), (36) into Eq. (39) and integrating through the thickness of the plate, Eq. (47) can be rewritten as:

$$ \begin{aligned} & \int_{S} {\left[{N_{x} \delta \varepsilon_{x}^{0} + N_{y} \delta \varepsilon_{y}^{0} + N_{xy} \delta \varepsilon_{xy}^{0} + M_{x} \delta k_{x}^{b} + M_{y} \delta k_{y}^{b} + M_{xy} \delta k_{xy}^{b} + S_{x} \delta k_{x}^{s}} \right.} \hfill \\ & \quad \left. {+ S_{y} \delta k_{y}^{s} + S_{xy} \delta k_{xy}^{s} + Q_{yz} \delta \gamma_{yz}^{s} + Q_{xz} \delta \gamma_{xz}^{s}} \right]{\text{d}}S + \int_{\varOmega} {f_{\text{e}} \left({\delta w_{\text{b}} + \delta w_{\text{b}}} \right)\;{\text{d}}S} \hfill \\ & \quad - \int\limits_{- h/2}^{h/2} {\int_{S} {\rho \left[{\left({u_{0,tt} - zw_{x,xtt}^{b} + fw_{x,xtt}^{s}} \right)\delta \left({u_{0} - zw_{x,x}^{b} + fw_{x,x}^{s}} \right) + \left({v_{0,tt} - zx_{y,ytt}^{b} + fw_{y,ytt}^{s}} \right)\delta \left({v_{0} - zx_{y,y}^{b} + fw_{y,y}^{s}} \right)} \right.}} \hfill \\ & \left. {\left({w_{,tt}^{b} + w_{,tt}^{s}} \right)\delta \left({w^{b} + w^{s}} \right)} \right]{\text{d}}S\;{\text{d}}z \hfill \\ \end{aligned} $$
(40)

where the stress resultants N, M, and S are defined by

$$ \begin{aligned} \left({N_{x},N_{y},N_{xy}} \right) & = \int\limits_{- h/2}^{h/2} {\left({\sigma_{x},\sigma_{y},\tau_{xy}} \right){\text{d}}z} \\ \left({M_{x},M_{y},M_{xy}} \right) & = \int\limits_{- h/2}^{h/2} {\left({\sigma_{x},\sigma_{y},\tau_{xy}} \right)z{\text{d}}z} \\ \left({S_{x},S_{y},S_{xy}} \right) & = \int\limits_{- h/2}^{h/2} {\left({\sigma_{x},\sigma_{y},\tau_{xy}} \right)f{\text{d}}z} \\ \left({Q_{xz},Q_{yz}} \right) & = \int\limits_{- h/2}^{h/2} {\left({\tau_{xz},\tau_{yz}} \right)g{\text{d}}z} \\ \end{aligned} $$
(41)

Based on the Winkler and Pasternak foundations, the effects of the surrounding elastic medium on the nanoplates are considered as follows:

$$ f_{\text{e}} = k_{\text{w}} w - k_{\text{p}} \nabla^{2} w = k_{\text{w}} \left({w_{\text{b}} + w_{\text{s}}} \right) - k_{\text{p}} \left({\frac{{\partial^{2}}}{{\partial x^{2}}} + \frac{{\partial^{2}}}{{\partial y^{2}}}} \right)\left({w_{\text{b}} + w_{\text{s}}} \right) $$
(42)

where \( f_{\text{e}} \) is the foundation reaction per unit area applied on lower nanoplate, \( k_{\text{w}} \) and \( k_{\text{p}} \) are spring and shear modulus, respectively.

Substituting Eq. (20) into Eq. (41) and integrating through the thickness of the plate, the stress resultants are given as:

$$ \left\{{\begin{array}{*{20}c} N \\ M \\ S \\ \end{array}} \right\} - \left({e_{0} a} \right)^{2} \left({\frac{{\partial^{2}}}{{\partial x^{2}}} + \frac{{\partial^{2}}}{{\partial y^{2}}}} \right)\left\{{\begin{array}{*{20}c} N \\ M \\ S \\ \end{array}} \right\} = \left[{\begin{array}{*{20}c} {A_{ij}} & {B_{ij}} & {B_{ij}^{f}} \\ {B_{ij}} & {D_{ij}} & {D_{ij}^{f}} \\ {B_{ij}^{f}} & {D_{ij}^{f}} & {F_{ij}^{f}} \\ \end{array}} \right]\left\{{\begin{array}{*{20}c} \varepsilon \\ \kappa \\ \eta \\ \end{array}} \right\},Q - \left({e_{0} a} \right)^{2} \left({\frac{{\partial^{2}}}{{\partial x^{2}}} + \frac{{\partial^{2}}}{{\partial y^{2}}}} \right)Q = \gamma A_{ij}^{f}, $$
(43)

where \( A_{ij} \) denote the extensional stiffnesses, \( D_{ij} \) the bending stiffnesses, \( B_{ij} \) the bending–extensional coupling stiffnesses and \( B_{ij}^{f} \), \( D_{ij}^{f} \),\( F_{ij}^{f} \),\( A_{ij}^{f} \) are the stiffnesses associated with the transverse shear effects, defined by

$$ \begin{aligned} \left\{{A_{ij},B_{ij},D_{ij},B_{ij}^{f},D_{ij}^{f},F_{ij}^{f}} \right\} & = \int\limits_{- h/2}^{h/2} {\left\{{1,z,z^{2},f\left(z \right),zf\left(z \right),f\left(z \right)^{2}} \right\}Q_{ij} \left(z \right){\text{d}}z} \quad \left({i,j = 1,2,6} \right) \\ \left\{{A_{ij}^{f}} \right\} & = \int\limits_{- h/2}^{h/2} {\left\{{g^{2}} \right\}Q_{ij} {\text{d}}z} \quad \left({i,j = 4,5} \right) \\ \end{aligned} $$
(44a)

The inertias \( I_{i} \) are defined by:

$$ \left\{{I_{1},I_{2},I_{3},I_{4},I_{5},I_{6}} \right\} = \int\limits_{- h/2}^{h/2} {\left\{{1,z,z^{2},f\left(z \right),zf\left(z \right),f\left(z \right)^{2}} \right\}\rho \left(z \right){\text{d}}z} $$
(44b)

The governing equations of equilibrium can be derived from Eq. (39) by integrating the displacement gradients by parts and setting the coefficients \( \delta u_{0} \),\( \delta \, v_{0} \), \( \delta \, w_{\text{b}} \), and \( \delta \, w_{\text{s}} \) to zero separately. Thus, one can obtain the equilibrium equations associated with the present RPT for the nonlocal plate.

$$ \begin{aligned} & \delta u_{0} :\;\frac{{\partial N_{x} }}{\partial x} + \frac{{\partial N_{xy} }}{\partial y} = I_{1} \frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} - I_{2} \frac{{\partial^{3} w_{\text{b}} }}{{\partial x\partial t^{2} }} + I_{4} \frac{{\partial^{3} w_{\text{s}} }}{{\partial x\partial t^{2} }} \\ & \delta v_{0} :\;\frac{{\partial N_{xy} }}{\partial x} + \frac{{\partial N_{y} }}{\partial y} = I_{1} \frac{{\partial^{2} v_{0} }}{{\partial t^{2} }} - I_{2} \frac{{\partial^{3} w_{\text{b}} }}{{\partial y\partial t^{2} }} + I_{4} \frac{{\partial^{3} w_{\text{s}} }}{{\partial y\partial t^{2} }} \\ & \delta w_{\text{b}} :\;\frac{{\partial^{2} M_{x} }}{{\partial x^{2} }} + 2\frac{{\partial^{2} M_{xy} }}{\partial x\partial y} + \frac{{\partial^{2} M_{y} }}{{\partial y^{2} }} - f_{\text{e}} = I_{2} \left( {\frac{{\partial^{3} u_{0} }}{{\partial x\partial t^{2} }} + \frac{{\partial^{3} v_{0} }}{{\partial y\partial t^{2} }}} \right) - I_{3} \left( {\frac{{\partial^{4} w_{\text{b}} }}{{\partial x^{2} \partial t^{2} }} + \frac{{\partial^{4} w_{\text{b}} }}{{\partial y^{2} \partial t^{2} }}} \right) \\ & \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad + I_{5} \left( {\frac{{\partial^{4} w_{\text{s}} }}{{\partial x^{2} \partial t^{2} }} + \frac{{\partial^{4} w_{\text{s}} }}{{\partial y^{2} \partial t^{2} }}} \right) + I_{1} \left( {\frac{{\partial^{2} w_{\text{b}} }}{{\partial t^{2} }} + \frac{{\partial^{2} w_{\text{s}} }}{{\partial t^{2} }}} \right) \\ & \delta w_{\text{s}} :\;\frac{{\partial^{2} S_{x} }}{{\partial x^{2} }} + 2\frac{{\partial^{2} S_{xy} }}{\partial x\partial y} + \frac{{\partial^{2} S_{y} }}{{\partial y^{2} }} - \frac{{Q_{xz} }}{\partial x} - \frac{{\partial Q_{yz} }}{\partial y} + f_{\text{e}} = I_{4} \left( {\frac{{\partial^{3} u_{0} }}{{\partial x\partial t^{2} }} + \frac{{\partial^{3} v_{0} }}{{\partial y\partial t^{2} }}} \right) - I_{5} \left( {\frac{{\partial^{4} w_{\text{b}} }}{{\partial x^{2} \partial t^{2} }} + \frac{{\partial^{4} w_{\text{b}} }}{{\partial y^{2} \partial t^{2} }}} \right) \\ & \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad + I_{6} \left( {\frac{{\partial^{4} w_{\text{s}} }}{{\partial x^{2} \partial t^{2} }} + \frac{{\partial^{4} w_{\text{s}} }}{{\partial y^{2} \partial t^{2} }}} \right) + I_{1} \left( {\frac{{\partial^{2} w_{\text{b}} }}{{\partial t^{2} }} + \frac{{\partial^{2} w_{\text{s}} }}{{\partial t^{2} }}} \right) \\ \end{aligned} $$
(45)

In this part we present some formulations for the free vibration of generic higher-order shear plate models generalized in a nonlocal framework. This nonlocal model depends on a single characteristic length \( \left({e_{0} a} \right)^{2} \), responsible of the small scale effects. The nonlocal generalization of the linear elastic constitutive law Eq. (9) using the nonlocal theory of Eringen [32–34] can be presented in the following differential format:

$$ \begin{aligned} & \left({- I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} \partial x^{2}}} + I_{2} \frac{{\partial^{3} w_{\text{b}}}}{{\partial t^{2} \partial x^{3}}} - I_{4} \frac{{\partial^{3} w_{\text{s}}}}{{\partial t^{2} \partial x^{3}}} - I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} \partial y^{2}}} + I_{2} \frac{{\partial^{3} w_{\text{b}}}}{{\partial x\partial y^{2} \partial t^{2}}} - I_{4} \frac{{\partial^{3} w_{\text{s}}}}{{\partial x\partial y^{2} \partial t^{2}}}} \right)\left({e_{0} a} \right)^{2} \\ & \quad + \left({I_{1} \frac{{\partial^{2} u}}{{\partial t^{2}}} - I_{2} \frac{{\partial^{3} w_{\text{b}}}}{{\partial x\partial t^{2}}} + I_{4} \frac{{\partial^{3} w_{\text{s}}}}{{\partial x\partial t^{2}}}} \right) = A_{11} \frac{{\partial^{2} u}}{{\partial x^{2}}} + A_{66} \frac{{\partial^{2} u}}{{\partial y^{2}}} + \left({A_{12} + A_{66}} \right)\frac{{\partial^{2} v}}{\partial x\partial y} - B_{11} \frac{{\partial^{3} w_{\text{b}}}}{{\partial x^{3}}} \\ & \quad - \left({B_{12} + 2B_{66}} \right)\frac{{\partial^{3} w_{\text{b}}}}{{\partial y^{2} \partial x}} + B_{11}^{f} \frac{{\partial^{3} w_{\text{s}}}}{{\partial x^{3}}} + \left({B_{12}^{f} + 2B_{66}^{f}} \right)\frac{{\partial^{3} w_{\text{s}}}}{{\partial y^{2} \partial x}} \\ \end{aligned} $$
(46a)
$$ \begin{aligned} & \left({- I_{1} \frac{{\partial^{2} v}}{{\partial t^{2} \partial y^{2}}} + I_{2} \frac{{\partial^{3} w_{\text{b}}}}{{\partial t^{2} \partial y^{3}}} - I_{4} \frac{{\partial^{3} w_{\text{s}}}}{{\partial t^{2} \partial y^{3}}} - I_{1} \frac{{\partial^{2} v}}{{\partial t^{2} \partial x^{2}}} + I_{2} \frac{{\partial^{3} w_{\text{b}}}}{{\partial t^{2} \partial y\partial x^{2}}} - I_{4} \frac{{\partial^{3} w_{\text{s}}}}{{\partial t^{2} \partial y\partial x^{2}}}} \right)\left({e_{0} a} \right)^{2} \\ & \quad + \left({I_{1} \frac{{\partial^{2} v}}{{\partial t^{2}}} - I_{2} \frac{{\partial^{3} w_{\text{b}}}}{{\partial y\partial t^{2}}} + I_{4} \frac{{\partial^{3} w_{\text{s}}}}{{\partial y\partial t^{2}}}} \right) = \left({A_{12} + A_{66}} \right)\frac{{\partial^{2} u}}{\partial x\partial y} + A_{66} \frac{{\partial^{2} v}}{{\partial x^{2}}} + A_{22} \frac{{\partial^{2} v}}{{\partial y^{2}}} - \left({B_{12} + 2B_{66}} \right)\frac{{\partial^{3} w_{\text{b}}}}{{\partial x^{2} \partial y}} \\ & \quad - B_{22} \frac{{\partial^{3} w_{\text{b}}}}{{\partial y^{3}}} + \left({B_{12}^{f} + 2B_{66}^{f}} \right)\frac{{\partial^{3} w_{\text{s}}}}{{\partial x^{2} \partial y}} - B_{22}^{f} \frac{{\partial^{3} w_{\text{s}}}}{{\partial y^{3}}} \\ \end{aligned} $$
(46b)
$$ \begin{aligned} & \quad - \frac{\partial}{{\partial x^{2}}}\left({I_{2} \left({\frac{{\partial^{3} u}}{{\partial x\partial t^{2}}} + \frac{{\partial^{3} v}}{{\partial y\partial t^{2}}}} \right) - I_{3} \left({\frac{{\partial^{4} w_{\text{b}}}}{{\partial x^{2} \partial t^{2}}} + \frac{{\partial^{4} w_{\text{b}}}}{{\partial y^{2} \partial t^{2}}}} \right) + I_{5} \left({\frac{{\partial^{4} w_{\text{s}}}}{{\partial x^{2} \partial t^{2}}} + \frac{{\partial^{4} w_{\text{s}}}}{{\partial y^{2} \partial t^{2}}}} \right) + I_{1} \left({\frac{{\partial^{2} w_{\text{b}}}}{{\partial t^{2}}} + \frac{{\partial^{2} w_{\text{s}}}}{{\partial t^{2}}}} \right) + f_{\text{e}}} \right)\left({e_{0} a} \right)^{2} \\ & \quad - \frac{\partial}{{\partial y^{2}}}\left({I_{2} \left({\frac{{\partial^{3} u}}{{\partial x\partial t^{2}}} + \frac{{\partial^{3} v}}{{\partial y\partial t^{2}}}} \right) - I_{3} \left({\frac{{\partial^{4} w_{\text{b}}}}{{\partial x^{2} \partial t^{2}}} + \frac{{\partial^{4} w_{\text{b}}}}{{\partial y^{2} \partial t^{2}}}} \right) + I_{5} \left({\frac{{\partial^{4} w_{\text{s}}}}{{\partial x^{2} \partial t^{2}}} + \frac{{\partial^{4} w_{\text{s}}}}{{\partial y^{2} \partial t^{2}}}} \right) + I_{1} \left({\frac{{\partial^{2} w_{\text{b}}}}{{\partial t^{2}}} + \frac{{\partial^{2} w_{\text{s}}}}{{\partial t^{2}}}} \right) + f_{\text{e}}} \right)\left({e_{0} a} \right)^{2} \\ & \quad + I_{2} \left({\frac{{\partial^{3} u}}{{\partial x\partial t^{2}}} + \frac{{\partial^{3} v}}{{\partial y\partial t^{2}}}} \right) - I_{3} \left({\frac{{\partial^{4} w_{\text{b}}}}{{\partial x^{2} \partial t^{2}}} + \frac{{\partial^{4} w_{\text{b}}}}{{\partial y^{2} \partial t^{2}}}} \right) + I_{5} \left({\frac{{\partial^{4} w_{\text{s}}}}{{\partial x^{2} \partial t^{2}}} + \frac{{\partial^{4} w_{\text{s}}}}{{\partial y^{2} \partial t^{2}}}} \right) + I_{1} \left({\frac{{\partial^{2} w_{\text{b}}}}{{\partial t^{2}}} + \frac{{\partial^{2} w_{\text{s}}}}{{\partial t^{2}}}} \right) + f_{\text{e}} \\ & \quad = B_{11} \frac{{\partial^{3} u}}{{\partial x^{3}}} + \left({B_{12} + 2B_{66}} \right)\frac{{\partial^{3} u}}{{\partial x\partial y^{2}}} + \left({B_{12} + 2B_{66}} \right)\frac{{\partial^{3} v}}{{\partial x^{2} \partial y}} + B_{22} \frac{{\partial^{3} v}}{{\partial y^{3}}} - D_{11} \frac{{\partial^{4} w_{\text{b}}}}{{\partial x^{4}}} - 2\left({D_{12} + 2D_{66}} \right)\frac{{\partial^{4} w_{\text{b}}}}{{\partial x^{2} \partial y^{2}}} \\ & \quad - D_{22} \frac{{\partial^{4} w_{\text{b}}}}{{\partial y^{4}}} - D_{11}^{f} \frac{{\partial^{4} w_{\text{s}}}}{{\partial x^{4}}} - 2\left({D_{12}^{f} + 2D_{66}^{f}} \right)\frac{{\partial^{4} w_{\text{s}}}}{{\partial x^{2} \partial y^{2}}} - D_{22}^{f} \frac{{\partial^{4} w_{\text{s}}}}{{\partial y^{4}}} \\ \end{aligned} $$
(46c)
$$ \begin{aligned} & \quad - \frac{\partial}{{\partial x^{2}}}\left({I_{4} \left({\frac{{\partial^{3} u}}{{\partial x\partial t^{2}}} + \frac{{\partial^{3} v}}{{\partial y\partial t^{2}}}} \right) - I_{5} \left({\frac{{\partial^{4} w_{\text{b}}}}{{\partial x^{2} \partial t^{2}}} + \frac{{\partial^{4} w_{\text{b}}}}{{\partial y^{2} \partial t^{2}}}} \right) + I_{6} \left({\frac{{\partial^{4} w_{\text{s}}}}{{\partial x^{2} \partial t^{2}}} + \frac{{\partial^{4} w_{\text{s}}}}{{\partial y^{2} \partial t^{2}}}} \right) + I_{1} \left({\frac{{\partial^{2} w_{\text{b}}}}{{\partial t^{2}}} + \frac{{\partial^{2} w_{\text{s}}}}{{\partial t^{2}}}} \right) - f_{\text{e}}} \right)\left({e_{0} a} \right)^{2} \\ & \quad - \frac{\partial}{{\partial y^{2}}}\left({I_{4} \left({\frac{{\partial^{3} u}}{{\partial x\partial t^{2}}} + \frac{{\partial^{3} v}}{{\partial y\partial t^{2}}}} \right) - I_{5} \left({\frac{{\partial^{4} w_{\text{b}}}}{{\partial x^{2} \partial t^{2}}} + \frac{{\partial^{4} w_{\text{b}}}}{{\partial y^{2} \partial t^{2}}}} \right) + I_{6} \left({\frac{{\partial^{4} w_{\text{s}}}}{{\partial x^{2} \partial t^{2}}} + \frac{{\partial^{4} w_{\text{s}}}}{{\partial y^{2} \partial t^{2}}}} \right) + I_{1} \left({\frac{{\partial^{2} w_{\text{b}}}}{{\partial t^{2}}} + \frac{{\partial^{2} w_{\text{s}}}}{{\partial t^{2}}}} \right) - f_{\text{e}}} \right)\left({e_{0} a} \right)^{2} \\ & \quad + I_{4} \left({\frac{{\partial^{3} u}}{{\partial x\partial t^{2}}} + \frac{{\partial^{3} v}}{{\partial y\partial t^{2}}}} \right) - I_{5} \left({\frac{{\partial^{4} w_{\text{b}}}}{{\partial x^{2} \partial t^{2}}} + \frac{{\partial^{4} w_{\text{b}}}}{{\partial y^{2} \partial t^{2}}}} \right) + I_{6} \left({\frac{{\partial^{4} w_{\text{s}}}}{{\partial x^{2} \partial t^{2}}} + \frac{{\partial^{4} w_{\text{s}}}}{{\partial y^{2} \partial t^{2}}}} \right) + I_{1} \left({\frac{{\partial^{2} w_{\text{b}}}}{{\partial t^{2}}} + \frac{{\partial^{2} w_{\text{s}}}}{{\partial t^{2}}}} \right) - f_{\text{e}} \\ & \quad = B_{11}^{f} \frac{{\partial^{3} u}}{{\partial x^{3}}} + \left({B_{12}^{f} + 2B_{66}^{f}} \right)\frac{{\partial^{3} u}}{{\partial x\partial y^{2}}} + \left({B_{12}^{f} + 2B_{66}^{f}} \right)\frac{{\partial^{3} v}}{{\partial x^{2} \partial y}} + B_{22}^{f} \frac{{\partial^{3} v}}{{\partial y^{3}}} - D_{11}^{f} \frac{{\partial^{4} w_{\text{b}}}}{{\partial x^{4}}} - 2\left({D_{12}^{f} + 2D_{66}^{f}} \right)\frac{{\partial^{4} w_{\text{b}}}}{{\partial x^{2} \partial y^{2}}} \\ & \quad - D_{22}^{f} \frac{{\partial^{4} w_{\text{b}}}}{{\partial y^{4}}} - F_{11}^{f} \frac{{\partial^{4} w_{\text{s}}}}{{\partial x^{4}}} - 2\left({F_{12}^{f} + 2F_{66}^{f}} \right)\frac{{\partial^{4} w_{\text{s}}}}{{\partial x^{2} \partial y^{2}}} - F_{22}^{f} \frac{{\partial^{4} w_{\text{s}}}}{{\partial y^{4}}} + A_{55}^{f} \frac{{\partial^{2} w_{\text{s}}}}{{\partial x^{2}}} + A_{44}^{f} \frac{{\partial^{2} w_{\text{s}}}}{{\partial y^{2}}} \\ \end{aligned} $$
(46d)

2.3.4 Analytical solutions for vibration problems nonlocal plates

For the analytical solution of Eq. (46), the Navier method is used under the specified boundary conditions. The displacement functions that satisfy the equations of boundary conditions in the Table 1 are selected as the following Fourier series [44–46]:

$$ \left\{{\begin{array}{*{20}c} u \\ v \\ {w_{\text{b}}} \\ {w_{\text{s}}} \\ \end{array}} \right\} = \sum\limits_{i = 1}^{\infty} {\sum\limits_{j = 1}^{\infty} {\left\{{\begin{array}{*{20}c} {U_{mn} \frac{{\partial X_{m} \left(x \right)}}{\partial x}Y_{n} \left(y \right){\text{e}}^{i\omega t}} \\ {V_{mn} X_{m} \left(x \right)\frac{{\partial Y_{n} \left(y \right)}}{\partial x}{\text{e}}^{i\omega t}} \\ {W_{bmn} X_{m} \left(x \right)Y_{n} \left(y \right){\text{e}}^{i\omega t}} \\ {W_{smn} X_{m} \left(x \right)Y_{n} \left(y \right){\text{e}}^{i\omega t}} \\ \end{array}} \right\}}} $$
(47)

where \( U_{mn} \), \( V_{mn} \),\( W_{{{\text{b}}mn}} \), and \( W_{{{\text{s}}mn}} \) are arbitrary parameters and \( \omega = \omega_{mn} \) denotes the eigenfrequency associated with (mth, nth) eigenmode.

Table 1 The admissible functions \( X_{m} \left(x \right) \) and \( Y_{n} \left(y \right) \) [45]
Full size table

The functions \( X_{m} \left(x \right) \) and \( Y_{n} \left(y \right) \) are suggested here to satisfy at least the geometric boundary conditions given in Table 1, and represent approximate shapes of the deflected surface of the plate.

These functions, for the different cases of boundary conditions, are listed in Table 1 [45] noting that \( \eta_{m} = \frac{m\pi}{{a_{1}}},\;\zeta_{n} = \frac{n\pi}{{b_{1}}} \).

Substituting Eq. (47) into equations of motion (46) we get the below eigenvalue equations for any fixed value of m and n, for free vibration problem:tabl

$$ \left({\left[K \right] - \omega^{2} \left[M \right]} \right)\left\{\Delta \right\} = \left\{0 \right\} $$
(48)

where \( \left\{\Delta \right\} \) denotes the columns, and \( \left[K \right] \) is stiffness matrix and \( \left[M \right] \) refers to the mass matrix in the case of free vibration.

$$ \left\{\Delta \right\} = \left\{{\begin{array}{llll} {U_{mn}} \\ {V_{mn}} \\ {W_{bmn}} \\ {W_{smn}} \\ \end{array}} \right\},\;\left[K \right] = \left[{\begin{array}{*{20}c} {K_{11}} &\quad {K_{12}} &\quad {K_{13}} &\quad {K_{14}} \\ {K_{12}} &\quad {K_{22}} &\quad {K_{23}} &\quad {K_{24}} \\ {K_{13}} &\quad {K_{23}} &\quad {K_{33}} &\quad {K_{34}} \\ {K_{14}} &\quad {K_{24}} &\quad {K_{34}} &\quad {K_{44}} \\ \end{array}} \right],\;\left[M \right] = \left[{\begin{array}{*{20}c} {M_{11}} &\quad {M_{12}} &\quad {M_{13}} &\quad {M_{14}} \\ {M_{12}} &\quad {M_{22}} &\quad {a_{23}} &\quad {M_{24}} \\ {M_{13}} &\quad {M_{23}} &\quad {M_{33}} &\quad {M_{34}} \\ {M_{14}} &\quad {M_{24}} &\quad {M_{34}} &\quad {M_{44}} \\ \end{array}} \right] $$
(49)

The elements \( K_{ij} = K_{ji} \) of the coefficient matrix \( \left[K \right] \) are given by:

$$ \begin{aligned} K_{11} & = A_{11} e_{1} + A_{66} e_{2}, \\ K_{12} & = \left({A_{12} + A_{66}} \right)e_{2}, \\ K_{13} & = - B_{11} e_{1} - \left({B_{12} + 2B_{66}} \right)e_{2}, \\ K_{14} & = B_{11}^{f} e_{1} + \left({B_{12}^{f} + 2B_{66}^{f}} \right)e_{2}, \\ K_{21} & = \left({A_{12} + A_{66}} \right)e_{3}, \\ K_{22} & = A_{22} e_{4} + A_{66} e_{3}, \\ K_{23} & = - B_{22} e_{4} - \left({B_{12} + 2B_{66}} \right)e_{3}, \\ K_{24} & = B_{22}^{f} e_{4} + \left({B_{12}^{f} + 2B_{66}^{f}} \right)e_{3}, \\ K_{31} & = B_{11} e_{5} + \left({B_{12} + 2B_{66}} \right)e_{6}, \\ K_{32} & = B_{22} e_{7} + \left({B_{12} + 2B_{66}} \right)e_{6}, \\ K_{33} & = \left({\left({e_{8} + e_{9}} \right)k_{\text{w}} - \left({e_{5} + 2e_{6} + e_{7}} \right)k_{\text{p}}} \right)\left({e_{0} a} \right)^{2} - e_{10} k_{\text{w}} + \left({e_{8} + e_{9}} \right)k_{\text{p}} - e_{5} D_{11} - e_{7} D_{22} - 2\left({D_{12} + 2D_{66}} \right)e_{6}, \\ K_{34} & = \left({\left({e_{8} + e_{9}} \right)k_{\text{w}} - \left({e_{5} + 2e_{6} + e_{7}} \right)k_{\text{p}}} \right)\left({e_{0} a} \right)^{2} - e_{10} k_{\text{w}} + \left({e_{8} + e_{9}} \right)k_{\text{p}} + D_{22}^{f} e_{7} + D_{11}^{f} e_{5} + 2\left({D_{12}^{f} + 2D_{66}^{f}} \right)e_{6}, \\ K_{41} & = B_{11}^{f} e_{5} + \left({B_{12}^{f} + 2B_{66}^{f}} \right)e_{6}, \\ K_{42} & = B_{22}^{f} e_{7} + \left({B_{12}^{f} + 2B_{66}^{f}} \right)e_{6}, \\ K_{43} & = \left({\left({e_{5} + 2e_{6} + e_{7}} \right)k_{p} - \left({e_{8} + e_{9}} \right)k_{\text{w}}} \right)\left({e_{0} a} \right)^{2} + e_{10} k_{\text{w}} - \left({e_{8} + e_{9}} \right)k_{p} - D_{11}^{f} e_{5} - D_{11}^{f} e_{7} - 2\left({D_{12}^{f} + 2D_{66}^{f}} \right)e_{6}, \\ K_{44} & = \left({\left({e_{5} + 2e_{6} + e_{7}} \right)k_{\text{p}} - \left({e_{8} + e_{9}} \right)k_{w}} \right)\left({e_{0} a} \right)^{2} + e_{10} k_{\text{w}} - \left({e_{8} + e_{9}} \right)k_{p} + F_{11}^{f} e_{5} + F_{22}^{f} e_{7} + 2\left({F_{12}^{f} + 2F_{66}^{f}} \right)e_{6} \\ & \quad - A_{44}^{f} e_{9} - A_{55}^{f} e_{8} \\ \end{aligned} $$
(50)

The elements \( M_{ij} = M_{ji} \) of the coefficient matrix \( \left[M \right] \) are given by:

$$ \begin{aligned} M_{11} & = I_{1} \left({e_{11} - \left({e_{1} + e_{2}} \right)\left({e_{0} a} \right)^{2}} \right), \\ M_{12} & = 0, \\ M_{13} & = I_{2} \left({\left({e_{1} + e_{2}} \right)\left({e_{0} a} \right)^{2} - e_{11}} \right), \\ M_{14} & = I_{4} \left({e_{11} - \left({e_{1} + e_{2}} \right)\left({e_{0} a} \right)^{2}} \right), \\ M_{21} & = 0, \\ M_{22} & = I_{1} \left({\left({e_{3} + e_{4}} \right)\left({e_{0} a} \right)^{2} - e_{12}} \right), \\ M_{23} & = I_{2} \left({e_{12} - \left({e_{3} + e_{4}} \right)\left({e_{0} a} \right)^{2}} \right), \\ M_{24} & = I_{4} \left({\left({e_{3} + e_{4}} \right)\left({e_{0} a} \right)^{2} - e_{12}} \right), \\ M_{31} & = I_{2} \left({\left({e_{5} + e_{6}} \right)\left({e_{0} a} \right)^{2} - e_{8}} \right), \\ M_{32} & = I_{2} \left({\left({e_{6} + e_{7}} \right)\left({e_{0} a} \right)^{2} - e_{9}} \right), \\ M_{33} & = \left({\left({e_{8} + e_{9}} \right)I_{1} - \left({e_{5} + 2e_{6} + e_{7}} \right)I_{3}} \right)\left({e_{0} a} \right)^{2} - e_{10} I_{1} + \left({e_{8} + e_{9}} \right)I_{3}, \\ M_{34} & = \left({\left({e_{8} + e_{9}} \right)I_{1} + \left({e_{5} + 2e_{6} + e_{7}} \right)I_{5}} \right)\left({e_{0} a} \right)^{2} - e_{10} I_{1} - \left({e_{8} + e_{9}} \right)I_{5}, \\ M_{41} & = I_{4} \left({\left({e_{5} + e_{6}} \right)\left({e_{0} a} \right)^{2} - e_{8}} \right),\;M_{42} = I_{4} \left({\left({e_{6} + e_{7}} \right)\left({e_{0} a} \right)^{2} - e_{9}} \right), \\ M_{43} & = e_{10} I_{1} + \left({e_{8} + e_{9}} \right)I_{5} - \left({\left({e_{8} + e_{9}} \right)I_{1} + \left({e_{5} + 2e_{6} + e_{7}} \right)I_{5}} \right)\left({e_{0} a} \right)^{2}, \\ M_{44} & = e_{10} I_{1} - \left({e_{8} + e_{9}} \right)I_{6} + \left({\left({e_{5} + 2e_{6} + e_{7}} \right)I_{6} - \left({e_{8} + e_{9}} \right)I_{1} +} \right)\left({e_{0} a} \right)^{2}, \\ \end{aligned} $$
(51)

in which

$$ \begin{aligned} \left\{{e_{1},e_{2},e_{11}} \right\} & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {X^{\prime} \left(x \right)Y\left(y \right)\left\{{X^{\prime \prime \prime} \left(x \right)Y\left(y \right),\;X^{\prime} \left(x \right)Y^{\prime \prime} \left(y \right),\;X^{\prime} \left(x \right)Y\left(y \right)} \right\}{\text{d}}x{\text{d}}y}} \\ \left\{{e_{3},e_{4},e_{12}} \right\} & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {X\left(x \right)Y^{\prime} \left(y \right)\left\{{X^{\prime \prime} \left(x \right)Y^{\prime} \left(y \right),\;X\left(x \right)Y^{\prime \prime \prime} \left(y \right),\;X\left(x \right)Y^{\prime} \left(y \right)} \right\}{\text{d}}x{\text{d}}y}} \\ \left\{{e_{5},e_{6},e_{7}} \right\} & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {X\left(x \right)Y\left(y \right)\left\{{X^{\prime \prime \prime \prime} \left(x \right)Y\left(y \right),\;X^{\prime \prime} \left(x \right)Y^{\prime \prime} \left(y \right),\;X\left(x \right)Y^{\prime \prime \prime \prime} \left(y \right)} \right\}{\text{d}}x{\text{d}}y}} \\ \left\{{e_{8},e_{9},e_{10}} \right\} & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {X\left(x \right)Y\left(y \right)\left\{{X\left(x \right)Y\left(y \right),\;X\left(x \right)Y^{\prime \prime} \left(y \right),\;X\left(x \right)Y\left(y \right)} \right\}{\text{d}}x{\text{d}}y}} \\ \end{aligned} $$
(52)

For nontrivial solutions of Eq. (48), the following determinants should be zero:

$$ {\text{Det}}\left({\left[K \right] - \omega^{2} \left[M \right]} \right) = 0 $$
(53)

The exact solution of Eq. (53) for the FGM nanoplate under various boundary conditions can be constructed. The plate is assumed to have simply-supported (S) and clamped (C) edges or have combinations of them, and they are given as:

3 Results and discussion

The analytical free vibration solutions presented in Eqs. (48) and (53) are numerically evaluated here for an isotropic plate to discuss the effects of nonlocal parameter \( \left({e_{0} a} \right)^{2} \) on the plate vibration response. The material properties used in the present study are as follows:\( E_{\text{m}} = 70\;{\text{GPa}},\quad \rho_{\text{m}} = 2707\;{\text{kg}}/{\text{m}}^{3} \) for aluminum, \( E_{\text{c}} = 380\;{\text{GPa}},\quad \rho_{\text{c}} = 3800\;{\text{kg}}/{\text{m}}^{3} \) for alumina, \( \nu_{\text{c}} = \nu_{\text{m}} = \nu = 0.3 \)where \( E,\nu,\rho \) are Young modules, Poisson’s ratio and plate density.

In all examples, the parameters of the found are given in the dimensionless form \( K_{\text{w}} = {{k_{\text{w}} a_{1}^{4}} \mathord{\left/{\vphantom {{k_{\text{w}} a_{1}^{4}} D}} \right. \kern-0pt} D}_{\text{c}} \), \( K_{\text{p}} = {{k_{\text{p}} a_{1}^{2}} \mathord{\left/{\vphantom {{k_{\text{p}} a_{1}^{2}} D}} \right. \kern-0pt} D}_{\text{c}} \) and \( \bar{\omega} = \omega a_{1}^{2} \sqrt {\left({{{\rho_{\text{c}} h} \mathord{\left/{\vphantom {{\rho_{\text{c}} h} {D_{\text{c}}}}} \right. \kern-0pt} {D_{\text{c}}}}} \right)} \) where \( D_{\text{c}} = {{E_{\text{c}} h^{3}} \mathord{\left/{\vphantom {{E_{\text{c}} h^{3}} {12\left({1 - \nu^{2}} \right)}}} \right. \kern-0pt} {12\left({1 - \nu^{2}} \right)}} \) is the reference bending rigidity of the plate.

In this work, an analytical method was used to study the free vibration analysis of FGM nanoplates subjected with porosities resting on Winkler Pasternak elastic foundations based on two new variable refined plates theories. This theoretical formulation included the CPT, the first order shear deformation theory (FPT) and the higher order shear deformation theories (TPT, SPT and present model). The present results have shown the influences of porosity \( \left(\alpha \right) \) and nonlocal parameters \( \left({e_{0} a} \right)^{2} \), constituent material distribution and plate aspect ratio on the natural frequencies of the plate.

Figure 2a, b illustrates the shear strain shape function of different models. This figure also shows that [18] the present model has the same shape functions determining the same distribution of the transverse shear strains and stresses along the thickness. In the first-order shear deformation plate theory (FPT) Reissner–Mindlin [13, 14], the in-plane displacements are expanded up to the first term in the thickness coordinate, and the relations of normals to the mid-surface are assumed independent of the transverse deflection. Note that the condition in (31) is not satisfied and then the FPT yields a constant value of transverse shearing strain through the thickness of the plate Fig. 2b, and thus requires shear correction factors in order to ensure the proper amount of transverse energy. The actual values of shear correction coefficients of the present FPT are 5/6.

Fig. 2
figure 2

Shape strain functions of different shear deformation theories of the plate

Full size image

The TPT [18] accounts not only for transverse shear strains, but also for a parabolic variation of the transverse shear strains through the thickness. The forms of the assumed displacement functions for (TPT) Reddy [18] and (SPT) Touratier [43], the present model are satisfied the conditions of zero transverse shear stresses on the top and bottom surfaces of the plate (Fig. 2b). No shear correction factors are needed in computing the shear stresses for other theories, because a correct representation of the transverse shearing strain is given. It can be seen that the present model is in good agreement of (TPT) Reddy [18] and (SPT) Touratier [43]

In Table 2, the effects of plate aspect ratio (b 1 = a 1), side-to-thickness ratio (a 1 = h) and nonlocal parameter (e o a)2 on the natural frequencies of simply supported nanoplates for differents theory (CPT) [47], FPT [47], TPT [47], and the present result are given. However, the \( \bar{\omega} \) slightly decreases as the nonlocal parameter increases and plate aspect ratio decreases. It can be observed that the CPT [47] gives results higher than those obtained by the shear deformation plate theories, indicating to the shear deformation influence, It can be seen that the present result is in good agreement of (TPT) [47] and (FPT) [47].

Table 2 The first nondimensional higher order frequencies \( \bar{\omega} = \omega h\sqrt {{\rho \mathord{\left/{\vphantom {\rho G}} \right. \kern-0pt} G}} \) of simply supported plate
Full size table

Table 3 presents the natural frequency \( \bar{\omega} \) of a local (\( \left({e_{0} a} \right)^{2} = 0 \)) and nonlocal (\( \left({e_{0} a} \right)^{2} = 4 \)) FGM square nanoplate without or resting on elastic foundations for different values of inhomogeneity parameter (p) compared with results of Sobhy [48]. It is found that the presence of elastic foundations has a significant effect on the results, where it leads to a considerable increase the natural frequency \( \bar{\omega} \). On the other hand, with the change in the power law index (p) (inhomogeneity parameter), regardless of the elastic foundations, the natural frequency decreases as the parameter (p) increases. It is also noted that the frequency of the nonlocal theory is always smaller than of the local theory, the present results are in good agreement with the solutions of Sobhy [48].

Table 3 The frequency \( \bar{\omega} = {{\omega b^{2}} \mathord{\left/{\vphantom {{\omega b^{2}} {\pi^{2}}}} \right. \kern-0pt} {\pi^{2}}}\sqrt {{{\rho_{\text{c}} h} \mathord{\left/{\vphantom {{\rho_{\text{c}} h} {D_{\text{c}}}}} \right. \kern-0pt} {D_{\text{c}}}}} \), of a square functionally graded material nanoplate without or resting on elastic foundations for different values of inhomogeneity parameter (\( {{a_{1}} \mathord{\left/{\vphantom {{a_{1}} h}} \right. \kern-0pt} h} = 10 \))
Full size table

Table 4 presents dimensionless fundamental frequencies of FGM nanoplates with and without porosity parameter (α) for deferent value of nonlocal parameter \( \left({e_{0} a} \right)^{2} \) and volume fraction of material (p) for the various theories (CPT, FPT, TPT, SPT) compared with the present result. In general, the frequency results decrease as the increase of nonlocal parameter and volume fraction of material (p) values for with and without porosity for deferent theories. The present results are in good agreement with the solutions of (FPT), (TPT) and (SPT) theories.

Table 4 Effects of volume fraction index p and nonlocal parameter on the free vibration \( \bar{\omega} = \omega a_{1}^{2} \sqrt {\left({{{\rho_{\text{c}} h} \mathord{\left/{\vphantom {{\rho_{\text{c}} h} {D_{\text{c}}}}} \right. \kern-0pt} {D_{\text{c}}}}} \right)} \) of simply supported functionally graded nanoplate
Full size table

Figures 3 and 4 show the variation of fundamental frequencies with the side-to-thickness ratio for square FGM nanoplate with and without porosity parameter (α) and volume fraction of material (p) for the various theories (CPT, FPT,TPT, SPT) compared with the present result, respectively. It can be observed that the CPT gives results higher than those obtained by the first shear plate theory (FPT), third plate theory (TPT) and sinusoidal plate theory (SPT) and the present results, but I note that the fundamental frequencies due to FPT, TPT, SPT, and present model increase with increasing the side-to-thickness ratio and decrease with increasing values of porosity volume index (\( \alpha \)) and the present result is in good agreement with the solutions of the FPT, TPT and SPT.

Fig. 3
figure 3

The effect of thickness ratio (\( {{a_{1}} \mathord{\left/{\vphantom {{a_{1}} h}} \right. \kern-0pt} h} \)) on nondimensional fundamental frequency of (SSSS) square plate (\( p = 3.5,\;\left({e_{0} a} \right)^{2} = 0\;,K_{\text{w}} = K_{\text{p}} = 0 \))

Full size image
Fig. 4
figure 4

The effect of thickness ratio (\( {{a_{1}} \mathord{\left/{\vphantom {{a_{1}} h}} \right. \kern-0pt} h} \)) on nondimensional fundamental frequency of (CCCC) square plate (\( p = 2,\;\left({e_{0} a} \right)^{2} = 1\;,K_{\text{w}} = 100,K_{\text{p}} = 10 \))

Full size image

In Fig. 5. The plate aspect ratio is taken as 1, and the side-to-thickness ratio is taken as 5, 10, 15, 25, 30, 35, 40, 45, 50; while the nonlocal parameter is considered as 0, 1, 3, 4, 5. Note that when \( \left({e_{0} a} \right)^{2} = 0 \), one obtains the results of local model for FGM nanoplates with and without porosity parameter (α) respectively. I note that the fundamental frequencies of the present result increases with increasing the side to-thickness ratio and decrease with increasing of the values of porosity volume index (α).

Fig. 5
figure 5

The effect of thickness ratio and nonlocal parameters \( \left({e_{0} a} \right)^{2} \) on nondimensional fundamental frequency of (CSCS) square plate (\( p = 1.5,\;K_{\text{w}} = 100,\;K_{\text{p}} = 10 \))

Full size image

Table 5 present the effects of plate aspect ratio \( \left({{{b_{1}} \mathord{\left/{\vphantom {{b_{1}} a}} \right. \kern-0pt} a}_{1}} \right) \), Effects of elastic foundation stiffness \( K_{\text{w}} \), \( K_{\text{p}} \) and porosity volume index (α) on the fundamental frequency for the various boundary conditions (SSSS), (CCCC) and (CSCS) for FGM nanoplates for different theories are given. The CPT give result higher than those obtained by the FPT, TPT, SPT and the present results, The maximum difference between present theory and the CPT appears in the case of (CCCC) plate and (CSCS). The fundamental frequency decrease with increase porosity volume index. It can be seen that the present result is in good agreement with the solutions of the FPT, TPT and SPT.

Table 5 Effects of elastic foundation stiffnesses \( K_{\text{w}},\;K_{\text{p}} \) and the aspect ratio \( \frac{b}{a} \) on the free vibration \( \bar{\omega} = \omega a_{1}^{2} \sqrt {\left({{{\rho_{\text{c}} h} \mathord{\left/{\vphantom {{\rho_{\text{c}} h} {D_{\text{c}}}}} \right. \kern-0pt} {D_{\text{c}}}}} \right)} \) of three boundaries conditions square plates \( p = 3.5,\;{a \mathord{\left/{\vphantom {a h}} \right. \kern-0pt} h} = 10 \), \( \left({e_{0} a} \right)^{2} = 1 \), \( m = n = 1 \)
Full size table

Figures 6 and 7 reveals the variation of fundamental frequency of the side- to-thickness ratio (\( {{a_{1}} \mathord{\left/{\vphantom {{a_{1}} h}} \right. \kern-0pt} h} \))for various values of foundation parameters (\( K_{\text{w}} \), \( K_{\text{p}} \)) for FGM nanoplates with and without porosity parameter (α). It is to be seen that the fundamental frequency increases with the increase of Winkler Pasternak elastic foundations (\( K_{\text{w}} \),\( K_{\text{p}} \)).

Fig. 6
figure 6

The effect of thickness ratio (\( {{a_{1}} \mathord{\left/{\vphantom {{a_{1}} h}} \right. \kern-0pt} h} \)) and Winkler elastic foundation \( K_{\text{w}} \) on nondimensional fundamental frequency of (CCSS) square plate (\( p = 2.5,\;\left({e_{0} a} \right)^{2} = 0.5,\;K_{\text{p}} = 10 \))

Full size image
Fig. 7
figure 7

The effect of thickness ratio (\( {{a_{1}} \mathord{\left/{\vphantom {{a_{1}} h}} \right. \kern-0pt} h} \)) and Pasternak elastic foundation \( K_{\text{p}} \) on nondimensional fundamental frequency of (CCSS) square plate (\( p = 2.5,\;\left({e_{0} a} \right)^{2} = 0.5 \), \( K_{\text{w}} = 100 \))

Full size image

Table 6 shows the variation of fundamental frequencies with the side-to-thickness ratio and volume fraction of material (p) for the various boundary conditions for porous FGM nanoplate are given, the various theories (CPT, FPT,TPT, SPT) compared with the present result respectively in Table 6. the CPT gives result higher than those obtained by the FPT, TPT, SPT and the present results. The maximum difference between present theory and the CPT appears in the case of (CCCC) plate and (CCCS). the fundamental frequency increase with increase volume fraction of material (p) and the side-to-thickness ratio \( \left({{{a_{1}} \mathord{\left/{\vphantom {{a_{1}} h}} \right. \kern-0pt} h}} \right) \) the same for Fig. 8. It can be seen that the present result is in good agreement with the solutions of the FPT, TPT and SPT.

Table 6 Effects of index parameter p and side-to-thickness ratio \( \left({{{a_{1}} \mathord{\left/{\vphantom {{a_{1}} h}} \right. \kern-0pt} h}} \right) \) on the free vibration \( \bar{\omega} \) of functionally graded material square nanoplate
Full size table
Fig. 8
figure 8

The effect of thickness ratio \( {{a_{1}} \mathord{\left/{\vphantom {{a_{1}} h}} \right. \kern-0pt} h} \) on nondimensional fundamental frequency of various boundary square plate (\( p = 2,\left({e_{0} a} \right)^{2} = 2,\;\alpha = 0.2,\;K_{\text{w}} = 100,\;K_{\text{p}} = 0 \)

Full size image

Figure 9 shows the influence of porosities on natural frequencies of (CCCC) FGM nanoplate for various volume fractions of material (p). The numerical result based on HSPT in this figure reveals that the fundamental frequencies decrease as the porosity parameter (α) and volume fraction of material (p) increases.

Fig. 9
figure 9

The effect of (p) and porosity volume index \( \alpha \) on nondimensional fundamental frequency of (CCCC) square plate (\( \left({e_{0} a} \right)^{2} = 1.5,\;K_{\text{w}} = 100,\;K_{\text{p}} = 10 \))

Full size image

4 Conclusion

Functionally graded materials are a new class of composite structures that are of great interest for engineering design and manufacture. In this study, a nonlocal elasticity model for free vibrations of FGMs nano plate on elastic medium with porosities was developed using exponential shear deformation plate theory. The model can be extended to the analysis of the vibrations of beams, plates, shells, solid, etc. The model allows the analysis of the small-size effects such as micro metric or nano metric effects. In the present model, the number of unknown functions was reduced to only two functions. The obtained results show that the frequency values decrease as of (p) values for every boundary condition increase. The frequencies of the plates increase dramatically within the range of spring constant factors around 100 to 10. Additionally, the porosity within functionally graded plates is one of the important aspects that lead to considerable changes in frequencies. The frequencies decrease as the porosity volume fraction increases for every value of the volume fraction index. Our results are in good agreements with those founded in the literature. For testing the fiability and the accuracy of the developed model, it is recommend to compare it with finite element model. This comparison will be done in future work of the authors.