1 Introduction

The Swift–Hohenberg equation is an evolutive nonlinear equation with four order derivatives in space. It was first proposed by J. B. Swift and P. C. Hohenberg to study the effects of thermal fluctuations on the Rayleigh–Bénard instability Swift and Hohenberg (1977). The Swift–Hohenberg equation is derived from the following free energy functional:

$$\begin{aligned} {\mathcal {E}} (\phi ) = \int _\varOmega \left( \frac{1}{4}\phi ^4+\frac{1-\epsilon }{2}\phi ^2 -|\nabla \phi |^2+\frac{1}{2}(\Delta \phi )^2 \right) \mathrm{d}{} \mathbf{x}, \end{aligned}$$

where the phase field \(\phi (\mathbf{x},t)\) approximates the number density of atoms in a binary mixture in the domain \(\varOmega = \varPi _{i=1}^d (0,L_i) \subset {{\mathbb {R}}}^d\) (\(\mathrm{d}=2\) or 3). \(\Delta \) is the Laplacian operator and the temperature-related parameter \(\epsilon \) is constant. For simplicity of exposition, here we consider the periodic boundary condition for the density field. Then, under the constrained gradient flow in a \(L^2\) space, the Swift–Hohenberg equation can be written by:

$$\begin{aligned} \frac{\partial \phi }{\partial t}(\mathbf{x},t) =&-\, \frac{\delta {\mathcal {E}}}{\delta \phi } =-\phi ^3(\mathbf{x},t)-(1-\epsilon )\phi (\mathbf{x},t)\nonumber \\&-\,2\Delta \phi (\mathbf{x},t)-\Delta ^2\phi (\mathbf{x},t) , \quad \mathbf{x} \in \varOmega , \quad 0<t \le T, \end{aligned}$$
(1)

where \({\delta {\mathcal {E}}}/{\delta \phi }\) denotes the variational derivative of \({{\mathcal {E}}}\) with respect to the variation \(\phi \). Taking the derivative of \({\mathcal {E}}(\phi )\) with respect to t, we obtain

which leads to the inequality,

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} {\mathcal {E}}(\phi ) \le 0. \end{aligned}$$

The review by Cross and Greenside (2009) outlined a wide range of applications of the Swift–Hohenberg equation including but not limited to biology, sociology, crystallography, and of course fluid. As the Swift–Hohenberg equation is a nonlinear partial differential equation, we can not generally obtain the analytic solution for the arbitrary initial conditions. Therefore, it is very important to develop an accurate and efficient numerical scheme to solve the Swift–Hohenberg equation.

Up to now, there are many schemes proposed to study the Swift–Hohenberg equation (Xi et al. 1991; Viñals et al. 1991; Elder et al. 1992; Christov et al. 1997; Staliunas and Sánchez-Morcillo 1998; Lloyd et al. 2008; Cheng and Warren 2008; Zhao et al. 2016a, b; Yang and Han 2017; Li et al. 2017; Abbaszadeh et al. 2019; Nikolay 2016; Dehghan and Abbaszadeh 2017; Christov and Pontes 2002; Gomez and Nogueira 2012; Lee 2017). A challenge is how to increase the stability and the accuracy of the numerical approximation for the solution. For instance, to ensure the stability of the discrete numerical scheme, the time step size (\(\Delta t\)) in Euler method is required \(\Delta t \sim O(h^4)\), where h is the mesh size in space. Therefore, the Euler method for the Swift–Hohenberg equation is very expensive to calculate the long time interval in practice (Cheng and Warren 2008; Gomez and Nogueira 2012). Christov and Pontes (2002) developed a computationally efficient second order in time implicit difference scheme which allowed strict implementation of a discrete approximation of the Lyapunov functional. Gomez and Nogueira (2012) proposed a new fully discrete algorithm for the Swift–Hohenberg equation which inherits the nonlinear stability property of the continuum equation irrespective of the time step. Lee presented semi-analytical Fourier spectral methods based on the operator splitting method for solving the Swift–Hohenberg equation to achieve high-order time accuracy (Lee 2017). However, most of the existing approaches proposed in the literature are with first-/second-order accurate in time and space. In recent years, high-order compact difference methods have been developed for simulating the diffusion equation (Dehghan and Mohammadi 2015; Mohammadi and Dehghan 2010; Mohammadi et al. 2009; Mohebbi and Dehghan 2010; Zouraris 2018). We are not aware of any results on fourth-order space and second-order time discretization for the Swift–Hohenberg equation.

This paper is focused on developing the compact finite-difference scheme, which is second-order accurate in time and fourth-order accurate in space with good stability. An adaptive time step method is adopted to improve the efficiency of the proposed scheme. This is motivated by the successful application of the compact finite difference scheme in Cahn–Hilliard equation (Lee et al. 2014; Li et al. 2016) and the phase field crystal equation (Li and Kim 2017). A nonlinearly stabilized splitting scheme constructed by the Newton-type iterative method is used so that our proposed scheme could allow large time step. Furthermore, the multigrid technique (Trottenberg et al. 2001; Kim et al. 2004) is added to accelerate the convergence of the resulting linear system. Several numerical examples including a convergence test of the proposed scheme, comparison with second-order scheme, a test of the stability of the proposed scheme, extension of the adaptive time step method, comparison with the phase field crystal equation, a study of the effect of computational domain and boundary condition, crystal growth in a supercooled liquid, and an evolution of Swift–Hohenberg equation in three dimensions, will be performed to verify the accuracy, stability and efficiency of our proposed method.

The remainder of this paper is organized as follows. In Sect. 2, we derive the fourth-order compact finite difference scheme. Section 3 presents some numerical experiment results. Finally, a short conclusion is given in Sect. 4.

2 Numerical solution

Let \(\varOmega = (0,L_x)\times (0,L_y)\), we denote a discrete computational domain by \(\varOmega _h = \{(x_i,y_j)\ :\ x_i = (i-0.5)h,\ y_j = (j-0.5)h,\ 1\le i\le N_x,\ 1\le j\le N_y\}\), where \(N_x\) and \(N_y\) are positive even integers and \(h=L_x/N_x=L_y/N_y\) is the space size. Let \(\phi _{ij}\) be the approximation of \(\phi (x_i,y_j)\). We define the 9-point discrete Laplacian operator \(\Delta _{c}\) (Lee et al. 2014) as:

$$\begin{aligned} \Delta _{c}\phi _{ij} =&\frac{ 4(\phi _{i-1,j}+\phi _{i+1,j}+\phi _{i,j-1}+\phi _{i,j+1}) }{6h^2} \nonumber \\&+ \, \frac{ \phi _{i-1,j-1}+\phi _{i-1,j+1}+\phi _{i+1,j-1}+\phi _{i+1,j+1}-20\phi _{ij} }{6h^2}. \end{aligned}$$
(2)

Similarly, the 27-point discrete Laplacian operator in 3-dimensional space (Li et al. 2016) is defined as:

$$\begin{aligned} \Delta _{c}\phi _{ijk} =&[ 14(\phi _{i+1,j,k}+\phi _{i-1,j,k} +\phi _{i,j+1,k}+\phi _{i,j-1,k}+\phi _{i,j,k+1}+\phi _{i,j,k-1}) \nonumber \\&+ \, 3(\phi _{i+1,j+1,k}+\phi _{i+1,j-1,k} + \phi _{i+1,j,k+1}+\phi _{i+1,j,k-1} + \phi _{i-1,j+1,k}+\phi _{i-1,j-1,k}\nonumber \\&+\, \phi _{i-1,j,k+1}+\phi _{i-1,j,k-1} + \phi _{i,j+1,k+1}+\phi _{i,j-1,k-1} + \phi _{i,j+1,k-1}+\phi _{i,j-1,k+1})\nonumber \\&+ \, \phi _{i-1,j+1,k+1}+\phi _{i-1,j-1,k-1} + \phi _{i-1,j+1,k-1}+\phi _{i-1,j-1,k+1} + \phi _{i+1,j+1,k+1}\nonumber \\&+ \, \phi _{i+1,j-1,k-1} + \phi _{i+1,j+1,k-1}+\phi _{i+1,j-1,k+1}-128\phi _{i,j,k} ] / (30h^2). \end{aligned}$$
(3)

Then using the Taylor series, we obtain

$$\begin{aligned} \Delta \phi _{ij}= & {} \left( \frac{\partial ^2\phi }{\partial x^2}+\frac{\partial ^2\phi }{\partial y^2}\right) _{ij}=\Delta _{c}\phi _{ij}-\frac{h^2}{12} \Delta ^2 \phi _{ij} + O(h^4), \end{aligned}$$
(4)

and

$$\begin{aligned} \Delta \phi _{ijk}= & {} \left( \frac{\partial ^2\phi }{\partial x^2}+\frac{\partial ^2\phi }{\partial y^2}+\frac{\partial ^2\phi }{\partial z^2}\right) _{ijk}=\Delta _{c}\phi _{ijk}-\frac{h^2}{12} \Delta ^2 \phi _{ijk} + O(h^4), \end{aligned}$$
(5)

for two-dimensional and three-dimensional spaces, respectively. Here \(\Delta ^2 \phi = \Delta (\Delta \phi )\) is the biharmonic operator. Now, we derive the fourth-order spatially accurate compact finite difference scheme for Swift–Hohenberg equation. Before that, we rewrite Eq. (1) as:

$$\begin{aligned}&\phi _t=-\phi ^3-(1-\epsilon )\phi -\Delta \kappa , \end{aligned}$$
(6)
$$\begin{aligned}&\kappa =2\phi +\Delta \phi . \end{aligned}$$
(7)

Here, \(\kappa \) holds the periodic boundary condition, because we assumed this condition for \(\phi \). Let \(\phi ^n\) and \(\kappa ^n\) be the approximations of \(\phi (\cdot ,n\Delta t)\) and \(\kappa (\cdot ,n\Delta t)\), respectively. We can discretize Eq. (6) as:

$$\begin{aligned} \phi _t=-\phi ^3-(1-\epsilon )\phi -\Delta \kappa = -\phi ^3-(1-\epsilon )\phi -\Delta _c \kappa + \frac{h^2}{12}\Delta ^2\kappa + O(h^4). \end{aligned}$$
(8)

Here, Eqs. (4) and (5) are used for two- and three-dimensional space, respectively. By replacing \(\Delta \kappa \) as \(-\phi ^3-(1-\epsilon )\phi -\phi _t\) in Eq. (8), we get:

$$\begin{aligned} \phi _t= & {} -\phi ^3-(1-\epsilon )\phi -\Delta _c \kappa + \frac{h^2}{12}\Delta (-\phi _t-\phi ^3-(1-\epsilon )\phi )+ O(h^4)\nonumber \\= & {} -\phi ^3-(1-\epsilon )\phi -\Delta _c \kappa + \frac{h^2}{12}\Delta _c(-\phi _t-\phi ^3-(1-\epsilon )\phi )+ O(h^4). \end{aligned}$$
(9)

To obtain a second-order accuracy in time scheme, we use a backward differentiation formula time for Eq. (9):

$$\begin{aligned}&\frac{3\phi ^{n+1} - 4\phi ^{n}+\phi ^{n-1}}{2\Delta t} = - \,({\phi }^{n+1})^3- (1-\epsilon )\phi ^{n+1}-\Delta \kappa ^{n+1}\nonumber \\&\quad - \frac{h^2}{12}\Delta _c\Big ( \frac{3\phi ^{n+1} - 4\phi ^{n}+\phi ^{n-1}}{2\Delta t}+(\phi ^{n+1})^3+(1-\epsilon )\phi ^{n+1}\Big )+ O(\Delta t^2+h^4), \quad \end{aligned}$$
(10)

with \(\phi ^{-1}=\phi ^{0}\). It is difficult to solve \(\Delta _c({\phi }^{n+1})^3\), which is a Laplacian for the nonlinear term \(({\phi }^{n+1})^3\). Therefore, we replace \(\Delta _c({\phi }^{n+1})^3\) by \(\Delta _c({\tilde{\phi }}^{n+1})^3\), retaining the second-order accuracy in time:

$$\begin{aligned}&\frac{3\phi ^{n+1} - 4\phi ^{n}+\phi ^{n-1}}{2\Delta t} = -({\phi }^{n+1})^3- (1-\epsilon )\phi ^{n+1}-\Delta \kappa ^{n+1}\nonumber \\&\quad - \frac{h^2}{12}\Delta _c\Big ( \frac{3\phi ^{n+1} - 4\phi ^{n}+\phi ^{n-1}}{2\Delta t}+({{\tilde{\phi }}}^{n+1})^3+(1-\epsilon )\phi ^{n+1}\Big )+ O(\Delta t^2+h^4). \quad \end{aligned}$$
(11)

Here, the one-time value \({\tilde{\phi }}^{n+1}\) is calculated using an extrapolation from the previous two values, i.e., \({\tilde{\phi }}^{n+1}=2{\phi }^{n}-{\phi }^{n-1}\).

To obtain a high-order stable scheme, we use an implicit scheme for Eq. (7) as:

$$\begin{aligned} \kappa ^{n+1}= & {} 2{\tilde{\phi }}^{n+1} +\Delta _c\phi ^{n+1} - \frac{h^2}{12}\Delta ^2\phi ^{n+1}+ O(h^4)\nonumber \\= & {} 2{\tilde{\phi }}^{n+1} +\Delta _c\phi ^{n+1}- \frac{h^2}{12}\Delta _c( \kappa ^{n+1}-2{\tilde{\phi }}^{n+1})+ O(h^4). \end{aligned}$$
(12)

Finally, our proposed schemes are written as:

$$\begin{aligned}&\frac{3\phi ^{n+1} - 4\phi ^{n}+\phi ^{n-1}}{2\Delta t} = -({\phi }^{n+1})^3- (1-\epsilon )\phi ^{n+1}-\Delta \kappa ^{n+1}\nonumber \\&\quad - \, \frac{h^2}{12}\Delta _c\Big ( \frac{3\phi ^{n+1} - 4\phi ^{n}+\phi ^{n-1}}{2\Delta t}+({{\tilde{\phi }}}^{n+1})^3+(1-\epsilon )\phi ^{n+1}\Big ), \end{aligned}$$
(13)
$$\begin{aligned}&\quad \kappa ^{n+1} = 2{\tilde{\phi }}^{n+1} +\Delta _c\phi ^{n+1}- \frac{h^2}{12}\Delta _c( \kappa ^{n+1}-2{\tilde{\phi }}^{n+1}). \end{aligned}$$
(14)

We use a nonlinear multigrid method (Trottenberg et al. 2001; Kim et al. 2004) to solve the nonlinear discrete system (13, 14) at the implicit time level. Since \(({\phi }^{n+1})^3\) is nonlinear with respect to \({\phi }^{n+1}\), we use the Newton-type iterative method (Li and Kim 2017) to linearize \(({\phi }^{n+1})^3\). Despite it being difficult to exactly prove that our proposed method has a good stability property, the results of the numerical tests presented in Sect. 3 indicate that our proposed scheme allows much larger time steps.

3 Numerical results

3.1 Convergence test

We verify the convergence predicted by our proposed method by evolving the same initial condition as a function of time with increasingly finer values for both time spacing and grid spacing. The initial profile of the density field is given by:

$$\begin{aligned}&\phi (x,y,0)=0.01(\cos (\pi x)+\cos (\pi y)+\cos (0.25\pi x)+\cos (0.25\pi y)). \end{aligned}$$
(15)

on the domain \((0,50)\times (0,50)\). The simulation is evolved to time \(t=100\) with \(\epsilon =0.2\). To obtain the convergence rate for temporal discretization, we consider the same test by fixing the space step size as \(h = 1\) and choosing a set of decreasing time steps \(\Delta t =0.25\), 0.125, \(\ldots \), and 0.078125. Since there is no closed-form analytical solution for this problem, we use the Cauchy Error to measure the error without knowing the exact solution. The Cauchy error of a grid is defined as the difference between the numerical solutions obtained using the time step \(\Delta t\) and the next finer time space \(\Delta t/2\). To obtain the convergence rate for spatial discretization, we use the grid sizes as \(16\times 16\), \(32\times 32\), \(\ldots \), and \(512\times 512\). The time step \(\Delta t=2h^2\) is fixed. We define the Cauchy error between the numerical solution \(\phi _{h}\) and the next finer grid cells covering it to be: \( e_{ij}^{h/\frac{h}{2}} =\phi _{ij}^h-(\phi _{2i,2j}^{h/2}+\phi _{2i-1,2j}^{h/2}+\phi _{2i,2j-1}^{h/2}+\phi _{2i,2j}^{h/2})/4\). The errors of temporal and spatial refinements are given Tables 1 and 2, respectively. The results indicate the convergence of the results under spatial and temporal refinements is evident.

Table 1 \(L_2\) errors with various time steps
Full size table
Table 2 \(L_2\) errors with various mesh grids
Full size table

To demonstrate the convergence rate, we show the fitting plots together in Fig. 1a, b. The data define a straight line with slopes 2.048 and 3.922, respectively. From these results, we can see that our proposed numerical scheme is second-order accurate with respect to time and fourth-order accurate with respect to space.

Fig. 1
figure 1

a The \(L_2\) normal errors of temporal refinement. b The \(L_2\) normal errors of spatial refinement

Full size image

3.2 Comparison with second-order scheme

It is not difficult to present a second-order accurate (in time and space) finite-difference nonlinear scheme as:

$$\begin{aligned}&\frac{3\phi ^{n+1} - 4\phi ^{n}+\phi ^{n-1}}{2\Delta t} = -({\phi }^{n+1})^3- (1-\epsilon )\phi ^{n+1}-\Delta _c\kappa ^{n+1}, \end{aligned}$$
(16)
$$\begin{aligned}&\kappa ^{n+1} = 2{\tilde{\phi }}^{n+1} +\Delta _c\phi ^{n+1}. \end{aligned}$$
(17)

There are other well-established methods (Gomez and Nogueira 2012), which are second-order accurate in time and space. The performance of our time discretization, that is, backward differentiation, is with second-order accuracy which has been widely superior to numerical simulation. For this reason, we will focus on the space discretization method. In this section, we will compare the performance of our proposed numerical scheme with the second-order schemes (16) and (17). The initial condition is set as:

$$\begin{aligned} \phi (x,y,0)=0.1+0.02\cos \left( \frac{\pi x)}{100}\right) \sin \left( \frac{\pi y}{100}\right) +0.05\sin \left( \frac{\pi x}{20}\right) \cos \left( \frac{\pi y}{20}\right) . \end{aligned}$$
(18)

on the domain \((0,100)\times (0,100)\). The calculation is run until \(t=50\) with the time step \(\Delta t=1\) and \(\epsilon =0.2\).

Figure 2a, b show the solutions obtained by our proposed fourth-order scheme and second-order scheme, respectively. From left to right, they are the results obtained with the grid sizes \(64\times 64\), \(128\times 128\), \(256\times 256\), and \(512\times 512\), respectively. From these results, we can find that to get similar numerical solutions obtained by fourth-order scheme, more mesh grids should be used in the second-order scheme.

Fig. 2
figure 2

The solutions with our proposed fourth-order scheme (a) and second-order scheme (b). From left to right, the grid sizes \(64\times 64\), \(128\times 128\), \(256\times 256\), and \(512\times 512\) are used, respectively

Full size image

Table 3 shows the averaged CPU times versus the number of mesh grid (\(N_xN_y\)). The CPU time is recorded on a 3.4 GHz PC with 16G main memory. The result suggests that the difference of used CPU time for the two mentioned schemes is not significant.

Table 3 Average CPU times (in s) versus the number of mesh grid (\(N_xN_y\))
Full size table

The straight fitting plot shown in Fig. 3 implies that the multigrid solver achieves the \(O(N_xN_y)\) efficiency for the mentioned two cases.

Fig. 3
figure 3

Logarithm of averaged CPU time versus number of mesh gird (\(N_xN_y\)) in multigrid solver

Full size image
Fig. 4
figure 4

Evolution of the Swift–Hohenberg equation with much larger time step \(\Delta t=100\)

Full size image

3.3 Stability of the proposed scheme

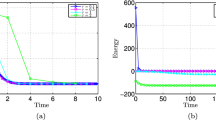
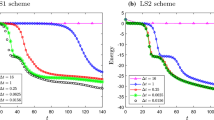
In this section, we will examine the stability of our proposed scheme with the initial condition \(\phi (x,y,0)=0.05+0.05\text{ rand }(x,y)\) on a square domain \((0,128)\times (0,128)\) with the mesh grid \(128\times 128\), where rand() is a random number between \(-\,1\) and 1. Figure 4 shows the evolution of the Swift–Hohenberg equation with much larger time step \(\Delta t=100\). Here, \(\epsilon =0.2\) is used. As can be seen, the numerical solutions do not blow up and the energy is decreasing, which confirms that our proposed scheme can use large time steps. However, although a larger time step can be used, the evolution is less accurate, i.e., the energy with \(\Delta t = 100\) is increasing for some time (see Fig. 4). To verify the evolving patterns with the small time steps, a set of different time steps \(\Delta t = 0.5\), 1, 2, and 4 are considered. Figure 5a–d shows the numerical solutions with different time steps at time \(t=2000\). Figure 5e shows energy evolutions with four different time steps. The accuracy is observed to increase as the time step is decreased, while the difference tends to be obvious for large time steps (see the box region in Fig. 5). Therefore, a high accurate numerical solution would require a smaller time step. While, the stability of numerical scheme is useful. Owning to the good stability, we can develop an efficient adaptive time step algorithm to reduce the computational cost.

Fig. 5
figure 5

a–d Numerical solutions with different time steps at time \(t=2000\). e Energy evolutions with four different time steps

Full size image

3.4 Adaptive time step method for the Swift–Hohenberg equation

Observing all the cases in Sect. 3.3, we can see that when the early-time dynamics are captured with a small time step, the accuracy of the numerical results will be better compared with those obtained with larger time steps. On the other hand, because the long-time simulation converges to the steady-state solution, a large time step should be used to reduce the computational cost. The use of a large time step is possible because of the good stability of our proposed scheme. This suggests that performance of our proposed scheme could be enhanced by using an adaptive time step. We previously proposed a similar method (Li et al. 2017), which has a computationally efficient adaptive time step for the Cahn–Hilliard equation. The adaptive time-step strategy is realized using the following procedure. Set the minimum and maximum time step sizes, \(\Delta t_{\min }\) and \(\Delta t_{\max }\), respectively. Let \(\Delta t^0\) be an initial time step (here we set \(\Delta t^0 = \Delta t_{\min }\)). Then, for \(n=1,2, \ldots ,\) we define the next time step to be

$$\begin{aligned} \Delta t^n = \left\{ \begin{array}{ll} \Delta t_{\min }, ~&{} \text{ if } t<t_0, \\ \min \left[ \max \left( \frac{\lambda }{\Vert \phi ^n - \phi ^{n-1} \Vert _\infty }, \Delta t_{\min } \right) , \Delta t_{\max } \right] , ~&{} \text{ otherwise }. \end{array} \right. \end{aligned}$$
(19)

where \( \Vert \phi ^n - \phi ^{n-1}\Vert _\infty \) is the maximum value of \(\Vert \phi ^n - \phi ^{n-1}\Vert \) and \(\lambda \) is a tolerance to choose a suitable time step. Next, we study the effectiveness of the adaptive time step strategy by comparing the numerical solutions with uniform time step and adaptive time step. The initial condition is the same as those in Sect. 3.3. In this test, we chose \(t_0=100\), \(\Delta t_{\min }=0.5\), \(\Delta t_{\max }=50\), and \(\lambda =0.4\). The simulation is run up to T = 20,000. To compare the results obtained by the adaptive time step, we run the computation with a uniform time step \(\Delta t=0.5\).

Fig. 6
figure 6

Energy evolutions with uniform time step and adaptive time step. The inscribed small figures are the density field \(\phi \) computed with uniform time step (top) and adaptive time step (bottom)

Full size image

Figure 6 shows the comparison of the numerical results obtained using uniform time step and adaptive time step. We notice that the density fields obtained by two cases are qualitatively similar. For the CPU times, the taken CPU times are 148.95 min and 10.05 min for uniform time step and adaptive time step, respectively, which implies that the computational cost can be significantly reduced using the adaptive time step.

Fig. 7
figure 7

The density field at time \(t=1000\) with two different values of \(\phi _\mathrm{ave}\) for Eqs. (1) and (20). a, b Results obtained by Eq. (20). c, d Results obtained by Eq. (1)

Full size image

3.5 Comparison with the phase field crystal equation

The phase field crystal model (PFC), which is related to the dynamic density functional theory of freezing (Elder and Grant 2004; Marconi and Tarazona 1999), has an important advantage over many atomistic models in that the characteristic time is determined by the diffusion time scale and not by that of the atomic vibrations. The phase field crystal model can be derived from the mass-constrained gradient flow in a \(H^{-1}\) Hilbert space of a free energy functional of the Swift–Hohenberg type as:

$$\begin{aligned} \frac{\partial \phi }{\partial t} =\Delta \frac{\delta {\mathcal {E}}}{\delta \phi }=\Delta (\phi ^3+(1-\epsilon )\phi +2\Delta \phi +\Delta ^2\phi ). \end{aligned}$$
(20)

There are many schemes proposed to study the phase field crystal equation (Cheng and Warren 2008; Wise et al. 2009; Lee et al. 2015; Vignal et al. 2015; Clayton and Knap 2016; Li et al. 2019), since both Eqs. (1) and (20) are derived from the same energy functional in the different space, we will compare the dynamics of these two equations. Equation (20) is solved by a fourth-order spatially accurate and practically stable compact finite-difference scheme (Li and Kim 2017). The same initial condition \(\phi (x,y,0)=\phi _\mathrm{ave}+0.05\text{ rand }(x,y)\) is used on a square domain \((0,128)\times (0,128)\) with a mesh grid \(256\times 256\). The time step \(\Delta t=1\) and \(\epsilon =0.2\) are chosen. Since the phase field crystal model satisfies mass conservation, we can consider this problem by performing a numerical experiment with different initial conditions \(\phi _\mathrm{ave}=0.05\) and  0.15. The density field at time \(t=1000\) with two different values of \(\phi _\mathrm{ave}\) for Eqs. (1) and (20) is shown in Fig. 7. The results show that, depending on the value of the initial average \(\phi _\mathrm{ave}\), different patterns for Eq. (20) are produced, e.g., hexagonal (Fig. 7a) and striped (Fig. 7b). While as can be seen in Fig. 7c, d, Eq. (1) produces the striped patterns.

Fig. 8
figure 8

Evolution of a mass(\(\sum \sum \phi ^n/\sum \sum \phi ^0\)) and b energy using \(\phi _\mathrm{ave}\) for Eqs. (1) and (20)

Full size image

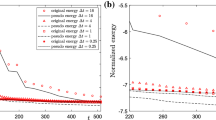
Figure 8a, b show the time evolution of the scaled total energy mass (\(\sum \sum \phi ^n/\sum \sum \phi ^0\)) and energy, respectively. The discrete mass for Eq. (20) is observed to be conserved and Eq. (1) does not hold the mass conservation. The discrete energies for Eqs. (1) and (20) are observed to be non-increasing from one time step to the next conserved to be some constant energy level. Furthermore, we can see that by Eq. (1), the energy is decreasing faster and conserved at a lower energy level compared to using Eq. (20).

Fig. 9
figure 9

The density field at time \(t=1000\) with different values of \(\epsilon \). Here, only Eq. (1) is considered

Full size image

Figure 9 shows the density field at time \(t=1000\) with different values of \(\epsilon =0.01\), 0.1, and 0.5. Here, only Eq. (1) is considered. The same initial conditions are used as the above test. Here, \(\phi _\mathrm{ave}=0.05\) is fixed. The results show that, depending on the value of parameter \(\epsilon \), striped and hexagonal patterns can be produced.

3.6 Effect of computational domain and boundary conditions

The length of the chosen computational domain and boundary condition can affect the patterns of density field. To investigate the effect of computational domain and boundary condition on pattern formation, we simulate our scheme with the same random initial conditions on a square domain \(\varOmega =(0,100)\times (0,100)\) and \(\varOmega =(0,200)\times (0,200)\). The parameters \(\Delta t=1\), \(\epsilon =0.2\), and \(h=100/64\) are used. Here,we also consider the periodic and Neumann boundary conditions. Note that using the ghost cells, different boundary conditions in the finite difference framework are easily satisfied. Figure 10 shows the density field with periodic boundary condition and Neumann boundary condition. The results suggest that as the domain size increases, we have more complex striped pattern and need more computational time to get a conserved result. Furthermore, we can see that with the periodic boundary condition, the phases interact across the boundary. And with the Neumann boundary, the phases are perpendicular to the domain boundary.

Fig. 10
figure 10

a, b The density field with periodic boundary condition. c, d The density field with Neumann boundary condition. From top to bottom, they are the results at \(t=1000\) and \(t=3000\), respectively

Full size image

3.7 Crystal growth in a supercooled liquid

Next, we consider the growth of a polycrystal in a supercooled liquid. Similar numerical examples can be found in Li and Kim (2017) and Elder and Grant (2004). We start our simulation with a constant density field \(\phi _\mathrm{ave}=0.285\) on a domain \(\varOmega =(0,500)\times (0,500)\) with a \(512\times 512\) mesh grid. As seeds for nucleation, we place three random perturbations on three small square patches with the following expression:

$$\begin{aligned} \phi (x,y)=\phi _\mathrm{ave}+A\text{ rand }(x,y). \end{aligned}$$

Here A is amplitude. The centers of four small square patches are located at (375, 125), (375, 375), and (125, 250) and the length of each square is 10. The amplitudes are chosen as \(A=0.1\), 0.2, and 0.4 in turn. The parameters are set to be \(\Delta t=1\) and \(\epsilon =0.25\). In this test, the boundary conditions are chosen as be homogeneous Neumann boundaries for \(\phi \) and \(\kappa \). Figure 11 shows snapshots of the crystal microstructure at several times. Three different crystal grains grow and eventually become large enough to form grain boundaries.

Fig. 11
figure 11

Growth of a polycrystal in a supercooled liquid. The computational time is listed below each figure

Full size image

3.8 Swift–Hohenberg equation in three dimensions

This example deals with the numerical simulation of Swift–Hohenberg equation in three dimensions. The initial condition is chosen as \(\phi ({x,y,z},0) =0.05+0.05\text{ rand }(x,y,z)\) on the computational domain \((0,128)\times (0,128)\times (0,128)\). Here,we assume periodic boundary conditions in all directions. The computation is run up to \(t=1000\) with the time step \(\Delta t=1\). The parameters \(\epsilon =0.2\) and \(h=1\) are used. Figure 12 shows the time evolution of the energy functional and the density field. It can be observed that our proposed scheme can work well in three dimensions. The energy decreases at all times, which suggests that our method has a good stability property.

Fig. 12
figure 12

Evolution of Swift–Hohenberg equation in three dimensions

Full size image

4 Conclusions

In this paper, we presented a high-order accurate compact scheme for the Swift–Hohenberg equation. We discretized this equation by a fourth-order compact finite-difference formula in space and a backward differentiation with second-order accurate in time, respectively. A stabilized splitting scheme was presented and a Newton-type iterative method was introduced to deal with the nonlinear term. The resulting discrete systems were solved by a fast and efficient nonlinear multigrid solver. Adaptive time step method was implemented to reduce the computational cost. Various numerical simulations including a convergence test of the proposed scheme, comparison with second-order scheme, a test of the stability of the proposed scheme, extension of the adaptive time step method, comparison with the phase field crystal equation, a study of the effect of computational domain and boundary condition, and an evolution of Swift–Hohenberg equation in three dimensions, were performed to demonstrate the efficiency of our proposed method.