1 Introduction

In this article, we consider the Swift–Hohenberg (SH) equation with quadratic-cubic nonlinearity [1,2,3]:

$$\begin{aligned} \phi _t = -(\phi ^3 - g\phi ^2 + (-\epsilon +(1+{\varDelta })^2)\phi ), \end{aligned}$$
(1)

where \(\phi = \phi (\mathbf{x},t)\) is the density field in the domain \(\mathbf{x} ~\in ~{\varOmega }\subset {{\mathbb {R}}}^d\), where \(d = 2\) or 3 is the space dimension and the subscript t represents the derivative with respect to time t, g is a nonnegative constant, \(\epsilon \) is a positive parameter, and \(\epsilon < 1\) in general. The SH equation has extensive applications in physical and industrial fields, such as biological tissue [4], thermal convection [1], crystallography [5], and pattern formations [6]. One can derive the SH equation (1) by taking the variational derivative of the following energy functional:

$$\begin{aligned} {\mathcal {E}}(\phi ) = \int _{\varOmega }\left( \frac{1}{4}\phi ^4 - \frac{g}{3}\phi ^3 + \frac{1}{2}\phi (-\epsilon +(1+{\varDelta })^2)\phi \right) \mathrm{{d}}{} \mathbf{x}. \end{aligned}$$
(2)

We take the derivative of Eq. (2) with respect to time t and we obtain

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{d}}t}{\mathcal {E}}(\phi )= & {} -\int _{\varOmega }\phi ^2_t \,\mathrm{{d}}{} \mathbf{x} \le 0, \end{aligned}$$

which indicates the energy functional of the SH equation is nonincreasing. To numerically study the dynamics of the SH equation, one important criterion of constructing numerical scheme is whether the energy dissipation law is satisfied at larger time steps. In the past thirty years, many scholars have developed various practical numerical schemes for the SH equation [7,8,9,10,11,12]. However, most of the previous works only have first-order temporal accuracy. To obtain the desired results under larger time steps, high-order (at least second-order) accurate schemes are necessary. Sarmiento et al. [13] developed an adaptive second-order accurate and energy stable method for the SH model with controllable dissipation. Lee [14] proposed a high-order semi-analytical Fourier spectral method for the SH equation. Su et al. [5] numerically studied the SH equation by using a compact difference method. Their works only focus on the case of \(g = 0\) (no cubic nonlinearity). Note that the case of \(g \ne 0\) usually causes some challenges in constructing energy stable numerical schemes. Based on the idea of convex splitting, Lee [3] recently proposed nonlinearly energy stable schemes for the SH equation. Here, the nonlinear part is treated implicitly and Newton-type linearization is needed in the iteration. Moreover, the convex splitting method has been successfully applied to various phase-field models with SH-type free energy. For example, Wise et al. [15] developed an unconditionally stable finite-difference scheme for the phase-field crystal (PFC) equation. Hu et al. [16] proposed an efficient and energy stable nonlinear-multigrid method for solving the PFC model. Guan et al. [17] developed a hexagonal finite difference scheme for the PFC amplitude equations in two-dimensional space. Wang and Wise [18] developed an energy stable finite difference method for the modified PFC equation by using the convex splitting approach. Later, Baskaran et al. [19] proposed an efficient and stable nonlinear-multigrid method for solving the modified PFC model. Cheng et al. [20] constructed an energy stable scheme for the square PFC equation by using the Fourier pseudo-spectral method and BDF2 temporal discretization. For more details of convergence and error estimations of second-order convex splitting methods for three-dimensional PFC model and modified PFC model, please refer to [21, 22].

In this work, we want to develop the desired numerical schemes satisfying the following advantages: (1) Accuracy (at least second-order accuracy), (2) Energy stability (the energy dissipation law is satisfied), and (3) Efficiency (linear system with constant coefficients), for the Allen–Cahn (AC) equation [23,24,25,26], Cahn–Hilliard (CH) equation [27, 28], PFC equation [29], etc. The recently developed Lagrange multiplier approach [30], invariant energy quadratization (IEQ) approach [31], and scalar auxiliary variable (SAV) approach [32] are the popular ways to construct efficient and energy stable schemes with high-order accuracy. The classical Lagrange multiplier approach is valid for the problems with fourth-order polynomial potential, such as the AC, CH, and PFC equations [30, 33]. One can use an auxiliary variable to replace the quadratic nonlinear terms in the equation to construct energy stable schemes. For the SH equation with cubic nonlinearity, it is hard to show the energy stability if we replace all quadratic parts with an auxiliary variable. For the IEQ and SAV approaches, we admit that they not only satisfy the energy dissipation law for various gradient flows, but also naturally satisfy the boundedness of total energy because the auxiliary variable is defined in the form of square-root. They are good methods for the phase-field models with nonlinear terms satisfying the bounded-from-below condition. However, if we consider the SH equation with cubic nonlinearity, there is no criterion guiding us to choose an exact constant to guarantee the term beneath the square-root be always positive because the variable \(g > 0\). If an improper constant is used, the value beneath the square-root may be negative, and then the computation cannot be conducted. Therefore, for the SH equation in the case of \(g \ne 0\), the classical Lagrange multiplier, IEQ, and SAV approaches may be not very practical [34]. In a recent work of Liu and Li [35], a step-by-step solving scheme based on the SAV approach was proposed for the AC, CH, and PFC equations. This new approach weakens the condition of classical SAV approach and inherits the advantages of classical SAV approach. The similar ideas can also be found in a recent work [36] for phase-field surfactant model.

Inspired by the ideas in [35], we develop linear and energy stable numerical schemes for the SH equation with \(g \ge 0\). In our schemes, the bounded below restriction of classical SAV approach is weakened, i.e., we only require that the auxiliary variable is not zero. Moreover, the density field \(\phi \) and auxiliary variable are decoupled with each other, and thus we can solve them in a step-by-step way, i.e., the density field is updated by solving only one semi-implicit system with constant coefficients and then the auxiliary variable can be directly updated by an explicit way. Different with the classical SAV approach, the calculation of inner product is not needed any more, the whole algorithm is significantly simplified. To the best of our knowledge, this is the first work using the modified SAV approach [35] to treat the SH equation with \(g \ge 0\).

The organization of the rest of this work is as follows. In Sect. 2, we describe the equivalent form of governing equations. In Sect. 3, we present the temporally first- and second-order accurate schemes and analytically estimate the energy dissipation law. In Sect. 4, various computational experiments are performed. The conclusion are given in Sect. 5.

2 Governing equations

In this section, we describe the equivalent governing equations based on the improved SAV approach. Defining the following auxiliary variable

$$\begin{aligned} U = E(\phi ) + C, \end{aligned}$$
(3)

where \(E(\phi ) = \int _{\varOmega }\left( \frac{1}{4}\phi ^4 - \frac{g}{3}\phi ^3 - \frac{\epsilon }{2}\phi ^2 \right) \mathrm{{d}}{} \mathbf{x}\) and C is a constant ensuring \(E(\phi ) + C \ne 0\). Based on the property \({\mathcal {E}}(\phi ^0) \ge {\mathcal {E}}(\phi )\), where \({\mathcal {E}}(\phi ^0)\) is the initial total energy functional, we can find

$$\begin{aligned} {\mathcal {E}}(\phi ^0) - E(\phi ) = {\mathcal {E}}(\phi ^0) - {\mathcal {E}}(\phi ) + \int _{\varOmega }\frac{1}{2}\phi (1+{\varDelta })^2\phi \, \mathrm{{d}}{} \mathbf{x} \ge 0. \end{aligned}$$
(4)

Thus, we can use \(C = -{\mathcal {E}}(\phi ^0) - \gamma \), where \(\gamma \) is any positive constant and we use \(\gamma = 0.0001\) in this work. Therefore, the total energy function (2) can be written to be the following equivalent form:

$$\begin{aligned} {\mathcal {E}}(\phi ,U)= & {} \int _{\varOmega }\frac{1}{2}\phi (1+{\varDelta })^2 \phi \mathrm{{d}}{} \mathbf{x} + U - C \nonumber \\= & {} \int _{\varOmega }\frac{1}{2}\phi ^2 - |\nabla \phi |^2 + \frac{1}{2}({\varDelta }\phi )^2 \mathrm{{d}}{} \mathbf{x} + U - C , \end{aligned}$$
(5)

where the periodic boundary condition is considered. By taking the variational derivative of Eq. (5) with respect to \(\phi \) and taking the derivative of U with respect to time t, we derive the following equivalent governing equations:

$$\begin{aligned}&\phi _t = -\frac{U}{E(\phi )+C} F'(\phi ) - \phi - 2{\varDelta }\phi - {\varDelta }\kappa , \end{aligned}$$
(6)
$$\begin{aligned}&\kappa = {\varDelta }\phi , \end{aligned}$$
(7)
$$\begin{aligned}&U_t = \int _{\varOmega }\frac{U}{E(\phi )+C} F'(\phi ) \phi _t \,\mathrm{{d}}{} \mathbf{x}, \end{aligned}$$
(8)

where \(F(\phi ) = \frac{1}{4}\phi ^4 - \frac{g}{3}\phi ^3 - \frac{\epsilon }{2}\phi ^2\) and \(F'(\phi )\) represents the derivative with respect to \(\phi \). By taking the inner product of Eq. (6) with \(-\phi _t\), we have

$$\begin{aligned} -\Vert \phi _t\Vert ^2 = \left( \frac{U}{E(\phi )+C}F'(\phi ), \phi _t\right) + (\phi ,\phi _t) + (2{\varDelta }\phi ,\phi _t) + ({\varDelta }\kappa , \phi _t), \end{aligned}$$
(9)

where \((a,a) = \Vert a\Vert ^2\) is the \(L^2\)-inner product.

By taking the inner product of Eq. (7) with \({\varDelta }\phi _t\), we get

$$\begin{aligned} (\kappa ,{\varDelta }\phi _t) = ({\varDelta }\kappa , \phi _t) = ({\varDelta }\phi , {\varDelta }\phi _t). \end{aligned}$$
(10)

By combining Eqs. (9) and (10) and using Eq. (8), we obtain

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{d}}t}U + \frac{1}{2}\frac{\mathrm{{d}}}{\mathrm{{d}}t}\Vert \phi \Vert ^2 - \frac{\mathrm{{d}}}{\mathrm{{d}}t}\Vert \nabla \phi \Vert ^2 + \frac{1}{2}\frac{\mathrm{{d}}}{\mathrm{{d}}t}\Vert {\varDelta }\phi \Vert ^2 = -\Vert \phi _t\Vert ^2 \le 0, \end{aligned}$$
(11)

which implies the equivalent total energy functional (5) satisfies the energy dissipation law. Here, we adopt the periodic boundary condition or the following homogeneous Neumann boundary condition:

$$\begin{aligned} \nabla \phi \cdot \mathbf{n}|_{\partial {\varOmega }} = 0, ~~\nabla \kappa \cdot \mathbf{n}|_{\partial {\varOmega }} = 0, \end{aligned}$$

where \(\mathbf{n}\) is the unit outward vector to the domain boundary \(\partial {\varOmega }\). Based on the equivalent governing equations (6)–(8), we will construct linearly first- and second-order schemes in the next section. For the energy stable schemes, the periodic and the above homogeneous Neumann boundary conditions are commonly used because the effects from boundary can be easily removed. Recently, Espath et al. [37] proposed generalized SH models based on a second-gradient phase-field theory with general boundary condition. For a general boundary condition, some technical works are needed to construct energy stable scheme and we will consider this interesting issue in the future.

3 Proposed temporal schemes

3.1 Linearly first-order scheme (LS1)

For Eqs. (6)–(8), we propose the following temporally first-order accurate numerical scheme

$$\begin{aligned}&\frac{\phi ^{n+1}-\phi ^n}{{\varDelta }t} = -\frac{U^n}{E(\phi ^n)+C}F'(\phi ^n) - \phi ^{n+1} - 2{\varDelta }\phi ^n - {\varDelta }\kappa ^{n+1}, \end{aligned}$$
(12)
$$\begin{aligned}&\kappa ^{n+1} = {\varDelta }\phi ^{n+1}, \end{aligned}$$
(13)
$$\begin{aligned}&\frac{U^{n+1}-U^n}{{\varDelta }t} = \int _{\varOmega }\frac{U^n}{E(\phi ^n)+C}F'(\phi ^n) \frac{\phi ^{n+1}-\phi ^n}{{\varDelta }t} \mathrm{{d}}{} \mathbf{x}, \end{aligned}$$
(14)

where superscripts \(n+1\) and n represent the solutions at \(n+1\) and n time level, and \({\varDelta }t\) is the time step. Next, we prove the proposed first-order scheme (12)–(14) satisfies the discrete energy dissipation law, i.e., \({\mathcal {E}}(\phi ^{n+1},U^{n+1}) \le {\mathcal {E}}(\phi ^{n},U^{n})\), where

$$\begin{aligned} {\mathcal {E}}(\phi ^{n},U^{n}) = U^n + \frac{1}{2}\Vert \phi ^n\Vert ^2 - \Vert \nabla \phi ^n\Vert ^2 + \frac{1}{2}\Vert {\varDelta }\phi ^n\Vert ^2 - C. \end{aligned}$$

By taking the inner product of Eq. (12) with \(-(\phi ^{n+1}-\phi ^n)\), we have

$$\begin{aligned} -\frac{1}{{\varDelta }t}\Vert \phi ^{n+1}-\phi ^n\Vert ^2= & {} \left( \frac{U^n}{E(\phi ^n)+C}, \phi ^{n+1}-\phi ^n\right) + (\phi ^{n+1},\phi ^{n+1}-\phi ^n)\nonumber \\&+ ( 2{\varDelta }\phi ^n, \phi ^{n+1}-\phi ^n) + ({\varDelta }\kappa ^{n+1}, \phi ^{n+1}-\phi ^n). \end{aligned}$$
(15)

By using the following identity:

$$\begin{aligned} (a,a-b) = \frac{1}{2}( |a|^2 - |b|^2 + |a-b|^2 ), \end{aligned}$$

we can rewrite Eq. (16) to be

$$\begin{aligned} -\frac{1}{{\varDelta }t}\Vert \phi ^{n+1}-\phi ^n\Vert ^2= & {} \left( \frac{U^n}{E(\phi ^n)+C}, \phi ^{n+1}-\phi ^n\right) + \frac{1}{2}\left( \Vert \phi ^{n+1}\Vert ^2 - \Vert \phi ^n\Vert ^2 \Vert \phi ^{n+1}-\phi ^n\Vert ^2 \right) \nonumber \\&+ \left( \Vert \nabla \phi ^n\Vert ^2 - \Vert \nabla \phi ^{n+1}\Vert ^2 +\Vert \nabla \phi ^n-\nabla \phi ^{n+1}\Vert ^2\right) + ({\varDelta }\kappa ^{n+1}, \phi ^{n+1}-\phi ^n). \end{aligned}$$
(16)

By taking the inner product of Eq. (13) with \({\varDelta }(\phi ^{n+1}-\phi ^n)\), we obtain

$$\begin{aligned} (\kappa ^{n+1},{\varDelta }(\phi ^{n+1}-\phi ^n)) = ({\varDelta }\kappa ^{n+1}, \phi ^{n+1}-\phi ^n) = \frac{1}{2}\left( \Vert {\varDelta }\phi ^{n+1}\Vert ^2 -\Vert \nabla \phi ^n \Vert ^2 + \Vert {\varDelta }\phi ^{n+1}-{\varDelta }\phi ^n\Vert ^2 \right) . ~~~~~~ \end{aligned}$$
(17)

By combine Eqs. (16) and (17) and using Eq. (14), we obtain

$$\begin{aligned}&U^{n+1}-U^n+\frac{1}{2}\Vert \phi ^{n+1}\Vert ^2 - \frac{1}{2}\Vert \phi ^n\Vert ^2 - \Vert \nabla \phi ^{n+1}\Vert ^2 + \Vert \nabla \phi ^n\Vert ^2 \nonumber \\&\quad + \frac{1}{2}\Vert {\varDelta }\phi ^{n+1}\Vert ^2 - \frac{1}{2}\Vert {\varDelta }\phi ^n\Vert ^2 = -\frac{1}{{\varDelta }t}\Vert \phi ^{n+1}-\phi ^n\Vert ^2 -\frac{1}{2}\Vert \phi ^{n+1}-\phi ^n\Vert ^2 - \frac{1}{2}\Vert {\varDelta }\phi ^{n+1}-{\varDelta }\phi ^n \Vert ^2 \le 0, \end{aligned}$$
(18)

which implies \({\mathcal {E}}(\phi ^{n+1},U^{n+1}) \le {\mathcal {E}}(\phi ^{n},U^{n})\), and the discrete energy dissipation law is proved.

Table 1 Convergence rates and \(L^2\)-errors with different time steps
Full size table
Fig. 1
figure 1

Temporal evolutions of discrete total energy with respect to a LE1 scheme and b LS2 scheme

Full size image
Fig. 2
figure 2

Effects of numerical parameters on the pattern formations

Full size image
Fig. 3
figure 3

Temporal evolution of normalized total energy. Here, the final time indicates the numerically steady state

Full size image
Fig. 4
figure 4

Temporal evolution of striped pattern

Full size image
Fig. 5
figure 5

Temporal evolution of hexagonal pattern

Full size image
Fig. 6
figure 6

Temporal evolutions of normalized total energy with respect to different values of g

Full size image
Fig. 7
figure 7

Temporal evolution of grain growth with \((\epsilon ,g) = (0.25,0)\)

Full size image

3.2 Linearly second-order scheme (LS2)

For Eqs. (6)–(8), the proposed temporally second-order accurate scheme is written to be

$$\begin{aligned}&\frac{\phi ^{n+1}-\phi ^n}{{\varDelta }t} = -\frac{U^*}{E(\phi ^*)+C}F'(\phi ^*)-\frac{\phi ^{n+1}+\phi ^n}{2}-2{\varDelta }\phi ^* - {\varDelta }\kappa ^{n+\frac{1}{2}}, \end{aligned}$$
(19)
$$\begin{aligned}&\kappa ^{n+\frac{1}{2}} = \frac{1}{2}\left( {\varDelta }\phi ^{n+1}+ {\varDelta }\phi ^n \right) , \end{aligned}$$
(20)
$$\begin{aligned}&\frac{U^{n+1}-U^n}{{\varDelta }t} = \int _{\varOmega }\frac{U^*}{E(\phi ^*)+C} F'(\phi ^*)\frac{\phi ^{n+1}-\phi ^n}{{\varDelta }t} d\mathbf{x}, \end{aligned}$$
(21)

where \(\phi ^* = \frac{3}{2}\phi ^n - \frac{1}{2}\phi ^{n-1}\) and \(U^* = \frac{3}{2}U^n - \frac{1}{2}U^{n-1}\). Next, we prove the proposed second-order scheme (19)–(21) satisfies the discrete pseudo-energy dissipation law, i.e., \(\tilde{{\mathcal {E}}}(\phi ^{n+1},\phi ^n, U^{n+1}) \le \tilde{{\mathcal {E}}}(\phi ^{n},\phi ^{n-1}, U^{n})\), where

$$\begin{aligned} \tilde{{\mathcal {E}}}(\phi ^{n},\phi ^{n-1}, U^{n})= & {} U^n + \frac{1}{2}\Vert \phi ^n\Vert ^2 - \Vert \nabla \phi ^n\Vert ^2 + \frac{1}{2}\Vert {\varDelta }\phi ^n\Vert ^2 +\frac{1}{2}\Vert \nabla (\phi ^n-\phi ^{n-1})\Vert ^2 - C. \end{aligned}$$

By taking the inner product of Eq. (19) with \(-(\phi ^{n+1}-\phi ^n)\), we have

$$\begin{aligned} -\frac{1}{{\varDelta }t}\Vert \phi ^{n+1}-\phi ^n\Vert ^2= & {} \left( \frac{U^*}{E(\phi ^*)+C}F'(\phi ^*),\phi ^{n+1}-\phi ^n\right) +\frac{1}{2}\left( \Vert \phi ^{n+1}\Vert ^2 - \Vert \phi ^n\Vert ^2\right) \nonumber \\&- (\nabla (3\phi ^n-\phi ^{n-1}),\nabla (\phi ^{n+1}-\phi ^n)) + \left( {\varDelta }\kappa ^{n+\frac{1}{2}},\phi ^{n+1}-\phi ^n\right) , \end{aligned}$$
(22)

where the integral by parts and periodic boundary condition are used. By using the following identity:

$$\begin{aligned} \left( 3b-c, a - b \right)= & {} \left( a+b - \left( a-2b+c\right) , a-b\right) \\= & {} |a|^2 - |b|^2 - \frac{1}{2}\left( |a-b|^2 - |b-c|^2 + | a-2b + c |^2 \right) , \end{aligned}$$

we can rewrite Eq. (22) to be

$$\begin{aligned}&-\frac{1}{{\varDelta }t}\Vert \phi ^{n+1}-\phi ^n\Vert ^2 = \left( \frac{U^*}{E(\phi ^*)+C}F'(\phi ^*),\phi ^{n+1}-\phi ^n\right) +\frac{1}{2}\left( \Vert \phi ^{n+1}\Vert ^2 - \Vert \phi ^n\Vert ^2\right) \nonumber \\&\qquad \qquad - (\Vert \nabla \phi ^{n+1}\Vert ^2 - \Vert \nabla \phi ^n\Vert ^2 - \frac{1}{2}( \Vert \nabla (\phi ^{n+1}-\phi ^n)\Vert ^2 - \Vert \nabla (\phi ^n-\phi ^{n-1})\Vert ^2\nonumber \\&\qquad \qquad + \Vert \nabla (\phi ^{n+1}-2\phi ^n+\phi ^{n-1})\Vert ^2)) + \left( {\varDelta }\kappa ^{n+\frac{1}{2}},\phi ^{n+1}-\phi ^n\right) , \end{aligned}$$
(23)

By using Eq. (20), we have

$$\begin{aligned}&-\frac{1}{{\varDelta }t}\Vert \phi ^{n+1}-\phi ^n\Vert ^2 = \left( \frac{U^*}{E(\phi ^*)+C}F'(\phi ^*),\phi ^{n+1}-\phi ^n\right) +\frac{1}{2}\left( \Vert \phi ^{n+1}\Vert ^2 - \Vert \phi ^n\Vert ^2\right) \nonumber \\&\qquad \qquad - (\Vert \nabla \phi ^{n+1}\Vert ^2 - \Vert \nabla \phi ^n\Vert ^2 - \frac{1}{2}( \Vert \nabla (\phi ^{n+1}-\phi ^n)\Vert ^2 - \Vert \nabla (\phi ^n-\phi ^{n-1})\Vert ^2\nonumber \\&\qquad \qquad + \Vert \nabla (\phi ^{n+1}-2\phi ^n+\phi ^{n-1})\Vert ^2)) + \frac{1}{2}(\Vert \nabla \phi ^{n+1}\Vert ^2-\Vert \nabla \phi ^n\Vert ^2), \end{aligned}$$
(24)

By using Eq. (21), we derive

$$\begin{aligned}&U^{n+1}-U^n + \frac{1}{2}\Vert \phi ^{n+1}\Vert ^2 - \frac{1}{2}\Vert \phi ^n\Vert ^2 - \Vert \nabla \phi ^{n+1}\Vert ^2 + \Vert \nabla \phi ^n\Vert ^2\nonumber \\&\quad +\frac{1}{2}\Vert \nabla (\phi ^{n+1}-\phi ^n)\Vert ^2 - \frac{1}{2}\Vert \nabla (\phi ^n-\phi ^{n-1})\Vert ^2 + \frac{1}{2}\Vert \nabla (\phi ^{n+1}-2\phi ^n +\phi ^{n-1})\Vert ^2\nonumber \\&\quad +\frac{1}{2}\Vert \nabla \phi ^{n+1}\Vert ^2 - \frac{1}{2}\Vert \nabla \phi ^n\Vert ^2 = -\frac{1}{{\varDelta }t}\Vert \phi ^{n+1}-\phi ^n\Vert ^2 \le 0, \end{aligned}$$
(25)

which implies \(\tilde{{\mathcal {E}}}(\phi ^{n+1},\phi ^n,U^{n+1}) \le \tilde{{\mathcal {E}}}(\phi ^{n},\phi ^{n-1},U^{n})\). Moreover, we can easily find that \(\tilde{{\mathcal {E}}}(\phi ^{n},\phi ^{n-1},U^{n}) \ge {\mathcal {E}}(\phi ^{n},U^{n})\). Therefore, we get the following chain of inequalities by assuming \(\phi ^{-1} \equiv \phi ^{0}\)

$$\begin{aligned} {\mathcal {E}}(\phi ^n,U^n) \le \tilde{{\mathcal {E}}}(\phi ^n,\phi ^{n-1},U^n) \le \dots \le \tilde{{\mathcal {E}}}(\phi ^0,\phi ^{-1},U^0) = {\mathcal {E}}(\phi ^0,U^0), \end{aligned}$$
(26)

which indicates the total energy at any time level is bounded by the initial energy. The proof is completed.

Remarks We can find that the proposed first- and second-order schemes are both linear systems with constant coefficients. Furthermore, the density field \(\phi \) and auxiliary variable U are decoupled with each other, and thus we can update \(\phi \) by solving only one semi-implicit system and then directly update U by an explicit way. Different with the classical SAV approach, we do not need to calculate the inner product at first; the whole algorithm is significantly simplified. Although our method satisfies the discrete energy dissipation law and does not depend on the positivity restriction which is necessary in the classical SAV method, it is hard for us to theoretically prove the boundedness of discrete energy. The results in Sects. 4.4 and 4.5 show that the total energy is still bounded at the numerical level. In this work, we only focus on the practicability and efficiency of the proposed schemes. To the best of authors’ knowledge, the convergence analysis of this modified SAV approach for phase-field models is still an open question. In a recent work of Shen and Xu [38], detailed convergence and error estimations were given for the classical SAV schemes. We will refer to the ideas in [38] to consider the convergence analysis of the proposed schemes for the SH equation and PFC-type equations in the future.

Fig. 8
figure 8

Temporal evolution of grain growth with \((\epsilon ,g) = (0.025,1)\)

Full size image
Fig. 9
figure 9

Temporal evolution of grain growth with \((\epsilon ,g) = (0.1,0.4)\)

Full size image

4 Numerical experiments

In this work, we only focus on constructing first- and second-order, linear, and energy stable temporal schemes; the standard finite difference method is used to spatially discretize the governing equations and the spatial step is defined as \(h = L/N\), where L is the length of computational domain and N is the mesh size. To accelerate the convergence of the resulting linear systems, an efficient linear multigrid algorithm is used. Please refer to [39,40,41] for some details of multigrid algorithm. In all simulations, we will consider the periodic boundary condition.

4.1 Accuracy test

To verify the desired first- and second-order temporal accuracy of the proposed schemes in Sect. 3, we consider the following initial condition

$$\begin{aligned} \phi (x,y,0) = \sin \left( \frac{2\pi }{16}\right) \cos \left( \frac{2\pi }{16} \right) \end{aligned}$$
(27)

in the domain \({\varOmega }= (0,32)^2\). The parameters are \(h = 0.125, ~\epsilon = 0.25, ~g = 1\). We take the solution with finer time step \({\varDelta }t^{r} = 0.01h^2\) as the reference solution. The increasing finer time steps: \({\varDelta }t = 320{\varDelta }t^{r}\), \(160{\varDelta }t^{r}\), \(80{\varDelta }t^{r}\), \(40{\varDelta }t^{r}\), \(20{\varDelta }t^{r}\), and \(10{\varDelta }t^{r}\) are considered. Table 1 illustrates the \(L^2\)-norm errors [42] and convergence rates [42] of \(\phi \) at \(t = 0.1\). As we can observe, the desired first- and second-order accuracies can be obtained by using the corresponding LS1 and LS2 schemes.

4.2 Energy stability

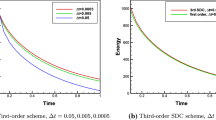
To test the energy stability of the proposed LS1 and LS2 schemes, the initial condition [3, 10, 43] is written to be

$$\begin{aligned} \phi (x,y,0)= & {} 0.07 - 0.02\cos \left( \frac{2\pi (x-12)}{32} \right) \sin \left( \frac{2\pi (y-1)}{32} \right) \nonumber \\&-\,0.01\sin ^2\left( \frac{4\pi x}{32} \right) \sin ^2\left( \frac{4\pi (y-6)}{32} \right) \nonumber \\&+\, 0.02\cos ^2\left( \frac{\pi (x+10)}{32} \right) \sin ^2\left( \frac{\pi (y+3)}{32} \right) \end{aligned}$$
(28)

in the domain \({\varOmega }= (0,32)^2\). We use \(h = 0.25, ~\epsilon = 0.25\), and \(g = 1\). Figures 1a and b show the temporal evolutions of discrete total energy with respect to the LS1 and LS2 schemes, respectively. We can find that the energy curves are both nonincreasing in time. In the following numerical experiments, the second-order scheme (LS2) will be used for the purpose of better accuracy.

4.3 Effects of numerical parameters

We next consider the effects of numerical parameters (\(\epsilon \) and g) on the pattern formations in two-dimensional space \({\varOmega }= (0,32)^2\). We take the initial condition as

$$\begin{aligned} \phi (x,y,0) = 0.25 + 0.1~\hbox {rand}(x,y), \end{aligned}$$
(29)

where \(\hbox {rand}(x,y)\) is the random number between \(-1\) and 1. We use \(h = 0.125\) and \({\varDelta }t = 1\). Figure 2 presents the profiles with different values of \(\epsilon \) and g at \(t = 512\), and the results indicate that the effect of g is more obvious than the effect of \(\epsilon \).

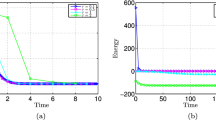
4.4 Long-time simulation of pattern formation

In this subsection, we briefly investigate the energy evolution in a long-time simulation. The computational domain and initial condition are unchanged like those in Sect. 4.3. We use \(\epsilon = 0.25\) and \(g = 0.8\) to perform the numerical simulation until the steady state, i.e., \(\Vert \phi ^{n+1}-\phi ^n\Vert _2 < 10^6\), is arrived. The result in Fig. 3 indicates that the discrete energy functional is nonincreasing and bounded.

Fig. 10
figure 10

Temporal evolution of grain growth with \((\epsilon ,g) = (0.1,1)\)

Full size image
Fig. 11
figure 11

Temporal evolution of grain growth with \((\epsilon ,g) = (0.15,0.4)\)

Full size image

4.5 Pattern formations in 2D space

In this part, we consider the formations of two typical patterns (striped and hexagonal structures). We take the initial condition to be

$$\begin{aligned} \phi (x,y,0) = 0.15 + 0.1~\hbox {rand}(x,y), \end{aligned}$$
(30)

in the domain \({\varOmega }= (0,128)^2\). We use \(h = 0.5, ~{\varDelta }t = 0.1\), and \(\epsilon = 0.25\). We consider \(g = 0\) and \(g = 1\) for the patterns with striped and hexagonal structures, respectively. The temporal evolutions are shown in Figs. 4 and 5. The results in Fig. 6 show that the discrete energy dissipation is satisfied.

Fig. 12
figure 12

Temporal evolutions of normalized total energy with respect to different values of \((\epsilon , g)\)

Full size image

4.6 Grain growth in supercooled liquid

Here, we first consider the two-dimensional grain growth in supercooled liquid. The following initial condition is used

$$\begin{aligned} \phi (x,y,0) = 0.278 + \alpha ~\hbox {rand}(x,y), \end{aligned}$$
(31)

in the domain \({\varOmega }= (0,500)^2\). Here, \(\alpha = 0.1, ~0.2\), and 0.4 for three square nuclei locating at (375, 125), (375, 375), and (125, 250). The length of three square nuclei is 10. The spatial and time steps are set to be \(h = 0.9766\) and \({\varDelta }t = 0.1\). The following three sets of parameters \((\epsilon ,g) = (0.25,0), ~(0.025,1)\), and (0.1, 0.4) are used to generate different patterns. As shown in Figs. 7, 8, and 9, we can find that the patterns of striped structure, hexagonal structure, and hybrid structure can be generated by manipulating the values of \(\epsilon \) and g.

Next, we consider the combining effects of \(\epsilon \) and g on the grain growth in three-dimensional space. The initial condition is taken to be

$$\begin{aligned} \phi (x,y,z,0) = 0.278 + \alpha ~ \hbox {rand}(x,y,z), \end{aligned}$$
(32)

in the domain \({\varOmega }= (0,128)^3\). We use \(h = 1\) and \({\varDelta }t = 0.1\). Here, \(\alpha = 0.1, ~0.2\), and 0.4 with respect to three square nuclei locating at (35, 64, 64), (85, 64, 64), and (64, 64, 95), respectively. The length of three nuclei is 10. The following three sets of parameters \((\epsilon ,g) = (0.1,1)\), and (0.15, 0.4) are used. As shown in Figs. 10 and 11, the combining effects of \(\epsilon \) and g control the formations of hexagonal and striped patterns. The energy curves with respect to different patterns are plotted in Fig. 12, and we find that the energy dissipation law is satisfied.

5 Conclusions

We proposed linear and energy stable numerical schemes for the Swift–Hohenberg equation with \(g \ge 0\). A modified SAV approach was used to construct temporally first- and second-order accurate discretizations. Different from the classical SAV approach, the proposed schemes did not need to calculate the inner product at first. We analytically proved the energy stability. The pattern formations in two- and three-dimensional spaces were investigated numerically. The results showed that the proposed scheme gave desired first- and second-order accuracies and energy stability. Note that the proposed schemes can be easily improved by combining a stabilization technique. Because this extension is simple and straightforward, we leave it for interested readers.