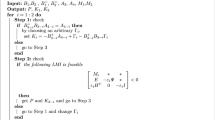1 Introduction

In the past few decades, research on two-dimensional (2-D) state space representation has rapidly increased. The 2-D linear models were introduced in the 1970s (Fornasini and Marchesini 1976; Givone and Roesser 1972) and have found many physical applications such as digital data filtering, image processing (Roesser 1975), thermal power engineering (Roesser 1975). Thus a considerable interest has been devoted to 2-D systems and a number of results have been presented in the literature. To mention a few, the stability analysis problem of 2-D systems has been addressed in Kar and Singh (2003), Ooba (2000) and Badie et al. (2018a, b). Moreover, the \(H_{\infty }\) control problem for 2-D state-delayed systems has been studied in Xu and Yu (2009), Feng et al. (2012) and Ghous and Xiang (2015, 2016), and the authors in Peng and Guan (2009) and Zhang et al. (2011) presented a solution to \(H_{\infty }\) filtering problem of 2-D systems. Yet, all the results mentioned above are only for linear certain 2-D systems without parameter uncertainties. As is well known, almost all existing physical and engineering systems unavoidably include uncertainties because of the existence of external disturbance, modeling inaccuracies, component aging, parameter variations or parameter fluctuation in the process of implementations. The term uncertainty refers to the differences or errors between models and real systems and whatever methodology is used to express these errors will be called a representation of uncertainty. In general, the norm-bounded uncertainty is one of the important representation of parametric uncertainty where the mathematical description of the uncertain system explicitly exhibits a nominal model located at the center of the hyper ellipsoid of uncertainty in the parameter space (Hmamed et al. 2013; Yao et al. 2013). Another important description of uncertainty is the so-called polytopic uncertainty, where the set of system parameters is supposed to be uncertain and unknown but belonging to a known convex polytopic domain, and the nominal system is located at the center of this convex polytopic domain (Peaucelle et al. 2000; Kau et al. 2005). In recent years, a great deal of attention has been devoted to the robustness analysis and synthesis for 2-D systems with polytopic uncertainties, and we can cite for example (El-Kasri et al. 2013; Boukili et al. 2016; El-Amrani et al. 2017; Tadepalli and Leite 2018; Badie et al. 2018).

On the other hand, the robust stability analysis problem is an important issue for many physical and engineering applications, as it is the initial requirement for any design. The Lyapunov stability theory has become an efficient method for dealing with this problem, and it is well known that the reduction in conservatism in robust stability criteria can be achieved mainly from the construction of an appropriate Lyapunov functional. In particular, existing stability methods for uncertain systems with polytopic uncertainties are classified into two types: quadratic stability conditions and parameter-dependent stability conditions. In the first case, the stability of a polytope of matrices can be checked by using a single Lyapunov matrix for all the sub-models, and therefore, the obtained stability condition is rather conservative and sometimes very restrictive, but it does not contain a large number of decision variables. Therefore, it is very simple to be checked numerically. The parameter-dependent stability condition is introduced in order to overcome the conservativeness of the quadratic stability condition. For one-dimensional (1-D) systems with polytopic uncertainties, many considerable efforts have been made to develop parameter-dependent approaches (see Ramos and Peres 2002; Leite and Peres 2003; Oliveira and Peres 2006), and in the past few years, the notion of parameter dependence was further extended to 2-D systems. For instance, in Alfidi and Hmamed (2007), new robust stability conditions for 2-D linear continuous-time systems described by Roesser model have been given. In Hmamed et al. (2008) the problem of robust stability of uncertain two-dimensional discrete systems described by Fornasini–Marchesini second model has been investigated. In Jia et al. (2013) the problem of stability analysis and control synthesis of uncertain 2-D discrete systems in the Roesser model has been studied.

Motivated by the idea to overcome the limitations of the quadratic stability conditions, and further to improve the parameter-dependent technique. In this paper, we consider the problem of robust stability for a class of uncertain polytopic 2-D discrete systems described by the Roesser model. Based on parameter-dependent Lyapunov function combined with Finsler’s lemma new sufficient conditions for robust stability analysis are derived. The obtained conditions are expressed in terms of LMIs and can be viewed as general cases of some existing conditions. Two numerical examples are given to demonstrate the merits of the proposed methods.

The rest of this paper is organized as follows: In Sect. 2, the problem under study is formulated and some preliminary results are given. In Sect. 3, new sufficient conditions are proposed for verifying the robust asymptotical stability of the uncertain 2-D discrete-time systems described by the Roesser model. Numerical examples are given to illustrate the results in Sect. 4. Finally, some conclusions are also given in Sect. 5.

Notations Throughout the paper, \(\mathbb {R}^{n}\) denotes the n-dimensional real Euclidean space, \(\mathbb {R}^{n\times m}\) denotes the set of \(n\times m\) matrices. I and \(\mathbf 0 \) represent identity matrix and zero matrix, respectively. The superscripts ‘T’ stand for the matrix transpose. \(P >0\) means that P is real symmetric and positive definite. sym(M) is the shorthand notation for \(M+M^\mathrm{T}\) and \(\text {diag}\{...\}\) denotes a block diagonal matrix. In symmetric block matrices or long matrix expressions, we use an asterisk \((*)\) to represent a term that is induced by symmetry.

2 Problem Statement and Preliminaries

Consider a 2-D discrete linear system represented by the Roesser state-space model of the form Roesser (1975):

$$\begin{aligned} \left[ \begin{array}{c} x^{h}(k+1,l) \\ x^{v}(k,l+1) \\ \end{array} \right] =\left[ \begin{array}{cc} A^{11} &{}\quad A^{12} \\ A^{21} &{}\quad A^{22} \\ \end{array} \right] \left[ \begin{array}{c} x^{h}(k,l) \\ x^{v}(k,l) \\ \end{array} \right] , \end{aligned}$$
(1)

where \(x^{h}(k,l)\in \mathbb {R}^{n_{h}}\), \(x^{v}(k,l)\in \mathbb {R}^{n_{v}}\), are the horizontal and the vertical states, respectively. \(A^{11}\), \(A^{12}\), \(A^{21}\), \(A^{22}\), are constant matrices with appropriate dimensions. The boundary conditions for system (1) are specified as:

$$\begin{aligned} \left\{ \begin{array}{ll} x^{h}(0,l)=f(l),\\ x^{v}(k,0)=g(k). \end{array} \right. \end{aligned}$$
(2)

To simplify the notation, identify in the state-space model (1) the matrix

$$\begin{aligned} A=\left[ \begin{array}{cc} A^{11} &{}\quad A^{12} \\ A^{21}&{}\quad A^{22} \\ \end{array} \right] , \end{aligned}$$

and define the vectors:

$$\begin{aligned} x^{+}(k,l)=\left[ \begin{array}{c} x^{h}(k+1,l) \\ x^{v}(k,l+1) \\ \end{array} \right] ,\quad x(k,l)=\left[ \begin{array}{c} x^{h}(k,l) \\ x^{v}(k,l) \\ \end{array} \right] , \end{aligned}$$

Hence, Eq. (1) is rewritten as:

$$\begin{aligned} x^{+}(k,l)= & {} Ax(k,l). \end{aligned}$$
(3)

We first present the notion of asymptotic stability of 2-D discrete systems (1).

Definition 1

Du and Xie (2002) The 2-D discrete systems (1) is said to be asymptotically stable if \(\sup _{k,l}||x(k,l)||<\infty \) and \(\lim _{k,l \rightarrow \infty }x(k,l)=0\), with all boundary conditions in (2) such that \(\sup _{l}||x^{h}(0,l)||<\infty \), \(\sup _{k}||x^{v}(k,0)||<\infty \).

The following lemma presents a sufficient condition for the asymptotic stability of 2-D discrete systems (1) in terms of an LMI.

Lemma 1

(Du and Xie 2002) The 2-D discrete systems (1) is asymptotically stable if there exists a block diagonal matrix \(P={\text {diag}}\{P^{h},P^{v}\}>0\) where \(P^{h}\in \mathbb {R}^{n_{h}\times n_{h}}\) and \(P^{v}\in \mathbb {R}^{n_{v}\times n_{v}}\) such that

$$\begin{aligned} A^\mathrm{T}PA-P<0, \end{aligned}$$
(4)

Suppose now that the system matrix A is not precisely known, but belongs to a convex bounded uncertain domain \(\mathcal {D}\) that is described by N vertices as follows:

$$\begin{aligned} A=A(\alpha )=\left[ \begin{array}{cc} A^{11}(\alpha ) &{}\quad A^{12}(\alpha ) \\ A^{21}(\alpha ) &{}\quad A^{22}(\alpha ) \\ \end{array} \right] \in \mathcal {D}, \end{aligned}$$
(5)

where

$$\begin{aligned} \mathcal {D}:=\left\{ \begin{array}{c} A(\alpha ):A(\alpha )=\displaystyle \sum _{i=1}^{N}\alpha _{i}A_{i}; \sum _{i=1}^{N}\alpha _{i}=1;\alpha _{i}\ge 0\\ \end{array} \right\} \end{aligned}$$
(6)

with the matrix

$$\begin{aligned} A_{i}=\left[ \begin{array}{cc} A_{i}^{11} &{}\quad A_{i}^{12} \\ A_{i}^{21} &{}\quad A_{i}^{22} \\ \end{array} \right] , \end{aligned}$$

representing the ith vertex of the polytope

Remark 1

As shown in Jin and Park (2001), the polytopic model uncertainty described in (6) can be utilized to represent the uncertain domain more exactly and cover large classes of uncertainties than the norm-bounded uncertainty.

We start our study by defining robust stability of system (1) under the structured model (6).

Definition 2

System (1) is robustly stable in the uncertainty domain (6) if there exists matrix \(P(\alpha )>0\) such that

$$\begin{aligned} A^{T}(\alpha )P(\alpha )A(\alpha )-P(\alpha )<0. \end{aligned}$$
(7)

An effective way of addressing such problem is to choose a single Lyapunov matrix \(P(\alpha )=P\) which solves inequality (7). Unfortunately, this approach is known to provide quite conservative results, but it constitutes one of the elementary results in the quadratic approach. The test for this class of stability, also known as a quadratic stability test, is summarized in the following lemma.

Lemma 2

(Jia et al. 2013) The 2-D discrete system (1) with parameter uncertainties satisfying (6) is robustly asymptotically stable if an appropriate-dimensional matrix \(P>0\) exists with

$$\begin{aligned}&P=\left[ \begin{array}{ll} P^{1} &{}\quad *\\ P^{3} &{}\quad P^{2}\\ \end{array} \right] ,\quad P^{1}\in \mathbb {R}^{nh\times nh},\\&\quad P^{2}\in \mathbb {R}^{nv\times nv},\quad P^{3}\in \mathbb {R}^{nv\times nh}, \end{aligned}$$

such that the following LMIs hold:

$$\begin{aligned}&A_{i}^{T}PA_{i}-P<0,\quad i=1,2,\ldots ,N;\end{aligned}$$
(8)
$$\begin{aligned}&{sym}(A_{i}^{T}PA_{j})-2P<0,\quad 1\le i <j\le N. \end{aligned}$$
(9)

The following lemma will be helpful in proving our main result.

Lemma 3

(Finsler’s lemma de Oliveira and Skelton 2001) Given \(\xi \in \mathbb {R}^{n},\)\(\Theta =\Theta ^{T}\in \mathbb {R}^{n\times n} \) and \( \mathcal {A}\in \mathbb {R}^{p\times n}\), if \( \text {rank}(\mathcal {A})<n. \) The following conditions are equivalent

  1. 1.

    \(\xi ^{T}\Theta \xi <0\) , \(\forall \mathcal {A}\xi =0\) , \(\xi \ne 0,\)

  2. 2.

    \(\exists \varGamma \in \mathbb {R}^{n\times p}\) such that \( \Theta +\varGamma \mathcal {A}+\mathcal {A}^{T}\varGamma ^{T}<0.\)

3 Main Results

In this section, based on the Lyapunov stability theorem combined with the Finsler’s lemma, new parameter-dependent approaches will be developed to studies the problem of robust stability of uncertain 2-D discrete systems described by the Roesser model under polytopic uncertainty.

Theorem 1

The 2-D discrete system (1) with parameter uncertainties satisfying (6) is robustly asymptotically stable if there exist symmetric positive definite matrices \(P_{i}=P_{i}^{T} > 0\), \(i\in \{1,\ldots ,N\}\) and any appropriately dimensioned matrices F and H, with

$$\begin{aligned} P_{i}=\left[ \begin{array}{cc} P_{i}^{h} &{}\quad 0 \\ *&{}\quad P_{i}^{v}\\ \end{array} \right] ,\quad P_{i}^{h}\in \mathbb {R}^{nh\times nh},P_{i}^{v}\in \mathbb {R}^{nv\times nv},\,\\ F=\left[ \begin{array}{cc} F^{h} &{}\quad 0 \\ 0 &{}\quad F^{v}\\ \end{array} \right] ,\quad F^{h}\in \mathbb {R}^{nh\times nh},F^{v}\in \mathbb {R}^{nv\times nv},\,\\ H=\left[ \begin{array}{cc} H^{h} &{}\quad 0 \\ 0 &{}\quad H^{v}\\ \end{array} \right] ,\quad H^{h}\in \mathbb {R}^{nh\times nh},H^{v}\in \mathbb {R}^{nv\times nv}, \end{aligned}$$

such that for all \(i\in \{1,\ldots ,N\}\) the following matrix inequalities hold:

$$\begin{aligned} \left[ \begin{array}{cc} -\,P_{i}+{sym}(FA_{i}) &{}\quad -\,F+A_{i}^{T}H \\ *&{}\quad P_{i}-{sym}(H) \\ \end{array} \right] <0. \end{aligned}$$
(10)

Proof

Consider the following parameter-dependent Lyapunov function for the uncertain 2-D system (1)

$$\begin{aligned} V(k,l)= & {} V^{h}(k,l)+V^{v}(k,l),\nonumber \\ V^{h}(k,l)= & {} x^{hT}(k,l)P^{h}(\alpha )x^{h}(k,l),\nonumber \\ V^{v}(k,l)= & {} x^{vT}(k,l)P^{v}(\alpha )x^{v}(k,l), \end{aligned}$$
(11)

where \(P^{h}(\alpha )=P^{h}(\alpha )^{T}>0\), \(P^{v}(\alpha )=P^{v}(\alpha )^{T}>0\) are parameter-dependent Lyapunov matrices to be determined.

The difference of Lyapunov function V(i, j) is given by

$$\begin{aligned} \Delta V(i,j)= & {} \Delta V^{h}(i,j)+\Delta V^{v}(i,j),\nonumber \\ \Delta V^{h}(i,j)= & {} x^{hT}(k+1,l)P^{h}(\alpha )x^{h}(k+1,l)\nonumber \\&-\,x^{hT}(k,l)P^{h}(\alpha )x^{h}(k,l),\nonumber \\ \Delta V^{v}(i,j)= & {} x^{vT}(k,l+1)P^{v}(\alpha )x^{v}(k,l+1)\nonumber \\&-\,x^{vT}(k,l)P^{v}(\alpha )x^{v}(k,l). \end{aligned}$$
(12)

and define

$$\begin{aligned} P(\alpha )=\left[ \begin{array}{cc} P^{h}(\alpha ) &{}\quad 0 \\ *&{}\quad P^{v}(\alpha ) \\ \end{array} \right] , \end{aligned}$$

Then \(\Delta V(i,j)\) in (12) can be rewritten as

$$\begin{aligned} \Delta V(i,j)= & {} x^{+T}(k,l)P(\alpha )x^{+}(k,l)-x^{T}(k,l)P(\alpha )x(k,l)\nonumber \\= & {} \xi ^{T}(k,l)\varPi (\alpha )\xi (k,l). \end{aligned}$$
(13)

where

$$\begin{aligned} \xi (k,l)=\left[ \begin{array}{c} x(k,l) \\ x^{+}(k,l) \\ \end{array} \right] , \quad \varPi (\alpha )=\left[ \begin{array}{cc} -\,P(\alpha ) &{}\quad 0 \\ *&{}\quad P(\alpha ) \\ \end{array} \right] . \end{aligned}$$

It is well known that it suffices to show that the following inequality is valid

$$\begin{aligned} \varPi (\alpha )<0, \end{aligned}$$
(14)

to prove that the 2-D discrete system (1) with polytopic uncertainties in (6) is robustly asymptotically stable.

To this end, defining

$$\begin{aligned} \varGamma =\left[ \begin{array}{c} F \\ H^{T} \\ \end{array} \right] ,\qquad \, \mathcal {A}(\alpha )^{T}=\left[ \begin{array}{c} A(\alpha )^{T} \\ -\,I \\ \end{array} \right] . \end{aligned}$$
(15)

where F and H are matrices with appropriate dimensions

It follows from system (1) that \(\mathcal {A}(\alpha )\xi (k,l)=0\) for all nonzero \(\xi (k,l)\ne 0\), according to Finsler’s lemma, the condition (14) with \(\mathcal {A}\xi (k,l)=0\), \(\xi (k,l)\ne 0\) is equivalent to the following inequality:

$$\begin{aligned} \varPi (\alpha )+\varGamma \mathcal {A}(\alpha )+\mathcal {A}^{T}(\alpha )\varGamma ^{T}<0. \end{aligned}$$
(16)

Assuming the corresponding parameter-dependent matrix of the following affine form

$$\begin{aligned} P(\alpha )=\sum _{i=1}^{N}\alpha _{i}P_{i}, \end{aligned}$$
(17)

and considering (6), the condition in (16) can be rewritten as

$$\begin{aligned} \sum _{i=1}^{N}\alpha _{i}\left( \begin{array}{c} \varPi _{i}+\varGamma \mathcal {A}_{i}+\mathcal {A}^{T}_{i}\varGamma ^{T} \\ \end{array} \right) <0. \end{aligned}$$
(18)

Thus, if the LMI (10) holds, inequality (18) obviously holds, which guarantees the robust asymptotical stability of the uncertain 2-D discrete system (1). This completes the proof. \(\square \)

Remark 2

Assume that system (1) is not subject to any uncertainty, that is, \(N = 1\). The stability condition of 2-D discrete system given by Lemma 1 is a special case of Theorem 1. Actually, if we set \(F=0\); \(H=P_{i}\) in (10), according to the Schur complement (Boyd et al. 1994), we can see that the inequality (10) reduces to (4). In addition, it is well known that Lemma 1 is the starting point of many papers investigating analysis and design problems of 2-D discrete system. So the proposed method in Theorem 1 can be extended to robust analysis and design problems to get less conservative results.

Remark 3

Compared to 1-D systems, the analysis of 2-D systems are not easy due to their complex structures for which the dynamics depend on two independent variables. Theorem 1 gives a sufficient condition for the asymptotic stability of uncertain 2-D discrete systems described by the Roesser model. Note that if system (1) reduces to a 1-D system with polytopic uncertainty, Theorem 1 coincides with the asymptotic stability for 1-D systems investigated in Peaucelle et al. (2000). Thus, Theorem 1 can be viewed as an extension of existing results on the asymptotic stability for 1-D systems to the 2-D case.

Theorem 2

The \(2-D\) discrete system (1) with parameter uncertainties satisfying (6) is robustly asymptotically stable if there exist symmetric positive definite matrices \(P_{i}=P^{T}_{i} > 0\) and any appropriately dimensioned matrices \(F_{i}\) and \(H_{i}\), \(i\in \{1,\ldots ,N\}\) with

$$\begin{aligned} P_{i}=\left[ \begin{array}{cc} P_{i}^{h} &{}\quad 0 \\ *&{}\quad P_{i}^{v}\\ \end{array} \right] ,\quad P^{h}_{i}\in \mathbb {R}^{nh\times nh},P^{v}_{i}\in \mathbb {R}^{nv\times nv},\,\\ F_{i}=\left[ \begin{array}{cc} F_{i}^{h} &{}\quad 0 \\ *&{}\quad F_{i}^{v}\\ \end{array} \right] ,\quad F^{h}_{i}\in \mathbb {R}^{nh\times nh},F^{v}_{i}\in \mathbb {R}^{nv\times nv},\,\\ H_{i}=\left[ \begin{array}{cc} H_{i}^{h} &{}\quad 0 \\ *&{}\quad H_{i}^{v}\\ \end{array} \right] ,\quad H^{h}_{i}\in \mathbb {R}^{nh\times nh},H^{v}_{i}\in \mathbb {R}^{nv\times nv}, \end{aligned}$$

such that the following LMIs hold:

$$\begin{aligned} \left[ \begin{array}{cc} \varXi ^{1}_{i} &{}\quad \varXi ^{2}_{i} \\ *&{}\quad \varXi ^{3}_{i}\\ \end{array} \right] <-\,I,&i=1,\ldots ,N \end{aligned}$$
(19)
$$\begin{aligned} \hline&\nonumber \\ \left[ \begin{array}{cc} \varXi ^{4}_{i,j} &{}\quad \varXi ^{5}_{i,j} \\ *&{}\quad \varXi ^{6}_{i,j}\\ \end{array} \right] <\frac{1}{(1-N)^{2}}I,&\left. \begin{array}{cc} i=1,\ldots ,N, &{} \\ i\ne j,\\ j=1,\ldots ,N, &{} \\ \end{array} \right. \end{aligned}$$
(20)
$$\begin{aligned} \hline&\nonumber \\ \left[ \begin{array}{cc} \varXi ^{7}_{i,j,p} &{}\quad \varXi ^{8}_{i,j,p} \\ *&{}\quad \varXi ^{9}_{i,j,p}\\ \end{array} \right] <\frac{6}{(1-N)^{2}}I,&\left. \begin{array}{c} i=1,\ldots ,N-2, \\ j=i+1,\ldots ,N-1, \\ p=j+1,\ldots ,N, \\ \end{array} \right. \nonumber \\ \end{aligned}$$
(21)

where

$$\begin{aligned} \varXi _{i}^{1}= & {} -P_{i}+{sym}(F_{i}A_{i})\\ \varXi _{i}^{2}= & {} -F_{i}+A_{i}^{T}H_{i}\\ \varXi _{i}^{3}= & {} P_{i}-{sym}(H_{i})\\ \varXi _{i,j}^{4}= & {} -2P_{i}-P_{j}+{sym}(F_{i}A_{i}+F_{i}A_{j}+F_{j}A_{i})\\ \varXi _{i,j}^{5}= & {} -2F_{i}-F_{j}+A_{i}^{T}H_{i}+A_{i}^{T}H_{j}+A_{j}^{T}H_{i}\\ \varXi _{i,j}^{6}= & {} 2P_{i}+P_{j}-2{sym}(H_{i})-{sym}(H_{j})\\ \varXi _{i,j,p}^{7}= & {} -2P_{i}-2P_{j}-2P_{p}+{sym}(F_{i}A_{j} +F_{i}A_{p}\\&+F_{j}A_{i}+F_{j}A_{p}+F_{p}A_{i}+F_{p}A_{j})\\ \varXi _{i,j,n}^{8}= & {} -2F_{i}-2F_{j}-2F_{p}+A_{i}^{T}H_{j}+A_{i}^{T}H_{p}\\&+\,A_{j}^{T}H_{i}+A_{j}^{T}H_{p}+A_{p}^{T}H_{i}+A_{p}^{T}H_{j}\\ \varXi _{i,j,p}^{9}= & {} 2P_{i}+2P_{j}+2P_{p}-2{sym}(H_{i}+H_{j}+H_{p}). \end{aligned}$$

Proof

Similar to the proof of Theorem 1 and by choosing

$$\begin{aligned} \varGamma =\varGamma (\alpha )=\sum _{i=1}^{N}\alpha _{i}\varGamma _{i}, \qquad \varGamma _{i}=\left[ \begin{array}{c} F_{i} \\ H^{T}_{i} \\ \end{array} \right] , \end{aligned}$$
(22)

where \(F_{i}\) and \(H_{i}\) are matrices with appropriate dimensions. Then we obtain

$$\begin{aligned} \varPi (\alpha )+\varGamma (\alpha )\mathcal {A}(\alpha )+\mathcal {A}^{T}(\alpha )\varGamma ^{T}(\alpha )<0. \end{aligned}$$
(23)

In addition defining

$$\begin{aligned} \varUpsilon (\alpha )=\varPi (\alpha )+{sym}(\varGamma (\alpha )\mathcal {A}(\alpha )). \end{aligned}$$
(24)

By considering (6), \(\varUpsilon (\alpha )\) can be rewritten as

$$\begin{aligned} \varUpsilon (\alpha )= & {} \left( \displaystyle \sum _{i=1}^{N}\alpha _{i} \right) ^{2}\varPi (\alpha )+\left( \displaystyle \sum _{i=1}^{N}\alpha _{i} \right) {sym}(\varGamma (\alpha )\mathcal {A}(\alpha ))\\= & {} \sum _{i=1}^{N}\alpha _{i}^{3}\left( \varPi _{i}+{sym}(\varGamma _{i}\mathcal {A}_{i}) \right) \\&+\sum _{i=1}^{N}\sum _{j\ne i;j=1}^{N}\alpha _{i}^{2}\alpha _{j}\left( 2\varPi _{i}+\varPi _{j}\right. \\&+\left. \,{sym}(\varGamma _{i}\mathcal {A}_{i})+{sym}(\varGamma _{i}\mathcal {A}_{j})+\,{sym}(\varGamma _{j}\mathcal {A}_{i})\right) \\&+\sum _{i=1}^{N-2}\sum _{j=i+1}^{N-1}\sum _{p=j+1}^{N}\alpha _{i}\alpha _{j}\alpha _{p}\left( 2\varPi _{i}\right. \\&+\,2\varPi _{j}+2\varPi _{p}+{sym}(\varGamma _{i}\mathcal {A}_{j})\\&+\,{sym}(\varGamma _{i}\mathcal {A}_{p})+{sym}(\varGamma _{j}\mathcal {A}_{i})+{sym}(\varGamma _{j}\mathcal {A}_{p})\\&\left. +\,{sym}(\varGamma _{p}\mathcal {A}_{i})+{sym}(\varGamma _{p}\mathcal {A}_{j}) \right) . \end{aligned}$$

Imposing conditions (1920)–(21), one gets

$$\begin{aligned} \varUpsilon (\alpha )< & {} - \left( \begin{array}{c} \displaystyle \sum _{i=1}^{N}\alpha _{i}^{3}-\frac{1}{(N-1)^{2}}\sum _{i=1}^{N}\sum _{j\ne i;j=1}^{N}\alpha _{i}^{2}\alpha _{j} \end{array} \right. \nonumber \\&\left. \begin{array}{c}-\,\displaystyle \frac{6}{(N-1)^{2}}\sum _{i=1}^{N-2}\sum _{j=i+1}^{N-1}\sum _{p=j+1}^{N}\alpha _{i}\alpha _{j}\alpha _{p}\end{array} \right) I\nonumber \\= & {} -\varXi (\alpha )I. \end{aligned}$$
(25)

Now, to analyze the sign of \(\varXi (\alpha )\), define \(\varPhi (\alpha )\) and \(\varPsi (\alpha )\) as

$$\begin{aligned} \varPhi (\alpha )= & {} \sum _{i=1}^{N}\sum _{j=1}^{N}\alpha _{i}(\alpha _{i}-\alpha _{j})^{2}\nonumber \\= & {} (N-1)\sum _{i=1}^{N}\alpha _{i}^{3}-\sum _{i=1}^{N}\sum _{j\ne i;j=1}^{N}\alpha _{i}^{2}\alpha _{j}\ge 0.\nonumber \\ \varPsi (\alpha )= & {} \sum _{i=1}^{N}\sum _{j\ne i;j=1}^{N-1}\sum _{p\ne i,j;p=2}^{N}\alpha _{i}(\alpha _{j}-\alpha _{p})^{2}\nonumber \\= & {} (N-2)\sum _{i=1}^{N}\sum _{j\ne i;j=1}^{N}\alpha _{i}^{2}\alpha _{j}\nonumber \\&-\,6\sum _{i=1}^{N-2}\sum _{j=i+1}^{N-1}\sum _{p=j+1}^{N}\alpha _{i}\alpha _{j}\alpha _{p}\ge 0. \end{aligned}$$
(26)

Considering (26), \( \varXi (\alpha )\) in (25) can be rewritten as

$$\begin{aligned} \varXi (\alpha )=\frac{1}{(N-1)}\varPhi (\alpha )+\frac{1}{(N-1)^{2}}\varPsi (\alpha )\ge 0. \end{aligned}$$
(27)

Inequality (25), together with condition (27), implies that (23) holds, which guarantees the robust asymptotical stability of the uncertain 2-D discrete system (1). This completes the proof. \(\square \)

Remark 4

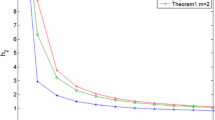
From the substitution (22), it can be seen that the quadratic slack variables in Theorem 1 are replaced by parameter-dependent slack variables in Theorem 2. As a result, Theorem 2 includes as particular case the result of Theorem 1. It will be shown in the Illustrative examples section that the condition proposed in Theorem 2 is the least conservative in comparison with Theorem 1 and Lemma 2.

Remark 5

The numbers of decision variables in Lemma 2, Theorem 1, and Theorem 2 are shown in Table 1.

Table 1 Numbers of decision variables for different methods
Full size table
Table 2 Number of stable polytopes confirmed by the different methods the different methods for \(2\le n\le 4\), and \(3\le N\le 4\)
Full size table
Fig. 1
figure 1

State trajectory of \(x^{h}(k,l)\): first vertex

Full size image
Fig. 2
figure 2

State trajectory of \(x^{v}(k,l)\): first vertex

Full size image

4 Illustrative Examples

Example 1

In this example, an exhaustive numerical comparison is provided to illustrate the effectiveness and less conservatism of the proposed robust stability approaches.

Fig. 3
figure 3

State trajectory of \(x^{h}(k,l)\): second vertex

Full size image
Fig. 4
figure 4

State trajectory of \(x^{v}(k,l)\): second vertex

Full size image
Fig. 5
figure 5

State trajectory of \(x^{h}(k,l)\): third vertex

Full size image

Thus, 1000 systems were randomly generated for each pair \(\{n,N\}\), \((n=n_{h}+n_{v})\), \(2\le n\le 4\) and \(3\le N\le 4\), giving a total of 8000 stable polytopes. Each of these polytopes was evaluated using Lemma 2, Theorem 1, and Theorem 2 to check whether the conditions successfully confirmed the robust stability. The comparisons are given in Table 2.

Example 2

Consider the uncertain 2-D discrete linear system \(n=2\)\((n_{h}=1, n_{v}=1)\), \(N=3\) given by

$$\begin{aligned} A_{1}= & {} \left[ \begin{array}{cc} 0.0356 &{}\quad 0.8862\\ 0.2469 &{}\quad 0.0089 \end{array} \right] ,A_{2}=\left[ \begin{array}{cc} 0.8149 &{}\quad 0.1405\\ 0.8799 &{}\quad 0.0954 \end{array} \right] ,\\ A_{3}= & {} \left[ \begin{array}{cc} 0.6480 &{}\quad 0.4334\\ 0.1398 &{}\quad 0.7519 \end{array} \right] . \end{aligned}$$

which define the stable polytope. The uncertain systems have not been identified as stable by any of the Lemma 2 and Theorem 1. However, the stability can be verified using Theorem 2, with a solution given as:

$$\begin{aligned} P_{1}= & {} \left[ \begin{array}{cc} 35.3331 &{}\quad 0\\ 0 &{}\quad 75.6912 \end{array} \right] , P_{2}=\left[ \begin{array}{cc} 119.0324 &{}\quad 0\\ 0 &{} \quad 26.5928 \end{array} \right] ,\\ P_{3}= & {} \left[ \begin{array}{cc} 41.3948 &{}\quad 0\\ 0 &{}\quad 69.0670 \end{array} \right] ,\\ F_{1}= & {} \left[ \begin{array}{cc} 10.2249 &{}\quad 0\\ 0 &{} \quad 9.0197 \end{array} \right] , F_{2}=\left[ \begin{array}{cc} 42.0977 &{}\quad 0\\ 0 &{}\quad 0.7606 \end{array} \right] ,\\ F_{3}= & {} \left[ \begin{array}{cc} 9.7406 &{}\quad 0\\ 0 &{}\quad 17.6507 \end{array} \right] ,\\ H_{1}= & {} \left[ \begin{array}{cc} 43.3014 &{}\quad 0\\ 0 &{}\quad 59.3318 \end{array} \right] , H_{2}=\left[ \begin{array}{cc} 74.2898 &{}\quad 0\\ 0 &{}\quad \quad 31.3625 \end{array} \right] ,\\ H_{3}= & {} \left[ \begin{array}{cc} 34.4231 &{} 0\\ 0 &{}\quad 48.5846 \end{array} \right] . \end{aligned}$$

The trajectories of the horizontal and vertical states of the three vertices are shown in Figs. 1, 2, 3, 4, 5 and 6 where the initial conditions are set as

$$\begin{aligned} x^{h}(0,l)=\left\{ \begin{array}{ll} 6\cos (l), &{} l<30 \\ 0, &{} l\ge 30, \end{array} \right. \qquad x^{v}(k,0)=\left\{ \begin{array}{ll} 4\sin (k), &{} k<30 \\ 0, &{} k\ge 30. \end{array} \right. \end{aligned}$$
Fig. 6
figure 6

State trajectory of \(x^{v}(k,l)\): third vertex

Full size image

Remark 6

From Remark 5, it can be seen that the the number of decision variables used in Theorem 2 is larger than those used in Lemma 2 and Theorem 1. The main reason for obtaining such larger number is that Theorem 2 is derived based on the use of the parameter-dependent Lyapunov functions (17), and the introduction of the parameter dependent slack variables (22). As a result, proposed stability conditions gives better results but with high computational cost. In the future research, we will focus on reducing the number of decision variables and solving the robust control synthesis problem.

5 Conclusions

This paper has presented sufficient conditions for robust stability of uncertain 2-D discrete systems described by the Roesser model under polytopic uncertainty. These stability criteria are less conservative for two reasons: one is that they are parameter-dependent; another is the introduction of two slack parameters by using Finsler’s lemma. All these results are expressed in the terms of LMIs which can be easily solved by LMI Toolbox in MATLAB. Two numerical examples have been given to verify the less conservative nature of the new approaches.