Breakable Fuzzy Multi-stage Transportation Problem

Abstract

In this paper, we investigate two new transportation models with breakability and restriction on transportation. Sometime in transportation process the items which are transported, have got damaged due to bad conditions of the road and vehicle. Here we consider the problem that there are so many plants and customers and the goods are transported in n-stages. We formulate two transportation models under crisp and fuzzy environment where we consider the transportation parameters are crisp and fuzzy in nature, respectively. We also consider the breakability (takes the deterministic value for the respective models) at each stages. For the fuzzy model, generalized triangular fuzzy number and mean of $\alpha$-cut method are considered. Numerical illustration is provided to illustrate the developed models.

1 Introduction

Hitchcock [9] originally proposed the classical transportation problem in 1941. The transportation processes may not be operated always directly between the suppliers and customers. It may happened in multiple stages using different warehouses at different stages. Geoffrion and Graves [6] were the pioneers who studied the two-stage distribution problem.

There are some literature listed in [1, 4, 5, 7, 8, 10, 13, 14, 16–19] to solve such transportation problems (TPs). Mahapatra et al. [11] applied fuzzy multi-objective mathematical programming technique to a reliability optimization model. Sreenivas and Srinivas [15] formulated and studied the probabilistic TPs. Recently, Ojha et al. [12] solved a multi-item TP using fuzzy tolerance and Baidya et al. [2, 3] solved two problems using safety factors and uncertainties in transportation of units.

In spite of the above progresses, there are some gaps in the formulation and solution of multi-item multi-stage TPs. Some researchers [5, 8, 9] have solved the two-stage TPs, but none has investigated the multi-stage TPs. In the literature, no TP model is formulated taking breakability for n-stages. Here the proposed multi-stage models are formulated as a constrained linear programming problem and solved using gradient-based non-linear optimization technique. The formulation of the respective models is new in this research area of TPs. Very few TP models are formulated and solved in different environments such as crisp and fuzzy.

After observing the above gaps, we formulated and solved two new transportation models with breakability as deterministic. Here we consider the units are first transported from plants to destination centers (DCs) and then DCs to customers. Sometime all the transportation parameters are not known to us precisely and for these reason we formulate the model by considering the transportation parameters as fuzzy in nature. Generalized triangular fuzzy number (GTFN) and Mean of $\alpha$-cut (MC) method are used to develop the fuzzy model. The numerical examples are provided to illustrate the models and solved using the LINGO.13 optimization software. The optimal results are also obtained with some restriction at each DC.

2 Preliminaries

Definition 2.1

(Generalized fuzzy numbers) A fuzzy subset of the real line ${\mathbb {R}}$ with membership function $f_{\tilde{A}}$ is defined as $\tilde{A} =(a, b, c, d;w)$, which is called generalized fuzzy number with the following properties:

(a) $f_{\tilde{A}}$ is a continuous mapping from ${\mathbb {R}}$ to the closed interval [0, w], $0\leqslant w\leqslant 1$; (b) $f_{\tilde{A}} \left( x \right) =0$ for all $x\in (-\infty ,a]$; (c) $f_{\tilde{A}}$ is strictly increasing on [a, b]; (d) $f_{\tilde{A}} \left( x\right) =w$ for all $x\in [b, c]$, where $w$ is a constant and $0<w\leqslant 1$; (e) $f_{\tilde{A}}$ is strictly decreasing on [c, d]; (f) $f_{\tilde{A}} \left( x\right) =0$ for all $x\in [d, +\infty )$; where $0<w\leqslant 1$, a, b, c, and d are real numbers.

Especially, a generalized trapezoidal fuzzy number can be defined as $\tilde{A} =(a, b, c, d;w)$, where $a\leqslant b\leqslant c\leqslant d, 0\leqslant w\leqslant 1$, its membership function is defined by

$$\begin{aligned} f_{\tilde{A}} \left( x\right) =\left\{ {{ \begin{array}{ll} 0,&{}\quad x<a, \\ \frac{(x-a)}{(b-a)},&{}\quad a\leqslant x\leqslant b, \\ w,&{}\quad b\leqslant x\leqslant c, \\ \frac{(x-c)}{(d-c)},&{}\quad c\leqslant x\leqslant d ,\\ 0,&{}\quad x>d. \end{array}}}\right. \end{aligned}$$

If $w=1$, then the generalized fuzzy number $\tilde{A}$ is called normal trapezoidal fuzzy number and is denoted by $A=(a, b, c, d)$. If $a=b$ and $c=d$, then $\tilde{A}$ is called a crisp interval. If $b=c$, then $\tilde{A}$ is called a generalized triangular fuzzy number. If $a=b=c=d$, then $\tilde{A}$ is called real number. Figure 1 shows two different generalized trapezoidal fuzzy number $\tilde{A}=(0.1, 0.2, 0.3, 0.4; 1.0)$ and $\tilde{B} =(0.1, 0.2, 0.3, 0.4; 0.8)$. Compared with normal fuzzy number, the generalized fuzzy numbers can deal with uncertain information in a more flexible manner. For example, in decision-making situation, the values $w_{1}$ and $w_{2}$ represent the degree of confidence of the opinions of the decision makers’ $\tilde{A}$ and $\tilde{B}$, respectively, where $w_{1}=1$ and $w_{2} =0.8$.

Fig. 1

Two generalized trapezoidal fuzzy number $\tilde{A}$ and $\tilde{B}$

Property 2.2

• (a) If GTFN $\tilde{A} =\left( {a,b,c;w}\right) ~and~Y=kA~\left( {with~k>0}\right) \,then\, \tilde{Y} =k\tilde{A}$ is a GTFN $\left( {ka,kb,kc;w}\right)$.

• (b) If $Y=kA~\left( {with~k<0}\right) \,then\,\tilde{Y} =k\tilde{A}$ is a GTFN $(kc, kb, ka; w)$, where k is a constant.

Property 2.3

If $\tilde{A}_{1}=\left( {a_{1}, b_{1}, c_{1};w_{1}}\right) \,and\, \tilde{A}_{1}=\left( {a_{2}, b_{2}, c_{2};w_{2}}\right) ,\,then\, \tilde{A}_{1}\oplus \tilde{A}_{2}$ is a fuzzy number $\left( {a_{1}+a_{2}, b_{1}+b_{2}, c_{1}+c_{2};min\left( w_{1},w_{2}\right) }\right)$.

2.1 Method for Defuzzification of Fuzzy Numbers (MC Method)

Defuzzification is the transformation of the fuzzy number to deterministic number. Lots of methods exist in the literature to translate the fuzzy number into a deterministic value. Here we discuss the defuzzification method proposed by Yager [17]. Let $\tilde{A}$ be a fuzzy number, then the defuzzification of $\tilde{A}$ is given by $\tilde{A} =\int \nolimits _{0}^{\alpha _{\mathrm{max}}} m[a_{\alpha }^{\mathrm{L}},a_{\alpha }^{\mathrm{R}}]\mathrm{d}\alpha$ where $\alpha _{\mathrm{max}}$ is the height of $\tilde{A},\,A_{\alpha } =[a_{\alpha }^{\mathrm{L}}, a_{\alpha }^{\mathrm{R}}]$ is an $\alpha$-cut, $\alpha \in \left[ {0,1}\right] \,\mathrm{and}\,\left[ {a_{\alpha }^{\mathrm{L}}, a_{\alpha }^{\mathrm{R}}}\right]$ is the mean value of the elements of that $\alpha$-cut, $m\left[ {a_{\alpha }^{\mathrm{L}}, a_{\alpha }^{\mathrm{R}}}\right] =\frac{a_{\alpha }^{\mathrm{L}}\,+\,a_{\alpha }^{\mathrm{R}}}{2}$ where $a_{\alpha }^{\mathrm{L}}\,\mathrm{and}\,a_{\alpha }^{\mathrm{R}}$ are the left and right limits of the $\alpha$-cut of the fuzzy number $\tilde{A}$.

Defuzzification of $\tilde{A}_{\mathrm{GTFN}} =(a_{1},a_{2},a_{3};w)$ by MC method $\tilde{A} =w(\frac{a_{1}\,+\,2a_{2}\,+\,a_{3}}{4})$. Here $a_{\alpha }^{\mathrm{L}}=a_{1}+\frac{\alpha }{w}(a_{2}-a_{1})$ and $a_{\alpha }^{\mathrm{R}}=a_{3}-\frac{\alpha }{w}(a_{3}-a_{2})$.

3 Multi-item Multi-stage Transportation Model

3.1 Assumptions and Notations

The following assumptions and notations are used throughout the model.

• (i) $q$: number of items, $q=1,2,\cdots , Q$.

• (ii) $M$: number of plant in TP for stage-1.

• (iii) $N^{l}$: number of DCs in TP for stage-$l$, $l=1, 2, \cdots n$.

• (iv) $C_{ijq}^{1}$, $C_{jkq}^{2},{\cdots }$, $C_{stq}^{m}$, $C_{tpq}^{n}$: crisp unit transportation cost to transport the commodities from $i$th plant to $j$th DC of $q$th item for stage-1, $j$th plant to $k$th DC of $q$th item for stage-2,$\cdots$, $s$th plant to $t$th DC of $q$th item for stage-m, $t$th plant to $p$th DC of $q$th item for stage-n, respectively.

• (v) $\tilde{C}_{ijq}^{1}$, $\tilde{C}_{jkq}^{2},\cdots$, $\tilde{C}_{stq}^{m}$, $\tilde{C}_{tpq}^{n}$: fuzzy unit transportation cost to transport the commodities from $i$th plant to $j$th DC of $q$th item for stage-1, $j$th plant to $k$th DC of $q$th item for stage-2,$\cdots$, $s$th plant to tth DC of qth item for stage-m, tth plant to pth DC of qth item for stage-n, respectively.

• (vi) $x_{ijq}^{1}$, $x_{jkq}^{2},\cdots$, $x_{stq}^{m}$, $x_{tpq}^{n}$: the amount which is transported from $i$th plant to $j$th DC of $q$th item for stage-1, jth plant to kth DC of $q$th item for stage-2,$\cdots$, $s$th plant to tth DC of $q$th item for stage-m, tth plant to pth DC of $q$th item for stage-$n$, respectively.

• (vii) $a_{iq}^{1}$, $\tilde{a}_{iq}^{1}$: crisp and fuzzy capacity for ith plant at stage-1 of $q$th item, respectively.

• (viii) $a_{kq}^{2}$, $\tilde{a}_{kq}^{2}$: crisp and fuzzy capacity for kth DC at stage-2 of $q$th item, respectively.

• (ix) $b_{jq}^{1}$, $\tilde{b}_{jq}^{1}$: crisp and fuzzy capacity of jth DC at stage-1 for $q$th item, respectively.

• (x) $e_{pq}$, $\tilde{e}_{pq}$: crisp and fuzzy, random and fuzzy-random requirement of $p$th customer for $q$th item.

• (xi) $\alpha _{ijq}$, $\beta _{jkq},\cdots \gamma _{tpq}$: rate of breaking of the units due to transportation from ith plant to jth DC of qth item at stage-1, jth plant to kth DC of qth item at stage-2,$\cdots$, tth DC to $p$th customer of $q$th item at stage-$n$, respectively.

3.2 Formulation of Transportation Models

Here we formulate two breakable multi-item multi-stage TP under crisp and fuzzy environments. The transportation parameters should be fuzzy in nature due to deficient evidence. For this reason, we formulate a transportation model with fuzzy transportation parameters.

Model-1 Formulation of breakable multi-item multi-stage transportation problem under crisp environment

$$\begin{aligned} \mathrm{min}~Z&= \sum \limits _{q=1}^{Q}\sum \limits _{i=1}^{M} \sum \limits _{j=1}^{N^{1}} C_{ijq}^{1}x_{ijq}^{1}+ \sum \limits _{q=1}^{Q}\sum \limits _{j=1}^{N^{1}} \sum \limits _{k=1}^{N^{2}} C_{jkq}^{2}x_{jkq}^{2}\nonumber \\&\quad +\, \cdots +\sum \limits _{q=1}^{Q}\sum \limits _{s=1}^{N^{\left( {m-1}\right) }} \sum \limits _{t=1}^{N^{m}} C_{stq}^{m}x_{stq}^{m}\nonumber \\&\quad +\, \sum \limits _{q=1}^{Q}\sum \limits _{t=1}^{N^{m}} \sum \limits _{p=1}^{N^{n}} C_{tpq}^{n}x_{tpq}^{n} \end{aligned}$$

(3.1)

Subject to the constraints,

$$\begin{aligned}&\sum \limits _{j=1}^{N^{1}} x_{ijq}^{1}\leqslant a_{iq}^{1},\qquad \left( {\mathrm{Supply~constraint~for~stage{\text {-}}1}}\right) \nonumber \\&\sum \limits _{i=1}^{M}x_{ijq}^{1}\left( {1-\alpha _{ijq}}\right) \leqslant b_{jq}^{1},\quad \left( {\mathrm{Demand~constraint~for~stage{\text {-}}1}}\right) \end{aligned}$$

(3.2)

$$\begin{aligned}&\sum \limits _{k=1}^{N^{2}} x_{jkq}^{2}\leqslant \sum \limits _{i=1}^{M}x_{ijq}^{1}\left( {1-\alpha _{ijq}}\right) ,\quad \left( \mathrm{Supply~constraint~for~stage{\text {-}}2}\right) \nonumber \\&\sum \limits _{j=1}^{N^{1}} x_{jkq}^{2}\left( {1-\beta _{jkq}}\right) \leqslant a_{kq}^{2},\quad \left( \mathrm{Demand~constraint~for~stage{\text {-}}2}\right) \\&\cdots \nonumber \end{aligned}$$

(3.3)

$$\begin{aligned}&\sum \limits _{p=1}^{N^{n}} x_{tpq}^{n}\leqslant \sum \limits _{s=1}^{N^{\left( {m-1}\right) }} x_{stq}^{m}\left( {1-\gamma _{stq}}\right) ,\quad \left( {\mathrm{Supply~constraint~for~stage{\text {-}}}\textit{n}}\right) \nonumber \\&\sum \limits _{t=1}^{N^{m}} x_{tpq}^{n}\geqslant e_{pq},\quad \left( \mathrm{Demand~constraint~for~stage{\text {-}}}\textit{n}\right) \\&\qquad \left( \sum \limits _{q=1}^{Q}\sum \limits _{i=1}^{M} \sum \limits _{j=1}^{N^{1}} x_{ijq}^{1}\right) \left( 1-\alpha _{ijq}\right) \nonumber \\&\quad =\left( \sum \limits _{q=1}^{Q}\sum \limits _{j=1}^{N^{1}} \sum \limits _{k=1}^{N^{2}} x_{jkq}^{2}\right) \left( {1-\beta _{ijq}}\right) \nonumber \\&\quad =\cdots =\left( \sum \limits _{q=1}^{Q}\sum \limits _{s=1}^{{N}^{\left( {m-1}\right) }} \sum \limits _{t=1}^{N^{m}} x_{stq}^{m}\right) \left( 1-\gamma _{ijq}\right) \nonumber \\&\quad =\sum \limits _{q=1}^{Q}\sum \limits _{t=1}^{N^{m}} \sum \limits _{p=1}^{N^{n}} x_{tpq}^{n}\nonumber \\&x_{ijq}^{1}\geqslant 0, x_{jkq}^{2}\geqslant 0,\cdots , x_{stq}^{m}\geqslant 0, x_{tpq}^{n}\geqslant 0,\quad \hbox {for all}\quad i=1,2,\cdots ,M,\nonumber \\&\qquad j=1,2,\cdots ,N^{1},\,k=1,2,\cdots ,~ N^{2},\,t=1,2,\cdots ,~N^{{m}},\nonumber \\&\qquad p=1,2,\cdots ,~N^{n},~q=1,2,\cdots ,Q\nonumber . \end{aligned}$$

(3.4)

Model-2 Formulation of Multi-item Multi-stage Transportation Problem with Fuzzy Penalties, Supplies, Demands, and Crisp Breakability

Sometime the transportation parameters are not known to us precisely but some insufficient or past data are known from past record. For this reason, we consider the unit transportation costs, availabilities at plants, and demands at destination centers or customers are fuzzy in nature.

$$\begin{aligned} \mathrm{min}~Z&= \sum \limits _{q=1}^{Q}\sum \limits _{i=1}^{M} \sum \limits _{j=1}^{N^{1}} \tilde{C}_{ijq}^{1}x_{ijq}^{1}+\sum \limits _{q=1}^{Q} \sum \limits _{j=1}^{N^{1}} \sum \limits _{k=1}^{N^{2}} \tilde{C}_{jkq}^{2}x_{jkq}^{2}\nonumber \\&\quad +\cdots +\sum \limits _{q=1}^{Q}\sum \limits _{s=1}^{N^{\left( {m-1}\right) }} \sum \limits _{t=1}^{N^{m}} \tilde{C}_{stq}^{m}x_{stq}^{m}\nonumber \\&\quad +\, \sum \limits _{q=1}^{Q}\sum \limits _{t=1}^{N^{m}} \sum \limits _{p=1}^{N^{n}} \tilde{C}_{tpq}^{n}x_{tpq}^{n} \end{aligned}$$

(3.5)

Subject to the constraints,

$$\begin{aligned}&\sum \limits _{j=1}^{N^{1}} x_{ijq}^{1}\leqslant \tilde{a}_{iq}^{1},\quad \left( {\mathrm{Supply~constraint~for~stage{\text {-}}1}}\right) \nonumber \\&\sum \limits _{i=1}^{M}x_{ijq}^{1}\left( {1-\alpha _{ijq}}\right) \leqslant \tilde{b}_{jq}^{1},\quad \left( {\mathrm{Demand~constraint~for~stage{\text {-}}1}} \right) \end{aligned}$$

(3.6)

$$\begin{aligned}&\sum \limits _{k=1}^{N^{2}} x_{jkq}^{2}\leqslant \sum \limits _{i=1}^{M}x_{ijq}^{1}\left( {1-\alpha _{ijq}} \right) ,\quad \left( \mathrm{Supply~constraint~for~stage{\text {-}}2}\right) \nonumber \\&\sum \limits _{j=1}^{N^{1}} x_{jkq}^{2}\left( {1-\beta _{jkq}}\right) \leqslant \tilde{a}_{kq}^{2},\quad \left( \mathrm{Demand~constraint~for~stage{\text {-}}2}\right) \\&\cdots \nonumber \end{aligned}$$

(3.7)

$$\begin{aligned}&\sum \limits _{p=1}^{N^{n}} x_{tpq}^{n}\leqslant \sum \limits _{s=1}^{N^{\left( {m-1}\right) }} x_{stq}^{m}\left( {1-\gamma _{stq}}\right) ,\quad \left( \mathrm{Supply~constraint~for~stage{\text {-}}}\textit{n}\right) \nonumber \\&\sum \limits _{t=1}^{N^{m}} x_{tpq}^{n}\geqslant \tilde{e}_{pq},\quad \left( \mathrm{Demand~constraint~for~stage{\text {-}}}\textit{n}\right) \\&\qquad \left( \sum \limits _{q=1}^{Q}\sum \limits _{i=1}^{M} \sum \limits _{j=1}^{N^{1}} x_{ijq}^{1}\right) \left( 1-\alpha _{ijq} \right) \nonumber \\&\quad =\left( \sum \limits _{q=1}^{Q}\sum \limits _{j=1}^{N^{1}} \sum \limits _{k=1}^{N^{2}} x_{jkq}^{2}\right) \left( {1-\beta _{ijq}}\right) \nonumber \\&\quad =\cdots =\left( \sum \limits _{q=1}^{Q}\sum \limits _{s=1}^{N^{\left( {m-1}\right) }} \sum \limits _{t=1}^{N^{m}} x_{stq}^{m}\right) \left( 1-\gamma _{ijq}\right) \nonumber \\&\quad =\sum \limits _{q=1}^{Q}\sum \limits _{t=1}^{N^{m}} \sum \limits _{p=1}^{N^{n}} x_{tpq}^{n}\nonumber \\&x_{ijq}^{1}\geqslant 0, x_{jkq}^{2}\geqslant 0,\cdots , x_{stq}^{m}\geqslant 0, x_{tpq}^{n}\geqslant 0,\, \hbox {for all} \quad i=1,2,\cdots , M,\nonumber \\&\qquad j=1,2,\cdots ,~N^{1},~k=1,2,\cdots , ~N^{2},\,t=1,2,\cdots ,\,N^{m},\nonumber \\&\qquad p=1,2,\cdots , \,N^{n},\,q=1,2,\cdots ,~Q \nonumber . \end{aligned}$$

(3.8)

4 Numerical Example

Let a company produces three items as products-$\hbox {I}_{1}$ and $\hbox {I}_{2}$ at three origins-$\hbox {O}_{1}$, $\hbox {O}_{2}$, $\hbox {O}_{3}$, which is supplied to three customers-$\hbox {C}_{1}$, $\hbox {C}_{2}$, $\hbox {C}_{3}$ via DCs-DC-1, DC-2, and DC-3. Assuming that to transport the items from origins to DCs and DCs to customers the percentage of breaking units are 4 and 3, respectively. Here we consider two cases depending on the availability of DCs. Case-1: All DCs as DC-1, DC-2, and DC-3 are open; Case-2: DC-1 and DC-2 are open but DC-3 is not available due to some problems.

The capacities of origins, DCs, requirements of the customers, and unit transportation cost (in $) to transport the items from origin to DC and also DC to customer are as follows:

Crisp unit transportation costs

$$\begin{aligned} \begin{array}{llllll} C_{111}^{1}=1, &{} C_{121}^{1}=1.8, &{} C_{131}^{1}=2, &{} C_{211}^{1}=1.5, &{} C_{221}^{1}=1.3, &{} C_{231}^{1}=2.4,\\ C_{311}^{1}=1.1, &{} C_{321}^{1}=1.9, &{} C_{331}^{1}=1.1, &{} C_{112}^{1}=1.4, &{} C_{122}^{1}=1.8, &{} C_{132}^{1}=2.3,\\ C_{212}^{1}=1.5, &{} C_{222}^{1}=1.3, &{} C_{232}^{1}=1.4, &{} C_{312}^{1}=1, &{} C_{322}^{1}=2.1, &{} C_{332}^{1}=2.2,\\ C_{113}^{1}=2.4, &{} C_{123}^{1}=1.8, &{} C_{133}^{1}=1.7, &{} C_{213}^{1}=2.5, &{} C_{223}^{1}=1.3, &{} C_{233}^{1}=1.4,\\ C_{313}^{1}=1.1, &{} C_{323}^{1}=2.3, &{} C_{333}^{1}=2.8, &{} C_{111}^{2}=1.1, &{} C_{121}^{2}=1.9, &{} C_{131}^{2}=2,\\ C_{211}^{2}=1.2, &{} C_{221}^{2}=1, &{} C_{231}^{2}=2.4, &{} C_{311}^{2}=1.3, &{} C_{321}^{2}=1.9, &{} C_{331}^{2}=2.1,\\ \end{array} \end{aligned}$$

$$\begin{aligned} \begin{array}{llllll} C_{112}^{2}=3.4, &{} C_{122}^{2}=2.1, &{} C_{132}^{2}=2.3, &{} C_{212}^{2}=1.5, &{} C_{222}^{2}=1.2, &{} C_{232}^{2}=2.4,\\ C_{312}^{2}=2, &{} C_{322}^{2}=2.1, &{} C_{332}^{2}=3.2, &{} C_{113}^{2}=1.4, &{} C_{123}^{2}=1.8, &{} C_{133}^{2}=2.7,\\ C_{213}^{2}=2.5, &{} C_{223}^{2}=1.3, &{} C_{233}^{2}=2.4, &{} C_{313}^{2}=2.1, &{} C_{323}^{2}=2.3, &{} C_{333}^{2}=3.8. \end{array} \end{aligned}$$

Crisp capacities of plants, DC, and demands of the customers

$$\begin{aligned} \begin{array}{lllllllll} a_{11}^{1}=42, &{} a_{21}^{1}=43, &{} a_{31}^{1}=47, &{} a_{12}^{1}=48, &{} a_{22}^{1}=54, &{} a_{32}^{1}=40,&{} a_{13}^{1}=50, &{}\\ \quad a_{23}^{1}=56, &{} a_{33}^{1}=51,\\ b_{11}^{1}=46, &{} b_{21}^{1}=44, &{} b_{31}^{1}=41, &{} b_{12}^{1}=50, &{} b_{22}^{1}=42, &{} b_{32}^{1}=29,&{} b_{13}^{1}=51, &{}\\ \quad b_{23}^{1}=40, &{} b_{33}^{1}=25,\\ e_{11}^{1}=25, &{} e_{21}^{1}=28, &{} e_{31}^{1}=31, &{} e_{12}^{1}=25, &{} e_{22}^{1}=26, &{} e_{32}^{1}=29,&{} e_{13}^{1}=30, &{}\\ \quad e_{23}^{1}=28, &{} e_{33}^{1}=29. \end{array} \end{aligned}$$

Fuzzy unit transportation costs

$$\begin{aligned} \begin{array}{lll} \tilde{C}_{111}^{1}=\left( {0.5,1.0,1.19;0.98}\right) ,&{} \tilde{C}_{121}^{1}=\left( {1.3,1.8,1.9;0.90}\right) ,&{}\\ \quad \tilde{C}_{131}^{1}=\left( {1.7,2.0,2.20;0.96}\right) ,\\ \tilde{C}_{211}^{1}=\left( {1.2,1.5,1.9;0.92}\right) ,&{} \tilde{C}_{221}^{1}=\left( {1.1,1.3,1.7;0.96}\right) ,&{}\\ \quad \tilde{C}_{231}^{1}=\left( {2.1,2.4,2.5;0.87}\right) ,\\ \tilde{C}_{311}^{1}=\left( {1,1.1,1.4;0.99}\right) , &{} \tilde{C}_{321}^{1}=\left( {1.2,1.9,2.0;0.97}\right) ,&{}\\ \quad \tilde{C}_{331}^{1}=\left( {0.90, 1.1, 1.18;0.97}\right) ,\\ \tilde{C}_{112}^{1}=\left( {1.1,1.4,1.8;0.9}\right) ,&{} \tilde{C}_{122}^{1}=\left( {1.2,1.8,2.0;0.87}\right) ,&{}\\ \quad \tilde{C}_{132}^{1}=\left( {2.0,2.3,2.6;0.95}\right) ,\\ \tilde{C}_{212}^{1}=\left( {1.2,1.5,1.9;0.89}\right) ,&{} \tilde{C}_{222}^{1}=\left( {1.1,1.3,1.5;0.94}\right) ,&{}\\ \quad \tilde{C}_{232}^{1}=\left( {1.1,1.4,1.9;0.99}\right) ,\\ \tilde{C}_{312}^{1}=\left( {0.9,1.0,1.4;0.89}\right) , &{} \tilde{C}_{322}^{1}=\left( {1.5,2.1,2.6;1}\right) ,&{}\\ \quad \tilde{C}_{332}^{1}=\left( {2.0,2.2,2.7;0.99}\right) ,\\ \tilde{C}_{113}^{1}=\left( {2.22,2.4,2.45;0.87}\right) ,&{} \tilde{C}_{123}^{1}=\left( {1.2,1.8,1.9;0.88}\right) , &{}\\ \quad \tilde{C}_{133}^{1}=\left( {1.3,1.7,1.9;0.97}\right) ,\\ \tilde{C}_{213}^{1}=\left( {2.1,2.5,2.9;0.85}\right) , &{} \tilde{C}_{223}^{1}=\left( {1.0,1.3,1.8;0.98}\right) , &{}\\ \quad \tilde{C}_{233}^{1}=\left( {1.1,1.4,1.7;0.94}\right) ,\\ \tilde{C}_{313}^{1}=\left( {1.0,1.1,1.7;0.96}\right) , &{} \tilde{C}_{323}^{1}=\left( {2.1,2.3,2.8;0.97}\right) , &{}\\ \quad \tilde{C}_{333}^{1}=\left( {2.1,2.8,3.0;0.88}\right) ,\\ \tilde{C}_{111}^{2}=\left( {1.0,1.1,1.5;0.96}\right) ,&{} \tilde{C}_{121}^{2}=\left( {1.3,1.9,2.3;0.88}\right) , &{}\\ \quad \tilde{C}_{131}^{2}=\left( {1.88,2.0,2.33;0.92}\right) ,\\ \tilde{C}_{211}^{2}=\left( {0.90,1.2,1.60;0.91}\right) ,&{} \tilde{C}_{221}^{2}=\left( {0.95,1.0,1.29;0.99}\right) ,&{}\\ \quad \tilde{C}_{231}^{2}=\left( {2.1,2.4,2.5;0.95}\right) , \end{array} \end{aligned}$$

$$\begin{aligned} \begin{array}{lll} \tilde{C}_{311}^{2}=\left( {1.11,1.3,1.32;1}\right) , &{} \tilde{C}_{321}^{2}=\left( {1.3,1.9,2.8;0.92}\right) , &{}\\ \quad \tilde{C}_{331}^{2}=\left( {1.85,2.1,2.34;0.94}\right) ,\\ \tilde{C}_{112}^{2}=\left( {3.2,3.4,3.6;0.98}\right) , &{} \tilde{C}_{122}^{2}=\left( {1.78,2.1,2.39;0.97}\right) ,&{}\\ \quad \tilde{C}_{132}^{2}=\left( {2.13,2.3,2.82;0.82}\right) ,\\ \tilde{C}_{212}^{2}=\left( {1.2,1.5,1.6;0.91}\right) ,&{} \tilde{C}_{222}^{2}=\left( {0.92,1.2,1.34;0.95}\right) ,&{}\\ \quad \tilde{C}_{232}^{2}=\left( {2.1,2.4,2.7;0.94}\right) ,\\ \tilde{C}_{312}^{2}=\left( {1.87,2.0,2.18;0.99}\right) , &{} \tilde{C}_{322}^{2}=\left( {1.9,2.1,2.4;0.96}\right) , &{}\\ \quad \tilde{C}_{332}^{2}=\left( {2.76,3.2, 3.7;0.98}\right) ,\\ \tilde{C}_{113}^{2}=\left( {1.1,1.4, 1.46;0.92}\right) ,&{} \tilde{C}_{123}^{2}=\left( {1.55,1.8,1.85;0.87}\right) ,&{}\\ \quad \tilde{C}_{133}^{2}=\left( {2.3,2.7,3;0.88}\right) ,\\ \tilde{C}_{213}^{2}=\left( {1.9,2.5,2.8;0.96}\right) , &{} \tilde{C}_{223}^{2}=\left( {1.99,2.4,2.5;0.93}\right) , &{}\\ \quad \tilde{C}_{233}^{2}=\left( {1.0,1.3,1.5;0.85}\right) ,\\ \tilde{C}_{313}^{2}=\left( {1.87,2.1,2.23;0.94}\right) , &{} \tilde{C}_{323}^{2}=\left( {1.84,2.3,2.9;1}\right) ,&{}\\ \quad \tilde{C}_{333}^{2}=\left( {3.1,3.8,4;0.90}\right) . \end{array} \end{aligned}$$

Fuzzy capacities of plants, DC, and demands of the customers

$$\begin{aligned} \begin{array}{lll} \tilde{a}_{11}^{1}=\left( {40,42,43;1}\right) ,&{} \tilde{a}_{21}^{1}=\left( {42,43,45;0.92}\right) ,&{} \tilde{a}_{31}^{1}=\left( {45,47,48;0.93}\right) ,\\ \tilde{a}_{12}^{1}=\left( {45,48,50;0.90}\right) ,&{} \tilde{a}_{22}^{1}=\left( {51,54,55;0.88}\right) ,&{} \tilde{a}_{32}^{1}=\left( {38,40,41;0.90}\right) ,\\ \tilde{a}_{13}^{1}=\left( {47,50,52;0.95}\right) ,&{} \tilde{a}_{23}^{1}=\left( {55,56,58;0.80}\right) ,&{} \tilde{a}_{33}^{1}=\left( {49,51,53;0.94}\right) ,\\ \tilde{b}_{11}^{1}=\left( {45,46,47;0.96}\right) ,&{} \tilde{b}_{21}^{1}=\left( {42,44,46;0.97}\right) ,&{} \tilde{b}_{31}^{1}=\left( {40,41,43;0.94}\right) ,\\ \tilde{b}_{12}^{1}=\left( {47,50,51;0.97}\right) ,&{} \tilde{b}_{22}^{1}=\left( {41,42,44;0.95}\right) ,&{} \tilde{b}_{32}^{1}=\left( {27,29,30;0.97}\right) ,\\ \tilde{b}_{13}^{1}=\left( {50,51,53;1}\right) ,&{} \tilde{b}_{23}^{1}=\left( {38,40,42;0.94}\right) ,&{} \tilde{b}_{33}^{1}=\left( {23,25,26;0.99}\right) ,\\ \tilde{e}_{11}^{1}=\left( {23,25,26;0.85}\right) ,&{} \tilde{e}_{21}^{1}=\left( {26,28,29;0.88}\right) ,&{} \tilde{e}_{31}^{1}=\left( {27,31,32;0.91}\right) ,\\ \tilde{e}_{12}^{1}=\left( {23,25,27;0.94}\right) ,&{} \tilde{e}_{22}^{1}=\left( {25,26,28;0.99}\right) ,&{} \tilde{e}_{32}^{1}=\left( {27,29,31;0.91}\right) ,\\ \tilde{e}_{13}^{1}=\left( {28,30,31;0.93}\right) ,&{} \tilde{e}_{23}^{1}=\left( {25,28,30;0.94}\right) ,&{} \tilde{e}_{33}^{1}=(26,29,30;0.97). \end{array} \end{aligned}$$

5 Optimal Results

The problems defined above are solved by the gradient-based non-linear optimization technique generalized reduced gradient and the optimal results are presented in Table 1.

Table 1 Optimal result of different models

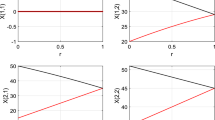
6 Sensitivity Analysis for Model-1

Here we present the sensitivity analysis for model-1 which is presented by Tables 2 and 3. Here in stage-1, the % of breakability taken as constants and the % of breakability at stage-2 are varied from 0 to 4 and total transportation costs as well as total loss at customer position are presented here. Interestingly, we notice that if we increase the % of breakability of stage-2, then the total transportation cost also increased because due to breakability, the customer order more quantity to satisfy the requirement (Figs. 2 and 3).

Fig. 2

Pictorial representation of sensitivity analysis of total cost and total loss at customer for model-1 (case-1)

Fig. 3

Pictorial representation of sensitivity analysis of total cost and total loss at customer for model-1 (case-2)

Table 2 Sensitivity analysis of total cost and total loss at customer for model-1 (case-1)

Table 3 Sensitivity analysis of total cost and total loss at customer for model-1 (case-2)

7 Discussion

Here we develop two classical transportation problems with breakability and illustrate numerically by taking a two-stage three-item classical transportation problem. Here we solve two models where model-1 is formulated with crisp environment but model-2 with fuzzy environment. Also we represent a sensitivity analysis of the model-1 with the geometrical representation. After careful investigation, we see that the transportation cost is increased if we increase the percentage of breakability for both stage-1 and stage-2. The decision maker always transports the quantity through the route where the transportation cost is minimum. But in case-2, when we close the DC-3, the decision maker is bound to transport the items through the route where the transportation cost is higher. For this reason, the minimum transportation costs for case-2 of all models are greater than the minimum transportation costs of case-1. However, the transportation cost for case-1 is more than that of case-2, which is as per our expectation.

8 Conclusion

In this manuscript, we show the solution of multi-item multi-stage transportation problem with breakability. Here we impose two models in transportation and in view of all the distribution centers are open and not all distribution centers are open, we discuss two cases. Sometimes the transportation parameters are vague in nature; so introducing the concept of generalized triangular fuzzy number, we solve the model-2 in two cases. Impreciseness is proceed in transportation problem, so we introduce these concepts in our model-2. The transportation cost in our result of all three models in case-I is less than the cost of the other three models in case-II which is as per our expectation. MC Method is used to convert the model-2 into its crisp equivalent, and LINGO.13 software is used to solve this reduced model. Since transportation problem plays an important role in our daily life, so our technique is highly fruitful.