1 Introduction

In machine learning and statistics, classification is the problem of identifying which of a set of categories (sub-populations) a new observation belongs to on the basis of a training set of data containing observations (or instances) whose category membership is known. The classification problems have practical applications in many areas of life, such as pattern recognition, regression forecasting, data processing, protein classification problem, meteorology, etc., [5, 6, 8, 26]. There are many methods for solving the classification problems, such as decision trees, neural networks, clustering algorithm, expectation-maximization (EM), support vector machine (SVM), etc., [3, 12]. Recently, a lot of attention has been paid to establishing the models and the algorithms which give a good trade-off of the better classification correctness versus the less computational efforts. Moreover, the more attention focuses on the simpler structure of models and the more sparse the solution for the classification problems is. The reader may be referred to the papers [17], Proximal SVM (PSVM) [11], etc.

SVM plays a key role in the classification problems and is used to transform the classification problems into an optimization problem. SVM has been widely used in many real-world problems such as pattern recognition, regression forecasting, data processing, etc., [1, 15, 16, 19, 20]. It is also an important achievement of machine learning theory in recent years. In 1995, Cortes and Vapnik formally proposed SVM based on statistical learning theory [9]. Vapnik first proposed the C-SVM and then gave the C-SVM with secondary relaxation variable [9, 27], where C is a regularization parameter to control the balance between the size of margin and the misclassification error. Then Schölkopf put forward the ν-SVM [23] to simplify the parameters adjustment of SVM, where ν is the upper bound of misclassification errors of the training samples, and simultaneously the lower bound of support vectors. From then on, there were a lot of extended SVMs, including one-class SVM [22, 25], Reduced SVM (RSVM) [18], Weighted SVM (WSVM) [8], LS-SVM (least squares SVM) [24], TSVM (Twin SVM) [17], PSVM [11], etc.

There are several standard methods for solving SVM such as modified gradient projection algorithm and interior-point methods, at least for small and medium size problems [4]. The alternating direction method of multipliers (ADMM) is mainly used in optimization problems with high dimension, and its initial point does not need to be feasible [2, 13, 14]. It is applicable in many cases, such as statistical learning, image processing, sensor networks, etc [4, 10, 13].

The original consensus problem is to deal with the optimization problem min f(x) = ∑ N i=1 f i (x) with the additive objective function such as ∑ N i=1 f i (x). Here \(x\in {\mathbb{R}}^{n}\) is called the global variable. Consensus can be viewed as a simple technique for turning the additive objective into separable objective which splits easily by introducing the local variables x i , i = 1, ···, N, that is, min f(x) = ∑ N i=1 f i (x i ) subject to x i  − z = 0, i = 1, ···, N. Boyd et al. pointed out that consensus problems have a long history, especially in conjunction with ADMM, (see, Boyd et al. [4]). Consensus models are usually used in the parallel optimization problems and require agreement among a number of processes for the same value. For a useful recent discussion of consensus algorithms, readers may refer to [23] and the references therein.

Motivated by recent attention in the context of consensus problems and algorithms, we note that the objective function in PSVM is \(\|w\|_{2}^{2}=\sum w_{i}^{2}\), and it can be handled by its own coordinate w i corresponding to the element x i in the train set. In this paper, we convert the original PSVM to the unconstrained form and also add 2l equality constraints to the model, where l is the number of the sample points. Then, we establish two consensus proximal support vector machines (PSVMs) models. The first one is to separate the objective functions into individual convex functions by using the number of the sample points of the training set. The constraints contain two types of the equations with global variables and local variables corresponding to the consensus points and sample points, respectively. To get more sparse solutions, the second one is consensus l 1−l 2 PSVM in which a sum of absolute values of global variables are added to the objective function. Consensus least squares SVM was proposed before [19]. The difference between our consensus PSVM and consensus LSSVM is that our formulation leads to the strong convex objective functions, and thus we add more l equality constraints to the model, where l means the number of sample points. While consensus l 1−l 2 PSVM aims to find a trade-off between classification performance and sparse solutions. These two consensus PSVMs are solved by the ADMM. As we mentioned above, consensus problem is to solve the problem in which a single global variable can be split into l parts. Therefore, ADMM can be derived either directly from the augmented Lagrangian or simply as a special case of the constrained optimization problem. Furthermore, they are implemented by the real-world data taken from the University of California, Irvine machine learning repository (UCI repository) and are compared with the existed models such as ℓ1-PSVM, ℓ p -PSVM, GEPSVM, PSVM, and SVM-light. Numerical results show that our models outperform to others with the classification accuracy and the sparse solutions.

The paper is organized as follows. In Sect. 2, we briefly recall the basic concepts of SVM and PSVM for binary classification problems. In Sect. 3, we present two consensus PSVMs that are consensus PSVM and consensus ℓ1−ℓ2 PSVM. The second model contains an ℓ1-norm term and an ℓ2-norm term. The ℓ2-norm term is responsible for the good classification performance, while ℓ1-norm term plays an important role on finding sparse solutions. Section 4 investigates the performance of the two models via ADMM and compares them with other five SVMs by the numerical examples of the real-world data taking from the UCI Repository. Finally, we conclude the paper and briefly give the goal of the future research in Sect. 5.

Notation

\(\mathbb{R}^{n}\) stands for the set of n-dimensional real vectors. \({\parallel\cdot\parallel}_{1}\) and \({\parallel\cdot\parallel}_{2}\) denote the ℓ1-norm and ℓ2-norm, respectively. The soft thresholding operator S is the proximity operator of ℓ1-norm. The penalty parameter ρ > 0 is used as the step size, and in this paper, we set ρ = 1. \(\varepsilon _{i}^{\text{primal}}\) and \(\varepsilon _{i}^{\text{dual}}, i=1,2\) means feasibility tolerances for the primal conditions and the dual ones. In the numerical experiments, we set \(\varepsilon _{i}^{\text{primal}}=10^{-4}\) and \(\varepsilon _i^{\text{dual}}=10^{-3}, i=1,2\), respectively.

2 Standard SVM and PSVM

In this section, we briefly recall some preliminaries of SVM and PSVM for binary classification problems. We will not go into the details of the SVM and PSVM, and readers may refer to [9, 11, 27].

First, we recall the linear separated case of a binary classification. Given a training set \(\{(x_{1},y_{1}),\cdots,(x_{l},y_{l})\}\subseteq {\mathbb{R}}^{n}\times \{-1,+1\}\), it is linearly separable if there exists a hyperplane w T x + b = 1 such that

$$ \begin{array}{lll} w^{\text{T}}x_{i}+b \geqslant 1 & if\; y_{i}=+1 &i=1,\cdots,l \\ w^{\text{T}}x_{i}+b \leqslant -1 & if\; y_{i}=-1 &i=1,\cdots,l \end{array} $$

Thus, the hard-margin SVM [9] can be formulated as follows:

$$ \begin{aligned} \mathop{\min}\limits_{w,b}\, &\frac{1}{2}\left\| w \right\|_{2}^2 \\ \hbox{s.t.}\, &y_{i}(w^{\text{T}}x_{i}+b)\geqslant 1 \quad i=1,\cdots,l \end{aligned} $$
(2.1)

where \(x_{i}\in {\mathbb{R}}^{n}, y_{i}\in \{-1,1\}, i=1,\cdots,l, w\in {\mathbb{R}}^{n}, b\in {\mathbb{R}}\). Geometrically the hard-margin SVM is illustrated in Fig. 1. When there exist wild points, the case is the nonlinear separated case. Introducing a slack variables \(\xi_{i},i=1,\cdots,l\) and a fixed penalty parameter C > 0 to the objective function of the hard-margin SVM, it can be converted to the soft-margin SVM [9] as follows:

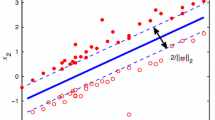
$$ \begin{aligned} \mathop{\min }\limits_{w,b,\xi } & \,\frac{1}{2}\left\| w \right\|_{2}^2 + C\sum\limits_{i = 1}^l {\xi _i} \\ \rm{s.t.} &\,y_{i}({w^\text{T}}{x_i} + b) \geqslant 1 - {\xi _i} \quad i=1,\cdots,l \\ &{\xi _i} \geqslant 0 \quad i=1,\cdots,l \end{aligned} $$
(2.2)

where \(x_{i}\in {\mathbb{R}}^{n}, y_{i}\in \{-1,1\}, \xi _i\in {\mathbb{R}}, \quad i=1,\cdots,l, w\in {\mathbb{R}}^{n}\), and \(b\in {\mathbb{R}}\). Figure 2 shows the geometric interpretation of the soft-margin SVM. The PSVM formulation is as good as the soft-margin SVM formulation with the advantage such as strong convexity of the objective function. It can give the explicit exact solution, whereas it is impossible to do that in the soft-margin SVM formulation. The formulation of PSVM [11] is as following.

$$ \begin{aligned} \mathop{\min}\limits_{w,b,\xi } &\,\frac{1}{2}\left( {\left\| w \right\|_2^2 + {b^2}} \right) + \frac{C}{2}\sum\limits_{i = 1}^l {\xi_i^2} \\ \hbox{s.t.} &\,y_{i}\left( {w^{\text{T}}x_{i} + b} \right) = 1 - \xi_{i},\quad i = 1, \cdots ,l \end{aligned} $$
(2.3)

where \(x_{i}\in {\mathbb{R}}^{n}, y_{i}\in \{-1,1\}, \eta_{i}\in {\mathbb{R}}, i=1,\cdots,l, w\in {\mathbb{R}}^{n},\) and \(b\in {\mathbb{R}}\). From Fig. 3, we can see that PSVM also aims to find the largest distance between two dashed lines, i.e., the bounding planes w T x + b = 1 and w T x + b =  −1. Here minimizing \(\frac{C}{2}\sum\limits_{i = 1}^l {\xi_i^2}\) means that the bounding planes are located as far as possible in the middle of positive points and negative points, respectively.

Fig. 1
figure 1

The points of the circle class (the negative samples) and the plus symbol class (the positive samples) with a full line showing a separation hyperplane w T x + b = 0 between them

Full size image
Fig. 2
figure 2

The points of the circle class (the negative samples) and the plus symbol class (the positive samples) with a full line showing a separation hyperplane w T x + b = 0 between them

Full size image
Fig. 3
figure 3

The points of the circle class (the negative samples) and the plus symbol class (the positive samples) with a full line showing a separation hyperplane w T x + b = 0 between them

Full size image

3 Two Consensus PSVM and Their Training Approaches

In this section, we start by reformulating the first consensus PSVM model. Then we consider the sparse solutions of the consensus PSVM and present the second one called the l 1−l 2 consensus PSVMs in which the objective function contains an ℓ1-norm term and an ℓ2-norm term. The ℓ2-norm term is responsible for the good classification performance, while ℓ1-norm term plays an important role on finding sparse solutions. The idea of consensus is based on parallel computing in which computational efforts can be shorted for solving large or complex problems. The consensus models are usually used in the parallel optimization.

3.1 Consensus PSVM

By introducing two types of the variables, the local variables \(w_i\in {\mathbb{R}}^{n}, b_i\in {\mathbb{R}}, i=1,\cdots,l\) and global variables \(z\in {\mathbb{R}}^{n}, d\in {\mathbb{R}}\). The original PSVM (2.3) can be converted to the consensus PSVM as follows:

$$ \begin{aligned} \mathop{\min}\limits_{w,b,z,d} & \,\lambda \left\| z \right\|_{2}^2 + \lambda {d^2} + \frac{1}{l}\sum\limits_{i = 1}^l {\left(1 - y_{i}\left(w_{i}^{\text{T}}x_{i} + b_{i} \right) \right)}^{2} \\ \hbox{s.t.} & \,w_{i} = z,\quad i = 1, \cdots ,l, \\ & b_i = d,\quad i = 1, \cdots ,l, \end{aligned} $$
(3.1)

where \(\lambda>0, x_{i}\in {\mathbb{R}}^{n}, y_{i}\in \{-1,1\}, w_{i}\in {\mathbb{R}}^{n}, b_{i}\in {\mathbb{R}},\quad i=1,\cdots,l, z\in {\mathbb{R}}^{n}, d\in {\mathbb{R}}\).

Obviously, the objective function is separable in (3.1). The splitting technique can be used to convert the implicit expression into the explicit one, and thus, the model contains more information. Moreover, (3.1) is called the global consensus model since all the local variables should be equal. We expect that the model would produce higher classification accuracy and computational efficiency than single model strategies.

The abbreviated form of consensus PSVM can be expressed as

$$ \begin{aligned} \mathop{\min}\limits_{w,b,z,d} & \,\sum\limits_{i = 1}^{l} f_{i}\left( w_{i},b_{i} \right) + g\left(z,d\right) \\ \rm{s.t.} &\,w_{i} - z = 0, \quad i = 1, \cdots ,l, \\ &b_{i} - d = 0, \quad i = 1, \cdots ,l, \end{aligned} $$
(3.2)

where \(\sum\limits_{i = 1}^{l} f_{i}\left(w_{i},b_{i} \right) = \frac{1}{l}\sum\limits_{i = 1}^{l} \left(1 - y_{i}\left( w_{i}^{\text{T}} x_{i} + b_{i} \right) \right)^{2}, g\left(z,d\right) = \lambda \left\| z \right\|_{2}^{2} + \lambda d^{2}.\)

Let α and β be the Lagrangian multipliers for the equality constraints in (5). The augmented Lagrangian function can be expressed as follows:

$$ L\left(w,b,z,d,\alpha ,\beta\right)= \sum\limits_{i = 1}^{l} f_{i}\left(w_{i},b_{i}\right) + g\left(z,d\right) +\sum\limits_{i = 1}^l {\alpha _{i}^{\text{T}}\left(w_{i} - z \right)} + \frac{\rho }{2}\sum\limits_{i = 1}^l {\left\| {{w_i} - z} \right\|_2^2}+ \sum\limits_{i = 1}^l {\beta _i^{\text{T}}\left( {{b_i} - d} \right)} + \frac{\rho }{2}\sum\limits_{i = 1}^l {\left\| {{b_i} - d} \right\|_2^2} $$

Here, we primarily give the optimal conditions of consensus PSVM,

$$ \left\{ \begin{array}{l} \nabla_{w_{i}}f_{i}\left(w_{i}^{*},b_{i}^{*}\right) + \alpha_{i}^{*} + \rho \left(w_{i}^{*} -z^{*}\right) = 0, \,i = 1, \cdots ,l,\\ \nabla_{b_{i}}f_{i}\left(w_{i}^{*},b_{i}^{*} \right) + \beta _{i}^{*} + \rho \left(b_{i}^{*} - d^{*} \right) = 0, \,i = 1, \cdots ,l,\\ \nabla _{z}g\left(z^{*}, d^{*}\right) + \sum\limits_{i = 1}^{l} \left(-\alpha_{i}^{*} - \rho \left(w_{i}^{*} - z^{*} \right) \right) = 0,\\ \nabla _{d}g\left(z^{*}, d^{*} \right) + \sum\limits_{i = 1}^{l} \left(- \beta_{i}^{*} - \rho \left(b_{i}^{*} - d^{*} \right) \right) = 0,\\ w_{i}^{*} - z^{*} = 0, \,i = 1, \cdots ,l,\\ b_{i}^{*} - d^{*} = 0, \,i = 1,\cdots ,l, \end{array}\right. $$

Subsequently, we give the stopping criteria due to the optimal conditions,

$$ \begin{aligned} 0 &= \nabla _{z}g(z^{k + 1},d^{k}) - \sum\limits_{i = 1}^{l} {\alpha _{i}^{k}} - \sum\limits_{i = 1}^{l} \rho \left(w_{i}^{k + 1} - z^{k + 1} \right) \\ &= \nabla _{z}g(z^{k + 1},d^{k}) - \sum\limits_{i = 1}^l {\alpha _{i}^k} - \sum\limits_{i = 1}^l {\rho \hat{r}_{i}^{k + 1}} \\ &= \nabla _{z}g(z^{k + 1},d^{k}) - \sum\limits_{i = 1}^l {\alpha _i^{k + 1}} \end{aligned} $$

and

$$ \begin{aligned} 0 &= \nabla _{d}g(z^{k + 1},d^{k + 1}) - \sum\limits_{i = 1}^{l} \beta _{i}^{k} - \sum\limits_{i = 1}^{l} \rho \left(b_{i}^{k + 1} - d^{k + 1} \right) \\ &= \nabla _{d}g(z^{k + 1},d^{k + 1}) - \sum\limits_{i = 1}^{l} \beta _{i}^{k} - \sum\limits_{i = 1}^{l} \rho \hat{s}_{i}^{k + 1} \\ &= \nabla _{d}g(z^{k + 1},d^{k + 1}) - \sum\limits_{i = 1}^{l} \beta _{i}^{k + 1} \end{aligned} $$

Obviously, the third and the fourth conditions are always satisfied.

The first and the second conditions involve the dual feasibility, so we have

$$ \begin{aligned} 0 &= \nabla _{w_{i}}f_{i}\left(w_{i}^{k + 1},b_{i}^{k} \right) + \alpha _{i}^{k} + \rho \left(w_{i}^{k + 1} - z^{k} \right) \\ &= \nabla _{w_{i}}f_{i}\left(w_{i}^{k + 1},b_{i}^{k}\right) + \alpha _{i}^{k} + \rho \left(w_{i}^{k + 1} - z^{k + 1}\right) + \rho \left(z^{k + 1} - z^{k} \right) \\ &= \nabla _{w_{i}}f_{i}\left(w_{i}^{k + 1},b_{i}^{k} \right) + \alpha _{i}^{k + 1} + \rho \left(z^{k + 1} - z^{k} \right), \quad i = 1, \cdots ,l \end{aligned} $$

and

$$ \begin{aligned} 0 &= \nabla _{b_{i}}f_{i}\left(w_{i}^{k + 1},b_{i}^{k + 1} \right) + \beta _{i}^{k} + \rho \left(b_{i}^{k + 1} - d^{k} \right) \\ &=\nabla _{b_{i}}f_{i}\left(w_{i}^{k + 1},b_{i}^{k + 1} \right) + \beta _{i}^{k} + \rho \left(b_{i}^{k + 1} - d^{k + 1} \right) + \rho \left(d^{k + 1} - d^{k} \right) \\ &= \nabla_{b_{i}}f_{i}\left(w_{i}^{k + 1},b_{i}^{k + 1} \right) + \beta _{i}^{k + 1} + \rho \left(d^{k + 1} - d^{k} \right), \quad i = 1, \cdots ,l, \end{aligned} $$

where \(r = \rho \left(z^{k + 1} - z^{k} \right)\) and \(s = \rho \left(d^{k + 1} - {d^k}\right)\) are called the dual residuals.

From the last two conditions, we can get the primal residuals as follows:

$$ \hat{r}_{i} = w_{i} - z, \hat{s}_{i} = b_{i} - d, \quad i = 1,\cdots,l. $$

Accordingly, the primal residuals can be written as

$$ \left\| \hat{r} \right\|_{2}^{2} = \sum\limits_{i = 1}^{l} \left\| w_{i} - z\right\|_{2}^{2}, \left\| \hat{s} \right\|_{2}^{2} = \sum\limits_{i = 1}^{l} \left\| b_{i} - d \right\|_{2}^{2}. $$

And therefore, the stopping criteria can be expressed as,

$$ \left\| \hat{r} \right\|_{2}^{2} \leqslant \varepsilon _{1}^{\text{primal}}, \left\| \hat{s} \right\|_{2}^{2} \leqslant \varepsilon _{2}^{\text{primal}}, \left\| r \right\|_{2}^{2} \leqslant \varepsilon _{1}^{\text{dual}}, \left\| s \right\|_{2}^{2} \leqslant \varepsilon _{2}^{\text{dual}}. $$

Now we can establish the consensus PSVM algorithm for classification problems,

Algorithm for Consensus PSVM

Given a training set \(T=\{(x_{1},y_{1}),\cdots,(x_{l},y_{l})\}\subseteq {\mathbb{R}}^{n}\times \{-1,1\}\) and select parameters λ and ρ. With the given iterate t k, we can get the new iterate t k+1 as follows:

  • Step 1. Update \(\tilde{t}^{k}=\{\tilde{w}_1^{k},\cdots,\tilde{w}_l^{k},\tilde{b}_1^{k},\cdots, \tilde{b}_l^{k},\tilde{z}^{k},\tilde{d}^{k},\tilde{\alpha}_1^{k}, \cdots,\tilde{\alpha}_l^{k},\tilde{\beta}_1^{k},\cdots,\tilde{\beta}_l^{k}\}\) in the alternating order by ADMM iterative scheme.

    $$ \begin{aligned} \tilde{w}_i^{k + 1} &:= \mathop{\arg \min }\limits_{w_{i}} \Big( \frac{1}{l}\left(1 - y_{i}\left(w_{i}^{\text{T}}x_{i} + b_{i}^{k} \right)\right)^{2} + {\alpha_{i}^{k}}^{\text{T}}\left(w_{i} - z^{k} \right) + \frac{\rho}{2}\left\|w_{i} - z^{k} \right\|_{2}^{2} \Big), \quad i = 1,\cdots,l,\\ \tilde{b}_{i}^{k + 1} &:= \mathop{\arg \min}\limits_{b_{i}} \Big( \frac{1}{l}\left(1 - y_{i}\left((\tilde{w}_{i}^{k + 1})^{\text{T}}x_{i} + b_{i} \right) \right)^{2} + {\beta_{i}^k}^{\text{T}}\left(b_{i} - d^{k} \right) + \frac{\rho}{2}\left\| b_{i} - d^{k} \right\|_{2}^{2} \Big), \quad i = 1,\cdots,l,\\ \tilde{z}^{k + 1} &:= \mathop{\arg\min}\limits_{z} \left( \lambda \left\| z \right\|_{2}^{2} + \sum\limits_{i = 1}^{l} \left(- {\alpha_{i}^{k}}^{\text{T}}z + \frac{\rho }{2}\left\|\tilde{w}_{i}^{k + 1} - z \right\|_{2}^{2} \right) \right), \\ \tilde{d}^{k + 1} &:=\mathop{\arg\min}\limits_{d} \left(\lambda d^{2} + \sum\limits_{i= 1}^{l}\left(- {\beta_{i}^{k}}^{\text{T}}d + \frac{\rho }{2}\left\| \tilde{b}_{i}^{k + 1} - d \right\|_{2}^{2}\right) \right), \\ \tilde{\alpha} _i^{k + 1} &:= \alpha _i^k + \rho \left( \tilde{w}_{i}^{k + 1} - \tilde{z}^{k + 1} \right), \quad i = 1, \cdots,l,\\ \tilde{\beta} _{i}^{k + 1} &:= \beta _i^k + \rho \left( \tilde{b}_{i}^{k + 1} - \tilde{d}^{k + 1} \right), \quad i = 1, \cdots,l. \end{aligned} $$

  • Step 2. Stopping criteria. Quit if the following conditions are satisfied.

    $$ \left\|\hat{r} \right\|_{2}^{2} \leqslant \varepsilon_{1}^{\text{primal}}, \left\|\hat{s} \right\|_{2}^{2} \leqslant \varepsilon_2^{\text{primal}}, \left\| r \right\|_{2}^{2} \leqslant \varepsilon_1^{\text{dual}}, \left\| s \right\|_{2}^{2} \leqslant \varepsilon _2^{\text{dual}}. $$

    Then, we get the solution \(t^{*}=\{w_1^{*},\cdots,w_l^{*},b_1^{*},\cdots,b_l^{*}, z^{*},d^{*},\alpha_1^{*},\cdots,\alpha_l^{*},\beta_1^{*},\cdots,\beta_l^{*}\}\).

  • Step 3. Construct the decision function as \(f\left( x \right) = \hbox{sgn} \left( (z^{*})^{\text{T}}{x}+ d^{*} \right)\).

According to the above algorithm for Consensus PSVM, it is evident that after each iteration t k, we can compute the consensus point \((\tilde{z}^{k+1},\tilde{d}^{k+1})\), in particular when the iteration reaches the stopping criteria, an optimal or near optimal consensus point (z *, d *) can be obtained.

What’s more, we briefly analyze the computational complexity of our methods. The complexity mainly relies on ADMM iterative scheme. For each iteration, \(w_{1},\cdots,w_{l}\) are solved at the same time. After solving \(w_{1},\cdots,w_{l}, b_{1},\cdots,b_{l}\) are also solved at the same time. Then z, d can be solved. At last, \(\alpha_{1},\cdots,\alpha_{l},\beta_{1},\cdots,\beta_{l}\) can be also solved simultaneously. Thus, each iteration contains only 4 flops. Compared with PSVM algorithm [11], the total cost of our methods is also small.

3.2 Consensus ℓ1−ℓ2 PSVM

To get more sparse solutions, we add a term of absolute values of global variables z to the objective function of consensus PSVM 5, then ℓ1−ℓ2 PSVM can be reformulated as following:

$$ \begin{aligned} \mathop{\min}\limits_{w,b,z,d} & \,\lambda \left\| z \right\|_{1} + \left(1 - \lambda\right)\left\| z \right\|_{2}^{2} + (1-\lambda) d^{2} + \frac{1}{l}\sum\limits_{i = 1}^{l} \left(1 - y_{i}\left( w_{i}^{{\text{T}}}x_{i} + b_{i} \right) \right)^{2} \\ \hbox{s.t.} &\,w_{i} = z, \quad i = 1, \cdots ,l, \\ & b_{i} = d, \quad i = 1, \cdots ,l, \end{aligned} $$
(3.3)

where \(\lambda \in \left[ {0,1} \right], x_{i}\in {\mathbb{R}}^{n}\), \(y_{i}\in \{-1,1\}, w_{i}\in {\mathbb{R}}^{n}, b_{i}\in {\mathbb{R}}\), \(i=1,\cdots,l, z\in {\mathbb{R}}^{n}, d\in {\mathbb{R}}\).

The augmented Lagrangian function of (6) can be expressed as

$$ \begin{aligned} L\left(w,b,z,d,\alpha ,\beta\right)&= \lambda \left\| z \right\|_{1} + \left(1 - \lambda\right)\left\| z \right\|_{2}^{2} + (1-\lambda) d^{2}+ \frac{1}{l}\sum\limits_{i = 1}^{l} \left(1 - y_{i}\left(w_{i}^{\text{T}}x_{i} + b_{i} \right)\right)^{2} + \sum\limits_{i = 1}^{l} \alpha _{i}^{\text{T}}\left(w_{i} - z \right)\\ & + \frac{\rho }{2}\sum\limits_{i = 1}^{l} \left\|w_{i} - z \right\|_{2}^{2} + \sum\limits_{i = 1}^{l} \beta _{i}^{\text{T}}\left(b_{i} - d \right) + \frac{\rho }{2}\sum\limits_{i = 1}^{l} \left\|b_{i} - d \right\|_{2}^{2} \end{aligned} $$

Thus, the iterative scheme of ADMM for solving (6) is as follows:

$$ \begin{aligned} w_{i}^{k + 1} &:= \mathop{\arg\min}\limits_{w_{i}} \Big( \frac{1}{l}\left(1 - y_{i} \left(w_{i}^{\text{T}}x_{i} + b_{i}^{k} \right)\right)^{2} + {\alpha_{i}^{k}}^{\text{T}} \left(w_{i} - z^{k} \right) + \frac{\rho }{2}\left\|w_{i} - z^{k} \right\|_{2}^{2} \Big), \,i=1,\cdots,l,\\ b_{i}^{k + 1} &:= \mathop{\arg\min}\limits_{b_{i}} \Big(\frac{1}{l} \left(1 - y_{i}\left((w_{i}^{k + 1})^{\text{T}}x_{i} + b_{i} \right)\right)^{2} + {\beta_{i}^{k}}^{\text{T}}\left(b_{i} - d^{k} \right)+ \frac{\rho }{2}\left\|b_{i}-d^{k} \right\|_{2}^{2} \Big), \,i=1,\cdots,l,\\ z^{k + 1} &:= S_{\frac{\lambda}{2(1 - \lambda ) + \rho l}}\bigg(\frac{\sum\limits_{i = 1}^{l} \rho w_{i}^{k + 1}+ \sum\limits_{i = 1}^{l} \alpha_{i}^{k}}{2(1 - \lambda ) + \rho l}\bigg),\\ d^{k + 1}&:=\mathop{\arg\min}\limits_d \left((1-\lambda) d^{2} + \sum\limits_{i = 1}^{l} \left( - {\beta_{i}^{k}}^{\text{T}}d + \frac{\rho}{2}\left\| b_{i}^{k + 1} - d \right\|_{2}^{2}\right) \right), \\ \alpha _{i}^{k + 1}&:=\alpha _{i}^{k} + \rho \left(w_{i}^{k + 1} - z^{k + 1} \right), \,i = 1, \cdots ,l,\\ \beta _{i}^{k + 1}&:=\beta _{i}^{k} + \rho \left(b_{i}^{k + 1} - d^{k + 1} \right), \,i = 1, \cdots ,l. \end{aligned} $$

Compared with ( 3.1), the ADMM iterative scheme is different in z-iteration,

$$ \begin{aligned} 1^{\circ} \quad z_{j}&>0, \\ &\,0 = 2\left(1 - \lambda\right)z_{j} + \lambda - \sum\limits_{i = 1}^{l} \alpha _{ij} - \sum\limits_{i = 1}^{l} \rho \left( w_{ij} - z_{j} \right), \\ &\,z_{j} = \frac{\sum\limits_{i = 1}^{l} \rho w_{ij} + \sum\limits_{i = 1}^{l} \alpha _{ij} - \lambda}{2\left(1 - \lambda\right) + \rho l}; \\ 2^{\circ}\quad z_{j}&<0,\\ &\,0 = 2\left(1 - \lambda\right)z_{j} - \lambda - \sum\limits_{i = 1}^{l} \alpha _{ij} - \sum\limits_{i = 1}^{l} \rho \left( w_{ij} - z_{j} \right), \\ &\,z_{j} = \frac{\sum\limits_{i = 1}^{l} \rho w_{ij} + \sum\limits_{i = 1}^{l} \alpha _{ij} + \lambda}{2\left(1 - \lambda\right) + \rho l}; \\ 3^{\circ}\quad z_{j}&=0,\\ &\,0= 2\left(1 - \lambda\right)z_{j} + \lambda h_{j} - \sum\limits_{i = 1}^{l} \alpha _{ij} - \sum\limits_{i = 1}^{l} \rho \left(w_{ij} - z_{j} \right),\\ &\,0= \lambda h_{j} - \sum\limits_{i = 1}^{l} \alpha _{ij} - \sum\limits_{i = 1}^{l} \rho w_{ij}, \\ &\, \left| \sum\limits_{i = 1}^{l} \rho w_{ij}+\sum\limits_{i = 1}^{l} \alpha _{ij} \right| \leqslant \left| \lambda\right|, \end{aligned} $$

where \(j=1,\cdots,n, \left\| {{h_j}} \right\|_2^2 \leqslant 1\).

At the last iteration, we can get z *,

$$ z_{j}^{*} = \max \left\{\frac{1}{2\left(1 - \lambda \right) + \rho l}\left(\left|\sum\limits_{i = 1}^{l} \rho w_{ij}^{*}+ \sum\limits_{i = 1}^{l} \alpha _{ij}^{*}\right| - \lambda \right),0 \right\}\hbox{sgn} \left(\frac{\sum\limits_{i = 1}^{l} \rho w_{ij}^{*}+ \sum\limits_{i = 1}^{l} \alpha _{ij}^{*} }{2\left(1 - \lambda\right) + \rho l} \right) $$

where \(j=1,\cdots,n\).

From the definition of the soft thresholding operator S, z * is given by,

$$ z_j^{*} = \left\{ \begin{array}{c} \frac{1}{2\left(1 -\lambda\right) + \rho l}\left(\sum\limits_{i = 1}^{l} \rho w_{ij}^{*} + \sum\limits_{i = 1}^{l}\alpha _{ij}^{*}- \lambda \right),\,\sum\limits_{i = 1}^{l} \rho w_{i}^{*}+ \sum\limits_{i = 1}^{l} \alpha _{i}^{*}>\lambda,\\ 0,\quad\quad\quad \left|\sum\limits_{i = 1}^l \rho w_{i}^{*}+ \sum\limits_{i = 1}^{l} \alpha _{i}^{*}\right|\leq \lambda,\\ \frac{1}{2\left(1 - \lambda\right) + \rho l}\left(\sum\limits_{i = 1}^{l} \rho w_{ij}^{*} + \sum\limits_{i = 1}^{l} \alpha _{ij}^{*} + \lambda \right),\,\sum\limits_{i = 1}^{l} \rho w_{i}^{*}+ \sum\limits_{i = 1}^{l} \alpha _{i}^{*}< -{\lambda}, \end{array} \right. $$

where \(j=1,\cdots,n\).

Equivalently, \({z^*} = S_{\frac{\lambda}{2(1 - \lambda ) + \rho l}}\left(\frac{\sum\limits_{i = 1}^{l} \rho w_{i}^{*}+ \sum\limits_{i = 1}^{l} \alpha _{i}^{*}}{2(1 - \lambda ) + \rho l} \right)\).

4 Numerical Experiments

In this section, we firstly report results on five synthetic datasets in Table 1 in terms of the classification accuracy. Then eight real-world datasets are taken from the UCI Repository, including Heart disease, Australian credit approval, Sonar, Pima Indians diabetes, Spambase, Mushroom, BUPA liver, and Ionosphere (Table 2). They are used to evaluate the classification performance and the execution time of our approaches in Tables 3, 4, and 5, respectively. Compared with real-world datasets, the dimension of synthetic datasets is lower, and the number of sample points is smaller. Two classes of sample points are selected better in synthetic datasets, and thus, they are easier to separate. While sample points of real-world datasets may be crowded together, and they are hard to be controlled by the artificial means (Table 6).

Table 1 Performance of classification on five problems with synthetic data
Full size table
Table 2 Datasets from the UCI Repository
Full size table
Table 3 Classification accuracy rates obtained by consensus PSVM, consensus ℓ1−ℓ2 PSVM, ℓ p -PSVM, and ℓ1-PSVM [7]
Full size table
Table 4 Classification accuracy rates obtained by consensus PSVM, consensus ℓ1−ℓ2 PSVM, GEPSVM, PSVM, and SVM-light [21]
Full size table
Table 5 Average time on the four datasets obtained by consensus PSVM, consensus ℓ1−ℓ2 PSVM, PSVM [11]
Full size table
Table 6 Sparse solutions and classification accuracy obtained by consensus ℓ1−ℓ2 PSVM and ℓ1-PSVM [7]
Full size table

The consensus PSVM training approaches are implemented on a PC with an Intel Pentium IV 1.73 GHz CPU, 1,024 MB RAM, the Windows XP operating system, and the Matlab 2011a development environment. In the following experiments, we set the penalty parameter ρ = 1 and set the termination tolerances \(\varepsilon _i^{\text{primal}}=10^{-4}\) and \(\varepsilon _i^{\text{dual}}=10^{-3}, i=1,2\), respectively. The variables \(\tilde{w}_i^{0}, \tilde{b}_i^{0}, \tilde{z}^{0}, \tilde{d}^{0}, \tilde{\alpha}_i^{0}\) and \(\tilde{\beta}_i^{0},\, i=1,\cdots,l\) are initialized to zero.

Figure 4 shows the iterative process of the problem with the synthetic data, including 50 positive instances and 50 negative instances. The examples split into ten groups, in the worst case, each group contains only the examples of the same kind. The circles and crosses stand for two different classes.

Fig. 4
figure 4

The iterative process of the problem

Full size image

Firstly, we give the classification accuracy of our approaches for the synthetic data in Table 1.

To demonstrate the performance of our methods better, we report results on the following datasets from the UCI Repository.

We summarize the classification performances of consensus PSVM and consensus ℓ1−ℓ2 PSVM for the real-world data in Tables 3 and 4, respectively. And we also compare them with the numerical results of ℓ1-PSVM, ℓ p -PSVM, GEPSVM, PSVM, and SVM-light in terms of the classification accuracy, respectively.

The numerical results ℓ1-PSVM and ℓ p -PSVM are taken from [7], those of PSVM are from [11] and those of GEPSVM and SVM-Light are from [21], respectively.

The first column of the following tables lists the names of datasets. The second column lists the results obtained by our consensus PSVM and they are labeled in bold which are tried to emphasize the effectiveness.

From Table 3, we can see that our approaches succeed in getting the highest correctness among the approaches.

In addition, we give the iterations of our first approach in Fig. 5.

Fig. 5
figure 5

The iterations of the three problems, including Heart, Australian and Sonar

Full size image

It is obvious that our methods outperform GEPSVM, PSVM, and SVM-light in Table 4. Likewise, we give the iterations of our first approach in Fig. 6.

Fig. 6
figure 6

The iterations of the three problems, including Pima, Spambase, and Mushroom

Full size image

Table 5 contains the execution time of our methods. From the average time, it is evident that our first approach is faster than PSVM.

Finally, we compare our second approach, i.e., consensus ℓ1−ℓ2 PSVM with ℓ1-PSVM [7] in terms of more sparse solutions and higher classification accuracy. For each dataset, including Heart disease, Australian credit approval, and Sonar, we choose the appropriate parameter λ for consensus ℓ1−ℓ2 PSVM. Table 6 shows the numerical results, where \(\sharp\) means the number of zero variables in w * of ℓ1-PSVM and z * of consensus ℓ1−ℓ2 PSVM.

From the experiments, we find that if \(\lambda\rightarrow 0\) in consensus ℓ1−ℓ2 PSVM, the classification performance of the model is better. While \(\lambda\rightarrow 1\) in consensus ℓ1−ℓ2 PSVM, more sparse solutions can be obtained. We also find that the assumption that the larger λ is, the better classification performance of consensus PSVM is not valid.

5 Conclusions and Future Research

We have proposed two consensus PSVMs for the classification problems, and the two consensus PSVMs have been solved by the ADMM. Furthermore, they have been implemented by the real-world data taken from the University of California, Irvine Machine Learning Repository (UCI Repository) and are compared with the existed models such as ℓ1-PSVM, ℓ p -PSVM, GEPSVM, PSVM, and SVM-light. Numerical results show that our models outperform others with the classification accuracy and the sparse solutions. Moreover, we can see that consensus ℓ1−ℓ2 PSVM succeeds in finding more sparse solutions with higher accuracy than ℓ1-PSVM.

We considered the binary linear classification problems and investigated the numerical behaviors of two consensus PVSMs. Our future research will derive the analysis of computation complexity of ADMM for two models thoroughly. Furthermore, we will consider the multi-class classification and nonlinear classification. We presume that the classification performance of consensus PSVM is related to the characteristic structure of the sample points. Thus, our next research will also analyze the relationship among the selection of λ, the characteristic structure of datasets, and the classification performance of consensus PSVM.

The size of datasets used in our numerical test is not large-scale problems in which the dimension of the problems is about hundred millions or more. ADMM has a great advantage in large-scale problems, and it has been applied in [4]. We plan to do such a large-scale experiment under the parallel environment with a distributed system (including several computers) or a clustering in the next step. Thus, our methods can be verified and extended better.