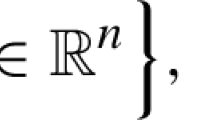Robust and Sparse Support Vector Machines via Mixed Integer Programming

Abstract

In machine learning problems in general, and in classification in particular, overfitting and inaccuracies can be obtained because of the presence of spurious features and outliers. Unfortunately, this is a frequent situation when dealing with real data. To handle outliers proneness and achieve variable selection, we propose a robust method performing the outright rejection of discordant observations together with the selection of relevant variables. A natural way to define the corresponding optimization problem is to use the $\ell _0$ norm and recast it as a mixed integer optimization problem (MIO) having a unique global solution, benefiting from algorithmic advances in integer optimization combined with hardware improvements. We also present an empirical comparison between the $\ell _0$ norm approach, the 0–1 loss and the hinge loss classification problems. Results on both synthetic and real data sets showed that, the proposed approach provides high quality solutions.

1 Introduction

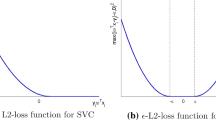
In support vector machine (SVM) classification, the natural way to quantify the performance of a classifier is via the 0–1 loss. This loss is non-convex and considered to be $\mathcal {NP}$-Hard. To this end, the hinge loss, which is convex, was introduced for the first time with [1]. Since then, it has become one of the most popular classifiers. An important reason behind the popularity of SVM is its significant empirical success in various applications such as data mining, engineering and bio-informatics [2]. In Fig. 1, the difference between the hinge-loss and the 0–1 loss is shown.

Considering training examples $x_{i} \in \mathbb {R}^{p}$ with their respective labels $y_{i} \in \{-1,1 \}, \quad i=1,\ldots ,n$. The main goal of SVM is to find a hyperplane (classifier) by introducing hard margins for separable data and soft margins for linearly non-separable data, the purpose of which is to separate data as far as possible from the hyperplane. A decision hyperplane can be defined by an intercept term b and a decision hyperplane normal vector w which is perpendicular to the hyperplane. This vector is commonly referred to, in the machine learning, literature as the weight vector. To choose among all the hyperplanes that are perpendicular to the normal vector, we specify the intercept term b. Because the hyperplane is perpendicular to the normal vector, all points x on the hyperplane satisfy $w^{T}x +b= 0$. Let the margin be defined as the distance from the hyperplane to the closest point across both classes. It can be shown that the width of the margin is equal to $\frac{2}{||w||_{2}}$, thus maximizing this width is equivalent to minimizing the norm $||w||_{2}^{2}$ (or $\frac{1}{2}||w||_{2}^{2}$). To obtain the optimal hyperplane, one should solve the following optimization problem:

$$\begin{aligned} \left. \begin{array}{cll} \displaystyle \min _{w,\xi } &{} \frac{1}{2} \displaystyle \Vert w\Vert _2^2 + C \sum _{i=1}^{n}\xi _{i}&{} \\ \text{ s.t. } &{} \displaystyle y_{i}(w^{T}x+b) \ge 1- \xi _{i} &{} i=1 \ldots n \\ &{} \displaystyle \xi _{i} \ge 0 &{} i=1 \ldots n \end{array} \right. \end{aligned}$$

(1)

where $\xi$ is a slack variable and C is a parameter controlling the trade-off between a large margin and a less constrained violation. The dual problem can be formulated through the use of Lagrange multipliers:

$$\begin{array}{ll} \displaystyle \max _{\alpha } &{} \displaystyle C\sum _{i=1}^{n} \alpha _{i} - \frac{1}{2} \sum _{i=1}^{n} \sum _{i=1}^{n} \alpha _{i} \alpha _{j} y_{i} y_{j}x_{i}^{T}x_{j} \\ \text{ s.t } &{} \displaystyle 0 \le \alpha _{i} \le C \quad \quad i=1,\ldots ,n \\ &{} \displaystyle \sum _{i=1}^{n}\alpha _{i} y_{i}= 0 \end{array}$$

Both the primal and dual are convex quadratic optimization problems. Because the dual problem has fewer decision variables, and the majority of these variables tend to be equal to zero, it is typically the problem solved in practice [3].

While algorithmic advances in integer optimization combined with hardware improvements have resulted in an astonishing 200 billion factor speedup in solving Mixed Integer Optimization (MIO) problems [4], this rapid development of MIO enabled [5] to reformulate the 0–1 loss classification problem as a mixed integer optimization problem and use it to solve small-scale classification problems.

In addition to all benefits listed above, SVM suffers from the existence of outliers and the existence of irrelevant features (especially for high dimensional data sets). Indeed, in the past three decades, the dimensionality of the data involved in machine learning and data mining tasks has increased explosively. Data with extremely high dimensionality has presented serious challenges to existing learning methods [3, 6]. With the presence of a large number of features, a learning model tends to overfit, resulting in their performance degenerates. Feature selection for SVM has been widely studied. For example, [7] introduced an algorithm based upon finding the features which minimize bounds on the leave-one-out error. The search can be efficiently performed via gradient descent. [8] proposed an approach that takes existing theoretical bounds on the generalization error for SVMs instead of performing cross-validation. This is computationally faster than k-fold cross-validation. Additionally, in general, the error bounds have a higher bias than cross-validation in practical situations they often have a lower variance and can thus reduce the overfitting of the wrapper algorithm. A convex energy-based framework to jointly perform feature selection and SVM parameter learning for linear and non-linear kernels was proposed by [9]. They also showed the equivalence between their approach and the $\ell _1$ SVM. In a recent work, [10] developed an efficient method for sparse support vector machines with $\ell _0$ norm approximation. The proposed method approximates the $\ell _0$ minimization through solving a series of $\ell _2$ optimization problems, which can be formulated with dual variables.

Furthermore, in practical applications, training samples are often contaminated by noise and some even have wrong labels [11]. These are usually known as outliers. In order to mitigate the effects of outliers, different approaches have been proposed to improve the robustness of SVM. [12] suggested to use the distance between each training sample and its class center to calculate an adaptive margin so as to reduce the influence of outliers. Weighted SVM (WSVM) or fuzzy SVM was also proposed to deal with outliers [13,14,15]. In WSVM, different weights are assigned to different training samples which can show their importance in the training data set. Several weight functions have been proposed [13,14,15]. [16] presented a novel combinatorial technique, which was called random gradient descent (RGD) tree, to identify and remove outliers in SVM and developed a new algorithm called RGD-SVM. [17] proposed the re-scaled hinge loss which is a monotonic, bounded and non-convex loss. Introducing a Ramp Loss function into one-class SVM optimization to reduce outliers influence was suggested by [18]. Then the outliers are identified and removed from the training set. The final classification surface is obtained on the remaining training samples. [19] introduced a new robust loss function (called $L_q$ loss) based on the concept of quantile and correntropy, which can be seen as an improved version of quantile loss function. To deal with label outliers, [20] introduced a variable $\varDelta y_{i}\in \{0,1\}$ where 1 indicates that the label was incorrect and has in fact been flipped, and 0 indicates that the label was correct. They also introduced a variable $\varDelta x_{i}$ to deal with uncertainty of features. They proposed the use of mixed integer optimization problems to solve the obtained problem. However, the algorithm is not sparse.

To obtain a sparse and robust least squares support vector machines (SR-LSSVM), [21] proposed the SR-LSSVM algorithm to obtain a sparse solution of the robust least squares SVM (R-LSSVM) [22, 23] by applying a low-rank approximation of the kernel matrix.

Contributions:

In this paper, we address the problem of both feature selection and outlier detection using the $\ell _0$ norm. We summarize our contributions in this paper below:

• We present an approach jointly performing feature selection and outlier detection for SVM classification;

• We propose to recast the presented problem as a mixed integer optimization problem which allows the use of efficient solvers (Gurobi) to solve it. Note that the sub-optimality (near-optimality) of the obtained solution is guaranteed even if we terminate the algorithm early;

• We present computational results on both real and synthetic datasets and compare the proposed approach with the classical 0–1 loss and hinge loss classification problems. The results show that the proposed approach provides high quality solutions.

The remainder of the paper is organized as follows. In Sect. 2, we present our approach for variable selection and outliers detection using the $\ell _0$ norm together with its formulation as a mixed integer optimization problem allowing to obtain the global solution. Section 3 reports empirical evidence on synthetic data sets, while empirical results on real data sets were presented in Sect. 4. Finally, the paper is concluded in Sect. 5.

2 Linear Binary Classification

We have n training points, where each input $x_{i}$ has p attributes and is in one of two classes $y_{i} \in \{-1,1\}$. Under linear assumption, the classification function can be expressed as $f(x,w)=w^{T}x+b.$ The goal is to predict the target class $\hat{y} \in \{-1,1\}$ which is defined by:

$$\begin{aligned} \hat{y_{i}}= \left\{ \begin{array}{cl} \displaystyle 1 &{} f(x_{i},w) \ge 0 \\ -1 &{} f(x_{i},w) < 0 \\ \end{array} \right. \end{aligned}$$

(2)

The natural way to quantify the performance of a classifier is using the 0–1 loss function: for a given instance x and a true binary label $y \in \{-1, 1\}$, we incur a loss of 1 if $sign(yf) <0$, and 0 otherwise, that is:

(3)

The 0–1 loss classification problem can be written as

(4)

Problem (4) is non-convex, to this end it has been replaced by a convex surrogate such as the hinge loss. However, advances in integer optimization resulted an impressive speedup in solving mixed integer optimization problems (MIO). To this end, [5] proposed to recast the problem of 0–1 loss classification (4) as a mixed integer optimization problem, that is:

$$\begin{aligned} \left. \begin{array}{cll} \displaystyle \min &{} \displaystyle \sum _{i=1}^{n}l_i &{} \\ \text{ s.t. } &{} \displaystyle y_{i}(w^{T}x_{i}+b) \ge 1- Ml_{i} \\ &{} \displaystyle l \in \{0,1\}^{n} &{} \end{array} \right. \end{aligned}$$

(5)

where M is a sufficiently large constant. Since this formulation suffers from infinite number of optimal solutions and it lacks from the generalization ability, [5] proposed a maximum margin 0–1 loss classifier defined as follows:

$$\begin{aligned} \left. \begin{array}{cll} \displaystyle \min &{}\displaystyle \sum _{i=1}^{n}l_i + Cw^{T}w&{} \\ \text{ s.t. } &{} \displaystyle y_{i}(w^{T}x_{i}+b) \ge 1- Ml_{i} \\ &{} \displaystyle l \in \{0,1\}^{n} &{} \end{array} \right. \end{aligned}$$

(6)

where C is a positive parameter, and showed the efficiency of this approach for small-scale classification problems.

Fig. 1.

Illustration of the hinge loss which is a convex surrogate to the 0–1 loss. The 0–1 loss is shown in blue and the hinge loss is shown in red. (Color figure online)

2.1 Introducing Binary Variables

Variable selection involves the $\ell _0$ norm function to count the number of useful variables. This counting function can be represented by introducing p binary variables $z_{j} \in \{0,1\}$ such that

$$ \Vert w \Vert _0 = \sum _{j=1}^p z_{j} \quad \text{ and } \quad z_{j} = 0 \Leftrightarrow w_j = 0. $$

Different approaches can be used to force $z_{j} = 0 \Leftrightarrow w_j = 0$ into an optimization problem, such as:

• 1. Replace $w_j$ by $z_j w_j$ for $j=1,\dots ,p$,

• 2. Set $|w_j| (1-z_j) = 0$ for $j=1,\dots ,p$ or $\displaystyle \sum _{j=1}^p |w_j| (1-z_j) = 0$,

• 3. Use a big-M constraint, $|w_j| \le M_v z_j$ for $j=1,\dots ,p$ and for some fixed constant $M_v$ large enough (such as $M_v \ge \max _j |w_j^\star |$, $w_j^\star$ being the solution of the optimization problem),

• 4. Treat $z_{j} = 0 \Leftrightarrow w_j = 0$ as logical implications (also called indicator constraints or special ordered set SOS-1). Note that this kind of logical implication can be efficiently handled in a branch-and-bound procedure for MIO problems.

We now discuss and give a short overview of the advantages and drawbacks of each approach. The two first approaches involve nonlinear interaction terms between binary and continuous variables. Their interest lies in the possibility of obtaining interesting continuous relaxations. The main advantage of the big M method (approach 3) is that it brings only linear inequality constraints but the value of the M term needs to be chosen carefully since it shows a great deal of practical influence on the solver performance. Logical implications (approach 4) have the advantage of avoiding these types of problems, as they do not rely on a separate constant value. However, they tend to have weaker relaxations, a condition which may lead to longer solve times in a model. In this paper we will use the third approach for our implementation.

2.2 Our Approach

To deal with the problem of outlier detection, we propose to add a variable $\tau$ so that Problem (1) becomes:

$$\begin{aligned} \left. \begin{array}{cll} \displaystyle \min _{w,\xi ,\tau } &{} \frac{1}{2} \displaystyle \Vert w\Vert _2^2 + C \sum _{i=1}^{n}|\xi _{i}-\tau _i|&{} \\ \text{ s.t. } &{} \displaystyle y_{i}(w^{T}x+b) \ge 1- \xi _{i} &{} i=1 \ldots n \\ &{} \displaystyle ||w||_{0} \le k_{v} &{} \\ &{} \displaystyle ||\tau ||_{0} \le k_{o} &{} \\ &{} \displaystyle \xi _{i} \ge 0 &{} i=1 \ldots n \end{array} \right. \end{aligned}$$

(7)

where the $\ell _0$ norm of a vector w counts the number of nonzeros in w. In this formulation, $k_v$ represents the number of features to be selected while $k_{o}$ represents the number of outliers to be detected. We note that in Problem (7), $\tau (i) \ne 0$ means that the observation “i” is an outlier. In Fig. 2 we can see the effect of an outlier on the hinge-loss classifier. Furthermore, it can be also seen that the MIO approach can still recover the true classifier even in the presence of the outlier.

Fig. 2.

Example of synthetically generated data in two dimensions to show the effect of an outlier on the Hinge-loss classification. The true generating hyperplane in green, the Hinge-loss hyperplane in blue and the MIO approach hyperplane in red. (Color figure online)

2.3 A MIO Formulation

To solve (7) exactly, we recast it as a mixed integer optimization problem. Two binary variables z and t are introduced to control the sparsity levels for w and $\tau$ respectively. The MIO formulation of (7) is as follows:

$$\begin{aligned} \left. \begin{array}{cll} \displaystyle \min _{w,\xi , \tau , t, z, b } &{} \frac{1}{2} \displaystyle \Vert w\Vert _2^2 + C \sum _{i=1}^{n}|\xi _{i}-\tau _{i}|&{} \\ \text{ s.t. } &{} \displaystyle \sum _{j=1}^{p} z_j \le k_v&{} \\ &{} \displaystyle |w_j | \le z_j M_v &{} j=1 \ldots p \\ &{} \displaystyle \sum _{i=1}^n t_i \le k_o &{} \\ &{} \displaystyle |\tau _i | \le t_i M_o &{} i=1 \ldots n \\ &{} \displaystyle y_{i}(w'x_{i}+b) \ge 1 -\xi _{i} &{} i=1 \ldots n\\ &{} \displaystyle \xi _{i} \ge 0 &{} i=1 \ldots n \end{array} \right. \end{aligned}$$

(8)

where $w \in \mathbb {R}^p$, $\tau ,\xi \in \mathbb {R}^n$, $t \in \{0,1\}^n$, $z \in \{0,1\}^p$ and $b \in \mathbb {R}$.

When $k_{v}=0$ and $k_{o}=0$, no feature selection nor outlier detection are performed, the resulting problem is the classical hinge loss classification problem. In the above formula, $M_{v}$ and $M_{o}$ are two big values.

2.4 Solving the Problem Using Gurobi

To overcome the absolute value in the objective function, we introduce two new variables $\alpha ^+$ and $\alpha ^-$, such that $\xi _{i}-\tau _{i}=\alpha ^{+}_{i}-\alpha ^{-}_{i}$, and $|\xi _{i}-\tau _{i}|=\alpha ^{+}_{i}+\alpha ^{-}_{i}$, where $\alpha ^{+}_{i},\alpha ^{-}_{i} \ge 0$ for $i=1 \ldots n$. Then the new obtained problem is as follows:

$$\begin{aligned} \left. \begin{array}{cll} \displaystyle \min _{w,\xi , \tau , t, z, b } &{} \frac{1}{2} \displaystyle \Vert w\Vert _2^2 + C \sum _{i=1}^{n}(\alpha _{i}^{+}+\alpha _{i}^{-})&{} \\ \text{ s.t. } &{} \displaystyle \sum _{j=1}^{p} z_j \le k_v&{} \\ &{} \displaystyle |\beta _j | \le z_j M_v &{} j=1 \ldots p \\ &{} \displaystyle \sum _{i=1}^n t_i \le k_o &{} \\ &{} \displaystyle |\tau _i | \le t_i M_o &{} i=1 \ldots n \\ &{} \displaystyle y_{i}(w'x_{i}+b) \ge 1 -\xi _{i} &{} i=1 \dots n\\ &{} \displaystyle \xi _{i}-\tau _{i}=\alpha ^{+}_{i}-\alpha ^{-}_{i} &{} i=1\ldots n\\ &{} \displaystyle \xi _{i} \ge 0 &{} i=1 \ldots n\\ &{} \displaystyle \alpha _{i}^{+} \ge 0 &{} i=1 \ldots n\\ &{} \displaystyle \alpha _{i}^{-} \ge 0 &{} i=1 \ldots n \end{array} \right. \end{aligned}$$

(9)

2.5 Computational Cost

Fig. 3.

The evolution of the MIO for the breast cancer prognostic data set with $n=194$ and $p=33$. The top panel shows the evolution of upper and lower bounds with time when $k_o=5\%$, while the bottom panel shows the evolution of upper and lower bounds with time when $k_o=2.5\%$. The left panel shows the evolution of upper and lower bounds with time when $k_v=p$, while the right panel shows the evolution of upper and lower bounds with time when $k_v=0.8p$. For all panels, $C=1$.

In Fig. 3, the left panel shows the evolution of upper and lower bounds with time when $k_{v}=p$, while the right panel shows this evolution when $k_{v}=0.8p.$ By comparing the left and the right panels, we can see that the computational time increased from 1200 s to 1800 s (top panel) and from 4 s to 8 s (bottom panel). This means that the value of $k_{v}$ has an influence on the computational cost.

Similarly, the top panel shows the evolution of upper and lower bounds with time when $k_{o}=5\%$, while the bottom panel shows this evolution when $k_{o}=2.5\%$. A simple comparison between the top and the bottom panels sheds the light on how much increasing the value of $k_{o}$ (percentage of outliers to detect) will increase the time needed to certify optimality. Indeed, decreasing $k_{o}$ from 5% to 2.5% resulted a significant decrease of the computational cost, that is from 1200 s to only 4 s, and from 1800 s to only 8 s.

We note that optimal solutions are found in a few seconds in the top panel examples, but it takes 20–30 min to certify optimality via the lower bounds. We also note that the computational time depends on the value of C and the big-M values.

3 Experiments on Synthetic Data Sets

To report the robustness of the proposed approach, we evaluated its performance on synthetically generated data sets. In these experiments, we run the classical hinge-loss classifier and the MIO approach to recover the separating hyperplane classifier.

3.1 Experimental Setup

The experiment uses data in $\mathbb {R}^2$. The data are generated synthetically as follows:

• 1. Twenty-five points are generated as multivariate random normal, N(3.5e, I) where e is the vector of ones and I is the identity matrix. These points are given the label $+1$.

• 2. Twenty-five points are generated as multivariate random normal, $N(-3.5e,I)$. These points are given the label $-1$.

• 3. Ten outlier points are introduced as multivariate random normal N(0, 3I), where 0 is the vector of zeros. The labels are randomly generated as either −1 or +1.

We split the data $75\%$/$25\%$ into training and validation sets, which we used to tune the parameters for both methods. To create the test set, we generated 1000 points in the same way as items 1 and 2 above.

Fig. 4.

Example of synthetically generated data in two dimensions alongside the true generating hyperplane

An example of a data set generated according to this procedure is shown in Fig. 4. By the symmetry of this data generation process, we can see that the true hyperplane separating the two clusters of points is given by $e^{T}x=0$. The goal of the experiment is to show how closely the two methods can recover the truth in the data. We are interested in the following two measures:

• Accuracy: We measure and evaluate the out-of sample accuracy of the trained classifiers on the test set, defined by:

  $$Accuracy=\frac{TP+TN}{TP+FP+TN+FN}$$

  where TP and TN represent the quantity of correct positive and correct negative samples, respectively; FN and FP respectively represent the number of misclassification negative and positive samples. The higher the values of the Accuracy, the better the model is.

• Similarity: To evaluate the ability of each method to recover the truth in the data, we measure the cosine of the angle between the separating hyperplane generated by the methods and the true hyperplane.

We recall that the cosine of the angle $\alpha$ between two vectors u and v is given by:

$$cos(\alpha )=\frac{u.v}{||u||\times ||v||}$$

3.2 Results

Table 1. Performance results for synthetic data experiments

This experiment was repeated 1000 times. We present the means of the two measures for each method in Table 1. The results show that the MIO approach improved the performance of classification. In fact, the accuracy increased by about $1\%$ and that it recovered the truth better than the classical hinge loss classifier (cosine value closer to 1 means smaller angle between hyperplanes and thus better recovery).

4 Experiments on Real Data Sets

To evaluate the effectiveness of the proposed method, we carry out numerical simulations on twelve real-world data sets from the University of California Irvine (UCI) Machine Learning Repository. All experiments are implemented using MATLAB-Gurobi interface. The experiment environment is: PC with Intel Core i7 4700MQ (2.40 GHz) with 8 GB memory. We note that for each problem instance, we used a time limit of 15 min for Gurobi to optimize the classification problem.

We recall that to obtain: the hinge-loss classification problem solution we solved Problem (1), the 0–1 loss problem solution we solved Problem (6). The solution of the MIO approach was found by solving Problem (7).

4.1 Experimental Setup

To evaluate the performance of the proposed approach, we considered two scenarios:

• 1. In the first scenario, $10\%$ of the training and validation sets labels were randomly flipped. The aim is to study the robustness of the mixed integer programming approach.

• 2. In the second scenario, we wanted to mimic real-world setting, hence data sets were not modified.

For both scenarios, each data set was normalized using the min-max scaling and was split randomly into three parts: the training set ($60\%$), the validation set ($20\%$), and the testing set ($20\%$). The training set was used to train each classifier for a variety of combinations of input parameters. For each combination of parameters, the accuracy on the validation set was calculated, and this was used to select the best combination of parameters for each classifier. Finally, the classifier was trained by using these best parameters on the combined training and validation sets, before reporting the out-of-sample accuracy on the testing set. All methods were trained, validated, and tested on the same random splits, and computational experiments were repeated five times for each data set with different splits. For each data set and classification method, we report the average out-of-sample accuracy across all five splits. C was chosen from the set $[10^{-4},10^{-3},\ldots ,10^4]$, $k_v$ was set to $k_v=p$ for the first scenario, and chosen from the set [p, 0.8p, 0.6p] for the second scenario that is no feature selection was performed, $80\%$ and $60\%$ of features are selected respectively. $k_o$ was chosen from the set [0.025n, 0.05n, 0.1n] that is $2.5\%$, $5\%$ and $10\%$ of outliers to be detected respectively.

Table 2. Out of sample accuracy averaged across five seeds for each classification method on all data sets. (first scenario)

Table 3. Out of sample accuracy averaged across five seeds for each classification method on all data sets. (second scenario)

4.2 Results and Discussion

Tables 2 and 3 present the means of the accuracy for each method. We note that n stands for training points and p for attributes. The robustness of the proposed approach is shown in Table 2. In fact, it had a superior performance on 9 data sets, and a tie for one data set, when $10\%$ of labels were flipped. An important remark is that no variable selection was performed during this scenario so the comparison between the MIO approach and the hinge-loss classification is based only on the robustness of the MIO approach. This side by side comparison sheds the light on the significant improvement obtained with the MIO approach.

The second scenario is closer to the real world setting. The data sets are taken without any change or modification. From Table 3, it is clear that the prediction accuracy of our approach is higher than those of the compared algorithms for almost all datasets. We can remark a significant accuracy improvement for some datasets. For example, we obtained about $11\%$ improvement for Arrythmia dataset. In general, it can be seen that the proposed approach provides high quality solutions. We also note that the pairwise comparison of the 0–1 classification against the hinge loss classification shows that none of the two losses dominates the other. Indeed each loss showed better results on six data sets, while a tie was obtained for one data set. An important caveat to emphasize upfront is that the $\ell _0$ robust regression algorithm was given 15 min time limit per problem instance per subset size. This practical restriction may have caused this algorithm to under perform in some cases.

5 Conclusion

In this paper, we propose a method for support vector machine which solves the underlying optimization problem that handles both feature selection and outlier detection. We formulate the problem as a mixed integer optimization problem and use an efficient commercial solver (Gurobi) to solve it. Furthermore, we present an empirical comparison between this method, the classical hinge-loss and the 0–1 loss classification methods. The experimental results have verified the superior performance of the proposed method. In terms of computational efficiency, the MIO solution can already be adopted for relatively small data sets. For the high dimensional case, a screening procedure would be suggested to reduce the computational cost.