Manifold proximal support vector machine with mixed-norm for semi-supervised classification

Abstract

Since labeling all the samples by the user is time-consuming and fastidious, we often obtain a large amount of unlabeled examples and only a small number of labeled examples in classification. In this context, the classification is called semi-supervised learning. In this paper, we propose a novel semi-supervised learning methodology, named Laplacian mixed-norm proximal support vector machine Lap-MNPSVM for short. In the optimization problem of Lap-MNPSVM, the information from the unlabeled examples is used in a form of Laplace regularization, and $l_p$ norm ($0\,<\,p\,<\,1$) regularizer is introduced to standard proximal support vector machine to control sparsity and the feature selection. To solve the nonconvex optimization problem in Lap-MNPSVM, an efficient algorithm is proposed by solving a series systems of linear equations, and the lower bounds of the solution are established, which are extremely helpful for feature selection. Experiments carried out on synthetic datasets and the real-world datasets show the feasibility and effectiveness of the proposed method.

1 Introduction

In many real situations, there are plentiful unlabeled training examples since the acquisition of labels is time-consuming and fastidious. In such situations, semi-supervised learning tries to utilize the unlabeled examples to improve learning performance, especially when there are limited labeled training examples. During the past decade, semi-supervised learning has received significant attention and a lot of approaches have been developed [1, 2–10].

Among the many semi-supervised learning methods, manifold regularization (MR) is one of the most interesting frameworks [11–14]. The MR introduces a meaningful regularization term to capture the geometric information from the data and makes the smoothness of the classifier along the intrinsic manifold. Following the MR framework, Belkin et al. proposed a Laplacian support vector machine (Lap-SVM) [12], which is able to handle both the transductive and inductive cases. Qi et al. [28] proposed Laplacian twin support vector machine (Lap-TSVM), which constructs a nonparallel classifier for semi-supervised learning.

The semi-supervised learning methods proposed in this paper are closely related with the proximal support vector machine (PSVM) [15] and the $p$-norm (0 < p < 1) support vector machine ($p$-norm SVM) [21–24] for supervised classification problem. Different from the standard 2-norm SVM, PSVM generates the linear classifier based on proximity to one of two parallel planes that are pushed as far apart as possible. It only requires solving a simple nonsingular system of linear equations (LEs), while the standard 2-norm support vector machine classifier requires a more costly solution of a quadratic program. The $p$-norm SVM comes from the good contribution on the $p$-norm ($p\in [0,1]$) in the optimization communities [17–25], where the 2-norm penalty in the standard linear SVM is replaced by the $p$-norm $(p \in (0, 1))$ penalty.

In this paper, we introduced two extra regularizers into the optimization problem of PSVM. One is the manifold regularizer, which captures the geometric structure of the unlabeled and labeled examples, the other is the $p$-norm, which can control the sparsity of hyperplane and realize feature selection. The proposed method is called Laplacian mixed-norm proximal support vector machine (Lap-MNPSVM). Our Lap-MNPSVM can realize classification and feature selection simultaneously. Unfortunately, the optimization problem of our Lap-MNPSVM is neither convex nor differentiable; it is therefore difficult to be solved directly. We propose an algorithm to find its approximate solution via solving a series systems of LEs. And the lower bounds for the absolute value of nonzero components in every local optimal solution are established, which are extremely helpful to eliminate the zero components in any numerical solution. The numerical experimental results have shown that our Lap-MNPSVM is more effective than some popular semi-supervised learning methods such as transductive SVM (TSVM) [27], Laplacian Regularized Least Square Classifier (Lap-RLS) [12], Laplacian SVM (Lap-SVM) [12] and Laplacian Twin SVM (Lap-TSVM) [28].

This paper is organized as follows. In Sect. 2, we briefly introduce some works related to this paper first and then describe our Lap-PPSVM in detail including solving and analyzing the involved optimization problem in it. In Sect. 3, numerical experiments are given to demonstrate the effectiveness of our method. We conclude this paper in Sect. 4.

2 Methods

In this section, we first remind proximal support vector machine (PSVM) and the semi-supervised manifold regularization; then, we carry out our Lap-MNPSVM.

We describe our notation firstly. All vectors are column vectors unless transposed to a row vector by a super script $\top$. For a vector $x$ in $R^n, [x]_i(i=1,2,\ldots ,n)$ denotes the $i$th component of $x$. $|x|$ denotes a vector in $R^n$ of absolute value of the components of $x$. $\Vert x\Vert _p$ denotes the value $(|[x]_1|^p+\cdots +|[x]_n|^p)^{\frac{1}{p}}$. Strictly speaking, when $0 < p < 1 \Vert x\Vert _p$ is not a norm in general sense.¹ But, we still follow the term $p$-norm because of simplicity and the consistence with the other references such as [17–25]. $\Vert x\Vert _0$ is the number of nonzero components of $x$. For two vectors $x =([x]_1, \ldots , [x]_n)^\top \in R^n$ and $y ([y]_1, \ldots , [y]_n)^\top \in R^n, (x\cdot y)$ denotes the inner product of $x$ and $y, x\otimes y$ generates a new vector with the $i$-th element $[x]_i[y]_i, i=1,2,\ldots ,n$.

Consider the semi-supervised classification problem with the training set $T$

$$\begin{aligned} T=\{(x_1,y_1),\ldots ,(x_l,y_l), x_{l+1}, \ldots , x_{l+u}\}, \end{aligned}$$

(1)

where $x_j\in R^n, \; j=1,2, \ldots , l+u$ and $y_j \in \{1, -1\}(j=1,\ldots ,l)$. Denote the inputs of all examples $X=\{x_i\}_{i=1}^{l+u} \in R^{(l+u) \times n}$ and each row $X_i \in R^n$ is the input of the i-th example. Suppose the inputs of labeled examples denoted by $X_l=\{x_i\}_{i=1}^l \in R^{l\times n}$, the outputs of the labeled examples denoted by $Y_l=\{y_i\}_{i=1}^l \in R^{l \times 1}$. Our goal is to construct a classifier utilizing both labeled and unlabeled examples, which can realize the feature selection and give a better generalization performance.

2.1 Proximal support vector machine (PSVM)

For supervised classification problem, instead of the standard support vector machine (SVM) that classifies the examples by assigning them to one of two disjoint half spaces in input or feature space, PSVM assigns examples to the closer one of two parallel super planes. Its optimization problem is as follows,

$$\begin{aligned} \min _{ w,\,b,\,\xi }&\frac{1}{2}\left( \Vert {\varvec{w}}\Vert _2^2+b^2\right) +\frac{C}{2}\displaystyle \sum _{i=1}^l\xi _i^2\ , \end{aligned}$$

(2)

$$\begin{aligned} \text{ s.t. } \quad &y_i(({\varvec{w}}\cdot {\varvec{x}}_i)+b)= 1-\xi _i\;,\; i=1,\ldots ,l\;. \end{aligned}$$

(3)

The first term in (2) is the regularizer, optimizing it can maximize the margin between two boundary hyperplanes ($( w \cdot x )+b=1$ and $( w \cdot x)+b=-1$) and avoid over-fitting. Minimizing the second term is to minimize the empirical risk. It is clear that PSVM requires only solving a nonsingular system of LEs.

2.2 Semi-supervised manifold regularization

Recently, manifold learning techniques [11, 13, 16] have attracted much attention as they can preserve some geometric information of the data. Particularly, for semi-supervised learning (SSL), Belkin et al. [12] introduced a meaningful regularization term:

$$\begin{aligned} \Vert f\Vert _M^2=\sum _{ij=1}^{l+u}w_{ij}(f(x_i)-f(x_j))^2=f'Lf, \end{aligned}$$

(4)

where $f= (f(x_1), \ldots , f(x_{l+u}))^\top$ represents the decision function values over all the training examples, $W=(w_{ij}) \in R^{(l+u) \times (l+u)}, w_{ij}$ is the edge-weight pre-defined for a pair of points $(x_i, x_j)$, and $D$ is the diagonal matrix given by $D_{ii}=\sum _{j=1}^{l+u}w_{ij}, L=D-W$. It is easy to see that the MR term contains all the information from the labeled and unlabeled examples and is suitable for SSL.

2.3 Laplacian mixed-norm proximal SVM (Lap-MNPSVM)

2.3.1 Linear Lap-MNPSVM

Now, we are in a position to present our novel algorithm—the Laplacian p-norm proximal support vector machine (Lap-MNPSVM) by modifying the above problems (2–3). We hope our algorithm can automatically realize feature selection and classification simultaneously. To realize the former, we replace the $\Vert w\Vert _2^2$ in the objective function (2) by $\frac{1}{2}\Vert w\Vert _2^2+\frac{1}{2}\Vert w\Vert _p^p \; (0<p<1)$. To realize the latter, we add the extra regularization term (4) to the objective function (2), making our Lap-MNPSVM is suitable for SSL. This leads to the optimization problem:

$$\begin{aligned} \min _{ w,\,b,\,\xi }&\frac{1}{2}\left( \Vert w\Vert _2^2+b^2\right) +\frac{1}{2}\Vert w\Vert _p^p+\frac{C}{2}\displaystyle \sum _{i=1}^l\xi _i^2+\frac{\lambda }{2}\sum _{ij=1}^{l+u}w_{ij}(f(x_i)-f(x_j))^2\ , \end{aligned}$$

(5)

$$\begin{aligned}&\text{ s.t. } \quad y_i(({\varvec{w}}\cdot {\varvec{x}}_i)+b)= 1-\xi _i\;,\; i=1,\ldots,l\;, \end{aligned}$$

(6)

where $w_{ij}=\exp (-\frac{\Vert x_i-x_j\Vert _2}{\sigma }), \sigma$ is the parameter that can be adjusted. Substituting the equality constraints and $f(x_i)=(w\cdot x_i)+b$ into the objective function, we get the simplified version:

$$\begin{aligned}&\min _{ w,\,b} \frac{1}{2}\left( \Vert w\Vert _2^2+b^2\right) +\frac{1}{2}\Vert w\Vert _p^p+\frac{C}{2}\displaystyle \sum _{i=1}^l[y_i-((w\cdot x_i)+b)]^2 \nonumber \\&\quad +\frac{\lambda }{2}\sum _{ij=1}^{l+u}w_{ij}[((w\cdot x_i)+b)-((w\cdot x_j)+b)]^2\ , \end{aligned}$$

(7)

where $C (C>0), \lambda (0 \le \lambda \le 1), \mu > 0$ and $p (0< p <1)$ are parameters.

We now give the geometric interpretation of problem (7). The first term is the regularizer, optimizing it can maximize the margin between two boundary hyperplanes. The second term is also the regularizer that can control the sparsity² of the final classification hyperplane. The third term minimizes the squared sum of errors, which makes the examples to be classified as correct as possible. The last term, (MR) term aims at to exploit the geometric information inside all the examples, and enforces $f(x)=(w\cdot x)+b$ smoothness along the intrinsic manifold M. In addition, regularization parameter $\lambda$ is introduced to balance the relative significance between the empirical risk term and MR term.

Note that, it is rather difficult to find the global solution of problem (7) because its objective function is neither convex nor differentiable. For the issue of nondifferentiable, we approximate $\Vert w\Vert _p^p =\sum _{i=1}^n |[w]_i|^p$ by $\sum _{i=1}^n (|[w]_i|+\varepsilon )^p$ and get the following problem

$$\begin{aligned}\min _{ w,\,b} F_p(w,b)&=\frac{1}{2}\left( \Vert w\Vert _2^2+b^2+\sum _{i=1}^n (|[w]_i|+\varepsilon )^p\right) +\frac{C}{2}\displaystyle \sum _{i=1}^l[y_i-(( w\cdot x_i)+b)]^2 \nonumber \\ & \quad +\frac{\lambda }{2}\sum _{i=1}^{l+u}\sum _{j=1}^{l+u}w_{ij}[(( w\cdot x_i )+b)-(( w\cdot x_j)+b)]^2\, \end{aligned}$$

(8)

here, $\varepsilon >0$ is a very small number. But this term is still concave due to $0< p < 1.$ To solve this issue, the convex term $\frac{1}{2} \Vert \beta \otimes w\Vert _2^2$ is used to approximate the concave term $\sum _{i=1}^n (|[w]_i|+\varepsilon )^p$, $\beta$ is adjustable to fit the approximation. Thus, we get the following convex quadratic program that approximated problem (7):

$$\begin{aligned}&\min _{ w,\,b} \frac{1}{2}\left( \Vert w\Vert _2^2+b^2\right) +\frac{1}{2}\Vert \beta \otimes w\Vert _2^2 \\ & \quad +\frac{C}{2}\displaystyle \sum _{i=1}^l[y_i-((w\cdot x_i)+b)]^2 \\&\quad +\frac{\lambda }{2}\sum _{ij=1}^{l+u}w_{ij}[((w\cdot x_i)+b)-((w\cdot x_j)+b)]^2\ . \end{aligned}$$

(9)

In order to get better approximation, we adjust $\beta$ successively. This is an iterative process as follows:

Given an initial $\beta^{(0)}= \left(\beta _1^{(0)}, \ldots \beta _n^{(0)}\right)^\top$, suppose that the current $(w^{(k)},b^{(k)})$ is estimated by solving (9) with $\beta =\beta ^{(0)}$. Set $(w^{(k+1)},b^{(k+1)})$ as the solution to the following weighted optimization problem:

$$\begin{aligned}\min _{ w,\,b} F_2(w,b)&=\frac{1}{2}\left( \Vert w\Vert _2^2+b^2\right) +\frac{1}{2}\left( \Vert \beta ^{(k+1)} \otimes w\Vert _2^2\right) +\frac{C}{2}\displaystyle \sum _{i=1}^l[y_i-((w\cdot x_i)+b)]^2\nonumber \\&\quad +\frac{\lambda }{2}\sum _{ij=1}^{l+u}w_{ij}[((w\cdot x_i)+b)-((w\cdot x_j)+b)]^2\ , \end{aligned}$$

(10)

where $\beta ^{(k+1)}=\left( \beta _1^{(k+1)}, \ldots \beta _n^{(k+1)} \right) ^\top$ is the weight vector and is required to satisfy:

$$\begin{aligned} p\left( |[w^{(k)}]_i|+\varepsilon \right) ^{p-1}\hbox {sign}\left( [w^{(k)}]_i\right) =\left[ \beta _i^{(k+1)}\right] ^2[w^{(k)}]_i. \end{aligned}$$

(11)

Equation (11) means that the objective function of (8) has the same steepest descent direction as the objective function of problem (10) at the current $(w^{(k)},b^{(k)})$, i.e.,

$$\begin{aligned} \nabla F_p(w^{(k)},b^{(k)})=\nabla F_2(w^{(k)},b^{(k)}), \end{aligned}$$

(12)

So a reasonable choice is

$$\begin{aligned} \beta _i^{(k+1)}=\sqrt{p(|[w^{(k)}]_i|+\varepsilon )^{p-2}}. \end{aligned}$$

(13)

Based on the above discussion, we can get the approximated solution $(w^{(k+1)},b^{(k+1)})$ of problem (7) by solving (10). Note that problem (10) is a unconstrained quadratic programming. Its KKT condition leads to solving the following LEs:

$$\begin{aligned} (B+C \bar{X_l}^\top \bar{X_l} +\lambda \bar{X}^\top L\bar{X})\tilde{w}=\bar{X_l}^\top Y_l, \end{aligned}$$

(14)

where

$$\begin{aligned} \bar{X}=\left(\begin{array}{ll} x_1^\top & 1 \\ x_2^\top & 1 \\ \vdots & \vdots \\ x_{l+u}^\top & 1\end{array}\right)_{(l+u)\times (n+1)},\ \ \bar{X_l}=\left(\begin{array}{ll} x_1^\top & 1 \\ x_2^\top & 1 \\ \vdots \ & \vdots \\ x_{l}^\top & 1\end{array}\right)_{l\times (n+1)}, \tilde{w}=[w^\top b]^\top , \end{aligned}$$

and $B=\hbox {diag}(1+[\beta _1^{(k+1)}]^2, \ldots , 1+[\beta _n^{(k+1)}]^2, 1)$.

The above LEs can be solved by the powerful conjugate gradient (CG) algorithm [26] effectively , which is described as follows: Suppose the linear system is represented as

$$\begin{aligned} Ax = b, \end{aligned}$$

(15)

where $x$ is an unknown solution, $A$ is a symmetric and positive definite matrix, and $b$ is a vector. The whole procedure is shown by Algorithm 1.

So in this way it can be expected to find a solution of (7). Now, there arises another issue: Since we can only get the approximate local solution of problem (7) by iteratively solving weighted-biased SVM (14) using algorithm 1, how to identify the nonzero components in the solution? To solve this issue, we prove the following theorem, which can be used to identify nonzero components in any local optimal solutions from an approximate local optimal solution.

Theorem 1

For any local optimal solution $(w^*,b^*)$ to the problem (7), we have $[w^*]_i= 0$ if $[w^*]_i \in (-L_i, L_i)$, where $L_i=[ \frac{p}{2|C\sum _{j=1}^l[x_j]_i(y_j-b^*)|}]^\frac{1}{1-p}, ( i=1,2 \ldots n).$

Proof

Suppose $\Vert w^*\Vert _0=k.$ Without loss of generality, let $w^*=([w^*]_1,[w^*]_2,\ldots ,[w^*]_k,0,0,\ldots ,0)^T$ and $z^*=([w^*]_1,[w^*]_2,\ldots ,[w^*]_k)^T.$ Construct the new training set

$$\begin{aligned} \widetilde{T}=\{(\widetilde{x}_1,y_1),\ldots ,(\widetilde{x_l},y_l), \widetilde{x}_{l+1}, \ldots , \widetilde{x}_{l+u}\}, \end{aligned}$$

where $\widetilde{x}_i=([x_i]_1,[x_i]_2,\ldots , [x_i]_k)^\top$. We consider the following optimization problem

$$\begin{aligned}\min _{ z,\,b} F_p(z,b)&=\frac{1}{2}\left( \Vert z\Vert _2^2+\Vert z\Vert _p^p+b^2\right) \\ &\quad+\frac{C}{2}\displaystyle \sum _{i=1}^l[y_i-((z\cdot \widetilde{x}_i)+b)]^2 \\ &\quad +\frac{\lambda }{2}\sum _{ij=1}^{l+u}w_{ij}[((z\cdot \widetilde{x}_i)+b)-((z\cdot \widetilde{x}_j)+b)]^2\ . \end{aligned}$$

(16)

It is easy to know that $(z^*,b^*)$ is a local optimal solution of (16), according to the KKT condition, we have

$$\begin{aligned} I_nz^*+\widetilde{X}_l^\top \widetilde{X}_l z^*+\frac{1}{2}p|z^*|^{p-1}\hbox {sign}(z^*)+\widetilde{X}^\top (D-W)\widetilde{X}z^*=C\widetilde{X}_l^\top (Y_l- eb^*) \end{aligned}$$

(17)

where $I_n$ is a $n$ dimensional identity matrix and

$$\begin{aligned} \widetilde{X}=\left(\begin{array}{l} \widetilde{x}_1^\top \\ \widetilde{x}_2^\top \\ \vdots \ \\ \widetilde{x}_{l+u}^\top \end{array}\right)_{(l+u)\times k},\quad {\widetilde{X}}_l=\left(\begin{array}{l} \widetilde{x}_1^\top \\ \widetilde{x}_2^\top \\ \vdots \ \\ \widetilde{x}_{l}^\top \end{array}\right)_{l\times k}, e=\left(\begin{array}{l}1\\ 1\\ \vdots \ \\ 1\end{array}\right)_{l\times 1}. \end{aligned}$$

By (17), we have

$$\begin{aligned} \frac{1}{2}p|z^*|^{p-1} &\le |I_nz^*+ \widetilde{X}_l^\top \widetilde{X}_l z^*+\frac{1}{2}p|z^*|^{p-1}\hbox {sign}(z^*) \\ & \quad +\widetilde{X}^\top (D-W)\widetilde{X}z^*| \\ &= |C\widetilde{X}_l^\top (Y_l-eb^*)|. \end{aligned}$$

(18)

So,

$$\begin{aligned} \frac{1}{2}p|[z^*]_i|^{p-1} \le |C\sum _{j=1}^l[x_j]_i(y_j-b^*)|, \end{aligned}$$

(19)

which is equivalent to $|[z^*]_i| \ge \left[ \frac{p}{2|C\sum _{j=1}^l[x_j]_i(y_j-b^*)|}\right]^\frac{1}{1-p}.$ It means that for any local optimal solution $(w^*,\,b^*)$ of (7), we have $[w^*]_i \in (-L_i, L_i) \Rightarrow [w^*]_i=0, i=1,2, \ldots , n.$

Based on the above discussion, our novel algorithm is established as follows:

2.3.2 Nonlinear Lap-MNPSVM

In order to extend our model to the nonlinear case, we consider the following kernel-generated hyperplane

$$\begin{aligned} K(x,X^\top )u+b=0, \end{aligned}$$

(20)

where $K$ is an chosen kernel function: $K(x_i, x_j) = (\varphi (x_i)\cdot \varphi (x_j))$. The optimization problems for our nonlinear $l_p$ LSTSVM can be expressed as

$$\begin{aligned}&\min _{u,b } \frac{1}{2}\left( \Vert u\Vert _2^2+\Vert u\Vert _P^P+b^2\right) +\frac{C}{2}\sum _{i=1}^l(K(x_i,X^\top )u+b-y_i)^2\nonumber \\&\quad +\frac{\lambda }{2}\sum _{i,j=1}^{l+u}[(K(x_i,X^\top )u-K(x_j,X^\top )u)w_{ij}]^2. \end{aligned}$$

(21)

Now, we rewrite problem (21) into the following equivalent form:

$$\begin{aligned} \min _{u,b } \frac{1}{2}\left( \Vert u\Vert _2^2+\Vert u\Vert _P^P+b^2\right) +\frac{C}{2}\Vert \widetilde{K_l}\widetilde{u}-Y_l\Vert _2^2 +\frac{\lambda }{2}\widetilde{u}^\top \widetilde{K}L\widetilde{K}\widetilde{u}, \end{aligned}$$

(22)

where $\widetilde{u}=\left[\begin{array}{ll} u\\b \end{array}\right],\widetilde{K_l}= \left[\begin{array}{ll}K(X_l,X^\top )&e\end{array}\right],\widetilde{K}=\left[\begin{array}{ll} K(X,X^\top )&e\end{array}\right].$

With an entirely similar process to the linear case, problems (22) can be solved iteratively. At the $k$-th iteration, suppose that the current $(u, b)$ is estimated by $(u^{(k)},b^{(k)})$. Set $(u^{(k+1)},b^{(k+1)})$ as the solution to the following weighted QPP:

$$\begin{aligned} \min _{u,b }\frac{1}{2}\left( \Vert u\Vert _2^2+\Vert \beta ^{(k+1)} \otimes u\Vert _2^2+b^2\right) +\frac{C}{2}\Vert \widetilde{K_l}\widetilde{u}-Y_l\Vert ^2 +\frac{\lambda }{2}\widetilde{u}^\top \widetilde{K}L\widetilde{K}\widetilde{u}, \end{aligned}$$

(23)

where

$$\begin{aligned}{}[\beta ^{(k+1)}]_i=\sqrt{p\left( |u_1^{(k)}]_i|+\varepsilon \right) ^{p-2}}. \end{aligned}$$

(24)

Note that problems (23) is an unconstrained QPP, according to the KKT conditions, it is equivalent to the following LEs:

$$\begin{aligned} (\mathcal {B}_1+C\widetilde{K_l}^\top \widetilde{K_l}+\lambda \widetilde{K}L\widetilde{K})\widetilde{u}=\widetilde{K_l}^\top Y_l, \end{aligned}$$

(25)

where $\mathcal {B}_1=\hbox{diag}(1+ [\beta ^{(k+1)}]_1^2, \ldots , 1+ [\beta ^{(k+1)}]_{l+u}^2, 1).$ Then, we can use Algorithm 1 to solve the LEs (25). The optimal solutions $(u, b)$ can be obtained by almost the same iterative progress as algorithm 2, and a new data $x \in R^n$ are assigned to class $i (i = + 1 or - 1)$, depending on

$$\begin{aligned} f(x)=\hbox {sgn}{K(x,X^\top )u+b}. \end{aligned}$$

3 Experiment and results

To evaluate the performance of our Lap-MNPSVM, we investigate its classification accuracy and feature selection on synthetic dataset and some real-world datasets. We focus on the comparison between Lap-MNPSVM and several state-of-the-art semi-supervised classifiers, including TSVM, Lap-RLS, Lap-SVM and Lap-TSVM:

• TSVM [27]: Transductive SVM. It adopts the cluster assumption and attempts to seek a low-density region to separate classes (guided by the maximum margin principle), avoiding the boundary passing through the high-density region.

• Lap-RLS [12]: Laplacian Regularized Least Square Classifier. It adopts the manifold assumption and solves the optimization problem with the squared loss function (an extension of RLS [30] for SSL).

• Lap-SVM [12]: Laplacian SVM. It adopts the manifold assumption and uses the hinge loss to construct a parallel hyperplane classifier by seeking a maximum margin boundary on both labeled and unlabeled data (an extension of SVM for SSL).

• Lap-TSVM [28]: Laplacian Twin SVM. It also adopts the manifold assumption and exploits the geometric information embedded in the training data to construct a nonparallel hyperplane classifier (an extension of TWSVM for SSL).

Our algorithm code is written in MATLAB 2010 on a PC with an Intel Core I5 processor with 4 GB RAM. With regard to parameter selection, we employ the tenfold cross-validation technique on the training set. Parameters $C, \lambda$ and $\sigma$ in MR term are all selected from the set $\{2^i|i = -6, \ldots , 6\}, p$ is selected from the set $\{0.1, 0.2,\ldots , 0.9\}$.

3.1 Results

3.1.1 Comparison on UCI datasets

It is well known that the scale of the labeled examples is important to the semi-supervised learning. To investigate the impact of the ratio of labeled data on the performance of Lap-MNPSVM, each classifier is applied on several real-world datasets from the UCI machine learning repository, summarized in Table 1. These datasets represent a wide range of fields (include pathology, vehicle engineering, biological information and finance), sizes (from 155 to 1,437) and features (from 6 to 34). All datasets are normalized such that the features scale in $[-1, 1]$ before training. Similar to [2], our experiments are set up in the following way. First, each dataset is divided into two subsets: 70 % for training and 30 % for testing. Then, we randomly label $m$ of the training set and use the remainder as unlabeled examples, where m is the ratio of labeled examples. Finally, we transform them into semi-supervised tasks. Each experiment is repeated 10 times.

Table 1 Summary of UCI datasets

Accuracy ($A_{\rm cc}$) is utilized to evaluate the performance of classification and is defined as follows. Accuracy denotes the percentage of both positive points and negative points correctly predicted and is defined as follows:

$$\begin{aligned} A_{\rm cc}=\frac{\hbox {TP+TN}}{\hbox {TP+FP+TN+FN}}, \end{aligned}$$

where TP, TN, FP and FN denote the number of true positives, true negatives, false positives and false negatives, respectively.

Tables 2, 3, 4 list the learning results of each classifier and include the mean and deviation of test accuracy for various $m$ from 10 to 30 %. We have highlighted the best performance. The results reveal that increasing the ratio of labeled examples generally improves the classification performance for almost all classifiers.

Now, we focus on the performance of our Lap-MNPSVM. The results in Tables 2, 3, 4 show that Lap-MNPSVM is better than other methods on almost all datasets. The accuracy is improved in varying degrees using Lap-MNPSVM. In particular, on the dataset ‘Austrialian,’ ‘CMC’ and ‘Germen,’ there are over 10 % improvements using Lap-MNPSVM. Only on the dataset ‘BUPA,’ Lap-MNPSVM preforms obviously worse than other methods. But, from the perspective of average ‘mean’ and ‘std’ accuracy, given at the bottom of Tables 2, 3, 4, our Lap-MNPSVM owns the best performance among all. Lap-MNPSVM has not only the highest average accuracy but also the lowest standard deviation. This shows that Lap-MNPSVM performs better and more stable. In addition to better performance on classification accuracy, our Lap-MNPSVM can pick out the really relevant features, while the other methods can not. The reason may be that the Lap-MNPSVM considers two aspects simultaneously: classification and feature selection. By selecting the proper parameters in the Lap-MNPSVM model, it can balance the classification and feature selection better. In one word, our Lap-MNPSVM performs better than other methods.

Table 2 Mean and standard deviation (%) of test accuracy and the number of selected features at 10 % of labeled examples

Table 3 Mean and standard deviation (%) of test accuracy and the number of selected features at 20 % of labeled examples

Table 4 Mean and standard deviation (%) of test accuracy and the number of selected features at 30 % of labeled examples

3.1.2 Comparison on MNIST dataset

MNIST Dataset is a handwritten digit dataset and consists of gray scale images of handwritten digits from ‘0’ to ‘9’ as shown in Fig. 1. The size of each sample is $28 \times 28$ pixels. As the reference [28], we use digits 5 and 8 to form a binary classification problem. The size of labeled examples are 300, 600, and 1,200 separately (‘5’ and ‘8’ have the same number of samples.) Then, 420 ‘5’ and ‘8’ are randomly selected as unlabeled examples. All labeled and unlabeled examples together form the training set. The test dataset contains 1,500 examples. We use the training set to select the optimal parameters and learn the classifier and then test it on the test set. The experiments are repeated 10 times. Table 5 shows the result in the case of RBF kernel. We can see that Lap-MNPSVM has not only the best accuracy but also the best stability. The accuracy of Lap-MNPSVM is about 1 % higher than Lap-TSVM in various situations, and the standard deviation is only 0.4 at most. The reason of better performance of our Lap-MNPSVM may be that it has an adaptive norm which can be adjusted according to the dataset while the other methods has only the fixed norm for all datasets.

Fig. 1

An illustration of 10 subjects in MNIST dataset

Table 5 The testing accuracy of ‘5’ versus ‘8’ dataset. The size of the unlabeled data is 420

3.1.3 Comparison on synthetic dataset

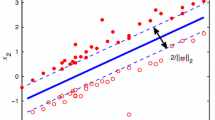
In this subsection, we compare the effectiveness of our Lap-MNPSVM with TSVM, Lap-SVM and Lap-TSVM for two semi-supervised synthetic datasets, in terms of the classification performance and decision boundary. Figure 2 shows the one-run results from this dataset of each classifier. It can be found that the decision boundary of TSVM, Lap-SVM and Lap-TSVM is too close to some positive examples, while our Lap-MNPSVM can obtain a more reasonable decision boundary than the others. Furthernore, from Table 6, we can see that our Lap-MNPSVM performs best because only it can achieve 100 % accuracy. The behind reason may be that our Lap-MNPSVM has an adaptive norm, which can be adjusted according to the dataset.

Table 6 Results on synthetic dataset

Fig. 2

The comparison on synthetic dataset. a Trueclass, b TSVM, c Lap-SVM, d Lap-TSVM, e Lap-MNPSVM

4 Conclusion

This paper proposes a novel algorithm named Laplacian mixed-norm proximal support vector machine (Lap-MNPSVM). For the corresponding optimization problem, an approximate local optimal solution is obtained by solving a series of LEs. Furthermore, we analyzing the lower bounds theoretically, which is extremely helpful to select the really relevant features. Our Lap-MNPSVM can automatically realize feature selection and classification for semi-supervised learning. Numerical experiments show that our Lap-MNPSVM is effective in both selecting relevant features and improving the classification accuracy, compared with some popular methods. In the future, one possible work will be extending Lap-MNPSVM to multi-class classification.