Application of Artificial Intelligence Techniques to Predict Strip Foundation Capacity Near Slope Surfaces

Abstract

In some situations, a foundation is built on or near the crest of a slope. As a result, the soil’s overall stability and bearing capacity dramatically reduced, depending on many geometrical and geotechnical factors. This study consists of two main parts: numerical analysis and artificial intelligence prediction. In the numerical section, simple two-dimensional numerical models have been employed using Plaxis 2D software to examine the bearing capacity and slope stability of a continuous foundation placed near a slope. It specifies foundation width and depth, soil cohesion, frictional and slope angles, and slope crest distances. A comprehensive database of simulated results was used to develop and validate ANN and EPR prediction expressions as well as the relevance of the input parameters. The results show that there is a positive relationship between all studied variables and (q_u/γH) except the slope angle β. The FOS increases as the footing distance away from the slope edge increases up to a critical b/B ratio; LE methods, however, yield a higher FOS value than FEM as a result of their differing approaches. It was determined that the essential distance between the slope crest and the continuous foundation edge is 6B after which the slope's impact diminishes. Based on the input variables sensitivity analysis, B, ϕ, and c were identified as the most effective input parameters. Finally, as a result of the case study analysis, the authors concluded that both ANN and EPR models are highly accurate with differences within 6%. The ANN model is superior to EPR but lacks a straightforward mathematical solution.

Introduction

Bearing capacity (BC) and settlement estimation are key factors for geotechnical engineers to consider when designing a foundation. These design requirements are affected by the geotechnical properties of the soil, the geometric characteristics of the footing, and the loading circumstances. However, due to the variability and anisotropy of soil formation, numerous methodologies have been developed to assess the BC of foundations on level ground under different circumstances [1, 2]. The foundation should be designed with an appropriate safety factor against shear collapse and permissible foundation settling. In hilly areas, the construction of the foundation on the slope is unavoidable. However, due to fast urbanization and population increase, many commercial or residential structures, such as bridge abutments, electric and mobile transmission towers, buildings, and elevated water tanks, will be located on or near the crest of earthen slopes. As a result, the behavior of the foundation on the slope crest/face will alter in terms of BC and overall structural stability. The established passive resistance zone towards the slope's face will reduce depending on the footing location from the slope edge and thereby the carrying capacity of earth slope footings will be less than that of level ground footings.

Several studies have published several methodologies and approaches for estimating the bearing resistance of foundations situated on earthen slopes. These strategies include experimental model testing [3, 4]; theoretical and analytical research [5,6,7,8]; and numerical methods [9,10,11]. Artificial intelligence (AI) methods, particularly Artificial Neural Networks (ANNs) and Evolutionary Polynomial Regression (EPR), are now widely used in geotechnical engineering for their superior prediction abilities in simulating complex material behavior. Researchers in geotechnical engineering have utilized ANN and EPR techniques since the 1990s in foundation engineering, specifically to assess settlement [12, 13] and estimate BC of individual shallow foundations resting on level ground [14,15,16].

Further, a broad variety of parameters have been studied using various hybrid learning models; such as the GWO-RF model to predict the splitting tensile strength of recycled aggregate concrete with glass fiber and silica fume [17]; PSO and BWOA techniques for predicting pavement material resilient modulus (MR) under wet-dry cycles [18]; PSO-RF and HHO-RF models to forecast pile set-up parameter `A` from CPT. However, HHO-RF is more efficient than PSO-RF, with R² and RMSE both equal to 0. 9328 and 0.0292 for training and 0. 9729 and 0.024 for test data, respectively [19]. All these prediction models aligned with experimental results using various assessment criteria and techniques, such as error criteria, Taylor diagrams, uncertainty analysis, scatter index analysis, and error distribution.

Some researchers used the ANN and EPR to estimate the bearing capacity (BC) on the sloped ground [10, 20,21,22], while others have applied EPR to evaluate various geotechnical engineering applications [23,24,25]. Nevertheless, in 2021, only Ebid et al. [22] used EPR to estimate BC factors for a strip foundation near an earthen slope crest using Meyerhof's approach. EPR models are offered in mathematical expression forms, making them simply accessible to the modeler. As a novel aspect of this study, two models have been constructed, utilizing ANN and EPR, to estimate BC on sloped grounds, which was not attempted in previous studies by Acharyya and Dey [21] and Acharyya et al. [10]. The current work seeks to examine the BC of individual continuous foundations set on an earthen-sloping crest through a comprehensive numerical analysis utilizing the PLAXIS 2D v20 finite element software. Many geometrical and geotechnical variables were investigated to achieve the study's objectives, including footing width (B), soil cohesion (c), soil friction angle (ϕ), footing embedment (D_f/B), slope angle (β) and setback distance (b/B). Based on the parametric analysis results, two models were developed using ANN and EPR techniques to construct a mathematical expression for estimating the BC of individual continuous foundations placed on an earthen slope. Further, to determine the relative relevance of the input parameters, a sensitivity analysis was performed on each model. These approaches greatly assist design and consulting engineers in estimating BC quickly and easily.

Method of Analysis

Model Geometry, Boundaries, and Meshing

As illustrated in Fig. 1, the slope model geometry was chosen so that isobar stresses would not reach the model's borders. The model boundaries are selected with the bottom boundary fully rigid and restricted in both vertical and horizontal directions. The vertical boundaries are fixed horizontally, but vertical deformation is allowed, while the slope face is kept free from movement.

Fig. 1

Model geometry

Sensitive Analysis

The model is divided into finite elements for numerical analysis. The mesh must be fine for reliable results. A coarse mesh hinders capturing soil and foundation characteristics. A fine mesh creates more elements and requires longer processing time. Hence, a sensitivity analysis was done to determine the ideal mesh size for the FE model, considering PLAXIS meshing options. These meshes are categorized as very coarse, coarse, medium, fine, and very fine. To reduce reliance on the numerical model, the optimal mesh element size is determined using non-dimensional average element size (NAES). Figure 2 shows how the elements' size affects the bearing pressure of the strip foundation on the earth's slope. A fine meshing approach with NAES of 0.04 yielded favorable results and was used in the current numerical model study. After properly defining soil, foundation, loads, and slope boundaries, automatic mesh generation is done. Figure 3 shows the geometry and meshing of the Plaxis 2D FE model.

Fig. 2

Mesh sensitivity

Fig. 3

Mesh generation and boundary fixation

Constitutive Modeling

The hardening soil model with small-strain stiffness (HSsmall) is used to simulate backfill and foundation soils. It is an expansion of the hardening soil (HS) model, considering increasing soil stiffness at low strains. Most soils have more stiffness at small strain levels than at engineering strain levels, and this stiffness changes nonlinearly with strain. This behavior is given in the HSsmall model by two extra material parameters,${\text{G}}_{0}^{{{\text{ref}}}}$, and $\gamma_{0.7}$ where ${\text{G}}_{0}^{{{\text{ref}}}}$ is the small-strain shear modulus and $\gamma_{0.7}$ is the strain level at which the shear modulus has decreased to approximately 70% of the small-strain shear modulus. This model has a cap yield surface (see Fig. 4) and accurately reproduces soil deformations better than other models because of its non-linear stress–strain relationship and calculated soil stiffness using various loading and unloading techniques [26, 27]. This study uses 15-node triangular elements with 2 degrees of freedom per node for modeling soil elements. These elements have 12 stress points, providing quicker convergence and more accurate results compared to 6-noded elements. The linear elastic (LE) model has been used for modeling the concrete foundation. Tables 1 and 2 display the soil and concrete foundation parameters employed in this study.

Fig. 4

a Different moduli of typical stress–strain HS small soil model, b The cap yield surface in principle stress space

Table 1 Soil properties

Table 2 Foundation properties

Finite Element Software and its Validation

In this work, PLAXIS 2D v20 software is used for numerical modeling and analysis. The software is a professional finite element package for the deformation and stability analysis issues in geotechnical engineering concerns such as tunnels, earth structures, deep excavations, etc. Many researchers have successfully utilized this program to explore the foundation behavior on earth slopes, bearing capacity, and slope stability evaluation [28,29,30].

To ensure PLAXIS accuracy in analysis, the findings of Abed and Hameed's [31] numerical analysis using PLAXIS 3D and the experimental work described by Lee and Manjunath [32] for a strip foundation set on an earth slope were used to verify the FE model. The comparison of analytical results in terms of load-deformation curves, as illustrated in Fig. 5a, revealed a close agreement in terms of both magnitude and trend. Furthermore, the assessment of the slope stability of the present numerical analysis is verified with the Limit Equilibrium Method (LEM) results conducted by [33]. The verification results exhibit good indication as illustrated in Fig. 5b. Thus, the verified model can be utilized for conducting a parametric study to explore the numerous design parameters' impact on the bearing pressure of a single strip foundation situated on a sloped soil surface.

Fig. 5

Verification of the numerical model

Artificial Intelligence (AI) Techniques

Artificial Neural Networks (ANNs) Approach

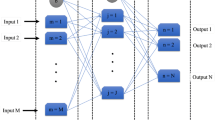
ANNs are mathematical tools and data processing systems used to express complex, nonlinear processes by connecting inputs and outputs. They consist of interconnected neurons that are arranged in layers and are connected within each layer by weights. ANNs are suitable for modeling the complex behavior of most geotechnical engineering materials with high variability, as they do not require making hypotheses about fundamental laws and have an advantage over traditional modeling methods.

The dataset is divided into three divisions: training, validation, and testing, each taking a percentage of the total input data. Weights are adjusted at the training stage until desired outputs are achieved. After the training phase is complete, validation data are used to assess the model's performance, and the testing dataset is used to find the ideal hidden layer node numbers.

There are several types of ANNs. The multilayer perceptron network model is one of the most frequent and frequently used network models, with three layer types: input, hidden, and output layers. The proposed network's input layer receives data, which is processed in the hidden layer(s), and the result is transferred to the output layer. The feed-forward–backward propagation (FFBP) algorithm is one of the most essential types of algorithms utilized in the ANN process [34, 35]. In this technique, the ANN must be fed input and output samples. The error-prone FFBP algorithm predicts data output and compares it to the actual output. When there is a mistake, the weights and biases of the various levels are reversed from the output layer to the input layer. This technique is repeated until the ANN error is as close to zero as possible. The network with the highest (R) value and the lowest error value gives the best ANN model, as judged by several metrics such as the correlation coefficient (R), Mean Squared Error (MSE), Root Mean Square Error (RMSE), Mean Absolute Error (MAE), and so on. The number of nodes in the hidden layer(s) is sensitive to the ANNs. Therefore, it should be optimal to maximize the performance of the network; very few nodes may cause under-fitting, meanwhile, many nodes may cause over-fitting, i.e., the training data will be modeled well, and the sum of the squared errors will be low, but the ANN will be modeling the noise in the data. As a result, the ANN's testing data will be poorly generalized [36]. The general stepwise of the ANN model used in this investigation is shown in Fig. 6.

Fig. 6

Flow chart of the utilized ANN model for predicting the ultimate bearing capacity of strip footings

Evolutionary Polynomial Regression (EPR) Technique

EPR is an AI approach based on evolutionary computing, combining the least squares method and Giustolisi and Savic's Genetic Algorithm (GA) to find optimal and simple scheme descriptions [37]. Unlike ANNs, EPR generates symbolic and straightforward mathematical models [38]. The EPR approach's fundamental features can be expressed in two steps. First, the optimum model architecture in polynomial expression form is chosen using an evolutionary seeking technique via genetic algorithms [39]. Second, numerical regression is performed using the least-squares technique.

Before beginning the EPR operation, some variables need to be modified to regulate the modeling architecture development process. These variables can be utilized to influence the optimization approach employed, such as the exponent ranges, the desired terms number in the mathematical model(s), mathematical structures, and the function types to generate the models. Applying the optimization process, EPR finds the most accurate symbolic model(s) of the studied system using the stated parameters and the optimization procedure.

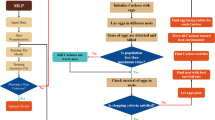
Following calibration of the EPR model(s), the best (optimal) model(s) from the chain of returning models can be chosen. The proposed EPR model(s) performance during the testing, validation, and training phases can be evaluated using analytical standard criteria (statistical measures) such as the correlation coefficient R, Coefficient of Determination (COD = R²), Mean Squared Error, MSE, and Root Mean Squared Error, RMSE [37]. The steps of the EPR method and the way it was applied in the study are illustrated in more detail by the flow chart shown in Fig. 7.

Fig. 7

EPR-MOGA analysis flow chart [40]

Results and Discussion

Numerical Results

Table 3 highlights the diverse geometrical and geotechnical soil variables utilized in the present research for the single-strip foundation model presented in Fig. 3 to calculate the normalized bearing capacity $q_{u} /\gamma H$ of a continuous foundation positioned on an earthen slope crest corresponding to a settlement of 5%B. The stated statistical information for all used data is presented in Table 4. The histograms combined with the normal distribution curve for inputs and output parameters are shown in Fig. 8.

Table 3 Used variables in the numerical analysis

Table 4 Statistical information of input and target data used in ANN and EPR models

Fig. 8

Histograms and normal distribution curves for inputs output parameters

Effect of Slope Angle and Foundation Setback

The effect of the foundation position b/B from the slope edge and the slope angle β on the $q_{u} /\gamma H$ of a continuous foundation built on an earthen slope crest is depicted in Fig. 9. This graph illustrates that as the inclination of the slope increases, the $q_{u} /\gamma H$ value decreases. This is due to the free flow of dirt on the slope surface outward and a reduction in soil confinement or passive resistance from the side slope, which results in a decrease in footing bearing pressure. The outcomes show that the $q_{u} /\gamma H$ value is strongly related to the b/B ratio up to a critical ratio. Hence, at a small setback distance ratio, slope instability increases, soil confinement, and passive resistance decrease, and the footing-soil system stiffness is adversely affected, resulting in a drop in bearing pressure. The slope angle impact fades away at around b/B = 6, and the $q_{u} /\gamma H$ does not vary significantly for the further b/B ratio. This conclusion supports the findings arrived by [20, 21]. Furthermore, the $q_{u} /\gamma H$ improvement rate is greater on steep gradient slopes than on low (gentle) gradient slopes.

Fig. 9

Combined influence of β and b/B ratio on $q_{u} /\gamma H$

Effect of Soil Cohesion

Figure 10 highlights the combined impact of the soil cohesion c variation and the b/B ratio on the $q_{u} /\gamma H$; it shows that both have considerable influence on the $q_{u} /\gamma H$ value. It depicts that the c and b/B ratio positively correlates with the $q_{u} /\gamma H$ magnitude, the enhancement in the $q_{u} /\gamma H$ becoming insignificant after b/B = 6, and the impact being more tangible at larger c values. Improvement of $q_{u} /\gamma H$ satisfies the reality that increases in soil cohesion include improvements in the shear resistance of the foundation soil.

Fig. 10

Impact of c and b/B ratio on $q_{u} /\gamma H$

Friction Angle Impact

Figure 11 depicts the combined effect of the friction angle ϕ and b/B ratio on $q_{u} /\gamma H$ value; both significantly impact the $q_{u} /\gamma H$. It is claimed that the ϕ and b/B ratio have a proportionate relationship with the $q_{u} /\gamma H$ value, the increase in the $q_{u} /\gamma H$ being inefficient after b/B = 6, and the impact became more pronounced at higher ϕ values. The increase in $q_{u} /\gamma H$ confirms that the changes in soil friction angle increase foundation soil shear resistance.

Fig. 11

Effect of ϕ and b/B ratio on $q_{u} /\gamma H$

Embedment Depth Impact

Figure 12 depicts the combined influence of the footing embedment depth D_f/B and the b/B ratios, both of which have a significant effect on the $q_{u} /\gamma H$ value. It is revealed that increasing of D_f/B and b/B ratios increases the $q_{u} /\gamma H$ value. This is due to rising soil confinement, which raises the passive resistance zone. Furthermore, increasing $q_{u} /\gamma H$ value becomes invaluable after b/B = 6 and has a greater influence at a higher D_f/B ratio.

Fig. 12

Effect of D_f/B and b/B ratios on $q_{u} /\gamma H$

Effect of Foundation Width

Figure 13 shows the combined impact of the foundation width B and b/B ratio on the $q_{u} /\gamma H$ value; it reveals that both have a significant effect on the $q_{u} /\gamma H$ value. The results observed that when the B and b/B ratio increased, so did the $q_{u} /\gamma H$ value, since a higher soil depth beneath the foundation contributed to its ability to sustain the applied load. Because soil collapse at a small b/B ratio is caused by a combination of bearing capacity and slope instability failure, the influence is more noticeable for larger b/B ratio; however, this increases in the $q_{u} /\gamma H$ value diminished after b/B = 6.

Fig. 13

Effect of B and b/B ratio on $q_{u} /\gamma H$

Effect of Type of Soil

Figure 14 depicts the combined effect of soil shear strength parameters, c, ϕ, and b/B ratio on the $q_{u} /\gamma H$ value. In general, for any soil type as the b/B ratio increases away from the slope crest the $q_{u} /\gamma H$ increases up to b/B = 6. In contrast, for constant b/B, soil B (c = 30 kPa, and ϕ = 32°) shows the highest $q_{u} /\gamma H$ value in comparison to soil A which has the lowest cohesion (c = 8 kPa) although (ϕ = 40°). This demonstrates that the internal friction angle has more effect than soil cohesion. In other words, soil C shows the lowest $q_{u} /\gamma H$ value resulting from (a decreased internal friction angle of 12° although the cohesion is increased to 40 kPa).

Fig. 14

Combined influence of c, ϕ, and b/B on $q_{u} /\gamma H$

Slope Stability

Figure 15 depicts the safety factor with the b/B ratios. It clearly showed that the FS increases as the b/B ratio increases up to b/B = 3 and 6 for a 100 kPa loading and a pressure corresponding to 5% B settlement, respectively. After that, the slope effect disappears and the FS and the critical footing setback greatly depend on the applied load. This is due to the rise in the passive confining zone as the foundation moved away further from the slope edge, as previously indicated.

Fig. 15

FOS with b/B ratio

Failure Mechanism

In the current research, the soil failure pattern generated beneath a continuous foundation placed on the slope crest has been analyzed for various β and b/B ratios to determine the key b/B ratio; then, the impact of the β fades away. Figure 16 displays how the slope affects the passive zone formed under the foundation and that the failure pattern is one-sided only and toward the slope direction up to b/B = 6, affecting the soil bearing pressure and overall slope stability. The failure mechanism established at b/B ≥ 6 is analogous to the failure mechanism developed on level ground or flat topography.

Fig. 16

Failure pattern generated under foundation with b/B ratio (B = 2m; D_f = 0.0 B; ϕ = 40°; c = 8; β = 40°)

ANN Model Results

In the current research, the varied parameters listed in Table 3 are used as input data to predict the $q_{u} /\gamma H$ output of a continuous foundation situated on the slope crest by applying the ANN tool available in MATLAB software, which provides many training functions and algorithms. The FFBP algorithm with Levenberg–Marquardt (TRIANLM) training function has been found efficient in the training process [35], and therefore, it is used to build the ANN model. Table 5 shows how the samples for training, testing, and validation are distributed using random division by the ANN “dividerand” function.

Table 5 Samples number used for strip foundation analysis

To assess the ANN performance, its predicted results, and the optimal hidden layer nodes (neurons), the R² and MSE criteria are considered based on trial and error. According to this analysis, the ANN structure that best fits predicted, and numerical results comprises a 6–5-1 architecture (see Table 6 and Fig. 17).

Table 6 Trials for selection of ANN model structure

Fig. 17

The ANN model structure (single strip foundation)

ANN structure performance

Figure 18 depicts the outcome of the $q_{u} /\gamma H$ training, validation, and testing processes in agreement with their magnitudes obtained from the FE simulation and those predicted by the ANN model, with R² values of 0.996, 0.995, and 0.996, respectively. Thus, Tables 7 and 8 listed the optimal connection weights and biases among ANN layers acquired due to the training process and then employed in both the testing and validation stages.

Fig. 18

Capability of ANN model for training, validation, and testing phases

Table 7 Input to hidden weights and thresholds (biases)

Table 8 Hidden to output weights and thresholds (biases)

First, the trained ANN model was coupled with the validation group data, which had been unused during both the training and testing processes, to create the ANN model. The validation phase process is useful in determining whether the ANN model can generalize the physical problem outcome. Figure 18b shows a superior match between those simulated by FE and the estimated $q_{u} /\gamma H$ magnitudes, emphasizing the best generalization capacity and performance of the 6–5-1 ANN model architecture (see Fig. 19). Second, the trained ANN model and its optimum related weights and biases are considered for the testing phase to check the prediction capacity of the network. Figure 18c indicates a good match between the FE simulation outcomes and those predicted by the ANN model. The high R² value in the testing phase demonstrates a certainty that the trained ANN has excellent prediction ability.

Fig. 19

Best validation performance

Input Parameter’s Importance

The research required to sort the input factors, highlighting their prioritized impact on the specific physical problem outcome, is known as "sensitivity searching." Such research helps in the "design of experiments" when a large number of physical or numerical simulations are needed, but only a few of them are chosen for real modeling due to the sensitive effect of the contributing independent (input) variables. Thus, sensitivity analysis aids in reducing the model simulations' number without affecting the generality of the conclusions. Many ways to differentiate the critical input variables (parameters) have been referred to in the literature [13, 41]. Garson's algorithm has been employed in the current research to evaluate the relevance of the input parameters. To accomplish this, first, compute the products (Table 9) of the input-hidden (Table 7) and hidden-output (Table 8) connection weights and then, calculate the input parameter importance using the following formula:

$${\text{Input}}_{{\text{X}}} = \sum\limits_{{{\text{N}} = 1}}^{5} {\frac{{\left| {{\text{Hidden}}_{{{\text{XN}}}} } \right|}}{{\sum\limits_{{{\text{Z}} = 1}}^{6} {\left| {{\text{Hidden}}_{{{\text{ZN}}}} } \right|} }}} \;{\text{(Garson}}^{\prime}{\text{s}}\;{\text{Algorithm}})$$

(1)

where Hidden_XN = the absolute connection weight values for input to output nodes, and Hidden_ZN = the absolute product connection weights values for the input-hidden and hidden-output nodes.

Table 9 Input-hidden and hidden-output weights product

Figure 20 shows the results of the sensitivity assessment for the presented ANN structure as per Garson’s algorithm. It displays that the foundation width, B, the internal friction angle, ϕ°, and soil cohesion, c, are the most relevant impact input parameters on the $q_{u} /\gamma H$ value of the continuous foundation placed on the earthen slope crest.

Fig. 20

Rank of input parameters

Mathematical Expression Development for (q _u /γH)

Based on the ANN model's ideal biases and weights obtained from the trained neural network model 6-5-1, a mathematical prediction expression is constructed [15, 36, 42, 43]. As shown in Eq. 2, it connects the input parameters (B, c, ϕ°, D_f/B, β, and b/B) with the output $q_{u} /\gamma H$ value corresponding to the 5% B settlement.

$$\left( {\frac{{q_{u} }}{\gamma H}} \right) = f_{sig} \left\{ {b_{o} + \sum\limits_{N = 1}^{h} {\left[ {\omega_{N} f_{sig} (b_{hN} + \sum\limits_{i = 1}^{m} {\omega_{iN} X_{i} )} } \right]} } \right\}$$

(2)

where $q_{u} /\gamma H$ = normalized bearing pressure; Xi = input variables; $f_{sig}$ = Tan-sigmoid transfer function; m = input variables number; h = hidden layer neurons; $\omega_{iN}$ = related weight between the ith input layer and Nth node of hidden layer; $\omega_{N}$ = related weight between Nth hidden layer node and output node; $b_{hN}$ = the Nth hidden layer bias (threshold); and $b_{o}$ = output layer bias.

The mathematical equation of the ANN model for $q_{u} /\gamma H$ of the strip foundation placed on the slope crest has been built with the weights and thresholds aid listed in Tables 7 and 8, as per the following expressions:

$$\begin{aligned} A_{1} = & - 0.0432B - 1.5697c - 0.8625\varphi - 0.1421\left( {\frac{{D_{f} }}{B}} \right) \\ & \quad + & 0.5150\beta - 0.6604\left( {\frac{b}{B}} \right) - 3.4056 \\ \end{aligned}$$

(3)

$$\begin{aligned} A_{2} =& - 0.1755 B - 0.0510 c + 0.2370 \varphi + 0.0501 \left( {\frac{{D_{f} }}{B}} \right) \\+ 0.0149\beta - 0.0224 \left( \frac{b}{B} \right) - 0.9481 \\ \end{aligned}$$

(4)

$$\begin{aligned} A_{3} = & - 2.106 B - 0.0403 c + 0.2104 \varphi + 0.0501 \left( {\frac{{D_{f} }}{B}} \right) \\+ 0.024 \beta - 0.0467 \left( \frac{b}{B} \right) - 3.0045 \\ \end{aligned}$$

(5)

$$\begin{aligned}A_{4} = & - 3.1733 B + 0.0360 c - 0.2108 \varphi - 0.0545 \left( {\frac{{D_{f} }}{B}} \right) \\ - 0.0425 \beta + 0.1035 \left( \frac{b}{B} \right) + 4.9441 \\ \end{aligned}$$

(6)

$$\begin{aligned} A_{5} = & + 0.0934 B + 0.0710 c - 0.2758 \varphi - 0.0535 \left( {\frac{{D_{f} }}{B}} \right) \\ - 0.0105 \beta + 0.0049 \left( \frac{b}{B} \right) + 0.7550 \\ \end{aligned}$$

(7)

$$B_{1} = - 22.3421 (e^{{A_{1} }} - e^{{ - A_{1} }} )/(e^{{A_{1} }} + e^{{ - A_{1} }} )$$

(8)

$$B_{2} = + 183.1677 (e^{{A_{2} }} - e^{{ - A_{2} }} )/(e^{{A_{2} }} + e^{{ - A_{2} }} )$$

(9)

$$B_{3} = - 100.4545 (e^{{A_{3} }} - e^{{ - A_{3} }} )/(e^{{A_{3} }} + e^{{ - A_{3} }} )$$

(10)

$$B_{4} = + 135.6964 (e^{{A_{4} }} - e^{{ - A_{4} }} )/(e^{{A_{4} }} + e^{{ - A_{4} }} )$$

(11)

$$B_{5} = + 78.9862 (e^{{A_{5} }} - e^{{ - A_{5} }} )/(e^{{A_{5} }} + e^{{ - A_{5} }} )$$

(12)

$$C_{1} = B_{1} + B_{2} + B_{3} + B_{4} + B_{5} - 157.3474$$

(13)

$$(q_{u} /\gamma H)_{{{\text{norm}}}} = (e^{{C_{1} }} - e^{{ - C_{1} }} )/(e^{{C_{1} }} + e^{{ - C_{1} }} )$$

(14)

where $(q_{u} /\gamma H)_{{{\text{norm}}}}$, in Eq. (14), is the normalized bearing capacity. To compute its value, before subjecting the input data for the parameters in Eqs. (3–7) to the network process, it should be normalized according to the used transfer functions between input and hidden layers (in this work, the TANSIG function is utilized), which normalizes the input parameters between ( − 1 and + 1) as per Eq. (15).

$$P_{i}^{n} = \frac{{2 (P_{i}^{a} - P_{i}^{\min } )}}{{(P_{i}^{\max } - P_{i}^{\min } )}} - 1$$

(15)

where $P_{i}^{a}$ and $P_{i}^{n}$ are the ith input or target vector components before and after normalization, respectively. $P_{i}^{\max }$ and $P_{i}^{\min }$ are the maximum and minimum values before the normalization of all input or target vector components.

The input and target dataset range of the present study are illustrated in Table 4, and the normalized expressions for the input parameters are displayed in Table 10.

Table 10 Normalized expressions for the input parameters

Using the same Eq. (15) above, the final (de-normalized) $q_{u} /\gamma H$ is calculated as follows:

$$\begin{aligned} (q_{u} /\gamma H)_{{denorm}} = & 0.5[(q_{u} /\gamma H)_{{norm}} + 1][(q_{u} /\gamma H)_{{\max }} \\ - & (q_{u} /\gamma H)_{{\min }} ] + (q_{u} /\gamma H)_{{\min }} \\ \end{aligned}$$

(16)

Substituting the target maximum and minimum values shown in Table 9, the final form of Eq. (16) can be written as follows (See Appendix A for calculation sample):

$$(q_{u} /\gamma H)_{denorm} = 2.722(q_{u} /\gamma H)_{n} + 2.826$$

(17)

EPR Model Results

One of the advantages of EPR is the ability to generate many models for a particular physical problem. This provides the modeler with the resilience to select the appropriate expression from the developed expressions depending on a parametric study or engineering judgment. In this investigation, the model with the fewest terms (for simplicity or decrease in complexity) the highest coefficient of determination (COD = R²) value, and the lowest MSE (to ensure maximum possible fitness) will be chosen as shown in Fig. 21. As with the ANN technique, the total dataset is divided into three sets: 70% for training, 15% for testing, and 15% of the invisible data in both the training and testing processes to validate the predicted EPR model. Trial-and-error is employed to get the most effective (optimal) EPR model; Table 11 describes the parameters used to construct the EPR model.

Fig. 21

COD and MSE for developed EPR models

Table 11 EPR setting parameters

The EPR model calculates the $q_{u} /\gamma H$ of a continuous foundation situated on an earthen slope crest, using the inputs B, c, ϕ, D_f/B, β, and b/B. The best EPR model explored in this study to capture the specific geotechnical engineering issue under consideration is summarized in Eq. (18):

$$\begin{aligned} \frac{{q_{u} }}{\gamma H} = & {0}{\text{.7278}}1 \frac{{\varphi^{2} }}{{\beta^{2} }} + 5.7045*10^{ - 2} \frac{c \varphi }{\beta } + 2.0964*10^{ - 3} B^{0.5} \beta \frac{b}{B}\\ & \quad + 3.5021\frac{{B \varphi^{0.5} D_{f} /B }}{\beta } + 1.6175*10^{ - 4} B^{1.5} \varphi^{2} (\frac{b}{B})^{0.5} \\ \end{aligned}$$

(18)

Figure 22 displays the comparison of outcomes determined using FE simulation with those predicted by the EPR model (Eq. 18) for the training, testing, and validation phases, respectively, with their corresponding correlation factors. As it appears in the figure, a strong relationship has been indicated between the FE simulation results and those prophesied by the EPR model.

Fig. 22

Results comparison obtained by FE and EPR

The sensitivity analysis has been done using the one-factor-at-a-time technique, which is considered one of the robust approaches [44] performed to understand the contribution of uncertainty of each input parameter to the model output. This method provides a clear indication of how a single parameter influences the overall outcome. This approach considered the variation range in input parameters of the standard deviation lower and upper than the mean [45]. The sensitivity evaluation results depict that the friction angle, cohesion, and foundation width are the most effective independent variables (inputs) that impact the dependent variable (target) for the proposed model as presented in Fig. 23.

Fig. 23

Sensitivity evaluation of input variables for the EPR model

Despite the two different approaches (Garson for ANN model and one-factor-at-a-time for EPR model) used in the sensitivity analysis of the input variables, the outcomes of both are compatible except for parameters arrangement.

The Distinction Between ANN- and EPR-Developed Models

Table 12 summarizes the performance evaluation of the constructed ANN and EPR models, whereas Table 13 depicts Pearson’s correlation heat map of input and output parameters. According to the stated evaluation indices, the ANN model performance is better than the EPR model in all phases. This indicates that the developed ANN model has more accuracy and capability to generate and predict outcomes than the EPR model, but with a more complex mathematical expression that is difficult to solve manually. This is because ANN does not generate a direct expression, whereas EPR generates a simple and clear mathematical equation that is easily solved manually. So in this regard, the EPR model has superiority over the ANN model. This conclusion is also supported by Fig. 24, which displays Taylor diagrams for both training and testing datasets, due to higher correlation and nearest standard deviation to the simulated FE outcomes.

Table 12 Comparison between ANN and EPR models

Table 13 Pearson’s correlation heat map of input and output parameters

Fig. 24

Taylor diagrams for the developed models, a Training data and b Testing data

Zawita Case Study (Duhok City/Kurdistan Region of Iraq)

Site Location and Geology

The investigated area of the Zawita case study is located about 60 km northeast of Duhok city in the Kurdistan Region of Iraq. It is a sub-district of Duhok City. Large parts of the soils in Duhok areas are interspersed with clay beds that vary in color from light brown to reddish brown. This soil is of variable thickness, covering moderately deep inclined rock strata. Duhok geological successions are the Bekhair and Duhok Mountains. Late Cretaceous and Paleocene sediments overlay Bekhair's anticline. In the northern part of Duhok City, it extends from the southeast toward the northwest, and in the southern part, it extends to Duhok Mountain. The southwestern part of the investigated area is of low relief and dominated mostly by Quaternary deposits. These formations formed from alterations in sand, silt, and clayey silt. Such formations to some extent are unstable from an engineering perspective. So, additional precautions in the design of the foundation are necessary.

Results of Analysis

Figure 25 shows the geometry, boundary conditions, and finite element mesh of the Zawita case study. The FE bearing capacity analysis is conducted using Plaxis 2D in plain strain conditions with a fine element mesh produced by 15-node elements that could result in an extra accurate computation of strain. Whereas Plaxis 2D and SLOPE/W software are used for slope stability analyses. The hardening soil model with a small strain is used to simulate the behavior of the selected slope. The model’s soil and concrete foundation properties are presented in Table 14.

Fig. 25

Slope schematic of Zawita case study

Table 14 Soil and foundation properties of Zawita case study [46]

Table 15 shows the bearing pressure results obtained using Plaxis 2D (FEM) for the various conditions of the case study slope model with those values derived from the ANN and EPR-developed models. The differentiation among the results displays acceptable compatibility despite the soil unit weight and slope angle of the chosen case study being not within the data range of the ANN and EPR selected models. It means that the selected models have a high capacity to generate plausible results.

Table 15 Comparison of bearing capacity values (in kPa) at 5.0% B settlement

Figure 26 illustrates the differences between ANN and EPR bearing pressure computed by FEM for D_f/B equal to 0 and 0.5. As shown, for D_f/B = 0, and B = 1 m, the percentage differences in ANN bearing pressure with FEM are 14.1, 7.7, and 7.4%, for b/B = 0, 2, and 4, respectively. The same slope status ratios decrease to 6.9, 1.8, and 4.8% when B = 2 m. Similarly, when D_f/B = 0.5, and B = 1 m, the differences with FEM are 7.5, 3.9, and 4.7%, and when B = 2 m, these ratios decrease to 2.8, 0.9, and 4.0% for the same slope situations. On the other hand, when D_f/B = 0, and B = 1 m, the EPR values differ from FEM by 8.8, 7.8, and 7.4%, for b/B = 0, 2, and 4, respectively. When B = 2 m, these ratios decrease to 9.7, 1.5, and 7.3% in similar situations. Also, when D_f/B = 0.5, and B = 1 m, the differences with FEM are 10.3, 7.9, and 6,4%, and when B = 2 m, these ratios decrease to 4.4, 2.1, and 7.5%, for the same b/B, respectively. As is evident from this figure, the average differences between both models are within 6% maximum, indicating that both models are highly accurate.

Fig. 26

ANN and EPR bearing capacity percentage differences from FEM

Based on Fig. 27, the contours of failure patterns developed under the foundation show that the failure is one-sided, toward the slope face, due to eliminating the passive zone.

Fig. 27

Contours of failure patterns generated under the foundation of some case study situations

Tables 16 and 17 and Fig. 28 depict the safety factor FOS of the slope stability analysis for various slope conditions of the case study using many approaches (FEM, Bishop, Morgenstern-Price, and Spencer). It was observed that for slope angle $\beta =$ 31° and any foundation width considered, the FOS increases as the footing setback b/B distance increases. The same trend was noticed in all analysis methods. Table 17 shows that FEM yields a lower FOS value than all LE methods. This is attributed to their fundamentally different approaches. Hence, the LE methods have more limitations than the FEM, resulting in a relatively defined critical failure surface, whereas the FEM showed a much wider and deeper zone of critical failure, and as a result revealed higher concentrations of plastic strain near the top of the slope. Also, LE methods do not consider the fundamental aspects of the stress–strain relationship, and thus, they cannot compute a realistic stress distribution [47, 48]. A comparison of LE methods considered in this study shows that safety factors calculated by the Simplified Bishop Method are approximately 2–4% lower than those obtained by other methods. However, it cannot be accepted for complex slopes with multiple failure factors, since it does not take into account interslice forces compared to Spencer’s or Morgenstern and Price's methods that satisfy both force and moment equilibrium.

Table 16 Safety factors for Zawita case study without loading

Table 17 Safety factors for Zawita case study at load corresponding to 5.0% B settlement

Fig. 28

Some case study stability analysis at q corresponding to 5% B settlement

Conclusions

This investigation presents two models using ANN and EPR techniques to predict the normalized bearing pressure q_u/γ H from data obtained by FE simulation of a continuous foundation on the earthen slope crest using different geometrical and geotechnical parameters such as (B, c, ϕ, D_f/B, β, and b/B). It is worth mentioning that the developed expressions are valid and accurate within the range of the parameters considered in this study, but outside of these limits, the foretelling must be validated. The following conclusions are drawn from the outcomes:

• The bearing capacity improved as B, c, ϕ, D_f/B, and b/B increased but it negatively related to β.

• The critical b/B ratio was found to be 6, after which the slope inclination influence vanished, and the foundation behaved like it was placed on the horizontal ground.

• The FOS increases as the foundation setback increases to reach the critical b/B ratio.

• The ANN and EPR techniques offer the best capable models to forecast the q_u/γH of the strip foundation situated on the slope crest, based on the high R² values achieved in the training, validation, and testing phases.

• The prediction precision of ANN and EPR models is close to each other; however, the EPR model can directly give a simple mathematical equation that is easily solved manually without needing to use any software, whereas the ANN model provides a complex expression that is difficult to solve manually.

• Based on the optimum weights and thresholds obtained from ANN and the more appropriate EPR model, an adequate mathematical expression for predicting q_u/γH of strip foundations located on the slope crest has been provided. This mathematical prediction expression will serve as a simple and quick tool for the geotechnical practicing and consulting engineers included in the hilly area planning and design.

• The sensitivity analysis using Garson’s technique indicated that the most important parameters that affect the q_u/γH value are B, ϕ, and c.

• The results of the selected case study proved that the chosen models of ANN and EPR are powerful and give acceptable results.

Appendix A: ANN case study result calculation sample

B (m)	c kN/m2	ϕ°	Df/B	βo	b/B
2	10	40	0	31	0

Geometry and soil parameters.

The normalized input parameters in the range (− 1, + 1) according to Table 10.

Parameter	Normalized expression	Normalized input parameter values
B (m)	Bnorm = 2B–3	= 2 (2)− 3 = 1
c (kPa)	cnorm = 0.05c–1	= 0.05 (10)− 1 = $-$ 0.5
ϕ°	ϕnorm = 0.0714ϕ–1.8571	= 0.0714 (40)− 1.871 = 0.985
Df/B	(Df/B)norm = 2(Df/B)–1	= 2(0)− 1= − 1
β°	βnorm = 0.08β–3.8	= 0.08 (31) − 3.8 = − 1.32
b/B	(b/B)norm = 0.2857(b/B)–1	= 0.2857(0) − 1 = − 1

Hidden layer no	Weights and bias for input-hidden layers from Table 6
	B	c	ϕ°	Df/B	βo	b/B	Bias
N1	– 0.0432	– 1.5697	– 0.8625	– 0.1421	0.5150	– 0.6604	– 3.4056
N2	– 0.1755	– 0.0510	0.2370	0.0501	0.0149	– 0.0224	– 0.9481
N3	– 2.1060	– 0.0403	0.2104	0.0501	0.0240	– 0.0467	– 3.0045
N4	– 3.1733	0.0360	– 0.2108	– 0.0545	– 0.0425	0.1035	4.9441
N5	0.0934	0.0710	– 0.2758	– 0.0535	– 0.0105	0.0049	0.7550

$$\begin{aligned} {\text{A}}1 = & - 0.0432*\left( 1 \right) - 1.5697*\left( { - 0.5} \right) - 0.8625*\left( {0.985} \right) \\ & - 0.1421*\left( { - 1} \right) + 0.515*\left( { - 1.32} \right) - 0.6604*\left( { - 1} \right) - 3.4056 = - 3.403 \\ \end{aligned}$$

$$\begin{aligned} {\text{A}}2 = & - 0.1755*\left( 1 \right) - 0.051*\left( { - 0.5} \right) + 0.2370*\left( {0.985} \right) \\ & + 0.0501*\left( { - 1} \right) + 0.0149*\left( { - 1.32} \right) - 0.0224*\left( { - 1} \right) - 0.9481 = - 0.909 \\ \end{aligned}$$

$$\begin{aligned} {\text{A}}3 = & - 2.106*\left( 1 \right) - 0.0403*\left( { - 0.5} \right) + 0.2104*\left( {0.985} \right) \\ & + 0.0501*\left( { - 1} \right) + 0.024*\left( { - 1.32} \right) - 0.0467*\left( { - 1} \right) - 3.0045 = - 4.915 \\ \end{aligned}$$

$$\begin{aligned} {\text{A}}4 = & - 3.1733*\left( 1 \right) + 0.036*\left( { - 0.5} \right) - 0.2108*\left( {0.985} \right) \\ & - 0.0545*\left( { - 1} \right) - 0.0425*\left( { - 1.32} \right) + 0.1035*\left( { - 1} \right) + 4.9441 = 1.549 \\ \end{aligned}$$

$$\begin{aligned} {\text{A}}5 = & 0.0934*\left( 1 \right) + 0.071*\left( { - 0.5} \right) - 0.2758*\left( {0.985} \right) \\ & - 0.0535*\left( { - 1} \right) - 0.0105*\left( { - 1.32} \right) + 0.0049*\left( { - 1} \right) + 0.755 = 0.600 \\ \end{aligned}$$

Weights and bias for hidden-output layers from Table 7
N1	N2	N3	N4	N5	Bias
– 22.3421	183.1677	– 100.4545	135.6964	78.9862	– 157.3474

$\left( {q_{u} /\gamma H} \right)$
Min	0.104
Max	5.548

$$B_{1} = - 22.3421 (e^{{A_{1} }} - e^{{ - A_{1} }} )/(e^{{A_{1} }} + e^{{ - A_{1} }} ) = 22.293$$

$$B_{2} = + 183.1677 (e^{{A_{2} }} - e^{{ - A_{2} }} )/(e^{{A_{2} }} + e^{{ - A_{2} }} ) = - 131.976$$

$$B_{3} = - 100.4545 (e^{{A_{3} }} - e^{{ - A_{3} }} )/(e^{{A_{3} }} + e^{{ - A_{3} }} ) = 100.444$$

$$B_{4} = + 135.6964 (e^{{A_{4} }} - e^{{ - A_{4} }} )/(e^{{A_{4} }} + e^{{ - A_{4} }} ) = 123.982$$

$$B_{5} = + 78.9862 (e^{{A_{5} }} - e^{{ - A_{5} }} )/(e^{{A_{5} }} + e^{{ - A_{5} }} ) = 42.412$$

$$C_{1} = B_{1} + B_{2} + B_{3} + B_{4} + B_{5} - 157.3474 = \left( {22.293 - 132.976 + 100.444 + 123.982 + 42.412} \right) - 157.3474 = - 0.193$$

$$\left( {q_{u} /\gamma H} \right)_{norm} = (e^{{C_{1} }} - e^{{ - C_{1} }} )/(e^{{C_{1} }} + e^{{ - C_{1} }} ) = - 0.191$$

$$\left( {q_{u} /\gamma H} \right)_{denorm} = 0.5 [\left( {q_{u} /\gamma H} \right)_{norm} + 1] [\left( {q_{u} /\gamma H} \right)_{\max } - \left( {q_{u} /\gamma H} \right)_{\min } ] + \left( {q_{u} /\gamma H} \right)_{\min } = 2.307$$

$$\left( {q_{u} } \right)_{denorm} = 2.307 (\gamma H) = 2.307(20.1)(9) = 417.3 kN/m^{2} , (See Table 14).$$