1 Introduction

Local slopes can highly affect adjacent engineering studies. In most civil engineering projects, the stability of the local slopes has been considered as a significant problem. Also, slope failures can cause various psychological damages, including property loss as well as human life in our world. For instance, Iranian Landslide Working Party (2007) reported that 187 people were killed due to the destructive effects of slope failure [1]. The impregnation level, along with different intrinsic characteristics of the soil, can impact the slope failure likelihood [2, 3]. Various studies have been conducted to propose impressive modelling for slope stability issue. Traditional methods have many shortcomings, such as the requirement of utilizing laboratory equipment and also high complexity barricade them from being an appropriate solution [4]. Nevertheless, because of their constraint in studying a particular slope state, for example, soil properties, height, slope angle, groundwater level, etc., these solutions have not commonly been considered as a general solution. Various sorts of numerical solutions, finite element model (FEM), and limit equilibrium methods (LEMs) are extensively chosen for the slope stability issue [5,6,7]. For providing a trustworthy method for slope stability study, scholars have focused on the expansion of design charts [8]. However, this method also has some defects. Producing an impressive design chart needs a lot of time and cost. Also, indicating the accurate mechanical factors is a problematic duty [9, 10]. Hence, because of efficiency, design charts commonly accompanied high precision, therefore the usage of artificial intelligence methods is more bolded [11, 12]. These methods can specify the non-linear relationship between the target factors as well as its key parameters, and this is an outstanding advantage of these approaches. Artificial neural network (ANN) commonly uses any determined number of hidden nodes [13, 14]. In geotechnical studies, different scholars stated that machine learning approaches such as support vector machine (SVM) and ANNs have proper efficiency [15,16,17,18,19]. The intricacy of the slope stability issue is obvious. What makes the problem even more complex and critical is creating different buildings in the presence of slopes that are showing a considerable value of loads used on a rigid footing. It is known that the interval of the slope’s crest along with the value of surcharge is considered as two factors that can affect the stability of the target slope [20]. Because of this fact, scholars have motivated to show a relationship to compute the factor of safety of pure slopes and sometimes the slopes taking a static load [21,22,23,24,25]. Chakraborty and Goswami [26] predicted the factor of safety for around 200 slopes to distinct geometric and shear strength factors by taking into account the multiple linear regression (MLR) along with ANN algorithms. In their work, a comparison study has been conducted to compare calculated results to a FEM model. They have obtained a proper rate of precision obtained for both practical models. In addition, they found that ANN had better performance compared to MLR. Lie et al. [27] utilized the random forest (RF) along with regression tree in functional soil–landscape simulations to regionalize the depth of the failure level and density of soil bulk. Although looking for more reliable analysis of the stability of the slopes various hybrid evolutionary algorithms has been successfully employed in plenty of studies [28,29,30,31], this study presents a novel optimization technique named Harris hawks’ optimization (HHO) incorporated with ANN to give a reliable approximation of the stability of soil slopes. Notably, the HHO is a recently proposed natural inspired metaheuristic algorithm, and the authors did not come across any previous study which applied this algorithm to the mentioned subject.

2 Methodology

2.1 Artificial neural network

The artificial neural network (ANN) is based on the interaction among the neurons in the biological neural apparatus. McCulloch and Pitts [32] proposed ANN for the first one. The algorithm of ANNs is generally utilized as approximators in a non-linear survey of input–output data [33,34,35,36,37,38]. These methods are commonly used for different engineering issues because of their specific mathematical solution in optimization tasks [22, 39,40,41,42,43,44,45,46,47]. Basically, the ANN algorithm includes a group of computational relationships that are commonly worked with each other. Multilayer perceptron (MLP) is known as one of the most appropriate methods between different algorithms of ANNs that used for classification as well as regression issues. The whole structure of the MLP algorithm is presented in Fig. 1. As can be observed, this model consists of three different types of layers. In this method, the number of hidden layers usually changes; however, it just can have input and output layers. Scholars determined that MLPs possess one hidden layer in terms of efficiency [48].

Fig. 1
figure 1

The structure of an MLP neural network with one hidden layer

Full size image

The MLP is basically employed for detecting the mathematical relations among different factors with the taking into account of one and even more activation function(s). We consider W1 and W2 as the weight matrices layers in the hidden and output sections, respectively. After that, the mentioned method is adjusted as below:

$$f(X) = b_{2} + W_{2} \times \left( {f_{A} \left( {b_{1} + W_{1} \times X} \right)} \right),$$
(1)

where \(f_{A}\) stands for the activation function. b1 and b2 stand for the bias matrices related to the neurons located in the hidden and output layers, respectively.

2.2 Harris hawks’ optimization algorithm

The algorithm of Harris hawks’ optimization (HHO) is inspired using the cooperative treatment along with the chasing manner of Harris’ hawks that is first expanded by Heidari et al. [49]. This algorithm has been successfully used for various scientific applications [50, 51]. Hawks attempting to surprise their prey and from different paths swooped on them, cooperatively. In addition, Harris hawks have the ability to choose chase type according to the distinct patterns of prey flight. It has three base stages in HHO, including amaze pounce, tracking the prey, and other different sorts of attacking strategies. Different phases of Harris hawks’ optimization (HHO) are shown in Fig. 2. The pseudo-code of HHO algorithm is also illustrated in Table 1. In a glance, the first stage is named “Exploration” and is modelled to mathematically wait, search, and discover the desired hunt. The second stage of this algorithm is transforming from exploration to exploitation, based on the external energy of a rabbit. Finally, in the third phase which is called “Exploitation”, considering the residual energy of the prey, hawks commonly take a soft and sometimes hard surround for hunting the rabbit from different directions.

Fig. 2
figure 2

Different phases of Harris hawks’ optimization (HHO) (after Heidari et al. [49])

Full size image
Table 1 Pseudo-code of the HHO algorithm (after Heidari et al. [49])
Full size table

2.2.1 Exploration

In each step, Harris’ hawks have been considered the best solutions. The iter + 1 (the Harris hawks’ position) is mathematically modelled by the following relation:

$$X\left({{\text{iter}} + 1} \right) = \left\{{\begin{array}{ll} {{X_{\text{rand}}}\left({\text{iter}} \right) - {r_1}\left| {{X_{\text{rand}}}\left({\text{iter}} \right) - 2{r_2}X\left({\text{iter}} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\text{if}}\;q \geqslant 0.5} \right.} \\ {\left({{X_{{\rm rabit}}}\left({iter} \right) - {X_m}\left({\text{iter}} \right)} \right) - {r_3}\left({LB + {r_4}\left({UB - LB} \right)} \right)\;\;{\text{if}}\;q < 0.5} \end{array}} \right.,$$
(2)

where iter means the present iteration, \(X_{\text{rand}}\) stands selected for hawk at the available population, \(r_{i}\), i = 1, 2, 3, 4…, q are random numbers that are between 0 and 1, \(X_{{\rm rabit}}\) stands for the rabbit position, and \(X_{m}\) is the mean position for hawks and that is computed as follows:

$$X_{m} \left( {\text{iter}} \right) = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} X_{i} \left( {\text{iter}} \right),$$
(3)

where \(X_{i}\) shows the every hawk place and N stands for the hawks size.

2.2.2 Transition from exploration to exploitation

The rabbit energy may be calculated by the below relation:

$$E = 2E_{0} \left( {1 - \frac{\text{iter}}{T}} \right),$$
(4)

where E is the external energy from rabbit and T stands for the maximum size about the iterations. In this relation, E stands for the energy of the rabbit, and \(E_{0} \in \left( { - 1. 1} \right)\) shows the inlet energy for each step. HHO may determine the rabbit state based on the variation trend of \(E_{0}\).

2.2.3 Exploitation

In this stage, for successful escape of the prey: if \(r < 0.5\). If \(\left| E \right| \ge 0.5\) HHO takes soft surround and if \(\left| E \right| < 0.5\) the HHO takes hard surround. To model the attacking stage, the algorithm of HHO used four distinct methods based on the escaping approaches of the prey as well as pursuing approaches of the Harris’ hawks: hard and soft surrounds, advanced rapid dives while soft surround, progressive rapid dives while hard surround. Particularly, \(\left| E \right| \ge 0.5\) means that the prey has enough energy for running out from the surround. Therefore, whether the rabbit runs out from the surround or not is based on two values of r and E.

A—soft surround: \(r \ge \frac{1}{2} {\text{and}} \left| E \right| \ge \frac{1}{2}\).

We can use the following relation:

$$X\left( {{\text{iter}} + 1} \right) = \Delta X\left( {\text{iter}} \right) - E\left| {JX_{{\rm rabit}} \left( {\text{iter}} \right) - \left. {X\left( {\text{iter}} \right)} \right|} \right.,$$
(5)
$$\Delta X\left( {\text{iter}} \right) = X_{{\rm rabit}} \left( {\text{iter}} \right) - X\left( {\text{iter}} \right),$$
(6)

where \(\Delta X\) stands for deference among the position vector of the prey, J = 2(1-\(r_{s}\)) stands for jump severity of the prey in the stage of escaping and \(r_{s} \in \left( {01} \right)\) shows a random number.

B—hard surround: \(r \ge \frac{1}{2} {\text{and}} \left| E \right| < \frac{1}{2}\).

We can use the following formula for showing the present positions:

$$X\left( {{\text{iter}} + 1} \right) = X_{{\rm rabit}} \left( {\text{iter}} \right) - E\left| {\left. {\Delta X\left( {\text{iter}} \right)} \right|} \right..$$
(7)

C—advanced rapid dives while soft surround: \(r < \frac{1}{2} \, {\text{and}} \, \left| E \right| \ge \frac{1}{2}\).

As stated for soft surround, previously, hawks find the next purpose using the below relation:

$$Y = X_{{\rm rabit}} \left( {\text{iter}} \right) - E\left| {JX_{{\rm rabit}} \left( {\text{iter}} \right) - \left. {X\left( {\text{iter}} \right)} \right|} \right..$$
(8)

The hawks can dive as the below relation:

$$Z = Y + S \times {\text{LF}}\left( D \right),$$
(9)

where D stands for the issue dimension and \(S_{1 \times D}\) shows a random vector along with the levy flight. We can calculate LF as follows:

$${\text{LF}}\left( D \right) = 0.01 \times \frac{\mu \times \sigma }{{\left| \vartheta \right|^{{\frac{1}{\beta }}} }}. \sigma = \left( {\frac{{\varGamma \left( {1 + \beta } \right) \times \sin \left( {\frac{\pi \beta }{2}} \right)}}{{\varGamma \left( {\frac{1 + \beta }{2}} \right) \times \beta \times 2^{{\left( {\frac{\beta - 1}{2}} \right)}} }}} \right) \cdot \beta = 1.5,$$
(10)

where \(\mu\) and \(\vartheta\) stand for random amounts among in the range of 0–1. Hence, for updating the hawks’ locations, the final approach can be shown as follows:

$$X\left({{\text{iter}} + 1} \right) = \left\{{\begin{array}{*{20}{c}} {Y\;\;\;{\text{\;if}}\;F\left(Y \right) < F\left({X\left({\text{iter}} \right)} \right)} \\ {Z\;\;\;\;{\text{if}}\;F\left(Z \right) < F\left({X\left({\text{iter}} \right)} \right)} \end{array}} \right.$$
(11)

D—advanced rapid dives while hard surround.

$$r < \frac{1}{2} \, {\text{and}} \, \left| E \right| < \frac{1}{2}.$$

In the present paper, the hawks were considered being near the rabbit. The behaviour of them can be modelled as follows:

$$X\left({{\text{iter}} + 1} \right) = \left\{{\begin{array}{*{20}{c}} {Y\;\;\;\;{\text{if}}\;F\left(Y \right) < F\left({X\left({\text{iter}} \right)} \right)} \\ {Z\;\;\;\;{\text{if}}\;F\left(Z \right) < F\left({X\left({\text{iter}} \right)} \right)} \end{array}} \right.$$
(12)

Y and Z should be calculated as follows:

$$Y = X_{{\rm rabit}} \left( {\text{iter}} \right) - E\left| {JX_{{\rm rabit}} \left( {\text{iter}} \right) - \left. {X\left( {\text{iter}} \right)} \right|} \right.,$$
(13)
$$Y = X_{{\rm rabit}} \left( {\text{iter}} \right) - E\left| {JX_{{\rm rabit}} \left( {\text{iter}} \right) - \left. {X\left( {\text{iter}} \right)} \right|} \right.,$$
(14)
$$Z = Y + S \times {\text{LF}}\left( D \right),$$
(15)

in which \(X_{m} \left( {\text{iter}} \right) {\text{shows}}\frac{1}{N}\mathop \sum \nolimits_{i = 1}^{N} X_{i} \left( {\text{iter}} \right)\) [52].

3 Data collection and methodology

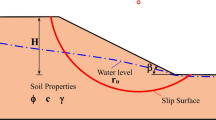
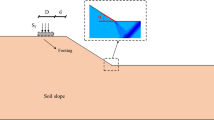
We can use a single-layer slope to obtain a reliable database. In this method, we should assume a purely cohesive soil, having only undrained cohesive strength (Cu), creates the body of this slope. The basic parameters that can have some influences on the strength of the slope versus the failure (i.e., the factor of safety) are the magnitude of the surcharge on the footing enchased onto the slope (w), setback distance ratio (b/B), and slope angle (β). Figure 3a shows these parameters. In this study, the Optum G2 software was used for computing the factor of safety. In most cases, the safety factor is a typical method to show the geotechnical stability as well as deformation in slopes [53] (see Fig. 3b). In this regard, various geometries of the slope angle (β) along with different rigid foundation (b/B) (i.e., around 630 possible cases) are drawn and then evaluated in Optum G2 for calculating the factor of safety. Other parameters were also considered into simulation including cohesive strength of the soil (Cu) and applied surcharge (w). The mechanical factors, including the ratio of Poisson, internal friction angle, and soil unit weight, were specified 0.35, 0°, and 18 kN/m3, respectively. Moreover, modulus of Young (E) differed for every amount of Cu. It is adjusted to be 1000, 2000, 3500, 5000, 9000, 15,000 and 30,000 kPa for amount of Cu 25, 50, 75, 100, 200, 300 and 400 kPa, respectively.

Fig. 3
figure 3

A graphical view of the designed slope in (a) the schematic view and (b) results of the horizontal strain diagram obtained from the Optum G2 (for b/B = 3, Cu = 75 kPa, β = 30°, and w = 50 KN/m2)

Full size image

An example of the utilized dataset is shown in Table 2. In this table, we illustrated the examples of the relation between the slope safety factor and its effective parameters. As can be observed, when Cu has high value, the slope ensures more stability. The factors of β (5°, 30°, 45°, 60°, and 75°), as well as w (50, 100, and 150 KN/m2), have been considered as adversely proportionate for the FOS. By increasing the values of β and w, the slope is more likely to be failing. The factor of safety cannot illustrate any considerable sensibility to the b/B ratio variations (0, 1, 2, 3, 4, and 5). Also, Table 2 shows that the safety factor does not specify any considerable sensitivity for the b/B ratio variations of 0, 1, 2, 3, 4, and 5.

Table 2 Example of the input and output datasets used for training and validating the applied models
Full size table

We have randomly divided the dataset into training and testing sub-classes that have the respective amounts of 0.8 (504 instances) and 0.2 (126 instances). It is important to note that the training instances are utilized for training the ANN and HHO–ANN models. The performance of these methods has been verified using the testing database. Also, k-fold cross-validation procedure is utilized to mitigate the bias caused by the random selection of the data [54,55,56] (see Fig. 4).

Fig. 4
figure 4

The k-fold cross-validation process, taking training and testing samples

Full size image

4 Results and discussion

4.1 Implementation and optimization

As stated previously, the main objective of this research is to present a new optimization of the artificial neural network, namely Harris hawks’ optimization, for the stability analysis of soil slopes by predicting the FOS. To this end, four slope stability conditioning factors, namely slope angle, the position of the rigid foundation, the strength of the soil, and the magnitude of the surcharge are considered to create the required dataset. After dividing the data into the training and testing parts, utilizing the programming language of MATLAB v.2014, the proposed ANN and HHO–ANN models were designed. Based on the authors’ experience, as well as a trial and error process, an MLP neural network with six hidden computational units in the middle layer was developed. In this sense, lots of theoretical attempts have revealed the efficiency of the MLP tool with one hidden layer [57, 58]. Notably, the activation function of “Tansig” was used to activate the calculations of these neurons. This function is expressed as follows:

$$\operatorname{Tan} {\rm sig}(x) = \frac{2}{{1 + {e^{- 2x}}}} - 1.$$
(16)

After determining the optimal structure of the ANN, the HHO algorithm was coupled with it. It is worth noting that the main aim of such optimization algorithms in incorporation with intelligent tools (e.g., ANFIS and ANN) is to find the most appropriate values for their computational parameters. In the case of MLP we used in this study, the HHO performs to find the solution for a mathematically defined problem which contains the weights and biases of the neurons. Ten different structures of HHO–ANN networks were tested based on the population size. In this sense, the population size was considered to vary from 50 to 500 with 50 intervals. Each model performed within 1000 repetitions when meaning square error was defined as the objective function (Table 3). Figure 5 shows the obtained convergence curves. According to this chart, the HHO–ANN having population size = 90 outperformed other tested models. It finally achieved the MSE = 2.469635486 in 4129 s. Remarkably, the majority of the reduction of the MSE occurred in the first 100 iterations.

Fig. 5
figure 5

The convergence curves of tested HHO–ANN networks

Full size image
Table 3 Optimized weight and biases of the ANN model
Full size table

4.2 Performance assessment

The outputs (i.e., the predicted FOS) of the ANN and HHO–ANN models were extracted and compared with the actual values to evaluate their prediction capability. Two error criteria of root mean square error (RMSE) and mean absolute error (MAE) are used to measure the prediction error. Moreover, the correlation between the observed and predicted FOSs is measured by the coefficient of determination (R2). These indices are expressed as follows:

$$R^{2} = 1 - \frac{{\sum\limits_{i = 1}^{N} {\left( {Y_{{i_{{\rm predicted}} }} - Y_{i_{{{\text{observed}} }}} } \right)^{2} } }}{{\sum\limits_{i = 1}^{N} {\left( {Y_{{i_{{\rm observed}} }} - Y_{i_{{{\text{observed}} }}} } \right)^{2} } }}$$
(17)
$${\text{MAE}} = \frac{1}{N}\sum\limits_{I = 1}^{N} {\left| {Y_{{i_{{\rm observed}} }} - Y_{{i_{{\rm predicted}} }} } \right|} ,$$
(18)
$${\text{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {\left[ {\left( {Y_{{i_{{\rm observed}} }} - Y_{{i_{{\rm predicted}} }} } \right)} \right]}^{2} } ,$$
(19)

where Yipredicted and Yiobserved stand for the predicted and actual FOSs, respectively. The term N symbolizes the number of samples and \(\overline{Y}_{\text{observed}}\) denotes the average value of the observed FOS.

Figure 6 illustrates the results of the ANN and HHO–ANN models. In these figures, the error (i.e., the difference between the actual and predicted) and histogram of the errors are also presented. Based on the results, applying the HHO algorithm has helped the ANN to have a better analysis of the relationship between the FOS and its conditioning factors. In this sense, the training RMSE was decreased by 26.52% (from 2.1388 to 1.5715). As for the MAE, the HHO reduced this error criterion by 32.31% (from 1.7151 to 1.1610). Furthermore, the obtained values of R2 (0.8778 vs. 0.9339) show more consistency for the outputs of the HHO–ANN. About the testing phase, it can be deduced that using the HHO increases the generalization power (i.e., predicting the unseen samples) of the ANN. More clearly, the testing RMSE and MAE fell by 20.47% (from 2.0806 to 1.6546) and 26.97% (from 1.6883 to 1.2330), respectively. Besides, the correlation analysis between the testing outputs of the ANN and HHO–ANN show that the R2 increases from 0.8220 to 0.9253.

Fig. 6
figure 6figure 6

The prediction results of the (a and b) ANN and (c and d) HHO–ANN models, respectively, for the training and testing samples

Full size image

4.3 Presenting the HHO-based predictive formula

Overall, it was found that the weights and biases which were suggested by the HHO algorithm can predict the FOS more efficiently than those found in the non-optimized ANN. Hence, in this part of the study, it was aimed to extract the FOS predictive formula from the HHO–ANN model. Notably, the calculated accuracy criteria indicate that it can estimate the FOS accurately, by taking into consideration four slope stability influential factors, namely slope angle, the position of the rigid foundation, strength of the soil, and applied surcharge. Equation 20 denotes the HHO–ANN formula:

$$\begin{array}{ll} {\text{FO}}{{\text{S}}_{{{\rm HHO}}-{\text{ANN}}}} & = -0.7312 \times {Z_1} - 0.9610 \times {Z_2} - 0.7498 \times {Z_3} \\ & \quad - 0.5534 \times {Z_4} - 0.1017 \times {Z_5} + 0.0691 \times {Z_6} + 0.9808,\\ \end{array}$$
(20)

where Z1, Z2, …, Z6 are calculated as shown in Table 3.

5 Conclusion

The complexity of environmental threats has driven scholars to employ evolutionary evaluative methods for dealing with them. The stability of the soil slopes is a crucial civil engineering issue which needs nonlinear analysis. In this paper, Harris hawks’ optimization was used as a novel hybrid metaheuristic technique for optimizing the performance of the artificial neural network in predicting FOS of the soil slope. In other words, the HHO was used to overcome the computational drawbacks of the ANN, through finding the best-fitted structure. Based on the results of the sensitivity analysis, the HHO–ANN with population size = 90 outperforms others. Moreover, the findings showed that synthesizing the HHO algorithm can effectively help the ANN to have more consistent learning and predicting of the slope failure pattern. Lastly, conducting comparative studies for comparing the potential of the used HHO algorithm with other well-known optimization techniques is a good idea for future works to determine the most appropriate technique for solving the mentioned problem.