Introduction

Panel flutter is an aeroelastic phenomenon causing fatigue damage on skin panels of an aircraft in a supersonic gas flow. If the flight speed is not too high, then the panel is stable. Panel flutter or problems associated with it have occurred on supersonic flight regimes on many supersonic aircraft from the Second World War to the present days: the German V-2 rocket in 1944, several experienced American aircraft in the 1950, hypersonic aircraft X-15, rocket Saturn V, American Apollo, Lockheed SR-71 Blackbird, F-117A, F-22. Usually, panel flutter, even in the case of destruction of separate panels, directly does not lead to the collapse, but it can lead to a significant loss of aircraft control, destruction of hydraulic systems and increase in background noise inside the aircraft [1].

At present, the panel flutter phenomenon studies are not enough, and effects of stresses in panel flutter occurrence remain an urgent task. Improving aircraft performance requires a reduction in mass and stiffness of the skin panels, which increases the possibility of panel flutter. Aircraft are designed and tested with flexible wings, adapted to the conditions of flight and having a thin-walled structure. Development of new geometric forms of aircraft and production of new materials, including composites and polymers changes the parameters of the airflow around the panels and their physical properties, which can also lead to flutter [1,2,3].

When the vehicle exceeds critical Mach number, the panel becomes unstable and begins to vibrate. These vibrations occur due to pumping energy from the flow to the panel and may have a large amplitude, resulting in aircraft fatigue damage or structural components [2].

Most studies till now devoted to the mathematical modeling panel flutter of shells exposed to the gas flow can be divided into two groups: using analytical or numerical methods. The purpose of works belonging to the first group is the conclusion of the analytic dependence of the critical flutter frequency as a function that depends on the parameters of a shell and the flow of gas. Second group can also be divided into two areas: Solving a differential formulation and an integrated formulation. A common point for this group is to reduce the original problem to the computation and analysis of complex eigenvalues of finite-dimensional analogue of the problem [3].

One of the main differences between them is as follows: In the first case, the equations of shell theory are written in the form of a differential equation or a system of differential equations and a numerical solution is constructed using the Galerkin method. In the second case, a variation formulation is used for solving the problem, such as virtual work, and a finite element method (FEM) is used for realization of numerical variation equations [4].

In most studies until now, effects of stresses in panel flutter are not studied. But in real situations (e.g., panels on the supersonic plane wing), many stresses apply to wing and its panels during the flight. As these stresses may change the flutter boundaries and stability of the plate, they can play a big role in structural designing of supersonic vehicles. Many researches in this field up to now have been done, which neglected these effects, and they cannot be assumed in real-case designing.

These effects for the flutter boundary of a rectangular plate (which mostly is used in real situations) by using the Galerkin method and spectral numerical solutions are not analyzed yet; therefore, the main purpose of this paper is using these numerical methods to analyze effects of these stresses on panel flutter characteristics and predict the most critical zones in a sample supersonic airplane structure.

Numerical Model

Formulation

The most famous methods in FEM are Ritz and Bubnov Galerkin. The characteristic feature of FEM is using local basis functions (shape functions). The main advantage of the method is the ability to divide any shape and area into finite elements, which permits calculation of stress and strain in real detail, including all their structural features [3].

As is known, in solving the problem of the dynamics in the force equilibrium equations of elasticity, inertia forces distributed over the volume details should be included. This approach may be realized within the framework of the finite element method. The problem in this case may not be the potential, and the Ritz method in the above formulation is not applicable; the main method of solving problems is the Bubnov–Galerkin method.

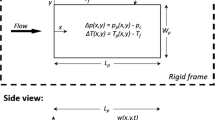
We assume that at the initial time the load was suddenly applied to the plate [5] (Fig. 1).

Fig. 1
figure 1

Panel figure

Full size image

To find the relation between small plate deflection w(x, y) and applied load distribution ΔP(x, y), biharmonic equation for Kirchhoff plate is used [2, 3, 5]:

$$D\left( {\frac{{\partial^{4} W}}{{\partial x^{4} }} + 2\frac{{\partial^{4} W}}{{\partial x^{2} \partial y^{2} }} + \frac{{\partial^{4} W}}{{\partial y^{4} }}} \right) = \Delta p$$
(1)

Equation (1) is a basic equation of bending a thin plate. It has the following properties:

  • Linearity (a consequence of the linearity of the geometric relationships);

  • Invariance with respect to the interchange of the coordinates (x, y) (this is a consequence of the isotropy of the material)

After solving Eq. (1), by deflection w(x, y), all the components of the stresses and strains at any point of the plate can be determined. However, the solution of this equation leads to the integration of constants. Finding them is possible by using the boundary conditions.

On the plate contour can be implemented the following main types of fixings:

  1. 1.

    Hinged

  2. 2.

    Rigidly clamped

  3. 3.

    The free edge

For satisfying the boundary conditions, deflection function w(x, y) and its derivative at the plate edges is assumed zero, which is corresponded only to the conditions of rigidly clamped fixing.

Deflection function w(x, y) will be found in the form of a linear combination of shape functions:

$$W = \sum {C_{i} W_{i} \left( {x,y} \right)}$$
(2)

Each set of basic functions w(x, y) and each set of constants Ci may be used, and Eq. (1) is put into correspondence with some loads p(x, y). By finding the best Ci, p*(x, y) coincides with the given load p(x, y), and then, expression (2) will give the exact solution.

In the case of incomplete (finite) set of shape functions, obtaining an exact solution is not always possible, and the load p*(x, y) is different from the set p(x, y) in the value of r(x, y), which is called the residue. So, by choosing the Ci, residual can be minimized, which can be carried out according to various standards. In the Bubnov–Galerkin method, the minimum residual does not perform work on any of the basic functions is considered:

$$\iint {r\left( {x,y} \right)W_{i} \left( {x,y} \right){\text{d}}x{\text{d}}y = 0}$$
(3)

which gives a system of N equations for determining the unknown constants Ci:

$$\iint {\left[ {D\left( {\frac{{\partial^{4} }}{{\partial x^{4} }}\sum {C_{i} W_{i} } + 2\frac{{\partial^{4} }}{{\partial x^{2} \partial y^{2} }}\sum {C_{i} W_{i} } + \frac{{\partial^{4} }}{{\partial y^{4} }}\sum {C_{i} W_{i} } } \right)} \right.\left. { - \Delta p\left( {x,y} \right)} \right]W_{j} \left( {x,y} \right){\text{d}}x{\text{d}}y = 0}$$
(4)

That is:

$$\sum {C_{i} } \iint {\left[ {D\left( {\frac{{\partial^{4} }}{{\partial x^{4} }}W_{i} + 2\frac{{\partial^{4} }}{{\partial x^{2} \partial y^{2} }}W_{i} + \frac{{\partial^{4} }}{{\partial y^{4} }}W_{i} } \right)*W_{j} {\text{d}}x{\text{d}}y} \right]} - \iint {\Delta P*}W_{j} {\text{d}}x{\text{d}}y = 0$$
(5)

Expression (5) is a system of linear equations of the form:

$$\sum {C_{i} K_{ij} - f_{i = 0} ,\quad i,j = 1 \ldots N}$$
(6)

Or in the traditional matrix form:

$$KC = F$$
(7)

Thus, the Bubnov–Galerkin method, as well as the Ritz method, reduces the problems of determining the stress–strain state to solve a system of linear equations. As seen from (5), the function should have fourth partial derivatives.

During the motion, the plate deflection at each point is a function of time: w = w(x, y, t). During accelerated motion arise the forces of inertia, which can be considered by the principle of d’Alembert:

$$D\left( {\frac{{\partial^{4} }}{{\partial x^{4} }}W_{{}} + 2\frac{{\partial^{4} }}{{\partial x^{2} \partial y^{2} }}W_{{}} + \frac{{\partial^{4} }}{{\partial y^{4} }}W_{{}} } \right) = \Delta p - h\rho \frac{{\partial^{2} W}}{{\partial t^{2} }}$$
(8)

So, the solution of this equation should be found:

$$W\left( {x,y,t} \right) = \sum {C_{i} \left( t \right)} W_{i} \left( {x,y} \right),\quad i = 1, \ldots ,N$$
(9)

By repeating the above transformation:

$$\iint {\left[ {D\left( {\frac{{\partial^{4} }}{{\partial x^{4} }}\sum {C_{i} W_{i} } + 2\frac{{\partial^{4} }}{{\partial x^{2} \partial y^{2} }}\sum {C_{i} W_{i} } + \frac{{\partial^{4} }}{{\partial y^{4} }}\sum {C_{i} W_{i} } } \right)} \right.}\left. { - \Delta p\left( {x,y} \right) + h\rho \sum {\frac{{\partial^{2} C_{i} }}{{\partial t^{2} }}W_{i} } } \right]W_{j} \left( {x,y} \right){\text{d}}x{\text{d}}y = 0$$
(10)

Or in matrix form:

$$M\ddot{C} + KC = 0$$
(11)

Here, C is a vector of unknown functions of time, and not the vector of unknown constants, and the dot denotes differentiation in time and the matrix M is the mass matrix.

From piston theory in fluid dynamics [2, 6], we can find P in Eq. (1), i.e.,

$$\Delta P = - (P - P_{\infty } ) = \frac{{ - 2q_{\infty } }}{{\sqrt {M^{2} - 1} }}\left( {\frac{{{\text{d}}W}}{{{\text{d}}x}} + \frac{1}{{U_{\infty } }}\frac{{M^{2} - 2}}{{M^{2} - 1}}\frac{{{\text{d}}W}}{{{\text{d}}t}}} \right)$$
(12)

Unsteady aerodynamic load at supersonic flow can be determined by piston theory, which is proposed by Lighthill [2]. Theory of the piston is based on the assumption that each surface element has the property of a piston, perpendicular to the flow moving at a speed equal to the downstream speed of w(x, y, t). This is recognized as the relation between the motion of and pressure on a piston in a tube where the total piston velocity includes both a convection term and the direct velocity. Here, the plate is the equivalent piston, and the fluid ‘tube’ is perpendicular to the plate.

In addition, by adding the stresses (Nx and Ny) into Eq. 1, this equation can be written in the complete form [7]

$$\begin{aligned} & D\left( {\frac{{\partial^{4} }}{{\partial x^{4} }}W + 2\frac{{\partial^{4} }}{{\partial x^{2} \partial y^{2} }}W + \frac{{\partial^{4} }}{{\partial y^{4} }}W} \right) + h\rho \frac{{\partial^{2} W}}{{\partial t^{2} }} + N_{x} \frac{{\partial^{2} W}}{{\partial x^{2} }} + N_{y} \frac{{\partial^{2} W}}{{\partial y^{2} }} \\ & = \frac{{2q_{\infty } }}{{\sqrt {M^{2} - 1} }}\left( {\frac{{{\text{d}}W}}{{{\text{d}}x}} + \frac{1}{{U_{\infty } }}\frac{{M^{2} - 2}}{{M^{2} - 1}}\frac{{{\text{d}}W}}{{{\text{d}}t}}} \right) \\ \end{aligned}$$
(13)

And in matrix form:

$$M\ddot{C} + B\dot{C} + KC = 0$$
(14)

An explicit solver with time step Δt = 0.0001 (s) is used, and results were compared with Matlab explicit solver (ODE) for validation and clearly demonstrated the accuracy of our solver.

Finding the Shape Functions

Trigonometric functions are often used as shape functions with this general form [8]:

$$\hat{f} = \sum\limits_{m - 1}^{M} {C_{m} \sin (m\pi x/L)}$$
(15)

Functions must satisfy these conditions for a clamped plate:

$$\begin{aligned} & w\left( {0,y} \right) = w\left( {a,y} \right) = w\left( {x,0} \right) = w\left( {x,b} \right) = 0 \\ & w_{x} \left( {0,y} \right) = w_{x} \left( {a,y} \right) = w_{x} \left( {x,0} \right) = w_{x} \left( {x,b} \right) = 0 \\ & w_{y} \left( {0,y} \right) = w_{y} \left( {a,y} \right) = w_{y} \left( {x,0} \right) = w_{y} \left( {x,b} \right) = 0 \\ \end{aligned}$$
(16)

In this case, there is no boundary edge corresponding deflection (w = 0), and the internal normal to the contour of the boundary edges (x = 0, a and y = 0, b) do not rotate. Sinusoidal functions are good candidates for these conditions [9, 10] So, the shape functions are chosen in this form (Fig. 2):

$$W = \sin \frac{i\pi x}{a}\sin \frac{\pi x}{a}\sin^{2} \frac{\pi y}{b} , \quad i = 1, \, 2, \, 3, \, 4 \,$$
(17)
Fig. 2
figure 2

W1, W2

Full size image

Validation

To validate the present formulation, the flutter results for rectangular simply supported isotropic panels are obtained and compared with other computations.

For simply supported panels, functions must satisfy these conditions:

$$w\left( {0,y} \right) = w\left( {a,y} \right) = w\left( {x,0} \right) = w\left( {x,b} \right) = 0$$
(18)

In this case, there is no boundary edge corresponding deflection (w = 0).

So, the shape functions had been chosen in this form [2]:

$$W = \sin \frac{i\pi x}{a}\sin \frac{\pi y}{b} , \quad i = 1, \, 2, \, 3, \, 4$$
(19)

The nondimensional dynamic pressure (λ) in which flutter begins, for a square panel (a/b = 1) obtained 506 and for a rectangular panel (a/b = 2) obtained 1060. The present formulation is in good agreement with results obtained by Dowell [2] and Abdel-Motagaly et al. [11].

Results

First, the velocity of the flutter without any stress on the plate should be computed. So, assuming the following characteristics for plate, vibration frequencies of the plate have been analyzed using MATLAB coding:

  • a = 0.6 m

  • b = 0.3 m

  • h = 0.002 m

  • Material = aluminum

  • Material density = 2.7 g/cm3

  • Young’s modulus = 70 GPa

  • Poisson’s ratio = 0.35

Assuming no stress condition for plate means Nx = Ny = 0. So, Eq. 13 should be written in this form:

$$\begin{aligned} & D\left( {\frac{{\partial^{4} }}{{\partial x^{4} }}W + 2\frac{{\partial^{4} }}{{\partial x^{2} \partial y^{2} }}W + \frac{{\partial^{4} }}{{\partial y^{4} }}W} \right) + h\rho \frac{{\partial^{2} W}}{{\partial t^{2} }} \\ & = \frac{{ - 2q_{\infty } }}{{\sqrt {M^{2} - 1} }}\left( {\frac{{{\text{d}}W}}{{{\text{d}}x}} + \frac{1}{{U_{\infty } }}\frac{{M^{2} - 2}}{{M^{2} - 1}}\frac{{{\text{d}}W}}{{{\text{d}}t}}} \right) \\ \end{aligned}$$
(20)

To find the speed of starting panel flutter, natural frequencies for panel have been computed and vibration graphs (Z vs. time) for typical point of the panel at different speeds have been drawn. For this reason, the central point of panel has been selected [x = 0.3, y = 0.15 (m)]. Results were as below:

U = 500, m = 1.47

See Fig. 3.

Fig. 3
figure 3

Deformation of central point versus time at 500 m/s

Full size image

U = 700, m = 2.05

See Fig. 4.

Fig. 4
figure 4

Deformation of central point versus time at 700 m/s

Full size image

U = 800, m = 2.35

See Fig. 5.

Fig. 5
figure 5

Deformation of central point versus time at 800 m/s

Full size image

U = 830, m = 2.44

See Fig. 6.

Fig. 6
figure 6

Deformation of central point versus time at 830 m/s

Full size image

U = 850, m = 2.5

See Fig. 7.

Fig. 7
figure 7

Deformation of central point versus time at 850 m/s

Full size image

It can be seen from Fig. 6 that flutter starts at the speed of 830 m/s. Since in flutter situations, two frequencies coincide, it is possible to find an accurate flutter speed. It means that flutter occurs when two frequencies get complex numbers [12]. Using this method, the first velocity in which two frequencies coincide has been computed. By MATLAB coding, the first panel flutter speed had been computed as 808 m/s.

Analysis of the Effect of Stresses on Panel Flutter

For analyzing the stress effects on panel flutter, the complete form of Eq. 13 should be used. For this reason, by adding the stresses gradually and computing the flutter velocity by a method which had been explained in the previous section, graphics of relationship between flutter dynamic pressure and longitudinal and lateral stresses has been drawn.

From Fig. 8, the relationship between divergence velocity and longitudinal stresses is clear. Compressive stresses reduce flutter speed and stability, and stretching increases them. And from Fig. 9, the relationship between divergence velocity and lateral stresses is clear. Compressive stresses reduce flutter speed and stability, and stretching increases them too, but longitudinal stresses (particularly the stretching stresses) have a greater effect on plate stability than lateral stresses.

Fig. 8
figure 8

Flutter velocity versus Nx

Full size image
Fig. 9
figure 9

Flutter velocity versus Ny

Full size image

Conclusions

The modeling for analysis of panel flutter and effect of stresses on divergence speed are presented. A numerical model using Galerkin method is developed with piston theory in supersonic aerodynamics to detect the vibration characteristics of a rectangular panel. This model allows designing the geometrical and material features of panels to avoid dynamic instability of a supersonic aircraft structure.

It is demonstrated that increasing the velocity of fluid will lead to decreasing the vibration frequencies. Also, longitudinal (in direction of flow) compressive stresses in the panel will decrease the divergence velocity, which means that compressive longitudinal stress will increase the panel dynamical instability, and stretching stress in this direction will decrease it. Furthermore, compressive stresses in lateral (perpendicular to the flow) direction will increase the panel dynamical instability, and stretching stress in this direction will decrease it.

Using this information, the most dynamic stable and unstable zones in airplane structures can be determined. The safest zones are shown in red color in Fig. 10, and the most critical zones are shown in green color in Fig. 11.

Fig. 10
figure 10

The safest zones on airplane structure

Full size image
Fig. 11
figure 11

The most critical zones on airplane structure

Full size image

Since the maximum stress applied to the airplane wing skin is created from bending stress caused by the lift force, compressive stress is applied on the upper wing skin and stretching stress perpendicular to the flow is applied on the lower wing skin. These stresses have the maximum value near the root of the wing, so the safest zones are located on the lower wing skin near the root, because the compressive lateral stress decreases the stability.

In addition, the most critical zones are located on the upper wing skin near the root, because the compressive lateral stress increases the instability. In aircraft structural design, this instability should be considered in computing the wing skin material, thickness and aspect ratio of panels.