1 Introduction

Understanding vibration and stability of structures interacting with fluid is of great importance due to its extensive applications in various industries such as aeronautics, shipbuilding, space vehicles, submarines and civil engineering. Vibration characteristics of a structure like natural frequencies and mode shapes will be affected by the presence of fluid around structure as it can vary the kinetic energy of the overall system. Numerous studies of fluid–structure interaction problems have been investigated for a variety of fluids and different geometries [1,2,3,4, 14, 21, 23,24,25,26, 34, 35, 44] Some experimental studies on the natural frequencies of the plate interacting with fluid were carried out during the past years. For instance, [22] investigated the free vibration response of a rectangular plate in contact with bounded fluid by the acoustic and modal test. Also, [27] experimentally studied the hydroelastic vibration of free-edge annular plates to obtain added virtual mass incremental factors. They utilized the Hankel transformation technique in conjunction with the Fourier–Bessel series approach to achieve added virtual mass incremental factors. The dynamic behavior of non-rectangular plates in contact with bounded fluid was considered by Watts et al. [42] based on a semi-analytical technique. They applied the element-free Galerkin approach and moving Kriging shape functions based on Mindlin plate theory for modeling the structure. Jeong [17] developed a hydroelastic model to analyze the vibration of two annular plates coupled with a bounded compressible fluid based on the Rayleigh–Ritz method by taking the finite element approach. He showed that by increasing the compressibility of the fluid, the natural frequencies decrease.

Stability analysis of various structures subjected to the aerodynamic forces received a great deal of attention due to its prominent role in structural design of aircrafts during several decades. Hence, extensive research related to the aeroelasticity can be found in the literature [7, 9, 11,12,13, 18, 28, 30, 36, 38, 39, 45]. Most of these works investigated the flutter analysis of elastic structures exposed to supersonic air flow [5, 6, 15, 25, 26, 29, 31, 43]. Flutter is a dynamic instability that may appear in supersonic airflow conditions and can damage the structure. When flutter instability occurs, the amplitude of the vibrating structure increases with time. Therefore, the proper design of the lifting surfaces and panels of space and aeronautical vehicles is crucial to prevent flutter instability.

Sawyer [33] investigated buckling and flutter analysis of simply supported laminate plate using the Galerkin approach. According to his paper, bending-extensional coupling and bending-twisting stiffness terms create instability on the behavior of flutter and buckling. Khalafi and Fazilati [19] studied free vibration and supersonic flutter analysis of variable stiffness composite laminated (VSCL) square and skew panels under yawed flow based on the isogeometric approach. They applied first-order shear deformation theory (FSDT) along with the linear piston theory to investigate vibrational and stability behavior of the laminates composed of curvilinear fibers. Zhou et al. [46] developed a unified solution to analyze supersonic flutter characteristics of coupled plate subjected to thermal force with classical and elastic boundary conditions. They expanded the displacement field of FSDT into a combination of two-dimensional Fourier series with auxiliary functions to satisfy arbitrary boundary conditions. Bochkarev and Lekomtsev [8] employed the finite element method to study aero- and hydro-elastic stability of plates interacting with gas flow and ideal fluid for different boundary conditions. They presented various stability diagrams to show the stabilizing and destabilizing effects of gas flow on the dynamic behavior of the structure.

saThe aim of this paper is to study supersonic flutter of rectangular plates interacting with the incompressible, irrotational and inviscid fluid subjected to sloshing on one side of the plate. Both the fifth-order shear deformation theory (FOSDT) and classical plate theory (CPT) are utilized to model the plate along with the first-order piston theory for considering aerodynamic force. Within the framework of Hamilton’s principle, governing equations and boundary conditions are derived and then discretized by the Galerkin method. After validation, the effect of various parameters on vibrational and flutter behavior of the plate are discussed.

2 Formulation

2.1 Geometrical model

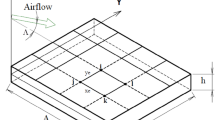
An isotropic rectangular plate with mass density \(\rho \), length a, width b and thickness h interacting with an ideal fluid from one side and subjected to supersonic aerodynamic flow from another side is considered with the coordinates of x and y along the in-plane directions and z along the thickness direction as shown in Fig. 1. The considered fluid is bounded by a rigid tank with width c and depth \({b}_{1}\).

Fig. 1
figure 1

Geometry of the isotropic plate under supersonic flow on one side in the direction of the arrow (in the x–y plane) and interacting with sloshing liquid on the other side

Full size image

2.2 Modified shear deformation theories

The modified shear deformation theories are a group of plate theories that consider nonlinear distributions for the transverse shear stresses along the thickness of the structure. These nonlinear distributions commonly provide the shear stress-free surface conditions on the bottom and top surfaces of the structure. Based on the modified shear deformation theories (MSDT) with the common hypothesis of neglecting thickness deformation, the displacement field can be described as

$$\begin{aligned}&u_{1}\left( x,y,z,t \right) =u\left( x,y,t \right) -\left( z+\frac{h}{2}\right) \frac{\partial w\left( x,y,t \right) }{\partial x}+F\left( z+\frac{h}{2}\right) \zeta (x,y,t),\nonumber \\&u_{2}\left( x,y,z,t \right) =v\left( x,y,t \right) -\left( z+\frac{h}{2}\right) \frac{\partial w\left( x,y,t \right) }{\partial y}+F\left( z+\frac{h}{2}\right) \psi (x,y,t),\nonumber \\&u_{3}\left( x,y,z,t \right) =w(x,y,t),\nonumber \\&f\left( z \right) =F\left( z+\frac{h}{2}\right) , \end{aligned}$$
(1)

where \(u_{1}\left( x,y,t \right) \), \(u_{2}\left( x,y,t \right) \) and \(u_{3}\left( x,y,t \right) \) are the displacement of an arbitrary point along the x axis, y axis and z axis, respectively. F(z) is a continuous function that controls the distribution of transverse shear stress along the thickness of the plate. In this paper, we have considered fifth-order shear deformation theory (FOSDT) of Khorshidi and Karimi [25, 26], and classical plate theory (CPT) by setting \(F\left( {z} \right) =z\left( \frac{1}{h}-\frac{2}{h^{3}}z^{2}+\frac{8}{{5h}^{5}}z^{4} \right) \) and \(F(z)=0\). respectively. u, v and w denote the displacements of middle-surface (\({z}=h/2\)) in the x, y and z-direction, respectively. The unknowns \(\psi \) and \(\zeta \) are the functions related to the shear slopes in the xoz plane and in the yoz plane. As it is seen in Eq. (1), the in-plane displacement components (u1 and u2) include two parts; the first part which is the same as in classical plate theory and the second one which catches shear deformation effects. Additionally, the kinematics of FOSDT includes just five unknowns (\(u, v, w, \psi \) and \(\zeta )\). Within the framework of linear elasticity, the components of linear strain can be written as

$$\begin{aligned} \varepsilon _{xx}= & {} \frac{\partial u}{\partial x}-\left( z+\frac{h}{2}\right) \frac{\partial ^{2}w}{\partial x^{2}}+f(z)\frac{\partial \zeta }{\partial x},\nonumber \\ \varepsilon _{yy}= & {} \frac{\partial v}{\partial y}-\left( z+\frac{h}{2}\right) \frac{\partial ^{2}w}{\partial y^{2}}+f(z)\frac{\partial \psi }{\partial y},\nonumber \\ \varepsilon _{xy}= & {} \frac{1}{2}\left( \left( \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x} \right) -2\left( z+\frac{h}{2}\right) \frac{\partial ^{2}w}{\partial x\partial y}+f(z)\left( \frac{\partial \psi }{\partial x}+\frac{\partial \zeta }{\partial y} \right) \right) ,\nonumber \\ \varepsilon _{xz}= & {} \frac{1}{2}\xi \frac{\partial f\left( z \right) }{\partial z}, \quad \varepsilon _{yz}=\frac{1}{2}\psi \frac{\partial f\left( z \right) }{\partial z}. \end{aligned}$$
(2)

For the considered isotropic plate under the assumption of the plane-stress condition, the components of the stress field can be written as

$$\begin{aligned} \sigma _{xx}= & {} \frac{E}{1-\upsilon ^{2}}(\varepsilon _{xx}+\upsilon \varepsilon _{yy}),\nonumber \\ \sigma _{yy}= & {} \frac{E}{1-\upsilon ^{2}}(\varepsilon _{yy}+\upsilon \varepsilon _{xx}),\nonumber \\ \sigma _{xy}= & {} \frac{E}{2(1+\upsilon )}\varepsilon _{xy},\nonumber \\ \sigma _{xz}= & {} \frac{E}{2(1+\upsilon )}\varepsilon _{xz},\nonumber \\ \sigma _{yz}= & {} \frac{E}{2(1+\upsilon )}\varepsilon _{yz}, \end{aligned}$$
(3)

in which E and \(\nu \) are Young’s modulus and Poisson’s ratio, respectively.

2.3 Piston theory

The piston theory has been extensively applied to evaluate the aerodynamic load of supersonic flow. This theory relates the local normal component of fluid velocity to the local pressure caused by the motion of the structure, in other words, this inviscid aerodynamic model is a simple point-function relationship between the surface deformation and aerodynamic pressure. Piston theory can be utilized for large Mach numbers or high reduced frequencies of unsteady motion, and the surface involved must be nearly plane. In fact, it has been shown that the local pressure exerted on the structure can be written in the expansions of thickness ratio and the inverse of the Mach number. For high Mach numbers, the contribution of higher-order terms is negligible and as a result, a point-function relationship will be obtained for anticipating aerodynamic load on the surface of the panel [32]. Generally, different types of nonlinear and linear panel flutter are depicted in Table 1. A great deal of research has shown that first-order piston theory has proper and acceptable accuracy for flows with Mach number greater than 1.7. The aerodynamic pressure exerted on the structure according to the first-order piston theory can be expressed as [10]

$$\begin{aligned} {{P}}_{a}= & {} -\left( \varUpsilon _{1}\frac{\partial w\left( {{x}},{{y}},{{t}} \right) }{\partial x}\cos \theta +\varUpsilon _{1}\frac{\partial w\left( {{x}},{{y}},{{t}} \right) }{\partial y}\sin \theta +\varUpsilon _{2}\frac{\partial w\left( {{x}},{{y}},{{t}} \right) }{\partial t}\right) ,\nonumber \\ \varUpsilon _{1}= & {} \frac{\rho _{\infty }U_{\infty }^{2}}{\sqrt{M^{2}-1} },\nonumber \\ \varUpsilon _{2}= & {} \frac{1}{U_{\infty }}\frac{\rho _{\infty }U_{\infty }^{2}}{\sqrt{M^{2}-1} }\frac{M^{2}-2}{M^{2}-1}, \end{aligned}$$
(4)

where \(M, \theta \), \(\rho _{\infty }\) and \(U_{\infty }\) are Mach number, yaw angle, air density and air stream velocity, respectively, and t denotes the time It must be noted that the supersonic flow is parallel to the plate surface, and the yaw angle is measured from the positive direction of the x-axis as seen in Fig. 1.

Table 1 Comparison study of flutter characteristics for isotropic square plate
Full size table

2.4 Formulation of fluid–structure interaction

According to the linearity of the present problem, it is possible to consider the motions of fluid as a combination of bulging modes and sloshing modes. Sloshing modes are caused by the rigid motions of the tank, whereas bulging modes are due to the effects of plate vibration on the fluid. As the fluid is assumed to be ideal, the fluid potential velocity \(\varPhi _{0}\) is definable for that as follows:

$$\begin{aligned} \vec {V}={\vec {\nabla }\varPhi }_{0}, \end{aligned}$$
(5)

where \(\vec {\nabla }\) denotes the gradient operator. Moreover, the continuity equation for an ideal fluid can be expressed as

$$\begin{aligned} \vec {\nabla }\vec {V}=0. \end{aligned}$$
(6)

Substituting Eq. (5) into Eq. (6) leads to the Laplace equation as follows:

$$\begin{aligned} \nabla ^{2}\phi _{0}=\frac{\partial ^{2}\phi _{0}}{\partial x^{2}}+\frac{\partial ^{2}\phi _{0}}{\partial y^{2}}+\frac{\partial ^{2}\phi _{0}}{\partial z^{2}}=0. \end{aligned}$$
(7)

The fluid potential velocity can be divided into fluid potential velocity due to fluid sloshing \(\varPhi _{\mathrm{S}}\) and fluid bulging \(\varPhi _{\mathrm{B}}\):

$$\begin{aligned} \varPhi _{0}=\varPhi _{\mathrm{B}}+\varPhi _{\mathrm{S}}. \end{aligned}$$
(8)

The fluid boundary conditions are simply satisfied using this division. By inserting Eq. (8) into Eq. (7), the governing equations of the fluid are obtained:

$$\begin{aligned}&\nabla ^{2}\phi _{\mathrm{B}}=0, \end{aligned}$$
(9)
$$\begin{aligned}&\nabla ^{2}\phi _{\mathrm{S}}=0. \end{aligned}$$
(10)

Impermeability constraints on the boundaries of the fluid can be written as follows:

$$\begin{aligned}&\hbox {at}\, x=0 \Rightarrow \frac{\partial \phi _{\mathrm{B}}}{\partial x}=\frac{\partial \phi _{\mathrm{S}}}{\partial x}=0,\nonumber \\&\hbox {at}\, x=a \Rightarrow \frac{\partial \phi _{\mathrm{B}}}{\partial x}=\frac{\partial \phi _{\mathrm{S}}}{\partial x}=0,\nonumber \\&\hbox {at}\, y=0 \Rightarrow \frac{\partial \phi _{\mathrm{B}}}{\partial y}=\frac{\partial \phi _{\mathrm{S}}}{\partial y}=0,\nonumber \\&\hbox {at}\, z=c \Rightarrow \frac{\partial \phi _{\mathrm{B}}}{\partial z}=\frac{\partial \phi _{\mathrm{S}}}{\partial z}=0,\nonumber \\&\hbox {at}\, z=0 \Rightarrow \frac{\partial \phi _{\mathrm{S}}}{\partial z}=0. \end{aligned}$$
(11)

The assumption of no bulging mode on the free surface of the fluid leads to

$$\begin{aligned} \hbox {at}\, y=b_{1} \Rightarrow \phi _{\mathrm{B}}=0. \end{aligned}$$
(12)

The velocities of the fluid and the vibrating plate are equal at the interface of the container and the plate because they hold their perfect contact during vibration, so the following boundary condition is the fundamental coupling equation which relates the motions of the fluid to the structure:

$$\begin{aligned} \hbox {at}\, z=0 \Rightarrow \frac{\partial \phi _{\mathrm{B}}}{\partial z}=\frac{\partial w}{\partial t}. \end{aligned}$$
(13)

Under the assumption of harmonic oscillation of the fluid and based on the separation of variables method, the fluid potential velocity due to fluid sloshing and fluid bulging can be separated as

$$\begin{aligned}&\varPhi _{\mathrm{B}}\left( {{x}},{{y}},{z},{{t}} \right) =X_{\mathrm{B}}(x)Y_{\mathrm{B}}(y)Z_{\mathrm{B}}(z)\, {\dot{T}}(t), \end{aligned}$$
(14)
$$\begin{aligned}&\varPhi _{\mathrm{S}}\left( {{x}},{{y}},{z},{{t}} \right) =X_{\mathrm{S}}(x)Y_{\mathrm{S}}(y)Z_{\mathrm{S}}(z)\,{\dot{T}}(t). \end{aligned}$$
(15)

Substitution Eqs. (14, 15) into Eqs. (9, 10), one obtains

$$\begin{aligned}&\frac{1}{{X}_{\mathrm{B}}(x)}\frac{d^{2}{X}_{\mathrm{B}}(x)}{\mathrm{d}x^{2}} +\frac{1}{{Y}_{\mathrm{B}}(y)}\frac{d^{2}{Y}_{\mathrm{B}}(y)}{\mathrm{d}y^{2}} +\frac{1}{{Z}_{\mathrm{B}}(z)}\frac{d^{2}{Z}_{\mathrm{B}}(z)}{\mathrm{d}z^{2}}=0, \end{aligned}$$
(16)
$$\begin{aligned}&\frac{1}{{X}_{\mathrm{S}}(x)}\frac{d^{2}{X}_{\mathrm{S}}(x)}{\mathrm{d}x^{2}} +\frac{1}{{Y}_{\mathrm{S}}(y)}\frac{d^{2}{Y}_{\mathrm{S}}(y)}{\mathrm{d}y^{2}} +\frac{1}{{Z}_{\mathrm{S}}(z)}\frac{d^{2}{Z}_{\mathrm{S}}(z)}{\mathrm{d}z^{2}}=0. \end{aligned}$$
(17)

Equations (16, 17) can easily be converted to the following decoupled equations:

$$\begin{aligned}&\frac{1}{{X}_{\mathrm{B}}(x)}\frac{d^{2}{X}_{\mathrm{B}}(x)}{\mathrm{d}x^{2}}=\pm \, p_{1}^{2},\nonumber \\&\frac{1}{{Y}_{\mathrm{B}}(y)}\frac{d^{2}{Y}_{\mathrm{B}}(y)}{\mathrm{d}y^{2}}=\pm \, q_{1}^{2},\nonumber \\&\frac{1}{{Z}_{\mathrm{B}}(z)}\frac{d^{2}{Z}_{\mathrm{B}}(z)}{\mathrm{d}z^{2}}=\mp \left( p_{1}^{2}+q_{1}^{2}\right) , \end{aligned}$$
(18)
$$\begin{aligned}&\frac{1}{{X}_{\mathrm{S}}(x)}\frac{d^{2}{X}_{\mathrm{S}}(x)}{\mathrm{d}x^{2}}=\pm \, p_{2}^{2},\nonumber \\&\frac{1}{{Y}_{\mathrm{S}}(y)}\frac{d^{2}{Y}_{\mathrm{S}}(y)}{\mathrm{d}y^{2}}=\mp \left( p_{2}^{2}+q_{2}^{2}\right) ,\nonumber \\&\frac{1}{{Z}_{\mathrm{S}}(z)}\frac{d^{2}{Z}_{\mathrm{S}}(z)}{\mathrm{d}z^{2}}=\pm \, q_{2}^{2}, \end{aligned}$$
(19)

where \(p_{1}^{2} \, p_{2}^{2}\), \(q_{1}^{2}\) and \(q_{2}^{2}\) are arbitrary nonnegative real numbers.

General solution for Eqs. (18, 19) can be written as

$$\begin{aligned} {X}_{\mathrm{B}}(x)= & {} a_{1}\sin {\left( p_{1}x \right) +a_{2}\cos {(p_{1}x)}},\nonumber \\ {Y}_{\mathrm{B}}(y)= & {} a_{3}\sin {\left( q_{1}y \right) +a_{4}\cos {(q_{1}y)}},\nonumber \\ {Z}_{\mathrm{B}}(z)= & {} a_{5}e^{\sqrt{p_{1}{}^{2}+q_{1}{}^{2}} z}+a_{6}e^{-\sqrt{p_{1}{}^{2}+q_{1}{}^{2}} z}, \end{aligned}$$
(20)
$$\begin{aligned} {X}_{\mathrm{S}}(x)= & {} a_{7}\sin {\left( p_{2}x \right) +a_{8}\cos {(p_{2}x)}},\nonumber \\ {Y}_{\mathrm{S}}(y)= & {} a_{9}\sin {\left( q_{2}y \right) +a_{10}\cos {(q_{2}y)}},\nonumber \\ {Z}_{\mathrm{S}}(z)= & {} a_{11}e^{\sqrt{p_{2}{}^{2}+q_{2}{}^{2}} z}+a_{12}e^{-\sqrt{p_{2}{}^{2}+q_{2}{}^{2}} z}. \end{aligned}$$
(21)

Using Eqs. (11–13), and employing the method of separation of variables, the following expression can be found for the fluid velocity potential associated with the bulging and sloshing modes:

$$\begin{aligned}&\displaystyle \phi _{\mathrm{B}}\left( x,y,z,t \right) =\sum \limits _{l_{1}=0}^\infty {\sum \limits _{k_{1}=0}^\infty {A_{l_{1},k_{1}}\left( t \right) \cos \left( \frac{l_{1}\pi x}{a} \right) } {\cos }\left( \frac{\left( 2k_{1}+1 \right) \pi y}{2b_{1}}\right) (e^{S_{1}z}+e^{S_{1}(2c-z)})}, \nonumber \\ \end{aligned}$$
(22)
$$\begin{aligned}&\displaystyle \phi _{\mathrm{S}}\left( x,y,z,t \right) =\sum \limits _{i_{1}=0}^{N_{s}} \sum \limits _{j_{1}=0}^{M_{s}} {B_{i_{1},j_{1}}\left( t \right) \cos {\left( \frac{i_{1}\pi x}{a} \right) {\cosh }(S_{2}y){\cos }\left( \frac{j_{1}\pi z}{c}\right) }},\nonumber \\&\displaystyle \quad {(l}_{1}=k_{1}=0,1,2,\ldots ),(i_{1}=j_{1}=0,1,2,\ldots ),\nonumber \\&S_{1}=\pi \sqrt{{(l_{1}/a)}^{2}+{(2k_{1}+1/(2b_{1}))}^{2}}, \nonumber \\&S_{2}=\pi \sqrt{{(i_{1}/a)}^{2}+{(j_{1}/c)}^{2}}, \end{aligned}$$
(23)

where \({N}_{{s}}\) and \({M}_{{s}}\) specify the terms required to have acceptable accuracy in Eq. (23). \(A_{l_{1},k_{1}}\left( t \right) \) and \(B_{i_{1},j_{1}}\left( t \right) \) are unknown Fourier coefficients relating to the bulging and sloshing modes, respectively. \(A_{l_{1},k_{1}}\left( t \right) \) can be easily obtained with satisfying the boundary condition at the interface of the fluid and plate, i.e., Eq. (13) as follows:

$$\begin{aligned} A_{l_{1},k_{1}}\left( t \right)= & {} \frac{\frac{{\mathrm {coff}}}{ab_{1}}\int _0^a \int _0^{b_{1}} {\frac{\partial w(x,y,t)}{\partial t}\cos \left( \frac{l_{1}\pi x}{a} \right) \cos \left( \frac{\left( 2k_{1}+1\right) \pi y}{2b_{1}} \right) \mathrm{d}y\mathrm{d}x} }{S_{1}\left( 1-e^{{S_{{1}}(2c)}} \right) },\nonumber \\ \hbox {coff}= & {} \left\{ {\begin{array}{ll} 1&{} \hbox {if}\quad l_{1}=k_{1}=0, \\ 2&{} \hbox {if}\quad l_{1}\quad \hbox {or}\quad k_{1}=0, \\ 4&{} \hbox {if}\quad l_{1}\quad \hbox {and}\quad k_{1}=0. \\ \end{array}} \right. \end{aligned}$$
(24)

The kinetic energies of the fluid due to the bulging and sloshing modes can be written as [25, 26]

$$\begin{aligned} T_{\mathrm{fB}}= & {} -\frac{1}{2}\rho _{F}\int _{{V}_{\mathrm{f}}} {\left| {\vec {\nabla }\varPhi }_{\mathrm{B}} \right| ^{2}\mathrm{d}V_{\mathrm{f}}} =-\frac{1}{2}\rho _{F}\int _0^a \int _0^{b_{1}} {\varPhi _{\mathrm{B}}\left( x,y,0,{{t}} \right) \frac{\partial {w(x,}y,{t)}}{\partial t}\mathrm{d}y\mathrm{d}x}, \nonumber \\ T_{\mathrm{fS}}= & {} -\frac{1}{2}\rho _{F}\int _{V_{\mathrm{f}}} {\left| {\vec {\nabla }\varPhi }_{\mathrm{S}} \right| ^{2}\mathrm{d}V_{\mathrm{f}}} =-\frac{1}{2}\rho _{F}\int _0^a \int _{0}^{b_{1}} {\varPhi _{\mathrm{S}}\left( x,y,0,{{t}} \right) \frac{\partial {w(x,}y,{t)}}{\partial t}\mathrm{d}y\mathrm{d}x}. \end{aligned}$$
(25)

An additional equation from the concept of linearized sloshing [2, 3] at the free surface of the fluid can be easily employed as follows:

$$\begin{aligned} \left. \rho _{\mathrm{f}}\frac{\partial \varPhi _{\mathrm{B}}}{\partial y} \right| _{y=b_{1}}+\left. \rho _{\mathrm{f}}\frac{\partial \varPhi _{\mathrm{S}}}{\partial y} \right| _{y=b_{1}}-\left. \rho _{\mathrm{f}}\frac{\omega ^{2}}{g}\varPhi _{\mathrm{S}} \right| _{y=b_{1}}=0, \end{aligned}$$
(26)

where g denotes the acceleration of gravity.

2.5 Equations of motion

The governing equations of motion for the assumed plate are derived using Hamilton’s principle. Therefore, the time integral of the Lagrangian L must be extremized for the considered system in any possible time interval as follows:

$$\begin{aligned} \delta \int _{t_{1}}^{t_{2}} {L\mathrm{d}t=\delta \int _{t_{1}}^{t_{2}} {(T_{\mathrm{p}}+T_{\mathrm{fS}}+T_{\mathrm{fB}}-U+W)\mathrm{d}t=0}}, \end{aligned}$$
(27)

where \(\delta \) and L denote the variation operator and the Lagrangian, respectively. \(T_{\mathrm{p}}\) represents the kinetic energy of the plate, U is the strain energy and W expresses the work done by external force, and they are defined as

$$\begin{aligned} U= & {} \frac{1}{2}\int _A \int _{-h}^0 \left( \sigma _{xx}\varepsilon _{xx}+\sigma _{yy}\varepsilon _{yy} +2\sigma _{xy}\varepsilon _{xy}+{2\sigma }_{xz}\varepsilon _{xz}+2\sigma _{yz}\varepsilon _{yz} \right) \mathrm{d}z \mathrm{d}A, \end{aligned}$$
(28)
$$\begin{aligned} T_{\mathrm{p}}= & {} \frac{1}{2}\rho _{\mathrm{p}}\int _A \int _{-h}^0 \left( \left( \frac{\partial u_{1}}{\partial t}\right) ^{2}+{\left( \frac{\partial u_{2}}{\partial t}\right) }^{2}+{\left( \frac{\partial u_{3}}{\partial t}\right) }^{2}\right) \mathrm{d}z\mathrm{d}A, \end{aligned}$$
(29)
$$\begin{aligned} W= & {} \frac{1}{2}\int _A {\Delta pw}\; \mathrm{d}A. \end{aligned}$$
(30)

Inserting Eqs. (28–30) and Eq. (25) in Eq. (27), and considering Eqs. (2–4) lead to the final displacement form of the governing equations:

$$\begin{aligned}&C_{1}\frac{\partial ^{2}u}{\partial y^{2}}+C_{2}\frac{\partial ^{2}\zeta }{\partial y^{2}}{+\left( A_{1}+C_{1} \right) \frac{\partial ^{2}v}{\partial x\partial y}+\left( A_{2}+C_{2} \right) \frac{\partial ^{2}\psi }{\partial x\partial y}+B}_{1}\frac{\partial ^{2}u}{\partial x^{2}}+B_{2}\frac{\partial ^{2}\zeta }{\partial x^{2}}=\left( I_{1}\frac{\partial ^{2}u}{\partial t^{2}}+I_{4}\frac{\partial ^{2}\zeta }{\partial t^{2}} \right) , \end{aligned}$$
(31)
$$\begin{aligned}&B_{1}\frac{\partial ^{2}v}{\partial y^{2}}+B_{2}\frac{\partial ^{2}\psi }{\partial y^{2}}+{(A}_{1}+C_{1})\frac{\partial ^{2}u}{\partial x\partial y}+\left( A_{2}+C_{2} \right) \frac{\partial ^{2}\zeta }{\partial x\partial y}+C_{1}\frac{\partial ^{2}v}{\partial x^{2}}+C_{2}\frac{\partial ^{2}\psi }{\partial x^{2}}=\left( I_{1}\frac{\partial ^{2}v}{\partial t^{2}}+I_{4}\frac{\partial ^{2}\psi }{\partial t^{2}} \right) ,\nonumber \\ \end{aligned}$$
(32)
$$\begin{aligned}&{{-(D}_{3}+D_{4})\frac{\partial \psi }{\partial y}-2{(D}_{1}+D_{2})\frac{\partial ^{2}w}{\partial y^{2}}+B_{3}\frac{\partial ^{3}\psi }{\partial y^{3}}+B}_{4}\frac{\partial ^{4}w}{\partial y^{4}}{-(D}_{3}+D_{4})\frac{\partial \zeta }{\partial x}+\left( A_{3}+2C_{3} \right) \frac{\partial ^{3}\zeta }{\partial x\partial y^{2}}\nonumber \\&\qquad -{2(D}_{1}+D_{2})\frac{\partial ^{2}w}{\partial x^{2}}+\left( A_{3}+2C_{3} \right) \frac{\partial ^{3}\psi }{\partial y\partial x^{2}}+2\left( A_{4}+2C_{4} \right) \frac{\partial ^{4}w}{\partial y^{2}\partial x^{2}}+B_{3}\frac{\partial ^{3}\zeta }{\partial x^{3}}+B_{4}\frac{\partial ^{4}w}{\partial x^{4}}+{{P}}_{a}\nonumber \\&\quad =\left( -\frac{1}{2}\rho _{\mathrm{f}}\left( \varPhi _{\mathrm{B}}\left( x,{{y}},0,{{t}} \right) +\varPhi _{\mathrm{S}}\left( x{,y,0,t} \right) \right) +I_{1}\frac{\partial ^{2}w}{\partial t^{2}}-I_{2}\frac{\partial ^{4}w}{\partial y^{2}\partial t^{2}}-I_{2}\frac{\partial ^{4}w}{\partial x^{2}\partial t^{2}}-I_{5}\frac{\partial ^{3}\psi }{\partial y\partial t^{2}}-I_{5}\frac{\partial ^{3}\zeta }{\partial x\partial t^{2}} \right) , \end{aligned}$$
(33)
$$\begin{aligned}&-D_{5}\zeta +C_{2}\frac{\partial ^{2}u}{\partial y^{2}}+C_{5}\frac{\partial ^{2}\zeta }{\partial y^{2}}-(D_{3}+D_{4})\frac{\partial w}{\partial x}+\left( A_{2}+C_{2} \right) \frac{\partial ^{2}v}{\partial x\partial y}+\left( A_{5}+C_{5} \right) \frac{\partial ^{2}\psi }{\partial x\partial y}\nonumber \\&\qquad +\left( A_{3}+2C_{3} \right) \frac{\partial ^{3}w}{\partial x\partial y^{2}}+B_{2}\frac{\partial ^{2}u}{\partial x^{2}}+B_{5}\frac{\partial ^{2}\zeta }{\partial x^{2}}+B_{3}\frac{\partial ^{3}w}{\partial x^{3}}=\left( I_{3}\frac{\partial ^{2}\zeta }{\partial t^{2}}+I_{4}\frac{\partial ^{2}u}{\partial t^{2}}+I_{5}\frac{\partial ^{3}w}{\partial x\partial t^{2}}\right) , \end{aligned}$$
(34)
$$\begin{aligned}&-D_{5}\psi -(D_{3}+D_{4})\frac{\partial w}{\partial y}+B_{2}\frac{\partial ^{2}v}{\partial y^{2}}+B_{5}\frac{\partial ^{2}\psi }{\partial y^{2}}+B_{3}\frac{\partial ^{3}w}{\partial y^{3}}+\left( A_{2}+C_{2} \right) \frac{\partial ^{2}u}{\partial x\partial y}\nonumber \\&\qquad +\left( A_{5}+C_{5} \right) \frac{\partial ^{2}\zeta }{\partial x\partial y}+C_{2}\frac{\partial ^{2}v}{\partial x^{2}}+C_{5}\frac{\partial ^{2}\psi }{\partial x^{2}}+\left( A_{3}+2C_{3} \right) \frac{\partial ^{3}w}{\partial y\partial x^{2}}\nonumber \\&\quad =\left( I_{4}\frac{\partial ^{2}v}{\partial t^{2}}+I_{3}\frac{\partial ^{2}\psi }{\partial t^{2}}+I_{5}\frac{\partial ^{3}w}{\partial y\partial t^{2}} \right) . \end{aligned}$$
(35)

2.6 Solution procedure

In this section, we apply the Galerkin weighted residual method to derive solutions for vibration analysis of the simply supported plate. The considered problem has six unknown functions including \(u,v,w,\psi ,\zeta \) and \(\varPhi _{\mathrm{S}}\), and six coupled partial differential equations including Eqs. (31–35) and (26) We must expand the unknown functions in infinite series form in the Galerkin method to minimize the weighted residuals. It can be approximated to the exact solution of the problem by considering the adequate terms in these series. In this paper, trigonometric functions are employed to express unknown functions as follows:

$$\begin{aligned} \{u\left( x,y,t \right) ,\zeta \left( x,y,t \right) \}= & {} \sum \limits _{n=1}^N \sum \limits _{m=1}^M {{\{u}_{m,{n}}, \zeta _{m,{n}}\}\cos {\left( \frac{m\pi x}{a} \right) \sin \left( \frac{n\pi y}{b} \right) }e^{{p}t}},\nonumber \\ \{v\left( x,y,t \right) ,\psi \left( x,y,t \right) \}= & {} \sum \limits _{n=1}^N \sum \limits _{m=1}^M {{\{v}_{m,{n}}, \psi _{m,{n}}\}{\sin {\left( \frac{m\pi x}{a} \right) \cos \left( \frac{n\pi y}{b} \right) }e}^{{p}t}}, \nonumber \\ w\left( x,y,t \right)= & {} \sum \limits _{n=1}^N \sum \limits _{m=1}^M {w_{m,{n}}\sin {\left( \frac{m\pi x}{a} \right) \sin \left( \frac{n\pi y}{b} \right) }e^{{p}t}}. \end{aligned}$$
(36)

Substituting expressions (36) into Eqs. (31–35) and (26), then multiplying the residual functions by the corresponding eigenfunctions, and using the orthogonality lead to a homogeneous system of linear algebraic equations as follows:

$$\begin{aligned} \left[ M \right] \left[ {\ddot{Q}} \right] +\left[ C \right] \left[ {\dot{Q}} \right] +\left[ K \right] \left[ Q \right] =0, \end{aligned}$$
(37)

where [K], [C] and [M] represent the stiffness matrix, damping matrix and mass matrix of the presented model. To solve Eq. (37), we can add the following equation, as aerodynamic damping used here is not proportional:

$$\begin{aligned} \left[ M \right] \left[ {\dot{Q}} \right] -\left[ M \right] \left[ {\dot{Q}} \right] =0. \end{aligned}$$
(38)

By augmenting Eq. (38) in Eq. (37), one obtains

$$\begin{aligned}&\left[ R \right] \left[ {\dot{q}} \right] +\left[ S \right] \left[ q \right] =0, \nonumber \\&\left[ R \right] =\left[ \frac{\left[ 0 \right] \left[ M \right] }{\left[ M \right] \left[ C \right] } \right] ,\left[ S \right] =\left[ \frac{-\left[ M \right] [0]}{ \left[ 0 \right] [K]} \right] ,\left[ q \right] =\left[ {\begin{array}{l} \left[ {\dot{Q}} \right] \\ \left[ Q \right] \\ \end{array}} \right] . \end{aligned}$$
(39)

Assuming solutions of the form \([q]=[f] e^{{p}t}\) and inserting in Eq. (39), the following equation can be written:

$$\begin{aligned} \left( \varOmega \left[ {R} \right] +{[S]} \right) \left[ q \right] =0. \end{aligned}$$
(40)

By multiplying Eq. (40) in \({[S]}^{-1}\) , the following eigenvalue problem is obtained:

$$\begin{aligned} \left( {[S]}^{-1}\left[ {R} \right] +\frac{1}{{p}}I \right) \left[ q \right] =0. \end{aligned}$$
(41)

The non-trivial solution of the relation (37) is obtained when the following determinant equals zero:

$$\begin{aligned} \hbox {det}\left( {[S]}^{-1}\left[ {R} \right] +\frac{1}{{p}}I \right) =0. \end{aligned}$$
(42)

Frequencies of the presented model can be easily obtained as \(\varOmega =\varOmega _{R}+i\omega \) by solving the above characteristic equation, i.e., Eq. (42), in which \(\varOmega _{R}\) is the aerodynamic damping and \(\omega \) represents the natural frequency of the system. Natural frequencies of the system can be obtained by vanishing the aerodynamic force (\(U_{\infty }=0)\).

As the aerodynamic force rises, the eigenvalues and eigenfunctions of the structure vary, and finally the sign of the aerodynamic damping changes from negative to positive at a critical dynamic pressure(\(\lambda _{\mathrm{cr}})\). In fact, instability begins at this critical dynamic pressure and the panel’s amplitude grows exponentially with time.

3 Numerical results

3.1 Validation studies

The solution methodology mentioned in the previous section for the out of plane vibration and stability analysis of the system were coded in mathematical analytical software. Since no research has been carried out for flutter behavior of a plate in interaction with the fluid, demonstration of reliability, applicability and effectiveness of the present model is investigated for two special cases including critical dynamic pressure of a plate in vacuum environment and wet frequencies of an isotropic plate.

Unless otherwise expressed, it is assumed that Young’s modulus \({E}=200\,\hbox {GPa}\), Poisson’s ratio \(\upsilon =0.3\), plate density \(\rho _{\mathrm{p}}=7800\,\hbox {kg/m}^{3}\), fluid density \(\rho _{\mathrm{f}}=1000\, \hbox {kg/m}^{3}\) and the length of the plate \(a=1\,\hbox {m}\). The following parameters are employed to express numerical results in tables and figures.

  • thickness ratio: \(\delta =\frac{a}{h}\)

  • aspect ratio: \(\eta =\frac{a}{b}\)

  • fluid depth ratio: \(\tau =\frac{b_{1}}{a}\)

  • fluid width ratio: \(\varsigma =\frac{c}{a}\)

  • frequency parameter: \({\tilde{\omega }}=\frac{\omega }{2 \pi }a^{2}\sqrt{\rho _{\mathrm{p}} h/D} \)

  • damping parameter: \({\tilde{\varOmega }}_{R}=\frac{\varOmega _{R}}{2 \pi }a^{2}\sqrt{\rho _{\mathrm{p}} h/D} \)

Moreover, the ratios of the frequency and damping of the plate under supersonic flow to the fundamental frequency of the dry plate are denoted by \({\bar{\omega }}_{(m,n)}=\frac{{\tilde{\omega }}_{(m,n)}}{{\tilde{\omega }}_{dry-(1,1)}}\) and \({\bar{\varOmega }}_{(m,n)}=\frac{{\tilde{\varOmega }}_{R(m, n)}}{{\tilde{\omega }}_{\mathrm{dry}-(1,1)}}\), respectively.

3.1.1 Flutter boundary of an isotropic plate

To confirm the effectiveness of the present formulation with previously published works in the case of flutter behavior, the critical dynamic pressure parameter (\({\bar{\lambda }}_{\mathrm{cr}})\) and critical flutter frequency (\({\tilde{\omega }}_{\mathrm{cr}})\) of an isotropic plate with \(\delta =100\) and \(\upsilon =0.3\) are compared with those reported by Singha and Ganapathi [37], Valizadeh et al. [41] and Grover et al. [16] in Table 2. It is seen that there is an excellent agreement between the present model and available results in the literature for the flutter boundary of a plate in contact with air.

Table 2 Frequency parameter of isotropic plate coupled with bounded fluid
Full size table

3.1.2 Frequencies of an isotropic plate interacting with inviscid fluid

As another validation study, the frequencies corresponding to various modes of a square plate coupled with water for different percentages of fluid depth are tabulated in Table 3. The obtained results in this table are calculated for \({a}={b}=10\,\hbox {m}\), \({h}=0.15\,\hbox {m}\), \({c}=100\,\hbox {m}\), \({E}=25\,\hbox {GPa}\), \(\upsilon =0.15\). As observed, again, suitable compatibility is seen by comparing the current model and available data including Ritz solution of Khorshid and Farhadi [20] and the finite element of Uğurlu et al. [40]. As seen in Tables 2 and 3, results reported by CPT are greater than those obtained by FOSDT. This is due to the fact that the rotary inertia and transverse shear deformations have dissimilar effects through the thickness of the structure in CPT and FOSDT. In fact, CPT neglects transverse shear stress and rotary inertia effects and therefore overestimates natural frequencies.

3.2 Convergence study

The Galerkin method can provide reliable solutions depending on the choice of trial functions and the number of terms used in the series. Table 3 shows the convergence study of frequency parameter and critical dynamic pressure parameter for the vibrating plate in contact with fluid in order to establish necessary degrees of freedom in the expansion of the displacements and rotations relating to the structure. It is seen that by increasing the required terms in series, the natural frequencies and critical dynamic pressure approach to more desirable amounts. Besides, it can be concluded that \({N}={M}=10\) leads to accurate results in this study. The numerical results reported in Table 3 were calculated for \(\tau =\varsigma =0.5\), \(\eta =1\) and \(\delta =10\).

Table 3 Convergence of frequency parameter and critical dynamic pressure for isotropic plate in contact with liquid (\({N}_{1}={M}_{1}=6\))
Full size table

3.3 Results and discussion

In this section, results for stability and vibration analysis of rectangular plates coupled with inviscid fluid under supersonic flow are presented in tabular and graphical form for variou parameters of the plate, fluid and aerodynamic force. Since the present problem may seem complicated, the four following cases of the system are considered to demonstrate vibration and flutter behavior of the plate:

  1. Case (a)

    A rectangular plate without liquid interaction in the absence of supersonic flow, i.e., \({U_{\infty }=b}_{1}=0\)

  2. Case (b)

    A rectangular plate without liquid interaction in the presence of supersonic flow, i.e., \({b}_{1}=0\)

  3. Case (c)

    A rectangular plate interacting with liquid in the absence of supersonic flow, i.e., \(U_{\infty }=0\)

  4. Case (d)

    A rectangular plate interacting with liquid in the presence of supersonic flow.

Fig. 2
figure 2

Various of mode shapes and natural frequencies of the isotropic plate, a without liquid in the absence of aerodynamic force, b without liquid and in the presence of supersonic flow, c interacting with liquid in the absence of supersonic flow, d interacting with liquid in the presence of supersonic flow

Full size image
Fig. 3
figure 3

Variations of the first five frequency ratios (\({\bar{\omega }})\) and damping ratios (\({\bar{\varOmega }})\) of the square plate without liquid versus variations of the dynamic pressure parameter (\({\bar{\lambda }})\)

Full size image
Fig. 4
figure 4

Variations of the first five frequency ratios (\({\bar{\omega }})\) and damping ratios (\({\bar{\varOmega }})\) of the square plate in contact with liquid (\(\tau =0.4)\) versus variations of the dynamic pressure parameter (\({\bar{\lambda }})\)

Full size image
Fig. 5
figure 5

Variations of the first five frequency ratios (\({\bar{\omega }})\) and damping ratios (\({\bar{\varOmega }})\) of the square plate in contact with liquid (\(\tau =0.8)\) versus variations of the dynamic pressure parameter (\({\bar{\lambda }})\)

Full size image

Figure 2 shows different eight dry and wet mode shapes of the isotropic plate for four abovementioned cases a–d. Herein \(\lambda _{\mathrm{cr}\hbox {-}\mathrm{dry}}\) and \(\lambda _{\mathrm{cr}\hbox {-}\mathrm{wet}}\) express the critical dynamic pressure parameter in the second and fourth case, respectively. It is seen than mode shapes are entirely symmetric in the absence of aerodynamic flow, while the symmetry of mode shapes is violated in the presence of supersonic air flow. It must be mentioned that by increasing the supersonic flow velocity the position of peaks shifts and some nodes appear in mode shapes. Instability of the square plate under consideration (case b) begins when the dynamic pressure parameter is greater than \(\lambda _{\mathrm{cr}\hbox {-}\mathrm{dry}} =511.22\), and two first mode shapes of the plate merge to each other. As seen in case (c), the coupling between plate and fluid changes the mode shapes as compared to case (a), and it creates a remarkable distortion in the wet mode shapes especially for higher modes. This is due to the bulging and sloshing effects of fluid on the overall kinetic energy of the system. For the square plate coupled with fluid, i.e., case (d), instability begins later than a plate in vacuum at \(\lambda _{\mathrm {cr}\hbox {-}\mathrm{wet}} =619.542\). Additionally, it is seen that in contrast to case (b) the flutter phenomenon occurs due to the coalescence of the second and third modes. The numerical results for Fig. 2 are extracted for \(\delta =100\), \(\eta =1\) and \(\tau =\varsigma =0.5\)

Figures 3, 4 and 5 show the variations of the frequency ratio (\({\bar{\omega }})\) and damping ratio (\({\bar{\varOmega }})\) against variations of dynamic pressure (\({\bar{\lambda }})\) of the supersonic flow for the first five modes of the system with \(\delta =40\). Figure 3 is equivalent to case (a), and the tank is empty of fluid. From this figure, it is seen that the first and second modes of the plate coalesce into one mode at \({\bar{\lambda }}=446.74\). If increasing dynamic pressure goes on, other instabilities will occur at higher dynamic pressure. For instance, a second instability happens at \({\bar{\lambda }}=902.34\) The tank has been considered to be full of fluid by 40% in Fig. 4. According to this figure, the second mode shape of the system is coupled to the third mode shape at \({\bar{\lambda }}=560.12\). In contrast to the previous case, i.e., Fig. 3, this instability is not permanent and coalescence of modes is eliminated at \({\bar{\lambda }}_{R}=988.95\). In other words, a post-stable region is formed due to the effects of fluid. Herein, \({\bar{\lambda }}_{R}\) denotes the critical dynamic pressure which coupling of modes is released. Fluid depth ratio is assumed to be 0.8 in Fig. 5. As seen from this figure, changing the level of fluid alters the kinetic energies related to the bulging and sloshing modes, and as a consequence new branches of instability appear in Fig. 5. In fact, the first coupling of modes occurrs due to the approaching third and fourth mode shapes. Moreover, the length of the post-stable region (\(\hbox {LPSR}={\bar{\lambda }}_{R}-{\bar{\lambda }}_{\mathrm{cr}})\) has been enhanced from 428.83 to 465.84 as compared to the previous case.

Fig. 6
figure 6

Variations of the first five frequency ratios (\({\bar{\omega }})\) of the square plate in contact with liquid (\(\tau =0.5)\) versus variations of the dynamic pressure parameter (\({\bar{\lambda }})\) using classical plate theory (CPT) and fourth-order shear deformation theory (FOSDT)

Full size image

Figure 6 displays the effects of supersonic flow on the first five wet frequencies of a square plate with \(\tau =\varsigma =0.5\) formulated on CPT and FOSDT. It is evident that natural frequencies and critical dynamic pressure predicted by CPT are greater than those predicted by FOSDT which is due to the effects of transverse shear deformation and rotary inertia on dynamic and stability behavior of the structure. It can be concluded that transverse shear deformation has a destabilizing effect, and it can expedite the flutter phenomenon. The thickness ratio of the plate is taken to be \(\delta =10\) in this figure to highlight the transverse shear deformation effects.

Fig. 7
figure 7

Effects of fluid depth ratio on critical dynamic pressure parameter of the plate interacting with liquid

Full size image

Figure 7 depicts the influences of fluid depth ratio on the stability of the square plate. It is observed from this figure that, apart from the depth ratio, the existence of fluid around the structure creates a postponement in the occurrence of flutter. In addition, some jumping points appear in this figure which is due to the shifting of the mode shapes involved in the flutter. Moreover, it can be concluded that the variations of the critical dynamic pressure versus fluid depth ratio vary monotonically as far as there is no changing in mode shapes participating in the flutter. It is worth mentioning that the flutter onset varies sharply for the low values of the fluid depth ratio. However, this rate reduces as the fluid depth ratio increases. This means that the stability of the system mainly depends on the fluid near the bottom of the tank rather than the fluid near the free surface of the tank.

Fig. 8
figure 8

Effects of fluid depth ratio on the length of post-stable region of the plate interacting with liquid

Full size image

As discussed in the previous figures, the presence of fluid can form a temporary instability in the dynamic behavior of the wet plate. Figure 8 displays effects of fluid depth ratio on the length of post-stable region (LPSR). There are four different regions depending on the level of fluid according to this figure. The first region (\(\tau <0.17)\) is formed due to the coalescence of the first two mode shapes, and the conventional supersonic flutter instability occurs. When \(0.17<\tau <0.38\), again, the first and second mode shapes are coupled to each other but with forming a post-stable region. It is seen that for greater values of \(\tau >0.17\), a post-stable region arises because of the coupling of higher modes. For values of fluid depth ratio between 0.38 and 0.61, the second and third mode shapes and for higher values of fluid depth ratio (\(\tau >0.61)\), the third and fourth mode shapes coalesce into a single mode. It can be concluded that the length of the post-stable region rises as the fluid depth ratio increases. Numerical results in Figs. 7 and 8 have been calculated for a plate with \(\delta =40\)

4 Conclusion

In this work, both the fifth-order shear deformation theory and classical plate theory are adopted to investigate the vibrational and flutter behavior of isotropic plates coupled to fluid. The fluid is considered to be inviscid, irrotational and incompressible and the fluid velocity potential due to sloshing and bulging motions is derived satisfying the Laplace equation. The linear piston theory is employed to evaluate the supersonic aerodynamic pressure over the plate. Governing equations of the rectangular plate subjected to supersonic flow on one side and coupled to fluid on the other side are obtained on the basis of Hamilton’s principle. Rotations and displacements of the plate are assumed in terms of trigonometric functions, and the Galerkin approach is taken to obtain the dynamic response of the simply supported plate. Convergence and comparison studies confirm the validity and reliability of the current model. Numerical results reveal that the presence of fluid has a significant effect on the dynamic response of the system, and that it gives a distortion of the mode shapes in vacuum. Also, it is observed that fluid–structure interaction has a major effect on the flutter behavior of the system. It may change the modes participating in the flutter instability and give rise to a post-flutter stable region depending on the level of fluid. Additionally, it is observed that the extension of the post-stable region is influenced by the fluid depth ratio, and that it increases by enhancing the fluid level.