Investigation of aeroelastic instabilities for a thin panel in turbulent flow

Abstract

The dynamic response of a thin buckled panel in a supersonic wind-tunnel experiment is investigated. Measured time histories of the panel displacement and velocity show co-existing, nonlinear responses with features of periodic and chaotic oscillations. Fully coupled computational analyses are conducted in order to study and interpret the aeroelastic phenomena observed during the experiments. A computationally efficient modeling framework is formulated with a nonlinear structural reduced-order model and enriched piston theory aerodynamics for the mean flow. The simulations predict the onset of the chaotic motions observed in the experiments, albeit with an approximately 21% increase in the oscillation amplitude. A linearized equation governing the distance between neighboring solutions is derived and used to compute the largest Lyapunov exponent in order to prove the existence of chaos. A modified Riks analysis highlights the co-existence of multiple equilibrium positions which predisposes the nonlinear system to chaos. The system’s sensitivity to cavity pressure, temperature differential, and initial conditions is also investigated. Variation of the cavity pressure and temperature differential yields additional regions of dynamic activity that were not explored during the experiments.

1 Introduction

The intersection of nonlinear plate dynamics and high-speed flow has been, and continues to be, an active area of computational research [8, 10, 17, 18, 22, 24, 30, 32, 38, 41]. Plates represent a basic structural component in the design of aerospace vehicles, particularly with regards to the aircraft’s outer mold line. The weight-constrained nature of these platforms motivates the use of thin panels that inevitably operate in the nonlinear regime. Moreover, coupling between the extreme environmental loads associated with high-speed flows and the nonlinear structure drives unanticipated responses that are path-dependent and evolve over long time records [30]. These issues highlight the importance of carefully designed experiments and computational studies in order to develop and improve fluid-structure interaction (FSI) models as well as understand the physical mechanisms governing the coupled problem.

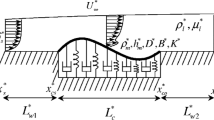
Experiments on FSI are necessary for a comprehensive understanding of the flow physics and the associated structural response. Early FSI experiments focused on identification of panel flutter boundaries for evaluation of engineering-level tools and to provide guidelines on avoiding detrimental aeroelastic behavior during the design process [14,15,16, 21, 43]. However, the use of discrete instrumentation limited the ability to characterize the loads and response over the entire test article. In addition, the experiments did not consider post-flutter behavior. These issues have stimulated a renewed interest in FSI experiments [5, 7, 11, 12, 39, 40, 44, 46], many of which have relied on recent advances in full-field measurement techniques to characterize the structural response, loading conditions, and flow-field. Small-amplitude forcing of the test articles due to turbulent boundary layer pressure fluctuations and shock/boundary-layer interaction (SBLI) was measured in a majority of the experiments. However, Spottswood et al. [44] and Brouwer et al. [5] demonstrated that modulation of the temperature differential between the frame and panel as well as the cavity pressure in a wind tunnel, as illustrated in Fig. 1, can excite large-amplitude, cross-well oscillations for a buckled panel. The experimental results from the latter demonstrated that a transition from chaotic to periodic dynamics occurred as the temperature differential decreased. Additionally, Daub et al. [12] measured large-amplitude, transient motions of a thin panel excited by heating in the absence of an SBLI which eventually subsided as the temperature increased. While such data are clearly important, there are several limitations associated with aeroelastic experiments. First, ground-based facilities are unable to replicate all flow and boundary conditions necessary for an in-depth exploration of the parameter space [23]. In addition, the coupled nature of the problem restricts the ability to study the independent effects of various flow mechanisms on the aeroelastic instabilities and post-flutter behavior. Finally, prohibitive operational costs limit the use of experiments to adequately explore the operational space.

Fig. 1

Top and side view of a generic thin panel and rigid support showing the cavity pressure, $p_c$, static pressure differential, $\varDelta p$, and the temperature differential between the frame and panel, $\varDelta T$. The subscripts p and f denote the panel and frame properties, respectively

Given these restrictions, computational modeling must play a role in the analysis of FSI. While high-fidelity models such as computational fluid dynamics (CFD) and finite element (FE) are necessary for a comprehensive understanding of the fluid and structural domains, respectively, computational costs generally prohibit their use for aeroelastic predictions over the life of a structure [3]. This has motivated the use of model reduction strategies to study FSI [8,9,10, 13, 17, 18, 22, 24, 32, 37, 38]. The computational frameworks are generally formulated with a nonlinear, Galerkin-based structural model coupled to piston theory aerodynamics. Dowell [19] and Mei et al. [32] provide excellent reviews on panel flutter including the influence of panel geometry, boundary conditions, cavity acoustics, static pressure differentials, and thermal effects. Notable findings include the sensitivity of the flutter boundary to small variations in the static pressure differential and that thermal buckling can lead to an earlier onset of dynamic instabilities. Thermal buckling also has the potential to produce non-simple periodic as well as chaotic motions [8, 20]. The co-existence of multiple potential wells for a buckled structure that grow further apart as the temperature differential increases results in the onset of chaos. Nydick et al. [38] also demonstrated that panel curvature can produce similar behavior to that of a buckled structure. More recent studies have focused on incorporating three-dimensional flow effects, viscous-inviscid interactions, and SBLI into the fluid loads using an enriched piston theory formulation [4, 9]. In particular, SBLI has been shown to produce significant variations in the flutter boundaries and post-flutter response. Finally, Miller et al. [37], Deshmukh et al. [13], and Freydin et al. [24] demonstrated that turbulent boundary layer fluctuating pressure loads affect instability onset. To date, correlations between the simulations and experiments demonstrate the ability of reduced-order models (ROMs) to reasonably capture flutter onset for a wide range of parameters.

The Air Force Research Laboratory Structural Sciences Center recently conducted a series of experiments in the Research Cell 19 (RC-19) wind tunnel to explore the response of a thin panel to turbulent flows. Multiple instances of coexisting, nonlinear panel responses were measured using full-field, non-contact techniques. A calibrated, reduced-order computational aeroelastic framework is implemented in this study to investigate the underlying physics governing the measured panel behavior. The models enable efficient exploration of the highly nonlinear parameter space including the effects of different operating conditions, modeling assumptions, and initial conditions on the aeroelastic response. This is in contrast to the experiments, where exploring these effects is generally not feasible. The computational results will guide the development of future experiments targeting aeroelastic instabilities and inform the continued enhancement of the reduced-order framework.

The remainder of the paper is organized as follows. The computational models for aeroelastic response prediction are detailed in Sect. 2. This includes a discussion of the enriched piston theory model for the prediction of unsteady pressure and the nonlinear structural ROM. An approach to identify chaos using the governing aeroelastic equations is presented in Sect. 3. A brief overview of the RC-19 experiments is discussed in Sect. 4. The computational configuration as well as model calibration, evaluation, and application are presented in Sects. 5–8. In regards to model calibration, measurements of the installed panel are used to update the structural model parameters. Time histories of the measured deformation are then used to benchmark the aeroelastic model. Identification of chaos in the aeroelastic response is discussed in Sect. 9. Concluding remarks are provided in Sect. 10.

2 Computational models for fluid-structure interactions

A reduced-order simulation framework for efficient and robust aeroelastic response prediction is constructed. The formulation relies on a piston theory model for the mean pressure loading and does not include fluctuations from the turbulent boundary layer. The sensitivity of the predictions to acoustic loading from the turbulent boundary layer is a topic of future research. A steady Reynolds-averaged Navier–Stokes (RANS) analysis is also used to enrich the piston formulation and is assumed to capture three-dimensional as well as boundary layer effects for flow over a flat, rigid plate. This enrichment is necessary when considering the effects of SBLI on FSI, which is an objective of ongoing research. The structure is approximated using a nonlinear ROM, which is applicable to a broad range of structural configurations.

2.1 Enriched Piston theory

Piston theory is a simple and effective strategy for aeroelastic load prediction [33]:

$$\begin{aligned} \begin{aligned}&p(x,y,t) \\&\quad = p_{\infty } + \gamma p_{\infty } \Bigg \{ c_1 \frac{v_n(x,y,t)}{a_{\infty }} + c_2 \left( \frac{v_n(x,y,t)}{a_{\infty }} \right) ^2\\&\qquad + c_3 \left( \frac{v_n(x,y,t)}{a_{\infty }} \right) ^3 \Bigg \} \end{aligned}\nonumber \\ \end{aligned}$$

(1)

where the piston velocity, $v_n$, is given as:

$$\begin{aligned} v_n(x,y,t) = U_{\infty } w'(x,y,t) + {\dot{w}}(x,y,t) \end{aligned}$$

(2)

In the above equations, p is the pressure, U is the velocity, a is the speed of sound, $w'$ is the surface inclination in the x-direction, ${\dot{w}}$ is the surface velocity, and the subscript $\infty$ denotes freestream conditions. Since the experiments were conducted for a Mach number of approximately 2.0, the coefficients $c_1$, $c_2$, and $c_3$ are obtained from the second-order theory of Van Dyke [45]:

$$\begin{aligned} \begin{aligned} c_1&= \frac{M_{\infty }}{\sqrt{M_{\infty }^2 - 1}} \\ c_2&= \frac{M_{\infty }^4 (\gamma +1) - 4(M_{\infty }^2 - 1)}{4(M_{\infty }^2 - 1)^2} \\ c_3&= 0 \end{aligned} \end{aligned}$$

(3)

As the Mach number, M, tends to infinity, Van Dyke’s expression converges to second-order classical piston theory [29]. Note that piston theory is a quasi-steady model for the aerodynamic pressure. This assumption is reasonable due to the disparity between the extreme fluid velocities and the frequencies associated with structural vibration [30]. In order to extend these expressions to a broader range of flow conditions, including those with three-dimensional flow effects and inviscid–viscous interactions, the freestream conditions in Eqs. 1–3 are replaced by local flow quantities that vary spatially along the surface [4]:

$$\begin{aligned}&p(x,y,t) \nonumber \\&\quad = p_{l}(x,y) + \gamma p_{l}(x,y) \Bigg \{ \frac{M_{l}(x,y)}{\sqrt{M_{l}(x,y)^2 - 1}} \frac{v_n(x,y,t)}{a_{l}(x,y)} \nonumber \\&\qquad + \frac{M_{l}(x,y)^4 (\gamma +1) - 4(M_{l}(x,y)^2 - 1)}{4(M_{l}(x,y)^2 - 1)^2}\nonumber \\&\qquad \left( \frac{v_n(x,y,t)}{a_{l}(x,y)} \right) ^2 \Bigg \} \end{aligned}$$

(4)

$$\begin{aligned}&v_n(x,y,t) = U_{l}(x,y) w'(x,y,t) + {\dot{w}}(x,y,t) \end{aligned}$$

(5)

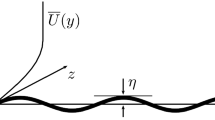
where the local quantities are denoted by the subscript l and are extracted from a steady RANS analysis over a flat, rigid surface. Surface inclination and velocity effects are then included in Eq. 4 as a quadratic perturbation about $p_l$. The local pressure is computed at the surface since it is assumed to be constant through the boundary layer. However, the local speed of sound, $a_l$, and local velocity, $U_l$, are not constant through the boundary layer as illustrated in Fig. 2. Thus, both quantities are extracted along an effective shape, which is assumed to capture the displacement effects of the flat plate boundary layer on the external flow [1]. The effective shape for flow over an undeformed surface is extracted using a modified piston theory model, as described in McNamara et al. [31]. Note that a comparison of the aeroelastic predictions using classical and enriched piston theory is provided in Sect. 8.

Fig. 2

Representative velocity contours for a turbulent boundary layer (TBL) over a flat plate showing the approximate locations of the boundary layer thickness, $\delta _{TBL}$, and effective shape

2.2 Structural reduced-order model

A structural ROM with nonlinear geometric effects is implemented in order to reduce the computational costs associated with structural response prediction. Construction of a robust structural ROM requires the identification of key features in the structural response which must be included in the basis identification. The governing equation for the structural ROM is formulated in the undeformed reference configuration as:

$$\begin{aligned} \frac{\partial }{\partial {\varvec{X}}_k}\left( {\varvec{F}}_{ij} {\varvec{S}}_{ij}\right) + \rho _0{\varvec{b}}_i^0 = \rho _0\ddot{u}_i \end{aligned}$$

(6)

where ${\varvec{S}}$ is the second Piola–Kirchhoff stress tensor, $\rho _0$ is the density with respect to the reference configuration, $\ddot{u}$ is the acceleration field, ${\varvec{b}}^0$ is the vector of body forces, and ${\varvec{F}}$ is the deformation gradient tensor:

$$\begin{aligned} {\varvec{F}}_{ij} = \varvec{\delta }_{ij} + \frac{\partial u_i}{\partial {\varvec{X}}_j} \end{aligned}$$

(7)

which is a function of the displacement field, u, and the Kronecker delta, $\varvec{\delta }$. The above equations are assumed to depend on the position, ${\varvec{X}} \in \varOmega _0$. The stress–strain relation is obtained from the Duhamel–Neumann form of the Helmholtz free energy equation [25]:

$$\begin{aligned} {\varvec{S}}_{ij}= & {} \rho _0 \left( \frac{\partial {\mathcal {F}}}{{\varvec{E}}_{ij}} \right) _T \nonumber \\= & {} {\varvec{C}}_{ijkm} \left[ {\varvec{E}}_{km} - \varvec{\alpha }_{km} \left( T - T_{ref} \right) \right] \end{aligned}$$

(8)

where ${\mathcal {F}}$ is the Helmholtz free energy per unit mass, ${\varvec{E}}$ is the green strain tensor, ${\varvec{C}}$ is the fourth-order elasticity tensor, $\varvec{\alpha }$ is the second-order tensor of thermal expansion, T is the temperature, and $T_{ref}$ is the reference temperature.

The displacement, $u_i$, and temperature, T, fields are defined in modal form as:

$$\begin{aligned} u_i({\varvec{X}},t)= & {} \varSigma _{j = 1}^{N_U} \eta _j(t)U_i^{(j)}({\varvec{X}}) \quad \mathrm {for} \,\,\,\, i = 1 - 3\end{aligned}$$

(9)

$$\begin{aligned} T({\varvec{X}},t)= & {} \varSigma _{j = 1}^{N_T} \tau _j(t){\mathcal {T}}^{(j)}({\varvec{X}}) \end{aligned}$$

(10)

where $\eta _j(t)$ and $\tau _j(t)$ are the time-dependent generalized coordinates. The variables $U_i^{(j)}({\varvec{X}})$ and ${\mathcal {T}}^{(j)}({\varvec{X}})$ represent the basis functions satisfying the boundary conditions. The number of temperature and displacement basis functions are specified by $N_T$ and $N_U$, respectively. After substitution of Eqs. 9 and 10 into Eqs. 6–8, the resulting equation is discretized using Galerkin’s method. This yields a set of nonlinear ordinary differential equations for the generalized coordinates:

$$\begin{aligned} \begin{aligned}&{\varvec{M}}_{ij}\ddot{\eta }_{j} + {\varvec{D}}_{ij}{\dot{\eta }}_{j} + \left( {\varvec{K}}_{ij}^{(1)} - {\varvec{K}}_{ijm}^{(th)} \tau _m \right) \eta _j + {\varvec{K}}_{ijm}^{(2)}\eta _j\eta _m \\&\quad + {\varvec{K}}_{ijmn}^{(3)} \eta _j \eta _m \eta _n = {\varvec{F}}_i^{(ae)} + {\varvec{F}}_{ij}^{(th)}\tau _j \end{aligned}\nonumber \\ \end{aligned}$$

(11)

where ${\varvec{M}}_{ij}$ denotes the elements of the mass matrix, and ${\varvec{K}}_{ij}^{(1)}$, ${\varvec{K}}_{ijm}^{(2)}$, and ${\varvec{K}}_{ijmn}^{(3)}$ are the linear, quadratic, and cubic stiffness coefficients, respectively. The ${\varvec{F}}_i^{(ae)}$ term represents the modal forces from the aerodynamic loading. The terms ${\varvec{K}}_{ijm}^{(th)}$ and ${\varvec{F}}_{ij}^{(th)}$ are the change in linear stiffness and force induced by a temperature variation of the form $1 \times {\mathcal {T}}^{(j)}$. Note that the quadratic and cubic stiffness coefficients are exact representations with physical meaning and not merely the outcome of a truncated approximation. The method of indirect evaluation of the coefficients in Eq. 11 from the finite element method is used [35]. Finally, a viscous damping term, ${\varvec{D}}_{ij}$, is included in Eq. 11 to represent dissipation mechanisms. The Rayleigh damping model is adopted:

$$\begin{aligned} {\varvec{D}}_{ij} = \alpha _d {\varvec{M}}_{ij} + \beta _d {\varvec{K}}_{ij} \end{aligned}$$

(12)

where $\alpha _d$ and $\beta _d$ are mass and stiffness proportional Rayleigh damping coefficients which are identified using the damping ratios of the first three panel frequencies. These quantities were obtained from an impact hammer test of the panel after installation in the wind tunnel. The resulting $\alpha _d$ and $\beta _d$ are $15\,\hbox {s}^{-1}$ and $8\times 10^{-7}\,\hbox {s}$, which leads to damping ratios between 0.3% and 1.4% for all bending modes in the basis.

3 Identification of chaos in fluid-structure interactions

During recent tests in the RC-19 wind tunnel, multiple instances of chaotic oscillations were observed. Computational aeroelastic studies on similar configurations have also noted the potential for chaos [8, 20, 27, 38, 41]. However, most of these studies relied on indirect tests for chaos, including phase portraits, Poincaré maps, and plots of the power spectrum computed from a fast Fourier transform. A more rigorous test for chaos involves computing the largest Lyapunov exponent (LLE). In this study, the governing equations for the aeroelastic system are used to directly compute the LLE.

Direct calculation of the LLE involves analyzing the dynamics of the distance between two neighboring solutions. In the case of chaotic motions, the neighboring solutions will diverge exponentially with exponent $\lambda$, which are referred to as Lyapunov exponents. First, the governing fluid model and structural ROM are combined into a single equation. In order to simplify the analysis, a linear enriched piston model is used in place of the second-order model. This assumption is not expected to impact the findings since both models are capable of producing chaotic attractors, as discussed in Sect. 8. The governing equation is then written as:

$$\begin{aligned} \begin{aligned}&{\varvec{M}}_{ij}\ddot{\eta }_{j} + \left( {\varvec{D}}_{ij} + {\varvec{D}}^{(pt)}_{ij} \right) {\dot{\eta }}_{j} \\&\quad + \left( {\varvec{K}}_{ij}^{(1)} - {\varvec{K}}_{ijm}^{(th)} \tau _m + {\varvec{K}}_{ij}^{(pt)} \right) \eta _j \\&\quad + {\varvec{K}}_{ijm}^{(2)}\eta _j\eta _m + {\varvec{K}}_{ijmn}^{(3)} \eta _j \eta _m \eta _n \\&\quad = \left( {\varvec{F}}_i^{(pt)} + {\varvec{F}}_{ij}^{(th)}\tau _j \right) \end{aligned} \end{aligned}$$

(13)

where ${\varvec{D}}^{(pt)}_{ij}$ is the modal aerodynamic damping, ${\varvec{K}}^{(pt)}_{ij}$ is the modal aerodynamic stiffness, and ${\varvec{F}}^{(pt)}_{i}$ is a modal force. These terms are defined as:

$$\begin{aligned} \begin{aligned} {\varvec{D}}^{(pt)}_{ij}&= {\varvec{T}}_{ir} {\varvec{L}}_{rr}^{(2)} \phi _{rj} \\ {\varvec{K}}^{(pt)}_{ij}&= {\varvec{T}}_{ir} {\varvec{L}}_{rr}^{(1)} \phi '_{rj} \\ {\varvec{F}}^{(pt)}_{i}&= - {\varvec{T}}_{ir} \varDelta p_r \end{aligned} \end{aligned}$$

(14)

In Eq. 14, $\varDelta p_r$ is the spatially varying static pressure differential, $\phi$ is a matrix containing the displacement basis functions for the structural ROM such that $\phi _{rj} = U^{(j)}_r$, and ${\varvec{T}}_{ir}$ is the transfer matrix used to project the pressure onto the modes. Note that the number of rows and columns in ${\varvec{T}}_{ir}$ is defined by the number of modes in the ROM, $N_m$, and the number of nodes in the FE mesh, $N_{FE}$, respectively. The diagonals of the square matrices ${\varvec{L}}^{(1)}$ and ${\varvec{L}}^{(2)}$ are computed from the linear piston model as:

$$\begin{aligned} \begin{aligned} {\varvec{L}}_{rr}^{(1)}&= \frac{\gamma p_l M_l U_l}{a_l \sqrt{M_l^2 - 1}} \\ {\varvec{L}}_{rr}^{(2)}&= \frac{\gamma p_l M_l}{a_l \sqrt{M_l^2 - 1}} \end{aligned} \end{aligned}$$

(15)

where the subscript l denotes the local flow conditions which are defined at each point on the surface of the FE mesh.

Direct calculation of the Lyapunov exponents involves analyzing the distance, ${\varvec{d}}$, between two nearby solutions, $\varvec{\eta }$ and $\varvec{\eta }^{(2)}$, where $\varvec{\eta }^{(2)} = \varvec{\eta } + {\varvec{d}}$. In other words, this approach involves solving for the dynamics of ${\varvec{d}}$ in the vicinity of the solution $\varvec{\eta }$. Re-labeling Eq. 13 yields:

$$\begin{aligned} {\varvec{M}}_{ij}\ddot{\eta }_{j} + \tilde{{\varvec{D}}}_{ij} {\dot{\eta }}_{j} + \tilde{{\varvec{K}}}_{ij} \eta _j + {\varvec{R}}_i(\varvec{\eta }) = \tilde{{\varvec{F}}}_i \end{aligned}$$

(16)

where $\tilde{{\varvec{D}}}_{ij}$, $\tilde{{\varvec{K}}}_{ij}$, and $\tilde{{\varvec{F}}}_{i}$, represent the combined damping, linear stiffness, and force terms, respectively, in Eq. 13. The nonlinear restoring force is given by ${\varvec{R}}_i(\varvec{\eta })$. Similarly, the dynamics of $\varvec{\eta }^{(2)}$ are governed by:

$$\begin{aligned}&{\varvec{M}}_{ij}\ddot{(\eta _j + d_j)} + \tilde{{\varvec{D}}}_{ij} \dot{(\eta _j + d_j)} + \tilde{{\varvec{K}}}_{ij} (\eta _j + d_j) \nonumber \\&\quad + {\varvec{R}}_i(\varvec{\eta } + {\varvec{d}}) = \tilde{{\varvec{F}}}_i \end{aligned}$$

(17)

Since the time differentiation is a linear operator, subtracting Eq. 16 from Eq. 17 yields:

$$\begin{aligned} {\varvec{M}}_{ij}\ddot{d}_j + \tilde{{\varvec{D}}}_{ij} {\dot{d}}_j + \tilde{{\varvec{K}}}_{ij} d_j + {\varvec{R}}_i(\varvec{\eta } + {\varvec{d}}) - {\varvec{R}}_i({\varvec{d}}) = 0\nonumber \\ \end{aligned}$$

(18)

Expanding the nonlinear restoring force and retaining only the linear terms with respect to ${\varvec{d}}$ results in the final form of the linearized equations:

$$\begin{aligned}&{\varvec{M}}_{ij}\ddot{d}_j + \tilde{{\varvec{D}}}_{ij} {\dot{d}}_j + \tilde{{\varvec{K}}}_{ij} d_j + {\varvec{K}}_{ijm}^{(2)} \left( \eta _j d_m + d_j \eta _m \right) \nonumber \\&\quad + {\varvec{K}}_{ijmn}^{(3)} \left( \eta _j \eta _m d_n + \eta _j d_m \eta _n + d_j \eta _m \eta _n\right) = 0 \nonumber \\ \end{aligned}$$

(19)

Note that the forcing does not appear on the right hand side. Instead the nonlinear stiffness changes as a function of $\varvec{\eta }(t)$, which is an input to the linearized equation.

Fig. 3

RC-19 modified test section showing the pressure taps, thin panel, and cavity

Next, ${\varvec{d}}$ is assumed to take the form:

$$\begin{aligned} {\varvec{d}} = \sum _{i=1}^{N} A_i e^{\lambda _i t} \varvec{\varphi }_i \end{aligned}$$

(20)

where $\varvec{\varphi }_i$ is a mode shape, $A_i$ are constants and $\lambda _i$ are the eigenvalues (i.e. Lyapunov exponents). For large time, the response will be completely dominated by the LLE. Thus, if the aeroelastic response is computed for a sufficiently large time, then ${\varvec{d}}$ is governed by $\lambda _{LLE}$:

$$\begin{aligned} |{\varvec{d}}(large\,\, t)| \rightarrow C e^{\lambda _{LLE} t} \end{aligned}$$

(21)

where $C = A_{LLE} |\varvec{\varphi }_{LLE}|$ is a constant. Thus, the LLE is estimated as:

$$\begin{aligned} ln(|{\varvec{d}}(large\,\, t)|) = ln(C) + \lambda _{LLE} t \end{aligned}$$

(22)

For small t, the approximation $C \approx |{\varvec{d}}_0|$ is introduced where $|{\varvec{d}}_0|$ is the initial separation. The final result is:

$$\begin{aligned} \lambda _{LLE} = \lim _{t \rightarrow \infty } \frac{1}{t}\frac{|{\varvec{d}}(t)|}{|{\varvec{d}}_0|} \end{aligned}$$

(23)

In order to solve for $\lambda _{LLE}$, the time history of the modal weights is extracted from the aeroelastic simulations and substituted into the linearized equation governing the perturbation dynamics, Eq. 19. The equation is initialized by randomly selecting sufficiently small values for ${\varvec{d}}$ and $\dot{{\varvec{d}}}$. While these initial quantities do not necessarily need to be small, a smaller value helps avoid rapid divergence of the equation. Equation 19 is marched forward in time using a Newmark-$\beta$ scheme with Newton–Raphson subiterations to achieve convergence. The estimate for $\lambda _{LLE}$, Eq. 23, is monitored as a function of time.

4 RC-19 experimental overview

The RC-19 is a continuous Mach 1.5 – 3 supersonic wind tunnel consisting of four separate interchangeable walls that can be configured to meet a range of experimental requirements [26]. The rectangular test section, detailed in Table 1, was modified in previous experiments [44] to accommodate a flexible panel flush with the top wall, as indicated in Fig. 3. The panel was machined from a $0.305\times 0.152\times 0.0127$ m block of AISI 4140 alloy steel. A pocket was machined into the block leaving a compliant panel with the dimensions listed in Table 1. Note that the thin panel was scaled so that the first three vibration modes are below 500 Hz. A pressurized cavity was located on the opposite side of the panel and contained a clear quartz window through which the backside panel dynamics were measured using three-dimensional digital image correlation (DIC). The speckle pattern of randomly distributed dots for the DIC on the cavity side of the panel is shown in Fig. 4.

Table 1 RC-19 and compliant panel geometry

Fig. 4

Cavity side of the thin panel instrumented with the strain gage and thermocouples. The retroreflective dot represents the LDV location, $x/L_p = 0.35$, $y/L_p = 0.16$

In addition to the full-field displacement measurements from DIC, discrete sensors were also used to characterize the loading environment and flexible panel response. The panel was instrumented with two type-K thermocouples (TC) to record temperatures on the thick frame and cavity side of the panel, as shown in Fig. 4. Note that the thermocouples were used sparingly and only near the edges of the thin panel in order to limit the effects of the sensors on the panel dynamics. A Micro-Measurements WK-06-125AD-350 foil strain gage was also positioned near the thermocouple on the cavity side of the panel. A Polytec OFV-552 fiber optic dual-beam Laser Doppler Vibrometer (LDV) was used to record panel velocities at the fixed point labeled in Fig. 4.

Table 2 Operating conditions

The operating conditions for the experiment are listed in Table 2. While the wind tunnel configuration is designed to produce a nominal freestream Mach number of 2.0 in the test section, measurements of the boundary layer as well as the cavity pressures required to excite a post-flutter response in Brouwer et al. [5] support the lower value in Table 2. At the start of the experiment, the panel was installed and the tunnel started. The cavity was sealed once the transient panel response due to start-up subsided. A static pressure differential was then applied through modulation of the cavity pressure, $p_c$. The temperature differential, $\varDelta T$, between the panel and frame was also monitored. The $\varDelta T$ induces stresses due to constrained thermal expansion that alters the dynamic behavior of the panel. In the absence of full-field temperature measurements, the panel and frame thermocouples were used to approximate the temperature differential as:

$$\begin{aligned} \varDelta T_{TC} = T_{TC, p} - T_{TC, f} \end{aligned}$$

(24)

where $T_{TC, p}$ and $T_{TC, f}$ are the discrete measurements of temperature from the thermocouples on the panel and frame, respectively. Note that a majority of the thin panel quickly reached an adiabatic condition once exposed to the heated flow, whereas the frame heated up at a slower rate due to its larger mass. Thus, the temperature differential between the panel and frame thermocouple, $\varDelta T_{TC}$, decreased as a function of time. At each cavity pressure, ten seconds of strain gage and LDV data were recorded at a rate of 25 kHz. These measurements were also used for in situ monitoring of the panel behavior. When a large dynamic response was observed, approximately three seconds of DIC were recorded at a frame rate of 5 kHz. This recording time was set based on camera memory limitations and the desire to obtain data at multiple cavity pressures. These steps were repeated until the dynamic behavior subsided. The cavity pressure was then increased in order to return to the starting condition. Additional data were recorded when the dynamic motions resumed.

5 Aeroelastic model development

The computational configuration for the fluid and structural models of the thin panel in supersonic, turbulent flow is discussed in detail below. This includes the steady RANS analysis, which is used to compute the local flow conditions for enriched piston theory, and the nonlinear structural ROM. The structural ROM is evaluated relative to a finite element model for various static loading conditions. The coupling procedure for the aeroelastic simulations is also presented. Finally, measurements of the installed panel are used to calibrate the structural ROM in order enhance the accuracy of the aeroelastic model for dynamic response prediction.

5.1 Fluid model configuration

The required steady-state RANS flow solution for the enriched piston theory model is computed using the NASA Langley CFL3D code [2, 28]. The code uses an implicit, finite-volume algorithm based on upwind-biased spatial differencing to solve the RANS equations. Closure of the equations for viscous flow is achieved using the Menter k-$\omega$ turbulence model [34].

Fig. 5

Reynolds-averaged Navier–Stokes (RANS) CFD mesh

The computational domain for the RC-19 experiments in Fig. 5 is generated using the dimensions listed in Table 1. The mesh consists of 501 points in the x-direction, 97 points in the y-direction, and 153 points exponentially distributed from the surface. In addition, 401 and 73 points are evenly distributed over the surface in the x and y-directions, respectively. The average $y^+$ normal to the surface is 0.16. A freestream boundary condition is specified at the leading edge of the computational domain and a trip to turbulence is specified 0.5 m upstream of the leading edge of the panel. In order to simplify the computations, the tunnel side walls are not modeled. Instead, an extrapolation boundary condition is specified at both computational boundaries in the y-direction. This yields a nominally two-dimensional flow field. All computations are conducted assuming an adiabatic wall condition. The operating conditions in Table 2 yield a mean surface pressure and adiabatic temperature of ${\bar{p}}_{\text{ RANS }} = 51.0~\hbox {kPa}$ and ${\bar{T}}_{\text{ RANS }} = 377$ K, respectively. Note that the average surface pressure is slightly larger than the freestream pressure of 48.4 kPa due to the inclusion of the flat plate boundary layer in the steady RANS analysis, as illustrated in Fig. 2. Moreover, the presence of the boundary layer produces minimal variation in the local flow quantities extracted for enriched piston theory. In the absence of full-field pressure measurements, the local pressure from the RANS solution is also used to define the static pressure differential for both the experiments and simulations:

$$\begin{aligned} \varDelta p (x,y) = p_{\text{ RANS }}(x,y) - p_c \end{aligned}$$

(25)

Note that Eq. 25 applies to aeroelastic simulations with enriched piston theory. When classical piston theory is used, $p_{\text{ RANS }}$ is replaced by $p_{\infty }$, which makes $\varDelta p$ a constant.

5.2 Structural reduced-order model (ROM)

A converged structural model is constructed using a commercial FE software, Abaqus$^{\textregistered }$, and contains 10,000 thin shell triangular (S3) elements. These elements are suitable for modeling finite strains and large deformations. The required mesh resolution is identified based on the convergence of the free vibration frequencies and the response to uniform static loading. Bilinear interpolation is used to compute the nodal degrees of freedom. The shell behavior is described using a co-rotational formulation based on the Koiter–Sanders theory for thin shells [6]. The structure is assumed to be clamped on all sides. The aerodynamic pressure from the RANS simulation is applied on the surface of the structure using the subroutines available in Abaqus$^{\textregistered }$. A temperature difference, $\varDelta T_{\text{ Sim }}$, between the spatially varying panel temperature and a constant frame temperature is also applied in the simulations. The sign convention is consistent with Eq. 24. The RANS prediction of the adiabatic wall temperature is used to define the spatial distribution of $\varDelta T_{\text{ Sim }}$, whereas the mean is defined by the user.

Table 3 Modal frequencies for the compliant panel

The first 15 mode shapes from the unstressed state of the panel are selected to represent the displacement field in the ROM. The frequencies for the first seven modes are listed in Table 3 along with the corresponding pre-test modal frequencies. The ROM frequencies are identical to those from the FE model. Note that the pre-test frequencies were measured before placing the panel in the wind tunnel and therefore do not include the effect of the pre-load imparted during installation. The thermal mode for the ROM is assumed to have a distribution corresponding to that of the steady RANS adiabatic wall temperature where the mean is shifted to match a user-defined average temperature differential. Note that for all simulations using the structural ROM this average temperature differential is reported as $\overline{\varDelta T}_{\text{ Sim }}$.

Fig. 6

Comparison of the static response from Abaqus$^{\textregistered }$and the structural ROM. $y/L_p = 0.25$, $\overline{\varDelta T}_{\text{ Sim }} = 11.1~K$, $p_{\infty } = 48.4~kPa$, $Re_{L_p} = 7.70\times 10^6$

The predictive accuracy of the structural ROM is assessed through a comparison of the static response for various loading conditions, as illustrated in Fig. 6. The selected cavity pressures produce deformations into and out of the cavity. The deformations along the midspan, $y/L_p = 0.25$, in Fig. 6 indicate that the ROM adequately captures the static response for a range of cavity pressures. A similar comparison is not conducted for dynamic simulations due to the computational limitations associated with Abaqus$^{\textregistered }$for long-duration analyses.

Fig. 7

Effect of fundamental frequency on the aeroelastic response prediction. $p_{\infty } = 48.4~kPa$, $Re_{L_p} = 7.70\times 10^6$

5.3 Aeroelastic simulation procedure

Before conducting a coupled aeroelastic analysis, a steady RANS simulation is computed over the flat, rigid surface in order to obtain the local flow quantities for enriched piston theory as well as the adiabatic wall temperature. Next, two different initialization procedures are considered for the dynamic simulations in order to assess the sensitivity of the coupled system to different initial conditions. For the first initial condition, a static structural analysis is conducted using the ROM for a given $\varDelta p$ and $\varDelta T_{\text{ Sim }}$. The static pressure differential is then removed, so that the resulting buckled shape is only due to $\varDelta T_{\text{ Sim }}$. This shape is then used to initialize the dynamic simulation. Note that at the onset of the dynamic analysis, the aerodynamic loading includes the fluid-structural coupling terms from piston theory as well as the static pressure differential, $\varDelta p$. The latter term functions as an additional instantaneous perturbation to the nonlinear system since it was removed in the static analysis. While generally larger in magnitude, this perturbation serves to mimic the effect of cavity pressure modulation in the experiments. This initialization procedure is used for all simulations unless otherwise noted. For the alternate initial condition, $\varDelta p$ is included in the static solution and only the surface inclination and velocity terms from piston theory are added at the start of the dynamic analysis. This typically yields a smaller perturbation to the nonlinear system compared to the first initial condition.

A loosely coupled, partitioned framework is implemented for the fluid and structural solvers [36]. Before each time step in the dynamic analysis, the fluid solution is updated using the most recent surface deformations. After the time step, the pressure loads are extracted for the structural solver. The structural ROM is discretized in time using the Newmark-$\beta$ integration scheme, where Newton–Raphson subiterations are used for convergence. A time step size of $1\times 10^{-5}~\hbox {s}$ is used for all coupled simulations and was selected based on a time convergence study of the dynamic response. This corresponds to a step size of approximately 0.0024 of the first natural period.

5.4 Model calibration

In an attempt to model the measured response of the thin panel, an initial series of simulations are conducted using the unmodified aeroelastic model detailed above. The pre-calibration predictions in Fig. 7 assume a fundamental frequency of 238 Hz. The oscillation amplitude normalized by panel thickness, $w/h_{Amp}$, and standard deviation of velocity, $\sigma _{Velocity}$, are provided as functions of $p_c$ and $\overline{\varDelta p}$ on the lower and upper x-axes, respectively. The mean static pressure differential, $\overline{\varDelta p}$, is computed using the steady RANS mean pressure. The deformation power spectral density (PSD) is also provided for the cases with the largest oscillation amplitude. Similar to the experiments, computations are conducted over a range of cavity pressures in order to induce a dynamic response. Due to the continuous variation in $\varDelta T_{TC}$ throughout the experiments, the simulations are initially evaluated at the mean of all $\varDelta T_{TC}$ which is approximately 13.6 K.

Data from the DIC and LDV are also provided. The measured mean oscillation amplitude in Fig. 7 (a) is extracted from the DIC data along the midspan at $x/L_p = 0.75$, whereas the standard deviation of velocity, Fig. 7b, is obtained from the time history of the LDV output. Note that the arrows in both plots denote the direction of cavity pressure modulation. The measured oscillation amplitude and standard deviation of velocity contain a peak in the vicinity of $p_c = 51.0~\hbox {kPa}$ or $\overline{\varDelta p} \approx 0~\hbox {kPa}$, the amplitude of which decreases with $\varDelta T_{TC}$. This behavior is due in part to a change in the in-plane stress with the temperature differential. Again, $\varDelta T_{TC}$ decreased throughout the experiments since a majority of the panel achieved an adiabatic condition whereas the frame continued to heat up.

In contrast to the measured response, the pre-calibration simulations predict a static deformation for several combinations of cavity pressure and $\overline{\varDelta T}_{\text{ Sim }}$ due to the omission of fluctuating pressure loads from the turbulent boundary layer. If these loads are included in the fluid model, the simulations are expected to recover the small-amplitude, forced oscillations observed in the experiments. The unmodified ROM yields smaller oscillation amplitudes and standard deviations of velocity relative to the experiments. The simulated response also produces two distinct regions of dynamic activity. The first region corresponds to larger amplitude oscillations with cavity pressures near 51.0 kPa or $\overline{\varDelta p} \approx 0~\hbox {kPa}$. The second region occurs for $\overline{\varDelta p} < 0~\hbox {kPa}$. This region exhibits an approximately continuous increase in amplitude, which is in contrast to the discontinuity in amplitude for $\overline{\varDelta p} \approx 0~\hbox {kPa}$. The deformation PSD for the case with the maximum oscillation amplitude is compared with the measured response in Fig. 7c. In addition to the decrease in amplitude, the predicted dominant frequency is 386 Hz compared to 257 Hz in the measured response, an error of 50%.

Fig. 8

Strain PSD associated with small-amplitude oscillations during tunnel startup used to identify the first natural frequency of the panel. $p_{\infty } = 48.4~kPa$, $Re_{L_p} = 7.70\times 10^6$

Fig. 9

Effect of $\varDelta T$ and $p_c$ on the aeroelastic response where the square symbols denote selected cases in Figs. 10 and 11. The mean static pressure differential, $\overline{\varDelta p}$, and $p_c$ are provided on the upper and lower x-axes, respectively. $p_{\infty } = 48.4~kPa$, $Re_{L_p} = 7.70\times 10^6$

Installation of the thin panel in the wind tunnel imparts a pre-load. Characterizing the impact of this load on the panel frequencies using traditional modal testing is difficult since the panel is not easily accessible once installed. Thus, the time history of the panel strain during tunnel startup is used to estimate the fundamental panel frequency. Note that during startup of the RC-19 tunnel, a normal shock passes through the test section. Before this normal shock reaches the panel, the panel is not exposed to the flow but exhibits a small-amplitude forced response due to tunnel vibrations. The PSD of the strain during the time period before the normal shock reaches the panel, Fig. 8, indicates that $f_1 \approx 260$ Hz for the installed panel. The ROM is adjusted to match the fundamental frequency of the installed panel by replacing the first entry in the linear stiffness matrix, ${\varvec{K}}^{(1)}_{11}$, with $(2 \pi f_1)^2$. The results using the modified structural ROM are labeled as the post-calibration simulations in Fig. 7. While the simulated oscillations have an amplitude and standard deviation of velocity that exceeds the measured response for $\overline{\varDelta p} \approx 0~\hbox {kPa}$, the dominant frequencies are identical. Interestingly, both of the structural ROMs reproduce the broad peak present in the measured response, which is indicative of chaotic, cross-well behavior. Given the results in Fig. 7, the modified structural ROM with $f_1 = 260$ Hz is used for all remaining simulations.

6 Aeroelastic model evaluation relative to experiments

As evidenced by the simulations and experimental data in Sect. 5.4, the temperature differential and cavity pressure have a profound impact on the response. Note that these are the primary parameters used to induce flutter in both the simulations and experiments since the dynamic pressure is fixed at $q_{\infty } = 128~\hbox {kPa}$. This is in contrast to classical panel flutter studies [19, 32] where $q_{\infty }$ is varied in order to elicit a post-flutter response. The effects of the temperature differential and cavity pressure are examined in greater detail through the construction of system response maps which are then used to investigate the aeroelastic phenomena observed in the experiments. This includes the large-amplitude, cross-well chaotic and periodic oscillations that occur for $\overline{\varDelta p} \approx 0~\hbox {kPa}$. Note that the use of reduced-order models enables the creation of these maps. Each pixel in the predicted response map represents an aeroelastic simulation computed for a given combination of $\varDelta T_{\text{ Sim }}$ and $p_c$. In contrast to high-fidelity simulation tools which incur significant computational costs, the reduced fluid and structural models require approximately 30 minutes on a single processor to simulate a minute of response. Additionally, constructing the system response map is an embarrassingly parallel process since each simulation is obtained independent of the others. Thus, the total wall time is highly dependent on the number of available computer processors.

Fig. 10

Effect of $\varDelta T$ and $p_c$ on the simulated deformation time history for cases with $\overline{\varDelta p} \approx 0~\hbox {kPa}$ in Fig. 9. $x/L_p = 0.75$, $y/L_p = 0.25$, $p_{\infty } = 48.4$ kPa, $Re_{L_p} = 7.70\times 10^6$

First, consider the simulated response maps of the oscillation amplitude and standard deviation of velocity in Fig. 9. The results are shown in terms of $p_c$ on the lower x-axis and $\varDelta T$ on the y-axis. The mean static pressure differential, computed using the RANS pressure prediction, is provided on the upper x-axis. Data from the DIC and LDV are also shown. The experiments start from an initial $p_c$ and $\varDelta T_{TC}$ of 55.2 kPa and 16.7 K, respectively. The measured temperature differential, $\varDelta T_{TC}$, decreases for each measurement since the frame temperature lagged behind that of the thin panel in the experiments. The panel experiences large-amplitude motions for experimental conditions near $p_c = 51.0~\hbox {kPa}$ and $\varDelta T_{TC} = 15.0$ K. These deformations also exhibit features of chaos as noted above.

A large number of the simulations in Fig. 9 yield a static response due to the omission of turbulent boundary layer induced fluctuating pressure loads. The predicted response is expected to recover the small-amplitude forced oscillations if the acoustic loads are included in the fluid model. Visual inspection of Fig. 9 illustrates that the simulations predict flutter onset for $\overline{\varDelta p} \approx 0~\hbox {kPa}$. The decrease in oscillation amplitude with $\varDelta T$ as well as the attenuation of the post-flutter response with increasing $|\overline{\varDelta p}|$ are also captured. However, the oscillation amplitude is larger in the simulations compared to the experiments for similar $\varDelta T$. This difference is likely tied to uncertainty in the distribution of $\varDelta T_{\text{ Sim }}$. In the simulations, the steady RANS prediction of the adiabatic wall temperature is used to define the distribution of $\varDelta T_{\text{ Sim }}$. While a majority of the panel achieves an adiabatic wall condition in the experiments, there is a thermal gradient near the panel edge as the temperature transitions from the hot panel to the cooler frame. This gradient is not accounted for in the simulations. Moreover, the panel thermocouple is located in this region of elevated temperature gradients, which introduces additional uncertainty in the discrete measurement of $\varDelta T_{TC}$. Thus, obtaining full-field surface temperature data is a primary test objective for future entries in RC-19.

Fig. 11

Effect of $\varDelta T$ and $p_c$ on the simulated deformation time history for cases with $\overline{\varDelta p} < 0~\hbox {kPa}$ in Fig. 9. $x/L_p = 0.75$, $y/L_p = 0.25$, $p_{\infty } = 48.4$ kPa, $Re_{L_p} = 7.70\times 10^6$

Other potential sources of error between the simulations and experiments include differences in the initial conditions as well as the omission of turbulent boundary layer pressure fluctuations. In regards to the former, each simulation is computed for an independent set of parameters and therefore neglects any hysteresis present in the experiments due to the continuous changes in $\varDelta T$ and $p_c$. A consequence of this omission is that the simulations and each observation in the experiments start from different initial conditions. This can lead to significant variation in the final solution, especially for nonlinear systems. Initial condition dependence is discussed further in Sect. 7. Next, the range of cavity pressures for which the cross-well behavior occurs is larger in the experiments compared to the simulations. The authors suspect that this difference is due to the absence of the turbulent boundary layer induced acoustic loads in the fluid model. While the cross-well oscillations are clearly an aeroelastic phenomenon, the pressure fluctuations likely influence the onset of this behavior as well as the intermittent snap-through observed in Spottswood et al. [44]. Additional simulations exploring these hypotheses are currently underway.

In addition to the response maps, the time histories and PSDs for a selected number of cases exhibiting aperiodic and periodic motions are also provided in Figs. 10 and 11. The results in Fig. 10 correspond to simulations where the cavity pressure is near the mean of the static surface pressure, i.e. $\overline{\varDelta p} \approx 0$. This condition tends to produce the largest amplitude oscillations. It is evident from the deformation time history along the midspan at $x/L = 0.75$ in Fig. 10 that the large-amplitude responses are centered about a zero mean with features of chaos. This is consistent with the PSDs, where there is a broad dominant peak at a lower frequency. Interestingly, a larger $\varDelta T$ yields an increase in the oscillation amplitude, a broadening of the dominant peak, and an increase in higher-frequency content in the response. The increase in oscillation amplitude is also observed in Fig. 9a. The thin panel is buckled for these simulations since the critical temperature is approximately 5.6 K. Buckling can lead to large-amplitude, cross-well oscillations due to the existence of co-existing equilibrium wells. In this case, the wells correspond to the static buckled positions of the panel into and out of the flow. The depth of the wells increases with $\varDelta T$, resulting in larger oscillation amplitudes and standard deviations of velocity for the cross-well motions.

Fig. 12

Comparison of the time history for the cross-well oscillations with features of chaos. $y/L_p = 0.25$, $p_{\infty } = 48.4~kPa$, $Re_{L_p} = 7.70\times 10^6$

As the magnitude of $\overline{\varDelta p}$ increases in Figs. 9 and 11, the dynamic response transitions to periodic and the amplitude decrease. This is particularly evident for $\overline{\varDelta T}_{\text{ Sim }} < 7.5$ K in Fig. 9, where for a given $\overline{\varDelta T}_{\text{ Sim }}$ there is typically a decrease in amplitude as the magnitude of the static pressure differential increases. Note that for a constant $\overline{\varDelta T}_{\text{ Sim }}$, the mean deformation grows with the pressure differential which stiffens the structure and causes the oscillations to diminish. In this region of the parameter space, the aeroelastic response exhibits features of chaotic and periodic attractors depending on the operating conditions. This is consistent with the behavior observed in the experiment as the cavity pressure was returned to the initial condition. The panel response also shifts from cross-well oscillations centered about a mean deformation of zero to single-well motions about a buckled shape, as shown in Fig. 11a.

Fig. 13

Comparison of the time history of the periodic deformations. $y/L_p = 0.25$, $p_{\infty } = 48.4~kPa$, $Re_{L_p} = 7.70\times 10^6$

For $\overline{\varDelta T}_{\text{ Sim }}$ in the range of [7.5, 10] K and $\overline{\varDelta p}$ near 0 kPa, the variation in amplitude is discontinuous as the response shifts from large-amplitude, cross-well to small-amplitude, single-well simple harmonic motions. The latter result is illustrated by the dashed red line in Fig. 11a corresponding to $p_c = 52.7~\hbox {kPa}$, $\overline{\varDelta p} = -1.71~\hbox {kPa}$, and $\overline{\varDelta T}_{\text{ Sim }} = 8.8$ K. Note that these oscillations have an amplitude of approximately 0.6h. For reference, the measured amplitudes for conditions without cross-well motions in the experiments are in the range of 0.2h to 0.5h. These low-amplitude, forced oscillations are governed by the turbulent boundary layer induced pressure fluctuations. Thus, the simulated simple harmonic oscillations are likely unobservable in the experiments since these motions may be obscured by the forced response arising from the turbulent boundary layer acoustic loading.

For the largest static pressure and temperature differentials, the maps in Fig. 9 exhibit two regions of dynamic response. A subset of these responses are also shown in Fig. 11b. Similar results are not shown for $\overline{\varDelta p} > 0~\hbox {kPa}$ due to the approximate symmetry in the system. The responses in this region primarily resemble periodic attractors, although there are limited cases of potentially chaotic behavior. The periodic motions are typically quite complex and tend to exhibit multiple frequencies. This type of periodic behavior is characteristically similar to that measured during a previous entry in RC-19 [44]. In contrast to the results for $\overline{\varDelta p} \approx 0~\hbox {kPa}$, the oscillation amplitude decreases with increasing $\overline{\varDelta T}_{\text{ Sim }}$. This trend is also consistent with a thermally buckled structure and is tied to the stiffening of the panel as $\overline{\varDelta T}_{\text{ Sim }}$ increases. Given the comparison between the simulated and measured responses in Fig. 9, larger temperature and static pressure differentials are required in the experiment in order to study these two upper lobes in the response map. Note that this is a test objective for future campaigns in RC-19.

Fig. 14

Effect of initial condition on the oscillation amplitude response map for the thin panel where the mean static pressure differential, $\overline{\varDelta p}$, and $p_c$ are provided on the upper and lower x-axes, respectively. $x/L_p = 0.75$, $y/L_p = 0.25$, $p_{\infty } = 48.4~kPa$, $Re_{L_p} = 7.70\times 10^6$

A detailed comparison of the measured and predicted time histories of the response along the midspan are provided in Figs. 12 and 13. The responses in Fig. 12 exhibit a large, broad peak in the PSD at a lower frequency which is indicative of chaotic oscillations. The dominant frequency is approximately 260 Hz. Two different predictions corresponding to a higher and lower $\overline{\varDelta T}_{\text{ Sim }}$ are provided. For the more extreme temperature differential, there is a 0.8% and 7.5% difference in $p_c$ and $\varDelta T$, respectively, between the computations and experiments. While the responses exhibit similar mean deformations, there are some differences in the higher frequency content. Possible explanations for this discrepancy include the omission of turbulent boundary layer fluctuating pressure loads as well as improper damping of the higher modes in the Rayleigh damping model. Nevertheless, there is good agreement in the frequency content, particularly with regard to the broad, dominant peak. The error in the dominant frequency is approximately 1%. The simulations also overestimate the oscillation amplitude by 20.5%. This error is likely due to differences in the estimated and actual distributions of $\varDelta T$. As noted above, there is a gradient in $\varDelta T$ near the panel edges in the experiments as the temperature transitions from an adiabatic wall condition over a majority of the panel to the cooler frame. This gradient is not included in the thermal mode for the ROM. The panel thermocouple is also located in this region of elevated temperature gradients, which introduces additional uncertainty in the magnitude of the temperature differential. As $\overline{\varDelta T}_{\text{ Sim }}$ decreases, the location of the dominant peak in the PSD does not change appreciably. Instead, the amplitude approaches the experimental condition, where the error in oscillation amplitude is 9.5% for the simulated response in Fig. 12d. However, the error in $\varDelta T$ is significantly higher at 34.0%. Again, uncertainty in the estimated distribution of the temperature differential is a probable source of error. Finally, these comparisons indicate that the panel is buckled in both the computations as well as the experiments. Moreover, the depth of the potential wells for the buckled panel decreases with the temperature, resulting in smaller amplitude, aperiodic oscillations.

The measured periodic oscillations are compared with the corresponding companion simulations in Fig. 13. While there is only a 4.6% difference between the predicted and measured cavity pressured, the error in $\varDelta T$ and oscillation amplitude are 44.5% and 31.7%, respectively. The simulated response captures the dominant frequency peak at 236 Hz in the PSD as well as the corresponding harmonics. Note that the decrease in frequency relative to the results in Fig. 12 is due to a reduction in the cavity pressure and temperature differential for the buckled panel. However, there is an additional peak in the simulated PSD at 113 Hz with harmonics at higher frequencies that is not observed in the experiments. Again, a potential source of error is the discrepancy between the estimated and actual distributions of $\varDelta T$. This uncertainty highlights the need for accurate full-field temperature measurements. In addition, the simulated response occurs about a positive, i.e. into the flow, mean deformation in Fig. 13c, whereas the mean of the measured response in Fig. 13b is into the cavity. This result is consistent with the sign of $\overline{\varDelta p}$ for the simulations and experiments. While the temperature differential is relatively low, it is still above the critical buckling temperature of 5.6 K. Therefore, both the simulated and measured periodic oscillations are likely cross-well with a bias towards one of the co-existing equilibrium positions. Furthermore, the difference in the buckling direction of the mean shapes suggests the existence of additional dynamic solutions for $\overline{\varDelta p} > 0~\hbox {kPa}$ that are not present in Fig. 9. Possible explanations for the lack of dynamic activity in this region include differences in initial conditions between the computations and experiments as well as the omission of hysteresis effects in the model predictions.

7 Initial condition dependence of the aeroelastic model

As mentioned in Sect. 6, each simulation is computed for an independent set of parameters using the first initialization procedure discussed in Sect. 5.3. Thus, the predicted responses neglect any hysteresis effects due to the continuous changes in $\varDelta T$ and $p_c$ during the experiments. A potential consequence of this omission is that the simulations and experiments start from different initial conditions. Note that even minor perturbations in the initial condition for a nonlinear coupled system can yield significant differences in the final solution. Initial condition dependence of the aeroelastic simulations is assessed using the alternate initialization presented in Sect. 5.3. For this approach, the static solution used to initialize the dynamic simulations includes the effects of the temperature and static pressure differentials. The aeroelastic coupling terms from piston theory are then added at the start of the dynamic simulation. This alternate initialization results in a smaller perturbation and reduces the regions of dynamic activity in Fig. 14a compared to Fig. 9a, particularly at lower $\overline{\varDelta T}_{\text{ Sim }}$. The large-amplitude, cross-well behavior is still evident for $\overline{\varDelta p} \approx 0~\hbox {kPa}$ in Fig. 14a, as are the two regions of predominantly periodic oscillations at higher $\overline{\varDelta T}_{\text{ Sim }}$. Although not shown, the time histories of the simulated responses in these regions are characteristically similar to those provided in Figs. 10 and 11.

Once the dynamic oscillations settle, a mode 1 velocity perturbation is applied to the results in Fig. 14a in order to observe the effects on the coupled response. Interestingly, a comparison of Figs. 14b and 9a illustrates that the perturbed system recovers a majority of the oscillations originally observed. These results indicate the presence of multiple dynamic solutions for the nonlinear system, which is a particularly troublesome scenario when designing aerospace structures. The system response map for the perturbed solution also exhibits oscillations that are not present in any of the previous results and suggests that other unobserved dynamic solutions likely exist. This is particularly evident for lower $p_c$, i.e., the left side of Fig. 14b. Although not shown, oscillations in this region exhibit frequencies and amplitudes similar to the simulated responses provided in Fig.11. However, the oscillations are centered about a mean deformation that is into the cavity since $\overline{\varDelta p} > 0~\hbox {kPa}$. This is consistent with the measured results in Fig. 13a.

Fig. 15

Aeroelastic response prediction for the thin panel using classical linear piston theory. $x/L_p = 0.75$, $y/L_p = 0.25$, $p_{\infty } = 48.4~kPa$, $Re_{L_p} = 7.70\times 10^6$

Fig. 16

Diagnostic plots for the time histories of the measured and simulated chaotic, cross-well oscillations in Fig. 12. $y/L_p = 0.25$, $x/L_p = 0.75$, $p_{\infty } = 48.4~kPa$, $Re_{L_p} = 7.70\times 10^6$. Experiment: $p_c = 51.5~kPa$, $\overline{\varDelta p} = -0.47~kPa$, $\varDelta T_{TC} = 14.7~K$. Simulations: $p_c = 51.1~kPa$, $\overline{\varDelta p} = -0.06~kPa$, $\overline{\varDelta T}_{\text{ Sim }} = 13.6~K$

8 Effect of different fluid models on the aeroelastic response

All of the system response maps presented in the previous sections exhibit asymmetry about $\overline{\varDelta p} = 0~\hbox {kPa}$ for lower temperature differentials. Symmetry in the response reappears for $\overline{\varDelta T}_{\text{ Sim }}$ larger than approximately 11.0 K. This behavior is likely tied to the inclusion of flat plate boundary layer displacement effects in the local flow conditions used to enrich piston theory. At lower $\overline{\varDelta T}_{\text{ Sim }}$, the buckled panel is softer and the effects of the boundary layer on the response are more pronounced. The panel stiffness increases with $\overline{\varDelta T}_{\text{ Sim }}$ which minimizes these effects. Note that boundary layer displacement effects due to surface inclination are not included in the current fluid model formulation but are expected to intensify the asymmetry. Additional computations exploring this hypothesis are currently underway.

While the symmetry of the nonlinear system was not explicitly explored during the experiments in RC-19, previous computational studies on nonlinear panel oscillations [17, 18] have noted symmetry in related configurations. However, these studies relied on a classical linear piston theory as opposed to the enriched model used in this study. Therefore, the effect of the fluid model on the response is evaluated in Fig. 15 using classical piston theory with the original initial condition procedure detailed in Sect. 5.3 and implemented in Sect. 6. Although not shown, simulations conducted with first-order enriched piston theory produced almost identical results to those with second-order enriched piston theory in Fig. 9, including the asymmetry. It is evident that replacing the enriched piston model with the classical linear version yields a symmetric response, centered about the freestream pressure of 48.4 kPa. The classical model still predicts the large-amplitude, cross-well behavior for static pressure differentials near zero in Fig. 15b as well as the transition to periodic attractors as the temperature and static pressure differentials increase. The differences in the response maps obtained using the classical and enriched piston theory models indicate the need for additional experiments to explore the symmetry of the aeroelastic system.

Fig. 17

Computation of $\lambda _{LLE}$ for the aeroelastic response. $p_c = 51.1~kPa$, $\overline{\varDelta p} = -0.06~kPa$, $p_{\infty } = 48.4~kPa$, $Re_{L_p} = 7.70\times 10^6$

Fig. 18

Modified Riks analysis for a thermally buckled panel where the starting point of the analysis is denoted by x. $x/L_p = 0.75$, $y/L_p = 0.25$, $\overline{\varDelta T}_{\text{ Sim }} = 11.7~K$, $p_{\infty } = 48.4~kPa$, $Re_{L_p} = 7.70\times 10^6$

9 Identification of chaos in the aeroelastic system

The results in Sects. 6–8 illustrate that large-amplitude oscillations with features of chaos occur for $\overline{\varDelta p} \approx 0~\hbox {kPa}$. As shown in Fig. 12, this behavior is present in both the simulations and experiments. Several indirect tests are applied to the data in Fig. 12 in order to support the existence of chaos. The results are provided in Fig. 16. The deformation, w, and velocity, ${\dot{w}}$, time histories are extracted along the midspan at $x/L_p = 0.75$. A visual evaluation of the plots reveals evidence of chaos. The phase portraits contain an irregular set of open loops, there is clear broad frequency content in the power spectra, and the Poincaré maps consists of multiple unevenly spaced points. While these indirect tests are generally required when dealing with experimental data, a more rigorous test for chaos involves computing the LLE using the approach outlined in Sect. 3.

The LLE is computed for a subset of oscillations from the response map in Fig. 9. The cavity pressure for the selected cases is 51.1 kPa, i.e. $\overline{\varDelta p} \approx 0~\hbox {kPa}$, and $\overline{\varDelta T}_{\text{ Sim }}$ ranges from 5.7 K to 11.7 K. Although not included in this analysis, there are sporadic regions of dynamic behavior for $\overline{\varDelta T}_{\text{ Sim }} > 11.7$ K that were identified as chaotic. The time histories of the modal response for each case are substituted into Eq. 19, and the solution is marched forward in time. The estimate for $\lambda _{LLE}$, Eq. 23, is monitored as a function of time. After an initial series of oscillations, $\lambda _{LLE}$ quickly converges to an approximately constant value, as shown in Fig. 17 (a). Note that the LLE is zero for periodic responses and positive for chaos. The solution is not shown for $t > 2$ s since the system rapidly diverges due to the large $\lambda _{LLE}$.

The computed range of $\lambda _{LLE}$ for the selected aeroelastic simulations is [61, 222] Hz, which is consistent with the values reported in Cheng and Mei [8]. However, these values are 1 to 2 orders of magnitude larger compared to the $\lambda _{LLE}$ for many classical low-order systems such as Logistic, Hénon, Lorenz, and Rössler. These systems are typically normalized to have a natural frequency of unity. Thus, the $\lambda _{LLE}$ is normalized by the frequency of the aeroelastic system, denoted as $f_{AE}$. The normalized LLE, shown in Fig. 17b, represents the approximate growth rate of the distance between nearest neighbors per period of the aeroelastic response. The computed range of $\lambda _{LLE}/f_{AE}$ for the selected cases is [0.22, 0.80]. All of the values are positive, which proves that the motions are chaotic. Interestingly, $\lambda _{LLE}/f_{AE}$ linearly increases with $\overline{\varDelta T}_{\text{ Sim }}$. While this result is still under investigation, a possible explanation is that the depth of the co-existing wells grows with the temperature differential, which in turn yields increasingly chaotic oscillations with larger amplitudes. This is consistent with the observations in Sect. 6.

Since the fluid load predictions do not include turbulent boundary layer fluctuating pressures, the self-excited chaotic response is a product of aeroelastic coupling. As noted previously, the presence of co-existing equilibria for buckled structures can predispose the system to chaos. Here, the equilibrium positions correspond to the static buckled shapes of the thin panel into and out of the flow. A static load-displacement curve is computed using the arc-length method [42] in order to confirm the existence of multiple equilibrium solutions. The thermal force induced by $\overline{\varDelta T}_{\text{ Sim }}$ is fixed for this analysis and the force due to the static pressure differential is allowed to vary. The results are shown in Fig. 18 for a point along the midspan at $x/L_p = 0.75$. In addition to the load-displacement curve, the first eigenvalue of the tangent stiffness matrix is provided as a function of the displacement at $x/L_p = 0.75$. A stable system will exhibit eigenvalues with a positive real component, whereas an unstable system will produce eigenvalues with a negative real component. The undamped eigenvalues will also tend to zero as the system approaches an unstable point. The complex behavior of the nonlinear system is clear from the results in Fig. 18, which further highlight the presence of co-existing potential wells.

10 Concluding remarks

Co-existing, nonlinear dynamic responses of a thin panel in turbulent flow were captured in a supersonic wind-tunnel experiment. A reduced-order computational framework is developed in this study to explore and interpret the observed aeroelastic behavior. A quasi-steady enriched piston theory model is used for the prediction of the mean flow. Fluctuating pressures from the turbulent boundary layer are not considered. The structure is approximated using a nonlinear reduced-order model (ROM) which is calibrated so that the fundamental frequency matches that of the installed panel. The sensitivity of the system to various parameters is investigated in terms of the oscillation amplitude and standard deviation of velocity. These analyses yield the following conclusions:

• 1. There is reasonable agreement in the prediction of the post-flutter response using the reduced aeroelastic model. In particular, the computations predict the self-excited chaotic motions observed in the experiment with excellent agreement in terms of the dominant frequency but overestimate the oscillation amplitude by approximately 21%.

• 2. The fundamental frequency has a pronounced effect on the coupled response. Thus, calibration of this quantity in the structural ROM is necessary in order to reproduce the observed aeroelastic behavior. Estimates of the installed panel frequencies are required for this analysis.

• 3. System response maps constructed for the aeroelastic configuration highlight the importance of the temperature differential between the panel and frame. Differences in the spatial variation of the temperature differential are a primary source of error between the theory and experiments. Higher-fidelity modeling of the temperature differential or full-field measurements of the surface temperature is needed in order to confirm this hypothesis.

• 4. The static pressure differential is also a key parameter. For values near zero, the oscillations exhibit features of chaos with corresponding amplitudes that increase with the temperature differential. This behavior is consistent with a buckled panel, where the depth of the co-existing potential wells increases with the temperature differential, resulting in larger deformations. As the magnitude of the pressure differential increases, the system transitions to predominantly periodic attractors. These conditions were not explored during previous entries in RC-19 and motivate the need for additional experimental campaigns targeting these conditions.

• 5. A linearized equation governing the distance between neighboring aeroelastic solutions is derived. The cross-well oscillations for static pressure differentials near zero are proven to be chaotic with a normalized largest Lyapunov exponent ranging from 0.22 to 0.80. The coexistence of multiple stable equilibria predisposes the aeroelastic system to self-excited chaos. The omission of boundary layer induced pressure fluctuations highlights that the chaotic motions are an aeroelastic phenomena. However, these fluctuations likely influence the onset of the cross-well behavior.

• 6. The nonlinear system is sensitive to initial conditions and perturbations. Thus, characterizing the initial conditions in the experiments is critical for accurate response predictions. The simulated results also indicate the existence of multiple dynamic solutions for the coupled system, which significantly complicates structural design and analysis.

• 7. A classical piston theory model produces symmetry in the system response map about a zero static pressure differential. When the effects of a flat plate boundary layer are introduced in enriched piston theory, the response exhibits some asymmetry. This is particularly evident at lower temperature differentials. The asymmetry is expected to be more pronounced when boundary layer effects due to surface deformation are included in the piston model. Exploring asymmetry in the coupled response is an objective for future experiments in RC-19.

The comparisons between the computations and experiments afford valuable insight into the aeroelastic behavior observed in the experiments as well as the accuracy bounds of the computational framework. In general, the agreement suggests that the reduced-order fluid and structural models reasonably capture the pertinent physics for fluid-structure interactions in turbulent flows. However, future work is required to explore the effects of turbulent boundary layer pressure fluctuations on the aeroelastic response. This effort will primarily rely on semi-empirical models due to the computational costs associated with large-eddy simulation and direct numerical simulation predictions. Continued assessment of the reduced-order framework will also focus on modeling the effects of shock/boundary-layer interactions on the aeroelastic response. These efforts will provide an improved understanding of the physical mechanisms that govern the panel behavior and will guide the design of future experiments targeting aeroelastic instabilities.