1 Introduction

During the last three decades, investigation of linear and nonlinear excitations of ion-acoustic (IA) wave features is one of the crucial and familiar aspects of theoretical as well as experimental electron-positron-ion plasma environments because of its enormous occurrence in different astrophysical situations, for example, pulsar magnetospheres [1], active galactic nuclei [2], cold neutron stars, and white dwarfs [3]. Following to their extensive applications in micro-electronic components and nano-electronic devices, quantum plasmas become one of the captivating areas of theoretical and laboratory plasma studies [4,5,6]. Furthermore, quantum plasmas also exist in astrophysical situations [7], high-intensity laser experiments [4], and ultra cold plasmas [8]. Bonitz et al. [9] reported strapping correlations in quantum Coulomb systems (dense plasmas and semiconductors). In this environment, electrons and positrons begin to be degenerated owing to impact of Pauli-exclusive principle and statistical assumption. One can explore the physical concern demanded in plasmas using quantum hydrodynamic fluid equations [9, 10]. For example, Silva et al. [10] reported quantum effects on nonlinear features of white-dwarfs. On the other hand, plasma components may become ultra-relativistic when the rest energy of plasma components become comparable with the Fermi energy and induce to the crumple of star under its colossus gravitational force [11, 12]. Furthermore, the massive ions, related to degenerate plasma pressure, play a crucial character on the features and dynamics of IA wave phenomena. Recently, Esfandyari-Kalejahi et al. [13] reported IA solitons with arbitrary amplitude in dense plasmas. The authors mentioned that plasma components perceived collisionless for the Fermi-blocking operation based on Pauli-exclusion principle, obey statics of zero-temperature Fermi gas, where ions act as classical fluid components. Hafez et al. [14] reported small-amplitude IASWs in a dense plasma. Very recently, Hafez [15] studied interactions of IA two solitons and three solitons in dense plasmas.

rgb 1,0.501961,0.752941rgb 0,0,0Recently, a new class of nonlinear waves in plasmas, called supernonlinear waves [16], was reported in the literature for the first time. The authors [16] proposed topological classification of such supernonlinear waves and suitable notations for their study. Dubinov and Kolotkov [17] also coined the name “supersolitons” in plasma considering a model of five species. Later on, Dubinov and Kolotkov affirmed that at least 4 components were needed to admit supersolitons in plasmas. Maharaj et al. [18] obtained the existence domains of supersolitons in a dusty plasma. Verheest et al. [19,20,21,22] showed that various three-species plasmas could generate supersolitons. It was observed that supersolitons [23] may exist in space plasma environments (Auroral zone).

Recently, appertaining the bifurcation analysis of dynamical systems, some works [24,25,26,27,28,29,30,31,32,33,34] were published on investigation of distinct qualitative attributes of different nonlinear wave features in various plasma systems. Das et al. [35, 36] investigated nonlinear wave features in dusty plasmas with collisional effects through perturbed dynamical systems. Very recently, different numerical methods [37, 38] were applied to obtain traveling wave solutions of nonlinear evolution equations. Saha and Tamang [39] reported effect of nonextensive electrons on supernonlinear waves in auroral plasma. However, there is no study on bifurcation analysis of superperiodic waves in a dense plasma. In this present study, we report bifurcation analysis of IA superperiodic waves in dense plasmas employing bifurcation analysis of dynamical systems [40,41,42,43]. In this case, positron concentration (α) acts as the controlling parameter in the qualitative changes of IA superperiodic waves in dense plasmas.

The remaining part of the paper is composed as follows: we consider basic quantum hydrodynamics fluid equations in Section 2. In Section 3, we form a planar dynamical system for our plasma model. We procure all probable phase plots and bifurcation analysis of IA superperiodic waves in Section 4. Section 5 is taken for conclusion.

2 Basic Equations

A dense unmagnetized plasma is considered that is composed of mobile positive ions, positrons, and electrons. In this case, electrons and positrons are described by zero-temperature Fermi-gas statistics, where ions are treated as classical fluid. To investigate the semi-classical elucidation of nonlinear dynamics for IA waves, we consider normalized quantum hydrodynamic fluid equations [13,14,15] as:

$$ \begin{array}{@{}rcl@{}} \frac{\partial n_{i}}{\partial t}+ \frac{\partial}{\partial x} (n_{i}u_{i})=0, \end{array} $$
(1)
$$ \begin{array}{@{}rcl@{}} \frac{\partial u_{i}}{\partial t}+ u_{i}\frac{\partial u_{i}}{\partial x} =-\frac{\partial \phi}{\partial x}, \end{array} $$
(2)
$$ \begin{array}{@{}rcl@{}} \frac{\partial^{2} \phi}{\partial x^{2}}=(1+\phi)^{\frac{3}{2}}-\alpha(1-\sigma_{F} \phi)^{\frac{3}{2}}-\beta n_{i}, \end{array} $$
(3)

where ni denotes number density of ions, ui denotes velocity of ions, x is space variable, ϕ denotes electrostatic potential, and t is time. The variables are normalized as: \(n_{i} \rightarrow n_{i} n_{i0}\), \(u_{i}\rightarrow v_{Fe}u_{i}\), \(\phi \rightarrow (2k_{B} T_{F_{e}}/e)\phi \), \(x\rightarrow (v_{F_{e}}/\omega _{pi})x\), \(t\rightarrow (1/\omega _{pi})t\), where \(v_{Fe}=\sqrt {2k_{B} T_{Fe}/m_{i}}\), \(\omega _{pi}=\sqrt {e^{2} n_{e0}/\varepsilon _{0}m_{i}}\), α = np0/ne0, σF = TFe/TFp, ni0 is unperturbed number density of ions, ne0(np0) is the unperturbed number density of Fermi-electrons (positrons), TFe(TFp) indicates temperature of Fermi-electrons (positrons), KB indicates the Boltzmann constant, and mi indicates mass of ions. At equilibrium condition, the charge neutrality condition is acquired as β = ni0/ne0 = 1 − α. It is crucial to note that σF = TFe/TFp is interpreted [13] as σF = α− 2/3 for non-relativistic case, and σF = α− 1/3 in case of ultra-relativistic Fermi-gas, which may be prevailed by simplifying the following Chandrasekhar mathematical expression [11] for electron degeneracy pressure \(P=(\pi {m_{e}}^{4} {c_{s}^{5}}/3h^{3})[r(2r^{2}-3)\sqrt {1+r^{2}}+3sinh^{-1}(r)]\), with r = (pFe/mecs), h denotes the Planck constant, cs indicates light’s speed, and me denotes mass of electrons.

3 Planar Dynamical System

To obtain planar dynamical system (DS) from the plasma system, we contemplate a transformation

$$ \xi=x-vt, $$
(4)

here, v indicates velocity of IA traveling wave. With the help of (4) and applying boundary conditions u = 0, n = 1, and ϕ = 0 as \(\xi \rightarrow \pm \infty \) in (1) and (2), one can obtain

$$ n_{i}=\frac{v}{\sqrt{v^{2}-2\phi}}, $$
(5)

and from (3), we get

$$ \frac{d^{2}\phi}{d\xi^{2}}= a\phi+b\phi^{2}+c\phi^{3}+d\phi^{4}, $$
(6)

where \(a=\frac {3}{2}(1+\sigma _{F} \alpha )-\frac {\beta }{v^{2}}\), \(b=\frac {3}{8}(1-{\sigma _{F}^{2}}\alpha )-\frac {3\beta }{2v^{4}}\), \(c=-\frac {1}{16}(1+{\sigma _{F}^{3}}\alpha )-\frac {5\beta }{2v^{6}}\) and \(d=\frac {3}{128}(1-{\sigma _{F}^{4}}\alpha )-\frac {35\beta }{8v^{8}}\).

Equation (6) can be expressed in the form of following DS

$$ \left\{ \begin{array}{ll} \frac{d\phi}{d \xi}=z, \\ \frac{dz}{d\xi}=a\phi+b\phi^{2}+c\phi^{3}+d\phi^{4}. \end{array} \right. $$
(7)

Here, equations in (7) represent a DS consisting of four physical parameters α,β,σF, and v. We consider non-relativistic and ultra-relativistic situations for investigating the DS (7). For non-relativistic case σF = α− 2/3 and for ultra-relativistic case σF = α− 1/3. Again, β = 1 − α. Thus, the DS (7) depends directly on two physical parameters, which are positron concentration (α) and velocity of IA traveling wave (v). In this study, the parameter (α) may be varied keeping a fixed value of v.

4 Bifurcation of Superperiodic Waves

Employing the bifurcation analysis of DS [40]–[43] to the system (7), we investigate bifurcation of superperiodic waves through symbolic computation. The phase plots of a DS may vary consequentially based on the number of critical points and actual number of enveloped separatrix layers [16]. Any trajectory in phase plot of a DS provides one traveling wave solution for the considered plasma. For classification of trajectories in the phase plot, we denote: SPTm,n (PTm,n) for superperiodic trajectory (periodic trajectory) [16], SHTm,n (HTm,n) for superhomoclinic trajectory (homoclinic trajectory), where m indicates the number of critical points covered by the trajectory and n indicates the number of separatrix layers covered by the trajectory. Therefore, to investigate bifurcation of superperiodic waves (periodic waves) of the system (6), we may require to obtain all probable superperiodic trajectories (periodic trajectories) of the system (7) based on parameters α and v in the system (7). The system (7) has four critical points at E1(ϕ1, 0), E2(ϕ2, 0), E3(ϕ3,0), and E4(ϕ4,0), where \(\phi _{1}=0,~~\phi _{2,3,4}=-\frac {p}{3}+2\sqrt {-\frac {g}{3}}cos(\frac {\psi }{3}+\frac {2k\pi }{3}), ~~k=0,1,2,\) with \(cos \psi = \left \{\begin {array}{ccc} -\sqrt {\frac {h^{2}/4}{-g^{3}/27}}, & \text {if~} h>0;\\ \sqrt {\frac {h^{2}/4}{-g^{3}/27}}, & \text {if~} h<0 \end {array}\right .\) and \(\frac {h^{2}}{4}+\frac {g^{3}}{27}<0\), \(p=\frac {c}{d},~q=\frac {b}{d}\), \(~r=\frac {a}{d}\), \(g=\frac {1}{3}(3q-p^{2})\) and \(h=\frac {1}{27}(2p^{3}-9pq+27r)\). Let A(ϕi,zi) indicates Jacobian matrix of system of (7) at a critical point (ϕi,zi). Also, we consider J = det(A(ϕi,zi)), then (ϕi,zi) becomes a saddle critical point if J < 0, and a center critical point for J > 0.

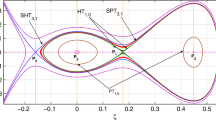
In Fig. 1, we display a phase plot of the nonlinear system (7) for α = 0.82 and v = 2.2 in non-relativistic case. In this situation, the system (7) has four critical points E1, E2, E3, and E4 and two varieties of qualitatively different trajectories, such as homoclinic trajectories (HT1,0) and periodic trajectories (PT1,0). It is essential to note that for the homoclinic trajectories (HT1,0) represented by red curves, one can get solitary wave solutions, and for periodic trajectories (PT1,0) shown by blue curves, one can get periodic wave solutions [24]–[25] which are shown in Fig. 2.

Fig. 1
figure 1

Phase plot of dynamical system (7) for α = 0.82 and v = 2.2 in non-relativistic case

Full size image
Fig. 2
figure 2

Periodic waves of the system (6) corresponding to periodic trajectories. a Around the critical point E3.b Around the critical point E2 present in Fig. 1

Full size image

In Fig. 3, we illustrate a phase plot of the nonlinear system (7) for α = 0.83 and v = 2.2 in non-relativistic case. In this case, there exist four critical points E1, E2, E3, and E4 and three varieties of qualitatively distinct trajectories, such as two homoclinic trajectories (HT1,0), two distinct families of periodic trajectories (PT1,0), superhomoclinic trajectory (SHT3,1) and superperiodic trajectories (SPT3,1). Because of the pair of homoclinic trajectories (HT1,0) shown by red curves, one can get solitary waves (compressive and rarefactive), and for periodic trajectories (PT1,0) represented by blue curves, one can get two distinct families of periodic waves [24]-[25] of similar type, one of which is shown in Fig. 4a. Furthermore, we have supersolitary wave corresponding to the superhomoclinic trajectory (SHT3,1) represented by magenta curve and superperiodic wave which is shown in Fig. 4b, for the superperiodic trajectory (SPT3,1) represented by black curve in Fig. 3.

Fig. 3
figure 3

Phase plot of dynamical system (7) for α = 0.83 and v = 2.2 in non-relativistic case

Full size image
Fig. 4
figure 4

a Periodic and b Superperiodic waves of the system (6) keeping same parametric values as in Fig. 3

Full size image

In Fig. 5, we delineate a phase plot of the nonlinear system (7) for α = 0.4 and v = 2.2 in ultra-relativistic case. In this case, we have four critical points E1, E2, E3, and E4 and two distinct varieties of qualitatively different trajectories, such as homoclinic trajectories (HT1,0) and periodic trajectories (PT1,0). It is fascinating to note that for the homoclinic trajectories (HT1,0) represented by red curves, one can get solitary waves, and for periodic trajectories (PT1,0) shown by blue curves, one can get periodic waves [24]–[25] which are presented in Fig. 6.

Fig. 5
figure 5

Phase plot of dynamical system (7) for α = 0.4 and v = 2.2 in ultra-relativistic case

Full size image
Fig. 6
figure 6

Periodic waves of the system (6) corresponding to periodic trajectories. a Around the critical point E3.b Around the critical point E2 present in Fig. 5

Full size image

In Fig. 7, we manifest a phase plot of the nonlinear system (7) for α = 0.5 and v = 2.2 in ultra-relativistic case. In this case, we have four critical points E1, E2, E3, and E4 and three varieties of qualitatively distinct trajectories, such as two homoclinic trajectories (HT1,0), a pair of families of periodic trajectories (PT1,0), superhomoclinic trajectory (SHT3,1), and superperiodic trajectories (SPT3,1). For the pair of homoclinic trajectories (HT1,0) shown by red curves, one can have solitary waves (compressive and rarefactive), and for periodic trajectories (PT1,0) shown by blue curves, one can have a pair of families of nonlinear periodic waves [24]-[25] of similar type, one of which is shown in Fig. 8a. Furthermore, we have supersolitary wave for the superhomoclinic trajectory (SHT3,1) represented by the magenta curve, and superperiodic wave which is shown in Fig. 8b, for the superperiodic trajectory (SPT3,1) shown by the black curve in Fig. 7.

Fig. 7
figure 7

Phase plot of dynamical system (7) for α = 0.5 and v = 2.2 in ultra-relativistic case

Full size image
Fig. 8
figure 8

a Periodic and b superperiodic waves of the system (6) keeping the same parametric values as Fig. 7

Full size image

5 Conclusions

Bifurcations of IA superperiodic waves have been reported in dense plasmas composed of electrons, positive ions, and positrons with electrons and positrons, where electrons and positrons obey zero-temperature Fermi-gas statistics, and where ions act as a classical fluid. The bifurcation analysis of DS has been applied successfully to present all probable phase plots incorporating superhomoclinic trajectory, and superperiodic trajectory depending on positron concentration (α). Using symbolic computation, IA superperiodic wave solutions have been found for ultra-relativistic environment as well as non-relativistic environment. It has been observed that positron concentration (α) plays a key role in the bifurcation analysis of IA superperiodic wave solutions. The results of this work may be applied to investigate the salient features of IA superperiodic waves in cold neutron stars [11, 12].