1 Introduction

The study of linear and nonlinear wave propagations in quantum plasmas has been a topic of interest due to a variety of the applications of quantum plasma media, such as in ultra-small electronic devices, dense astrophysical objects and high-intensity laser-produced plasmas [1,2,3,4]. In such media, the plasma behaves like a degenerate fluid and the dynamic role of quantum mechanics is outstanding [5]. In this situation, the thermal de Broglie wavelength of charged species becomes same or larger than the average inter-particle distance [6,7,8]. Description of the various nonlinear wave propagations in the magnetized and electrostatic plasmas has been thoroughly investigated by many researchers [9,10,11]. The balancing between nonlinearity and dispersion effects gives rise to the nonlinear structures [12].

Electron-acoustic waves (EAWs) are low frequency electrostatic plasma waves. Ions and cold electrons provide inertia and form a neutralizing stationary background, whereas the hot electrons provide the restoring force for EAWs. On the other hand, in ion-acoustic waves (IAWs) the inertia is provided by the heavily mass ions [13]. The theory of EAWs was first proposed by Freid and Gould [14]. They discovered that besides the Langmuir and ion-acoustic waves, another heavily damped acoustic-like wave (called EAW) may exist which greatly differed from these two waves [14,15,16]. Propagation of EAWs has been studied in magnetized [17, 18] as well as unmagnetized plasmas [19, 20]. The phase velocity of EAWs is between the cold and hot electron thermal velocities. Dubouloz et al. have given experimental observation of the EAWs in magnetized as well as unmagnetized, one-dimensional, collisionless plasma consisting of three components [21, 22]. Propagation of both linear and nonlinear EAWs in unmagnetized plasmas has been studied by many researchers [23,24,25].

The conventional Boltzmann–Gibbs (B-G) statistic was not suitable to describe the feature of a system with long-range interactions. In such a case, nonextensive distribution is widely considered. Tsalli’s q-nonextensive distribution is an extension of B-G’s thermostatistics. One can in general write the entropy as \(S_q=k\frac{1-\sum _{i=1}^{i=W}(P_i)^q}{q-1}\) , wherein entropic index that depicts quality of nonextensivity is denoted by q and the probabilities connected with microscopic states are denoted by \(P_i\). Solving mathematically for \(S_q\), by considering non-negative entropy, it was verified that \(q =1\) attributed to Boltzmann’s distribution, \(q>1\) indicated subextensive distribution and \(q <1\) denoted nonextensivity of plasma particles. Further Verheest [26] has suggested that \(\frac{1}{3}<q<1\) is the suitable range of nonextensivity. So in this manuscript we have taken the value of q within the restricted range of \(\frac{1}{3}<q<1\) in order to investigate the impact of q-nonextensivity of hot electrons.

The concept of planar dynamical system (PDS) is extensively used to study nonlinear waves in different plasmas [27,28,29,30,31,32,33,34,35,36,37,38,39]. Very recently, Saha et al. [29] showed the existence of different types of nonlinear waves, viz. periodic, kink and anti-kink waves in dense quantum plasma in the framework of Burger equation by using the concept of PDS. Sahu et al. [30] discussed nonlinear propagation of electron-acoustic solitons in a quantum plasma. El-Shamy et al [31] investigated a dense semiconductor quantum plasma consisting of electrons and holes to study electrostatic solitons in the framework of the Korteweg–de Vries equations. Bifurcation theory of PDS has been popularly used to study nonlinear waves [27, 40,41,42,43,44,45,46]. Samanta et al. [27] applied the bifurcation theory of PDS to examine propagation of nonlinear waves in a quantum plasma. El-Shamy [40] investigated bifurcation of monotonic and oscillatory magnetosonic shock waves in a degenerate quantum plasma. Recently, propagation of dust-acoustic waves in a four-component plasma was investigated using bifurcation theory by El-Monier and A. Atteya [44]. Shahein and El-Shehri [45] carried out bifurcation analysis of rogue wave under the framework of modified nonlinear Schrödinger equation in an electron-positron-ion plasma with superthermal electrons and relativistic ions.

Supernonlinear waves (SNWs), a new category of nonlinear waves in plasmas, distinguished by the nontrivial topology of their phase plots were revealed by Dubinov et al. [47] for the very first time. They suggested suitable notations and topological classification of such waves for the study. Saha and Tamang [32] were the first to employ bifurcation theory of planar dynamical system to report SNWs in plasmas. Since then, many researchers have employed bifurcation theory to investigate arbitrary amplitude [33,34,35,36] and small-amplitude [37,38,39] supernonlinear waves in different plasmas. Taha and El-Taibany [36] investigated bifurcation of dust-acoustic SNWs employing the generalized (r, q) distribution function. They found that double spectral indices r and q played a significant role in bifurcation of the nonlinear and supernonlinear dust-acoustic waves. SNWs have also been studied in many plasma systems using Sagdeev’s pseudopotential technique [48, 49].

Coexistence of trajectories better known as multistability is one of the recent research advances and consequently demands more investigation. It was first observed in a Q-switch laser model [50]. Basically, it describes the phenomenon where a dynamical system has two or more simultaneous solutions for one fixed set of parameters [51, 52]. Natiq et al. [53] showed multistability phenomena like the coexistence of chaos with quasiperiodic attractors, butterfly chaotic attractor with two point attractors and symmetric Hopf bifurcation in a low-dimensional plasma model. Recently, coexistence of attractors was shown by Saha et al. [37] in an electron-ion quantum plasma. Very recently, Abdikian et al. [39] investigated electron-acoustic SNWs in classical plasma in the framework of nonlinear Schrödinger equation and reported multistability phenomenon. But, effects of temperature ratio and number density ratio on electron-acoustic periodic and superperiodic waves were not reported. Also, coexistence of chaotic, quasiperiodic and superperiodic trajectories was not established. Characteristics of supernonlinear and coexistence features for small-amplitude electron-acoustic waves in an adiabatic quantum plasma in the framework of the modified-KdV equation have not been studied before to the best of our knowledge. In our present manuscript, we will investigate characteristics of supernonlinear and coexistence features for small-amplitude electron-acoustic waves in an adiabatic quantum plasma in the framework of the modified-KdV equation.

In the present work, we study the QEAWs by applying a one-dimensional model of a quantum plasma consisting of a cold and hot electron fluids and stationary ions. Using the reductive perturbation method, we obtained the modified KdV equation as the evolution equation. We present basic set of normalized equations in Sect. 2. Modified KdV equation is derived in Sect. 3. Phase plane analysis is addressed in Sect. 4. In Sect. 5, we have shown coexistence of trajectories for QEAWs. Finally, conclusion is provided in Sect. 6.

2 Basic set of normalised equations

The nonlinear dynamics of the low-frequency quantum electron-acoustic plasma mode is described by [3, 29, 38, 54, 55, 57]:

$$\begin{aligned}&\frac{\partial n}{\partial t}+\frac{\partial }{\partial x}(nu)=0, \end{aligned}$$
(1)
$$\begin{aligned}&\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}=\frac{\partial \phi }{\partial x}-\frac{\sigma }{n}\frac{\partial p}{\partial x}+\alpha \frac{H^2}{2}\frac{\partial }{\partial x} \bigg (\frac{\partial ^2 \sqrt{n}/\partial x^2}{\sqrt{n}}\bigg ),\nonumber \\ \end{aligned}$$
(2)
$$\begin{aligned}&\frac{\partial p}{\partial t}+u\frac{\partial p}{\partial x}+\gamma p\frac{\partial u}{\partial x}=0, \end{aligned}$$
(3)
$$\begin{aligned}&\frac{\partial ^2 \phi }{\partial x^2}=\mu n_h+n-(1+\mu ), \end{aligned}$$
(4)

where \(n_h=(1+(q-1)\sigma \phi )^{\frac{1}{q-1}+\frac{1}{2}}\).

Earlier pre-factor of the Bohm potential (\(\alpha \)) was considered as 1 which was strongly criticized as it gave rise to unphysical predictions [56]. In one-dimensional case with strong degeneracy limit, the pre-factor of Bohm potential for low frequency wave is \(-1/3\) [57, 58], which will be used in our present manuscript.

The variables \(t,~x,~u, n, n_h\) and \(\phi \) are time variable, space variable, velocity of cold electrons, number density of cold electrons, number density of hot electrons and electrostatic potential, respectively. They are normalized by the inverse of cold electron plasma frequency \(\omega ^{-1}_{pc}=\bigg (\dfrac{m_e}{4\pi n_{0}e^2}\bigg )^{\frac{1}{2}}\), the parameter \(\dfrac{C_e}{\omega _{pc}}\), \(C_e=\bigg (\dfrac{k_B T_c}{m_e}\bigg )^{1/2}\), unperturbed number density of cold electrons \(n_0\), unperturbed number density of hot electrons \(n_{h0}\) and \(\bigg (\dfrac{k_B T_c}{e}\bigg )\), respectively. Here \(\sigma =\dfrac{T_c}{T_h}\) is the cold to hot electron temperature ratio and \(\gamma =\dfrac{C^c_p}{C^c_v}\) where \(C^c_p(C^c_v)\) is the specific heat of electron at constant pressure (volume), p is the cold electron pressure normalized by \(n_{0}k_BT_h\). We have set \(\mu =\dfrac{n_{0}}{n_{h0}}\) and \(H=\dfrac{\hbar \omega _{pc}}{m_e C_e^2}\). One can expand the nonextensive electron as follows:

$$\begin{aligned} n_h=1+C_1\phi +C_2\phi ^2+C_3\phi ^3, \end{aligned}$$
(5)

where \(C_1=(1+q)\sigma /2\), \(C_2=(1+q)(3-q)\sigma ^2/8,\) and \(C_3=(1+q)(3-q)(3q-5)\sigma ^3/48\).

3 Modified KdV equation

In order to procure the modified KdV equation for the electrostatic potential in this degenerate quantum plasma, the independent variables are stretched as follows:

$$\begin{aligned} \xi =\epsilon (x-v_{ph}t),~\text {and}~\tau =\epsilon ^3t, \end{aligned}$$
(6)

where \(\epsilon \) is a small (\(0<\epsilon \le 1\)) expansion parameter characterizing the nonlinearity strength and \(v_{ph}\) is the phase velocity and determined later.

$$\begin{aligned} \left. \begin{array}{ll} n = 1+\epsilon n^{(1)}+\epsilon ^2 n^{(2)}+\cdots \\ p = 1+\epsilon p^{(1)}+\epsilon ^2 p^{(2)}+\cdots \\ u = \epsilon u^{(1)}+\epsilon ^2 u^{(2)}+\cdots \\ \phi =\epsilon \phi ^{(1)}+\epsilon ^2\phi ^{(2)}+\cdots \end{array} \right. \end{aligned}$$
(7)

After substituting Eq. (7) in Eqs. (1)–(5), one can collect the first-order terms of \(\epsilon \) as

$$\begin{aligned} \left. \begin{array}{ll} n^{(1)}=-\dfrac{\phi ^{(1)}}{v_{ph}^2-\gamma \sigma },\\ u^{(1)}=-\dfrac{v_{ph}\phi ^ {(1)}}{v_{ph}^2-\gamma \sigma },\\ p^{(1)}=-\dfrac{\gamma \phi ^{(1)}}{v_{ph}^2-\gamma \sigma }. \end{array} \right. \end{aligned}$$
(8)

Eliminating \(n^{(1)},~u^{(1)}\) and \(~p^{(1)}\), we can obtain linear dispersion relation as

$$\begin{aligned} v_{ph}=\sqrt{\dfrac{1+C_1\gamma \mu \sigma }{C_1\mu }}. \end{aligned}$$
(9)

From the next power of \(\epsilon \), one can derive

$$\begin{aligned} \left. \begin{array}{ll} n^{(2)}=\dfrac{(3v_{ph}^2+(\gamma -2)\gamma \sigma )(\phi _1^{(1)})^2-2(v_{ph}^2-\gamma \sigma )^2\phi ^{(2)}}{2(v_{ph}^2-\gamma \sigma )^3},\\ u^{(2)}=\dfrac{v_{ph}(v_{ph}^2+\gamma ^2\sigma )(\phi _1^{(1)})^2-2v_{ph}(v_{ph}^2-\gamma \sigma )^2\phi ^{(2)}}{2(v_{ph}^2-\gamma \sigma )^3},\\ p^{(2)}=\dfrac{\gamma (v_{ph}^2(2+\gamma )-\gamma \sigma )(\phi _1^{(1)})^2-2\gamma (v_{ph}^2-\gamma \sigma )^2\phi ^{(2)}}{2(v_{ph}^2-\gamma \sigma )^3}. \end{array} \right. \nonumber \\ \end{aligned}$$
(10)

While Poisson’s equation (4), gives [59,60,61]

$$\begin{aligned} \left( C_1\mu v_{ph}^2-1+C_1\gamma \mu \sigma \right) \phi ^{(2)}=\frac{1}{2}\frac{C_2\mu (v_{ph}^2-\gamma \sigma )^2}{v_{ph}}\left( \phi ^{(1)}\right) ^2, \end{aligned}$$
(11)

that can be written as \(\phi ^{(2)}=\dfrac{P}{2}\left( \phi ^{(1)}\right) ^2\). It is obvious from the last equation that the coefficient of \(\phi ^{(2)}\) is identically zero, because of linear dispersion relation (9). As \(\phi ^{(1)}\ne 0\), it is supposed that P could be at least of order \(\epsilon \) and this term should be included in the next order of the equation of motion.

Collecting the third order of \(\epsilon \), one can write

$$\begin{aligned}&\dfrac{\partial n^{(3)}}{\partial \xi }=-\dfrac{1}{4(v_{ph}^2-\gamma \sigma )^5}\bigg (8v_{ph}(v_{ph}^2-\gamma \sigma )^3\dfrac{\partial \phi ^{(1)}}{\partial \tau }\nonumber \\&\quad +\,2(15v_{ph}^4+v_{ph}^2\gamma (-18+13\gamma +\gamma ^2)\sigma \nonumber \\&\quad +\,\gamma ^2(6-7\gamma +2\gamma ^2)\sigma ^2)(\phi ^{(1)})^2\dfrac{\partial \phi ^{(1)}}{\partial \xi }\nonumber \\&\quad -\,4(v_{ph}^2-\gamma \sigma )^2 \bigg ( 3v_{ph}^2+(-2+\gamma )\gamma \sigma )\phi ^{(1)}\dfrac{\partial \left( \dfrac{P}{2}\left( \phi ^{(1)}\right) ^2\right) }{\partial \xi }\nonumber \\&\quad +\,(v_{ph}^2-\gamma \sigma )^2(-4(3v_{ph}^2+(-2+\gamma )\gamma \sigma )\dfrac{P}{2}\left( \phi ^{(1)}\right) ^2\dfrac{\partial \phi ^{(1)}}{\partial \xi }\nonumber \\&\quad +\,(v_{ph}^2-\gamma \sigma )\left( 4(v_{ph}^2-\gamma \sigma )\dfrac{\partial \phi ^{(3)}}{\partial \xi }-H^2\alpha \dfrac{\partial ^3 \phi ^{(1)}}{\partial \xi ^3} \right) \bigg ) \bigg ),\nonumber \\&\quad \dfrac{\partial u^{(3)}}{\partial \xi }=\dfrac{1}{4(v_{ph}^2-\gamma \sigma )^5}\bigg (-4\left( v_{ph}^2-\gamma \ \sigma \right) ^3\left( v_{ph}^2+\gamma \sigma \right) \dfrac{\partial \phi ^{(1)}}{\partial \tau }\nonumber \\&\quad +\,v_{ph}\bigg (-2(3v_{ph}^4+v_{ph}^2\gamma ^2(7+\gamma )\sigma \nonumber \\&\quad +\,\gamma ^3(-1+2\gamma )\sigma ^2)(\phi ^{(1)})^2\dfrac{\partial \phi ^{(1)}}{\partial \xi }\nonumber \\&\quad +\,4(v_{ph}^2-\gamma \sigma )^2(v_{ph}^2+\gamma ^2\sigma )\phi ^{(1)}\dfrac{\partial \dfrac{P}{2}\left( \phi ^{(1)}\right) ^2}{\partial \xi }\nonumber \\&\quad -\,(v_{ph}^2-\gamma \sigma )^2\bigg (-4(v_{ph}^2+\gamma ^2\sigma )\dfrac{P}{2}\left( \phi ^{(1)}\right) ^2\dfrac{\partial \phi ^{(1)}}{\partial \xi }\nonumber \\&\quad +\,(v_{ph}^2-\gamma \sigma )\bigg (4(v_{ph}^2-\gamma \sigma )\dfrac{\partial \phi ^{(3)}}{\partial \xi } -H^2\alpha \dfrac{\partial ^3 \phi ^{(1)}}{\partial \xi ^3}\bigg )\bigg )\bigg ),\nonumber \\&\quad \dfrac{\partial p^{(3)}}{\partial \xi }=\dfrac{\gamma }{4(v_{ph}^2-\gamma \sigma )^5}\bigg (8v_{ph}(v_{ph}^2-\gamma \sigma )^3\dfrac{\partial \phi ^{(1)}}{\partial \tau }\nonumber \\&\quad +\,2(v_{ph}^4(8+6\gamma +\gamma ^2)+v_{ph}^2\gamma (-7+\gamma +2\gamma ^2)\sigma \nonumber \\&\quad -\,(-2+\gamma )\gamma ^2\sigma ^2)(\phi ^{(1)})^2\dfrac{\partial \phi ^{(1)}}{\partial \xi }\nonumber \\&\quad -\,4(v_{ph}^2-\gamma \sigma )^2(v_{ph}^2(2+\gamma )-\gamma \sigma )\phi ^{(1)}\dfrac{\partial \dfrac{P}{2}\left( \phi ^{(1)}\right) ^2}{\partial \xi }\nonumber \\&\quad +\,(v_{ph}^2-\gamma \sigma )^2\bigg (-4(v_{ph}^2(2+\gamma )-\gamma \sigma )\dfrac{P}{2}\left( \phi ^{(1)}\right) ^2\dfrac{\partial \phi ^{(1)}}{\partial \xi }\nonumber \\&\quad (v_{ph}^2-\gamma \sigma )\bigg (4(v_{ph}^2-\gamma \sigma )\dfrac{\partial \phi ^{(3)}}{\partial \xi }-H^2\alpha \dfrac{\partial ^3 \phi ^{(1)}}{\partial \xi ^3}\bigg )\bigg )\bigg ). \end{aligned}$$
(12)

Using the above equations, one can get the modified KdV as

$$\begin{aligned} \frac{\partial \psi }{\partial \tau }+P\psi \frac{\partial \psi }{\partial \xi }+3Q\psi ^2 \frac{\partial \psi }{\partial \xi }+R\frac{\partial ^3 \psi }{\partial \xi ^3}=0, \end{aligned}$$
(13)

in which

$$\begin{aligned} \left. \begin{array}{ll} P=-\dfrac{1}{2v_{ph}}\bigg (3+\dfrac{2C_2}{C_1^2\mu }+C_1\gamma (1+\gamma )\mu \sigma \bigg ),\\ Q=\dfrac{-6C_3+C_1^3\mu ^2(6-7\gamma +2\gamma ^2+C_1v_{ph}^2(6+\gamma -5\gamma ^2)\mu )+3C_1^2v_{ph}^4(1+\gamma )^2\mu ^2}{4C_1^2v_{ph}\mu },\\ R=\dfrac{-H^2\alpha +4(v_{ph}^2-\gamma \sigma )^2}{8v_{ph}}, \end{array} \right. \end{aligned}$$

where \(\psi =\phi ^{(1)}\).

4 Phase plane analysis

We transform the modified KdV equation (13) with dual power nonlinearity to a planar dynamical system by applying the following Galilean transformation:

$$\begin{aligned} \zeta =\xi -V\tau , \end{aligned}$$
(14)

where V is the speed of the moving frame. Then modified KdV equation (13) becomes

$$\begin{aligned} -V\frac{\mathrm{d}\psi }{\mathrm{d}\zeta }+P\psi \frac{\mathrm{d}\psi }{\mathrm{d}\zeta }+3Q\psi ^2\frac{\mathrm{d} \psi }{\mathrm{d} \zeta }+R\frac{\mathrm{d}^3 \psi }{\mathrm{d} \zeta ^3}=0. \end{aligned}$$
(15)

Integrating Eq. (15) and applying \(\psi \rightarrow 0\), \(\dfrac{\mathrm{d}\psi }{\mathrm{d}\zeta }\rightarrow 0\), \(\dfrac{\mathrm{d}^2\psi }{\mathrm{d}\zeta ^2}\rightarrow 0\) as \(\zeta \rightarrow \pm \infty \), we have

$$\begin{aligned} -V\psi +\frac{P}{2}\psi ^2+Q\psi ^3+R\frac{\mathrm{d}^2 \psi }{\mathrm{d} \zeta ^2}=0. \end{aligned}$$
(16)

Then from Eq. (16) we can deduce the following dynamical system:

$$\begin{aligned} \left\{ \begin{array}{ll} \dfrac{\mathrm{d}\psi }{\mathrm{d} \zeta }=z, \\ \dfrac{\mathrm{d}z}{\mathrm{d} \zeta }=\dfrac{V}{R}\psi -\dfrac{P}{2R}\psi ^2-\dfrac{Q}{R}\psi ^3. \end{array} \right. \end{aligned}$$
(17)

The system (17) has the following equilibrium points:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}E_0(0,0),\\ &{}E_1\bigg (\frac{-P-\sqrt{P^2+16QV}}{4Q},0\bigg ),\\ &{}E_2\bigg (\frac{-P+\sqrt{P^2+16QV}}{4Q},0\bigg ). \end{array}\right. } \end{aligned}$$

The Jacobian matrix \(J_{E_i}\) of the system (17) at an arbitrary equilibrium point \(E_i(\psi ^*,0)\), \(i=0,1,2\), is:

$$\begin{aligned} J_{E_{i}}= \begin{bmatrix} 0 &{} 1\\ \dfrac{V}{R}-\dfrac{P}{R}\psi ^*-\dfrac{3Q}{R}\psi ^{*2} &{}0 \end{bmatrix}. \end{aligned}$$

Now, determinant of this Jacobian matrix at \(E_i(\psi ^*,0)\) is

$$det(J_{E_i})=-\dfrac{V}{R}+\dfrac{P}{R}\psi ^*+\dfrac{3Q}{R}\psi ^{*2}.$$

Therefore, determinant of this Jacobian matrix at \(E_0,~E_1\) and \(E_2\) is as follows:

$$\begin{aligned} det(J_{E_0})= & {} -\dfrac{V}{R},\\ det(J_{E_1})= & {} -\dfrac{V}{R}+\dfrac{P}{R}\bigg (\dfrac{-P-\sqrt{P^2+16QV}}{4Q}\bigg )\\&+\dfrac{3Q}{R}\bigg (\dfrac{-P-\sqrt{P^2+16QV}}{4Q}\bigg )^2,\\ det(J_{E_2})= & {} -\dfrac{V}{R}+\dfrac{P}{R}\bigg (\dfrac{-P+\sqrt{P^2+16QV}}{4Q}\bigg )\\&+\dfrac{3Q}{R}\bigg (\dfrac{-P+\sqrt{P^2+16QV}}{4Q}\bigg )^2. \end{aligned}$$
Fig. 1
figure 1

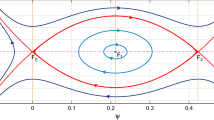
Phase plot of PDS (17) for \(\sigma =0.5,~\mu =0.77,~H=1.4,~\gamma =3,~V=0.1,~\alpha =-1/3\) and \(q=0.35\)

Full size image

The equilibrium point \(E_i(\psi ^*,0)\) is a centre if \(det(J_{E_i})>0\) and a saddle if \(det(J_{E_i})<0\), for \(i=0,1\) and 2 [62].

Figure 1 represents a phase plot of the PDS (17) for \(\sigma =0.5,~\mu =0.77,~H=1.4,~\gamma =3,~V=0.1,~\alpha =-1/3\) and \(q=0.35\) depicting three equilibrium points \(E_0,~E_1\) and \(E_2\) where equilibrium points \(E_1\) and \(E_2\) are centres and \(E_0\) is a saddle. For Fig. 1, we have chosen parameter values depending on physical condition and properties under restriction of phase plane analysis for Fig. 1 (values of the \(J_{E_i}\)). Here equilibrium points \(E_0\) and \(E_2\) are enclosed by a family of nonlinear periodic trajectories (\(NPT_{1,0}\)) for QEAWs. On the other hand, from the equilibrium point \(E_1\), a pair of nonlinear homoclinic trajectories (\(NHT_{1,0}\)) for QEAWs begin and terminate. A family of supernonlinear periodic trajectories (SNPT\(_{2,1}\)) for QEAWs enclosing equilibrium points \(E_0,~E_1\) and \(E_2\) are also portrayed in Fig. 1. For the two families of periodic trajectories for QEAWs surrounding \(E_0\) and \(E_2\), we get periodic wave solutions and for the family of supernonlinear periodic trajectories for QEAWs we get supernonlinear periodic wave solutions.

The periodic and superperiodic wave solutions corresponding to NPT enclosing equilibrium point \(E_2\) and SNPT shown in Fig. 1 are presented by bold green and red curves on left and right sides of Fig. 2. By keeping values of other parameters same as in Fig. 1, we show effect of one parameter on quantum electron-acoustic (QEA) periodic wave (left) and QEA superperiodic wave (right). For example, in Fig. 2a, b, keeping other parametric values same as Fig. 1, temperature ratio (\(\sigma \)) is increased from 0.5 to 0.53 and the wave solutions are depicted by dashed black curves and impact of enhancement of temperature ratio on periodic and superperiodic wave solutions are shown. Proceeding in the similar manner, effects of number density ratio (\(\mu \)), velocity of the moving frame (V) and nonextensivity parameter (q) are shown in Fig. 2c–h, respectively.

Fig. 2
figure 2

Variation of electron-acoustic periodic wave solutions (left) and superperiodic wave solutions (right) for different values of a, b ratio between cold and hot electron temperatures \(\sigma \), c, d ratio of number densities between unperturbed hot and cold electrons \(\mu \), e, f velocity of the moving frame V and g, h nonextensivity parameter q with other values of parameters same as figure 1

Full size image
Fig. 3
figure 3

a Coexistence of quasiperiodic trajectories for QEAWs initiated by \((-0.32,~0.005,~0)\) (blue) and (0.299,  0.005,  0) (black) with chaotic trajectory initiated by \((-0.03,~0.005,~0)\) (red) with \(\sigma =0.05,~\mu =0.78,~H=1.4,~\gamma =3,~V=0.1,~q=0.9,~\alpha =-\dfrac{1}{3},~f_0=0.014\) and \(\omega =0.09\), b enlarged view of quasiperiodic trajectory, c–e time series plots of a and f Lyapunov exponent spectrum w.r.t. \(f_0\) initiated by \((-0.03,~0.005,~0)\) with other parameters same as a

Full size image
Fig. 4
figure 4

a Enlarged view of quasiperiodic trajectories initiated by \((-0.11,~0,0)\) (green), b coexistence of superperiodic trajectory initiated by \((-0.2,~0.02,0)\) (black) and quasiperiodic trajectories initiated by \((-0.11,~0,0)\) (green) and (0.372,  0, 0) (blue) for QEAWs with \(\sigma =0.05,~\mu =0.78,~H=1.4,~\gamma =3,~V=0.1,~q=0.9,~\alpha =-\dfrac{1}{3},~f_0=0.001\) and \(\omega =0.003\), c enlarged view of quasiperiodic trajectories initiated by (0.372,  0, 0) (blue), d–f time series plots of b

Full size image
Fig. 5
figure 5

a Enlarged view of chaotic trajectory initiated by (0.27,  0.005, 0), b coexistence of superperiodic trajectory initiated by (0.65,  0.005, 0) (black), quasiperiodic trajectories initiated by (0.38,  0.005, 0) (blue) and (0.54,  0.005, 0) (cyan) and chaotic trajectory initiated by (0.27,  0.005, 0) (red) for QEAWs with \(\sigma =0.05,~\mu =0.77,~H=1.4,~\gamma =3,~V=0.1,~q=0.9,~\alpha =-\dfrac{1}{3},~f_0=0.01\) and \(\omega =0.002\), c enlarged view of quasiperiodic trajectory initiated by (0.38,  0.005, 0) (blue), d–g time series plot of b, h Lyapunov exponent spectrum initiated by (0.27,  0.005, 0) w.r.t. \(f_0\) with other parameter values same as b

Full size image

From Fig. 2a, b, we observe that an increase in temperature ratio of cold and hot electrons shortens amplitudes of both QEA superperiodic and periodic wave solutions. On the other hand, it elevates width of QEA superperiodic wave solution and decreases width of QEA periodic wave solution. Similar effects can be observed in Fig. 2c–f when values of number density ratio of unperturbed cold and hot electrons and nonextensivity parameter are enhanced. Finally, enhancement of velocity of the moving frame V causes widths of both periodic and superperiodic wave solutions for QEAWs to shorten and their amplitudes to elevate. From all these figures, one can deduce that QEA periodic and superperiodic wave solutions depend on temperature ration (\(\sigma \)), number density ratio (\(\mu \)), nonextensivity parameter (q) and velocity of moving frame (V).

Figure 2b indicates that the amplitude of the superperiodic wave depends inversely to the ratio between cold and hot electron temperature (\(\sigma \)). In this regard it is worth noting that in plasmas, particle disperse due to convection. The tendency toward rarefield regions from compressed regions is persuaded due to the thermal motions of the ions. Figure 2d shows that the amplitude of the superperiodic wave is inversely proportional to the ratio of number densities between unperturbed hot and cold electrons (\(\mu \)). This is because by choosing of a high ratio parameter means that more ions need to bunch in order to prepare the Debye sheath which is actually impossible since the ions are much less mobile compared to electrons. Hence, for sustaining the structure, their amplitude must be inversely proportional to the ratio parameter. From Fig. 2h, we found that the amplitude of the superperiodic wave is inversely proportional to the nonextensive parameter (q). This is true, because by picking up high value of this parameter means that we move further away from Boltzmann’s distribution, i.e., we have chosen the very fast hot electrons. Thus the ions should move fast and is impossible because for ion’s mass.

5 Coexistence of trajectories

We employ an exterior force \(f_0cos(\omega \zeta )\) to the PDS (17) in order to show coexistence of trajectories of QEAWs. The consequent perturbed dynamical system thus obtained is as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \dfrac{\mathrm{d}\psi }{\mathrm{d}\zeta }=z,\\ \dfrac{\mathrm{d}z}{\mathrm{d}\zeta }= \dfrac{V}{R}\psi -\dfrac{P}{2R}\psi ^2-\dfrac{Q}{R}\psi ^3+f_0cos(W),\\ \dfrac{\mathrm{d}W}{\mathrm{d}\zeta }=\omega ,\end{array} \right. \end{aligned}$$
(18)

where \(f_0\) is the strength and \(\omega \) is the frequency of exterior force.

Nonlinear dynamical systems may have more than one simultaneous solution for a fixed parameter set and different initial states. This phenomenon is termed as coexistence of trajectories or multistability. To show coexisting features of QEAWs in our plasma system we will plot phase spaces of system (17) for a particular set of parameters and different initial states. To establish the phenomenon of coexistence of trajectories for QEAWs, we fix parameter values at \(\sigma =0.05,~\mu =0.78,~H=1.4,~\gamma =3,~V=0.1,~q=0.9,~\alpha =-\dfrac{1}{3},~f_0=0.014\) and \(\omega =0.09\). We have chosen fixed values of the parameters depending on physical conditions and properties at different initial conditions to show multistability behaviour of electron-acoustic waves. Initial conditions are varied from \((\psi ,z,W)=(-0.32,~0.005,~0)\) (blue) to \((-0.03,~0.005,~0)\) (red) to (0.299,  0.005,  0) (black) and we observe a corresponding change in phase plot from quasiperiodic to chaotic to quasiperiodic phenomena. This coexistence of two kinds of quasiperiodic trajectories and one type of chaotic trajectory for QEAWs is portrayed in Fig. 3a. Enlarged view of quasiperiodic orbit initiated by (0.299,  0.005,  0) (black) is depicted in Fig. 3b.

From this coexisting phase space (Fig. 3a), one can deduce that electrostatic potential (\(\psi \)) in our plasma system is sensitive to initial conditions. For the above parameter values, electrostatic potential shows quasiperiodic behaviours at initial states \((0.299,0.005,~0)\) and \((-0.32,~0.005,~0)\) and chaotic behaviour at \((-0.03,~0.005,~0)\). Figure 3c–e shows time series plots for initial values (0.299,  0.005,  0) (black), \((-0.03,0.005,~0)\) (red) and \((-0.32,~0.005,~0)\) (blue), respectively, with other parameter values same as Fig. 3a. From time series plots (Fig. 3c, e), irregular periodic nature of the two quasiperiodic trajectories (black and blue) shown in Fig. 3a can be clearly seen. Also aperiodic behaviour of the chaotic trajectory (red) shown in Fig. 3a can be clearly observed from corresponding time series plot shown in Fig. 3d. The chaotic phenomenon is further verified by one positive Lyapunov exponent (LE) in the LE spectrum (Fig. 3f). This LE spectrum is obtained numerically for the fixed parameter set with initial value \((-0.03,~0.005,~0)\).

Coexistence of superperiodic trajectory that is initiated by \((-0.2,~0.02,0)\) (black) and quasiperiodic trajectories that are initiated by \((-0.11,~0,0)\) (green) and (0.372,  0, 0) (blue) for QEAWs are shown in Fig. 4b. Here parameters are fixed at \(\sigma =0.05,~\mu =0.78,~H=1.4,~\gamma =3,~V=0.1,~q=0.9,~\alpha =-\dfrac{1}{3},~f_0=0.001\) and \(\omega =0.003\). It is remarkable to note that electrostatic potential shows sensitive dependence on initial conditions. For the above-mentioned parameter values, electrostatic potential shows superperiodic phenomenon at initial state \((-0.2,~0.02,0)\) and quasiperiodic phenomena at \((-0.11,~0,0)\) and (0.372,  0, 0). Enlarged views of quasiperiodic trajectories for QEAWs initiated by \((-0.11,~0,0)\) (green) and (0.372,  0, 0) (blue) are shown in Fig. 4a, c, respectively. The time series plots initiated by \((-0.2,~0.02,0)\) (black), (0.372,  0, 0) (blue) and \((-0.11,~0,0)\) (green) with other parameters same as Fig. 4b are given in Fig. 4d, e, respectively. Superperiodic behaviour of the black trajectory for QEAWs shown in Fig. 4b is clearly obvious from the time series given by Fig. 4d. Also, irregular periodic phenomena of the blue and green trajectories for QEAWs shown in Fig. 4b are evident from Fig. 4e, f, respectively.

In Fig. 5, we have parameters fixed at \(\sigma =0.05,~\mu =0.78,~H=1.4,~\gamma =3,~V=0.1,~q=0.9,~\alpha =-\dfrac{1}{3},~f_0=0.01\) and \(\omega =0.002\). We observe three types of trajectories for QEAWs coexisting together in Fig. 5b, viz. superperiodic trajectory initiated by (0.65,  0.005, 0) (black), quasiperiodic trajectories initiated by (0.38,  0.005, 0) (blue) and (0.54,  0.005, 0) (cyan) and chaotic trajectory initiated by (0.27,  0.005, 0) (red). Sensitive dependence on initial states can be clearly observed from the coexisting phase space. Electrostatic potential in our plasma system shows superperiodic behaviour at (0.65,  0.005, 0), quasiperiodic behaviour at (0.38,  0.005, 0) and (0.54,  0.005, 0) and chaotic behaviour at (0.27,  0.005, 0). Enlarged views of chaotic trajectory and quasiperiodic trajectory initiated by (0.27,  0.005, 0) (red) and (0.38,  0.005, 0) (blue), respectively, are shown in Fig. 5a, c, respectively. We show time series plots of different trajectories contained in Fig. 5b in Fig. 5d–g, with colours indicating the corresponding initial points. The superperiodic, quasiperiodic and chaotic natures of trajectories shown in Fig. 5b are supported by their corresponding time series plots. The LE spectrum w.r.t. the parameter \(f_0\) initiated by (0.27,  0.005, 0) with other parameters same as Fig. 5b is shown in 5 (h). The existence of one positive LE throughout the graph (Fig. 5d) justifies chaotic nature of the red trajectory shown in Fig. 5b.

6 Conclusion

An adiabatic quantum plasma with stationary ions, degenerate cold electrons and nonextensively distributed hot electrons has been considered. The modified KdV equation has been derived with dual power nonlinearity for highly nonlinear QEAWs using RPT. The modified KdV equation has been reduced to a planar dynamical system with three equilibrium points employing Galilean transformation. A phase plot consisting of three equilibrium points, two families of nonlinear periodic trajectories, a pair of homoclinic trajectories and a family of supernonlinear periodic trajectories for QEAWs has been portrayed. Effects of different parameters on periodic and superperiodic wave solutions for QEAWs have been presented by employing numerical computations. It has been observed that increase in parameters like temperature ratio \(\sigma \), number density ratio \(\mu \) and nonextensivity parameter q shortened amplitudes of electron-acoustic superperiodic waves and expanded its widths. On the other hand, enhancement of velocity of the moving frame V elevated amplitude of electron-acoustic superperiodic wave and contracted its width. It has been found that the amplitude of the nonlinear structures is indirectly proportional to the ratio of number densities (\(\mu \)), the cold to hot electron temperature ratio (\(\sigma \)) and the nonextensivity parameter (q), we have explained physically that confronts our results. Coexistence of quasiperiodic and chaotic trajectories, superperiodic and quasiperiodic trajectories and superperiodic, quasiperiodic and chaotic trajectories for QEAWs were observed in this plasma system using tools such as phase plots and time series plots. Such tools have been efficient in showing repetitive phenomena of periodic trajectories, aperiodic natures of chaotic trajectories and irregular periodic properties of quasiperiodic trajectories for QEAWs. LEs in a LE spectrum quantify the rate of convergence or divergence of close trajectories in a phase space. One principal criteria of chaos in a system is the existence of a positive LE in the LE spectrum. The chaotic behaviours of QEAWs in our system have been further verified by a positive LE in the LE spectrum. Lastly, electrostatic potential of our quantum adiabatic plasma system has been found to depend sensitively on initial conditions and a variety of qualitatively different phenomena were observed for fixed values of physical parameters.