Mathematics of Malaria and Climate Change

Abstract

This chapter is concerned with malaria and the impact of climate change on the spread of malarial diseases on the African continent. The focus is on mathematical models describing the dynamics of malaria under various climate scenarios. The models fit into the Ross–Macdonald framework, with extensions to incorporate a fuller description of the Anopheles mosquito life cycle and the basic physics of aquatic anopheline microhabitats. Macdonald’s basic reproduction number, $\mathcal {R}_0$, is used as the primary metric for malaria potential. It is shown that the inclusion of air–water temperature differences significantly affects predicted malaria potential. The chapter includes several maps that relate the local ambient temperature to malaria potential across the continent. Under plausible global warming scenarios, western coastal Africa is likely to see a small decrease in malaria potential, while central, and especially eastern highland Africa, may see an increase in malaria potential.

1 Introduction

Environmental conditions have always been of profound importance in shaping the epidemiology of infectious diseases. This fact is perhaps best exemplified by the ancient disease of malaria or, more precisely, the collection of closely related malarial diseases.

Caused by plasmodium parasites, malaria is spread via the Anopheles mosquito. Five species are known to cause the disease in humans, namely P. falciparum, P. vivax, P. ovale, P. malariae, and P. knowlesi [4]. The first of these, P. falciparum, accounts for nearly all global malaria mortality, and most of these deaths occur in children under the age of five in sub-Saharan Africa [105].

The life cycles of both Plasmodium and Anopheles depend sensitively and nonlinearly on temperature. Thus, anthropogenic global warming may shift and/or expand the geographic range of malarial disease. This phenomenon has been the object of much mathematical modeling and is also the topic of interest in the current chapter. What do mathematical models tell us about the effects of climate change on the dynamics of malaria? Our geographic focus is on Africa, given the burden of disease on this continent.

Outline of the Chapter

The chapter is organized as follows. In Sect. 4.2, we provide basic information about malaria: the history of the disease, biology of malaria, its immunology and epidemiology, and the influence of weather and climate on the dynamics of the disease. We then move to mathematics in Sect. 4.3.1. After an overview of the panoply of mathematical models of malaria, we introduce the Ross–Macdonald framework, which forms the basis for most modeling efforts. We discuss thermal-response functions for the various parameters in this framework, and map the resulting malaria potential as a function of temperature across the globe, with and without climate change. In Sect. 4.4, we incorporate elements of the more complex vector life cycle into the Ross–Macdonald framework. We present the hydrodynamics of an immature anopheline habitat and compare predicted anopheline abundance—obtained with the extended model, which includes rainfall, the vector life cycle, and hydrodynamics—with historical data from the WHO’s Garki Project in northern Nigeria. We close this section with several maps of malaria potential over the African continent under different modeling options. We summarize our conclusions in the final Sect. 4.5.

2 Basic Information About Malaria

It is generally believed that a combination of local and global environmental changes caused the initial spread of P. falciparum malaria in proto-agricultural Africa, around 10,000 years ago, when the last ice age ended with a period of global warming, and the onset of the climatically stable Holocene Epoch created conditions favorable to agriculture [22]. Warmer temperatures and increased anopheline habitat created by the clearing of forests for crops, along with concentrated human settlements, created the conditions for both vector and parasite to thrive [83, 103]. By historical times, P. falciparum and P. vivax had likely spread to much of the inhabited world, even reaching Britain within the last 1000 years [83].

2.1 History of Malarial Disease

In antiquity, it was known that in certain seemingly unhealthy areas the population was prone to, among other ailments, periodic fevers (a hallmark of malarial disease), especially in the summer and autumn. By the late eighteenth century, it was established that, while certain diseases apparently spread directly from person to person (a process termed contagion), others were endemic to certain parts of the world and, it seemed, contracted from the environment itself. The putative cause of this latter form of transmission was termed miasma (Greek for “pollution”), a kind of poisonous air thought to emanate from soil or rotting matter, and it was believed that the high temperature, humidity, and soils of tropical areas, per se, gave rise to the disease [32].

The central role of low temperatures in limiting the range of malaria was recognized by the mid 1800s by German investigators, who determined that native malaria transmission was limited to areas with average summer temperatures above 15 or 16 ^∘C [65]. In the late nineteenth century (predating modern control programs), malarial disease was likely at its global maximum and clearly concentrated in the warm equatorial band, with its burden falling progressively toward the poles [65].

The close historical concordance between climate and malaria is illustrated visually in Fig. 4.1. The map in the left panel, reconstructed from the famous 1968 publication of Lysenko and Semashko [65], shows the approximate global burden of malarial disease at its global maximum, which happened in most areas in the late nineteenth century. Lysenko and Semashko drew upon a wide variety of sources to construct the first comprehensive map of the global distribution of malaria. Hay and colleagues more recently published a digitized version of this map [55], which has been used in multiple articles, for example, [45].

Fig. 4.1

(Left) The approximate distribution of malaria at its global maximum, based on the 1968 publication of Lysenko and Semashko [65]. The map was digitized by color-coding the textures of the original map, and then georeferenced and extracted using QGIS 2.14.3 with GRASS 7.04. (Right) Mean surface temperature and mean precipitation, based on the WorldClim 2.0 database [41]

Why certain tropical areas and marshy regions seemed so prone to malarial disease was finally discerned mechanistically in the late 1800s. Charles Laveran discovered writhing protozoan parasite within the red blood cells of malaria patients in 1880 [29], while Sir Ronald Ross (1857–1932), a British physician, discerned that these protozoans were spread victim to victim by the female Anopheles mosquito, which requires standing water and heat to breed [29]. Ross elucidated the malaria transmission cycle first in birds (1897) and later in humans, in Freetown, Sierra Leone (1899).

Economic and agricultural modernization, urbanization, and large-scale malaria control programs in the twentieth century led to a dramatic retreat of malaria across the globe [83]. The exception was Africa, where disease burden stayed near its peak until quite recently [22]. Figure 4.2 shows the P. falciparum parasite rate (fraction of 2–10 year olds with detectable blood-stage parasites) across continental Africa in 2000. (Data from the Malaria Atlas Project [53].) Figure 4.2 also shows the modern population across Africa. (Data from the Gridded Population of the World database, version 4 [25].) Population is mainly concentrated in warm coastal West Africa, where malaria is highly endemic (especially in heavily populated Nigeria), and in the cooler eastern highland areas surrounding Lake Victoria and in Ethiopia, where the malaria burden is appreciably lower. Since 2000, parasite rates as well as mortality rates in Africa have fallen dramatically [13].

Fig. 4.2

(Left) P. falciparum parasite rate (fraction of 2–10 year olds) across continental Africa in 2000 [53], which is fairly similar to the global maximum. (Right) African population distribution in 2010 [25]. In combination, these maps show the populations (as opposed to the areas) most at risk

2.2 Basic Biology

Plasmodium parasites, the causative agents of malaria, are eukaryotic protozoans belonging to the large order haemosporidia—a diverse assemblage of parasites that infect and transition between an array of vertebrate hosts and blood-sucking dipteran insect vectors (flies and mosquitoes), and that likely have existed almost as long as the dipterans themselves, at least 150 million years [22]. The consensus is that the haemosporidia first evolved as free-living, sexually reproducing parasites, which colonized the midguts of aquatic insects via a form of extracellular sexual reproduction known as sporogony. Subsequently, they evolved an additional form of intracellular asexual reproduction, known as schizogony, which occurs in the vertebrate host and dramatically increases the proliferation potential of the parasite [22, 88].

Plasmodia are known to infect mammals, lizards, birds, and, in the highly unusual case of the Mesnilium genus, amphibious fish via an unknown vector [88]. We therefore start the discussion of the malaria life cycle with the injection of motile sporozoites from the salivary glands of an infectious mosquito into the skin of its human victim. Within minutes, the sporozoites travel to the liver, where they infect hepatocytes, expand asexually via an initial round of “pre-erythrocyte” schizogony, and ultimately produce 30–40,000 merozoites per infected hepatocyte. The hepatocyte then ruptures, spilling the merozoites into the bloodstream, where they initiate the erythrocyte cycle of schizogony, repeatedly infecting and rupturing erythrocytes every 48 or 72 h, and thus yielding the classical tertian (in the cases of P. vivax and P. falciparum) and quartan (for P. malariae) malarial fevers [4].

Merozoites are not able to infect mosquitoes, so in a subset of infected erythrocytes, the invading merozoites ultimately terminally differentiate into male and female gametocytes, which are incapable of further schizogony but may initiate sporogony in the mosquito when they are ingested. Upon ingestion, the male and female gametocytes recombine extracellularly in the mosquito midgut, thus initiating the sexual sporogonic cycle, and undergo a series of transformations and invade into the mosquito body cavity, ultimately yielding an oocyte which, once mature, ruptures and releases many thousands of sporozoites that make their way to the unfortunate mosquito’s salivary glands, for the cycle to continue [4, 31]. This basic process and some of the key differences between the sporogonic and schizogonic cycles are summarized graphically in Fig. 4.3.

Fig. 4.3

The basic plasmodium life cycle in mosquito and man. Sporogony, which entails the sexual reproductive process beginning with ingested gametocytes and ending in salivary sporozoites, is depicted on the left, while asexual schizogony in man is shown on the right

The Anopheles mosquito also has a relatively complex life cycle, divided broadly into free-flying adult (imago) and aquatic juvenile stages. The adult female mosquito life cycle is dominated by the gonotrophic cycle, which entails the initial taking of a blood meal to fuel egg development, temperature-dependent blood digestion, and egg maturation, and is terminated with oviposition of eggs in an aquatic habitat, only to begin again. In water, the eggs hatch to become actively feeding, motile larvae divided into four instar stages, which eventually become nonfeeding pupae that yield adult mosquitoes [35].

2.3 Immunology and Epidemiology

Epidemiologically, malaria transmission was classified by Macdonald [66] in extremes as either stable or unstable. In the stable case, malaria is endemic (Greek for “in the people”). The population is very frequently exposed to infectious bites, inducing a basic level of immunity throughout the population (except in the youngest children), and thus, malaria incidence fluctuates but little, except for normal seasonal changes related to rainfall, temperature, etc. Epidemics (a marked increase in disease from the normal baseline) are unlikely, and malaria is also more difficult to control or, especially, eliminate. On the other hand, in the unstable case, malaria is characterized by low exposure to infectious bites, a varying and low level of population-level immunity, and hence vulnerability to dangerous and sudden epidemics. However, under such conditions, elimination is far more feasible.

Within endemic areas (and typically stable malaria), the unique immunology of malaria is of profound importance in shaping the burden of disease. When transmission is intense, clinical malaria is extremely common, severe, and frequently life-threatening during the first few years of life. It manifests itself as an uncomplicated febrile disease in adolescence and becomes quite rare by adulthood. Indeed, while historically on the order of 50% of all West African children succumbed to malaria before age five [22], Europeans long thought that adult Africans were incapable of acquiring or transmitting the disease [32]. However, adults very frequently have detectable parasites in their blood, yet no clinical symptoms. Thus, there exists a profound disparity between clinical immunity—protection against the clinical manifestations of disease such as fever, malaise, and, in more severe cases, profound anemia, multi-organ dysfunction, or cerebral malaria—and anti-parasite immunity—protection against infection by parasites per se [31]. Clinical immunity is slowly gained over the course of years as a consequence of numerous infectious bites, while true anti-parasite immunity is rarely, if ever, attained. However, it should be noted that, while blood-borne parasites are detected at nearly the same rates (in a binary sense) in old and young in holoendemic areas, the density of parasites in the old is vastly lower [101]. Furthermore, clinical immunity is relatively short-lived and requires frequent re-exposure for maintenance. Adults who move away from endemic areas become vulnerable to severe disease within just a few years [42], although protection against the most severe and life-threatening forms of disease may be longer-lasting [51, 52]. As a consequence, malaria eradication efforts are complicated by the waning of immunity induced by increased control. Thus, initially beneficial control measures have the potential to increase disease later in time [47]. In the worst case, when control measures lapse, transmission can shift to an unstable scenario with the potential for devastating epidemics. The latter scenario is not merely hypothetical and has occurred on multiple occasions from the 1960s onward [28, 103].

2.4 Weather and Climate

Vector and parasite life histories depend in highly nonlinear ways on temperature. Adult and immature aquatic mosquito survival is maximized at temperatures in the mid-20s (^∘C), with survival tailing off rather symmetrically at higher and lower temperatures. The developmental rates of plasmodium parasites, immature anophelines, and mosquito eggs, however, all generally increase with temperature up to at least 30 ^∘C. Temperature variability is also likely important in determining survival and development [12, 82], and temperatures may also vary appreciably across the micro-environments to which anophelines are regularly exposed [14, 77, 95].

Like temperature, precipitation and hydrology are fundamental environmental determinants of malarial disease. Malaria transmission often follows a highly seasonal pattern, where the most intense transmission occurs during the rainier season. For example, in the relatively arid African Sahel region, inter-annual variations in disease and Anopheles abundance are strongly linked to variations in rainfall [15]; in the Sahel and much of coastal West Africa, highly seasonal rainfall correlates with a highly seasonal pattern of malaria transmission [20]. Moreover, in the Sahel, clinical malaria incidence tends to track rainfall, but with a delay [16]. Monthly rainfall is also positively associated with malaria incidence in both the highlands [26] and coast of Kenya [59]. An. gambiae, which tends to breed in small, temporary pools associated with human activity, seems particularly sensitive to short-term rainfall patterns; Koenraadt et al. [60] observed a significant correlation between rainfall lagged by 1 week and adult An. gambiae numbers in a Kenyan village.

The relationship between anopheline abundance and rainfall is complex and varies across space and time. For example, the rainiest regions in Sri Lanka actually have the lowest malaria incidence, as strong rainfall results in constantly moving waters that make poor anopheline habitat, while drought may lead to standing waters that breed malaria mosquitoes [18]. However, the malaria incidence pattern still follows that of rainfall, as seasonal malaria cases peak a few months after the seasonal rainfall peak [18]. Thomson and colleagues [98, 99] observed a nonlinear, quadratic relationship between seasonal rainfall and the logarithm of malaria incidence in Botswana: while rain is necessary for habitat, excessive precipitation could wash out anopheline breeding grounds. An experiment by Paaijmans et al. [76] reported a similar phenomenon at the microscale. These authors monitored larvae attrition in artificial habitats over the course of the rainy season in western Kenya and observed that larval death rates were much greater on rainy nights. Bomblies et al. [16] also found the temporal pattern of rainy days during the rainy season itself to be important in explaining inter-annual variations in Anopheles abundance.

Malaria, whose distribution depends so profoundly upon temperature and environment, now threatens to change with anthropogenic global warming—warming that is driven principally by the continuously accelerating combustion of fossil fuels, and secondarily by global land-use changes, including deforestation, and large-scale agriculture [97]. Increasing global temperatures are expected to directly affect the capacity of Anopheles mosquitoes to transmit malaria.

3 Mathematical Modeling

Almost since the first elucidation of its life cycle, malaria has been a subject of mathematical modeling and analysis. In the early 1900s, Ross proposed some simple mechanistic models for malaria transmission [96]. Subsequently, George Macdonald developed a simple model for transmission that included the delay from mosquito infection to infectivity [66]. Macdonald also introduced the basic reproduction number ${\mathcal R}_0$— the average number of secondary cases a single initial case generates in a completely susceptible (uninfected and non-immune) population—as an indicator of malaria potential. Macdonald showed that this number is most sensitive to changes in the adult mosquito daily survival probability [66]. His work provided a theoretical justification for the Global Malaria Eradication Programme (GMEP, 1955–1969) of the World Health Organization (WHO). GMEP relied mainly upon indoor residual insecticide spraying for adult vector control, along with mass drug administration [71]. Since the pioneering contributions of Ross and Macdonald, the interest in malaria modeling has expanded considerably, and while many complex models exist, the majority are based upon the Ross–Macdonald framework [89].

Temperature may be incorporated into Ross–Macdonald-style models by making key parameters, such as adult mosquito survival, functions of ambient temperature. Such thermal-response functions are typically determined from experimental data, and allow us to predict malaria potential as a function of current and projected temperature patterns. The inclusion of rainfall in climate-focused mathematical models has varied. Some models ignore rainfall entirely, while others (generally when the focus is upon mapping malaria) apply some kind of mask or weighting according to either total or seasonal rainfall or an index of wetness such as NVDI [92] or soil moisture [100]. Several dynamical models have used relatively simple relations between rainfall and either oviposition or the larvae carrying capacity of the habitat [57, 104], while yet others—for example, [5, 6, 16]—have employed more physically realistic hydrodynamic modeling to drive the accumulation and loss of water within topographic depressions.

Even if we are interested in the role of temperature (the chief parameter altered by global warming) in determining malaria potential, it is unlikely that we can ignore rainfall and hydrodynamics completely, as the water temperature in aquatic microhabitats is an essential determinant of larval development time and survival. This temperature is, in general, not equal to the ambient temperature, especially in equatorial areas [77, 78]. In fact, the difference can vary with habitat size, time of year, and latitude.

In the last two decades, a large number of mathematical models, both statistical and mechanistic, have been developed to assess the possible impact of climate change upon malaria disease potential. A partial list of references includes [1, 3, 11, 12, 15, 16, 27, 30, 33, 39, 40, 57, 62,63,64, 67, 68, 70, 72, 74, 75, 84, 85, 92, 100, 104, 106], and one may also see Eikenberry and Gumel [37] for a recent review. These models have led to varying conclusions. Some of the earlier models predicted a large expansion in the global land area vulnerable to malaria [21, 67, 68, 84], while others predicted only smaller shifts in malaria range [45, 54, 90], as some areas where malaria is highly endemic become too hot to support the Anopheles vectors, while other cooler areas may become capable of more intense transmission. While the debate on expansion versus shift is still open, several recent process-based modeling efforts support the notion that, in western coastal Africa, the malaria burden may be minimally affected or decrease with global warming [92, 106], while central and eastern highland Africa may see greater disease potential [92]. The impact of global warming on the highlands of western Kenya (in eastern Africa) has been of particular interest in recent years, given the large population increase and concurrent large-scale deforestation [86, 87].

Our objective in this chapter is to introduce the basic mathematical tools necessary to address the question of how climate change may affect malaria potential. We focus mainly on models derived within the Ross–Macdonald framework.

3.1 Ross–Macdonald Framework

Sir Ronald Ross (1857–1932), the discoverer of the malaria life cycle, was a polymath who proposed several simple mathematical models for the transmission of malaria among humans and mosquitoes. The 1911 version is a system of two ordinary differential equations [96],

$$\displaystyle \begin{aligned} \begin{aligned} \frac{dX}{dt} &= a b m \, z \, (H - X) - r \, X, \\ \frac{dZ}{dt} &= a c \, x \, (M - Z) - g \, Z, \end{aligned} {} \end{aligned} $$

(4.3.1)

where H and X are, respectively, the total and infected human population, and similarly, M and Z the total and infected mosquito population. The parameters are a, the mosquito biting rate (bites/mosquito/day); b, the probability of human infection after an infectious bite (b = 1 in Ross’s original formulation); c, the probability of a human infecting a mosquito upon biting; m = M∕H, the number of mosquitoes per human; z = Z∕M, the fraction of infectious mosquitoes; x = X∕H, the proportion of infected humans or parasite rate; r, the human recovery rate (day⁻¹); and g, the mosquito death rate (day⁻¹). The last parameter is related to the daily survival probability p,

$$\displaystyle \begin{aligned} g = -\ln p . \end{aligned} $$

(4.3.2)

The Ross Institute and Hospital for Tropical Diseases was established shortly before Ross’s death in 1932. The British malariologist George Macdonald (1903–1967), who became its director in 1947, went on to develop a greatly influential model based upon the ideas of his predecessor but with two major modifications [66]. First, and most significantly, the delay from initial infection to infectivity in mosquito was included, with n denoting the time of the sporogonic cycle, also known as the extrinsic incubation period (EIP). Second, since humans may be infected by multiple Plasmodium strains, which are all cleared independently, Ross’s recovery parameter r was replaced by ρ(r, h), the rate at which new human infections occur. Here, r is the strain-specific rate of recovery and h the inoculation rate (to be defined shortly).

To obtain Macdonald’s model, we recast the system (4.3.1) as a set of delay differential equations,

$$\displaystyle \begin{aligned} \begin{aligned} \frac{dx}{dt} &= a b m \, z(t) (1 - x(t)) - \rho(h,r) x(t), \\ \frac{dz}{dt} &= a c \, x(t - n) (1 - z(t - n)) e^{-gn} - g \, z(t), \end{aligned} {} \end{aligned} $$

(4.3.3)

where x(t) is the parasite rate and z(t) now represents the fraction of mosquitoes that have completed the EIP to become infectious to humans. Thus, z(t) is equivalent to the “sporozoite rate,” the fraction of mosquitoes with sporozoites in saliva, denoted s by Macdonald. Note that the growth term in the z equation is now a function of x and z at time t − n, and also includes the factor e ^−gn to account for those mosquito deaths that occur before sporogony is complete. For example, if n = 10 days, and the daily survival probability is p = 0.9 (hence, g = 0.1054), then 65% of initially infected mosquitoes survive to become infectious; if p falls to 0.7, then fewer than 3% of infected mosquitoes survive to infectiousness.

Macdonald formulated his model solely in terms of x(t) by introducing the inoculation rate, h ≡ h(t) = abm z(t),

$$\displaystyle \begin{aligned} \frac{dx}{dt} = h (1 - x(t)) - \rho(r,h) x(t), \end{aligned} $$

(4.3.4)

While Macdonald originally gave an erroneous form for the overall recovery rate ρ(r, h), the correct form is [36, 96]

$$\displaystyle \begin{aligned} \rho(r,h) = \frac{h}{e^{h/r} - 1} . \end{aligned} $$

(4.3.5)

At equilibrium, the sporozoite rate is constant, z(t) = s, and

$$\displaystyle \begin{aligned} h = abms = \frac{a^2 b c m p^n x}{ax - \ln p} = \frac{a^2 bcmx}{ax + g} e^{-gn} . \end{aligned} $$

(4.3.6)

This model yields the following expression for Macdonald’s basic reproduction number:

$$\displaystyle \begin{aligned} {\mathcal R}_0 = \frac{a^2 b c m p^n}{-r \ln p} = \frac{a^2 b c m e^{-gn}} {r g}. \end{aligned} $$

(4.3.7)

The key conclusion is that ${\mathcal R}_0$ is most sensitive to p, the adult daily survival probability. Thus, the model provides a powerful theoretical justification for malaria eradication efforts based upon insecticidal measures, which underpinned the WHO’s Global Malaria Eradication Programme (GMEP). Somewhat later, the closely related vectorial capacity (VC) metric was defined [43] as the number of new malarial cases (or infectious bites) that could result from a single case in a single day. In terms of the Ross–Macdonald parameters [44], this metric is given by

$$\displaystyle \begin{aligned} \text{VC} = \frac{a^2 c m p^n}{-\ln p} = \frac{b}{r} {\mathcal R}_0. \end{aligned} $$

(4.3.8)

Thus, VC is the component of ${\mathcal R}_0$ that depends only on vectorial parameters and is independent of human parameters.

3.2 Thermal-Response Functions for Ross–Macdonald Parameters

Nearly all the Ross–Macdonald parameters depend in some way upon climate and weather. The most studied and basic relationships are the temperature dependence of survival (p or g), sporogonic duration and EIP (n), and mosquito biting rate (a), often taken as the inverse of the duration of the gonotrophic cycle. Less appreciated is the fact that both b and c depend on temperature as well, although this dependence is not typically included in models. This leaves only m lacking explicit temperature dependence. While taken as an imposed parameter in the Ross–Macdonald framework, m is clearly a function of the temperature-dependent parameters a and p, as well as the weather-dependent immature Anopheles life cycle, which is completely neglected by Ross–Macdonald models.

Adult Mosquito Survival (p or g)

Generally speaking, Anopheles survival peaks at temperatures in the mid- to low-20s celsius, and falls fairly symmetrically about this peak. However, rates of the developmental processes of gonotrophy (mosquito egg development) and sporogony (parasite development) hasten with increasing temperatures up to at least the low-30s, and may be modeled either by a hyperbolic, monotonically increasing function, or via an asymmetric, unimodal function that drops off rapidly at high temperatures. We briefly review some of the data and functional forms used to model these processes.

While several earlier models, most notably the epidemic potential models of Martens and colleagues, fitted a quadratic curve to three data points from 1949, more recent work has relied on a series of experiments by Bayoh [8], where adult An. gambiae was exposed to constant temperatures between 5 and 45 ^∘C at several different relative humidities (RHs). The data are equally well described by a quadratic curve; other authors (e.g., [11]) have used Gaussian distributions. The results are summarized in Fig. 4.4.

Fig. 4.4

Temperature-dependent Ross–Macdonald parameters. (Left) Mean daily survival S (top) and daily survival probability p (bottom), derived under the (false but expedient) assumption that survival is exponentially distributed. Data points show laboratory survival for An. gambiae at either 60 or 80% relative humidity (RH), obtained from [9], together with a quadratic fit to S (blue curve) and Mordecai et al.’s fit to p (red curve). (Middle) Biting rate a and its inverse, gonotrophic duration (1∕a). Data points from Lardeux et al. [61], and fits due to Moshkovsky’s formula (plus 24 h for stages I and III) [35], Lardeux et al. [61], and Mordecai et al. [70]. (Right) Sporogonic duration n and rate 1∕n. Data points compiled from a variety of sources as reported in [79], and fits using either Moshkovsky’s formula [35], or Briere functions due to either Paaijmans et al. [79] or Mordecai et al. [70]

If, as is typically (at least implicitly) assumed in most models, the probability of death does not vary with time—that is, p is independent of age—then the death rate g is the inverse of survival time, p = e ^−g = e ^−1∕S, and survival time is exponentially distributed. However, this assumption is actually false, as the probability of death increases with age in both laboratory and wild mosquito populations [91]. Such a phenomenon may be described using a variety of probability distributions; the most important ones are the Gompertz distribution, which is widely used and the best fit for many datasets, and the Gamma distribution, which may be straightforwardly incorporated into ODE models, as done, e.g., by Christiansen-Jucht et al. [27]. A discussion of this complication falls outside the scope of the chapter.

Gonotrophic Cycle and Mosquito Biting Rate (a)

The gonotrophic cycle is divided into three stages: (I) the search for a host and attack, (II) temperature-dependent blood meal digestion and egg maturation, and (III) oviposition in a suitable body of water [35]. Since only a single blood meal is usually necessary to nourish their eggs, and host attack is a risky energy-intensive process, female anophelines generally take only a single blood meal per cycle (stage I). The overall cycle length, which we denote G _C, can therefore be taken as the inverse of the biting rate, a (supposing, as with the adult survival time and death rate, that G _C is exponentially distributed and age-independent).

Stage II of the gonotrophic cycle is dominant in terms of time and relates to ambient temperature hyperbolically (at least up to fairly high temperatures). The classical formula of Moshkovsky is based upon the “sum of heat” hypothesis—that is, a certain amount of heat, integrated over time, is necessary to complete development—has been widely used to model this phenomenon. Moshkovsky’s expression for the duration of stage II, G _II, is

$$\displaystyle \begin{aligned} G_{II} = \frac{D}{T - T_{min}}, \end{aligned} $$

(4.3.9)

where $T_{\min }$ is the minimum temperature for development, $T > T_{\min }$ is the mean ambient temperature (^∘C), and D is an empirical constant measured in degree-days. Detinova [35] gave D = 37.1 and $T_{\min }$ = 9.9 for the European vector An. maculipennis at relative humidity RH =  70–80%, based on 1938 experiments by Shlenova [94].

The expression (4.3.9) is purely monotonic, while basic physiology suggests that very high temperatures should, at some point, impede egg development [70]. Thus, we may also use some asymmetric unimodal function, such as the Briere function [17], which relates the rate r of gonotrophy to temperature T as r(T) = cT(T − T ₀)(T _m − T)^1∕2. This relation was used by Mordecai et al. [70], with parameters based on much more recent experimental work by Lardeux et al. [61], who examined oviposition in An. pseudopunctipennis under different temperatures. Lardeux et al. [61] themselves employed a qualitatively similar unimodal function given graphically in Fig. 4.4.

Stage II generally dominates the gonotrophic cycle. To obtain the complete cycle length G _C, we may add about 24 h to G _II for stages I and III [35], although limited habitat availability may prolong stage III and additional time may be needed for the search for suitable waters [50].

Several aspects of mosquito biology can complicate the modeling of the biting rate and temperature. First, multiple blood meals may be taken per gonotrophic cycle, although this is generally only observed among newly emerged anophelines that lack sufficient nutritional reserves to fuel egg development from a single blood meal [93]. The time to first blood meal also takes 1–3 days and is temperature dependent [81]. Finally, and possibly quite significantly [24], malarial infection itself may alter anopheline feeding patterns, and infectious mosquitoes (i.e., those with sporozoites in their salivary glands) have been observed taking more frequent, smaller blood meals, while mosquitoes carrying pre-infectious plasmodium stages (e.g., oocysts) may take fewer blood meals [23].

Lastly, we note that several mathematical models have also assumed a constant hazard of death with each blood meal attempt, such that roughly half of all attempts end in death. This introduces a further “hidden” temperature dependency on adult mosquito survival. But this dependence is often ignored when a and p are considered as independent, imposed parameters.

Sporogonic Cycle Duration (n)

Similarly to gonotrophy, the duration of sporogony (or EIP), n, has been described classically using the formula of Moshkovsky (Eq. (4.3.9)), with D = 111 degree-days for P. falciparum and D = 105 degree-days for P. vivax, with $T_{\min } = 14.5\,^{\circ }$C for the relatively cold-tolerant P. vivax and $T_{\min } = 16\,^{\circ }$C for all other plasmodia.

Note that it has long been recognized that temperatures above 30–32 ^∘C can impede the sporogonic cycle [35, 66], although the major effect may be that higher temperatures impede the early stages of sporogony that immediately follow ingestion of a blood meal, but may not block development beyond the oocyst stage [38]. Okech et al. [73] also found that wild strains of West African An. gambiae developed under fluctuating field temperatures up to 33 ^∘C without apparent difficulty. In any case, such observations motivate, as for gonotrophy, the adoption of a unimodal Briere function as done by Mordecai et al. [70] and Paaijmans et al. [79], or a modification of Eq. (4.3.9) to block sporogony above, say, 32–34 ^∘C.

3.3 Temperature and Malaria Potential

Using the above relations, we compute the temperature-dependence of $\mathcal {R}_0$. The result, obtained with a quadratic fit to Bayoh’s adult mosquito survival data [8] and unimodal Briere functions for gonotrophy and sporogony, is shown in Fig. 4.5.

Fig. 4.5

Ross–Macdonald $\mathcal {R}_0$ as a function of temperature, based on the thermal-response functions detailed in the text for a, n, and p, while other parameters are representative of a malaria-endemic region

Given the above (or similar) relations relating key Ross–Macdonald parameters to temperature, one can construct a map representing malaria potential as a function of temperature, as multiple authors have done, often employing some index of transmission potential derived either from Macdonald’s $\mathcal {R}_0$ or from a newer model [30, 46, 67, 92], While such a map is sometimes framed as displaying (relative) $\mathcal {R}_0$ across space, as only vector- and parasite-specific parameters vary with temperature, it is perhaps more appropriate to cast it in terms of vectorial capacity (VC) (equivalent to $\mathcal {R}_0$ sans the human-specific components).

Probably the simplest possible approach to malaria mapping would be to calculate VC or $\mathcal {R}_0$ as a function of mean annual temperature. But this may be misleading, as temperatures are often only seasonally suitable for malaria and the relationship between temperature and $\mathcal {R}_0$ is nonlinear. As daily average temperatures are typically only available for global climate datasets at a monthly scale, this is the temporal resolution typically employed [30, 92], although an innovative work by Gething et al. [46] reconstructs approximate daily temperature variations, and daily temperature variation may be crucial to malaria potential [11, 82].

Using the WorldClim 2.0 database [41], we computed monthly values of Macdonald’s $\mathcal {R}_0$. Even at this time-scale and disregarding precipitation, malaria potential can vary quite appreciably over the year. The mean monthly $\mathcal {R}_0$, shown in Fig. 4.6, yields a crude measure of annual malaria potential as a function solely of temperature at the global scale. Note that we could simply use mean yearly temperatures instead, to yield a single $\mathcal {R}_0$ value at each location. However, this single yearly value varies somewhat from the mean of the $\mathcal {R}_0$ values calculated across each month individually, suggesting that weather variability is important to account for. In Fig. 4.6, we see surprisingly good visual concordance between the model and Lysenko’s historical malaria map. The main points of disagreement are in the extremely arid Saharan region and in the far Eurasian north, where the relatively cold-tolerant P. vivax historically caused short-lived epidemic malaria [65]. Malaria potential is also overestimated in the Kalahari Desert of southern Africa.

Fig. 4.6

(Left) Global malaria potential based on the Ross–Macdonald model, as a function of temperature alone, for 1970–2000 baseline conditions (per the WorldClim 2.0 database [41]). (Right) The same calculations using projected climate change under the HADCM3 model using the IPCC SRES A1B emissions scenario [102]

A variety of other (generally more sophisticated) metrics and methods may be followed in relating temperature to malaria potential. The above efforts do not incorporate precipitation or land cover at all, and precipitation may be included as an independent index of malaria potential (as done in [30]), or we may simply apply a precipitation mask to our map, such that transmission is prohibited anywhere rainfall is sufficiently low. We could also scale $\mathcal {R}_0$ with precipitation in some way, presuming it to be a marker of immature anopheline habitat availability. Ryan et al. [92] applied a mask based on the NDVI, and precipitation and soil moisture may also be more directly incorporated into the underlying model [100]. While we have simply employed VC/$\mathcal {R}_0$, other indices may be used, such as epidemic potential (a metric derived from VC by Martens et al. [67]), or an explicitly time-varying index proportional to VC, as employed by Gething et al. [46].

How might the malaria potential be affected by climate change in the Ross–Macdonald framework? Using the HADCM3 model—a down-sampled GCM climate projection—and the IPCC SRES A1B emissions scenario [102], we have calculated the projected monthly mean $\mathcal {R}_0$ for the 2080s. The results, shown in the right panel of Fig. 4.6, indicate a global expansion of land area that is at some risk and a shift in potential within Africa, where the areas at greatest risk shift roughly south and eastwardly. A similar phenomenon is seen in Figs. 4.13 and 4.14 (Sect. 4.4.2), where we compare predictions under the baseline Ross–Macdonald framework, using an augmented model that considers immature mosquito dynamics.

4 Augmented Ross–Macdonald Framework

In our discussions above, we have already alluded to multiple complicating factors that make the Ross–Macdonald framework likely insufficient for capturing the full range of climate effects on malaria epidemiology. Potentially most important, in our view, is the neglect of the immature anopheline life cycle, which is affected by a broad array of environmental factors, including temperature, rainfall, and local hydrodynamics and land use. These factors have been modeled in different ways by multiple authors. Here, we augment the basic Ross–Macdonald framework to explicitly include immature mosquito dynamics as well as adult vectors.

4.1 Modeling Immature Anophelines

Immature mosquitoes develop from egg, through four actively feeding larval instar stages, and to a final pupal stage. In a differential equations setting, we may variously lump these developmental stages. Here, we consider a model framework with all four larval instar stages,

$$\displaystyle \begin{aligned} \begin{aligned} \frac{dE}{dt} &= \varLambda - \sigma_E E - \mu_E E, \\ \frac{dL_1}{dt} &= \sigma_E E - \sigma_L L_1 - \mu_L L_1 - \varPhi , \\ \frac{dL_i}{dt} &= \sigma_L L_{i-1} - \sigma_L L_i - \mu_L L_i - \varPhi , \quad i = 2, 3, 4, \\ \frac{dP}{dt} &= \sigma_L L_4 - \sigma_P P - \mu_P P . \end{aligned} \end{aligned} $$

(4.4.1)

E(t), L ₁(t), …L ₄(t), and P(t) are the number of mosquitoes in the egg, first through fourth larval instar, and pupal stage, respectively, at time t; σ _i ≡ σ _i(T _W) is the temperature-dependent development rate for stage i (i = E, L, P); T _W represents water temperature; μ _i ≡ μ _i(T _W, R) is the death rate for stage i (i = E, L, P), which depends, in general, upon both the water temperature and rainfall history, denoted R. The rate at which eggs are oviposited by adult mosquitoes is given generically as Λ. The function $\varPhi \equiv \varPhi \left (\sum _i L_i, R\right )$ denotes density-dependent mortality among larvae, which is expected to depend upon rainfall, as this is the source of much anopheline habitat, and upon hydrodynamics more broadly, including topology, vegetation, soil type, etc.

This general framework for immature mosquito dynamics may be coupled to the Ross–Macdonald delay-differential description for adult mosquito dynamics by augmenting the system (4.3.3) by an equation for the total mosquito population, M,

$$\displaystyle \begin{aligned} \frac{dM}{dt} = \sigma_P P - g M. \end{aligned} $$

(4.4.2)

We first examine the temperature dependence of development and mortality rates, which is the weather dependency that has been studied most extensively and incorporated into models. Then we examine how this dependence affects an “augmented” version of Macdonald’s $\mathcal {R}_0$, which incorporates immature anopheline dynamics. We then turn to a discussion of rainfall and hydrodynamics, and examine the time-varying dynamics of anopheline populations and malarial infections when such behaviors are more fully accounted for. Furthermore, we use microscale hydrodynamic simulations to estimate the relation between air and water temperature as a function of time and latitude to refine the malaria potential map under the augmented Ross–Macdonald model.

Temperature-Dependent Parameters

Similar to sporogony and gonotrophy, the rates of immature anopheline development, σ _i, generally increase hyperbolically with temperature, at least up to a point. A purely monotonic relation for larval development time based on work done by Jepson in 1947 [58] has been used in multiple papers, while Bayoh et al. [9] used a unimodal function on the basis of experimental data; the same data were used by Mordecai et al. [70] for a morphologically extremely similar Briere function. The resulting development rates are summarized graphically in Fig. 4.7. Note, however, that while the unimodal functions go to zero because, beyond about 34 ^∘C, larvae fail to develop into adults, it is not clear whether this failure is actually due to increased attrition at high temperatures, rather than arrested development. Laboratory larval survival time as a function of temperature is also given in Fig. 4.7, based on [9, 10], with death rate and survival time described using a fourth-order polynomial fit.

Fig. 4.7

(Left) Immature anopheline development rates, along with unimodal fits due to Bayoh et al. [9], Mordecai et al. [70], or the monotonic relation by Jepson [58]. (Right, top) An. gambiae survival times as well as the fraction surviving to adulthood [10]. (This curve is shifted to the right relative to crude survival, as development is faster at higher temperatures.) (Right bottom) Survival time transformed to death rate, assuming exponentially distributed survival, and a fourth-order polynomial fit to the data

Basic Reproduction Number, ${\mathcal R}_0$

Considering the model framework for immature Anopheles dynamics given above, but excluding any dependence upon rainfall, we extend Macdonald’s ${\mathcal R}_0$ as follows. First, we simplify the general model by omitting density-dependent mortality in the larval compartment, and supposing that oviposition, Λ, is limited by a logistic term,

$$\displaystyle \begin{aligned} \varLambda = a \lambda M \left(1 - \frac{E}{K}\right) . \end{aligned} $$

(4.4.3)

Here, M is the total adult mosquito population, a the biting rate (necessarily equal to the oviposition rate), λ is eggs per oviposition, and K is a carrying capacity, which will generally be proportional to habitat availability as determined by land cover and precipitation patterns. We assume, furthermore, that all development (σ _i) and death (μ _i) parameters are constant, and that we have a single larval compartment. At steady-state, M is given by the expression

$$\displaystyle \begin{aligned} M = \left( \frac{\lambda a \sigma_E \sigma_L \sigma_P}{g (\mu_P + \sigma_P)(\sigma_L + \mu_L)} - \sigma_E - \mu_E \right) \frac{K}{\lambda a}, \end{aligned} $$

(4.4.4)

and m = M∕H. Using the thermal-response functions related above, and assuming for simplicity that the temperature-dependent death rates for all immature anophelines are equal, we get the curves for the normalized and absolute $\mathcal {R}_0$ as a function of the ambient temperature T _A given in Fig. 4.8.

Fig. 4.8

Normalized (top panels) and absolute values (lower panels) of $\mathcal {R}_0$ as a function of ambient temperature, T _A, under the augmented Ross–Macdonald model, including immature anopheline dynamics, for different constant values of ΔT = T _W − T _A. The standard Ross–Macdonald $\mathcal {R}_0$ curve is also given for comparison. As seen, higher water temperatures shift the curve markedly to the left, while colder water temperatures mainly reduce $\mathcal {R}_0$ at small T _A and decrease the magnitude of $\mathcal {R}_0$ across the entire T _A domain

When water and air temperatures are equal, immature dynamics may have only a small effect upon the optimum temperature for malaria transmission, as expressed by $\mathcal {R}_0$, but quite dramatically shift the $\mathcal {R}_0$ curve to the left when water is even a few degrees warmer than air. Interestingly, there is an asymmetry such that when water is colder than air, the temperature for peak $\mathcal {R}_0$ is affected minimally, but the absolute magnitude of $\mathcal {R}_0$ decreases across the entire temperature range, and $\mathcal {R}_0$ falls to zero at the lower temperature range. This pattern is also observed in Fig. 4.8.

4.2 Rainfall and Habitat Dependence

Rainfall

Many important anophelines rely upon ephemeral bodies of water often associated with human activity (ruts, hoofprints, etc.), the availability of which is strongly linked to recent rainfall patterns. In our generic model framework, the rainfall time-series, R, must be translated into some measure of habitat availability. Most commonly, this is manifested either at the level of oviposition or via density-dependent larval mortality; see, for example, [27, 57, 85, 104]. Seasonal anopheline abundance and rainfall patterns often track closely, as is strikingly illustrated in an example dataset drawn from the Garki Project [69] in Fig. 4.9. Thus, we may conclude that the Ross–Macdonald parameter m (mosquitoes per human) is fundamentally related to rainfall, as are $\mathcal {R}_0$ and vectorial capacity. Furthermore, the parameter m varies with temperature; this relationship is generally not independent of rainfall, as water temperature is partially determined by rainfall and habitat size, as can be demonstrated both experimentally (see, for example, [77, 78]) and from detailed mathematical modeling.

Fig. 4.9

Precipitation and An. gambiae counts (from pyrethrum spray collections) in the Ajura Village included in the Garki Project [69]. Seasonal peaks in mosquitoes clearly track the seasonal rainfall pattern, although within each season, total precipitation is a rather poor predictor of total mosquitoes collected

Several works have employed complex, realistic physical models of water accumulation to form Anopheline habitat, but simpler options exist [27, 57, 104]. White et al. [104] took larval carrying capacity (loosely speaking) to be a convolution of recent rainfall and some weighting function, with the best (of those considered) determined to be an exponential weighting of past rainfall. Earlier work by Hoshen and Morse [57] took the rate of oviposition to be linearly proportional to the sum of rainfall over the last 10 days. A more data-driven approach can also be taken. For example, Lunde et al. [64] calculated immature anopheline carrying capacity for different spatial grid-cells as a composite function of soil moisture and potential river length. The latter quantity was derived from the HydroSHEDS database, which provides data on the potential for water accumulation, given the topology of the Earth’s surface. Bomblies et al. [16] developed a more comprehensive model, explicitly including runoff, flow, and water accumulation within depressions at village scale topography, and coupled this to an agent-based model for malaria mosquitoes. This work also formed the basis for several more recent studies [15, 106].

Habitat

Regardless of how the accumulation and loss of habitat volume and/or surface area is determined, this metric must be translated into some kind of carrying capacity or density-dependent death term, etc. Several authors have assumed a biomass carrying capacity for anopheline ponds of about 300 mg m⁻², with stage-four instars weighing 0.45 mg [16, 33, 100]. Under the augmented Ross–Macdonald model, we may also simply limit oviposition via a logistic term, with the egg carrying capacity proportional to water surface area.

At the microscale, we can apply first principles from physics to describe water in a suitable depression as habitat for immature mosquitoes. Such a model can yield a time-varying immature carrying capacity, help elucidate the relationship between water and air temperature, give insight into the relationship between habitat parameters such as depth or shading and anopheline numbers, as well as justify or motivate simpler phenomenological relationships between anopheline habitat and rainfall.

Our first task is to define some habitat geometry that relates depth (d), surface area (A), and volume (V ). Options include, for example, a cylindrical geometry, right-angle cone, or a somewhat more general geometry proposed by Hayashi and colleagues [19, 56], which describes a depression by maximum surface area, maximum depth, and a dimensionless shape parameter, p.

The various mechanisms involved in microscale habitat hydrodynamics are schematically summarized in Fig. 4.10. Water volume is gained at a rate proportional to precipitation (both directly and via runoff over some catchment area), while it is lost through evaporation and infiltration into the soil. Volume balance is described by the ordinary differential equation

$$\displaystyle \begin{aligned} \frac{dV}{dt} = P (A + R_{\mathrm{frac}} (A_{\mathrm{catch}} - A)) - A (E + I), \end{aligned} $$

(4.4.5)

where P ≡ P(t) is the precipitation time-series (m); A _catch is the catchment area for precipitation runoff, with R _frac the fraction running off; E and I are volume losses due to evaporation (latent heat flux) and infiltration, respectively, with infiltration dominant in the Sahel [16, 34]. The infiltration rate varies nonlinearly; a simple expression is given in [5]. Washout, which happens when influx exceeds the maximum volume of the habitat, can serve as a source of larval mortality, as demonstrated experimentally in artificial habitats by Paaijmans et al. [76]. It has been incorporated into models, for example, by having larval mortality increase with precipitation [100] or via a quadratic relationship between egg survival and rainfall [85].

Fig. 4.10

Schematic for heat and volume balance in an anopheline microhabitat. Heat is gained and lost via both short- and long-wave radiation, precipitation, infiltration, runoff, and washout, while the same mechanisms lead directly or indirectly (i.e., via latent heat lost in the form of water vapor) to volume changes

As evaporation represents the loss of both water and heat, the heat balance of a habitat is directly coupled to its volume balance. This suggests a modeling complication of potentially fundamental importance: water and ambient temperatures are not necessarily equal, nor do they necessarily differ by a constant offset. The heat balance in a habitat can be described by an ordinary differential equation for the total heat, Q (joules),

$$\displaystyle \begin{aligned} \frac{dQ}{dt} = A (R_n - \lambda E - H - G) + P_Q - I_Q . \end{aligned} $$

(4.4.6)

Here, A is habitat surface area, R _n is net radiation per unit area, λE is latent heat flux (i.e., the heat contained in evaporating water), H is sensible heat flux, and G is heat flux through the surrounding soil [2, 6]. The units are m² for A and Wm⁻² for the quantities inside the parentheses. Heat is gained via precipitation and runoff, P _Q, and lost via infiltration, I _Q.

Further mathematical details and model formulations can be found in [5,6,7, 16, 77, 78, 85, 100].

Figure 4.11 demonstrates how rainfall in the Ajura village of the Garki Project might translate into habitat volume and adult mosquito populations. The results were obtained with the model represented in Fig. 4.10, assuming a relatively large habitat (maximum surface area 100 m² and maximum depth of 1.5 m). The graphs show that the “impulse response function”—that is, the habitat volume time-series response following a single pulse of rainfall—is essentially an exponential, concordant with the conclusions of White et al. [104].

Fig. 4.11

Simulated water temperatures, habitat volume, and adult mosquito populations (both total and infectious), based on ambient air temperature and precipitation data for the Garki region [69]. Maximum and minimum air temperatures were used to develop sinusoidally varying daily temperature profiles, and daily solar insolation was calculated from time of year and latitude (12.4^∘N). (Top) Smoothed time-series of ambient and (simulated) water temperatures. (Center) Precipitation and simulated habitat volume. (Bottom) Modeled adult Anopheles populations and corresponding data-points from the Ajura village

The top panel in Fig. 4.11 indicates that ambient and water temperatures can differ significantly. Water temperatures are typically around 2–6 ^∘C greater than air temperatures, and about 4 ^∘C greater on average. This is consistent with experiments by Paaijmans et al. [77, 78], who recorded diurnally varying ambient and water temperatures in a nearly equatorial area of Kenya in artificial anopheline habitats and found water to be several degrees warmer, especially at the height of the day.

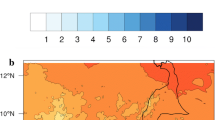
By modeling the heat balance of microhabitats, we can get a better idea of the likely difference ΔT = T _W − T _A across time and space and use this information to motivate an improved set of temperature-dependent malaria potential maps. Figure 4.12 shows how, under simulated diurnal temperature and solar radiation variation, water and ambient temperature vary over the course of a day. The variability in water temperature is greater for smaller habitats, although ΔT is fairly insensitive to habitat size. We also see from this figure that the average of ΔT is likely not constant but varies with T _A, such that ΔT is greater at lower ambient temperatures.

Fig. 4.12

Simulated water temperatures under sunny, low-wind conditions, for small and large habitats, at the equator and at 20^∘N, at the height of summer. The four panels on the left show how the minimum, mean, and maximum values of the water temperature, T _W, vary with mean air temperature, T _A. The two panels on the right show time-series of diurnally varying air and water temperatures in a small (top) and large (bottom) habitat. The average ΔT is similar across habitat sizes, but actual T _W is much more variable in the smaller habitat

Fig. 4.13

Temperature-dependent malaria potential (as measured by $\mathcal {R}_0$) across continental Africa. (Left) Baseline conditions (based on WorldClim 2.0 [41]). (Right) 2080s global warming conditions (based on the HADCM3 model and SRES A1B scenario [102]). (Top) Basic Ross–Macdonald framework. (Bottom) Augmented Ross–Macdonald model with ΔT = 0 ^∘C

Fig. 4.14

Similar to Fig. 4.13. Temperature-dependent malaria potential under baseline conditions (left) and 2080s global warming conditions (right). (Top) Augmented Ross–Macdonald model with ΔT = 3 ^∘C. (Bottom) ΔT varying with month and latitude

We emphasize that, while insolation at the equator is almost invariant throughout the year, there is nontrivial seasonal variability even at ±20^∘ latitude. Simulations suggest that, at 20^∘N under low-wind and sunny conditions, ΔT may range from about − 4 to + 1^∘C in winter, but around + 4 to + 8^∘C during summer. We have generated a set of ΔT data points as a function of month (using the first Julian day of the month), latitude, and average T _A, which yields a multiple linear regression for ΔT at any time and spatial point.

4.3 Malaria Potential Across Africa

Figures 4.13 and 4.14 show how temperature-dependent malaria potential varies across continental Africa under three scenarios, two where ΔT is fixed (ΔT = 0^∘C and ΔT = 3^∘C) and one where ΔT varies with date and latitude, under baseline conditions and a possible global warming scenario. All models predict a contraction in malaria potential under global warming in west coastal Africa. When ΔT is variable, the models predict appreciably more malaria potential in heavily populated eastern highland Africa compared to a fixed ΔT of 3 ^∘C.

5 Summary and Conclusions

Malaria epidemiology is fundamentally linked to weather and climate, and it remains to be seen how anthropogenic global warming will ultimately influence this disease. Multiple mathematical models have addressed this question, with somewhat varying conclusions, although the most likely outcome is a modest expansion of the global geographic areas potentially at risk. Within Africa, where almost the entire malaria burden is currently felt, there may be a shift in the areas and populations most at risk, from western to central and eastern Africa, particularly in some populous highland areas in western Kenya, Uganda, and Ethiopia. Furthermore, there are likely to be seasonal shifts in disease transmission [92], and precipitation, land use, and hydrology are all likely to be important environmental factors at local and regional scales [16, 86]. The goal of this chapter has been to establish the basic biology of malarial disease, and present in some detail how this is translated into the Ross–Macdonald framework (and extensions thereof), which forms the basis for hundreds of mathematical models and yields a widely used expression for the basic reproduction number, $\mathcal {R}_0$.

The Ross–Macdonald number $\mathcal {R}_0$ relates malaria potential to several key quantitative parameters. These parameters all depend on temperature, and at least one, namely the mosquito-to-human ratio (m), depends additionally on rainfall and land use. Because the Ross–Macdonald number forms the basis of many climate-focused mathematical malaria models, we have examined the thermal-response functions and data sources in detail for some of the key parameters, namely the duration of the sporogonic cycle (n), the mosquito biting rate (a), and the daily survival probability (p). Given these thermal-response functions, we can compute $\mathcal {R}_0$ as a function of temperature, and thus produce global and continental-scale maps of malaria potential, both under current and projected climatic conditions.

We extended the Ross–Macdonald framework to include a basic model for immature Anopheles dynamics. Using this augmented Macdonald framework, we show that the temperature-dependence of $\mathcal {R}_0$ may vary appreciably, depending upon how air and water temperature relate. This can significantly affect predicted malaria potential.

Precipitation and hydrodynamics are also fundamentally important to vectorial capacity. We examined how they may be reasonably modeled at the small scale to predict Anopheles abundance. We incorporated the effect of different air and water temperatures into the augmented Ross–Macdonald framework to generate malaria potential maps under various climate change scenarios. The results show that the populations of western Africa may be less susceptible to malaria under climate change, but those in the east may be more vulnerable. This finding is consistent with several more sophisticated modeling studies [92, 106]. Incorporating precipitation more directly into large-scale malaria potential maps is likely essential to reach a full understanding of the effect of global warming on malaria potential, but we defer that task to the future.

Finally, a variety of other phenomena affect malaria, and it is essential to at least mention some of these factors. From our discussion on modeling anopheline habitat, rainfall, and water heat- and volume-balance, we have already seen that water temperature may differ from ambient, and this difference can affect the optimum temperature for malaria transmission. In our discussion of mapping malaria potential under the Ross–Macdonald framework, we also demonstrated the importance of monthly temperature variations. It comes as no surprise then that daily variations in both ambient and water temperature also appreciably affect malaria potential, as has been demonstrated in several recent experimental and theoretical works [12, 14, 79, 80, 82]. Overall, temperature variability seems likely to asymmetrically affect malaria potential such that transmission is reduced at higher temperatures, while it may have a smaller effect at colder temperatures [12].

As elaborated in Sect. 4.2.3, the unique immunology of malaria is central to its epidemiology. But this fact has generally been ignored in mathematical malaria models that focus on the potential impact of climate change (but see, e.g., [106] for an exception). However, there exists a substantial mathematical literature focused on this aspect of the disease, dating at least to the influential Garki Model developed by Dietz et al. [36]. More recent works are [42, 47,48,49, 51, 52]. A full accounting for the interaction between climate and immunity is likely to be a fundamental challenge for the future.