Characterizations of balls by sections and caps

Abstract

Among others, we prove that if a convex body $\mathcal {K}$ and a ball ${\mathcal B}$ have equal constant volumes of caps and equal constant areas of sections with respect to the supporting planes of a sphere, then ${\mathcal K}\equiv {\mathcal B}$.

1 Introduction

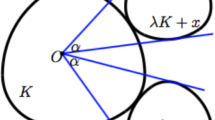
If the convex body $\mathcal M$, the kernel, contains the origin $O$, let $\hbar _{\mathcal M}({\varvec{u}})$ denote the supporting hyperplane of $\mathcal M$ that is perpendicular to the unit vector ${\varvec{u}}\in {\mathbb {S}}^{n-1}$ and contains in its same half space $\hbar ^-_{\mathcal M}({\varvec{u}})$ the origin $O$ and the kernel $\mathcal M$. Its other half space is denoted by $\hbar ^+_{\mathcal M}({\varvec{u}})$.

If the convex body $\mathcal K$ contains the kernel $\mathcal M$ in its interior, we define the functions

$$\begin{aligned} \mathrm{S}_{\mathcal M;\mathcal K}^{}({\varvec{u}})&= |\mathcal K\cap \hbar _{\mathcal M}({\varvec{u}})|, \quad (section\,function) \end{aligned}$$

(1.1)

$$\begin{aligned} \mathrm{C}_{\mathcal M;\mathcal K}^{}({\varvec{u}})&= |\mathcal K\cap \hbar ^+_{\mathcal M}({\varvec{u}})|, \quad (cap\,function) \end{aligned}$$

(1.2)

where $|\cdot |$ is the appropriate Lebesgue measure.

The goal of this article is to investigate the problem of determining $\mathcal K$ if some functions of the form (1.1) and (1.2) are given for a kernel $\mathcal M$.

Two convex bodies $\mathcal K$ and $\mathcal K'$ are called $\mathcal M$-equicapped if $\mathrm{C}^{}_{\mathcal M;\mathcal K}\equiv \mathrm{C}^{}_{\mathcal M;\mathcal K'}$, and they are $\mathcal M$-equisectioned if $\mathrm{S}^{}_{\mathcal M;\mathcal K}\equiv \mathrm{S}^{}_{\mathcal M;\mathcal K'}$. A convex body $\mathcal K$ is called $\mathcal M$-isocapped if $\mathrm{C}^{}_{\mathcal M;\mathcal K}$ is constant. It is said to be $\mathcal M$-isosectioned if $\mathrm{S}^{}_{\mathcal M;\mathcal K}$ is constant.

First we prove in the plane that

• (a) two convex bodies coincide if they are $\mathcal M$-equicapped and $\mathcal M$-equisectioned, no matter what $\mathcal M$ is (Theorem 3.1), and

• (b) any disc-isocapped convex body is a disc concentric to the kernel (Theorem 3.2).¹

Then, in higher dimensions we consider only such convex bodies that are sphere-equisectioned and sphere-equicapped with a ball, and prove that

• (1) a convex body that is sphere-equicapped and sphere-equisectioned with a ball, is itself a ball (Theorem 5.3);

• (2) a convex body that is twice sphere-equicapped (for two different concentric spheres) with a ball is itself a ball (Theorem 5.1);

• (3) a convex body that is twice sphere-equisectioned (for two different concentric spheres) with a ball is itself a ball (Theorem 5.2, but dimension $n=3$ excluded).

For more information about the subject we refer the reader to [1, 3] etc.

2 Preliminaries

We work with the $n$-dimensional real space ${\mathbb {R}}^n$, its unit ball is $\mathcal B=\mathcal B^n$ (in the plane the unit disc is $\mathcal D$), its unit sphere is ${\mathbb {S}}^{n-1}$ and the set of its hyperplanes is ${\mathbb {H}}$. The ball (resp. disc) of radius $\varrho >0$ centred to the origin is denoted by $\varrho \mathcal B=\varrho \mathcal B^{n}$ (resp. $\varrho \mathcal D$).

Using the spherical coordinates ${\varvec{\xi }}=(\xi _1,\ldots ,\xi _{n-1})$ every unit vector can be written in the form ${\varvec{u}}_{{\varvec{\xi }}}=(\cos \xi _1,\sin \xi _1\cos \xi _2,$ $\sin \xi _1\sin \xi _2\cos \xi _3,\ldots )$, the $i$th coordinate of which is $u_{{\varvec{\xi }}}^i=(\prod _{j=1}^{i-1}\sin \xi _j)\cos \xi _i$ ($\xi _n:=0$). In the plane we even use the ${\varvec{u}}_{\xi }=(\cos \xi ,\sin \xi )$ and ${\varvec{u}}_{\xi }^{\perp }={\varvec{u}}_{\xi +\pi /2}=(-\sin \xi ,\cos \xi )$ notations and in analogy to this latter one, we introduce the notation ${\varvec{\xi }}^{\perp }=(\xi _1,\dots ,\xi _{n-2},\xi _{n-1}+\pi /2)$ for higher dimensions.

A hyperplane $\hbar \in \mathbb {H}$ is parametrized so that $\hbar ({\varvec{u}}_{{\varvec{\xi }}},r)$ means the one that is orthogonal to the unit vector ${\varvec{u}}_{{\varvec{\xi }}}\in {\mathbb {S}}^{n-1}$ and contains the point $r{\varvec{u}}_{{\varvec{\xi }}}$, where $r\in {\mathbb {R}}$.² For convenience we also frequently use $\hbar (P,{\varvec{u}}_{{\varvec{\xi }}})$ to denote the hyperplane through the point $P\in {\mathbb {R}}^n$ with normal vector ${\varvec{u}}_{{\varvec{\xi }}}\in {\mathbb {S}}^{n-1}$. For instance, $\hbar (P,{\varvec{u}}_{{\varvec{\xi }}})=\hbar ({\varvec{u}}_{{\varvec{\xi }}},\langle \overrightarrow{OP},{\varvec{u}}_{{\varvec{\xi }}}\rangle )$, where $O=\mathbf{0}$ is the origin and $\langle .,.\rangle$ is the usual inner product.

On a convex body we mean a convex compact set $\mathcal K\subseteq {\mathbb {R}}^n$ with non-empty interior $\mathcal K^{\circ }$ and with piecewise $\mathrm{C}^1$ boundary $\partial \mathcal K$. For a convex body $\mathcal K$ we let $p_{\mathcal K}^{}:{\mathbb {S}}^{n-1}\rightarrow {\mathbb {R}}$ denote support function of $\mathcal K$, which is defined by $p_{\mathcal K}^{}({\varvec{u}}_{\xi })=\sup _{{\varvec{x}}\in \mathcal K}\langle {\varvec{u}}_{\xi },x\rangle$. We also use the notation $\hbar _{\mathcal K}({\varvec{u}})=\hbar ({\varvec{u}},p_{\mathcal K}^{}({\varvec{u}}))$. If the origin is in $\mathcal K^{\circ }$, another useful function of a convex body $\mathcal K$ is its radial function $\varrho _{\mathcal K}^{}:{\mathbb {S}}^{n-1}\rightarrow {\mathbb {R}}_+$ which is defined by $\varrho _{\mathcal K}^{}({\varvec{u}})=|\{r{\varvec{u}}:r>0\}\cap \partial K|$.

We need the special functions $I_x(a,b)$, the regularized incomplete beta function, $B(x;a,b)$, the incomplete beta function, $B(a,b)$, the beta function, and $\Gamma (y)$, Euler’s Gamma function, where $0<a,b\in {\mathbb {R}}, x\in [0,1]$ and $y\in {\mathbb {R}}$. We introduce finally the notation $|{\mathbb {S}}^{k}|:=2\pi ^{k/2}/\!\Gamma (k/2)$ as the standard surface measure of the $k$-dimensional sphere. For the special functions we refer the reader to [11, 12].

We shall frequently use the utility function $\chi$ that takes relations as argument and gives $1$ if its argument fulfilled. For example $\chi (1>0)=1$, but $\chi (1\le 0)=0$ and $\chi (x>y)$ is $1$ if $x>y$ and it is zero if $x\le y$. Nevertheless we still use $\chi$ also as the indicator function of the set given in its subscript.

A strictly positive integrable function $\omega :{\mathbb {R}}^n\!\setminus \!\mathcal B\rightarrow {\mathbb {R}}_+$ is called weight and the integral

$$\begin{aligned} V_{\omega }(f):=\int _{{\mathbb {R}}^n\setminus \mathcal B}f(x)\omega (x)dx \end{aligned}$$

of an integrable function $f:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ is called the volume of $f$ with respect to the weight $\omega$ or simply the $\omega$-volume of $f$. For the volume of the indicator function $\chi _{\mathcal S}^{}$ of a set $\mathcal S\subseteq {\mathbb {R}}^n$ we use the notation $V_{\omega }(\mathcal S):=V_{\omega }(\chi _{\mathcal S})$ as a shorthand. If more weights are indexed by $i\in {\mathbb {N}}$, then we use the even shorter notation $V_{i}(\mathcal S):=V_{\omega _i}(\mathcal S)=V_{i}(\chi _{\mathcal S}^{}) :=V_{\omega _i}(\chi _{\mathcal S}^{})$.

3 In the plane

We heard the following easy result from Kincses [5].

Theorem 3.1

Assume that the border of the strictly convex plane bodies $\mathcal M$ and $\mathcal K$ are differentiable of class $C^1$ and we are given $\mathcal M$ and the functions $\mathrm{S}_{\mathcal M;\mathcal K}^{}$ and $\mathrm{C}_{\mathcal M;\mathcal K}^{}$. Then $\mathcal K$ can be uniquely determined.

Proof

Fix the origin $\mathbf{0}$ in $\mathcal M^{\circ }$. In the plane ${\varvec{u}}_{\xi }=(\cos \xi ,\sin \xi )$, therefore we consider the functions

$$\begin{aligned} f(\xi )&:=\mathrm{S}_{\mathcal M;\mathcal K}^{}({\varvec{u}}_{\xi }) =|\hbar (p_{\mathcal M}^{}({\varvec{u}}_{\xi }),{\varvec{u}}_{\xi })\cap \mathcal K|\\ g(\xi )&:=\mathrm{C}_{\mathcal M;\mathcal K}^{}({\varvec{u}}_{\xi }) =|\hbar ^+(p_{\mathcal M}^{}({\varvec{u}}_{\xi }),{\varvec{u}}_{\xi })\cap \mathcal K| \end{aligned}$$

where $\hbar ^+$ is the appropriate half space bordered by $\hbar$.

Let ${\varvec{h}}(\xi )$ be the point, where $\hbar (p^{}_{\mathcal M}(\xi ),{\varvec{u}}_{\xi })$ touches $\mathcal M$. Then, as it is well known, ${\varvec{h}}(\xi )\!-\!p^{}_{\mathcal M}(\xi ){\varvec{u}}_{\xi }\!=\!p^{\prime }_{\mathcal M}(\xi ){\varvec{u}}_{\xi }^\perp$. Let ${\varvec{a}}(\xi )$ and ${\varvec{b}}(\xi )$ be the two intersections of $\hbar (p^{}_{\mathcal M}(\xi ),{\varvec{u}}_{\xi })$ and $\partial \mathcal K$ taken so that ${\varvec{a}}(\xi )={\varvec{h}}(\xi )+a(\xi ){\varvec{u}}_{\xi }^\perp$ and ${\varvec{b}}(\xi )={\varvec{h}}(\xi )-b(\xi ){\varvec{u}}_{\xi }^\perp$, where $a(\xi )$ and $b(\xi )$ are positive functions.

Then $f(\xi )=a(\xi )+b(\xi )$.

In the other hand, we have

$$\begin{aligned} g(\xi )&=\int _{\mathcal K\setminus \mathcal M} \chi (\langle {\varvec{x}},{\varvec{u}}_{\xi }\rangle \ge p_{\mathcal M}^{}(\xi )) \,d{\varvec{x}} =\int _{-\tfrac{\pi }{2}}^{\tfrac{\pi }{2}}\int _{0}^{\varrho ^{}_{\xi }(\zeta )}r\,dr\,d\zeta , \end{aligned}$$

where ${\varvec{h}}(\xi )+\varrho ^{}_{\xi }(\zeta ){\varvec{u}}_{\zeta }\in \partial \mathcal K$. Since $\frac{d\varrho ^{}_{\xi }(\zeta )}{d\xi }=\frac{d\varrho ^{}_{\xi }(\zeta )}{d\zeta }$, this leads to

$$\begin{aligned} 2g'(\xi )&=\int _{-\tfrac{\pi }{2}}^{\tfrac{\pi }{2}} \frac{d}{d\xi }\left( \int _{0}^{\varrho ^{}_{\xi }(\zeta )}2r\,dr\right) \,d\zeta =\int _{-\tfrac{\pi }{2}}^{\tfrac{\pi }{2}} 2\varrho ^{}_{\xi }(\zeta )\varrho ^{\prime }_{\xi }(\zeta ) \,d\zeta =a^2(\xi )-b^2(\xi ) \end{aligned}$$

that implies

$$\begin{aligned} a(\xi )=\frac{\frac{2g'(\xi )}{f(\xi )}+f(\xi )}{2} =\frac{2g'(\xi )+f^2(\xi )}{2f(\xi )} .\end{aligned}$$

This clearly determines $\mathcal K$. $\square$

If the kernel $\mathcal M$ is known to be a disc $\varrho \mathcal D$, then any one of the functions $\mathrm{S}_{\varrho \mathcal D;\mathcal K}^{}$ and $\mathrm{C}_{\varrho \mathcal D;\mathcal K}^{}$ can determine concentric discs by its constant value.

Theorem 3.2

Assume that one of the functions $\mathrm{S}_{\varrho \mathcal D;\mathcal K}^{}$ and $\mathrm{C}_{\varrho \mathcal D;\mathcal K}^{}$ is constant, where $\mathcal D$ is the unit disc. Then $\mathcal K$ is a disc centred to the origin.

Proof

If $\mathrm{S}_{\varrho \mathcal D;\mathcal K}^{}$ is constant, then this theorem is [1, Theorem 1].

If $\mathrm{C}_{\varrho \mathcal D;\mathcal K}^{}$ is constant, the derivative of $\mathrm{C}_{\varrho \mathcal D;\mathcal K}^{}$ is zero, hence—using the notations of the previous proof—$a(\xi )=b(\xi )$ for every $\xi \in [0,2\pi )$, that is, the point ${\varvec{h}}(\xi )$ is the midpoint of the segment $\overline{{\varvec{a}}(\xi ){\varvec{b}}(\xi )}$ on $\hbar (\varrho ,{\varvec{u}}_{\xi })$.

Let us consider the chord-map $C:\partial \mathcal K\rightarrow \partial \mathcal K$, that is defined by $C({\varvec{b}}(\xi ))={\varvec{a}}(\xi )$ for every $\xi \in [0,2\pi )$. This is clearly a bijective map. If ${\varvec{\ell }}_0\in \partial \mathcal K$, then by $a(\xi )=b(\xi )$ the whole sequence ${\varvec{\ell }}_i=C^i({\varvec{\ell }})$, where $C^i$ means the $i$ consecutive usage of $C$, are on a concentric circle of radius $|{\varvec{\ell }}_0|$. Moreover, every point ${\varvec{\ell }}_i$ ($i>0$) is the concentric rotation of ${\varvec{\ell }}_{i-1}$ with angle $\lambda =2\arccos (\tfrac{\varrho }{|{\varvec{\ell }}_0|})$. It is well known [4, Proposition 1.3.3] that such a sequence is dense in $\partial \mathcal K$ if $\tfrac{\lambda }{\pi }$ is irrational, or it is finitely periodic in $\partial \mathcal K$ if $\tfrac{\lambda }{\pi }$ is rational. However, if $\mathcal K$ is not a disc, then there is surely a point ${\varvec{\ell }}\in \partial \mathcal K$ for which $\tfrac{2\arccos (\tfrac{\varrho }{|{\varvec{\ell }}_0|})}{\pi }$ is irrational, hence $\mathcal K$ must be a concentric disc. $\square$

4 Measures of convex bodies

In this section the dimension of the space is $n=2,3,\dots$. As a shorthand we introduce the notations

$$\begin{aligned} \mathrm{S}_{\varrho ;\mathcal K}^{}({\varvec{u}}) :=&\mathrm{S}_{\varrho \mathcal B;\mathcal K}^{}(\hbar (\varrho ,{\varvec{u}}))=|\mathcal K\cap \hbar (\varrho ,{\varvec{u}})|, \end{aligned}$$

(4.1)

$$\begin{aligned} \mathrm{C}_{\varrho ;\mathcal K}^{}({\varvec{u}}) :=&\mathrm{C}_{\varrho \mathcal B;\mathcal K}^{}(\hbar (\varrho ,{\varvec{u}}))=|\mathcal K\cap \hbar ^+(\varrho ,{\varvec{u}})|, \end{aligned}$$

(4.2)

where $\varrho \mathcal B^{n}$ is the ball of radius $\varrho >0$ centred to the origin and $\hbar ^+$ is the appropriate half space bordered by $\hbar$.

Lemma 4.1

If the convex body $\mathcal K$ in ${\mathbb {R}}^n$ contains in its interior the ball $\varrho \mathcal B^n$, then

$$\begin{aligned} \int _{{\mathbb {S}}^{n-1}} \mathrm{C}_{\varrho ;\mathcal K}^{}({\varvec{u}}_{{\varvec{\xi }}})d{\varvec{\xi }} =\frac{\pi ^{n/2}}{\Gamma (\tfrac{n}{2})} \int _{\mathcal K\setminus \varrho \mathcal B} I_{1-\frac{\varrho ^2}{|{\varvec{x}}|^2}}\Big (\frac{n-1}{2},\frac{1}{2}\Big )\ d{\varvec{x}}. \end{aligned}$$

(4.3)

Proof

We have

$$\begin{aligned} \int _{{\mathbb {S}}^{n-1}}\!\! \mathrm{C}_{\varrho ;\mathcal K}^{}({\varvec{u}}_{{\varvec{\xi }}})d{\varvec{\xi }}&=\int _{{\mathbb {S}}^{n-1}}\int _{{\mathbb {R}}^n} \chi _{\mathcal K}^{}({\varvec{x}})\chi (\langle {\varvec{x}},{\varvec{u}}_{{\varvec{\xi }}}\rangle \ge \varrho ) \,d{\varvec{x}} d{\varvec{\xi }}\\&=\int _{\mathcal K\setminus \varrho \mathcal B} \int _{{\mathbb {S}}^{n-1}} \chi \left( \left\langle \frac{{\varvec{x}}}{|{\varvec{x}}|},{\varvec{u}}_{{\varvec{\xi }}}\right\rangle \ge \frac{\varrho }{|{\varvec{x}}|}\right) \,d{\varvec{\xi }} d{\varvec{x}} \end{aligned}$$

The inner integral is the surface of the hyperspherical cap. The height of this hyperspherical cap is $h=1-\tfrac{\varrho }{|{\varvec{x}}|}$, hence by the well-known formula [13] we obtain

$$\begin{aligned} \int _{{\mathbb {S}}^{n-1}} \chi \left( \left\langle \frac{{\varvec{x}}}{|{\varvec{x}}|},{\varvec{u}}_{{\varvec{\xi }}}\right\rangle \ge \frac{\varrho }{|{\varvec{x}}|}\right) \, d{\varvec{\xi }} =\frac{\pi ^{n/2}}{\Gamma (\tfrac{n}{2})} I_{\frac{|{\varvec{x}}|^2-\varrho ^2}{|{\varvec{x}}|^2}}\left( \frac{n-1}{2},\frac{1}{2}\right) . \end{aligned}$$

This proves the lemma. $\square$

Note that the weight in (4.3) is $\frac{\pi ^{}}{\Gamma (1)} I_{1-\frac{\varrho ^2}{|{\varvec{x}}|^2}}(\frac{1}{2},\frac{1}{2}) =2\arccos (\tfrac{\varrho }{|{\varvec{x}}|})$ for dimension $n=2$, and it is $\frac{\pi ^{3/2}}{\Gamma (\tfrac{3}{2})} I_{1-\frac{\varrho ^2}{|{\varvec{x}}|^2}}(1,\frac{1}{2}) =2\pi (1-\tfrac{\varrho }{|{\varvec{x}}|})$ for dimension $n=3$.

Lemma 4.2

Let the convex body $\mathcal K$ contain in its interior the ball $\varrho \mathcal B^{n}$. Then the integral of the section function is

$$\begin{aligned} \int _{{\mathbb {S}}^{n-1}} \mathrm{S}_{\varrho ;\mathcal K}^{}({\varvec{u}}_{{\varvec{\xi }}})d{\varvec{\xi }}&=|{\mathbb {S}}^{n-2}|\int _{\mathcal K\setminus \varrho \mathcal B^{n}} \frac{({\varvec{x}}^2-\varrho ^2)^{\frac{n-3}{2}}}{|{\varvec{x}}|^{n-2}} d{\varvec{x}}. \end{aligned}$$

(4.4)

Proof

Observe, that using (4.3) we have for any $\varepsilon >0$ that

$$\begin{aligned}&\frac{\Gamma (\tfrac{n}{2})}{\pi ^{n/2}} \int _0^{\varepsilon }\int _{{\mathbb {S}}^{n-1}} \mathrm{S}_{\varrho +\delta ;\mathcal K}^{}({\varvec{u}}_{{\varvec{\xi }}})d{\varvec{\xi }} d\delta \\&\quad =\frac{\Gamma (\tfrac{n}{2})}{\pi ^{n/2}} \int _{{\mathbb {S}}^{n-1}}\int _0^{\varepsilon } \mathrm{S}_{\varrho +\delta ;\mathcal K}^{}({\varvec{u}}_{{\varvec{\xi }}})d\delta d{\varvec{\xi }}\\&\quad =\frac{\Gamma (\tfrac{n}{2})}{\pi ^{n/2}} \int _{{\mathbb {S}}^{n-1}} \mathrm{C}_{\varrho ;\mathcal K}^{}({\varvec{u}}_{{\varvec{\xi }}})-\mathrm{C}_{\varrho +\varepsilon ;\mathcal K}^{}({\varvec{u}}_{{\varvec{\xi }}}) d{\varvec{\xi }}\\&\quad =\int _{\mathcal K\setminus \varrho \mathcal B} I_{\frac{|{\varvec{x}}|^2-\varrho ^2}{|{\varvec{x}}|^2}}\Big (\frac{n-1}{2},\frac{1}{2}\Big )\ d{\varvec{x}} -\int _{\mathcal K\setminus (\varrho +\varepsilon )\mathcal B} I_{\frac{|{\varvec{x}}|^2-(\varrho +\varepsilon )^2}{|{\varvec{x}}|^2}}\Big (\frac{n-1}{2},\frac{1}{2}\Big )\ d{\varvec{x}}\\&\quad =\int _{(\varrho +\varepsilon )\mathcal B\setminus \varrho \mathcal B} I_{\frac{|{\varvec{x}}|^2-\varrho ^2}{|{\varvec{x}}|^2}}\Big (\frac{n-1}{2},\frac{1}{2}\Big )\ d{\varvec{x}} \\&\qquad -\int _{\mathcal K\setminus (\varrho +\varepsilon )\mathcal B} I_{\frac{|{\varvec{x}}|^2-(\varrho +\varepsilon )^2}{|{\varvec{x}}|^2}}\Big (\frac{n-1}{2},\frac{1}{2}\Big ) -I_{\frac{|{\varvec{x}}|^2-\varrho ^2}{|{\varvec{x}}|^2}}\Big (\frac{n-1}{2},\frac{1}{2}\Big )\ d{\varvec{x}} , \end{aligned}$$

hence

$$\begin{aligned}&\lim _{\varepsilon \rightarrow 0}\frac{1}{\varepsilon } \frac{\Gamma (\tfrac{n}{2})}{\pi ^{n/2}} \int _0^{\varepsilon }\int _{{\mathbb {S}}^{n-1}} \mathrm{S}_{\varrho +\delta ;\mathcal K}^{}({\varvec{u}}_{{\varvec{\xi }}})d{\varvec{\xi }} d\delta \\&\quad =\lim _{\varepsilon \rightarrow 0}\frac{1}{\varepsilon } \int _{(\varrho +\varepsilon )\mathcal B\setminus \varrho \mathcal B} I_{\frac{|{\varvec{x}}|^2-\varrho ^2}{|{\varvec{x}}|^2}}\left( \frac{n-1}{2},\frac{1}{2}\right) \,d{\varvec{x}}\\&\qquad -\int _{\mathcal K\setminus \varrho \mathcal B} \lim _{\varepsilon \rightarrow 0}\frac{1}{\varepsilon }\left( I_{\frac{|{\varvec{x}}|^2-(\varrho +\varepsilon )^2}{|{\varvec{x}}|^2}} \left( \frac{n-1}{2},\frac{1}{2}\right) -I_{\frac{|{\varvec{x}}|^2-\varrho ^2}{|{\varvec{x}}|^2}}\left( \frac{n-1}{2},\frac{1}{2}\right) \right) \,d{\varvec{x}}\\&\quad =\lim _{\varepsilon \rightarrow 0}\frac{|{\mathbb {S}}^{n-1}|}{\varepsilon } \int _{\varrho }^{\varrho +\varepsilon } r^{n-1} I_{\frac{r^2-\varrho ^2}{r^2}}\left( \frac{n-1}{2},\frac{1}{2}\right) \,dr\\&\qquad -\int _{\mathcal K\setminus \varrho \mathcal B} \frac{d}{d\varrho }\left( I_{\frac{|{\varvec{x}}|^2-\varrho ^2}{|{\varvec{x}}|^2}} \left( \frac{n-1}{2},\frac{1}{2}\right) \right) \,d{\varvec{x}}\\&\quad =|{\mathbb {S}}^{n-1}|\varrho ^{n-1} I_{\frac{\varrho ^2-\varrho ^2}{\varrho ^2}}\left( \frac{n-1}{2},\frac{1}{2}\right) \\&\qquad -\frac{1}{B(\frac{n-1}{2},\frac{1}{2})} \int _{\mathcal K\setminus \varrho \mathcal B} \left( 1-\frac{\varrho ^2}{|{\varvec{x}}|^2}\right) ^{\frac{n-3}{2}} \left( \frac{\varrho ^2}{|{\varvec{x}}|^2}\right) ^{\tfrac{-1}{2}} \frac{-2\varrho }{|{\varvec{x}}|^2}\,d{\varvec{x}}\\&\quad =\frac{2}{B(\frac{n-1}{2},\frac{1}{2})} \int _{\mathcal K\setminus \varrho \mathcal B} \left( 1-\frac{\varrho ^2}{|{\varvec{x}}|^2}\right) ^{\frac{n-3}{2}} \frac{1}{|{\varvec{x}}|}\,d{\varvec{x}}. \end{aligned}$$

As

$$\begin{aligned} \frac{\pi ^{n/2}}{\Gamma (\tfrac{n}{2})}\frac{2}{B(\frac{n-1}{2},\frac{1}{2})} =\frac{2\pi ^{n/2}}{\Gamma (\frac{n-1}{2})\Gamma (\frac{1}{2})} =\frac{\frac{n-1}{2}}{\frac{n-1}{2}}\frac{2\pi ^{\frac{n-1}{2}}}{\Gamma (\frac{n-1}{2})} =\frac{(n-1)\pi ^{\frac{n-1}{2}}}{\Gamma (\frac{n-1}{2}+1)} =|{\mathbb {S}}^{n-2}|, \end{aligned}$$

the statement is proved. $\square$

Note that the weight in (4.4) is $\frac{2}{\sqrt{{\varvec{x}}^2-\varrho ^2}}$ in the plane, and $2\pi /|{\varvec{x}}|$ in dimension $n=3$, which is independent from $\varrho$!

A version of the following lemma first appeared in [9].

Lemma 4.3

Let $\omega _i \, (i=1,2)$ be weights and let $\mathcal K$ and $\mathcal L$ be convex bodies containing the unit ball $\mathcal B$. If $V_1(\mathcal K)\le V_1(\mathcal L)$ and

• (1) Either $\tfrac{\omega _2}{\omega _1}$ is a constant $c_{\mathcal K}$ on $\partial \mathcal K$ and $\frac{\omega _2}{\omega _1}(X) \left\{ \begin{array}{ll} \ge c_{\mathcal K},&{}if X\notin \mathcal K,\\ \le c_{\mathcal K},&{}if X\in \mathcal K, \end{array}\right.$ where equality may occur in a set of measure zero at most,

• (2) or $\tfrac{\omega _2}{\omega _1}$ is a constant $c_{\mathcal L}$ on $\partial \mathcal L$ and $\frac{\omega _2}{\omega _1}(X) \left\{ \begin{array}{ll} \le c_{\mathcal L},&{} if X\notin \mathcal L,\\ \ge c_{\mathcal L},&{} if X\in \mathcal L, \end{array}\right.$ where equality may occur in a set of measure zero at most,

then $V_2({\mathcal K})\le V_2({\mathcal L})$, where equality is if and only if $\mathcal K=\mathcal L$.

Proof

We have

$$\begin{aligned}&V_2(\mathcal L)\!-\!V_2(\mathcal K)\!=\!V_2(\mathcal L\!\setminus \mathcal K)\!-\!V_2(\mathcal K\!\setminus \mathcal L) \!=\! \int _{\mathcal L\setminus \mathcal K}\frac{\omega _2(x)}{\omega _1(x)}\omega _1(x)dx \!-\!\int _{\mathcal K\setminus \mathcal L}\frac{\omega _2(x)}{\omega _1(x)}\omega _1(x)dx \\&\quad \left\{ \begin{array}{ll} \!=\!0, &{}\quad \text {if }\, \mathcal K\triangle \mathcal L\!=\!\emptyset , \\ >c_{\mathcal K}(V_1(\mathcal L\!\setminus \mathcal K)\!-\!V_1(\mathcal K\!\setminus \mathcal L)) \!=\!c_{\mathcal K}(V_1(\mathcal L)-V_1(\mathcal K)), &{}\quad \text {if } \,\mathcal K\triangle \mathcal L\ne \emptyset \quad \mathrm{and}\quad (1), \\ >c_{\mathcal L}(V_1(\mathcal L\!\setminus \mathcal K)\!-\!V_1(\mathcal K\!\setminus \mathcal L)) \!=\!c_{\mathcal L}(V_1(\mathcal L)\!-\!V_1(\mathcal K)), &{}\quad \text {if }\, \mathcal K\triangle \mathcal L\ne \emptyset \quad \mathrm{and}\quad (2), \end{array}\right. \end{aligned}$$

that proves the theorem. $\square$

5 Ball characterizations

Although the following results are valid also in the plane, their points are for higher dimensions.

Theorem 5.1

Let $0<\varrho _1<\varrho _2<\bar{r}$ and let $\mathcal K$ be a convex body having $\varrho _2\mathcal B$ in its interior. If $\mathrm{C}_{\varrho _1;\mathcal K}^{}=\mathrm{C}_{\varrho _1;\bar{r}\mathcal B}^{}$ and $\mathrm{C}_{\varrho _2;\mathcal K}^{}=\mathrm{C}_{\varrho _2;\bar{r}\mathcal B}^{}$, then $\mathcal K\equiv \bar{r}\mathcal B$, where $\mathcal B$ is the unit ball.

Proof

Let $\bar{\omega }_1(r)=I_{\frac{r^2-\varrho _1^2}{r^2}}(\frac{n-1}{2},\frac{1}{2})$ and $\bar{\omega }_2(r)=I_{\frac{r^2-\varrho _2^2}{r^2}}(\frac{n-1}{2},\frac{1}{2})$ for every non-vanishing $r\in {\mathbb {R}}$, where $I$ is the regularized incomplete beta function, and define $\omega _1({\varvec{x}}):=\bar{\omega }_1(|{\varvec{x}}|)$ and $\omega _2({\varvec{x}}):=\bar{\omega }_2(|{\varvec{x}}|)$.

By formula (4.3) in Lemma 4.1 we have

$$\begin{aligned} \int _{\bar{r}\mathcal B\setminus \varrho _1\mathcal B^{n}}\omega _1({\varvec{x}})\,d{\varvec{x}} =\frac{\Gamma (\tfrac{n}{2})}{\pi ^{n/2}} \int _{{\mathbb {S}}^{n-1}} \mathrm{C}_{\varrho _1;\mathcal K}^{}({\varvec{u}}_{{\varvec{\xi }}})d{\varvec{\xi }} = \int _{\mathcal K\setminus \varrho _1\mathcal B^{n}}\omega _1({\varvec{x}})\,d{\varvec{x}}, \end{aligned}$$

and similarly

$$\begin{aligned} \int _{\bar{r}\mathcal B\setminus \varrho _2\mathcal B^{n}}\omega _2({\varvec{x}})\,d{\varvec{x}} =\frac{\Gamma (\tfrac{n}{2})}{\pi ^{n/2}} \int _{{\mathbb {S}}^{n-1}} \mathrm{C}_{\varrho _2;\mathcal K}^{}({\varvec{u}}_{{\varvec{\xi }}})d{\varvec{\xi }} = \int _{\mathcal K\setminus \varrho _2\mathcal B^{n}}\omega _2({\varvec{x}})\,d{\varvec{x}} . \end{aligned}$$

With the notations in Lemma 4.3, these mean $V_1(\mathcal K)=V_1(\bar{r}\mathcal B)$ and $V_2(\mathcal K)=V_2(\bar{r}\mathcal B)$.

Further, one can easily see that

$$\begin{aligned} 1<\frac{\omega _1({\varvec{x}})}{\omega _2({\varvec{x}})} =\frac{\bar{\omega }_1(|{\varvec{x}}|)}{\bar{\omega }_2(|{\varvec{x}}|)}=:q_n(|{\varvec{x}}|),\text {(n is the dimension)} \end{aligned}$$

is constant on every sphere, especially on $\bar{r}{\mathbb {S}}^{n-1}$.

As $\bar{\omega }_1$ and $\bar{\omega }_2$ are both strictly increasing, $q_n$ is strictly decreasing if and only if

$$\begin{aligned} \frac{\bar{\omega }_1'(r)}{\bar{\omega }_2'(r)}<\frac{\bar{\omega }_1(r)}{\bar{\omega }_2(r)}. \end{aligned}$$

(5.1)

First calculate for any $n\in {\mathbb {N}}$ that

$$\begin{aligned} \frac{\bar{\omega }_1'(r)}{\bar{\omega }_2'(r)} =\frac{\left( 1-\frac{\varrho _1^2}{r^2}\right) ^{\frac{n-3}{2}}\left( \frac{\varrho _1^2}{r^2}\right) ^{\tfrac{-1}{2}} \frac{2\varrho _1^2}{r^3}}{\left( 1-\frac{\varrho _2^2}{r^2}\right) ^{\frac{n-3}{2}}\left( \frac{\varrho _2^2}{r^2}\right) ^{\tfrac{-1}{2}} \frac{2\varrho _2^2}{r^3}} =\frac{(r^2-\varrho _1^2)^{\frac{n-3}{2}}\varrho _1}{(r^2-\varrho _2^2)^{\frac{n-3}{2}}\varrho _2}, \end{aligned}$$

then consider for $n\ge 4$ that

$$\begin{aligned} \frac{\bar{\omega }_1(r)B\left( \frac{n-1}{2},\frac{1}{2}\right) }{\left( 1-\frac{\varrho _1^2}{r^2}\right) ^{\frac{n-3}{2}}}&= \left( 1-\frac{\varrho _1^2}{r^2}\right) ^{\frac{3-n}{2}} \int _0^{1-\frac{\varrho _1^2}{r^2}}t^{\frac{n-3}{2}}(1-t)^{\frac{-1}{2}}\,dt \nonumber \\&= \int _0^{1}s^{\frac{n-3}{2}} \left( 1-s\left( 1-\frac{\varrho _1^2}{r^2}\right) \right) ^{\frac{-1}{2}} \left( 1-\frac{\varrho _1^2}{r^2}\right) \,ds\nonumber \\&= -2\int _0^{1}s^{\frac{n-3}{2}} \frac{d}{ds}\left( \left( 1-s\left( 1-\frac{\varrho _1^2}{r^2}\right) \right) ^{\frac{1}{2}}\right) \,ds\nonumber \\&= -2\left( \frac{\varrho _1}{r}-\frac{n-3}{2} \int _0^{1}s^{\frac{n-5}{2}} \left( 1-s\left( 1-\frac{\varrho _1^2}{r^2}\right) \right) ^{\frac{1}{2}} \,ds \right) \nonumber \\&= \frac{2\varrho _1}{r} \left( \frac{n-3}{2} \int _0^{1}s^{\frac{n-5}{2}} \left( \frac{r^2}{\varrho _1^2}(1-s)+s\right) ^{\frac{1}{2}} \,ds-1 \right) \!. \end{aligned}$$

(5.2)

From the two equations above we deduce

$$\begin{aligned} \frac{\bar{\omega }_1(r)}{\bar{\omega }_2(r)}\frac{\bar{\omega }_2'(r)}{\bar{\omega }_1'(r)}&= \frac{\frac{2\varrho _1}{r}\left( 1-\frac{\varrho _1^2}{r^2}\right) ^{\frac{n-3}{2}} \left( \frac{n-3}{2} \int _0^{1}s^{\frac{n-5}{2}} (\frac{r^2}{\varrho _1^2}(1-s)+s)^{\frac{1}{2}} \,ds-1 \right) }{\frac{2\varrho _2}{r}\left( 1-\frac{\varrho _2^2}{r^2}\right) ^{\frac{n-3}{2}} \left( \frac{n-3}{2} \int _0^{1}s^{\frac{n-5}{2}} (\frac{r^2}{\varrho _2^2}(1-s)+s)^{\frac{1}{2}} \,ds-1 \right) } \frac{(r^2-\varrho _2^2)^{\frac{n-3}{2}}\varrho _2}{(r^2-\varrho _1^2)^{\frac{n-3}{2}}\varrho _1}\\&= \frac{\frac{n-3}{2} \int _0^{1}s^{\frac{n-5}{2}} \left( \frac{r^2}{\varrho _1^2}(1-s)+s\right) ^{\frac{1}{2}} \,ds-1}{\frac{n-3}{2} \int _0^{1}s^{\frac{n-5}{2}} \left( \frac{r^2}{\varrho _2^2}(1-s)+s\right) ^{\frac{1}{2}} \,ds-1} \ge 1, \end{aligned}$$

where in the last inequality we used $\varrho _1<\varrho _2$. Thus, for $n\ge 4$ we have proved (5.1).

Assume now, that $n<4$. It is easy to see that

$$\begin{aligned} \bar{\omega }_1(r)-\bar{\omega }_2(r)&= \frac{1}{B\left( \frac{n-1}{2},\frac{1}{2}\right) }\int _{1-\tfrac{\varrho _2^2}{r^2}}^{1-\tfrac{\varrho _1^2}{r^2}}t^{\frac{n-3}{2}}(1-t)^{\tfrac{-1}{2}}\,dt , \end{aligned}$$

hence differentiation leads to

$$\begin{aligned} (\bar{\omega }_1'(r)&-\bar{\omega }_2'(r))B\left( \frac{n-1}{2},\frac{1}{2}\right) \\&= \left( 1-\frac{\varrho _1^2}{r^2}\right) ^{\frac{n-3}{2}}\left( \frac{\varrho _1^2}{r^2}\right) ^{\tfrac{-1}{2}} \frac{2\varrho _1^2}{r^3} -\left( 1-\frac{\varrho _2^2}{r^2}\right) ^{\frac{n-3}{2}}\left( \frac{\varrho _2^2}{r^2}\right) ^{\tfrac{-1}{2}} \frac{2\varrho _2^2}{r^3}\\&=\frac{2}{r^{n-1}}\left( (r^2-\varrho _1^2)^{\frac{n-3}{2}}\varrho _1-(r^2-\varrho _2^2)^{\frac{n-3}{2}}\varrho _2\right) \!. \end{aligned}$$

This is clearly negative for all $r$ if $n=2$ and $n=3$, hence

$$\begin{aligned} \frac{\bar{\omega }_1(r)}{\bar{\omega }_2(r)}\frac{\bar{\omega }_2'(r)}{\bar{\omega }_1'(r)} =\frac{\bar{\omega }_1(r)}{\bar{\omega }_2(r)}\left( \frac{\bar{\omega }_2'(r)-\bar{\omega }_1'(r)}{\bar{\omega }_1'(r)}+1\right) \ge \frac{\bar{\omega }_1(r)}{\bar{\omega }_2(r)}\ge 1 \end{aligned}$$

proving (5.1) for $n\le 3$.

Thus, $\frac{\bar{\omega }_1(r)}{\bar{\omega }_2(r)}$ is strictly monotone decreasing in any dimension, hence $\mathcal K\equiv \bar{r}\mathcal B$ follows from Lemma 4.3. $\square$

Theorem 5.2

Let $0<\varrho _1<\varrho _2<\bar{r}$ and the dimension be $n\ne 3$. If $\mathcal K$ is a convex body having $\varrho _2\mathcal B$ in its interior, and $\mathrm{S}_{\varrho _1;\mathcal K}^{}\equiv \mathrm{S}_{\varrho _1;\bar{r}\mathcal B}^{}$, $\mathrm{S}_{\varrho _2;\mathcal K}^{}\equiv \mathrm{S}_{\varrho _2;\bar{r}\mathcal B}^{}$, then $\mathcal K\equiv \bar{r}\mathcal B$.

Proof

Let $\bar{\omega }_1(r)=(r^2-\varrho _1^2)^{\frac{n-3}{2}}r^{2-n}$ and $\bar{\omega }_2(r)=(r^2-\varrho _2^2)^{\frac{n-3}{2}}r^{2-n}$ for every non-vanishing $r\in {\mathbb {R}}$, and define $\omega _1({\varvec{x}}):=\bar{\omega }_1(|{\varvec{x}}|)$ and $\omega _2({\varvec{x}}):=\bar{\omega }_2(|{\varvec{x}}|)$.

By formula (4.4) in Lemma 4.2 we have

$$\begin{aligned} \int _{\bar{r}\mathcal B\setminus \varrho _1\mathcal B^{n}}\omega _1({\varvec{x}})\,d{\varvec{x}} =\frac{1}{|{\mathbb {S}}^{n-2}|} \int _{{\mathbb {S}}^{n-1}} \mathrm{S}_{\varrho _1;\mathcal K}^{}({\varvec{u}}_{{\varvec{\xi }}})d{\varvec{\xi }} = \int _{\mathcal K\setminus \varrho _1\mathcal B^{n}}\omega _1({\varvec{x}})\,d{\varvec{x}}, \end{aligned}$$

and similarly

$$\begin{aligned} \int _{\bar{r}\mathcal B\setminus \varrho _2\mathcal B^{n}}\omega _2({\varvec{x}})\,d{\varvec{x}} =\frac{1}{|{\mathbb {S}}^{n-2}|} \int _{{\mathbb {S}}^{n-1}} \mathrm{S}_{\varrho _2;\mathcal K}^{}({\varvec{u}}_{{\varvec{\xi }}})d{\varvec{\xi }} = \int _{\mathcal K\setminus \varrho _2\mathcal B^{n}}\omega _2({\varvec{x}})\,d{\varvec{x}}. \end{aligned}$$

With the notations in Lemma 4.3, these mean $V_1(\mathcal K)=V_1(\bar{r}\mathcal B)$ and $V_2(\mathcal K)=V_2(\bar{r}\mathcal B)$.

The ratio $\frac{\omega _1({\varvec{x}})}{\omega _2({\varvec{x}})} =\frac{\bar{\omega }_1(|{\varvec{x}}|)}{\bar{\omega }_2(|{\varvec{x}}|)}$ is obviously constant on every sphere, especially on $\bar{r}{\mathbb {S}}^{n-1}$, and it is

$$\begin{aligned} \frac{\bar{\omega }_1(r)}{\bar{\omega }_2(r)} ={\left\{ \begin{array}{ll} \frac{\sqrt{r^2-\varrho _2^2}}{\sqrt{r^2-\varrho _1^2}} =\sqrt{1-\frac{\varrho _1^2-\varrho _2^2}{r^2-\varrho _1^2}},&{}\text { if } n=2,\\ 1,&{}\text { if } n=3,\\ \Big (1+\frac{\varrho _2^2-\varrho _1^2}{r^2-\varrho _2^2}\Big )^{\frac{n-3}{2}},&{}\text { if } n>3.\\ \end{array}\right. } \end{aligned}$$

Thus, $\frac{\bar{\omega }_1(r)}{\bar{\omega }_2(r)}$ is strictly monotone if the dimension $n\ne 3$, hence $\mathcal K\equiv \bar{r}\mathcal B$ follows from Lemma 4.3 for dimensions other than $3$. $\square$

This theorem leaves the question open in dimension $3$ if $\mathrm{S}_{\varrho _1;\mathcal K}^{}\equiv \mathrm{S}_{\varrho _1;\bar{r}\mathcal B}^{}$ and $\mathrm{S}_{\varrho _2;\mathcal K}^{}\equiv \mathrm{S}_{\varrho _2;\bar{r}\mathcal B}^{}$ imply $\mathcal K\equiv \bar{r}\mathcal B$. We have not yet tried to find an answer.

The following generalizes Theorem 3.1 for most dimensions, but only for spheres.

Theorem 5.3

Let $\varrho _1,\varrho _2\in (0,\bar{r})$ and let $\mathcal K$ be a convex body in ${\mathbb {R}}^n$ having $\max (\varrho _1,\varrho _2)\mathcal B$ in its interior. If $\mathrm{S}_{\varrho _1;\mathcal K}^{}\equiv \mathrm{S}_{\varrho _1;\bar{r}\mathcal B}^{}$ and $\mathrm{C}_{\varrho _2;\mathcal K}^{}\equiv \mathrm{C}_{\varrho _2;\bar{r}\mathcal B}^{}$, and

• (1) $n=2$ or $n=3$, or

• (2) $n\ge 4$ and $\varrho _1\le \varrho _2$,

then $\mathcal K\equiv \bar{r}\mathcal B$.

Proof

Let $\bar{\omega }_1(r)=(r^2-\varrho _1^2)^{\frac{n-3}{2}}r^{2-n}$ and and $\bar{\omega }_2(r)=I_{\frac{r^2-\varrho _2^2}{r^2}}(\frac{n-1}{2},\frac{1}{2})$ for every non-vanishing $r\in {\mathbb {R}}$, and define $\omega _1({\varvec{x}}):=\bar{\omega }_1(|{\varvec{x}}|)$ and $\omega _2({\varvec{x}}):=\bar{\omega }_2(|{\varvec{x}}|)$.

By formula (4.4) in Lemma 4.2 we have

$$\begin{aligned} \int _{\bar{r}\mathcal B\setminus \varrho _1\mathcal B^{n}}\omega _1({\varvec{x}})\,d{\varvec{x}} =\frac{1}{|{\mathbb {S}}^{n-2}|} \int _{{\mathbb {S}}^{n-1}} \mathrm{S}_{\varrho _1;\mathcal K}^{}({\varvec{u}}_{{\varvec{\xi }}})d{\varvec{\xi }} = \int _{\mathcal K\setminus \varrho _1\mathcal B^{n}}\omega _1({\varvec{x}})\,d{\varvec{x}}, \end{aligned}$$

and by formula (4.3) in Lemma 4.1 we have

$$\begin{aligned} \int _{\bar{r}\mathcal B\setminus \varrho _2\mathcal B^{n}}\omega _2({\varvec{x}})\,d{\varvec{x}} =\frac{\Gamma (\tfrac{n}{2})}{\pi ^{n/2}} \int _{{\mathbb {S}}^{n-1}} \mathrm{C}_{\varrho _2;\mathcal K}^{}({\varvec{u}}_{{\varvec{\xi }}})d{\varvec{\xi }} = \int _{\mathcal K\setminus \varrho _2\mathcal B^{n}}\omega _2({\varvec{x}})\,d{\varvec{x}}. \end{aligned}$$

With the notations in Lemma 4.3, these mean $V_1(\mathcal K)=V_1(\bar{r}\mathcal B)$ and $V_2(\mathcal K)=V_2(\bar{r}\mathcal B)$.

The ratio $\frac{\omega _2({\varvec{x}})}{\omega _1({\varvec{x}})} =\frac{\bar{\omega }_2(|{\varvec{x}}|)}{\bar{\omega }_1(|{\varvec{x}}|)}$ is obviously constant on every sphere, especially on $\bar{r}{\mathbb {S}}^{n-1}$, and it is

$$\begin{aligned} \frac{\bar{\omega }_2(r)}{\bar{\omega }_1(r)}&=\frac{\int _0^{1-\frac{\varrho _2^2}{r^2}}t^{\frac{n-3}{2}}(1-t)^{\frac{-1}{2}}\,dt}{(r^2-\varrho _1^2)^{\frac{n-3}{2}}r^{2-n}}\\&=\frac{\frac{2\varrho _2}{r}\left( 1-\frac{\varrho _2^2}{r^2}\right) ^{\frac{n-3}{2}} \left( \frac{n-3}{2} \int _0^{1}s^{\frac{n-5}{2}} \left( \frac{r^2}{\varrho _2^2}(1-s)+s\right) ^{\frac{1}{2}} \,ds-1 \right) }{\frac{1}{r}\left( 1-\frac{\varrho _1^2}{r^2}\right) ^{\frac{n-3}{2}}} \text {by}\quad (5.2)\\&=2\varrho _1\left( \frac{r^2-\varrho _2^2}{r^2-\varrho _1^2}\right) ^{\frac{n-3}{2}} \left( \frac{n-3}{2} \int _0^{1}s^{\frac{n-5}{2}} \left( \frac{r^2}{\varrho _2^2}(1-s)+s\right) ^{\frac{1}{2}} \,ds-1 \right) \\&=2\varrho _1\left( 1+\frac{\varrho _1^2-\varrho _2^2}{r^2-\varrho _1^2}\right) ^{\frac{n-3}{2}} \left( \frac{n-3}{2} \int _0^{1}s^{\frac{n-5}{2}} \left( \frac{r^2}{\varrho _2^2}(1-s)+s\right) ^{\frac{1}{2}} \,ds-1 \right) \end{aligned}$$

if $n>3$. For other values of $n$ we have

$$\begin{aligned} \frac{\bar{\omega }_2(r)}{\bar{\omega }_1(r)}&=\frac{\int _0^{1-\frac{\varrho _2^2}{r^2}}t^{\frac{n-3}{2}}(1-t)^{\frac{-1}{2}}\,dt}{(r^2-\varrho _1^2)^{\frac{n-3}{2}}r^{2-n}}\\&={\left\{ \begin{array}{ll} (r^2-\varrho _1^2)^{\frac{1}{2}} \int _0^{1-\frac{\varrho _2^2}{r^2}}t^{\frac{-1}{2}}(1-t)^{\frac{-1}{2}}\,dt ,&{}\text { if } n=2,\\ r\int _0^{1-\frac{\varrho _2^2}{r^2}}(1-t)^{\frac{-1}{2}}\,dt ,&{}\text { if } n=3.\\ \end{array}\right. } \end{aligned}$$

Thus, $\frac{\bar{\omega }_2(r)}{\bar{\omega }_1(r)}$ is strictly monotone increasing if $n=2,3$ and it is also strictly monotone increasing if $n>3$ and $\varrho _1\le \varrho _2$. In these cases Lemma 4.3 implies $\mathcal K\equiv \bar{r}\mathcal B$. $\square$

This theorem leaves open the case when $\varrho _1>\varrho _2$ in dimensions $n>3$. We have not yet tried to complete our theorem.

6 Discussion

Barker and Larman conjectured in [1, Conjecture 2] that in the plane $\mathcal M$-equisectioned convex bodies coincide, but they were unable to justify this in full.³ Nevertheless they proved, among others, that a $\mathcal D$-isosectioned convex body $\mathcal K$ in the plane is a disc concentric to the disc $\mathcal D$.

Having a convex body $\mathcal K$ that is sphere-isocapped with respect to two concentric spheres raises the problem if there is a concentric ball $\bar{r}\mathcal B$—obviously sphere-isocapped with respect to that two concentric spheres—that is sphere-equicapped to $\mathcal K$ with respect to that two concentric spheres. The very same problem exists also for bodies that are sphere-isosectioned with respect to two concentric spheres. So we have the following range characterization problems: Let $0<\varrho _1<\varrho _2$ and let $c_{1}>c_{2}>0$ be positive constants. Is there a convex body $\mathcal K$ containing the ball $\varrho _2\mathcal B$ in its interior and satisfying

• (i) $c_{1}\equiv \mathrm{C}_{\varrho _1;\mathcal K}^{}$ and $c_{2}\equiv \mathrm{C}_{\varrho _2;\mathcal K}^{}$ (raised by Theorem 5.1)?

• (ii) $c_{1}\equiv \mathrm{S}_{\varrho _1;\mathcal K}^{}$ and $c_{2}\equiv \mathrm{S}_{\varrho _2;\mathcal K}^{}$ (raised by Theorem 5.2)?

• (iii) $c_{1}\equiv \mathrm{S}_{\varrho _1;\mathcal K}^{}$ and $c_{1}\equiv \mathrm{C}_{\varrho _1;\mathcal K}^{}$ (raised by Theorem 5.3)?

In the plane if $\mathcal M$ is allowed to shrink to a point (empty interior), then $\mathrm{S}_{\mathcal M;\mathcal K}^{}$ is the X-ray picture at a point source [3] investigated by Falconer in [2]. The method used in Falconer’s article made Barker and Larman mention in [1] that in dimension $2$ the convex body $\mathcal K$ can be determined from $\mathrm{S}_{\mathcal M;\mathcal K}^{}$ and $\mathrm{S}_{\mathcal M';\mathcal K}^{}$ if $\partial \mathcal M$ and $\partial \mathcal M'$ are intersecting each other in a suitable manner. The method in the anticipated proof presented in [1] decisively depends on the condition of proper intersection.

Finally we note that determining a convex body by its constant width and constant brightness [8] sounds very similar a problem as the ones investigated in this paper. Moreover also the result is analogous to Theorem 5.3.