Some characterizations of the Euclidean ball

Abstract

In this paper the following result is proved, which is an extension of the one proved in García-Jiménez et al. (Monatsh Math 181:601–607, 2016): a convex body K in the n-dimensional Euclidean space is a Euclidean ball if one of its isoptic surfaces is homothetic to $\partial K$. We also proved some related characterizations of the Euclidean ball.

1 Introduction

Let $K\in \mathbb R^n$, $n\ge 2$, be a convex body, i.e., a compact and convex set with non-empty interior. The solid cone generated by K with apex z is denoted by $\text {cone}(K,z)$, i.e., $\text {cone}(K,z):=\{z+\mu (y-z): y\in K,\, \mu \ge 0\}.$ The boundary of $\text {cone}(K,z)$ is known as the support cone of K from z. Let $B^n(z,r)$ and $S^n(z,r)$ denote the Euclidean ball and sphere in $\mathbb R^n$, respectively, centred at z and with radius r. We say that the solid angle of $\text {cone}(K,x)$ is $\alpha$ if $\text {vol}_{n-1}(\text {cone}(K,x)\cap S^n(x,1))=\alpha$.

The isoptic surface of K of angle $\alpha$, denoted by $K_{\alpha }$, is the hypersurface such that from every point in $K_{\alpha }$, K is seen under a constant solid angle $\alpha$. In other words, for every $z\in K_{\alpha }$ we have that $\text {vol}_{n-1}(\text {cone}(K,z)\cap S^n(z,1))=\alpha$. There are some interesting characterizations of the Euclidean disc and ball, related with isoptic curves and isoptic surfaces in [3,4,5,6,7]. Here we are interested in some similar results

Consider the following two properties of the Euclidean ball in $\mathbb R^n$:

• (a) For a positive number $\lambda$, the solid angle (from the origin) under which is seen every ball of radius $\lambda$, which is exteriorly tangent to $B^n(O,1)$, is constant.

• (b) For a positive number $\lambda <1,$ the common support cone of $B^n(O,1)$ and every ball of radius $\lambda$, which is exteriorly tangent, subtend a constant solid angle.

We wonder if the above properties are characteristics of the Euclidean ball, in other words, we wonder if there exist any other convex body which have the property (a) or (b).

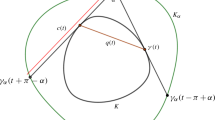
Problem 1. Let $K\subset \mathbb R^n$ be a convex body with the origin O in its interior and let $\lambda$ be a positive real number. Suppose every translate of $\lambda K$, which is tangent to K, is seen under a constant solid angle  $\alpha$ from O (Fig. 1). Is it true that K is a Euclidean ball?

Fig. 1

Homothetic copies tangent to K are seen under a constant angle

Problem 2. Let $K\subset \mathbb R^n$ be a convex body and let $\lambda <1$ be a positive real number. For every $x\in \mathbb R^n$ such that $\lambda K + x$ is tangent to K, the common support cone of K and $\lambda K + x$ has a constant solid angle $\alpha$ (Fig. 2). Is it true that K is a Euclidean ball?

Fig. 2

The common tangent lines intersect at a constant angle

With respect to Problem 1 the following result was proved in [3] and the particular case when $\lambda =1$ was proved by Yu in [9].

Theorem 1

Let K be a centrally symmetric convex body in $\mathbb R^n$, $n\ge 2$, centred at the origin O and let $\lambda$ be a positive number. Suppose every translate of $\lambda K$, which is tangent to K, is seen under a constant solid angle $\alpha$ from O. Then K is a Euclidean ball.

If K is a centrally symmetric set centred at the origin and z is a point in the boundary of K, then $\lambda K+ (1+\lambda )z$ is tangent to K at the point z. If the body $\lambda K+ (1+\lambda )z$ is seen from O under the fixed solid angle $\alpha$, then $\lambda K$ is also seen from $-(1+\lambda )z$ under the solid angle $\alpha$. It follows that the boundary of $(1+\lambda )K$ is an isoptic surface of $\lambda K$.

By the above comment, note that Theorem 1 says: let K be a centrally symmetric convex set, if for some $\alpha$ the isoptic $K_{\alpha }$ is homothetic to $\partial K$ then K is a Euclidean ball. However, we suspected the hypothesis over K of being a centrally symmetric set is unnecessary and this is what we obtained in Corollary 1.

In this paper we prove the following results.

Theorem 2

Let $K\subset \mathbb R^n$ be a convex body with the origin in its interior and let $\lambda >0$ be a real number. For every $x\in \mathbb R^n$ such that $x-\lambda K$ is tangent to K, the support cone of $x-\lambda K$ from O subtends a constant solid angle $\alpha .$ Then K is a Euclidean ball.

Corollary 1

Let K be a convex body in $\mathbb R^n$, $n\ge 2$. If $K_{\alpha }$ is homothetic to $\partial K$ for a solid angle $\alpha$, then K is a Euclidean ball.

Theorem 3

Let $K\subset \mathbb R^n$ be a convex body, $n\ge 2$, and let $0<\lambda <1$ be a real number. For every $x\in \partial K$ the common support cone of K and $\lambda K + x$ subtends a constant solid angle $\alpha$ from its apex. Then K is a Euclidean ball.

Corollary 2

Let $K\subset \mathbb R^n$ be a centrally symmetric convex body, $n\ge 2$, and let $\lambda <1$ be a positive real number. For every $x\in \mathbb R^n$ such that $\lambda K + x$ is tangent to K, the common support cone of K and $\lambda K + x$ subtends a constant solid angle $\alpha$ from its apex. Then K is a Euclidean ball.

2 Proof of Theorem 2

Let r be the minimal distance among the points in $\partial K$ to O. Clearly, $B^n(O,r)$ is the maximal ball contained in K with center at O. Without loss of generality we suppose that $r=1$. If $x\in \partial K\cap B^n(O,r)$ we say that x is a contact point of K. Let $r_2$ be the minimal number such that the ball $B^n(O,r_2)$ contains to K. Every point $x\in \partial K\cap S^n(O,r_2)$ is called a distant point of K. Finally, denote by $\alpha _n(\lambda )$ the solid angle under which is seen from O any ball of radius $\lambda$ which is tangent to $B^n(O,1)$.

The following two auxiliary lemmas are proved in [3] for a centrally symmetric set K, however, the hypothesis of central symmetry is only used to give a little stronger conclusion in Lemma 2. For completeness we give its proofs here.

Lemma 1

The solid angle $\alpha$ is equal to $\alpha _n(\lambda )$.

Proof. Let x be any contact point of K and z any distant point. We have that $(1+\lambda )x-\lambda K$ and $(1+\lambda )z-\lambda K$ are exteriorly tangent to K at x and z, respectively. Also, $(1+\lambda )x + B^n(O,\lambda )$ and $(1+\lambda )z + B^n(O,\lambda r_2)$ are exteriorly tangent to $B^n(O,1)$ and $B^n(O,r_2)$, at x and z, respectively. Clearly, $(1+\lambda )x + B^n(O,\lambda )$ and $(1+\lambda )z + B^n(O,\lambda r_2)$ are both seen from O under the solid angle $\alpha _n(\lambda )$. Since

$$\{(1+\lambda )x-\lambda K\}\supset \{(1+\lambda )x + B^n(O,\lambda )\}$$

and

$$\{(1+\lambda )z-\lambda K\}\subset \{(1+\lambda )z + B^n(O,\lambda r_2)\},$$

we have that $\alpha \ge \alpha _n(\lambda )$ and $\alpha \le \alpha _n(\lambda )$, respectively. We conclude that $\alpha =\alpha _n(\lambda )$. $\square$

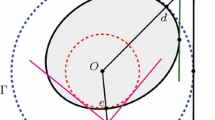
Given $u\in S^n(O,1)$ we define $D_u = \left\{ x \in S^n(O,1):\ \langle x,u \rangle = \frac{\lambda }{1+\lambda } \right\}$ (see Fig. 3).

Fig. 3

All points in $D_u$ are contact points

Lemma 2

Let $u\in \partial K$ be a contact point. Then all points in $D_u$ are contact points of K.

Proof. Since u is a contact point, we have that $u\in S^n(O,1).$ We know that $(1+\lambda )u-\lambda K$ and $(1+\lambda )u + B^n(O,\lambda )$ have the same support cone with apex O. If $\ell$ is a line through O and tangent to $(1+\lambda )u + B^n(O,\lambda )$ then is easy to see that the point of tangency is also in $\partial ((1+\lambda )u-\lambda K)$. This proves that all points in $D_u$ are contact points of K. $\square$

Now we are ready to prove Theorem 2.

Proof of Theorem 2. The proof for $n=2$ was already given in [3]. In order to prove the theorem for $n\ge 3$ it is sufficient to prove that all points in $S^n(O,1)$ are contact points of K. Let u be any contact point of K and consider $x\in S^n(O,1)$ such that $\langle x,u \rangle \ge \frac{\lambda }{1+\lambda }$. Since x is contained in the smaller cap of $S^n(O,1)$ which is bounded by $D_u$ (the one that contains u) and for every $z\in D_u$ we have that $u\in D_z$, we obtain that $D_u\cap D_x\ne \emptyset$. Let y be a point in $D_u\cap D_x$, and because all points in $D_u$ are contact points (by Lemma 2), it follows that all points in $D_y$ are contact points. Since $x\in D_y$, we obtain that x is a contact point of K, and because x is any point in the closed cap defined by $R_u:=\left\{ z\in S^n(O,1): \langle z,u \rangle \ge \frac{\lambda }{1+\lambda }\right\} ,$ we obtain that all points in the cap $R_u$ are contact points of K. Every point $z\in D_u$ gives another cap $R_z$ whose elements are all contact points. By compactness of $S^n(O,1)$ we have that the whole sphere $S^n(O,1)$ is covered by a finite number of regions $R_u$. Therefore, all points of $S^n(O,1)$ are contact points and hence K is a Euclidean ball. $\square$

Proof of Corollary 1. Without loss of generality we assume that the center of homothety of $\partial K$ and $K_{\alpha }$ is the origin O. Since K is contained in the interior of $K_{\alpha },$ we have that O is in the interior of K. Consider an arbitrary point $z\in K_{\alpha }$ and let $x_z$ be the point where the segment [O, z] intersects $\partial K$. Let $\lambda$ be the ratio of homothety between $K_{\alpha }$ and $\partial K$, i.e., $\lambda =\frac{|Oz|}{|Ox_z|}$, where |pq| denotes de length of the segment [p, q]. We have that the homothetic copy $(\lambda -1)K +z$ is tangent to K at the point $x_z$ and K is seen from z under the solid angle $\alpha$, this implies that $K-z$ is tangent to $(\lambda -1)K$ and is seen from O under the solid angle $\alpha$. We repeat this argument for every $z\in K_{\alpha }$ and get the conditions of Theorem 2, so we have that $(\lambda -1)K$ is a Euclidean ball and therefore K is a Euclidean ball. $\square$

3 Proof of Theorem 3

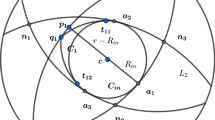
Proof of Theorem 3. Let $x\in \partial K$ be an arbitrary point and let $p_x$ be the apex of the common support cone of K and $\lambda K +x$. Clearly, $p_x$ is the center of homothety between the two bodies with the ratio $\lambda$, hence the points O, x, and $p_x$ are collinear (see Fig. 4). For every natural number $m\ge 2$ we denote by $x_m$ the second point of intersection of the ray from O to $p_x$ with the boundary of $\lambda ^m K +x_{m-1}$. We have that

$$x_m=(1+\lambda +\lambda ^2 +\cdots +\lambda ^m)x=\frac{\lambda ^{m+1}-1}{\lambda -1}x,$$

and since $0<\lambda <1$ we have that

$$p_x=\lim _{m\rightarrow \infty }x_m=\frac{1}{1-\lambda }x.$$

Since x is any point in the boundary of K we have that the locus of points $p_x$ is a surface homothetic to $\partial K$ with center of homothety at O and ratio $\frac{1}{1-\lambda }.$ Now, we apply Corollary 1 and conclude that K is a Euclidean ball. $\square$

Fig. 4

The points $p_x$ lie in the isoptic $K_{\alpha }$ which is homothetic to $\partial K$

Proof of Corollary 2. Without loss of generality we suppose the center of symmetry of K is O. Let z be any point in $\partial K$ and let $\lambda K+(1+\lambda )z$ be the homothetic copy tangent at z. Since the two bodies are homothetic the common support hyperplanes concur at the center of homothety, namely $p_z$. The center of $\lambda K+(1+\lambda )z$ is in $\partial (1+\lambda )K$, hence the common support hyperplanes of $(1+\lambda )K$ and $2\lambda K +(1+\lambda )z$ are parallel to the corresponding common support hyperplanes of K and $\lambda K+(1+\lambda )z$ (see Fig. 5). By similarity of triangles we can see that all the common support hyperplanes of $(1+\lambda )K$ and $2\lambda K +(1+\lambda )z$ concur at a point $q_z$ collinear with O and $p_z$. This is valid for every $z\in \partial K$, we then have the conditions of Theorem 3 for $(1+\lambda )K$ and $2\lambda K +(1+\lambda )z$, therefore K is a Euclidean ball. $\square$

Fig. 5

The common support cone of $(1+\lambda )K$ and $2\lambda K +(1+\lambda )z$ subtends a solid angle $\alpha$