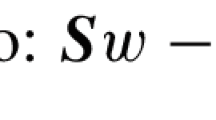Two Numerical Approaches to Stationary Mean-Field Games

Abstract

Here, we consider numerical methods for stationary mean-field games (MFG) and investigate two classes of algorithms. The first one is a gradient-flow method based on the variational characterization of certain MFG. The second one uses monotonicity properties of MFG. We illustrate our methods with various examples, including one-dimensional periodic MFG, congestion problems, and higher-dimensional models.

1 Introduction

Mean-field games (MFG) model problems with a large number of rational agents interacting noncooperatively [39–43]. Much progress has been achieved in the mathematical theory of MFG for time-dependent problems [13, 23–25, 27, 31, 34, 47, 48] and for stationary problems [22, 28, 32, 33, 46, 50] (also see the recent surveys [7, 11, 35]). Yet, in the absence of explicit solutions, the efficient simulation of MFG is important to many applications. Consequently, researchers have studied numerical algorithms in various cases, including continuous state problems [1–5, 8–10, 14, 36–38] and finite state problems [29, 30]. Here, we develop numerical methods for (continuous state) stationary MFG using variational and monotonicity methods.

Certain MFG, called variational MFG, are Euler–Lagrange equations of integral functionals. These MFG are instances of a wider class of problems—monotonic MFG. In the context of numerical methods, the variational structure of MFG was explored in [2]. Moreover, monotonicity properties are critical for the convergence of the methods in [1, 3, 4]. Recently, variational and monotonicity methods were used to prove the existence of weak solutions to MFG in [12, 13, 18, 44, 49].

Here, our main contributions are two computational approaches for MFG. For variational MFG, we build an approximating method using a gradient flow approach. This technique gives a simple and efficient algorithm. Nevertheless, the class of variational MFG is somewhat restricted. Monotonic MFG encompass a wider range of problems that include variational MFG as a particular case. In these games, the MFG equations involve a monotone nonlinear operator. We use the monotonicity to build a flow that is a contraction in $L^2$ and whose fixed points solve the MFG.

To keep the presentation elementary, we develop our methods for the one-dimensional MFG:

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{u_x^2}{2} + V(x)+b(x) u_x =\ln m+{\overline{H}},\\ -(m (u_x+b(x)))_x =0. \end{array}\right. } \end{aligned} \end{aligned}$$

(1.1)

To streamline the discussion, we study (1.1) with periodic boundary conditions. Thus, the variable x takes values in the one-dimensional torus, ${\mathbb {T}}$. The potential, V, and the drift, b, are given real-valued periodic functions. The unknowns are u, m, and ${\overline{H}}$, where $u$ and $m$ are real-valued periodic functions satisfying $m> 0$, and where ${\overline{H}}$ is a constant. The role of $\overline{H}$ is to allow for m to satisfy $\int _{{\mathbb {T}}} m\,\mathrm{d}x=1$. Furthermore, since adding an arbitrary constant to u does not change (1.1), we require

$$\begin{aligned} \int _{{\mathbb {T}}} u \,\mathrm{d}x=0. \end{aligned}$$

(1.2)

The system (1.1) is one of the simplest MFG models. However, its structure is quite rich and illustrates our techniques well. Our methods extend in a straightforward way to other models, including higher-dimensional problems. In particular, in Sect. 4, we discuss applications to a one-dimensional congestion model and to a two-dimensional MFG.

We end this introduction with a brief outline of our work. In Sect. 2, we examine various properties of (1.1). These properties motivate the ideas used in Sect. 3 to build numerical methods. Next, in Sect. 4, we discuss the implementation of our approaches and present their numerical simulations. We conclude this work in Sect. 5 with some final remarks.

2 Elementary Properties

We begin this section by constructing explicit solutions to (1.1). These are of particular importance for the validation and comparison of the numerical methods presented in Sect. 3. Next, we discuss the variational structure of (1.1) and show that (1.1) is equivalent to the Euler–Lagrange equation of a suitable functional. Because of this, we introduce a gradient flow approximation and examine some of its elementary properties. Finally, we explain how (1.1) can be seen as a monotone operator. This operator induces a flow that is a contraction in $L^2$ and whose stationary points are solutions to (1.1).

2.1 Explicit Solutions

Here, we build explicit solutions to (1.1). For simplicity, we assume that V and b are $C^\infty$ functions. Moreover, we identify ${\mathbb {T}}$ with the interval $[0,1]$.

Due to the one-dimensional nature of (1.1), if $\int _{\mathbb {T}}b\,\mathrm{d}x=0$, we have the following explicit solution

$$\begin{aligned} u(x)&=-\int _0^x b(y)\,\mathrm{d}y+ \int _{\mathbb {T}}\int _0^x b(y)\,\mathrm{d}y\, \mathrm{d}x,\quad m(x)=\frac{e^{V(x)-\frac{b^2(x)}{2}}}{\int _{{\mathbb {T}}} e^{V(y)-\frac{b^2(y)}{2}} \,\mathrm{d}y}, \\ \overline{H}&=\ln \left( \int _{{\mathbb {T}}} e^{V(y)-\frac{b^2(y)}{2}} \,\mathrm{d}y\right) . \end{aligned}$$

Suppose that $b=\psi _x$ for some $C^\infty$ and periodic function $\psi :{\mathbb {T}}\rightarrow {\mathbb {R}}$ with $\int _{{\mathbb {T}}} \psi \,\mathrm{d}x=0$. For

$$\begin{aligned} u(x)=\psi (x),\quad m(x)=\frac{e^{V(x)-\frac{\psi _x^2(x)}{2}}}{\int _{{\mathbb {T}}} e^{V(y)-\frac{\psi _y^2(y)}{2}} \,\mathrm{d}y}, \quad H=\ln \left( \int _{{\mathbb {T}}} e^{V(y)-\frac{\psi _y^2(y)}{2}} \,\mathrm{d}y\right) , \end{aligned}$$

the triplet $(u,m, \overline{H})$ solves (1.1). If $\int _{\mathbb {T}}b\,\mathrm{d}x\ne 0$, we are not aware of any closed-form solution.

Next, we consider the congestion model

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{u_x^2}{2 m^{1/2}} + V(x) =\ln m+{\overline{H}},\\ -(m^{1/2} u_x)_x =0. \end{array}\right. } \end{aligned} \end{aligned}$$

(2.1)

Remarkably, the previous equation has the same solutions as (1.1) with $b=0$. Namely, for $u(x)=0$, $m(x)=\frac{e^{V(x)}}{\int _{{\mathbb {T}}} e^{V(y)} \,\mathrm{d}y}$, and $\overline{H} = \ln \left( \int _{{\mathbb {T}}} e^{V(y)} \,\mathrm{d}y\right)$, the triplet $(u,m, \overline{H})$ solves (2.1). Thus, this model is particularly convenient for the validation of the numerical methods. However, we stress that our methods are valid for general congestion models satisfying monotonicity conditions.

2.2 Euler–Lagrange Equation

We begin by showing that (1.1) is equivalent to the Euler–Lagrange equation of the integral functional

$$\begin{aligned} J[u]= \int _{\mathbb {T}}e^{\frac{u_x^2}{2} + V(x)+b(x) u_x}\, \mathrm{d}x\end{aligned}$$

(2.2)

defined for $u\in D(J)= W^{2,2}({\mathbb {T}}) \cap L^2_0({\mathbb {T}})$, where $L^2_0({\mathbb {T}})= \{u\in L^2({\mathbb {T}}): u \text { satisfies }$(1.2)}.

Remark 2.1

(On the domain of J ) As proved in [16] (see [17, 19, 22, 27, 28, 46] for related problems), (1.1) admits a $C^\infty$ solution. By a simple convexity argument, this solution is the unique minimizer of

$$\begin{aligned} \begin{aligned} J[u] = \min _{v\in W^{1,2}({\mathbb {T}}) , \int _{\mathbb {T}}v\,\mathrm{d}x=0} J[v]. \end{aligned} \end{aligned}$$

Thus, the minimizers of J in $\{ v\in W^{1,2}({\mathbb {T}}) :\, \int _{\mathbb {T}}v\,\mathrm{d}x= 0\}$ are also minimizers of J in $\{ v\in W^{2,2}({\mathbb {T}}) :\, \int _{\mathbb {T}}v\,\mathrm{d}x= 0\}$. Hence, the domain of J is not too restrictive, and, due to this choice, our arguments are substantially simplified. In particular, because we are in the one-dimensional setting, $W^{2,2}({\mathbb {T}}) \subset W^{1,\infty }({\mathbb {T}})$.

We also observe that $L^2_0({\mathbb {T}})$ endowed with the $L^2({\mathbb {T}})$-inner product is a Hilbert space.

Lemma 2.2

For ${\overline{H}}=0$, (1.1) is equivalent to the Euler–Lagrange equation of J.

Proof

Let $u\in W^{2,2}({\mathbb {T}})\cap L^2_0({\mathbb {T}})$. We say that u is a critical point of J if

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}\varepsilon } J[u + \varepsilon v]_{\big |_{\varepsilon =0}} = 0 \end{aligned}$$

for all $v\in W^{2,2}({\mathbb {T}}) \cap L^2_0({\mathbb {T}})$. Fix any such v. For all $\varepsilon \in {\mathbb {R}}$, we have that

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}}{\mathrm{d}\varepsilon } J[u + \varepsilon v] = \int _{\mathbb {T}}e^{ \frac{u_x^2}{2} + \varepsilon u_x v_x + \varepsilon ^2 \frac{v_x^2}{2} + V(x) +b(x) u_x+\varepsilon b(x) v_x } (u_x v_x + b(x) v_x+\varepsilon v_x^2) \,\mathrm{d}x. \end{aligned} \end{aligned}$$

Define m by

$$\begin{aligned} \ln m= \frac{u_x^2}{2} + V(x)+b(x)u_x. \end{aligned}$$

(2.3)

Then, it follows that

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}}{\mathrm{d}\varepsilon } J[u + \varepsilon v]_{\big |_{\varepsilon =0}} = 0 \Leftrightarrow \int _{\mathbb {T}}m(u_x+b(x)) v_x \,\mathrm{d}x= 0 \Leftrightarrow -\int _{\mathbb {T}}(m(u_x+b(x)) )_x v \,\mathrm{d}x= 0. \end{aligned} \end{aligned}$$

Since $v\in W^{2,2}({\mathbb {T}})$ is an arbitrary function with zero mean, we conclude that u is a critical point of J if, and only if, (m, u) satisfies (1.1). $\square$

As mentioned in Remark 2.1, the functional J defined by (2.2) admits a unique minimizer. Moreover, since J is convex, any solution to the associated Euler–Lagrange equation is a minimizer. By (2.3), we have $m> 0$. In MFG, it is usual to require

$$\begin{aligned} \int _{{\mathbb {T}}} m \,\mathrm{d}x=1. \end{aligned}$$

To normalize m, we multiply m by a suitable constant and introduce the parameter ${\overline{H}}$, which leads us to (1.1).

2.3 Monotonicity Conditions

Let H be a Hilbert space with the inner product $\langle \cdot , \cdot \rangle _H$. A map $A:D(A)\subset H\rightarrow H$ is a monotone operator if

$$\begin{aligned} \langle A(w)-A(\tilde{w}), w-\tilde{w}\rangle _H \geqslant 0 \end{aligned}$$

for all $w, \tilde{w}\in D(A)$.

In the Hilbert space $L^2({\mathbb {T}})\times L^2({\mathbb {T}})$, we define

$$\begin{aligned} A \begin{bmatrix} m\\ u \end{bmatrix} = \begin{bmatrix} -\frac{u_x^2}{2} - V(x) -b(x) u_x+\ln m\\ -(m( u_x+ b(x)))_x \end{bmatrix} , \end{aligned}$$

(2.4)

with $D(A) = \{ (m,u) \in W^{1,2}({\mathbb {T}}) \times W^{2,2}({\mathbb {T}}): \, \inf _{\mathbb {T}}m >0\}$. Observe that $A$ maps $D(A)$ into $L^2({\mathbb {T}})\times L^2({\mathbb {T}})$ because $W^{1,2}({\mathbb {T}})$ is continuously embedded in $L^\infty ({\mathbb {T}})$.

The condition $\inf _{\mathbb {T}}m>0$ in the definition of D(A) is due to the singularity of $\ln m$. With a non-singular coupling term the condition would become $\inf _{\mathbb {T}}m\geqslant 0$. However, the proof that a smooth weak solution is a solution requires the condition $m>0$ (see, e.g., Remark 3.8 for a similar argument).

Lemma 2.3

The operator A given by (2.4) is a monotone operator in $L^2({\mathbb {T}})\times L^2({\mathbb {T}})$.

Proof

Let (m, u), $(\theta , v)\in D(A)\subset L^2({\mathbb {T}})\times L^2({\mathbb {T}})$. We have

$$\begin{aligned} \begin{aligned}&\left\langle A \begin{bmatrix}m \\ u \\ \end{bmatrix} - A \begin{bmatrix}\theta \\ v \\ \end{bmatrix} , \begin{bmatrix}m \\ u \\ \end{bmatrix} - \begin{bmatrix}\theta \\ v \\ \end{bmatrix} \right\rangle _{L^2({\mathbb {T}}) \times L^2({\mathbb {T}})} \\&\quad = \int _{\mathbb {T}}(\ln m - \ln \theta )(m-\theta ) \,\mathrm{d}x+ \int _{\mathbb {T}}\Big ( \frac{m}{2} + \frac{\theta }{2}\Big ) (u_x - v_x)^2\,\mathrm{d}x, \end{aligned} \end{aligned}$$

where we used integration by parts. Because $\ln (\cdot )$ is an increasing function and because $\theta , m>0$, the conclusion follows. $\square$

As observed in [41, 43], the monotonicity of A implies the uniqueness of the solutions. Here, we use the monotonicity to construct a flow that approximates solutions of (1.1).

2.4 Weak Solutions Induced by Monotonicity

Denote by $\langle \cdot , \cdot \rangle _{{\mathcal {D}}\times {\mathcal {D}}'}$ the duality pairing in the sense of distributions. We say that a triplet $(m, u, {\overline{H}})\in {\mathcal {D}}'\times {\mathcal {D}}' \times \mathbb {R}$ is a weak solution induced by monotonicity (or, for brevity, weak solution) of (1.1) if

$$\begin{aligned} \left\langle A \begin{bmatrix} \theta \\ v \\ \end{bmatrix} - \begin{bmatrix}\,\overline{H}\,\\ 0 \\ \end{bmatrix} , \begin{bmatrix}\theta \\ v \\ \end{bmatrix} - \begin{bmatrix}m \\ u \\ \end{bmatrix} \right\rangle _{{\mathcal {D}}\times {\mathcal {D}}'}\geqslant 0 \end{aligned}$$

for all $(\theta , v)\in {\mathcal {D}}\times {\mathcal {D}}$ satisfying $\inf _{\mathbb {T}}\theta >0$ and $\int _{{\mathbb {T}}} \theta \,\mathrm{d}x=1$.

2.5 Continuous Gradient Flow

Next, we introduce the gradient flow of the energy (2.2) with respect to the $L^2({\mathbb {T}})$-inner product. First, we extend J in (2.2) to the whole space $L^2_0({\mathbb {T}})$ by setting $J[u]=+\infty$ if $u \in L^2_0({\mathbb {T}}) \backslash W^{2,2}({\mathbb {T}})$. We will not relabel this extension.

The functional $J: L^2_0({\mathbb {T}}) \rightarrow [0,+\infty ]$ is proper, convex, and lower semicontinuous in $L^2_0({\mathbb {T}})$. The subdifferential of J is the map $\partial J: L^2_0({\mathbb {T}})\rightarrow 2^{L^2_0({\mathbb {T}})}$ defined for $u\in L^2_0({\mathbb {T}})$ by

$$\begin{aligned} \begin{aligned} \partial J[u]= \big \{ v\in L^2_0({\mathbb {T}}):\, J[w] \geqslant J[u] + \langle v, w-u \rangle _{L^2({\mathbb {T}})} \text { for all } w\in L^2_0({\mathbb {T}})\big \}. \end{aligned} \end{aligned}$$

The domain of $\partial J$, $D(\partial J)$, is the set of all $u\in L^2_0({\mathbb {T}})$ such that $\partial J[u] \not = \emptyset$.

The gradient flow with respect to the $L^2({\mathbb {T}})$-inner product and energy J is

$$\begin{aligned} \begin{aligned} \dot{\varvec{u}}(t) \in -\partial J [\varvec{u}(t)],\quad t\geqslant 0, \end{aligned} \end{aligned}$$

(2.5)

where $\varvec{u}: [0,+\infty ) \rightarrow L^2_0({\mathbb {T}})$. As we will see next, (2.5) is equivalent to

$$\begin{aligned} \begin{aligned} \dot{\varvec{u}}(t)= \big (\varvec{m}(t)((\varvec{u}(t))_x+ b(x))\big )_x,\quad t\geqslant 0, \end{aligned} \end{aligned}$$

(2.6)

where $\varvec{m}(t)$ is given by (2.3) with u replaced by $\varvec{u}(t)$. Moreover, if the solution $\varvec{u}$ to (2.6) is regular enough, then

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}J[\varvec{u}]=-\int _{{\mathbb {T}}} \Big [\big (\varvec{m} (\varvec{u}_x+b(x))\big )_x\Big ]^2 \,\mathrm{d}x\leqslant 0. \end{aligned}$$

Proposition 2.4

We have $D(\partial J) = W^{2,2}({\mathbb {T}}) \cap L^2_0({\mathbb {T}})$ and, for $u\in D(\partial J)$, $\partial J[u] = -\big (m (u_x+b(x))\big )_x$, where m is given by (2.3).

Proof

By [15, Thm. 1 in §9.6.1], $D(\partial J) \subset D(J)=\{u\in L^2_0({\mathbb {T}}):\, J[u]<+\infty \}= W^{2,2}({\mathbb {T}}) \cap L^2_0({\mathbb {T}})$.

Conversely, fix $u\in W^{2,2}({\mathbb {T}}) \cap L^2_0({\mathbb {T}})$, let m be given by (2.3), and set $v= -\big (m (u_x+b(x))\big )_x$. Then, $v\in L^2_0({\mathbb {T}})$ by the embedding $W^{2,2}({\mathbb {T}}) \subset W^{1,\infty }({\mathbb {T}})$ and by the periodicity of $u$, $m$, and $b$. Moreover, using the convexity of the exponential function, the integration by parts formula, and the conditions $m>0$ and $\frac{w_x^2}{2} - \frac{u_x^2}{2} \geqslant u_xw_x - u_x^2$, for each $w\in W^{2,2}({\mathbb {T}}) \cap L^2_0({\mathbb {T}})$, we obtain

$$\begin{aligned} \begin{aligned} J[w]&\geqslant J[u] + \int _{\mathbb {T}}m \Big ( \frac{w_x^2}{2} + b(x) w_x - \frac{u_x^2}{2} - b(x) u_x \Big )\, \mathrm{d}x\\&\geqslant J[u] + \int _{\mathbb {T}}m \big (u_x w_x - u_x^2 + b(x)(w_x - u_x)\big )\,\mathrm{d}x\\&= J[u] - \int _{\mathbb {T}}\big (m (u_x+b(x))\big )_x (w-u)\,\mathrm{d}x. \end{aligned} \end{aligned}$$

Because $w\in W^{2,2}({\mathbb {T}}) \cap L^2_0({\mathbb {T}})$ is arbitrary and because $J=+\infty$ in $L^2_0({\mathbb {T}}) \backslash W^{2,2}({\mathbb {T}})$, we obtain $v=-(m (u_x+b(x)))_x \in \partial J[u]$. Because $u\in W^{2,2}({\mathbb {T}}) \cap L^2_0({\mathbb {T}})$ is also arbitrary, we get $D(\partial J) \supset W^{2,2}({\mathbb {T}}) \cap L^2_0({\mathbb {T}})$.

To conclude the proof, we show that for $u\in D(\partial J)$, the function $-\big (m (u_x+b(x))\big )_x$ with m given by (2.3) is the unique element of $\partial J[u]$. Let $\bar{v}\in \partial J[u]$. Then, for all $\varepsilon >0$ and $w\in W^{2,2}({\mathbb {T}}) \cap L^2_0({\mathbb {T}})$, we have

$$\begin{aligned} \frac{J[u \pm \varepsilon w] - J[u]}{\varepsilon } \geqslant \pm \langle \bar{v}, w \rangle _{L^2({\mathbb {T}})}. \end{aligned}$$

Letting $\varepsilon \rightarrow 0^+$ and arguing as in the proof of Lemma 2.2, we obtain

$$\begin{aligned} \big \langle -\big (m (u_x+b(x))\big )_x, w\big \rangle _{L^2({\mathbb {T}})} \geqslant \pm \langle \bar{v}, w\rangle _{L^2({\mathbb {T}})}. \end{aligned}$$

Because $w\in W^{2,2}({\mathbb {T}}) \cap L^2_0({\mathbb {T}})$ is arbitrary, it follows that $\bar{v}= -\big (m (u_x+b(x))\big )_x$. $\square$

The following result about solutions to the gradient flow (2.6) holds by [15, Thm. 3 in §9.6.2] and by the fact that $W^{2,2}({\mathbb {T}}) \cap L^2_0({\mathbb {T}})$ is dense in $L^2_0({\mathbb {T}})$.

Theorem 2.5

For each $u\in W^{2,2}({\mathbb {T}}) \cap L^2_0({\mathbb {T}})$, there exists a unique function $\varvec{u} \in C([0,+\infty );L^2_0({\mathbb {T}}))$, with $\dot{\varvec{u}} \in L^\infty (0,+\infty ;L^2_0({\mathbb {T}}))$, such that

• (i) $\varvec{u}(0) =u,$

• (ii) $\varvec{u}(t) \in W^{2,2}({\mathbb {T}}) \cap L^2_0({\mathbb {T}})$ for each $t>0$,

• (iii) $\dot{\varvec{u}}(t) = \big (\varvec{m}(t) ((\varvec{u}(t))_x+ b(x))\big )_x$ for a.e. $t\geqslant 0$, where $\varvec{m}(t)$ is given by (2.3) with u replaced by $\varvec{u}(t)$.

2.6 Monotonic Flow

Because the operator A is monotone, the flow

$$\begin{aligned} \begin{bmatrix} \dot{\varvec{m}}\\ \dot{\varvec{u}} \end{bmatrix} = -A \begin{bmatrix} \varvec{ m}\\ \varvec{ u} \end{bmatrix} \end{aligned}$$

(2.7)

is a contraction in $L^2({\mathbb {T}}) \times L^2({\mathbb {T}})$. That is, if $(\varvec{m},\varvec{u})$ and $(\tilde{\varvec{m}}, \tilde{\varvec{u}})$ solve (2.7), then

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}t} \left( \Vert \varvec{u}-\tilde{\varvec{u}}\Vert ^2_{L^2({\mathbb {T}})}+\Vert \varvec{m}-\tilde{\varvec{m}}\Vert ^2_{L^2({\mathbb {T}})}\right) \\&\quad =-2 \left\langle A \begin{bmatrix} \varvec{m}\\ \varvec{u}\\ \end{bmatrix} - A \begin{bmatrix}\tilde{\varvec{m}} \\ \tilde{\varvec{u}} \\ \end{bmatrix} , \begin{bmatrix} \varvec{m}\\ \varvec{u}\\ \end{bmatrix} - \begin{bmatrix}\tilde{\varvec{m}} \\ \tilde{\varvec{u}} \\ \end{bmatrix} \right\rangle _{L^2({\mathbb {T}}) \times L^2({\mathbb {T}})}\leqslant 0, \end{aligned}$$

provided that for each $t \geqslant 0$, $(\varvec{m}(t),\varvec{u}(t))$, $(\tilde{\varvec{m}}(t), \tilde{\varvec{u}}(t)) \in D(A)$. The flow (2.7) has two undesirable features. First, it does not preserve probabilities; second, the flow may not preserve the condition $\varvec{m}>0$. To conserve probability, we modify (2.7) through

$$\begin{aligned} \begin{bmatrix} \dot{\varvec{m}}\\ \dot{\varvec{u}} \end{bmatrix} = -A \begin{bmatrix} \varvec{m}\\ \varvec{u} \end{bmatrix} + \begin{bmatrix} \,{\overline{H}}(t)\\ 0 \end{bmatrix} , \end{aligned}$$

(2.8)

where ${\overline{H}}(t)$ is such that $\frac{\mathrm{d}}{\mathrm{d}t} \int _{\mathbb {T}}\varvec{m}\,\mathrm{d}x=0$. A straightforward computation shows that (2.8) is still a contraction in $L^2({\mathbb {T}}) \times L^2({\mathbb {T}})$. More precisely, if $(\varvec{m},\varvec{u})$ and $(\tilde{\varvec{m}}, \tilde{\varvec{u}})$ solve (2.8) and satisfy $(\varvec{m}(t),\varvec{u}(t))$, $(\tilde{\varvec{m}}(t), \tilde{\varvec{u}}(t)) \in D(A)$ for all $t\geqslant 0$, $\int _{\mathbb {T}}\varvec{m}(0)\,\mathrm{d}x=1$, and $\int _{\mathbb {T}}\tilde{\varvec{m}}(0)\,\mathrm{d}x=1$, then

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \left( \Vert \varvec{u}-\tilde{\varvec{u}}\Vert ^2_{L^2({\mathbb {T}})}+\Vert \varvec{m}-\tilde{\varvec{m}}\Vert ^2_{L^2({\mathbb {T}})}\right) \leqslant 0. \end{aligned}$$

Furthermore, thanks to the nonlinearity $\ln (\cdot )$, positivity holds for the discretization of (2.8) that we develop in the next section. Therefore, the discrete analog of (2.8) is a contracting flow that preserves probability and positivity. Then, as $t\rightarrow \infty$, the solutions approximate (1.1).

3 Discrete Setting

Here, we discuss the numerical approximation of (1.1). We use a monotone scheme for the Hamilton–Jacobi equation. For the Fokker–Planck equation, we consider the adjoint of the linearization of the discrete Hamilton–Jacobi equation. This technique preserves both the gradient structure and the monotonicity properties of the original problem.

3.1 Discretization of the Hamilton–Jacobi Operator

We consider N equidistributed points on [0, 1], $x_i=\frac{i}{N}$, $i\in \{1,...,N\}$, and corresponding values of the approximation to u given by the vector $u=(u_1, ..., u_N)\in {\mathbb {R}}^N$. We set $h=\frac{1}{N}$. To incorporate the periodic conditions, we use the periodicity convention $u_0=u_N$ and $u_{N+1}= u_1$. For each $i\in \{1,...,N\}$, let $\psi _i: \mathbb {R}^N\rightarrow \mathbb {R}^2$ be given by

$$\begin{aligned} \begin{aligned} \psi _i (u) = (\psi _i^1(u),\psi _i^2(u)) = \Big (\frac{u_i - u_{i+1}}{h}, \frac{u_i - u_{i-1}}{h} \Big ) \end{aligned} \end{aligned}$$

for $u\in \mathbb {R}^N$. To discretize the operator

$$\begin{aligned} u\mapsto \frac{u_x^2}{2} + V(x)+b(x) u_x, \end{aligned}$$

we use a monotone finite difference scheme, see [6]. This scheme is built as follows. We consider a function $F:{\mathbb {R}}\times {\mathbb {R}}\times {\mathbb {T}}\rightarrow {\mathbb {R}}$ satisfying the following four conditions.

• 1. F(p, q, x) is jointly convex in (p, q).

• 2. The functions $p\mapsto F(p, q, x)$ for fixed (q, x) and $q\mapsto F(p, q, x)$ for fixed (p, x) are increasing.

• 3. $F(-p, p, x)=\frac{p^2}{2}+b(x)p+V(x)$.

• 4. There exists a positive constant, $c$, such that

  $$\begin{aligned} F(-p, q, x) + F(q', p, x') \geqslant - \frac{1}{c} + c\,p^2. \end{aligned}$$

  (3.1)

An example of such a function may be found in Sect. 4 below. Next, we set

$$\begin{aligned} F_i(p,q)=F(p,q, x_i). \end{aligned}$$

(3.2)

Let $G:\mathbb {R}^N\rightarrow \mathbb {R}^N$ be the function defined for $u\in \mathbb {R}^N$ by

$$\begin{aligned} G(u) = (G_1(u), ... , G_N(u))= \big ((F_1\circ \psi _1)(u), ... , (F_N\circ \psi _N)(u)\big ). \end{aligned}$$

(3.3)

Then, G(u) is a finite difference scheme for the Hamilton–Jacobi operator $\frac{u_x^2}{2}+V(x)+b(x)u_x$.

Remark 3.1

In the higher-dimensional case, the Hamilton–Jacobi operator can be discretized with a similar monotone scheme. See [45] for a systematic study of convergent monotone difference schemes for elliptic and parabolic equations.

3.2 The Variational Formulation

Here, we study the following discrete version, $\phi :\mathbb {R}^N \rightarrow \mathbb {R}$, of the functional (2.2):

$$\begin{aligned} \phi (u)= \sum _{i=1}^{N} h\, e^{G_i(u)},\quad u\in \mathbb {R}^N, \end{aligned}$$

(3.4)

where $G_i$ is given by (3.3).

Lemma 3.2

The function $\phi$ given by (3.4) is convex.

Proof

Fix $\lambda \in (0,1)$ and u, $v\in {\mathbb {R}}^N$. Because each $F_i$ is convex, because the exponential is an increasing convex function, and because $h>0$, we have

$$\begin{aligned} \begin{aligned} \phi (\lambda u + (1-\lambda )v)&= \sum _{i=1}^{N} h\, e^{F_i \big ( \lambda \frac{u_i - u_{i+1}}{h} + (1-\lambda ) \frac{v_i - v_{i+1}}{h}, \lambda \frac{u_i - u_{i-1}}{h} + (1-\lambda ) \frac{v_i - v_{i-1}}{h} \big ) } \\&\leqslant \sum _{i=1}^{N} h \, e^{\lambda F_i \big (\frac{u_i - u_{i+1}}{h}, \frac{u_i - u_{i-1}}{h} \big ) + (1-\lambda ) F_i \big (\frac{v_i - v_{i+1}}{h}, \frac{v_i - v_{i-1}}{h} \big )} \\&\leqslant \lambda \phi (u) + (1-\lambda ) \phi (v), \end{aligned} \end{aligned}$$

which completes the proof. $\square$

Lemma 3.3

Let $\phi$ be given by (3.4). Let ${\mathcal {L}}^*_u:\mathbb {R}^N\rightarrow \mathbb {R}^N$ represent the adjoint operator of the linearized operator ${\mathcal {L}}_u :\mathbb {R}^N\rightarrow \mathbb {R}^N$ of the function G at $u\in \mathbb {R}^N$. A vector $u\in \mathbb {R}^N$ is a critical point of $\phi$ if and only if there exists $\tilde{m}\in \mathbb {R}_+^N$ such that the pair $(\tilde{m},u)$ satisfies

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle G_i(u)= \ln \tilde{m}_i, \\ \displaystyle ({\mathcal {L}}_u^* \tilde{m})_i=0 \end{array}\right. } \end{aligned}$$

for all $i\in \{1,...,N\}$.

Proof

The proof is similar to the one for Lemma 2.2. $\square$

Remark 3.4

We observe that for $w\in \mathbb {R}^N$ and $i\in \{1,...,N\}$, we have

$$\begin{aligned} \begin{aligned} ({\mathcal {L}}_u^* w)_i&= \sum _{j=1}^N \partial _iG_j(u)w_j = \sum _{j=i-1}^{i+1} \frac{\partial }{\partial u_i} F_j(\psi _j(u))w_j \\&= \frac{1}{h} \bigg [ - \frac{\partial F_{i-1}}{\partial p} (\psi _{i-1}(u))w_{i-1} + \frac{\partial F_{i}}{\partial p} (\psi _{i}(u))w_{i} + \frac{\partial F_{i}}{\partial q} (\psi _{i}(u))w_{i} \\&\quad - \frac{\partial F_{i+1}}{\partial q} (\psi _{i+1}(u))w_{i+1}\bigg ]. \end{aligned} \end{aligned}$$

Simple computations show that ${\mathcal {L}}_u^* w$ is a consistent finite difference scheme for the Fokker–Planck equation.

3.3 The Discretized Operator

Motivated by the previous discussion, we discretize (1.1) through the finite difference operator

$$\begin{aligned} \begin{aligned} A^N \begin{bmatrix}m \\ u \\ \end{bmatrix} = \begin{bmatrix}\displaystyle -G(u) + \ln m \\ {\mathcal {L}}_u^* m \end{bmatrix}, \quad (m,u)\in \mathbb {R}^N_+ \times \mathbb {R}^N, \end{aligned} \end{aligned}$$

(3.5)

where $\ln m = (\ln m_1, ... , \ln m_N)$ and where G is given by (3.3). Accordingly, the analog to (1.1) becomes

$$\begin{aligned} A^N\begin{bmatrix}m^N \\ u^N \\ \end{bmatrix} = \begin{bmatrix}-{\overline{H}}^N \varvec{\iota } \\ 0 \\ \end{bmatrix}, \end{aligned}$$

(3.6)

where we highlighted the dependence on $N$ and where $\varvec{\iota }=(1, ..., 1)\in \mathbb {R}^N$. In (3.6), the unknowns are the vector $u^N$, the discrete probability density $m^N$, normalized to $h \sum _{i=1}^N m_i^N=1$, and the effective Hamiltonian ${\overline{H}}^N$.

We are interested in two main points. The first is the existence and approximation of solutions to (3.6). The second is the convergence of these solutions to solutions of (1.1). The first issue will be examined by gradient flow techniques and by monotonicity methods. The second issue is a consequence of a modified Minty method.

3.4 Existence of Solutions

Here, we prove the existence of solutions to (3.6). Our proof uses ideas similar to those of the direct method of the calculus of variations.

Proposition 3.5

Let $\phi$ be as in (3.4). Then, there exists $u^N\in {\mathbb {R}}^N$ with $\sum _{i=1}^N u_i^N=0$ that minimizes $\phi$. Moreover,

$$\begin{aligned} h\sum _{i=1}^{N} (u_i^N)^2\leqslant C \end{aligned}$$

(3.7)

for some positive constant $C$ independent of h. In addition, there exist $m^N\in \mathbb {R}^N$ with $h\sum _{i=1}^N m_i^N = 1$ and $\overline{H}^N \in \mathbb {R}^N$ such that the triplet $(u^N, m^N, \overline{H}^N)$ satisfies (3.6).

Proof

To simplify the notation, we will drop the explicit dependence on $N$ of $u^N$ and $m^N$. Accordingly, we simply write $u$ and $m$.

As in the direct method of the calculus of variations, we select a minimizing sequence, $(u^k)_{k\in \mathbb {N}} \subset {\mathbb {R}}^N$, for $\phi$ satisfying

$$\begin{aligned} \sum _{i=1}^N u_i^k=0. \end{aligned}$$

(3.8)

Then, there exists a positive constant, C, independent of k and $h$ such that $\sup _{k\in \mathbb {N}}\phi (u^k)\leqslant C$. Using Jensen’s inequality, for all $k\in \mathbb {N}$, we have that

$$\begin{aligned} h\sum _{i=1}^{N} G_i(u^k) \leqslant \tilde{C}, \end{aligned}$$

where $\tilde{C}$ is positive constant that is independent of k and $h$. This estimate together with (3.1)–(3.3) implies that

$$\begin{aligned} \sum _{i=1}^{N} \frac{|u_{i+1}^k-u_i^k|^2}{h}\leqslant \bar{C} \end{aligned}$$

for some positive constant $\bar{C}$ that is independent of k and $h$. By a telescoping series argument combined with the Cauchy inequality, for all $l,m\in \{1,...,N\}$, we have

$$\begin{aligned} |u_l^k-u_m^k|&\leqslant \sum _{i=1}^{N} |u_{i-1}^k-u_i^k|\leqslant \Big (\frac{1}{h}\Big )^{\frac{1}{2}} \left( \sum _{i=1}^{N} |u_{i-1}^k-u_i^k|^2\right) ^{\frac{1}{2}}\leqslant \bar{C}^{\frac{1}{2}}. \end{aligned}$$

The previous bound combined with (3.8) yields

$$\begin{aligned} \max _{1 \leqslant i \leqslant N} |u_i^k| \leqslant \bar{C}^{\frac{1}{2}}. \end{aligned}$$

By compactness and by extracting a subsequence if necessary, there exists $u\in {\mathbb {R}}^N$ with $\sum _{i=1}^N u_i=0$ such that $u^k\rightarrow u$ in $\mathbb {R}^N$. The continuity of $\phi$ implies that u is a minimizer of $\phi$. Furthermore, (3.7) holds.

Finally, by Lemma 3.3, we have

$$\begin{aligned} A^N\begin{bmatrix} \tilde{m} \\ u \\ \end{bmatrix} = \begin{bmatrix} 0\\ 0 \\ \end{bmatrix} \end{aligned}$$

for $\tilde{m}_i=e^{G_i(u)}$. By selecting ${\overline{H}}^N$ conveniently and by setting $m_i=e^{-{\overline{H}}^N}\tilde{m}_i$, we obtain $h\sum _{i=1}^{N} m_i=1$. Moreover, the triplet $(u,m, \overline{H}^N)$ satisfies (3.6). $\square$

Remark 3.6

The proof of the previous proposition gives an $\ell ^\infty$ bound for $u_i$, not just the $\ell ^2$ bound in (3.7). However, the technique used in the proof is one-dimensional since it is similar to the proof of the one-dimensional Morrey’s theorem. As stated in the proposition, inequality (3.7) is a discrete version of the Poincaré inequality; this inequality holds in any dimension. Finally, for our purposes, (3.7) is sufficient.

3.5 Monotonicity Properties

Next, we prove that the operator $A^N$ is monotone.

Lemma 3.7

The operator $A^N$ given by (3.5) is monotone in $\mathbb {R}^N \times \mathbb {R}^N$. More precisely, for all (m, u), $(\theta ,v) \in \mathbb {R}_+^N \times \mathbb {R}^N$,

$$\begin{aligned} \begin{aligned} \bigg \langle A^N \begin{bmatrix}m \\ u \\ \end{bmatrix} - A^N \begin{bmatrix}\theta \\ v \\ \end{bmatrix} , \begin{bmatrix}m \\ u \\ \end{bmatrix} - \begin{bmatrix}\theta \\ v \\ \end{bmatrix} \bigg \rangle _{\mathbb {R}^N \times \mathbb {R}^N} \geqslant 0. \end{aligned} \end{aligned}$$

(3.9)

Proof

Fix (m, u), $(\theta ,v) \in \mathbb {R}_+^N \times \mathbb {R}^N$. Using the definition of $A^N$ and the fact that $\ln (\cdot )$ is increasing, we obtain

$$\begin{aligned} \begin{aligned}&\bigg \langle A^N \begin{bmatrix}m \\ u \\ \end{bmatrix} - A^N \begin{bmatrix}\theta \\ v \\ \end{bmatrix} , \begin{bmatrix}m \\ u \\ \end{bmatrix} - \begin{bmatrix}\theta \\ v \\ \end{bmatrix} \bigg \rangle _{\mathbb {R}^N \times \mathbb {R}^N}\\&\quad = \sum _{i=1}^{N} \Big [\big (G_i(v) - G_i(u) + \ln m_i - \ln \theta _i\big ) (m_i - \theta _i) + \big (({\mathcal {L}}_u^* m)_i - ({\mathcal {L}}_v^* \theta )_i\big ) (u_i - v_i) \Big ]\\&\quad \geqslant \sum _{i=1}^{N} \big [ \big (G_i(v)-G_i(u)\big ) m_i + ({\mathcal {L}}_u^* m)_i (u_i - v_i)\big ] \\&\quad \quad + \sum _{i=1}^{N} \big [\big (G_i(u) - G_i(v)\big ) \theta _i - ({\mathcal {L}}_v^* \theta )_i (u_i - v_i)\big ]. \end{aligned} \end{aligned}$$

Moreover, by the periodicity convention, we have that

$$\begin{aligned} \begin{aligned} \sum _{i=1}^{N}({\mathcal {L}}_u^* m)_i (u_i - v_i)&= \frac{1}{h} \sum _{i=1}^{N} \bigg [ - \frac{\partial F_{i-1}}{\partial p} (\psi _{i-1}(u))m_{i-1} (u_i - v_i)+ \frac{\partial F_{i}}{\partial p} (\psi _{i}(u))m_{i} (u_i - v_i) \bigg ] \\&\quad +\frac{1}{h} \sum _{i=1}^{N} \bigg [ \frac{\partial F_{i}}{\partial q} (\psi _{i}(u))m_{i} (u_i - v_i)- \frac{\partial F_{i+1}}{\partial q} (\psi _{i+1}(u))m_{i+1} (u_i - v_i)\bigg ]\\&= \frac{1}{h} \sum _{i=1}^{N} \bigg [ - \frac{\partial F_{i}}{\partial p} (\psi _{i}(u))m_{i} (u_{i+1} - v_{i+1})+ \frac{\partial F_{i}}{\partial p} (\psi _{i}(u))m_{i} (u_i - v_i) \bigg ] \\&\qquad +\frac{1}{h} \sum _{i=1}^{N} \bigg [ \frac{\partial F_{i}}{\partial q} (\psi _{i}(u))m_{i} (u_i - v_i)- \frac{\partial F_{i}}{\partial q} (\psi _{i}(u))m_{i} (u_{i-1} - v_{i-1})\bigg ]\\&= \sum _{i=1}^{N} \bigg [ \frac{\partial F_{i}}{\partial p} (\psi _{i}(u)) (\psi _i^1(u) - \psi _i^1(v)) + \frac{\partial F_{i}}{\partial q} (\psi _{i}(u)) (\psi _i^2(u) - \psi _i^2(v)) \bigg ] m_i \\&= \sum _{i=1}^{N} \nabla F_{i} (\psi _{i}(u)) \cdot (\psi _i(u) - \psi _i(v)) m_i. \end{aligned} \end{aligned}$$

So, the estimate

$$\begin{aligned}&\sum _{i=1}^{N} \big [\big (G_i(v)-G_i(u)\big ) m_i + ({\mathcal {L}}_u^* m)_i (u_i - v_i)\big ] \nonumber \\&\qquad = \sum _{i=1}^{N} \big [F_i(\psi _i(v))-F_i(\psi _i(u))-\nabla F_{i} (\psi _{i}(u)) \cdot (\psi _i(v) - \psi _i(u))\big ] m_i\geqslant 0 \end{aligned}$$

(3.10)

follows from the convexity of each $F_i$ and from the positivity of each $m_i$. Similarly,

$$\begin{aligned} \begin{aligned} \sum _{i=1}^{N} \big [\big (G_i(u) - G_i(v)\big ) \theta _i - ({\mathcal {L}}_v^* \theta )_i (u_i - v_i)\big ] \geqslant 0, \end{aligned} \end{aligned}$$

which concludes the proof. $\square$

Remark 3.8

Because the operator $A^N$ is monotone, $(u^N, m^N, {\overline{H}}^N)$ with $m^N\in \mathbb {R}^N_+$ solves (3.6) if and only if the condition

$$\begin{aligned} \left\langle A^N \begin{bmatrix} \theta \\ v \\ \end{bmatrix} + \begin{bmatrix}{\overline{H}}^N\varvec{\iota }\\\ 0 \\ \end{bmatrix} , \begin{bmatrix}\theta \\ v \\ \end{bmatrix} - \begin{bmatrix}m^N \\ u^N \\ \end{bmatrix} \right\rangle _{\mathbb {R}^N \times \mathbb {R}^N}\geqslant 0 \end{aligned}$$

(3.11)

holds for every $(v, \theta )\in \mathbb {R}^N \times \mathbb {R}^N_+$. In fact, if $(u^N, m^N, {\overline{H}}^N)$ solves (3.6), then clearly (3.11) holds (with “$\geqslant$” replaced by “=”). Conversely, let $(\tilde{v}, \tilde{\theta })\in \mathbb {R}^N\times \mathbb {R}^N$ be arbitrary, and for $\delta >0$, define $(v,\theta ):= (u^N+\delta \tilde{v}, m^N + \delta \tilde{\theta })$. Because $m^N\in \mathbb {R}^N_+$, we have $( v, \theta )\in \mathbb {R}^N\times \mathbb {R}^N_+$ for all sufficiently small $\delta >0$; thus, (3.11) yields

$$\begin{aligned} \begin{aligned} \left\langle A^N \begin{bmatrix} u^N+\delta \tilde{v} \\ m^N + \delta \tilde{\theta } \\ \end{bmatrix} + \begin{bmatrix}{\overline{H}}^N\varvec{\iota }\\\ 0 \\ \end{bmatrix} , \begin{bmatrix}\tilde{\theta } \\ \tilde{v} \\ \end{bmatrix} \right\rangle _{\mathbb {R}^N \times \mathbb {R}^N}\geqslant 0. \end{aligned} \end{aligned}$$

Letting $\delta \rightarrow 0^+$, we obtain

$$\begin{aligned}\Big \langle A^N \begin{bmatrix} u^N \\ m^N \\ \end{bmatrix} + \begin{bmatrix}{\overline{H}}^N\varvec{\iota }\\\ 0 \\ \end{bmatrix} , \begin{bmatrix}\tilde{\theta } \\ \tilde{v} \\ \end{bmatrix} \Big \rangle _{\mathbb {R}^N \times \mathbb {R}^N}\geqslant 0. \end{aligned}$$

Because $(\tilde{v}, \tilde{\theta })\in \mathbb {R}^N\times \mathbb {R}^N$ is arbitrary, we conclude that $(u^N, m^N, {\overline{H}}^N)$ solves (3.6).

Definition 3.9

We say that $A^N$ is strictly monotone if (3.9) holds with strict inequality whenever (m, u), $(\theta ,v) \in \mathbb {R}_+^N \times \mathbb {R}^N$ satisfy $v\ne u$ and $\sum _{i=1}^{N} v=\sum _{i=1}^{N} u$.

3.6 Uniform Estimates

Estimates that do not depend on N play a major role in establishing the convergence of solutions of (3.6) to (1.1). Here, we prove elementary energy estimates that are sufficient to show convergence.

Proposition 3.10

Let $(u^N,m^N, {\overline{H}}^N)$ solve (3.6). Further assume that $\sum _{i=1}^{N} u^N_i=0$. Then, there exists a positive constant, C, independent of N such that

$$\begin{aligned} \frac{1}{N} \sum _{i=1}^{N} (u_i^N)^2\leqslant C \end{aligned}$$

(3.12)

and

$$\begin{aligned} \left| {\overline{H}}^N\right| \leqslant C. \end{aligned}$$

Proof

By Lemma 3.3, we have that $\phi (u^N) \leqslant C$, where $C= \phi (0)$. Then, arguing as in the proof of Proposition 3.5, we obtain the $\ell ^2$ bound in (3.12).

The bound for ${\overline{H}}^N$ is proven in two steps. First, we have

$$\begin{aligned} \frac{1}{N} \sum _{i=1}^{N} G_i(u^N)={\overline{H}}^N+\frac{1}{N} \sum _{i=1}^{N} \ln (m_i^N)\leqslant {\overline{H}}^N \end{aligned}$$

by Jensen’s inequality. Because $G_i$ is bounded from below, we obtain

$$\begin{aligned} {\overline{H}}^N\geqslant -C \end{aligned}$$

for some constant $C\geqslant 0$ independent of N. Second, for each $i\in \{1,..., N\}$, we multiply the ith equation in (3.6) by $m_i$ and the $(N+i)$th equation by $-u_i$. Adding the resulting expressions and summing over i, we get

$$\begin{aligned} \frac{1}{N} \sum _{i=1}^{N} m_i\left( G_i(u)-({\mathcal {L}}_u u)_i\right) ={\overline{H}}^N+\frac{1}{N} \sum _{i=1}^{N} m_i \ln m_i\geqslant {\overline{H}}^N \end{aligned}$$

by Jensen’s inequality. By the concavity of $G_i(u)$, we have

$$\begin{aligned} G_i(u)-({\mathcal {L}}_u u)_i=G_i(u)+({\mathcal {L}}_u (0-u))_i\leqslant G_i(0). \end{aligned}$$

Hence, ${\overline{H}}^N\leqslant C$ for some constant $C>0$ independent of N. $\square$

3.7 Convergence

Here, we show the convergence of solutions of (3.6) to weak solutions of (1.1).

Proposition 3.11

For $N\in {\mathbb {N}}$, let $(u^N,m^N, {\overline{H}}^N)\in {\mathbb {R}}^N\times {\mathbb {R}}^N\times \mathbb {R}$ be a solution of (3.6). Denote by $\bar{u}^N$ the step function in [0, 1] that takes the value $u^N_i$ in the interval $\left[ \frac{i-1}{N}, \frac{i}{N}\right]$ for $1\leqslant i\leqslant N$. Similarly, $\bar{m}^N$ is the step function associated with $m^N$. Then, up to a (not relabeled) subsequence, ${\overline{H}}^N\rightarrow {\overline{H}}$ in ${\mathbb {R}}$, $\bar{u}^N\rightharpoonup \bar{u}$ in $L^2([0,1])$, and $\bar{m}^N\rightharpoonup \bar{m}$ in $\mathcal {P}([0,1])$. Moreover, $(\bar{m}, \bar{u}, {\overline{H}})$ is a weak solution of (1.1).

Proof

According to Proposition 3.10, $|{\overline{H}}^N|$ and $\Vert \bar{u}^N\Vert _{L^2([0,1])}$ are uniformly bounded with respect to $N$. Moreover, $\Vert \bar{m}^N\Vert _{L^1([0,1])}=1$ by construction. Therefore, there exist ${\overline{H}}\in {\mathbb {R}}$, $\bar{u} \in L^2([0,1])$, and $\bar{m}\in \mathcal {P}([0,1])$ such that ${\overline{H}}^N\rightarrow {\overline{H}}$ in ${\mathbb {R}}$, $\bar{u}^N\rightharpoonup \bar{u}$ in $L^2([0,1])$, and $\bar{m}^N\rightharpoonup \bar{m}$ in $\mathcal {P}([0,1])$, up to a (not relabeled) subsequence.

Select $v, \theta \in C^\infty ({\mathbb {T}})$ satisfying $\theta > 0$ and $\int _{\mathbb {T}}\theta \,\mathrm{d}x=1$. Set $v^N_i=v\left( \frac{i}{N}\right)$ and $\theta ^N_i=\theta \left( \frac{i}{N}\right)$. Then, by Remark 3.8,

$$\begin{aligned} 0&\leqslant \left\langle A^N \begin{bmatrix} \theta ^N \\ v^N \\ \end{bmatrix} - \begin{bmatrix}{\overline{H}}^N\\ 0 \\ \end{bmatrix} , \begin{bmatrix}\theta ^N \\ v^N \\ \end{bmatrix} - \begin{bmatrix}m^N \\ u^N \\ \end{bmatrix} \right\rangle _{\mathbb {R}^N \times \mathbb {R}^N} \\&= O\left( \frac{1}{N}\right) + \left\langle A \begin{bmatrix} \theta \\ v \\ \end{bmatrix} - \begin{bmatrix}{\overline{H}}^N\\ 0 \\ \end{bmatrix} , \begin{bmatrix}\theta \\ v \\ \end{bmatrix} - \begin{bmatrix}\bar{m}^N \\ \bar{u}^N \\ \end{bmatrix} \right\rangle _{{\mathcal {D}}\times {\mathcal {D}}'}. \end{aligned}$$

The proposition follows by letting $N\rightarrow \infty$ in this last expression. $\square$

3.8 A Discrete Gradient Flow

To approximate (3.6), we consider two approaches. Here, we discuss a gradient-flow approximation.. Later, we examine a monotonicity-based method.

The discrete-time gradient flow is

$$\begin{aligned} \dot{\varvec{u}}=-({\mathcal {L}}_{\varvec{u}^*} \tilde{\varvec{m}})_i, \end{aligned}$$

(3.13)

where $\tilde{\varvec{m}}_i=e^{G_i(\varvec{u})}$. Because $\phi$ is convex, $\phi (\varvec{u}(t))$ is decreasing. Moreover, the proof of proposition 3.5 shows that $\phi$ is coercive on the set $\sum _{i=1}^N \varvec{u}_i=0$. Note that (3.13) satisfies

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \sum _{i=1}^{N} \varvec{u}_i=0. \end{aligned}$$

Consequently, $\varvec{u}(t)$ is bounded and converges to a critical point of $\phi$. Finally, we obtain a solution to (3.6) by normalizing $\tilde{\varvec{m}}_i$.

3.9 Dynamic Approximation

We can use the monotonicity of $A^N$ to build a contracting flow in $L^2$ whose fixed points satisfy (3.6). This flow is

$$\begin{aligned} \begin{bmatrix} \dot{\varvec{m}}\\ \dot{\varvec{u}} \end{bmatrix} = -A^N \begin{bmatrix} \varvec{m}\\ \varvec{u}\end{bmatrix} + \begin{bmatrix} {\overline{H}}^N(t) \varvec{\iota }\\ 0 \end{bmatrix}, \end{aligned}$$

where ${\overline{H}}^N(t)$ is such that the total mass is preserved; that is,

$$\begin{aligned} \sum _{i=1}^{N} \dot{\varvec{m}}_i=0. \end{aligned}$$

Due to the logarithmic nonlinearity, $\varvec{m}(t) > 0$ for all t. We further observe that

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \sum _{i=1}^{N} \varvec{u}_i=0. \end{aligned}$$

Moreover, if $(\bar{m}^N, \bar{u}^N, {\overline{H}}^N)$ is a solution of (3.6), then the monotonicity of $A^N$ implies that

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \left( \Vert \varvec{m}-\bar{m}^N\Vert ^2+\Vert \varvec{u}-\bar{u}^N\Vert ^2\right) \leqslant 0. \end{aligned}$$

Furthermore, if strong monotonicity holds (see Definition 3.9), the preceding inequality is strict if $(\varvec{m}, \varvec{u})\ne (m^N, u^N)$. In this case, $(\varvec{m}(t), \varvec{u}(t))$ is globally bounded and converges to $(m^N, u^N)$. Finally, this implies that ${\overline{H}}(t)$ converges to ${\overline{H}}^N$.

4 Numerical Results

Here, we discuss the implementation of our numerical methods, the corresponding results, and some extensions.

In our numerical examples, we construct F as follows. First, we build

$$\begin{aligned} F^Q(p,q)=\frac{1}{2} \left( \max \{p,q,0\}\right) ^2 \end{aligned}$$

and

$$\begin{aligned} F^D(p,q,x)= {\left\{ \begin{array}{ll} -b(x)p &{} \text {if } b(x)\leqslant 0,\\ b(x)q &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

We set

$$\begin{aligned} F(p,q,x)=F^Q(p,q)+F^D(p,q,x)+V(x). \end{aligned}$$

Then, $F_i$ is given by (3.2).

We implemented our algorithms in MATLAB and Mathematica with no significant differences in performance or numerical results. We present here the computations performed with the Mathematica code. To solve the ordinary differential equations, we used the built-in Mathematica ODE solver with the stiff backward difference formula (BDF) discretization of variable order.

4.1 Gradient Flow

For the gradient flow, we took $u(x,0)=0.2 \cos (2 \pi x)$ as the initial condition for u. We used $N=100$. We set $b=0$ and $V(x)=\sin (2 \pi x)$. Figures 1 and 2 feature the evolution of u and $m$, respectively, for $0\leqslant t\leqslant 1$. We can observe a fast convergence to the stationary solution $u=0$. Figure 3 illustrates the behavior of m at equally spaced times and compares it to the exact solution (in black).

Fig. 1

Gradient flow: u

Fig. 2

Gradient flow: m

Fig. 3

Gradient flow: m numeric for $0\leqslant t\leqslant 0.1$ versus exact (black line)

4.2 Monotonic Flow

Here, we present the numerical results for the monotonic flow. We set, as before, $b=0$ and $V(x)=\sin (2 \pi x)$. We used $u(x,0)=0.2 \cos (2 \pi x)$ and $m(x,0)=1+0.2 \cos (2 \pi x)$ as initial conditions for u and m, respectively. As previously, we used $N=100$. Figures 4 and 5 depict the convergence to stationary solutions for $0\leqslant t\leqslant 10$. Figure 6 shows the comparison of the values of m at equally spaced times with the stationary solution. Finally, Figs. 7 and 8 illustrate the solution (u, m) for the case $b(x)=\cos ^2(2 \pi x)$.

Fig. 4

Monotonic flow: u

Fig. 5

Monotonic flow: m

Fig. 6

Monotonic flow: m numerical versus exact (black line) for $t=0, 1,\ldots , 10$

Fig. 7

Monotonic flow: u with $b=\cos ^2(2 \pi x)$

Fig. 8

Monotonic flow: m with $b=\cos ^2(2 \pi x)$

In Table 1, we show the error in m and u in $L^\infty$ and the CPU time for the preceding problem at $T=100$; that is, we compute $\max _i|m(x_i)-m^N_i|$ and $\max _i|u(x_i)-u^N_i|$. We note that the error is extremely small because of the particular form of the solution. Here, the exact solution $u=0$ is also the exact numerical solution. We also observe that the CPU times increase substantially. Thus, as suggested to the authors by Y. Achdou, we consider the alternative monotone discretization

$$\begin{aligned} F(p,q)=\frac{1}{2}\left[ \max \{p,0\}^2+\max \{q,0\}^2\right] . \end{aligned}$$

The corresponding results (also for $T=100$) are shown in Table 2. To get a better sense of the convergence of the algorithm, we considered this last discretization for the case

$$\begin{aligned} b(x)=\cos ^2(2 \pi x), \end{aligned}$$

and $V(x)=\sin ( 2\pi x)$, $u(x,0)=0.2 \cos (2 \pi x)$, and $m(x,0)=1+0.2 \cos (2 \pi x)$ as before. The estimated errors are plotted in Table 3 and correspond to the difference between the solution computed with N nodes and the solution computed with 2N nodes. We see that the error decreases roughly linearly in $\frac{1}{N}$ as one would expect since the monotone discretization of the Hamilton–Jacobi equation is first-order accurate.

Table 1 MFG without congestion: error and CPU time for $F(p,q)=\frac{1}{2}\max \{p,q,0\}^2$

Table 2 MFG without congestion: error and CPU time for $F(p,q)=\frac{1}{2}\left[ \max \{p,0\}^2+\max \{q,0\}^2\right]$

Table 3 MFG without congestion: error and CPU time for $F(p,q)=\frac{1}{2}\left[ \max \{p,0\}^2+\max \{q,0\}^2\right]$ and $b\not =0$

Fig. 9

Congestion model: u

4.3 Application to Congestion Problems

Our methods are not restricted to (1.1) nor to one-dimensional problems. Here, we consider the congestion problem (2.1) and present the corresponding numerical results. We examine higher-dimensional problems in the next section.

The congestion problem (2.1) satisfies the monotonicity condition (see [32]). Moreover, this problem admits the same explicit solution as (1.1) with $b=0$. We chose $V(x)=\sin (2 \pi x)$, for comparison.

We took the same initial conditions as in the previous section and set $N=100$. We present the evolution of u and m in Figs. 9 and 10, respectively. In Fig. 11, we superimpose the exact solution, m, on the numerical values of m at equally spaced times. Finally, in Figs. 12 and 13, we consider the quartic mean-field game with congestion

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{u_x^4}{2 m^{1/2}}+\cos ^2(2 \pi x) u_x+\sin (2\pi x)-\ln m={\overline{H}}\\ -(2 u_x^3 m^{1/2})_x-(\cos ^2(2 \pi x) m)_x=0. \end{array}\right. } \end{aligned}$$

Fig. 10

Congestion model: m

Fig. 11

Congestion model: m numerical versus exact (black line) for $t=0, 1,\ldots , 10$

Fig. 12

Quartic congestion model: u

Fig. 13

Quartic congestion model: m

4.4 A Singular MFG

The logarithmic coupling in the MFG studied so far prevents m to vanish. However, m can vanish in many cases. The following example, taken from [26] (also see [20, 21]), illustrates this behavior. Consider the MFG

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{u_x^2}{2}+3 \sin (2 \pi x)=m+{\overline{H}}\\ -(m u_x)_x=0. \end{array}\right. } \end{aligned}$$

The solution of the preceding problem is $m=(3\sin (2\pi x)-{\overline{H}})^+$, where ${\overline{H}}$ is determined by the condition

$$\begin{aligned} \int _{{\mathbb {T}}}(3\sin (2\pi x)-{\overline{H}})^+ dx=1, \end{aligned}$$

and u is a viscosity solution of

$$\begin{aligned} \frac{u_x^2}{2}=({\overline{H}}-3\sin (2\pi x))^-. \end{aligned}$$

Here, the monotone flow fails to preserve the positivity of m. Thus, we introduce a regularized version of the monotone flow for which the set $m\geqslant 0$ is invariant. This regularized flow is obtained by discretizing the following continuous flow

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{\varvec{u}}=(\varvec{m}\varvec{u}_x)_x\\ \dot{\varvec{m}}=\frac{\lambda \varvec{m}^3}{1+\lambda \varvec{m}^3} \left( \frac{\varvec{u}_x^2}{2}+3 \sin (2 \pi x)-\varvec{m}-{\overline{H}}(t)\right) , \\ \end{array}\right. } \end{aligned}$$

where $\lambda$ is a regularization parameter. The results corresponding to $\lambda =100$ are shown in Fig. 14 (the evolution of m) and Fig. 15 (comparison between exact and numerical solution).

Fig. 14

Evolution of m for the modified monotone flow at $T=100$ for the singular MFG

Fig. 15

Comparison between numerical (blue) and exact (dashed) solution for the singular MFG (Color figure online)

4.5 Higher-Dimensional Examples

As a last example, we consider the following two-dimensional version of (1.1):

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{w_x^2}{2}+ \frac{w_y^2}{2} + W(x,y) =\ln m+{\overline{H}},\\ -(\theta (w_x))_x-(\theta (w_y))_y =0, \end{array}\right. } \end{aligned} \end{aligned}$$

(4.1)

with $W(x,y)=\sin (2 \pi x)+\sin (2 \pi y)$. Because $W(x,y)=V(x)+V(y)$ for $V(x)=\sin (2 \pi x)$, the solution to (4.1) takes the form $w(x,y)=u(x)+u(y)$ and $\theta (x,y)=m(x)+m(y)$, where (u, m) solves (1.1) with $b=0$.

We chose $w(x,y,0)=0.4 \cos (x+ 2 y)$, $\theta (x,y,0)=1+0.3 \cos (x- 3 y)$, and $N=20$. Figure 16 illustrates $\theta$ at $T=50$. The numerical errors for $\theta$ and w are shown in Figs. 17 and 18, respectively.

Fig. 16

Two-dimensional problem: numeric $\theta$ at $T=50$

Fig. 17

Two-dimensional problem: $\theta$ numerical error

Fig. 18

Two-dimensional problem: w numerical error

5 Final Remarks

Here, we developed two numerical methods to approximate solutions of stationary mean-field games. We addressed the convergence of a discrete version of (1.1), and the convergence to weak solutions through a monotonicity argument. Our techniques generalize to discretized systems that are monotonic, and that admit uniform bounds with respect to the discretization parameter.

In the cases we considered, our methods approximate well the exact solutions. While the gradient flow is considerably faster than the monotonic flow, this last method applies to a wider class of problems.

We selected a simple model for illustration purposes. In our numerical examples, however, we illustrated the convergence of the schemes in higher-dimensional problems and congestion MFG problems. Furthermore, our results can be easily extended to related problems—higher-dimensional cases, second-order MFG, or non-local (monotonic) problems. Additionally, our methods provide a natural guide for two future research directions. The first is the development of a general theory of convergence for monotone schemes and the extension of our methods to mildly non-monotonic MFG. The second is the study of time-dependent MFG. This last direction is particularly relevant since the coupled structure of MFG and the initial-terminal conditions that are usually imposed make these problems very challenging from the numerical point of view.