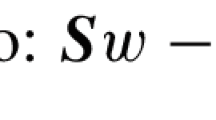Numerical Methods for Finite-State Mean-Field Games Satisfying a Monotonicity Condition

Abstract

Here, we develop numerical methods for finite-state mean-field games (MFGs) that satisfy a monotonicity condition. MFGs are determined by a system of differential equations with initial and terminal boundary conditions. These non-standard conditions make the numerical approximation of MFGs difficult. Using the monotonicity condition, we build a flow that is a contraction and whose fixed points solve both for stationary and time-dependent MFGs. We illustrate our methods with a MFG that models the paradigm-shift problem.

1 Introduction

The mean-field game (MFG) framework [24, 25, 27, 28] models systems with many rational players (see the surveys [18] and [19]). In finite-state MFGs, players switch between a finite number of states (see [16] for discrete-time and [7, 14, 17, 22], and [23] for continuous-time problems). Finite-state MFGs have applications in socio-economic problems, for example, in paradigm-shift and consumer choice models [8, 20, 21] or in corruption models [26]. They also arise in the approximation of continuous-state MFGs [1, 3, 6]. The MFG framework is a major paradigm change in the analysis of N-agent games. MFGs are an alternative approach to particle or agent-based models, which frequently are intractable from the analytical and numerical point of view and often provide no insight on the qualitative properties of the models. Finite-state MFGs are amenable to analytical tools and flexible enough to address a wide range of applications and to provide quantitative and qualitative information. However, in many cases of interest, they have no simple closed-form solution. Hence, the development of numerical methods is critical to applications of MFGs.

Finite-state MFGs comprise systems of ordinary differential equations with initial-terminal boundary conditions. Because of these conditions, the numerical computation of solutions is challenging. Often, MFGs satisfy a monotonicity condition that was first used in [27] and [28] to study the uniqueness of solutions. Besides the uniqueness of solutions, monotonicity implies the long-time convergence of MFGs (see [14] and [17] for finite-state models and [10] and [11] for continuous-state models). Moreover, monotonicity conditions were used in [15] to prove the existence of solutions to MFGs and in [6] to construct numerical methods for stationary MFGs. Here, we consider MFGs that satisfy a monotonicity condition and develop a numerical method to compute their solutions. For stationary problems, our method is a modification of the one in [6]. Our main advance here is how we handle initial-terminal boundary conditions, to which the methods from [6] cannot be applied directly.

We consider MFGs in which each player can be at a state in $I_d=\{1,\ldots ,d\}$, $d\in {\mathbb {N}}$, $d>1$, the players’ state space. Let $\mathcal {S}^d=\{\theta \in ({\mathbb {R}}_0^+)^d : \sum _{i=1}^d \theta ^i=1\}$ be the probability simplex in $I_d$. For a time horizon, $T>0$, the macroscopic description of the game is determined by a path $\theta : [0,T] \rightarrow \mathcal {S}^d$ that gives the probability distribution of the players in $I_d$. All players seek to minimize an identical cost. Each coordinate, $u^i(t)$, of the value function, $u: [0,T] \rightarrow {\mathbb {R}}^d$, is the minimum cost for a typical player at state $i\in I_d$ at time $0\le t\le T$. Finally, at the initial time, the players are distributed according to the probability vector $\theta _0\in \mathcal {S}^d$ and, at the terminal time, are charged a cost $u_T\in {\mathbb {R}}^d$ that depends on their state.

In the framework presented in [16], finite-state MFGs have a Hamiltonian, $h:{\mathbb {R}}^d\times \mathcal {S}^d\times I_d\rightarrow {\mathbb {R}}$, and a switching rate, $\alpha ^*_i:{\mathbb {R}}^d\times \mathcal {S}^d\times I_d\rightarrow {\mathbb {R}}_0^+$, given by

$$\begin{aligned} \alpha ^*_j=\frac{\partial h(\Delta _iz,\theta ,i) }{\partial z^j}, \end{aligned}$$

(1)

where $\Delta _i:{\mathbb {R}}^d\rightarrow {\mathbb {R}}^d$ is the difference operator

$$\begin{aligned} (\Delta _i u)^j=u^j-u^i. \end{aligned}$$

We suppose that h and $\alpha ^*$ satisfy the assumptions discussed in Sect. 2. Given the Hamiltonian and the switching rate, we assemble the following system of differential equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t^i = -h(\Delta _i u,\theta ,i)\\ \theta _t^i=\sum \nolimits _j \theta ^j \alpha ^*_i(\Delta _j u, \theta , j), \end{array}\right. } \end{aligned}$$

(2)

which, together with initial-terminal data

$$\begin{aligned} \theta (0) = \bar{\theta }_0 \text { and } u(T)=\bar{u}_T, \end{aligned}$$

(3)

with $\bar{\theta }_0\in \mathcal {S}^d$ and $\bar{u}_T\in {\mathbb {R}}^d$, determines the MFG.

Solving (2) under the non-standard boundary condition (3) is a fundamental issue in time-dependent MFGs. There are several ways to address this issue, although prior approaches are not completely satisfactory. First, we can solve (2) using initial conditions $\theta (0)=\bar{\theta }_0$ and $u(0)=u_0$ and then solve for $u_0$ such that $u(T)=\bar{u}_T$. However, this requires solving (2) multiple times, which is computationally expensive. A more fundamental difficulty arises in the numerical approximation of continuous-state MFGs by finite-state MFGs. There, the Hamilton–Jacobi equation is a backward parabolic equation whose initial-value problem is ill-posed. Thus, a possible way to solve (2) is to use a Newton-like iteration. This idea was developed in [1, 5] and used to solve a finite-difference scheme for a continuous-state MFG. However, Newton’s method involves inverting large matrices, whereas it is convenient to have algorithms that do not require matrix inversions. A second approach is to use a fixed-point iteration as in [12, 13]. Unfortunately, this iteration is not guaranteed to converge. A third approach (see [20, 21]) is to solve the master equation, which is a partial differential equation whose characteristics are given by (2). To approximate the master equation, we can use a finite-difference method constructed by solving an N-player problem. Unfortunately, even for a modest number of states, this approach is computationally expensive.

Our approach to the numerical solution of (2) relies on the monotonicity of the operator, $A:{\mathbb {R}}^d\times {\mathbb {R}}^d\rightarrow {\mathbb {R}}^d\times {\mathbb {R}}^d$, given by

$$\begin{aligned} A\left[ \begin{array}{c} \theta \\ u \end{array}\right] = \left[ \begin{array}{c} h(\Delta _i u,\theta ,i)\\ -\sum \nolimits _{j} \theta ^j \alpha ^*_i(\Delta _j u,\theta ,j) \end{array} \right] . \end{aligned}$$

(4)

More precisely, we assume that A is monotone (see Assumption 2) in the sense that

$$\begin{aligned} \left( A\left[ \begin{array}{c} \theta \\ u \end{array}\right] - A\left[ \begin{array}{c} \tilde{\theta }\\ \tilde{u} \end{array}\right] , \left[ \begin{array}{c} \theta \\ u \end{array}\right] - \left[ \begin{array}{c} \tilde{\theta }\\ \tilde{u} \end{array}\right] \right) \ge 0 \end{aligned}$$

for all $\theta , \tilde{\theta }\in \mathcal {S}^d$ and $u, \tilde{u}\in {\mathbb {R}}^d$. Building upon the ideas in [6] for stationary problems (also see the approaches for stationary problems in [4, 9, 29, 30]), we introduce the flow

$$\begin{aligned} \left[ \begin{array}{c} \theta _s\\ u_s \end{array}\right] =-A\left[ \begin{array}{c} \theta \\ u \end{array}\right] . \end{aligned}$$

(5)

Up to the normalization of $\theta$, the foregoing flow is a contraction provided that $\theta \in \mathcal {S}^d$. Moreover, its fixed points solve

$$\begin{aligned} A\left[ \begin{array}{c} \theta \\ u \end{array}\right] =0. \end{aligned}$$

In Sect. 3, we construct a discrete version of (5) that preserves probabilities; that is, it preserves both the total mass of $\theta$ and its non-negativity.

The time-dependent case is substantially more delicate. Our method to approximate its solutions is our main contribution. The operator associated with the time-dependent problem, $A:H^1(0,T; {\mathbb {R}}^d\times {\mathbb {R}}^d)\rightarrow L^2(0,T; \mathcal {S}^d\times {\mathbb {R}}^d)$, is

$$\begin{aligned} A\left[ \begin{array}{c} \theta \\ u \end{array}\right] = \left[ \begin{array}{c} -u_t+h(\Delta _i u,\theta ,i)\\ \theta _t-\sum \nolimits _{j} \theta ^j \alpha ^*_i(\Delta _j u,\theta ,j) \end{array} \right] . \end{aligned}$$

(6)

Under the initial-terminal condition in (3), A is a monotone operator. Thus, the flow

$$\begin{aligned} \left[ \begin{array}{c} \theta _s\\ u_s \end{array}\right] =-A\left[ \begin{array}{c} \theta \\ u \end{array}\right] \end{aligned}$$

(7)

for $(\theta , u)\in L^2(0,T; {\mathbb {R}}^d\times {\mathbb {R}}^d)$ is formally a contraction. Unfortunately, even if this flow is well defined, the preceding system neither preserves probabilities nor such boundary conditions (3). Thus, in Sect. 4, we modify (7) in a way that it becomes a contraction in $H^1$ and preserves the boundary conditions. Finally, we discretize this modified flow and build a numerical algorithm to approximate solutions of (2)-(3). Unlike Newton-based methods, our algorithm does not need the inversion of large matrices and scales linearly with the number of states. This is particularly relevant for finite-state MFGs that arise from the discretization of continuous-state MFGs. We illustrate our results in a paradigm-shift problem introduced in [8] and studied from a numerical perspective in [21].

We conclude this introduction with a brief outline of the paper. In the following section, we discuss the framework, main assumptions, and the paradigm-shift example that illustrates our methods. Next, we address stationary solutions. Subsequently, in Sect. 4, we discuss the main contribution of this paper by addressing the initial-terminal value problem. There, we outline the projection method, explain its discretization, and present numerical results. The paper ends with a brief concluding section.

2 Framework and main assumptions

Following [17], we present the standard finite-state MFG framework and describe our main assumptions. Then, we discuss a paradigm-shift problem from [8] that we use to illustrate our methods.

2.1 Standard Setting for Finite-State MFGs

Finite-state MFGs model systems with many identical players who act rationally and non-cooperatively. These players switch between states in $I_d$ in seeking to minimize a cost. Here, the macroscopic state of the game is a probability vector $\theta \in \mathcal {S}^d$ that gives the players’ distribution in $I_d$. A typical player controls the switching rate, $\alpha _j(i)$, from its state, $i\in I_d$, to a new state, $j\in I_d$. Given the players’ distribution, $\theta (r),$ at time r, each player chooses a non-anticipating control, $\alpha$, that minimizes the cost

$$\begin{aligned} u^i(t;\alpha )=E_{{\mathbf{i}}_t=i}^{\alpha } \left[ \int _t^T c({\mathbf{i}}_r,\theta (r),\alpha (r)) dr + u^{{\mathbf{i}}_T}(\theta (T))\right] . \end{aligned}$$

(8)

In the preceding expression, $c:I_d\times \mathcal {S}^d\times ({\mathbb {R}}_0^+)^d\rightarrow {\mathbb {R}}$ is a running cost, $\Psi \in {\mathbb {R}}^d$ is the terminal cost, and ${\mathbf{i}}_s$ is a Markov process in $I_d$ with switching rate $\alpha$. The Hamiltonian, h, is the generalized Legendre transform of $c(i,\theta ,\cdot )$:

$$\begin{aligned} h(\Delta _i z,\theta ,i) = \min _{\mu \in ({\mathbb {R}}^+_0)^d} \{ c(i,\theta ,\mu ) + \mu \cdot \Delta _i z\}. \end{aligned}$$

The first equation in (2) determines the value function, u,  for (8). The optimal switching rate from state i to state $j\ne i$ is given by $\alpha ^*_j(\Delta _iu,\theta ,i)$, where

$$\begin{aligned} \alpha ^*_j(z,\theta ,i)= {\text {argmin}}_{\mu \in ({\mathbb {R}}^+_0)^d} \{c(i,\theta ,\mu )+\mu \cdot \Delta _i z\}. \end{aligned}$$

(9)

Moreover, at points of differentiability of h, we have (1). The rationality of the players implies that each of them chooses the optimal switching rate, $\alpha ^*$. Hence, $\theta$ evolves according to the second equation in (2).

2.2 Main Assumptions

Because we work with the Hamiltonian, h, rather than the running cost, c, it is convenient to state our assumptions in terms of the former. For the relation between assumptions on h and c, see [17].

We begin by stating a mild assumption that ensures the existence of solutions for (2).

Assumption 1

The Hamiltonian $h(z,\theta , i)$ is locally Lipschitz in $(z, \theta )$ and differentiable in z. The map $z\mapsto h(z, \theta , i)$ is concave for each $(\theta , i)$. The function $\alpha ^*(z, \theta , i)$ given by (1) is locally Lipschitz.

Under Assumption 1, there exists a solution to (2)–(3) (see [17]). This solution may not be unique as the examples in [20] and [21] show. Monotonicity conditions are commonly used in MFGs to prove the uniqueness of solutions. For finite-state MFGs, the appropriate monotonicity condition is stated in the next Assumption. Before proceeding, we define $\Vert v \Vert _{\sharp }=\inf _{\lambda \in \mathbb {R}}\Vert v +\lambda \mathbf {1} \Vert$.

Assumption 2

There exists $\gamma >0$ such that the Hamiltonian, h, satisfies the following monotonicity property:

$$\begin{aligned} \theta \cdot (h(z,\tilde{\theta })-h(z,\theta ))+ \tilde{\theta }\cdot (h(\tilde{z},\theta )-h(\tilde{z},\tilde{\theta }) )\le -\gamma \Vert \theta -\tilde{\theta } \Vert ^2. \end{aligned}$$

Moreover, for each $M>0$, there exist constants, $\gamma _i$, such that on the set $\Vert w\Vert ,\Vert z\Vert _\sharp \le M$, h satisfies the following concavity property:

$$\begin{aligned} h(z,\theta ,i)-h( w,\theta ,i)-\alpha ^*(w,\theta ,i)\cdot \Delta _i(z-w)\le -\gamma _i\Vert \Delta _i (z-w)\Vert ^2. \end{aligned}$$

Under the preceding assumptions, (2)–(3) has a unique solution (see [17]). Here, the previous condition is essential to the convergence of our numerical methods, for both stationary problems in Sect. 3 and for the general time-dependent case in Sect. 4.

Remark 1

As shown in [17], Assumption 2 implies the inequality

$$\begin{aligned}&\sum _{i=1}^d (u^i-\tilde{u}^i) \left( \sum _j \theta ^j \alpha ^*(\Delta _j u,\theta ,j) - \sum _j \tilde{\theta }^j \alpha ^*(\Delta _j \tilde{u}, \tilde{\theta },j) \right) \\&\qquad + \sum _{i=1}^d (\theta ^i-\tilde{\theta }^i) \left( - h(\Delta _i u, \theta ,i) + k +h(\Delta _i \tilde{u}, \tilde{\theta },i) -\tilde{k}\right) \\&\quad \le -\gamma \Vert (\theta - \tilde{\theta })\Vert ^2 - \sum _{i=1}^d \gamma _i(\theta ^i+\tilde{\theta }^i) \Vert (\Delta _i u- \Delta _i \tilde{u})\Vert ^2 \end{aligned}$$

for any $u, \tilde{u}\in {\mathbb {R}}^d$, $\theta , \tilde{\theta }\in \mathcal {S}^d$, and $k, \tilde{k}\in {\mathbb {R}}$.

2.3 Solutions and Weak Solutions

Because the operator, A,  in (6) is monotone, we have a natural concept of weak solutions for (2)–(3). These weak solutions were considered for continuous-state MFGs in [6] and [15]. We say that $(u, \theta )\in L^2((0,T), {\mathbb {R}}^d)\times L^2((0,T), \mathcal {S}^d)$ is a weak solution of (2)–(3) if for all $(\tilde{u}, \tilde{\theta })\in H^1((0,T), {\mathbb {R}}^d)\times H^1((0,T), \mathcal {S}^d)$ satisfying (3), we have

$$\begin{aligned} \left\langle A\left[ \begin{array}{c} \tilde{\theta }\\ \tilde{u} \end{array}\right] , \left[ \begin{array}{c} \tilde{\theta }-\theta \\ \tilde{u}-u \end{array}\right] \right\rangle \ge 0. \end{aligned}$$

Any solution of (2)–(3) is a weak solution, and any sufficiently regular weak solution with $\theta >0$ is a solution.

Now, we turn our attention to the stationary problem. We recall (see [17]) that a stationary solution of (2) is a triplet, $(\bar{\theta },\bar{u}, \bar{k}) \in \mathcal {S}^d \times {\mathbb {R}}^d \times {\mathbb {R}},$ satisfying

$$\begin{aligned} {\left\{ \begin{array}{ll} h(\Delta _i \bar{u}, \bar{\theta }, i) = \bar{k} \\ \sum \nolimits _{j} \bar{\theta }^j \alpha ^*_i (\Delta _j \bar{u}, \bar{\theta },j) = 0 \end{array}\right. } \end{aligned}$$

(10)

for $i=1,\ldots ,d$. As discussed in [17], the existence of solutions to (10) holds under an additional contractivity assumption. In general, as for continuous-state MFGs, solutions for (10) may not exist. Thus, we need to consider weak solutions. For a finite-state MFG, a weak solution of (10) is a triplet, $(\bar{u}, \bar{\theta }, \bar{k})\in {\mathbb {R}}^d\times \mathcal {S}^d\times {\mathbb {R}},$ that satisfies

$$\begin{aligned} {\left\{ \begin{array}{ll} h(\Delta _i \bar{u}, \bar{\theta }, i) \ge \bar{k} \\ \sum \nolimits _{j} \bar{\theta }^j \alpha ^*_i (\Delta _j \bar{u}, \bar{\theta },j) = 0 \end{array}\right. } \end{aligned}$$

(11)

for $i=1,\ldots ,d$, with equality in the first equation for all indices,  i,  such that $\bar{\theta }^i>0$.

2.4 Potential MFGs

In a potential MFG, the Hamiltonian takes the form

$$\begin{aligned} h(\nabla _i u, \theta , i) = \tilde{h}(\nabla _i u,i) + f(\theta ,i), \end{aligned}$$

where $\tilde{h}: {\mathbb {R}}^d \times I_d \rightarrow {\mathbb {R}}$, $f:{\mathbb {R}}^d \times I_d \rightarrow {\mathbb {R}}$ and f is the gradient of a convex function, $F:{\mathbb {R}}^d \rightarrow {\mathbb {R}}$; that is, $f(\theta ,\cdot ) = \nabla _{\theta }F(\theta )$. We define $H:{\mathbb {R}}^d \times {\mathbb {R}}^d \rightarrow {\mathbb {R}}$ as

$$\begin{aligned} H( u, \theta ) = \sum _{i=1}^d \theta ^i \tilde{h}(\nabla _{i} u,i) + F(\theta ). \end{aligned}$$

(12)

Then, (2) can be written in Hamiltonian form as

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t=-D_\theta H(u, \theta )\\ \theta _t=D_u H(u, \theta ). \end{array}\right. } \end{aligned}$$

In particular, H is conserved as follows:

$$\begin{aligned} \frac{d}{dt}H(u,\theta )=0. \end{aligned}$$

In Sect. 4.6, we use this last property as an additional test for our numerical method.

2.5 A Case Study: The Paradigm-Shift Problem

A paradigm shift is a change in a fundamental assumption within a scientific theory. Scientists can simultaneous work in the context of multiple competing theories or problems. Their choice of theoretical grounding is made to maximize recognition (citations, awards, or prizes) and scientific activity (conferences or collaborations, for example). The paradigm-shift problem was formulated as a two-state MFG in [8]. Subsequently, it was studied numerically in [21] and [20] using an N-player approximation and PDE methods. Here, we present the stationary and time-dependent versions of this problem. Later, we use these versions to validate our numerical methods.

We consider the running cost, $c:I_d\times \mathcal {S}^d \times ({\mathbb {R}}_0^+)^2\rightarrow {\mathbb {R}},$ given by

$$\begin{aligned} c(i,\theta ,\mu ) = f(i,\theta ) + c_0(i,\mu ), \text { where } c_0(i,\mu ) = \frac{1}{2} \sum _{j\ne i}^2 \mu ^2_j. \end{aligned}$$

The functions $f=f(i,\theta )$ are productivity functions with constant elasticity of substitution, given by

$$\begin{aligned} {\left\{ \begin{array}{ll} f(1,\theta ) = \left( a_1 (\theta ^1)^r + (1-a_1)(\theta ^2)^r\right) ^{\frac{1}{r}}\\ f(2,\theta ) = \left( a_2 (\theta ^1)^r+ (1-a_2)(\theta ^2)^r\right) ^{\frac{1}{r}} \end{array}\right. } \end{aligned}$$

for $r\ge 0$ and $0\le a_1, a_2\le 1$. The Hamiltonian is

$$\begin{aligned} {\left\{ \begin{array}{ll} h(u,\theta ,1) = f(1,\theta ) - \frac{1}{2}\left( (u^1-u^2)^+\right) ^2,\\ h(u,\theta ,2) = f(2,\theta ) - \frac{1}{2}\left( (u^2-u^1)^+\right) ^2, \end{array}\right. } \end{aligned}$$

and the optimal switching rates are

$$\begin{aligned} \alpha _2^*(u,\theta , 1)&= (u^1-u^2)^+, \quad \alpha _1^*(u,\theta , 1) = -(u^1-u^2)^+,\\ \alpha _1^*(u,\theta , 2)&= (u^2-u^1)^+, \quad \alpha _2^*(u,\theta , 2) = -(u^2-u^1)^+. \end{aligned}$$

For illustration, we examine the case where $a_1=1$, $a_2=0$, and $r=1$ in the productivity functions above. In this case, $f=\nabla _\theta F(\theta )$ with

$$\begin{aligned} F(\theta )=\frac{(\theta ^1)^2+(\theta ^2)^2}{2}. \end{aligned}$$

Moreover, the game is potential with

$$\begin{aligned} H(u, \theta )=- \frac{1}{2}\left( (u^1-u^2)^+\right) ^2\theta ^1- \frac{1}{2}\left( (u^2-u^1)^+\right) ^2\theta ^2 +F(\theta ). \end{aligned}$$

Furthermore, $(\bar{\theta }, \bar{u},k)$ is a stationary solution if it solves

$$\begin{aligned} {\left\{ \begin{array}{ll} {\theta ^1}-\frac{1}{2}((u^1-u^2)^+)^2=k\\ {\theta ^2}-\frac{1}{2}((u^2-u^1)^+)^2=k, \end{array}\right. } \end{aligned}$$

(13)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} -\theta ^1(u^1-u^2)^+ + \theta ^2 (u^2-u^1)^+=0\\ \theta ^1(u^1-u^2)^+ - \theta ^2 (u^2-u^1)^+=0. \end{array}\right. } \end{aligned}$$

(14)

Since $\theta ^1+\theta ^2=1$, and using the symmetry of (13)–(14), we conclude that

$$\begin{aligned} (\bar{\theta }, \bar{u}, k) = \left( \left( \frac{1}{2},\frac{1}{2}\right) ,(p,p), \frac{1}{2} \right) , \quad p \in {\mathbb {R}}. \end{aligned}$$

(15)

The time-dependent paradigm-shift problem is determined by

$$\begin{aligned} {\left\{ \begin{array}{ll} u^1_t=-{\theta ^1}+\frac{1}{2}((u^1-u^2)^+)^2\\ u^2_t=-{\theta ^2}+\frac{1}{2}((u^2-u^1)^+)^2, \end{array}\right. } \end{aligned}$$

(16)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} \theta ^1_t=-\theta ^1(u^1-u^2)^+ + \theta ^2 (u^2-u^1)^+\\ \theta ^2_t=\theta ^1(u^1-u^2)^+ - \theta ^2 (u^2-u^1)^+, \end{array}\right. } \end{aligned}$$

(17)

together with initial-terminal conditions

$$\begin{aligned} \theta ^i(0) = \theta _0, \text { and } u^i(T) = u_T^i \end{aligned}$$

for $i=1,2$, $\theta _0\in \mathcal {S}^2$, and $u_T\in {\mathbb {R}}^2$.

3 Stationary Problems

To approximate the solutions of (10), we introduce a flow closely related to (5). This flow is the analog for finite-state problems of the one considered in [6]. The monotonicity in Assumption 2 gives the contraction property. Then, we construct a numerical algorithm using a Euler step combined with a projection step to ensure that $\theta$ remains a probability. Finally, we test our algorithm in the paradigm-shift model.

3.1 Monotone Approximation

To preserve the mass of $\theta$, we introduce the following modification of (5):

$$\begin{aligned} {\left\{ \begin{array}{ll} u_s^i = \sum \nolimits _{j} \theta ^j \alpha ^*_i(\Delta _j u,\theta ,j) \\ \theta _s^i = -h(\Delta _i u,\theta ,i)+k(s), \end{array}\right. } \end{aligned}$$

(18)

where $k:{\mathbb {R}}_0^+\rightarrow {\mathbb {R}}$ is such that $\sum _{i=1}^d \theta ^i(s) = 1$ for every $s\ge 0$. For this condition to hold, we need $\sum _{i=1}^d \theta _s^i=0$. Therefore,

$$\begin{aligned} k(s) = \frac{1}{d} \sum _{i=1}^d h(\Delta _i u,\theta ,i). \end{aligned}$$

(19)

Proposition 1

Suppose that Assumptions 1–2 hold. Let $(u,\theta )$ and $(\tilde{u}, \tilde{\theta })$ solve (18)–(19). Assume that $\sum _i \theta ^i(0)= \sum _i \tilde{\theta }^i(0)=1$ and that $\theta (s), \tilde{\theta }(s)\ge 0$. Then,

$$\begin{aligned}&\frac{d}{ds} \left( \Vert (u-\tilde{u}) \Vert ^2 + \Vert \theta -\tilde{\theta }\Vert ^2 \right) \\&\quad \le -\gamma \Vert (\theta - \tilde{\theta })(s)\Vert ^2 - \sum _{i=1}^d \gamma _i(\theta ^i+\tilde{\theta }^i)(s) \Vert (\Delta _i u- \Delta _i \tilde{u})(s)\Vert ^2. \end{aligned}$$

Proof

We begin with the identity

$$\begin{aligned}&\frac{1}{2} \frac{d}{ds} \sum _{i=1}^d \left[ (u^i-\tilde{u}^i)^2 + (\theta ^i- \tilde{\theta }^i)^2 \right] \\&\qquad = \sum _{i=1}^d (u^i-\tilde{u}^i) (u^i-\tilde{u}^i)_s + (\theta ^i-\tilde{\theta }^i) (\theta ^i-\tilde{\theta }^i)_s. \end{aligned}$$

Using (18) in the previous equality, we obtain

$$\begin{aligned}&\frac{1}{2} \frac{d}{ds} \sum _{i=1}^d \left[ (u^i-\tilde{u}^i)^2 + (\theta ^i- \tilde{\theta }^i)^2 \right] \\&\quad = \sum _{i=1}^d (u^i-\tilde{u}^i) \left( \sum _j \theta ^j \alpha ^*(\Delta _j u,\theta ,j) - \sum _j \tilde{\theta }^j \alpha ^*(\Delta _j \tilde{u}, \tilde{\theta },j) \right) \\&\qquad + \sum _{i=1}^d (\theta ^i-\tilde{\theta }^i) \left( - h(\Delta _i u, \theta ,i) + k +h(\Delta _i \tilde{u}, \tilde{\theta },i) -\tilde{k}\right) \\&\quad \le -\gamma \Vert (\theta - \tilde{\theta })(s)\Vert ^2 - \sum _{i=1}^d \gamma _i(\theta ^i+\tilde{\theta }^i)(s) \Vert (\Delta _i u- \Delta _i \tilde{u})(s)\Vert ^2, \end{aligned}$$

by Remark 1. $\square$

3.2 Numerical Algorithm

Let A be given by (4). Due to the monotonicity, for small $\mu$, the Euler map,

$$\begin{aligned} E_\mu \left[ \begin{array}{c} \theta \\ u \end{array} \right] = \left[ \begin{array}{c} \theta \\ u \end{array} \right] -\mu A\left[ \begin{array}{c} \theta \\ u \end{array} \right] , \end{aligned}$$

is a contraction, provided that $\theta$ is nonnegative; that is, the case when $\theta$ is a probability vector. However, $E_\mu$ may not keep $\theta$ non-negative and, in general, $E_\mu$ also does not preserve the mass. Thus, we introduce the following projection operator on $\mathcal {S}^d\times {\mathbb {R}}^d$:

$$\begin{aligned} P \left[ \begin{array}{c} \theta \\ u \end{array} \right] = \left[ \begin{array}{c} \varpi (\theta )\\ u \end{array} \right] , \end{aligned}$$

where $\varpi (\theta )_i=(\theta ^i+\xi )^+$ and $\xi$ is such that

$$\begin{aligned} \sum _i \varpi (\theta )_i=1. \end{aligned}$$

Clearly, P is a contraction because it is a projection on a convex set. Finally, to approximate weak solutions of (10), that is solutions (11), we consider the iterative map

$$\begin{aligned} \left[ \begin{array}{c} \theta _{n+1}\\ u_{n+1} \end{array} \right] = P E_\mu \left[ \begin{array}{c} \theta _{n}\\ u_{n} \end{array} \right] . \end{aligned}$$

(20)

We have the following result:

Proposition 2

Let $(\bar{\theta }, \bar{u}, \bar{k})$ solve (11). Then, $(\bar{\theta }, \bar{u} )$ is a fixed point for (20). Moreover, for any fixed point of (20), there exists $\bar{k}$ such that $(\bar{\theta }, \bar{u}, \bar{k})$ solves (11).

Finally, if $\mu$ is small enough and (11) has a weak solution, $(\bar{\theta }, \bar{u}, \bar{k})$, with $\bar{\theta }>0$, then the iterates in (20) are bounded and converge to $(\bar{\theta }, \bar{u} )$. Moreover, the solution is unique.

Proof

Clearly, a solution of (11) is a fixed point for (20). Conversely, let $(\bar{\theta }, \bar{u} )$ be a fixed point for (20). Then,

$$\begin{aligned} \bar{u}^i=\bar{u}^i+\mu \sum _{j} \bar{\theta }^j \alpha ^*_i (\Delta _j \bar{u}, \bar{\theta },j). \end{aligned}$$

Hence,

$$\begin{aligned} \sum _{j} \bar{\theta }^j \alpha ^*_i (\Delta _j \bar{u}, \bar{\theta },j)=0. \end{aligned}$$

Additionally, we have

$$\begin{aligned} \bar{\theta }^i=\left( \bar{\theta }^i- \mu h(\Delta _i \bar{u}, \bar{\theta }, i) +\xi \right) ^+ \end{aligned}$$

for some $\xi$. Thus, for $\bar{k}=\frac{\xi }{\mu }$,

$$\begin{aligned} h(\Delta _i \bar{u}, \bar{\theta }, i) \ge \bar{k}, \end{aligned}$$

with equality when $\bar{\theta }^i>0$.

If $\mu$ is small enough, $E_\mu$ is a contraction because A is a monotone Lipschitz map. Thus, if there is a solution of (11), the iterates in (20) are bounded. Then, the convergence follows from the monotonicity of $E_\mu$ and the strict contraction given by $\bar{\theta }>0$. $\square$

Remark 2

Concerning the convergence rate and the choice of the parameter $\mu$ in the preceding theorem, we observe the following. The operator A is locally Lipschitz. Thus, given bound on the initial conditions, we can assume the Lipschitz constant to be a number, $L>0$. By selecting

$$\begin{aligned} 0< \mu < \frac{2}{L}, \end{aligned}$$

we get that $E_{\mu }$ is a contraction and we may assume that the initial bound on data is preserved (for example, by looking at the norm of the difference between the iterates and a given stationary solution). If there is a strictly positive stationary solution, the convergence is exponential because, for u and $\tilde{u}$ with mean 0, we have

$$\begin{aligned}&\gamma \Vert (\theta - \tilde{\theta })(s)\Vert ^2 + \sum _{i=1}^d \gamma _i(\theta ^i+\tilde{\theta }^i)(s) \Vert (\Delta _i u- \Delta _i \tilde{u})(s)\Vert ^2 \\&\qquad \ge \, C \sum _{i=1}^d \left[ (u^i-\tilde{u}^i)^2 + (\theta ^i- \tilde{\theta }^i)^2 \right] . \end{aligned}$$

The constant, however, depends on the lower bounds on the stationary solution and thus, we do not have a direct estimate on the rate of convergence.

3.3 Numerical Examples

To illustrate our algorithm, we consider the paradigm-shift problem. The monotone flow in (18) is

$$\begin{aligned} {\left\{ \begin{array}{ll} u^1_s = -\theta ^1(u^1-u^2)^+ +\theta ^2 (u^2-u^1)^+\\ u^2_s = \theta ^1(u^1-u^2)^+ -\theta ^2 (u^2-u^1)^+, \end{array}\right. } \end{aligned}$$

(21)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} \theta ^1_s = -\theta ^1 + \frac{1}{2}((u^1-u^2)^+)^2+k(s)\\ \theta ^2_s = -\theta ^2 + \frac{1}{2}((u^2-u^1)^+)^2+k(s). \end{array}\right. } \end{aligned}$$

(22)

According to (19),

$$\begin{aligned} k(s) = \frac{1}{2} \left( \theta ^1 - \frac{1}{2}((u^1-u^2)^+)^2 + \theta ^2 - \frac{1}{2}((u^2-u^1)^+)^2 \right) . \end{aligned}$$

Now, we present the numerical results for this model using the iterative method in (20). We set $s\in [0,8]$ and discretize this interval into $N=300$ subintervals. First, we consider the following initial conditions:

$$\begin{aligned} u^1_0=4, \, u^2_0=2 \text { and } \theta ^1_0= 0.8, \, \theta ^2_0=0.2. \end{aligned}$$

The convergence towards the stationary solution is illustrated in Fig. 1a, b for $\theta$ and u. The behavior of k is shown in Fig. 2a. In Fig. 2b, we illustrate the contraction of the norm

$$\begin{aligned} \left\| \left[ \begin{array}{c} \theta (s)\\ u(s) \end{array} \right] - \left[ \begin{array}{c} \bar{\theta }\\ \bar{u} \end{array} \right] \right\| , \end{aligned}$$

Fig. 1

Evolution of $\theta$ and u with the monotone flow, for $s \in [0,8]$. The quantities corresponding to the state 1 and 2 are depicted in blue and orange, respectively. a Convergence of $\theta ^i$. b Convergence of $u^i$ (Color figure online)

Fig. 2

Evolution of k and contraction of the norm, $\Vert (\theta ,u)-(\bar{\theta },\bar{u})\Vert$. a Evolution of k. b Contraction of the norm

where $(\bar{\theta }, \bar{u})$ is the stationary solution in (15). Next, we consider the case in which the iterates of $E_\mu$ do not preserve positivity. In Fig. 3, we compare the evolution of $\theta$ by iterating $E_\mu$, without the projection and using (20). In the first case, $\theta$ may not remain positive, although, in this example, convergence holds. In Fig. 3, we plot the evolution through (20) of $\theta$ towards the analytical solution $\theta ^1=\theta ^2=0.5$. As expected from its construction, $\theta$ is always non-negative and a probability. The contraction of the norm is similar to the previous case, see Fig. 4.

Fig. 3

Comparison between the iterates of $E_\mu$ and $PE_\mu$ for $\theta ^1_0=0.8$, $\theta ^2_0=0.2$, $u^1_0=5$, and $u^2_0=2$. The quantities corresponding to the state 1 and 2 are depicted in blue and orange, respectively. a Non positivity of the distribution using $E_\mu$. b Convergence using (20) while preserving the positivity of $\theta$ (Color figure online)

Fig. 4

Evolution of the norm, $\Vert (\theta ,u)-(\bar{\theta },\bar{u})\Vert$, using the projection method

4 Initial-Terminal Value Problems

The initial-terminal conditions in (3) are the key difficulty in the design of numerical methods for the time-dependent MFG, (2). Here, we extend the strategy from the previous section to handle initial-terminal conditions. We start with an arbitrary pair of functions, $(u(t,0),\theta (t,0))$, that satisfies (3) and build a family $(u(t,s),\theta (t,s))$, $s\ge 0$, that converges to a solution of (2)–(3) as $s\rightarrow \infty$, while preserving the boundary conditions for all $s\ge 0$.

4.1 Representation of Functionals in $H^1$

We begin by discussing the representation of linear functionals in $H^1$. Consider the Hilbert space, $H^1_T=\{\phi \in H^1([0,T], {\mathbb {R}}^d): \phi (T)=0\}$. For $\theta , u\in H^1([0,T], {\mathbb {R}}^d)$, we consider the variational problem

$$\begin{aligned} \min _{\phi \in H^1_T} \int _0^T \left[ \frac{1}{2}(|\phi |^2 + |\dot{\phi }|^2) + \phi \cdot \left( \theta _t - \sum _j \theta ^j \alpha ^*(\Delta _j u, \theta ,j) \right) \right] dt. \end{aligned}$$

(23)

A minimizer, $\phi \in H^1_T$, of the preceding functional represents the linear functional

$$\begin{aligned} \eta \mapsto -\int _0^T\eta \cdot \left( \theta _t - \sum _j \theta ^j \alpha ^*(\Delta _j u, \theta ,j) \right) dt \end{aligned}$$

for $\eta \in H^1_T$, as an inner product in $H^1_T$; that is,

$$\begin{aligned} \int _0^T \left( \eta \cdot \phi + \dot{\eta } \cdot \dot{\phi } \right) dt = - \int _0^T \eta \cdot \left( \theta _t - \sum _j \theta ^j \alpha ^*(\Delta _j u, \theta ,j) \right) dt \end{aligned}$$

for $\phi ,\eta \in H^1_T$. The last identity is simply the weak form of the Euler–Lagrange equation for (23),

$$\begin{aligned} - \ddot{\phi }+ \phi = -\theta _t + \sum _j \theta ^j \alpha ^*(\Delta _j u, \theta ,j), \end{aligned}$$

(24)

whose boundary conditions are $\phi (T)=0$ and $\dot{\phi }(0)=0$. For $\theta , u\in H^1([0,T], {\mathbb {R}}^d)$, we define

$$\begin{aligned} \Phi (\theta , u, t)=\phi (t). \end{aligned}$$

(25)

Next, let $H^1_I=\{\psi \in H^1([0,T], {\mathbb {R}}^d): \psi (0)=0\}$. For $\theta , u\in H^1([0,T], {\mathbb {R}}^d)$, we consider the variational problem

$$\begin{aligned} \min _{\psi \in H^1_I} \int _0^T \left[ \frac{1}{2}(|\psi |^2 + |\dot{\psi }|^2) + \psi \cdot \left( u_t + h(\Delta _i u, \theta ,i) \right) \right] dt. \end{aligned}$$

(26)

The Euler–Lagrange equation for the preceding problem is

$$\begin{aligned} - \ddot{\psi }+ \psi = - u_t - h(\Delta _i u, \theta ,i), \end{aligned}$$

(27)

with the boundary conditions $\psi (0)=0$ and $\dot{\psi }(T)=0$. Moreover, if $\psi \in H^1_I$ minimizes the functional in (26), we have

$$\begin{aligned} \int _0^T \left( \eta \cdot \psi + \dot{\eta } \cdot \dot{\psi }\right) dt = \int _0^T \eta \cdot \left( - u_t - h(\Delta _i u, \theta ,i) \right) dt \end{aligned}$$

for $\eta , \psi \in H^1_I$. For $\theta , u\in H^1([0,T], {\mathbb {R}}^d)$, we define

$$\begin{aligned} \Psi (\theta , u, t)=\psi (t). \end{aligned}$$

(28)

4.2 Monotone Deformation Flow

Next, we introduce the monotone deformation flow,

$$\begin{aligned} {\left\{ \begin{array}{ll} u_s^i(t,s) = \Phi ^i(\theta (\cdot , s), u(\cdot , s), t)\\ \theta _s^i(t,s) = \Psi ^i(\theta (\cdot , s), u(\cdot , s), t), \end{array}\right. } \end{aligned}$$

(29)

where $\Phi$ and $\Psi$ are given in (25) and (28). As we show in the next proposition, for smooth enough solutions, the previous flow is a contraction in $H^1$. Moreover, if $(\theta , u)$ solve (2)–(3), we have

$$\begin{aligned} \Phi (\theta , u, t)=\Psi (\theta , u, t)=0. \end{aligned}$$

Hence, solutions of (2)–(3) are fixed points for (29).

Before stating the contraction property, we recall that the $H^1$-norm of a pair of functions is given by

$$\begin{aligned} \Vert (v, \eta )\Vert _{H^1}^2 = \int _0^T \left( |v|^2+|\dot{v}|^2+|\eta |^2+|\dot{\eta }|^2\right) dt \end{aligned}$$

for $v,\eta :[0,T]\rightarrow {\mathbb {R}}^d$.

Proposition 3

Let $(u, \theta )$ and $(\tilde{u}, \tilde{\theta })$ be $C^2$ solutions of (29). Suppose that $\theta , \tilde{\theta } \ge 0$. Then,

$$\begin{aligned} \frac{d}{ds}\Vert (u, \theta )-(\tilde{u}, \tilde{\theta })\Vert ^2_{H^1} \le 0, \end{aligned}$$

with strict inequality if $(u, \theta )\ne (\tilde{u}, \tilde{\theta })$.

Proof

We have

$$\begin{aligned}&\frac{1}{2} \frac{d}{ds} \int _0^T \left[ (u-\tilde{u})^2 + (u-\tilde{u})^2_t + (\theta -\tilde{\theta })^2 + (\theta - \tilde{\theta })^2_t \right] dt\\&\quad = \int _0^T \left[ (u-\tilde{u}) (u-\tilde{u})_s + (u-\tilde{u})_t (u-\tilde{u})_{ts}\right] dt\\&\qquad + \int _0^T \left[ (\theta -\tilde{\theta })(\theta -\tilde{\theta })_s + (\theta -\tilde{\theta })_t (\theta -\tilde{\theta })_{ts}\right] dt. \end{aligned}$$

Using (29), the term in the right-hand side of the previous equality becomes

$$\begin{aligned}&\int _0^T \left[ (u-\tilde{u}) (\phi -\tilde{\phi }) + (u-\tilde{u})_t (\phi -\tilde{\phi })_t \right] dt\\&\qquad + \int _0^T \left[ (\theta -\tilde{\theta }) (\psi - \tilde{\psi }) + (\theta -\tilde{\theta })_t(\psi -\tilde{\psi })_t\right] dt\\&\quad = \int _0^T (u-\tilde{u}) (\phi -\tilde{\phi }) dt + \left. \left[ (u-\tilde{u})(\phi -\tilde{\phi })_t \right] \right| _0^T \\&\qquad - \int _0^T (u-\tilde{u})(\phi - \tilde{\phi })_{tt} dt \\&\qquad + \int _0^T (\theta -\tilde{\theta }) (\psi -\tilde{\psi })dt + \left. \left[ (\theta -\tilde{\theta })(\psi -\tilde{\psi })_t \right] \right| _0^T \\&\qquad - \int _0^T (\theta -\tilde{\theta })(\psi -\tilde{\psi })_{tt} dt, \end{aligned}$$

where we used integration by parts in the last equality. Because $u(T)= \tilde{u}(T)$, $\theta (0) = \tilde{\theta }(0)$, $\phi _t(0) = \tilde{\phi }_t(0)$, $\psi _t(T) = \tilde{\psi }_t(T)$, and using (24) and (27), we obtain

$$\begin{aligned}&\frac{1}{2} \frac{d}{ds} \int _0^T (u-\tilde{u})^2 + (u-\tilde{u})^2_t + (\theta -\tilde{\theta })^2 + (\theta - \tilde{\theta })^2_t \nonumber \\&\quad = \int _0^T (u-\tilde{u}) \left( \sum \theta ^j \alpha ^*(\Delta _j u, \theta , j) - \sum \tilde{\theta } \alpha ^*(\Delta _j \tilde{u}, \tilde{\theta },j) \right) \nonumber \\&\qquad - \int _0^T (\theta - \tilde{\theta }) \left( h(\Delta _i u, \theta ,i) - h(\Delta _i \tilde{u},\tilde{\theta },i ) \right) \nonumber \\&\quad \le \int _0^T -\gamma \Vert (\theta - \tilde{\theta })(t) \Vert ^2 - \sum _{i=1}^d \gamma _i (\theta ^i + \tilde{\theta }^i)(t) \Vert (\Delta _i u - \Delta _i \tilde{u})(t) \Vert ^2 dt, \end{aligned}$$

(30)

due to Remark 1. $\square$

4.3 Monotone Discretization

To build our numerical method, we begin by discretizing (29). We look for a time-discretization of

$$\begin{aligned} A\left[ \begin{array}{c} \theta \\ u \end{array}\right] = \left[ \begin{array}{c} -\theta _t + f(u,\theta )\\ -u_t - h(u,\theta ) \end{array}\right] \end{aligned}$$

that preserves monotonicity, where $f(u,\theta )=\sum _j \tilde{\theta }^j \alpha ^*(\Delta _j \tilde{u}, \tilde{\theta },j)$.

With Hamilton–Jacobi equations, implicit schemes have good stability properties. Because the Hamilton–Jacobi equation in (29) is a terminal value problem, we discretize it using an explicit forward-in-time scheme (hence, implicit backward-in-time scheme). Then, to keep the adjoint structure of A at the discrete level, we are then required to choose an implicit discretization forward in time for the first component of A. Usually, implicit schemes have the disadvantage of requiring the numerical solution of non-linear equations at each time step. Here, we discretize the operator, A,  globally, and we never need to solve implicit equations.

More concretely, we split [0, T] into N intervals of length $\delta t=\frac{T}{N}$. The vectors $\theta _n\in \mathcal {S}^d$ and $u_n\in {\mathbb {R}}^d$, $0\le n\le N$ approximate $\theta$ and u at time $\frac{nT}{N}$. We set $\mathcal {M}_N=(\mathcal {S}^d\times {\mathbb {R}}^{d})^{N+1}$ and define

$$\begin{aligned} A^N\left[ \begin{array}{c} \theta \\ u \end{array}\right] _n = \left[ \begin{array}{c} -\frac{\theta _{n+1}^i-\theta _n^i}{\delta t}+f(u_{n+1}^i,\theta _{n+1}^i) + k_n\\ -\frac{u_{n+1}^i-u_n^i}{\delta t}-h(u_{n}^i,\theta _{n}^i) \end{array}\right] , \end{aligned}$$

(31)

where

$$\begin{aligned} k_n(s) = -\frac{1}{d} \sum _{i=1}^d \left( -\frac{\delta \theta ^i_n}{\delta t} + f(u_{n+1}^i,\theta _{n+1}^i)\right) \end{aligned}$$

and $\delta \theta ^i_n = \theta _{n+1}^i-\theta _n^i$. Next, we show that $A^N$ is a monotone operator in the convex subset of vectors in $\mathcal {M}$ that satisfy the initial-terminal conditions in (3). We denote by $\langle \cdot , \cdot \rangle$, the duality pairing in $(\mathcal {S}^d\times {\mathbb {R}}^d)^{N+1}$. More precisely, for $(\theta , u), (\tilde{\theta }, \tilde{u})\in (\mathcal {S}^d\times {\mathbb {R}}^d)^{N+1}$

$$\begin{aligned} \left\langle \left[ \begin{array}{c} \theta \\ u \end{array} \right] , \left[ \begin{array}{c} \tilde{\theta }\\ \tilde{u} \end{array} \right] \right\rangle =\sum _{k=0}^N \theta ^k\cdot \tilde{\theta }^k+u^k\cdot \tilde{u}^k. \end{aligned}$$

Proposition 4

$A^N$ is monotone in the convex subset $\mathcal {M}_N$ of all $(\theta , u)\in (\mathcal {S}^d\times {\mathbb {R}}^d)^{N+1}$ such that $\theta _0=\bar{\theta }_0$ and $u_{N}=\bar{u}_T$. Moreover, we have the inequality

$$\begin{aligned}&\left\langle A^N\left[ \begin{array}{c} \theta \\ u \end{array}\right] -A^N\left[ \begin{array}{c} \tilde{\theta }\\ \tilde{u} \end{array}\right] ,\left[ \begin{array}{c} \theta \\ u \end{array}\right] -\left[ \begin{array}{c} \tilde{\theta }\\ \tilde{u} \end{array}\right] \right\rangle \\&\quad \le \sum _{n=1}^{N-1} \left( -\gamma \Vert (\theta - \tilde{\theta })(t) \Vert ^2 - \sum _{i=1}^d \gamma _i (\theta ^i + \tilde{\theta }^i)(t) \Vert (\Delta _i u - \Delta _i \tilde{u})(t) \Vert ^2 \right) . \end{aligned}$$

Proof

We begin by computing

$$\begin{aligned}&\left\langle A^N\left[ \begin{array}{c} \theta \\ u \end{array}\right] -A^N\left[ \begin{array}{c} \tilde{\theta }\\ \tilde{u} \end{array}\right] ,\left[ \begin{array}{c} \theta \\ u \end{array}\right] -\left[ \begin{array}{c} \tilde{\theta }\\ \tilde{u} \end{array}\right] \right\rangle \\&\quad =\sum _{n=0}^{N-1} \Bigg [(\theta _n - \tilde{\theta }_n) \left( -\frac{u_{n+1}- u_{n}}{\delta t} - h(u_{n},\theta _{n}) + \frac{\tilde{u}_{n+1}-\tilde{u}_{n}}{\delta t} + h(\tilde{u}_{n},\tilde{\theta }_{n}) \right) \\&\qquad + (u_{n+1}-\tilde{u}_{n+1}) \Big ( -\frac{\theta _{n+1}-\theta _{n}}{\delta t} + f(u_{n+1},\theta _{n+1}) + k_{n}\\&\qquad + \frac{\tilde{\theta }_{n+1}-\tilde{\theta }_{n}}{\delta t} - f(\tilde{u}_{n+1},\tilde{\theta }_{n+1}) - \tilde{k}_n \Big )\Bigg ]. \end{aligned}$$

With the sums developed and the indices relabeled, the preceding expression becomes

$$\begin{aligned}&\sum _{n=1}^{N-1}\Bigg [ (\theta _n - \tilde{\theta }_n) \left( -\frac{u_{n+1}- u_{n}}{\delta t} - h(u_{n},\theta _{n}) + \frac{\tilde{u}_{n+1}-\tilde{u}_{n}}{\delta t} + h(\tilde{u}_{n},\tilde{\theta }_{n}) \right) \\&\qquad + (\theta _0-\tilde{\theta }_0) \left( - \frac{u_1-u_0}{\delta t} - h(u_0,\theta _0) + \frac{\tilde{u}_1 -\tilde{u}_0}{\delta t} +h(\tilde{u}_0,\theta _0) \right) \Bigg ]\\&\qquad +\sum _{n=1}^{N-1} \Bigg [(u_n-\tilde{u}_n) \left( -\frac{\theta _{n}-\theta _{n-1}}{\delta t} + f(u_{n},\theta _{n}) + \frac{\tilde{\theta }_{n}-\tilde{\theta }_{n-1}}{\delta t} - f(\tilde{u}_{n},\tilde{\theta }_{n}) \right) \\&\qquad +(u_{N}-\tilde{u}_{N})\left( -\frac{\theta _N-\theta _{N-1}}{\delta t} +f(u_N,\theta _N) + \frac{\tilde{\theta }_N-\tilde{\theta }_{N-1}}{\delta t}- f(\tilde{u}_N,\tilde{\theta }_N) \right) \Bigg ]. \end{aligned}$$

The second and last lines above are zero since $\theta _0=\tilde{\theta }_0=\bar{\theta }_0$ and $u_{N}=\tilde{u}_{N}=\bar{u}_T$. Using Remark 1, we obtain

$$\begin{aligned}&\left\langle A\left[ \begin{array}{c} \theta \\ u \end{array}\right] -A\left[ \begin{array}{c} \tilde{\theta }\\ \tilde{u} \end{array}\right] ,\left[ \begin{array}{c} \theta \\ u \end{array}\right] -\left[ \begin{array}{c} \tilde{\theta }\\ \tilde{u} \end{array}\right] \right\rangle \\&\quad \le \sum _{n=1}^{N-1} \left( -\gamma \Vert (\theta - \tilde{\theta })(t) \Vert ^2 - \sum _{i=1}^d \gamma _i (\theta ^i + \tilde{\theta }^i)(t) \Vert (\Delta _i u - \Delta _i \tilde{u})(t) \Vert ^2 \right) \\&\qquad - \sum _{n=1}^{N-1} (\theta _n-\tilde{\theta }_n) \left( \frac{u_{n+1}-\tilde{u}_{n+1}}{\delta t} - \frac{u_n-\tilde{u}_n}{\delta t} \right) \\&\qquad - \sum _{n=1}^{N-1} (u_n-\tilde{u}_n) \left( \frac{\theta _n -\tilde{\theta }_n}{\delta t}-\frac{\theta _{n-1}-\tilde{\theta }_{n-1}}{\delta t}\right) . \end{aligned}$$

We now show that the last two lines add to zero. Let $a_n = \theta _n-\tilde{\theta }_n$ and $b_n = u_n-\tilde{u}_n$. Accordingly, we have

$$\begin{aligned}&-\frac{1}{\delta t} \sum _{n=1}^{N-1} a_n(b_{n+1}-b_n) - \frac{1}{\delta t} \sum _{n=1}^{N-1} b_n (a_n-a_{n-1}) \\&\quad =- \frac{1}{\delta t}(b_N a_N - b_1 a_1)+\frac{1}{\delta t} \sum _{n=1}^{N-1} b_{n+1}(a_{n+1}-a_n) - \frac{1}{\delta t} \sum _{n=0}^{N-2} b_{n+1} (a_{n+1}-a_n)\\&\quad =\frac{1}{\delta t}(b_1a_0-b_Na_{N-1}) = 0, \end{aligned}$$

where we summed the first term by parts and relabeled the index, n,  in the last term of the first line. The last equality follows from the assumption in the statements, $a_0=\theta _0-\tilde{\theta }_0 = 0$ and $b_N = u_N-\tilde{u}_N = 0$. $\square$

Using the techniques in [6], we prove the convergence of the solutions of the discretized problem as $\delta t \rightarrow 0$. As usual, we discretize the time interval, [0, T], into $N+1$ equispaced points.

Proposition 5

Let $(\theta ^N, u^N)\in {\mathcal {M}}_N$ be a solution of

$$\begin{aligned} A^N\left[ \begin{array}{c} \theta ^N\\ u^N \end{array} \right] _n = \left[ \begin{array}{c} 0\\ 0 \end{array} \right] \end{aligned}$$

satisfying the initial-terminal conditions in (3). Suppose that $u^N$ is uniformly bounded. Consider the step functions $\bar{u}^N$ and $\bar{\theta }^N$ taking the values $\bar{u}^{N i}_n \in {\mathbb {R}}$ and $\bar{\theta }_n^{N i} \in \mathcal {S}$ in $[\frac{(n-1)T}{N},\frac{n T}{N}]$, with $0\le n \le N$, for $i\in I_d$, respectively. Then, extracting a subsequence if necessary, $\bar{u}^{N i} \rightharpoonup \bar{u}^i$ and $\bar{\theta }^{N i} \rightharpoonup \theta ^i$ weakly-* in $L^\infty$ for $i \in I_d$. Furthermore, $(\bar{u}, \bar{\theta })$ is a weak solution of (2).

Proof

Because $u^N$ is bounded by hypothesis and $\theta ^N$ is bounded since it is a probability measure, the weak-* convergence in $L^\infty$ is immediate. Hence, there exist $\bar{u}^i \in L^\infty ([0,T])$ and $\theta ^i \in L^\infty ([0,T])$ as claimed.

Let $\tilde{u}^{i}, \tilde{\theta }^{i} \in C^{\infty }([0,T])$, with $\tilde{\theta }^{i} \ge 0$ for all $i\in I_d$, and $\sum _{i \in I_d} \tilde{\theta }^i =1$. Suppose further that $\tilde{u}^{i}, \tilde{\theta }^{i}$ satisfy the boundary conditions in (3). Let $\tilde{u}_n^{N} = \tilde{u} \left( \frac{n}{N}T \right)$, $\tilde{\theta }_n^{N} = \tilde{\theta } \left( \frac{n}{N}T \right)$ be the vectors whose components are $\tilde{u}_n^{N i}$ and $\tilde{\theta }_n^{N i}$, respectively. By the monotonicity of $A^N$, we have

$$\begin{aligned} 0&\le \left\langle A^N\left[ \begin{array}{c} \tilde{\theta }^N \\ \tilde{u}^N \end{array} \right] , \left[ \begin{array}{c} \tilde{\theta }^N\\ \tilde{u}^N \end{array}\right] -\left[ \begin{array}{c} \theta ^N\\ u^N \end{array} \right] \right\rangle \\&= O \left( \frac{1}{N} \right) +\left\langle A \left[ \begin{array}{c} \tilde{\theta }\\ \tilde{u} \end{array}\right] , \left[ \begin{array}{c} \tilde{\theta }\\ \tilde{u} \end{array} \right] - \left[ \begin{array}{c} \bar{\theta }^N\\ \bar{u}^N \end{array} \right] \right\rangle , \end{aligned}$$

and taking the limit $N\rightarrow \infty$ gives the result. $\square$

4.4 Monotone Discretization for the $H^1$ Projections

Next, we discuss the representation of linear functionals for the discrete problem. For that, proceeding as in Sect. 4.1, we compute the optimality conditions of the discretized versions of (23) and (26).

Fix $(u,\theta )\in \mathcal {M}_N$ and consider the following discrete analog to (23):

$$\begin{aligned} \min _{\phi \in \tilde{H}^1_T} \delta t \sum _{n=1}^{N} \frac{1}{2} \left( \phi _n^2 + \left( \frac{\delta \phi _{n-1}}{\delta t}\right) ^2\right) + \phi _n \left( \frac{\delta \theta _{n-1}}{\delta t} - f(u_{n},\theta _{n}) \right) , \end{aligned}$$

where $\delta g_n = g_{n+1}-g_n$, and $\tilde{H}^1_T =\{\phi =(\phi _0, \ldots , \phi _N)\in ({\mathbb {R}}^d)^{(N+1)}:\phi _N=0\}$. The corresponding optimality conditions (the discrete Euler–Lagrange equation) is

$$\begin{aligned} -\frac{\delta (\delta \phi _{n-1})}{(\delta t)^2} + \phi _n = -\frac{\delta \theta _{n-1}}{\delta t} + f(u_{n},\theta _{n}), \end{aligned}$$

(32)

for $n=1,\ldots ,N-1$, coupled with the boundary conditions $\phi _N = 0$ and $\phi _{1}=\phi _0$.

A minimizer of the problem above represents the following discrete linear functional

$$\begin{aligned} \eta \mapsto - \sum _{n=1}^N \eta _n \cdot \left( \frac{\delta \phi _{n-1}}{\delta t} - f(u_n,\theta _n) \right) \delta t \end{aligned}$$

as an inner product in $\tilde{H}^1_T$

$$\begin{aligned} \sum _{n=1}^N \left( \eta _n \cdot \phi _n \delta t + \frac{1}{\delta t}\delta \eta _{n-1}\cdot \delta \phi _{n-1} \right) = - \sum _{n=1}^N\eta _n \cdot \left( \frac{\delta \phi _{n-1}}{\delta t} - f(u_n,\theta _n) \right) \delta t. \end{aligned}$$

For $(\theta _n,u_n) \in \mathcal {M}_N$, we define

$$\begin{aligned} \Phi (\theta _n,u_n) = \phi _n. \end{aligned}$$

(33)

We now examine a second discrete variational problem corresponding to (26). For $(u,\theta )\in \mathcal {M}_N$, we consider

$$\begin{aligned} \min _{\psi \in \tilde{H}^1_I} \delta t \sum _{n=0}^{N-1} \frac{1}{2} \left( \psi _n^2 + \left( \frac{\delta \psi _n}{\delta t}\right) ^2\right) + \psi _n \left( \frac{\delta u_n}{\delta t} + h(u_n, \theta _n) \right) , \end{aligned}$$

where $\tilde{H}^1_I =\{\psi =(\psi _0, \ldots , \psi _N)\in ({\mathbb {R}}^d)^{(N+1)}:\psi _0=0\}$.

The discrete Euler–Lagrange equation is

$$\begin{aligned} -\frac{\delta (\delta \psi _{n-1})}{(\delta t)^2} + \psi _n = - \frac{\delta u_n}{\delta t} - h(u_n, \theta _n) \end{aligned}$$

(34)

for $n=1,\ldots ,N-1$, together with the conditions $\psi _0=0$ and $\psi _N=\psi _{N-1}$.

From the Euler–Lagrange equation, we obtain the following representation formula in the Hilbert space $\{\psi \in H_n^1(\{0,\ldots ,N\}): \psi _0 = 0\}$:

$$\begin{aligned} \sum _{n=0}^{N-1} \left( \eta \cdot \psi + \delta \eta \cdot \delta \psi \right) \delta t = \sum _{0}^N \eta \cdot \left( - \frac{\delta u_n}{\delta t}-h(u_n,\theta _n) \right) \delta t. \end{aligned}$$

Finally, we define

$$\begin{aligned} \Psi (\theta _n,u_n) = \psi _n, \end{aligned}$$

(35)

for $(u,\theta )\in \mathcal {M}_N$.

Proposition 6

Let $\Phi$ and $\Psi$ be given by (33) and (35). Consider the following operator:

$$\begin{aligned} Q_A\left[ \begin{array}{c} \theta \\ u \end{array}\right] = \left[ \begin{array}{c} \Phi \\ \Psi \end{array}\right] . \end{aligned}$$

(36)

Let ${\mathcal {M}}_N^{\bar{\theta }_0,\bar{u}_T}$ be the set of all $(\theta , u) \in {\mathcal {M}}_N$ that satisfy the initial condition $\theta _0=\bar{\theta }_0$ and the terminal condition $u_N=\bar{u}_T$. Then, $Q_A$ is monotone with respect to the discrete $H^1_N$ inner product corresponding to the norm

$$\begin{aligned} \Vert (\eta , \nu )\Vert _{H^1_N}^2 = \sum _{n=0}^{N-1} |\eta _n|^2 + |\delta \eta _n|^2 + |\nu _n|^2 + |\delta \nu _n|^2. \end{aligned}$$

(37)

Proof

Let $(u,\theta )\in {\mathcal {M}}_N^{\bar{\theta }_0,\bar{u}_T}$ and $(\tilde{u}, \tilde{\theta })\in {\mathcal {M}}_N^{\bar{\theta }_0,\bar{u}_T}$. Let $\phi , \tilde{\phi }$ and $\psi , \tilde{\psi }$ be given by (33) and (35). We begin by computing

$$\begin{aligned}&\left\langle Q_A\left[ \begin{array}{c} \theta \\ u \end{array}\right] - Q_A\left[ \begin{array}{c} \tilde{\theta }\\ \tilde{u} \end{array}\right] ,\left[ \begin{array}{c} \theta \\ u \end{array}\right] -\left[ \begin{array}{c} \tilde{\theta }\\ \tilde{u} \end{array}\right] \right\rangle _{H^1_N} \nonumber \\&\quad =\sum _{n=0}^{N-1} \Bigg [ (\theta _n-\tilde{\theta }_n)(\psi _n - \tilde{\psi }_n) +\frac{\delta (\theta _n - {\tilde{\theta }}_n)}{\delta t} \frac{\delta (\psi _n - \tilde{\psi }_n)}{\delta t} \nonumber \\&\qquad + (u_n-\tilde{u}_n)(\phi _n-\tilde{\phi }_n) + \frac{\delta (u_n -{\tilde{u}}_n)}{\delta t}\frac{\delta ({\phi }_n-{\tilde{\phi }}_n)}{\delta t} \Bigg ]\nonumber \\&\quad =\sum _{n=0}^{N-1} (\theta _n-\tilde{\theta }_n)(\psi _n - \tilde{\psi }_n) + (u_n-\tilde{u}_n)(\phi _n-\tilde{\phi }_n) \nonumber \\&\qquad +\frac{1}{\delta t}\sum _{n=0}^{N-1}\left( \frac{\theta _{n+1}-\theta _n}{\delta t} - \frac{\tilde{\theta }_{n+1}-\tilde{\theta }_n}{\delta t}\right) (\delta {\psi }_n-\delta {\tilde{\psi }}_n)\nonumber \\&\qquad +\frac{1}{\delta t}\sum _{n=0}^{N-1}\left( \frac{u_{n+1}-u_n}{\delta t} - \frac{\tilde{u}_{n+1}-\tilde{u}_n}{\delta t} \right) (\delta {\phi }_n - \delta {\tilde{\phi }}_n). \end{aligned}$$

(38)

Reorganizing, we see that the previous two lines are equal to

$$\begin{aligned}&\frac{1}{(\delta t)^2} \sum _{n=0}^{N-1}\Bigg [ \left[ (\theta _{n+1}-\tilde{\theta }_{n+1})-(\theta _n-\tilde{\theta }_n)\right] (\delta {\psi }_n-\delta \tilde{\psi }_n)\nonumber \\&\quad +\left[ (u_{n+1}-\tilde{u}_{n+1})-(u_n-\tilde{u}_n)\right] (\delta {\phi }_n-\delta {\tilde{\phi }}_n)\Bigg ]. \end{aligned}$$

(39)

Using the notation

$$\begin{aligned} a_n=\theta _n-\tilde{\theta }_n, \quad b_n=\delta {\psi }_n-\delta {\tilde{\psi }}_n, \quad c_n=u_n-\tilde{u}_n, \text { and } d_n = \delta {\phi }_n-\delta {\tilde{\phi }}_n, \end{aligned}$$

we write (39) multiplied by $(\delta t)^2$ as

$$\begin{aligned} \sum _{n=0}^{N-1} b_n \delta a_n + d_n \delta c_n&= b_{N-1}\delta a_{N-1} + d_{N-1}\delta c_{N-1} +\sum _{n=0}^{N-2} b_n \delta a_n + d_n \delta c_n \nonumber \\&= b_{N-1}\delta a_{N-1} + d_{N-1}\delta c_{N-1} \nonumber \\&\quad + a_{N-1}b_{N-1} - a_0 b_0 -\sum _{n=0}^{N-2} a_{n+1} \delta b_n \nonumber \\&\quad + c_{N-1}d_{N-1} - c_0d_0 - \sum _{n=0}^{N-2} c_{n+1} \delta d_n, \end{aligned}$$

(40)

where we used summation by parts in the last equality. Because $\psi _N=\psi _{N-1}$, we have $b_{N-1}=0$. Moreover, since $\theta _0=\tilde{\theta }_0$, we have $a_0=0$, and $\phi _1=\phi _0$ implies that $d_0=0$. Thus, we further have

$$\begin{aligned} d_{N-1}\delta c_{N-1}&= d_{N-1}\left( u_N-\tilde{u}_N - (u_{N-1}-\tilde{u}_{N-1}) \right) \\&= -d_{N-1}(u_{N-1}-\tilde{u}_{N-1})\\&= -c_{N-1}d_{N-1}, \end{aligned}$$

where we used the terminal condition $u_N=\tilde{u}_N$. According to these identities, (40) becomes

$$\begin{aligned} \sum _{n=0}^{N-1} b_n \delta a_n + d_n \delta c_n&= -\sum _{n=0}^{N-2} a_{n+1} \delta b_n + c_{n+1} \delta d_n. \end{aligned}$$

Therefore, (39) can be written as

$$\begin{aligned} -\sum _{n=0}^{N-2}\frac{\theta _{n+1}-\tilde{\theta }_{n+1}}{(\delta t)^2} \left( \delta ^2 \psi _n - \delta ^2 \tilde{\psi }_n \right) -\sum _{n=0}^{N-2}\frac{u_{n+1}-\tilde{u}_{n+1}}{(\delta t)^2} \left( \delta ^2 \phi _n - \delta ^2 \tilde{\phi }_n \right) . \end{aligned}$$

(41)

Shifting the index $n+1$ into n in (41), we obtain

$$\begin{aligned} -\sum _{n=1}^{N-1}\frac{\theta _{n}-\tilde{\theta }_{n}}{(\delta t)^2} \left( \delta ^2 \psi _{n-1} - \delta ^2 \tilde{\psi }_{n-1} \right) -\sum _{n=1}^{N-1}\frac{u_{n}-\tilde{u}_{n}}{(\delta t)^2} \left( \delta ^2 \phi _{n-1} - \delta ^2 \tilde{\phi }_{n-1} \right) . \end{aligned}$$

Using the Euler–Lagrange equations (32) and (34) in the preceding expression yields

$$\begin{aligned}&-\sum _{n=1}^{N-1} (\theta _n-\tilde{\theta }_n) \left( \psi _n + \frac{u_{n+1}-u_n}{\delta t} + h(u_n,\theta _n) - \tilde{\psi }_n - \frac{\tilde{u}_{n+1}-\tilde{u}_n}{\delta t} - h(\tilde{u}_n,\tilde{\theta }_n)\right) \\&\quad -\sum _{n=1}^{N-1} (u_n-\tilde{u}_n) \left( \phi _n + \frac{\theta _n - \theta _{n-1}}{\delta t} - f(u_n,\theta _n) - \tilde{\phi }_n - \frac{\tilde{\theta }_n - \tilde{\theta }_{n-1}}{\delta t} + f(\tilde{u}_n, \tilde{\theta }_n)\right) . \end{aligned}$$

Finally, plugging the previous result into (38), we obtain

$$\begin{aligned}&\qquad -\sum _{=1}^{N-1} (\theta _n-\tilde{\theta }_n) \left( \frac{u_{n+1}-\tilde{u}_{n+1}}{\delta t} - \frac{ u_{n}- \tilde{u}_n}{\delta t} + h(u_n,\theta _n) - h(\tilde{u}_n, \tilde{\theta }_n) \right) \\&\qquad -\sum _{n=1}^{N-1} (u_n-\tilde{u}_n) \left( \frac{\theta _n - \tilde{\theta }_{n}}{\delta t} -\frac{\theta _{n-1}- \tilde{\theta }_{n-1}}{\delta t} - f(u_n,\theta _n) + f(\tilde{u}_n,\tilde{\theta }_n) \right) \\&\quad \le \sum _{n=1}^{N-1} -\gamma \Vert (\theta _n- \tilde{\theta }_n)\Vert ^2 -\sum _{i=1}^d \gamma _i(\theta ^i_n+\tilde{\theta }^i_n) \Vert (\Delta _i u_n-\Delta _i \tilde{u}_n)\Vert ^2 \end{aligned}$$

by using Remark 1 and arguing as at the end of Sect. 4.3. $\square$

4.5 Projection Algorithm

As shown in Sect. 3, the monotone flow may not keep $\theta$ positive. Thus, to preserve probabilities and prevent $\theta$ from taking negative values, we define a projection operator through the following optimization problem. Given $(\eta , w)\in {\mathcal {M}}_N$, we solve

$$\begin{aligned} {\left\{ \begin{array}{ll} \min _{\lambda ^i_n} \sum _{i=1}^d (\eta ^i_n - \lambda ^i_n)^2 \\ \sum _{i=1}^d \lambda ^i_n = 1, \quad \lambda ^i_n \ge 0 \end{array}\right. } \end{aligned}$$

(42)

for $n\in \{0,\ldots , N\}$. Then, we set

$$\begin{aligned} P \left[ \begin{array}{c} \eta \\ w \end{array}\right] _n= \left[ \begin{array}{c} \lambda _n\\ w_n \end{array}\right] \end{aligned}$$

for $0\le n \le N$. We note that if $\eta _n$ is a probability, then $\lambda _n=\eta _n$. Moreover, P is a contraction.

Now, we introduce the following iterative scheme:

$$\begin{aligned} w_{k+1} = P\left[ w_k - \upsilon Q_A [w_k]\right] , \end{aligned}$$

(43)

where $w_k = (\theta _k, u_k)$, $Q_A$ is defined in (36), and $\upsilon >0$ is the step size.

Proposition 7

For small enough $\upsilon$, the map (43) is a contraction. Moreover, if there exists a solution $(\tilde{\theta }, \tilde{u})$ of

$$\begin{aligned} {\left\{ \begin{array}{ll} -\frac{\tilde{\theta }_{n+1}^i-\tilde{\theta }_n^i}{\delta t}+f(\tilde{u}_{n+1}^i,\tilde{\theta }_{n+1}^i)=0\\ -\frac{\tilde{u}_{n+1}^i-\tilde{u}_n^i}{\delta t}-h(\tilde{u}_{n}^i,\tilde{\theta }_{n}^i)=0 \end{array}\right. } \end{aligned}$$

(44)

satisfying the initial-terminal conditions $\tilde{\theta }_0=\bar{\theta }_0$ and $\tilde{u}^N=\bar{u}_T$, the iterates of (43) satisfy

$$\begin{aligned} \sum _{n=1}^{N-1} \gamma \Vert (\theta _{n,k}- \tilde{\theta }_{n,k})\Vert ^2 +\sum _{i=1}^d \gamma _i(\theta ^i_{n,k}+\tilde{\theta }^i_{n,k}) \Vert (\Delta _i u_{n,k}-\Delta _i \tilde{u}_{n,k})\Vert ^2\rightarrow 0, \end{aligned}$$

as $k\rightarrow \infty$.

Proof

The operator $E_{\upsilon }$ is a contraction because $Q_A$ is a monotone Lipschitz map (see Proposition 6). The convergence in the statement follows from the series

$$\begin{aligned} \sum _{k=1}^\infty \sum _{n=1}^{N-1} \gamma \Vert (\theta _{n,k}- \tilde{\theta }_{n,k})\Vert ^2 +\sum _{i=1}^d \gamma _i(\theta ^i_{n,k}+\tilde{\theta }^i_{n,k}) \Vert (\Delta _i u_{n,k}-\Delta _i \tilde{u}_{n,k})\Vert ^2, \end{aligned}$$

being convergent. $\square$

Proposition 8

Let $(\bar{\theta }, \bar{u})\in {\mathcal {M}}_N$ solve

$$\begin{aligned} A^N\left[ \begin{array}{c} \theta \\ u \end{array}\right] = \left[ \begin{array}{c} 0\\ 0 \end{array}\right] , \end{aligned}$$

with $u_N=\bar{u}_T$ and $\theta _0=\bar{\theta }_0$. Then, $(\bar{\theta }, \bar{u})$ is a fixed point of (43).

Conversely, let $(\tilde{\theta }, \tilde{u})\in {\mathcal {M}}_N$ be a fixed point of (43) with $\tilde{\theta }>0$. Then, there exists a solution to (44), $(\bar{\theta }, \bar{u}),$ with $\bar{\theta }=\tilde{\theta }$ and $\bar{u}$ given by

$$\begin{aligned} \frac{\delta \bar{u}^i_n}{\delta t}= - h(\Delta _i \tilde{u},\theta ,i) \end{aligned}$$

(45)

with $\bar{u}_N=\bar{u}_T$.

Proof

The first claim of the proposition follows immediately from the definition of $Q_A$. To prove the second part, let $(\tilde{\theta },\tilde{u})\in {\mathcal {M}}_N$ be a fixed point of (43). For all $n\in \{0,\ldots ,N\}$ and $i \in I_d$, we have

$$\begin{aligned} \tilde{u}^i_n = \tilde{u}^i_n + \upsilon \phi _n(\tilde{u}_n, \tilde{\theta }_n). \end{aligned}$$

Therefore, $\phi _n(\tilde{u}_n, \tilde{\theta }_n)=0$. Hence, from (32), we conclude that

$$\begin{aligned} -\frac{\delta \tilde{\theta }_{n-1}}{\delta t} + f(\tilde{u}_{n},\tilde{\theta }_{n})=0. \end{aligned}$$

Furthermore, for $\tilde{\theta }_n^i = \lambda _n^i$, where $\lambda _n^i$ solves (42), we have

$$\begin{aligned} \tilde{\theta }_n^i&= P \left[ \tilde{\theta }_n^i - \upsilon \psi _n(\tilde{u}_n, \tilde{\theta }_n) \right] \\&= \left( \tilde{\theta }_n^i - \upsilon \psi _n(\tilde{u}_n, \tilde{\theta }_n) + \upsilon \kappa _n \right) ^+ \end{aligned}$$

for some $\kappa _n\ge 0$. If $\tilde{\theta }^i_n > 0$, $\psi _n(\tilde{u}_n, \tilde{\theta }_n)=\kappa _n$. Otherwise, $\psi _n(\tilde{u}_n, \tilde{\theta }_n) \ge \kappa _n$.

If $\tilde{\theta }^i_n > 0$, using the fact that $\psi$ solves (34), we gather

$$\begin{aligned} \frac{\delta \tilde{u}^i_n}{\delta t} - \frac{1}{d-1}\sum _{j \ne i} \frac{\delta \tilde{u}^j_n}{\delta t} = \frac{1}{d-1}\sum _{j \ne i} h(\Delta _j \tilde{u}_n,\theta ,j) - h(\Delta _i \tilde{u}_n,\theta ,i). \end{aligned}$$

Now, we define $\bar{u}$ as in the statement of the proposition. A simple computation gives

$$\begin{aligned} \frac{\delta \bar{u}^i_n}{\delta t}- \frac{\delta \bar{u}^j_n}{\delta t}= \frac{\delta \tilde{u}^i_n}{\delta t}- \frac{\delta \tilde{u}^j_n}{\delta t}. \end{aligned}$$

Hence, $\Delta _j \bar{u}_n=\Delta _j \tilde{u}_n$. Consequently,

$$\begin{aligned} \frac{\delta \bar{u}^i_n}{\delta t}= - h(\Delta _i \bar{u},\theta ,i). \end{aligned}$$

Thus, $(\bar{\theta }, \bar{u})$ solves (2). $\square$

Remark 3

The convergence of solutions of (44) to weak solutions of (2) follows from the Minty’s method and the monotonicity of the operator A as shown in Proposition 5.

4.6 Numerical Examples

Finally, we present numerical simulations for the time-dependent paradigm-shift problem. As explained before, we discretize the time variable, $t \in [0,T]$, into N intervals of length $\delta t=\frac{T}{N}$. We then have N equations for each state. Because $d=2$, this system consists of 4N evolving equations according to (43).

To compute approximate solutions to (16)–(17), we use the projection algorithm, (43), with $N=400$. We first consider a case in which the analytical solution can be computed explicitly. We choose $\theta ^1=\theta ^2=\frac{1}{2}$. Thus, from (16), it follows that $u^1=u^2$ are affine functions of t with $u^1_t=u^2_t-\frac{1}{2}$. Our results are depicted in Figs. 5, 6, and 7. In Fig. 5, for $t\in [0,T]$, $T=8$, we plot the initial guess ($s=0$) for $\theta$ and u, and the analytical solution. In Fig. 6, we see the evolution of the density of players and the value functions for $s\in [0,20]$. The final results, $s=20$, are shown in Fig. 7. Finally, in Fig. 8, we show the evolution of the $H^1$ norm of the difference between the analytical, $(\tilde{u}, \tilde{\theta })$, and computed, $(u,\theta )$, solutions. The norm $\Vert (\tilde{u}, \tilde{\theta }) - (u,\theta ) \Vert _{H^1([0,T])}^2(s)$ is computed as

$$\begin{aligned} \sum _{j=0}^{N-1} \sum _{i=1}^2 \delta t \left( |\tilde{u}^i_j - u^i_j |^2 + |\dot{\tilde{u}}^i_j - \dot{u}^i_j |^2 + |\tilde{\theta }^i_j -\theta ^i_j|^2 + |\dot{\tilde{\theta }}^i_j -\dot{\theta }^i_j|^2 \right) (s) \end{aligned}$$

for $s\ge 0$, where $v^i_j=v^i(t_j,s)$ and $\delta t$ is the size of the time-discretization step.

Fig. 5

The blue lines correspond to the initial values ($s=0$) for state 1, $(\theta ^1,u^1)$: the orange lines correspond to the initial values for state 2, $(\theta ^2,u^2)$; the green lines correspond to the analytical solution $\theta ^1=\theta ^2$ and $u^1=u^2$ for $t\in [0,8]$. a Initial condition $\theta (\cdot ,0)$ versus exact solution. b Initial condition $u(\cdot ,0)$ versus exact solution (Color figure online)

Fig. 6

Evolution, along parameter $s\in [0,20]$, of the density of distribution of players, $\theta (\cdot ,s)$, and the difference of the value functions for both sates, $(u^1-u^2)(\cdot ,s)$. a Distribution of players $\theta ^1(t,s)$. b Difference $(u^1-u^2)(t,s)$

Fig. 7

Final value of $u(\cdot ,s)$ and $\theta (\cdot ,s)$ for $s=20$. Note that the quantities for both states superpose. a Final distribution $\theta (\cdot ,20)$. b Final value function $u(\cdot ,20)$

Fig. 8

Evolution, with the parameter s, of the $H^1$-norm of the difference between the computed solution $(u,\theta )(\cdot ,s)$ and the analytical solution for the unconstrained probability case

The paradigm-shift problem is a potential MFG with the Hamiltonian corresponding to

$$\begin{aligned} \tilde{h}(\Delta _i u,i) = -\frac{1}{2} ((u^i-u^j)^+)^2, \text { and } F(\theta ) = \frac{\theta _1^2 + \theta _2^2}{2} \end{aligned}$$

in (12). Thus, as a final test to our numerical method, we investigate the evolution of the Hamiltonian. In this case, as expected, the Hamiltonian converges to a constant (see Fig. 9).

Fig. 9

Evolution of the Hamiltonian for $s\in [0,20]$

In the preceding example, while iterating (43), $\theta$ remains away from 0. In the next example, we consider a problem in which, without the projection P in (43), positivity is not preserved. We set $N=400$ and choose initial conditions as in Fig. 10. In Fig. 11, we show the evolution by (43) for $s\in [0,20]$. In Fig. 12, we see the final result for $s=20$. Finally, in Fig. 13, we show the evolution of the $H^1$ norm of the difference $\Vert (\tilde{u}, \tilde{\theta }) - (u,\theta ) \Vert _{H^1([0,T])}^2(s)$ for $s\in [0,20]$.

Fig. 10

The blue lines correspond to the initial values ($s=0$) for state 1, $(\theta ^1,u^1)$; the orange lines correspond to the initial values for state 2, $(\theta ^2,u^2)$. a Initial condition $\theta (\cdot ,s=0)$. b Initial condition $u(\cdot ,s=0)$ (Color figure online)

Fig. 11

Evolution of $u(\cdot ,s)$ and $\theta (\cdot ,s)$, for $s\in [0,20]$. The quantities for state 1 and 2 are depicted in blue and orange, respectively. a Distribution of players $\theta ^1$. b Value functions $u^1$ and $u^2$ (Color figure online)

Fig. 12

Final value of $u(\cdot ,s)$ and distribution $\theta (\cdot ,s)$, at $s=20$. The quantities for state 1 are depicted in blue and for state 2 in orange. a Distribution of players $\theta (\cdot ,20)$. b Value functions $u(\cdot ,20)$ (Color figure online)

Fig. 13

Evolution, with respect to the parameter s, of the $H^1$-norm of the difference of the solution $(u,\theta )(\cdot ,s)$ and the solution obtained at $s=20$: $\Vert (u,\theta )(\cdot ,s) - (u,\theta )(\cdot ,20)\Vert _{H^1}$

In Fig. 14, we plot the evolution of the Hamiltonian determined using the projection method. Again, we obtain the numerical conservation of the Hamiltonian.

Fig. 14

Evolution of the Hamiltonian with the s-dynamics that preserves the probability and the positivity of the distribution of players

5 Conclusions

As the examples in the preceding sections illustrate, we have developed an effective method for the numerical approximation of monotonic finite-state MFGs. As observed previously, [1,2,3, 5], monotonicity properties are essential for the construction of effective numerical methods to solve MFGs and were used explicitly in [6]. Here, in contrast with earlier approaches, we do not use a Newton-type iteration as in [1, 3] nor do we require the solution of the master equation as in [20, 21]. While for $d=2$, the master equation can be handled numerically as in the preceding references, this approach becomes numerically prohibitive when there is a large number of states. The master equation determines the value function $U(\theta , i, t)$, where $\theta \in \mathcal {S}^d$. A direct approach to the master equation requires a grid in $\mathcal {S}^d$, or equivalently in a subset of ${\mathbb {R}}^{d-1}$. However, when d is moderately large, a direct approach requires the storage of an extremely large number of points. With our approach, we only need 2d values for each time step. The key contribution of this work is the projection method that makes addressing the initial-terminal value problem possible. This was an open problem since the introduction of monotonicity-based methods in [6]. Our methods can be applied to discretizing continuous-state MFGs, and we foresee additional extensions. The first one concerns the planning problem considered in [2]. A second extension regards boundary value problems, which are natural in many applications of MFGs. Finally, our methods may be improved by using higher-order integrators in time, provided that monotonicity is preserved. These matters will be the subject of future research.