Heat transport study of ternary hybrid nanofluid flow under magnetic dipole together with nonlinear thermal radiation

Abstract

The distinctive enhancement of thermal efficiency and improvement of the energy exchange rate as applied in the dynamics of fuels and cooling in vehicles have led to a growing knowledge of hybrid nanofluid. However, the idea of water-based nanoliquid incorporating triple different forms of solid nanoparticles with different densities and outlines (known as ternary hybrid nanofluid) remains fantastic. In this work, we investigated the influence of nonlinear thermal radiation on the MHD (magnetohydrodynamics) flow of a couple stress water-based nano, hybrid, and ternary hybrid nanofluids on a stretching sheet. The nanoparticles SiO₂, TiO₂, and Al₂O₃ are immersed in base fluid H₂O resulting in ternary hybrid nanofluid (SiO₂ + TiO₂ + Al₂O₃/H₂O). Magnetic dipole effects are also factored into the model equation. Employing suitable similarity parameters, the dimensional equations of motion and heat that characterize the aforesaid transfer mechanism were transformed into nonlinear differential equations. The homotopy analysis method (HAM) is used to solve the transformed model set of equations via Mathematica software. Various graphs are used to evaluate and assess the effects of various identifying model factors on (nano, hybrid, and ternary hybrid nanofluid) velocity and temperature fields. In the presence of a magnetic dipole, a rise in $\phi$ reduces the fluid velocity and increases the temperature fields. Furthermore, the estimated values of the engineering quantities of importance ($C_{{\text{f}}}$, ${\text{Nu}}$) are tabulated and explained. It is also be observed that skin friction declines with the larger amount of the nanoparticle volume fractions $\phi_{{{\text{SiO}}_{2} }} ,\phi_{{{\text{TiO}}_{2} }} ,\phi_{{{\text{Al}}_{2} {\text{O}}_{3} }}$. Some potential uses for this research include high-temperature and cooling processes, aerospace technologies, medications, metallic coatings, and biosensors, to name a few.

Introduction

Nanofluids have recently been acknowledged as having a substantial impact on a wide range of technological industries, including industrial production, scientific investigation, and various engineering sectors due to their diverse utilizations and applications. Advanced freezing mechanisms, fuel production, modern technique of drugs transportation, various technical machinery and devices, sector of nano-fabrication, and the energy transfer and cooling of various electronics circuit are only a few examples in this direction. On the basis of such a wonderful outcome, a significant amount of research into the transportation of energy and flow properties has been carried out all over the world. Researchers have attempted a variety of methods to increase convection heat transmission in liquids via putting some nanomaterials like Cu, Ag, SiO₂, Fe₃O₄, Al₂O₃, TiO₂, CNTs, graphene, and various other solid materials in common base fluids like kerosene oil, water, CH₃OH, blood, C₂H₆O₂, and many more. In this direction, Ahmad et al. (2021) and Yahya et al. (2021) and many others scientists have produced remarkable research works on nanofluid flow in past few years.

In this consequence, the situation of an exhaustive mixture of conventional fluids containing two sorts of nanomaterials (hybrid nanofluid) has been identified after the extensive exploration of the above-mentioned fluid (nanofluid). Thermal conductivities, heat, and concentration of molecular densities, as well as the thicknesses and dimension of nanoparticles are all used to characterize the thermal performance of hybrid nanofluids. For hybrid nanofluids, there is no special way or formula for determining the thermal conductivity. For ethylene glycol base hybrid nanoliquids, Jamei et al. (2020) described conjugate heat transfer assessment. Using a two-step technique, Xian et al. (2020) synthesized powerful hybrid nanoliquids by combining the TiO₂ and graphene nanoparticles into purified water. The numerical calculation of stagnation point’s mobility of Ag + CuO/H₂O hybrid nanoparticles via an extending surface was explored by Arani and Aberoumand (2020). Roy et al. (2020) investigated the effect of viscoelastic distribution on the motion and energy transmission of a Cu − Al₂O₃/water hybrid nanofluid via a rotating drum for both assistive and resistive movements. In the literature, various researchers have worked on the flow and energy transmission of hybrid nanofluids, with important applications in engineering and science, including (Algehyne et al. 2020; Gul et al. 2021; Sharma et al. 2020; Mourad et al. 2022; Akbar et al. 2017; Said et al. 2022; Muhammad and Nadeem 2017; Chu et al. 2021). The ternary hybrid nanofluid, homogeneous mixing of three kinds of nanomaterials containing a unique base liquid, was recently introduced; however, the results of a few investigations appear interesting and informative. Mousavi et al. (2019) explored at the subtleties of CuO, MgO, and TiO₂ transport in H₂O. In general, the characteristics of ternary hybrid nanofluids is closely resembled those of a Newtonian liquid. Increased temperature diminishes the concentration of tri-hybrid nanofluids proportionally. Through the inclusion of various types of nanoparticles, the definite heat capacities of the common functional fluid can be improved. Sahoo and Kumar (2020) analyzed the various thermophysical characteristics of H₂O containing Al₂O₃, CuO, and TiO₂-ternary hybrid nanofluid at 35–50 °C. Some other researchers were interested in the related published work on ternary hybrid nanofluid and are Manjunatha et al. (2021), Nazir et al. (2021), and Wang et al. (2022a, b). Thermal converters, storage of food, bioscience, storage of solar collectors, ventilation mechanism, transportation, and double windowpanes are only few of the areas where this research has made a significant impact. Furthermore, this research has substantial practical implications in polymer nanocomposites manufacture, fuel reservoirs, advance cooling system, groundwater transportation, and thermal insulation.

Nanofluids with the MHD (magnetohydrodynamics) phenomenon are widely known for their ability to control fluid flow and enhance the energy efficiency of electrically charged liquids. Furthermore, when manufacturing operations are conducted at extreme temperatures, the impact of thermally nonlinear radiation gets much more important than the impact of linearly thermal radiations, and hence, it performs a critical part in the developed thermal properties. Fiberglass forming, melting and tinning copper cables, forming of crystallization, steam turbines, metallurgical work, designing of modern equipment, nuclear power stations, fibers turning and continual heating and cooling, and many other uses have developed. Emphasizing the importance of such investigation, Laxmi and Shankar (2016) solved numerically the nonlinear thermal radiations impression on MHD nanofluid motion through a porous extending surface. Khan et al. (2018) numerically introduced the new idea of activation energy of MHD convectional movement over a stretchable surface including nonlinearly thermal radiations. Narayana et al. (2021) deliberated the effect of nonlinear thermal radiations and numerical results of MHD couple stress Casson nanofluid over an extending sheet. Gireesha et al. (2021) contributed significantly to the study of nanofluid flows via a permeable stretching surface while accounting for the consequence of nonlinear radiations. Similarly, the thermal radiations linked through a magnetic field in the form of infrared radiations (IR) can also be used for biomedical purposes. Therefore, in this regard, Hayat et al. (2021) recently stated in their study that infrared radiation delivered via electromagnetic waves is beneficial in the medication of pulmonary and esophageal cancer, gastric acid reflux, muscle clotting, and skin problems. Naz et al. (2020) investigated the Carreau nanofluid flow through a flat cylinder along with suspended gyrotactic microorganisms and an inclined MHD.

In the field of fluid dynamics, the liquid flowing through a stretchable surface has formed a classical problem due to the existence of a closed-form approach, which is extremely rare. In addition, the study of fluid and heat exchange on an elastic media is important because of its numerous implications in technology and manufacturing procedures. Several scientists were impressed by these technological uses to explore the various fluid movements through expanding surfaces. The stream of bioconvection nanoliquid through a stretchable medium including the condition of anisotropic slip was examined by Amirsom et al. (2019). Sohail et al. (2020) examined the mixed convection flow of Casson fluid over stretching sheet with permeable medium. Using the Tiwari-Das idea, Lund et al. (2021) illustrated the viscous dissipation flow of hybrid nanoliquid. Also, the non-Fourier energy flux on nanoliquid flow across an extending surface was investigated by Gowda et al. (Punith Gowda et al. 2021). Khan et al. (2021) experimentally inspected the influence of a hybrid nanoliquid across a shrinking and extending disk. Scientists (Wu et al. 2011; Berrouk et al. 2008) have done some outstanding work on such discipline.

After examining relevant literature, the central goal of the current investigation is to study the nonlinearly changing thermal radiation and the influence of a magnetic dipole on the stream of a couple stress ternary hybrid nanofluid along a stretchable surface. The originality of current research work is displayed as follows.

• i. The ternary hybrid nanofluid with magnetic dipole is considered.

• ii. The couple stress are terminologies considered to sustain the uniformity of the ternary hybrid nanofluids.

• iii. The nonlinear thermal radiation is studied to improve the thermal analysis more precisely.

• iv. The comparative study of SiO₂/H₂O, TiO₂ + Al₂O₃/H₂O, and SiO₂ + TiO₂ + Al₂O₃/H₂O nano and hybrid nanofluids on the momentum and thermal boundary layer is explored.

We used the similarity variables to translate the leading PDEs into a system of coupled ODE’s form. The non-dimensional governing expressions are tackled by HAM technique and the outcomes of model problems are displayed as diagrams and graphs. The tabular forms are used to analyze the technical parameters such as $C_{{\text{f}}}$ and $Nu_{x}$. The current study could be beneficial in a lot of disciplines, including high-temperature and cooling technologies, aerospace technologies, pigments, medications, and biosensors, to mention just some. The composition of ternary hybrid nanofluid is illustrated in Fig. 1a.

Fig. 1

a Composition of ternary hybrid nanofluid. b System of coordinates and physical configuration of flow model

Mathematical formulation

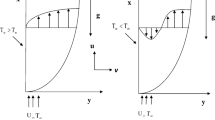
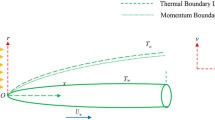
The mathematical analysis illustrates the ternary hybrid nanofluid flow through an extending sheet. The nanoparticles SiO₂, TiO₂, and Al₂O₃ are immersed in base fluid H₂O resulting ternary hybrid nanofluid (SiO₂ + TiO₂ + Al₂O₃/H₂O). The ternary hybrid nanofluid (SiO₂ + TiO₂₊Al₂O₃/H₂O) is flowing in a positive x-axis direction from left to right. The magnetic dipole is simply taken along the y-direction at a range c with a uniform magnetic field, as shown in figure. Because the material of surface is extensible, it can produce fluid movement when it is extended. Assume that the expanding velocity of sheet is $U_{w} = S\,x$. As in the present study, $O\left( u \right)$ = $O\left( 1 \right)$ = $O\left( x \right)$ and $O\left( v \right)$ = $O\left( \infty \right)$ = $O\left( y \right)$, the accepted boundary layer assumption in Wu et al. (2011) is used. The magnetic field effect is depicted in the figure by the round arcs containing arrows. Configuration of flow and physical geometry is explained and illustrated in Fig. 1b.

The assumptions and conditions of model

The present mathematical analysis is taken into consideration under some specific presumptions:

• Nonlinear thermal radiation

• A steady, incompressible and 2D flow.

• Magnetic dipole.

• Couple stress.

• SiO₂ + TiO₂ + Al₂O₃ nanoparticles are constantly dispersed in H₂O.

Governing model expressions

The basic flow and heat transfer equations using the conventional notations are expressed below (Muhammad and Nadeem 2017; Nazir et al. 2021) and (Andersson and Valnes 1998)

$$ \frac{\partial \,u}{{\partial \,x}} + \frac{\partial \,v}{{\partial \,y}} = 0, $$

(1)

$$ \rho_{{{\text{thnf}}}} \left( {u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}}} \right) = - \frac{\partial P}{{\partial x}} + \mu_{{\text{f}}} M\frac{\partial H}{{\partial x}} + \mu_{{{\text{thnf}}}} \frac{{\partial^{2} u}}{{\partial y^{2} }} - \eta^{*} \frac{{\partial^{4} u}}{{\partial y^{4} }}, $$

(2)

$$ \left( {\rho C_{p} } \right)_{{{\text{thnf}}}} \left( {u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}}} \right) = k_{{{\text{thnf}}}} \frac{{\partial^{2} T}}{{\partial y^{2} }} - \left( {u\frac{\partial H}{{\partial x}} + v\frac{\partial H}{{\partial y}}} \right)\mu_{{{\text{thnf}}}} T\frac{\partial M}{{\partial x}} + \frac{16}{3}\left( {\frac{{\sigma^{*} T_{\infty }^{3} }}{{k^{*} }}\frac{{\partial^{2} T}}{{\partial y^{2} }}} \right). $$

(3)

With boundary conditions

$$ \begin{gathered} \left. u \right|_{y = 0} = Sx = \,\,\,U_{{\text{w}}} ,\,\,\,\,\,\,\left. v \right|_{y = 0} = 0,\left. {\,\,\,\,\,T} \right|_{y} = \,\,0\,\, = T_{{\text{w}}} , \hfill \\ \left. u \right|_{y \to \infty } \to \,\,0,\,\,\,\,\,\,\,\,\left. T \right|_{y \to \infty } \to \,\,\,T_{\infty } = \,\,T_{{\text{c}}} . \hfill \\ \end{gathered} $$

(4)

Here velocities in x and y-axis are denoted $u$ and $v$. In Eq. (2), the symbols $\rho_{{{\text{thnf}}}}$ ternary hybrid nanofluid density,$\mu_{{{\text{hnf}}}}$ ternary hybrid nanofluid viscosity, $\mu_{{\text{f}}}$ viscosity of nanofluid, $P$ pressure, $H$ is the magnetic field, and $M$ magnetizations of magnetic field, $\eta^{*}$ couple stress material constant. In Eq. (3), the symbols show $\left( {\rho C_{{\text{p}}} } \right)_{{{\text{thnf}}}}$ ternary hybrid nanofluid specific heat, $K_{{{\text{hnf}}}}$ ternary hybrid nanofluid thermal conductivity, $T$ temperature field, $k^{*}$ mean absorption constant, and $\sigma^{*}$ Stefan Boltzmann constant. In Eq. (4), the symbols $T_{{\text{c}}}$, $T_{\infty }$ and $T_{{\text{w}}}$ curie, ambient and stretching wall temperatures, $S$ dimensionless constant. Additionally, it is assumed that the fluids temperature is $T = T_{\infty }$, such that $T_{{\text{w}}} < T_{\infty } < T_{{\text{c}}}$.

Magnetic dipole

Whenever a magnetic field is subjected to a spreading surface, the flow of nanofluid is altered, producing in a magnetic field domain that is symbolized by and quantitatively described as in Muhammad and Nadeem (2017); Andersson and Valnes 1998)

$$ \delta_{1} = \left( {\frac{x}{{x^{2} + \left( {c + y} \right)^{2} }}} \right)\frac{{\gamma_{1} }}{2\pi }. $$

(5)

In Eq. (5), the leading pint of the magnetic field is designated by $\gamma_{1}$. Also, the displacement of magnetic dipole is represented by c.

In the x- and y- directions, the horizontal and vertical components of $\left( H \right)$ are stated as

$$ x{\text{ - component of}}\;H:\frac{\partial H}{{\partial x}} = - \frac{{\partial \delta_{1} }}{\partial x} = \,\,\left\{ {\frac{{x^{2} - \left( {c + y} \right)^{2} }}{{\left( {x^{2} + \left( {c + y} \right)^{2} } \right)^{2} }}} \right\}\,\,\frac{{\gamma_{1} }}{2\pi }, $$

(6)

$$ y{\text{ - component of}}\;H:\frac{\partial H}{{\partial y}} = - \frac{{\partial \delta_{1} }}{\partial y} = \left\{ {\frac{{2\,\,\left( {c + y} \right)x}}{{\left( {x^{2} + \left( {c + y} \right)^{2} } \right)^{2} }}} \right\}\frac{{\gamma_{1} }}{2\pi }. $$

(7)

We acquire aforementioned two expressions for magnetic field elements by differentiating Eq. (5) with regard to $x$ and $y$, respectively. Because the magnetic force has a direct relationship with the gradient of $H$, hence $H$ can be stated mathematically as

$$ H = \sqrt {\left( {\frac{{\partial \delta_{1} }}{\partial x}} \right)^{2} + \left( {\frac{{\partial \delta_{1} }}{\partial y}} \right)^{2} } . $$

(8)

Using Eqs. (6) and (7) in Eq. (8), we get the following equations:

$$ \frac{\partial H}{{\partial x}} = \frac{{\gamma_{1} }}{2\pi }\frac{2x}{{\left( {y + c} \right)^{4} }}, $$

(9)

$$ \frac{\partial H}{{\partial x}} = \frac{1}{2\pi }\left( {\frac{{4x^{2} }}{{\left( {y + c} \right)^{5} }} - \frac{2}{{\left( {y + c} \right)^{3} }}} \right)\gamma_{1} . $$

(10)

Considering changes in temperature can induce alterations in magnetism, the effects on magnetism can be described as

$$ M = K_{1} \,\,\left( {T\,\, - \,\,T_{\infty } } \right). $$

(11)

Here, the magnetization is denoted by $M$, whereas the pyro-magnetic coefficient is denoted by $K_{1}$.

Transformation analysis

The dimensional model expressions of motion and energy are transformed into dimensionless shapes utilizing similarity transformations mentioned below (Muhammad and Nadeem 2017) and (Andersson and Valnes 1998)

$$ \psi \left( {\xi ,\eta } \right) = \left( {\frac{{\mu_{f} }}{{\rho_{f} }}} \right)\xi f\left( \eta \right),\,\,\,\Theta \left( {\xi ,\eta } \right) = \frac{{T_{c} - T}}{{T_{c} - T_{w} }} = \Theta_{1} \left( \eta \right) + \xi^{2} \Theta_{2} \left( \eta \right). $$

(12)

Therefore, $\Theta_{1} (\eta ,\xi )$ and $\Theta_{2} (\eta ,\xi )$ implies the non-dimensional temperature variables, non-dimensional stream function $f\left( \xi \right)$. $\xi$ and $\eta$ are the non-dimensional and continuous coordinates defined as

$$ \eta = y\left( {\frac{{\rho_{{\text{f}}} S}}{{\mu_{{\text{f}}} }}} \right)^{\frac{1}{2}} ,\,\,\,\,\xi = x\left( {\frac{{\rho_{{\text{f}}} S}}{{\mu_{{\text{f}}} }}} \right)^{\frac{1}{2}} . $$

(13)

The function presented in Eq. (12), directly satisfy Eq. (1), and the components of velocity are as follows:

$$ u\, = Sx\,\,f^{\prime}\left( \eta \right) = \frac{\partial \psi }{{\partial y}}\,\,\,\,\,{\text{and}}\,\,\,\,\,v = \,\,\, - \left( {S\mu_{f} } \right)^{\frac{1}{2}} \,\,\,f\left( \eta \right) = \,\frac{\partial \psi }{{\partial x}}. $$

(14)

Tri-hybrid nanomaterial and base fluid properties

The thermophysical properties of tri-hybrid nanofluid are stated as (Manjunatha et al. 2021; Nazir et al. 2021) and (Wang et al. 2022a) (Table 1)

$$ \frac{{\mu_{{{\text{thnf}}}} }}{{\mu_{{\text{f}}} }} = \frac{1}{{(1 - \phi_{{{\text{SiO}}_{2} }} )^{2.5} (1 - \phi_{{{\text{TiO}}_{2} }} )^{2.5} (1 - \phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} )^{2.5} }}, $$

(15)

$$ \frac{{\rho_{{{\text{thnf}}}} }}{{\rho_{{\text{f}}} }} = \left( {1 - \phi_{{{\text{SiO}}_{2} }} } \right)\left[ {\left( {1 - \phi_{{{\text{TiO}}_{2} }} } \right)\left\{ {\left( {1 - \phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} } \right) + \phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} \frac{{\rho_{{{\text{Al}}_{2} {\text{O}}_{3} }} }}{{\rho_{{\text{f}}} }}} \right\} + \phi_{{{\text{TiO}}_{2} }} \frac{{\rho_{{{\text{TiO}}_{2} }} }}{{\rho_{{\text{f}}} }}} \right] + \phi_{{{\text{SiO}}_{2} }} \frac{{\rho_{{{\text{SiO}}_{2} }} }}{{\rho_{{\text{f}}} }}, $$

(16)

$$ \begin{gathered} \frac{{(\rho c_{{\text{p}}} )_{{{\text{thnf}}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }} = \phi_{{{\text{SiO}}_{2} }} \frac{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{SiO}}_{2} }} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }} + \hfill \\ \left( {1 - \phi_{{{\text{SiO}}_{2} }} } \right)\left[ {\left( {1 - \phi_{{{\text{TiO}}_{2} }} } \right)\left\{ {\left( {1 - \phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} } \right) + \phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} \frac{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{Al}}_{2} {\text{O}}_{3} }} }}{{\left( {\rho cp} \right)_{{\text{f}}} }}} \right\} + \phi_{{{\text{TiO}}_{2} }} \frac{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{TiO}}_{2} }} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }}} \right], \hfill \\ \end{gathered} $$

(17)

$$ \begin{gathered} \frac{{k_{{{\text{thnf}}}} }}{{k_{{{\text{hnf}}}} }} = \left( {\frac{{k_{{{\text{Al}}_{2} {\text{O}}_{3} }} + 2k_{{{\text{hnf}}}} - 2\phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} \left( {k_{{{\text{hnf}}}} - k_{{{\text{Al}}_{2} {\text{O}}_{3} }} } \right)}}{{k_{{{\text{Al}}_{2} {\text{O}}_{3} }} + 2k_{{{\text{hnf}}}} + \phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} \left( {k_{{{\text{hnf}}}} - k_{{{\text{Al}}_{2} {\text{O}}_{3} }} } \right)}}} \right),\frac{{k_{{{\text{hnf}}}} }}{{k_{{{\text{nf}}}} }} = \left( {\frac{{k_{{{\text{TiO}}_{2} }} + 2k_{{{\text{nf}}}} - 2\phi_{{{\text{TiO}}_{2} }} \left( {k_{{{\text{nf}}}} - k_{{{\text{TiO}}_{2} }} } \right)}}{{k_{{{\text{TiO}}_{2} }} + 2k_{{{\text{nf}}}} + \phi_{{{\text{TiO}}_{2} }} \left( {k_{{{\text{nf}}}} - k_{{{\text{TiO}}_{2} }} } \right)}}} \right), \hfill \\ \frac{{k_{{{\text{nf}}}} }}{{k_{{\text{f}}} }} = \left( {\frac{{k_{{{\text{SiO}}_{2} }} + 2k_{f} - 2\phi_{{{\text{SiO}}_{2} }} \left( {k_{{\text{f}}} - k_{{{\text{SiO}}_{2} }} } \right)}}{{k_{{{\text{SiO}}_{2} }} + 2k_{f} + \phi_{{{\text{SiO}}_{2} }} \left( {k_{{\text{f}}} - k_{{{\text{SiO}}_{2} }} } \right)}}} \right), \hfill \\ \end{gathered} $$

(18)

$$ \begin{gathered} \frac{{\sigma_{{{\text{thnf}}}} }}{{\sigma_{{{\text{hnf}}}} }} = \left[ {1 + \frac{{3\left( {\frac{{\sigma_{{{\text{Al}}_{2} {\text{O}}_{3} }} }}{{\sigma_{{{\text{hnf}}}} }} - 1} \right)\phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} }}{{\left( {\frac{{\sigma_{{{\text{Al}}_{2} {\text{O}}_{3} }} }}{{\sigma_{{{\text{hnf}}}} }} + 2} \right) - \left( {\frac{{\sigma_{{{\text{Al}}_{2} {\text{O}}_{3} }} }}{{\sigma_{{{\text{hnf}}}} }} - 1} \right)\phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} }}} \right],\,\frac{{\sigma_{{{\text{hnf}}}} }}{{\sigma_{{{\text{nf}}}} }} = \left[ {1 + \frac{{3\left( {\frac{{\sigma_{{{\text{TiO}}_{2} }} }}{{\sigma_{{{\text{nf}}}} }} - 1} \right)\phi_{{{\text{TiO}}_{2} }} }}{{\left( {\frac{{\sigma_{{{\text{TiO}}_{2} }} }}{{\sigma_{{{\text{nf}}}} }} + 2} \right) - \left( {\frac{{\sigma_{{{\text{TiO}}_{2} }} }}{{\sigma_{{{\text{nf}}}} }} - 1} \right)\phi_{{{\text{TiO}}_{2} }} }}} \right], \hfill \\ \frac{{\sigma_{{{\text{nf}}}} }}{{\sigma_{{\text{f}}} }} = \left[ {1 + \frac{{3\left( {\frac{{\sigma_{{{\text{SiO}}_{{2}} }} }}{{\sigma_{f} }} - 1} \right)\phi_{{{\text{SiO}}_{{2}} }} }}{{\left( {\frac{{\sigma_{{{\text{SiO}}_{{2}} }} }}{{\sigma_{{\text{f}}} }} + 2} \right) - \left( {\frac{{\sigma_{{{\text{SiO}}_{{2}} }} }}{{\sigma_{{\text{f}}} }} - 1} \right)\phi_{{{\text{SiO}}_{{2}} }} }}} \right]. \hfill \\ \end{gathered} $$

(19)

Table 1 Nanoparticles and H₂O thermophysical characteristics (Manjunatha et al. 2021; Nazir et al. 2021; Nasir et al. 2018)

Both Eqs. (2), (3) become in form of ordinary differential equations after inserting the above-mentioned thermophysical parameters Eqs. (15–19) and transformations Eq. (14) in it

$$ f^{\prime\prime\prime} - \frac{{\rho_{{{\text{thnf}}}} }}{{\rho_{\,f} }}\frac{{\mu_{{\,{\text{f}}}} }}{{\mu_{{{\text{thnf}}}} }}\left[ {f^{{\prime}{2}} - ff^{\prime\prime} + \frac{{2\beta \,\Theta_{1} }}{{\rho_{{{\text{thnf}}}} }}\left( {\eta + \gamma^{*} } \right)^{4} } \right] - K^{*} f^{v} = 0, $$

(20)

$$ \begin{gathered} \left[ {\frac{{k_{{{\text{thnf}}}} }}{{k_{{{\text{bf}}}} }} + \frac{4}{3}Rd\left( {\frac{{\text{d}}}{{{\text{d}}\eta }}\left[ {1 + \left( {1 + \Theta_{{\text{w}}} } \right)\Theta_{1} } \right]^{3} } \right)} \right]\Theta^{\prime\prime}_{1} + \hfill \\ \frac{{(\rho C_{{\text{p}}} )_{{{\text{thnf}}}} }}{{(\rho C_{p} )_{{\text{f}}} }}\left[ {\Pr_{{\text{f}}} \left( {f\Theta^{\prime}_{1} - 2f^{\prime}\Theta_{1} } \right) + \frac{{2\beta \lambda f\left( {\Theta_{1} - \varepsilon } \right)}}{{\left( {\varepsilon + \gamma^{*} } \right)^{3} }} - 4\lambda f^{{\prime}{2}} } \right] = 0, \hfill \\ \end{gathered} $$

(21)

$$ \begin{gathered} \left[ {\frac{{k_{{{\text{thnf}}}} }}{{k_{{{\text{bf}}}} }} + \frac{4}{3}Rd\left( {\frac{{\text{d}}}{{{\text{d}}\eta }}\left[ {1 + \left( {1 + \Theta_{{\text{w}}} } \right)\Theta_{2} } \right]^{3} } \right)} \right]\Theta^{\prime\prime}_{2} - \hfill \\ \frac{{(\rho C_{{\text{p}}} )_{{{\text{thnf}}}} }}{{(\rho C_{{\text{p}}} )_{{\text{f}}} }}\left[ {\Pr_{{\text{f}}} \left( {4f\Theta^{\prime}_{2} - f^{\prime}\Theta_{2} } \right) - \frac{{2\,\beta \,\lambda \,f\,\Theta_{2} }}{{\left( {\varepsilon + \gamma^{*} } \right)^{3} }} + \lambda \beta \left( {\Theta_{1} - \varepsilon } \right)\left( {\frac{{2f^{\prime}}}{{\left( {\varepsilon + \gamma^{*} } \right)^{4} }} + \frac{4f}{{\left( {\varepsilon + \gamma^{*} } \right)^{5} }}} \right) - \lambda f^{{\prime\prime}{2}} } \right] = 0. \hfill \\ \end{gathered} $$

(22)

The corresponding transformed boundary condition are

$$ \begin{gathered} f\left( 0 \right) = 0,f^{\prime}\left( 0 \right) = 1,\Theta_{1} \left( 0 \right) = 1,\Theta_{2} \left( 0 \right) = 0, \hfill \\ f^{\prime}\left( \infty \right) = 0,\Theta_{1} \left( \infty \right) = 0,\Theta_{2} \left( \infty \right) = 0. \hfill \\ \end{gathered} $$

(23)

Table 2 lists the dimensionless formulas for all physical parameters.

Table 2 Model parameters and their mathematical expressions

The interest physical quantities

For the present model, the $C_{{\text{f}}}$ and ${\text{Nu}}_{x}$ are key engineering physical parameters described as

$$ \frac{1}{2}\,{\text{Re}}_{x}^{\frac{1}{2}} C_{{\text{f}}} = \frac{1}{{\left( {1 - \phi_{{{\text{SiO}}_{2} }} } \right)^{2.5} \left( {1 - \phi_{{{\text{TiO}}_{2} }} } \right)^{2.5} \left( {1 - \phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} } \right)^{2.5} }}f^{\prime\prime}\left( 0 \right), $$

(24)

$$ {\text{Re}}_{x}^{{ - \frac{1}{2}}} {\text{Nu}}_{x} = \left[ {\frac{{k_{{{\text{thnf}}}} }}{{k_{{{\text{bf}}}} }} + \frac{4}{3}Rd\left( {\frac{{\text{d}}}{{{\text{d}}\eta }}\left[ {1 + \left( {1 + \Theta_{{\text{w}}} } \right)\left( {\Theta_{1} + \Theta_{2} } \right)} \right]^{3} } \right)} \right]\left( {\Theta^{\prime}_{1} \left( 0 \right) + \eta^{2} \Theta^{\prime}_{2} \left( 0 \right)} \right), $$

(25)

whereas ${\text{Re}}_{x} = \frac{{xU_{{\text{w}}} \left( x \right)}}{{V_{{\text{f}}} }} = \frac{{Sx^{2} }}{{V_{{\text{f}}} l}}$, reveals the Reynold's number, which is dependent on the rate of change of displacement $U_{{\text{w}}} \left( x \right)$ as it extends. Also, coefficient of skin friction is represented as ${\text{Re}}_{x}^{\frac{1}{2}} C_{{\text{f}}}$ and Nusselt number is ${\text{Re}}_{x}^{{ - \frac{1}{2}}} {\text{Nu}}_{x}$.

Solution methodology

In this study, HAM is used to solve the nonlinear ordinary momentum and heat equation under permissible boundary conditions. The solution of extremely nonlinear problems is obtained using this method. When compared to perturbation approaches and other traditional investigative procedures, the HAM shows good performance. Because HAM provides us with a great deal of freedom in terms of choosing the form of mathematical expression of linear subproblems. Furthermore, the HAM operates independently of whether or not there are any small or massive physical variables in figuring out equation with boundary/initial constraints. Hence, Mathematica software is utilized for this determination. For the boundary value problem, the corresponding linear operators and their associated starting guesses are (Nasir et al. 2018)

$$ f(\eta ) = 1 - e^{ - \eta } ,\,\,\,\,\,\,\Theta_{1} (\eta ) = e^{ - \eta } ,\,\,\,\,\,\,\Theta_{2} (\eta ) = \eta e^{ - \eta } . $$

(26)

Therefore, inform of linear operators

$$ L_{f} (f) = f^{v} ,\,\,\,\,\,\,\,{\text{L}}_{{\Theta_{1} }} {(}\Theta_{1} ) = \Theta^{\prime\prime}_{1} ,\,\,\,\,\,\,\,\,{\text{L}}_{{\Theta_{2} }} {(}\Theta_{2} {) = }\Theta^{\prime\prime}_{2} . $$

(27)

Therefore, the linear operators $L_{{\text{f}}} ,\,\,\,L_{{\Theta_{1} }}$ and $L_{{\Theta_{2} }}$ are indicated as

$$ \begin{gathered} L_{f} (k_{1} + k_{2} \eta + k_{3} \eta^{2} + k_{4} \eta^{3} + k_{5} \eta^{4} ) = 0, \hfill \\ L_{{\Theta_{1} }} (k_{6} + k_{7} \eta ) = 0,\,\,\,\,L_{{\Theta_{2} }} (k_{8} + k_{9} \eta ) = 0, \hfill \\ \end{gathered} $$

(28)

where $k_{m} (m = 1,2 \ldots ,9)$ are arbitrary constant.

Results and discussion

In this research work, we utilized three different types of nanoparticles SiO₂ + TiO₂ + Al₂O₃ in base fluid H₂O that flows over a stretching surface. In the analytical inspection of the current mathematical model, the influences of ferrohydrodynamic interaction $\beta$, magnetic field strength $\gamma^{*}$, nanoparticle concentration parameter $\phi$, couple stress Parameter $K^{*}$, Prandtl number ${\text{Pr}}$, thermal radiation $Rd$ parameter are considered under some specific boundary conditions. For various values of model variables, numerical results are given using graphs and tables. The default range of fluid flow variables are taken on published works ((Muhammad and Nadeem 2017; Manjunatha et al. 2021; Nazir et al. 2021; Wang et al. 2022a)) as $\beta = 10$, $\gamma^{*} = 0.5$, $K^{*} = 0.1$, $\Pr = 6.7$, $Rd = 0.2,\,\,\varepsilon = 0.01$, and $\lambda = 0.1$.

Figure 2 depicts a comparison of SiO₂/H₂O nanofluid, TiO₂ + Al₂O₃/H₂O hybrid nanofluid, and SiO₂ + TiO₂ + Al₂O₃/H₂O ternary hybrid nanofluid on $f^{\prime}\left( \eta \right)$(velocity distribution) as ferrohydrodynamic parameter ($\beta$) is varied for various values. The $f^{\prime}\left( \eta \right)$ profile reduces as the magnitude of $\beta$ rises. In general, the availability of dimensionless parameters such as $\xi$, $\beta$ and $\varepsilon$ is required to perceive the ferromagnetic influence on the SiO₂/H₂O nanofluid, TiO₂ + Al₂O₃/H₂O hybrid nanofluid and SiO₂ + TiO₂ + Al₂O₃/H₂O ternary hybrid nanofluid flows. Additionally, the impact of magnetic dipole collects particles of the fluid which enhances nanofluid viscosity, causing a declination in $f^{\prime}\left( \eta \right)$ distribution to be detected. The fluid's $f^{\prime}\left( \eta \right)$ is significantly influenced by the high magnitude of $\beta$ throughout, and the value of $f^{\prime}\left( \eta \right)$ falls quicker in the presence of SiO₂ + TiO₂ + Al₂O₃/H₂O ternary hybrid nanofluid as compared to TiO₂ + Al₂O₃/H₂O hybrid nanofluid and SiO₂/H₂O nanofluid. Similarly, Fig. 3 illustrates the effect of $\beta$ on $\Theta_{1} \left( \eta \right)$ heat transmission in the context of SiO₂/H₂O nanofluid, TiO₂ + Al₂O₃/H₂O hybrid nanofluid and SiO₂ + TiO₂ + Al₂O₃/H₂O ternary hybrid nanofluid. In this case, we observe that an increment in $\beta$ enhances the $\Theta_{1} \left( \eta \right)$ profile. Physically, increasing $\beta$ causes friction within the fluid, which transforms mechanical energy to heat energy. Therefore, the $\Theta_{1} \left( \eta \right)$ profile becomes more prominent. Moreover, $\beta$ has a significant effect on $\Theta_{1} \left( \eta \right)$ profile and such effect grows more rapidly in SiO₂ + TiO₂ + Al₂O₃/H₂O ternary hybrid nanofluid as compared to TiO₂ + Al₂O₃/H₂O hybrid nanofluid and SiO₂/H₂O nanofluid. At other heat transmission profile $\Theta_{2} \left( \eta \right)$, an identical effect has been demonstrated for $\beta$ with a little change in behavior for SiO₂ + TiO₂ + Al₂O₃/H₂O ternary hybrid nanofluid, TiO₂ + Al₂O₃/H₂O hybrid nanofluid and SiO₂/H₂O nanofluid, as illustrated in Fig. 4. Figures 5, 6 and 7 present the effects of $\gamma$ (magnetic field strength factor) on $f^{\prime}\left( \eta \right)$ velocity field and temperatures fields $\Theta_{1} \left( \eta \right)$, $\Theta_{2} \left( \eta \right)$ in presence of SiO₂ + TiO₂ + Al₂O₃/H₂O ternary hybrid nanofluid, TiO₂ + Al₂O₃/ H₂O hybrid nanofluid, and SiO₂/H₂O nanofluid.

Fig. 2

Variations in $f^{\prime}\left( \eta \right)$ with various values of $\beta$

Fig. 3

Variations in $\Theta_{1} \left( \eta \right)$ with various values of $\beta$

Fig. 4

Variations in $\Theta_{2} \left( \eta \right)$ with various values of $\beta$

Fig. 5

Variations in $f^{\prime}\left( \eta \right)$ with various values of $\gamma$

Fig. 6

Variations in $\Theta_{1} \left( \eta \right)$ with various values of $\gamma$

Fig. 7

Variations in $\Theta_{2} \left( \eta \right)$ with various values of $\gamma$

Figure 5 illustrates a $f^{\prime}\left( \eta \right)$ profile assessment of SiO₂/H₂O nanofluid, TiO₂ + Al₂O₃/H₂O hybrid nanofluid, and SiO₂ + TiO₂ + Al₂O₃/H₂O ternary hybrid nanofluid, for varying values of the $\gamma$. The $f^{\prime}\left( \eta \right)$ of these fluids tends to decrease for high values of $\gamma$. Physically, for growing values of $\gamma$, a resistive force is generated, and as a result of such force, the $f^{\prime}\left( \eta \right)$ profile within the boundary layer is reduced. Also, the SiO₂/H₂O nanofluid exhibits a faster reduction in $f^{\prime}\left( \eta \right)$ profile than TiO₂ + Al₂O₃/H₂O hybrid nanofluid and SiO₂ + TiO₂ + Al₂O₃/H₂O ternary hybrid nanofluid, as shown in the diagram. In Fig. 6, the effect of $\gamma$ on $\Theta_{1} \left( \eta \right)$ profile is seen. We can see that $\Theta_{1} \left( \eta \right)$ is an increasing function in regard to $\gamma$. Because the scattering nanoparticles of ternary hybrid nanofluid are more impactful to magnetic field than the hybrid and nanofluid. The heat transmission effect of the ternary hybrid nanofluid is relatively higher than the both hybrid and nanoliquid, as density of fluid will improve the intermolecular overlap and thus boost the kinetic energy, which will increase the $\Theta_{1} \left( \eta \right)$ profile. Similarly, in Fig. 7, $\Theta_{2} \left( \eta \right)$ demonstrates an identical effect for $\gamma$ just a small modification in behavior for SiO₂ + TiO₂ + Al₂O₃/H₂O ternary hybrid nanofluid, TiO₂ + Al₂O₃/H₂O hybrid nanofluid, and SiO₂/H₂O nanofluid. Figures 8, 9 and 10 demonstrate the significance of $\phi$ (nanoparticles’ volume concentration) on $f^{\prime}\left( \eta \right)$ velocity field and temperatures fields $\Theta_{1} \left( \eta \right)$, $\Theta_{2} \left( \eta \right)$ in presence of SiO₂ + TiO₂ + Al₂O₃/H₂O ternary hybrid nanofluid, TiO₂ + Al₂O₃/H₂O hybrid nanofluid, and SiO₂/H₂O nanofluid.

Fig. 8

Variations in $f^{\prime}\left( \eta \right)$ with various values of $\phi$

Fig. 9

Variations in $\Theta_{1} \left( \eta \right)$ with various values of $\phi$

Fig. 10

Variations in $\Theta_{2} \left( \eta \right)$ with various values of $\phi$

Figure 8 shows that as the value of $\phi$ is enlarged, the $f^{\prime}\left( \eta \right)$ velocity of the existing fluid (nano, hybrid, and ternary hybrid nanofluid) declines. As we proceed away from the stretching surface, the $f^{\prime}\left( \eta \right)$ velocity decreases. Actuality, boosting the $\phi$ parameter leads the ferromagnetic fluid to condense, producing resistance in fluid motion and, as a result, the velocity of liquid decreases. Consequently, this figure shows that the velocity for TiO₂ + Al₂O₃/H₂O hybrid nanofluid and SiO₂/H₂O nanofluid are slower the velocity than SiO₂ + TiO₂ + Al₂O₃/H₂O ternary hybrid nanofluid in terms of flow rate. Figure demonstrates the effect of $\phi$ parameter on the $\Theta_{1} \left( \eta \right)$ temperature field of SiO₂/H₂O nanofluid, TiO₂ + Al₂O₃/H₂O hybrid nanofluid, and SiO₂ + TiO₂ + Al₂O₃/H₂O ternary hybrid nanofluid. The image shows that everywhere in the boundary layer region, there is a direct relationship between $\phi$ and $\Theta_{1} \left( \eta \right)$. According to the physical interpretation, SiO₂ + TiO₂ + Al₂O₃/H₂O ternary hybrid nanofluid has higher thermal conductivity than SiO₂/H₂O nanofluid, TiO₂ + Al₂O₃/H₂O hybrid nanofluid. Figure 10 illustrates an equivalent result of $\Theta_{2} \left( \eta \right)$ for SiO₂ + TiO₂ + Al₂O₃/H₂O ternary hybrid nanofluid, TiO₂ + Al₂O₃/H₂O hybrid nanofluid, and SiO₂/H₂O nanofluid with only a small variation in performance of fluid. Figure 11 depicts the effect of the $K^{*}$ (couple stress factor) on the $f^{\prime}\left( \eta \right)$ velocity profile of SiO₂ + TiO₂ + Al₂O₃/H₂O ternary hybrid nanofluid, TiO₂ + Al₂O₃/H₂O hybrid nanofluid, and SiO₂/H₂O nanofluid within the boundary layer. Increasing the values of $K^{*}$ produces a reduction in hybrid nanofluid movement due to a rise in drag force, which correlates to an apparent drop in fluid viscosity, as anticipated from the figure. Physically, the flow is delayed as a result of the addition of viscous effects which is generated by $K^{*}$, resulting in reduction in SiO₂ + TiO₂ + Al₂O₃/H₂O ternary hybrid nanofluid, TiO₂ + Al₂O₃/H₂O hybrid nanofluid, and SiO₂/H₂O nanofluid velocity profiles.

Fig. 11

Variations in $f^{\prime}\left( \eta \right)$ with various values of $K^{*}$

Figure 12 illustrates the characteristic of thermal profile $\Theta_{1} \left( \eta \right)$ for a different set of values $Rd$ (radiation parameter) in presence of SiO₂ + TiO₂ + Al₂O₃/H₂O ternary hybrid nanofluid, TiO₂ + Al₂O₃/H₂O hybrid nanofluid, and SiO₂/H₂O nanofluid. There is a direct relationship between $\Theta_{1} \left( \eta \right)$ and $Rd$ clearly as shown in the graph. When SiO₂ + TiO₂ + Al₂O₃/H₂O ternary hybrid nanofluid is utilized instead of TiO₂ + Al₂O₃/H₂O hybrid nanofluid, and SiO₂/H₂O nanofluid, therefore, the profiles show that thermal radiation has a greater impact on increasing the nanofluid temperature. Physically, strengthening radiative features stimulate the molecule mobility within the fluid, resulting in heat energy being converted through frequent collisions between nanoparticles. As a result, the $\Theta_{1} \left( \eta \right)$ temperature has improved. With only a minor difference in fluid outcomes for $\Theta_{2} \left( \eta \right)$ thermal profile. Figure 13 also a similar conclusion like $\Theta_{1} \left( \eta \right)$ for SiO₂ + TiO₂ + Al₂O₃/H₂O ternary hybrid nanofluid, TiO₂ + Al₂O₃/H₂O hybrid nanofluid, and SiO₂/H₂O nanofluid.

Fig. 12

Variations in $\Theta_{1} \left( \eta \right)$ with various values of $Rd$

Fig. 13

Variations in $\Theta_{2} \left( \eta \right)$ with various values of $Rd$

Skin friction declines with the larger amount of the nanoparticle volume fractions $\phi_{{{\text{SiO}}_{2} }} ,\phi_{{{\text{TiO}}_{2} }}$ and $\phi_{{{\text{Al}}_{2} {\text{O}}_{3} }}$. The tri-hybrid nanofluid creates more resistive forces to restrict the fluid motion and this happens when more nanoparticles are added to the base fluid. The comparison is shown in Fig. 14. The heat transfer rate varies with the variation of nanoparticle volume fractions $\phi_{{{\text{SiO}}_{2} }} ,\phi_{{{\text{TiO}}_{2} }} ,\phi_{{{\text{Al}}_{2} {\text{O}}_{3} }}$, as displayed in Figs. 15 and 16. The obtained results show that heat transfer rate improves with the larger amount of the nanoparticle volume fraction, as shown in Fig. 15. The improvement in the heat transfer rate is more prominent using the tri-hybrid nanofluids and this happens due to the effective thermal conductivity of $\phi_{{{\text{SiO}}_{2} }} ,\phi_{{{\text{TiO}}_{2} }} ,\phi_{{{\text{Al}}_{2} {\text{O}}_{3} }}$. The percentage-wise enhancement in the heat transfer rate as displayed in Fig. 16 shows that tri-hybrid nanofluid is more effective to increase the thermal efficiency of the fluid. In fact, from the experimental results, $\phi_{{{\text{Al}}_{2} {\text{O}}_{3} }}$ thermal conductivity provides a greater effect than $\phi_{{{\text{TiO}}_{2} }}$ and $\phi_{{{\text{SiO}}_{2} }}$. Therefore, the thermal performance increases with the stable dispersion of these three different types of nanoparticles in a single base fluid. Comparison for various values of $Nu_{x}$ is presented in Table 2.

Fig. 14

Skin friction under the influence of nanoparticle volume fractions

Fig. 15

Heat transfer rate under the influence of nanoparticle volume fraction

Fig. 16

Percentage-wise increase in the heat transfer rate under the influence of nanoparticle volume fraction

Conclusion

The flow and heat transport comparison of water base nanofluid, hybrid nanofluid, and ternary hybrid nanofluid across a stretched sheet is explored theoretically and numerically in this research work. Nonlinear thermal radiation and magnetic dipole effects are also considered. SiO₂, TiO₂, and Al₂O₃ are three nanoparticles studied in this work with H₂O as a base liquid. With the help of HAM, the boundary value problem is addressed analytically. The following results are some of the most noteworthy findings of the current work:

• In the presence of a magnetic dipole, $f^{\prime}\left( \eta \right)$ velocity of nano, hybrid, and tri-hybrid nanofluid decline as the value of volume concentration of nanoparticle ($\phi$) rises, while the temperature fields $\Theta_{1} \left( \eta \right),\,\Theta_{2} \left( \eta \right)$ show opposite trend. The velocity and temperature of turnery hybrid nanofluid present prominent results.

• By enhancing the values of $\beta$, the velocities of nano, hybrid, and tri-hybrid nanofluid decreases where the temperature fields increase more quickly.

• The $\Theta_{1} \left( \eta \right),\,\Theta_{2} \left( \eta \right)$ fields of fluid gradually decline by improving the Prandtl number, whereas it enhances by increasing the values of thermal radiation.

• Skin friction declines with the larger amount of the nanoparticle volume fractions $\phi_{{{\text{SiO}}_{2} }} ,\phi_{{{\text{TiO}}_{2} }} ,\phi_{{{\text{Al}}_{2} {\text{O}}_{3} }}$. The comparisons among these fluids are shown graphically.

• The heat transfer rate improves with the larger amount of the nanoparticle volume fraction. Also, prominent results presented by using the tri-hybrid.

• Therefore, the thermal performance increases with the stable dispersion of these three different types of nanoparticles in a single base fluid.

• We may deduce from the preceding study and graphs that the heat transfer rate in tri-hybrid nanofluid is much more effective than the hybrid and nanofluid.

Due to the relevance of modified nanofluid (tri-hybrid nanofluid), researchers and scientists may utilize these modified nanofluids for effective processing in emerging technologies and for cooling system in various electrical and electronic applications.