Introduction

In the present decade, researchers are interested in mixing up different nanoparticles with different base fluids in order to enhance the thermal conductivity of regular fluids such as water, propylene glycol, ethylene glycol, and kerosene oil. The resultant fluids, known as nanofluids, have different characteristics and can be used in biomedical applications in cooling, engineering, process industries, and cancer therapy. Thermal conductivity and heat transfer of convectional fluids are enhanced by dispersing the solid particles in the recent advances in nanotechnology and engineering. It is worth to highlight that the heat transfer coefficient increases as expected after the suspension of these particles. Physically, it is possible because the thermal conductivity of solid particles, such as metal and carbon nanotubes, is higher than that of regular base fluids. Therefore, heat transfer and thermal conductivity are enhanced. There are many advantages of these fluids such as better wetting, sufficient viscosity, and more stability [1]. Some commonly used nanoparticles are oxides (\({\text{Al}}_{2} {\text{O}}_{3}\)), metals (Al, Ag, Cu), nitrides (AlN, SiN), nonmetals (graphite, carbon nanotubes), carbides (SiC), etc. Generally, the diameter of these nanoparticles is between 1–100 nm. According to experimental studies by researchers [2,3,4,5,6,7,8], 5%, 10%, …, 55% volume fraction of nanoparticles are considered for a better rate of heat transfer and thermal conductivity of base fluids. It is discovered that the maximum effective rate of heat transfer is possible when the volume fraction of nanoparticles is 5%. There are many applications where nanofluids are used effectively such as fuel cell, transportation, biomedicine, and nuclear reactors. [9,10,11]. The better cooling performance, the higher thermal conductivity and the rate of heat transfer can be achieved by using a magnetic force. As an instance, continuous strips and drawing filaments can control the cooling rate with the help of electrically conducting nanofluids [12, 13]. Ferrofluids can be defined as the electrically conducting nanofluids where base fluids contain nanoparticles such as Hematite, Magnetite, Cobalt Ferrite or other compounds having iron. The thermal conductivity of nanofluids depends upon numerous factors such as size, shape, and volume fraction of the solid particles, the surrounding temperature, and base fluid [14,15,16].

It can be seen that many researchers considered different fluids and particles in order to enhance thermal conductivity. Lund et al. [17] considered sodium alginate as a base fluid in their studies and found dual solutions. Water-based nanofluid was studied by Bhatta et al. [18] and concluded that “enhancement in the heat transfer coefficient is noted due to the interaction of buoyancy parameter”. Hayat et al. [19] examined a nanofluid by considering two base fluids, namely kerosene oil and water with carbon nanotubes as the nanoparticles. Selimefendigil et al. [20] investigated \({\text{Fe}}_{3} {\text{O}}_{4}\)/water nanofluid in the channel and found that when the volume fraction of nanoparticles is 12–15%, Nusselt number increases more effectively. \({\text{TiO}}_{2}\)/water nanofluid was investigated by Kristiawan et al. [21] and stated that this nanofluid enhances the heat transfer rate and decreases the pressure. Dero et al. [22] examined Cu/water nanofluid and found dual solutions. Further, they performed a stability analysis to observe a stable solution. Some other development of nanofluid can be seen in these articles [23,24,25,26,27,28,29]. It is observed from the previous studies that the thermal conductivity of copper particles is higher as compared to the alumina and other solid nanoparticles. Further, solid particles of iron oxide are important to consider when the magnetic effect is incorporated. Therefore, both copper and iron oxide particles have been considered in this study in order to enhance the heat transfer rate effectively.

There are two fluid models in the computational fluid dynamics (CFD), namely Buongiorno’s model [30] and Tiwari and Das’s model [31]. Both models have been used intensively when researchers deal with nanofluid by numerical approaches. Due to the presence of nonlinearity in the governing equations, many researchers attempted to find multiple solutions as they have many applications in various fields of science. Khashi’ie et al. [32] successfully found dual solutions for three-dimensional MHD flow of nanofluid. Moreover, they considered Buongiorno’s model and examined the effect of thermophoresis and Brownian motion parameters. Mixed convection flow of water-based nanofluid was investigated by Jamaludin et al. [33]. Further, Tiwari and Das’s model [31] has been used to deal with governing equations, and they found dual solutions in the ranges of various parameters and performed stability analysis. Ali et al. [34] examined the MHD flow of micropolar nanofluid and found triple solutions. By performing stability analysis, they claimed that only the first solution is stable. Many important related references of non-uniqueness of solutions of nanofluids can be seen in these articles [35,36,37,38,39,40,41].

It can be concluded from the above-mentioned studies that researchers are still interested in searching for new kinds of fluids that are more capable of enhancing thermal conductivity and heat transfer rate. In this regard, researchers introduced new kinds of nanofluids called “hybrid nanofluids” recently. They believed that these fluids offer better thermal conductivity as compared to simple nanofluids. Hybrid nanofluid is the extension of nanofluid in which two different kinds of nanoparticles are suspended in a single base fluid [42]. There are many applications in numerous fields such as generator cooling, nuclear system cooling, drug reduction, biomedical, electronic cooling, the coolant in machining, and refrigeration where these kinds of fluid can be used effectively [43]. Ahmed et al. [44] studied hybrid nanofluid by considering nanoparticles and water as a base fluid and found a single solution. Devi and Devi [45] examined the hydromagnetic flow of \({\text{Cu}} - {\text{Al}}_{2} {\text{O}}_{3}\)/water hybrid nanofluid over the stretching surface and found a single solution. Their work was then extended by Waini et al. [46] for the multiple solutions. In the same year, the unsteady flow of hybrid nanofluid was examined by Waini et al. [47] and dual solutions were successfully noticed. There are only a few researchers who considered hybrid nanofluids for multiple solutions [48,49,50,51,52,53].

Motivated by the above works, our prime objective of this study is to find multiple solutions of hybrid nanofluid in the presence of magnetic, porous, and viscous dissipation effect over nonlinear permeable shrinking/stretching surfaces theoretically by employing of Tiwari and Das’s model [31] which has not been studied before. Two different kinds of nanoparticles are considered, namely Cu (copper) and \({\text{Fe}}_{3} {\text{O}}_{4}\) (iron oxide) in base fluid (water). It is expected that these findings would help those who are interested in increasing the heat transfer rate through experiments and finding multiple solutions for hybrid nanofluids.

Problem formulation

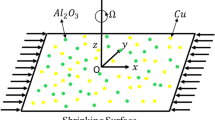
We have considered the two-dimensional laminar flow of electrically conducting hybrid nanofluid on nonlinearly shrinking/stretching surfaces with the effect of porous and viscous dissipation. Water is assumed as a base fluid, and copper and magnetite are considered as nanoparticles. Further, it is also assumed that the magnetic field effect is constant \(B = B_{0} x ^{(1-{\text{m}})/2}\) and applied in the perpendicular direction to hybrid nanofluid flow. It is also supposed that base fluid and the nanoparticles are in thermal equilibrium. The surface is stretched and shrunk along a velocity \(u_{{\text{w}}} \left( x \right) = ax^{{\text{m}}}\), where \(a\) is a constant and \(m\) is a power index. Velocity of wall mass suction is \(v_{{\text{w}}} \left( x \right) = - b\sqrt {c\vartheta } x^{{\left( {{\text{m}} - 1} \right)/2}}\) as seen in Fig. 1. The external forces and pressure gradients are ignored. By considering all the above assumptions, the governing equations of momentum and heat boundary layers in the model of Tiwari and Das [31] can be written as:

$$\frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0$$
(1)
$$u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} = \frac{{\mu_{{{\text{hnf}}}} }}{{\rho_{{{\text{hnf}}}} }}\frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{{\mu_{{{\text{hnf}}}} }}{{\rho_{{{\text{hnf}}}} }}\frac{u}{{K_{1} }} - \frac{{\sigma^{*} B ^{2} u}}{{\rho_{{{\text{hnf}}}} }}$$
(2)
$$u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} = \frac{{k_{{{\text{hnf}}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{hnf}}}} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{\mu_{{{\text{hnf}}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{hnf}}}} }}\left( {\frac{\partial u}{{\partial y}}} \right)^{2}$$
(3)
Fig. 1
figure 1

Physical models and coordinate systems

Full size image

The subjected boundary conditions are

$$\left\{ {\begin{array}{*{20}c} {v = v_{{\text{w}}} \left( x \right), u = u_{{\text{w}}} \left( x \right), T = T_{{\text{w}}} \, {\text{as}}\,y \to 0} \\ {u \to 0, T \to T_{\infty } \,{\text{as}}\,y \to \infty } \\ \end{array} } \right.$$
(4)

In this study, the following subsequent definitions are used [49,50,51], which are given in Table 1. Table 2 is constructed for the thermophysical features of nanomaterials and base.

Table 1 Thermophysical properties of hybrid nanofluid
Full size table
Table 2 The thermophysical properties of the base fluid (water) and the nanoparticles [13, 63]
Full size table

Now, the following variables of similarity transformation are introduced as:

$$\left\{ {\begin{array}{*{20}c} { v = - \sqrt {\frac{{c\vartheta \left( {m + 1} \right)}}{2}} x^{{\left( {{\text{m}} - 1} \right)/2}} \left[ {f\left( \eta \right) + \frac{m - 1}{{m + 1}}\eta f^{\prime}\left( \eta \right)} \right]} \\ {u = cx^{{\text{m}}} f^{\prime}\left( \eta \right), \eta = y\sqrt {\frac{{c\left( {m + 1} \right)}}{2\vartheta }} x^{{\left( {{\text{m}} - 1} \right)/2}} } \\ {\theta \left( \eta \right) = {\raise0.7ex\hbox{${\left( {T - T_{\infty } } \right)}$} \!\mathord{\left/ {\vphantom {{\left( {T - T_{\infty } } \right)} {\left( {T_{{\text{w}}} - T_{\infty } } \right)}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\left( {T_{{\text{w}}} - T_{\infty } } \right)}$}}} \\ \end{array} } \right.$$
(5)

The implementation of Eq. (5) into Eqs. (1–3) leads to the subsequent equations

$$f^{\prime\prime\prime} + \xi_{1} \left\{ {f^{^{\prime\prime}} f - \frac{2m}{{\left( {m + 1} \right)}}\left( {f^{\prime}} \right)^{2} } \right\} - \frac{2}{{\left( {m + 1} \right)}}\left\{ {M\left( {1 - \phi_{Cu} } \right)^{2.5} \left( {1 - \phi_{{Fe_{3} O_{4} }} } \right)^{2.5} + K} \right\}f^{\prime} = 0$$
(6)
$$\frac{{\xi_{2} }}{\Pr }\theta^{^{\prime\prime}} + \theta ^{\prime}f - \frac{4m}{{\left( {m + 1} \right)}} \theta f^{\prime} + \xi_{3} {\text{Ec}}\left( {f^{\prime\prime}} \right)^{2} = 0$$
(7)

Subject to boundary conditions

$$\left\{ {\begin{array}{*{20}c} {f\left( 0 \right) = - b\sqrt {\frac{2}{m + 1}} ,f^{\prime}\left( 0 \right) = \lambda , \theta \left( 0 \right) = 1} \\ {f^{\prime}\left( \eta \right) \to 0,\theta \left( \eta \right) \to 0 \,{\text{as}}\,\eta \to \infty } \\ \end{array} } \right.$$
(8)

In the above equations, we have

$$\left\{ \begin{gathered} M = \frac{{\sigma^{*} B_{0}^{2} }}{{c\rho_{{\text{f}}} }},K = \frac{{\vartheta_{{\text{f}}} }}{{cK_{1} x^{{\text{m}} - 1} }},\lambda = \frac{a}{c}, \Pr = \frac{{\vartheta_{{\text{f}}} }}{{\alpha_{{\text{f}}} }},{\text{Ec}} = \frac{{c^{2} \rho_{{\text{f}}} }}{{T_{0} \left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }} \hfill \\ \xi_{1} = \left( {1 - \phi_{{{\text{Cu}}}} } \right)^{2.5} \left( {1 - \phi_{{{\text{Fe}}_{{3}} {\text{O}}_{{4}} }} } \right)^{2.5} \left\{ {\left( {1 - \phi_{{{\text{Fe}}_{{3}} {\text{O}}_{{4}} }} } \right)\left[ {1 - \phi_{{{\text{Cu}}}} + \phi_{{{\text{Cu}}}} \left( {{\raise0.7ex\hbox{${\rho_{{{\text{Cu}}}} }$} \!\mathord{\left/ {\vphantom {{\rho_{{{\text{Cu}}}} } {\rho_{{\text{f}}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\rho_{{\text{f}}} }$}}} \right)} \right] + \phi_{{{\text{Fe}}_{{3}} {\text{O}}_{{4}} }} \left( {{\raise0.7ex\hbox{${\rho_{{{\text{Fe}}_{{3}} {\text{O}}_{{4}} }} }$} \!\mathord{\left/ {\vphantom {{\rho_{{{\text{Fe}}_{{3}} {\text{O}}_{{4}} }} } {\rho_{{\text{f}}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\rho_{{\text{f}}} }$}}} \right)} \right\} \hfill \\ \xi_{2} = \frac{{\left( {k_{{{\text{hnf}}}} /k_{{\text{f}}} } \right)}}{{\left\{ {\left( {1 - \phi_{{{\text{Fe}}_{{3}} {\text{O}}_{{4}} }} } \right)\left[ {1 - \phi_{{{\text{Cu}}}} + \phi_{{{\text{Cu}}}} \frac{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{Cu}}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }}} \right] + \phi_{{{\text{Fe}}_{{3}} {\text{O}}_{{4}} }} \frac{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{Fe}}_{{3}} {\text{O}}_{{4}} }} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }}} \right\}}} \hfill \\ \xi_{3} = \frac{1}{{\left( {1 - \phi_{{{\text{Cu}}}} } \right)^{2.5} \left( {1 - \phi_{{{\text{Fe}}_{{3}} {\text{O}}_{{4}} }} } \right)^{2.5} \left\{ {\left( {1 - \phi_{{{\text{Fe}}_{{3}} {\text{O}}_{{4}} }} } \right)\left[ {1 - \phi_{{{\text{Cu}}}} + \phi_{{{\text{Cu}}}} \frac{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{Cu}}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }}} \right] + \phi_{{{\text{Fe}}_{{3}} {\text{O}}_{{4}} }} \frac{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{Fe}}_{{3}} {\text{O}}_{{4}} }} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }}} \right\}}} \hfill \\ \end{gathered} \right.$$
(9)

The interesting physical quantities are the skin friction coefficient \(C_{{\text{f}}}\) and local Nusselt number \({\text{Nu}}_{{\text{x}}}\):

$$C_{{\text{f}}} = \frac{{2\mu_{{{\text{hnf}}}} }}{{\rho_{{\text{f}}} u_{{\text{w}}}^{2} }}\left( {\frac{\partial u}{{\partial y}}} \right)\left| {y = 0} \right., {\text{Nu}}_{{\text{x}}} = - \frac{{xk_{{{\text{hnf}}}} }}{{k_{{\text{f}}} \left( {T_{{\text{w}}} - T_{\infty } } \right)}}\left( {\frac{\partial T}{{\partial y}}} \right)\left| {y = 0} \right.$$
(10)

By applying Eq. (9) in Eq. (10), we have

$$\sqrt {\text{Re}} C_{{\text{f}}} = \frac{1}{{\left( {1 - \phi_{{{\text{Cu}}}} } \right)^{2.5} \left( {1 - \phi_{{{\text{Al}}_{{2}} {\text{O}}_{{3}} }} } \right)^{2.5} }}\sqrt {\frac{{\left( {m + 1} \right)}}{2}} f^{\prime\prime}\left( 0 \right); \sqrt {\frac{1}{{\text{Re}}}} {\text{Nu}}_{{\text{x}}} = - \frac{{k_{{{\text{hnf}}}} }}{{k_{{\text{f}}} }}\sqrt {\frac{{\left( {m + 1} \right)}}{2}} \theta^{\prime}\left( 0 \right)$$
(11)

where \({\text{Re}} = \frac{{cx^{{\text{m}}} }}{{\vartheta_{{\text{f}}} }}\) is local Reynolds number.

Stability analysis

There is a problem to know which solution is more stable when more than one solution exists in any fluid model. Researchers created a new method by introducing a new dimensionless time variable \(\tau\) [47, 48, 54, 55] in which they performed the stability analysis of solutions mathematically. This study is carried out by many researchers in their studies, some of them can be seen in these references [56,57,58,59]. The first step of performing the stability of the solution is to change the governing Eqs. (2–3) in unsteady form.

$$\frac{\partial u}{{\partial t}} + u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} = \frac{{\mu_{{{\text{hnf}}}} }}{{\rho_{{{\text{hnf}}}} }}\frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{{\mu_{{{\text{hnf}}}} }}{{\rho_{{{\text{hnf}}}} }}\frac{u}{{K_{1} }} - \frac{{\sigma^{*} B^{2} u}}{{\rho_{{{\text{hnf}}}} }}$$
(12)
$$\frac{\partial T}{{\partial t}} + u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} = \frac{{k_{{{\text{hnf}}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{hnf}}}} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{\mu_{{{\text{hnf}}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{hnf}}}} }}\left( {\frac{\partial u}{{\partial y}}} \right)^{2}$$
(13)

Equation (5) with new dimensionless variables for the unsteady problem can be written as

$$\left\{ {\begin{array}{*{20}c} { v = - \sqrt {\frac{{c\vartheta \left( {m + 1} \right)}}{2}} x^{{\left( {{\text{m}} - 1} \right)/2}} \left[ {f\left( \eta \right) + \frac{m - 1}{{m + 1}}\eta f^{\prime}\left( \eta \right)} \right]} \\ {u = cx^{{\text{m}}} f^{\prime}\left( \eta \right), \eta = y\sqrt {\frac{{c\left( {m + 1} \right)}}{2\vartheta }} x^{{\left( {{\text{m}} - 1} \right)/2}} } \\ {\theta \left( \eta \right) = {\raise0.7ex\hbox{${\left( {T - T_{\infty } } \right)}$} \!\mathord{\left/ {\vphantom {{\left( {T - T_{\infty } } \right)} {\left( {T_{{\text{w}}} - T_{\infty } } \right)}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\left( {T_{{\text{w}}} - T_{\infty } } \right)}$}},\tau = cx^{{{\text{m}} - 1}} t} \\ \end{array} } \right.$$
(14)

By putting Eq. (14) into Eqs. (12–13), we have:

$$f^{\prime\prime\prime} + \xi_{1} \left\{ {f^{^{\prime\prime}} f - \frac{2m}{{\left( {m + 1} \right)}}\left( {f^{\prime}} \right)^{2} } \right\} - \frac{2}{{\left( {m + 1} \right)}}\left\{ {M\left( {1 - \phi_{{{\text{Cu}}}} } \right)^{2.5} \left( {1 - \phi_{{{\text{Fe}}_{{3}} {\text{O}}_{{4}} }} } \right)^{2.5} + K} \right\}f^{\prime} - \frac{{2\xi_{1} }}{m + 1}\left[ {1 + \left( {m - 1} \right)\tau \frac{\partial f}{{\partial \eta }}} \right]\frac{{\partial^{2} f}}{\partial \eta \partial \tau } = 0$$
(15)
$$\frac{{\xi_{2} }}{\Pr }\theta^{^{\prime\prime}} + \theta ^{\prime}f - \frac{4m}{{\left( {m + 1} \right)}} \theta f^{\prime} + \xi_{3} {\text{Ec}}\left( {f^{\prime\prime}} \right)^{2} - \frac{2}{m + 1}\left[ {1 + \left( {m - 1} \right)\tau \frac{\partial f}{{\partial \eta }}} \right]\frac{\partial \theta }{{\partial \tau }} = 0$$
(16)

The new corresponding boundary conditions are

$$\left\{ {\begin{array}{*{20}c} {f\left( {0,\tau } \right) = - b\sqrt {\frac{2}{m + 1}} ,\frac{{\partial f\left( {0,\tau } \right)}}{\partial \eta } = \lambda , \theta \left( {0,\tau } \right) = 1} \\ {\frac{{\partial f\left( {\eta ,\tau } \right)}}{\partial \eta } \to 0,\theta \left( {\eta ,\tau } \right) \to 0\,{\text{as}}\,\eta \to \infty } \\ \end{array} } \right.$$
(17)

The unknown functions are needed to define; these functions depend on the time parameter, in order to obtain the stability of solutions

$$\left\{ {\begin{array}{*{20}c} {f\left( {\eta ,\tau } \right) = f_{0} \left( \eta \right) + e^{ - \gamma \tau } F\left( {\eta ,\tau } \right)} \\ {\theta \left( {\eta ,\tau } \right) = \theta_{0} \left( \eta \right) + e^{ - \gamma \tau } G\left( {\eta ,\tau } \right)} \\ \end{array} } \right.$$
(18)

where \(f_{0} \left( \eta \right)\) and \(\theta_{0} \left( \eta \right)\) are the small relatives of \(F\left( {\eta ,\tau } \right)\) and \(G\left( {\eta ,\tau } \right)\), respectively, which indicate the steady solutions of Eqs. (6–7). Further, \(\gamma\) is the unknown eigenvalue parameter, which will provide the infinite number of the values of eigenvalue. By introducing Eq. (18) into Eqs. (15–16), we get

$$\begin{aligned} & \frac{{\partial^{3} F}}{{\partial \eta^{3} }} + \xi_{1} \left\{ {f_{0} \frac{{\partial^{2} F}}{{\partial \eta^{2} }} + F\frac{{d^{2} f_{0} }}{{d\eta^{2} }} - \frac{4m}{{\left( {m + 1} \right)}}\frac{{df_{0} }}{d\eta }\frac{\partial F}{{\partial \eta }}} \right\} - \frac{2}{{\left( {m + 1} \right)}}\left\{ {M\left( {1 - \phi_{{{\text{Cu}}}} } \right)^{2.5} \left( {1 - \phi_{{{\text{Fe}}_{{3}} {\text{O}}_{{4}} }} } \right)^{2.5} + K} \right\}\frac{\partial F}{{\partial \eta }} \\ & \quad + \frac{{2\xi_{1} }}{m + 1}\left[ {1 + \left( {m - 1} \right)\tau \frac{{df_{0} }}{d\eta }} \right]\gamma \frac{\partial F}{{\partial \eta }} = 0 \\ \end{aligned}$$
(19)
$$\frac{{ \xi_{2} }}{\Pr }\frac{{\partial^{2} G}}{{\partial \eta^{2} }} + \frac{{d\theta_{0} }}{d\eta }F + \frac{\partial G}{{\partial \eta }}f_{0} - \frac{4m}{{\left( {m + 1} \right)}}\left( {\theta_{0} \frac{\partial F}{{\partial \eta }} + G\frac{{df_{0} }}{d\eta }} \right) + 2{\text{Ec}} \xi_{3} \frac{{d^{2} f_{0} }}{{d\eta^{2} }}\frac{{\partial^{2} F}}{{\partial \eta^{2} }} + \frac{2}{m + 1}\left[ {1 + \left( {m - 1} \right)\tau \frac{{df_{0} }}{d\eta }} \right]\gamma G = 0$$
(20)

The steady solutions of the equation can be obtained by keeping \(\tau = 0\), where \(F\left( {\eta ,\tau } \right)\) and \(G\left( {\eta ,\tau } \right)\) are reduced to \(F_{0}\) and \(G_{0}\), respectively, in Eqs. (19–20). In order to find the initial decay or growth of the solutions, we have to solve the following system of linearized eigenvalue problems

$$\xi_{1} F_{0}^{\prime\prime\prime} + \xi_{1} \left\{ {f_{0} F_{0}^{^{\prime\prime}} + F_{0} f_{0}^{^{\prime\prime}} } \right\} - \frac{2}{{\left( {m + 1} \right)}}\left\{ {M\left( {1 - \phi_{{{\text{Cu}}}} } \right)^{2.5} \left( {1 - \phi_{{{\text{Fe}}_{{3}} {\text{O}}_{{4}} }} } \right)^{2.5} + K} \right\}F_{0}^{^{\prime}} + \frac{{2\xi_{1} }}{m + 1}\left( {\gamma - 2mf_{0}^{^{\prime}} } \right)F_{0}^{^{\prime}} = 0$$
(21)
$$\frac{{ \xi_{2} }}{\Pr }G_{0}^{^{\prime\prime}} + \theta_{0}^{^{\prime}} F_{0} + G_{0}^{^{\prime}} f_{0} + 2{\text{Ec}} \xi_{3} f_{0}^{^{\prime\prime}} F_{0}^{^{\prime\prime}} - \frac{4m}{{\left( {m + 1} \right)}}\theta_{0} F_{0}^{^{\prime}} + \frac{2}{m + 1}\left( {\gamma - 2mf_{0}^{^{\prime}} } \right)G_{0} = 0$$
(22)

Subject to boundary conditions

$$\left\{ {\begin{array}{*{20}c} {F_{0} \left( 0 \right) = 0, F_{0}^{^{\prime}} \left( 0 \right) = 0, G_{0} \left( 0 \right) = 0} \\ {F_{0}^{^{\prime}} \left( \eta \right) \to 0, G_{0} \left( \eta \right) \to 0\,{\text{as}}\, \eta \to \infty } \\ \end{array} } \right.$$
(23)

We followed the procedure of the Mustafa et al. [60] and Lund et al. [61], in which they stated that the one boundary condition should be relaxed to find the values of eigenvalue. In this problem, \(F_{0}^{^{\prime}} \left( \eta \right) \to 0\,{\text{as}}\, \eta \to \infty\) is converted into \(F_{0}^{^{\prime\prime}} \left( 0 \right) = 1\).

Results and discussion

The prime concern of the current segment is to demystify the physical importance of numerical results presented in graphical representation. Flow along with heat transfer and viscous dissipation of \({\text{H}}_{{2}} {\text{O}}\)-based hybrid nanofluid (\({\text{Cu}} - {\text{Fe}}_{{3}} {\text{O}}_{{4}}\)) over a nonlinear shrinking sheet has been inspected numerically with Runge–Kutta fourth order along with the shooting technique. In this study, the thermophysical properties of Devi and Devi [45] have been used as it has been proven that their results have good agreement with the experimental results of Suresh et al. [62]. Henceforth, we expect that these results would provide good direction and understanding in order to enhance the rate of heat transfer numerically and experimentally. We compared the results of coefficient of skin friction for \({\text{Al}}_{{2}} {\text{O}}_{{3}} - {\text{Cu}}/{\text{H}}_{{2}} {\text{O}}\) hybrid nanofluid for different values of \(\phi_{{{\text{Cu}}}}\) when \(\phi_{{{\text{Al}}_{{2}} {\text{O}}_{{3}} }} = 0.1, S = 0, \Pr = 6.135, \lambda = 1,M = \beta = 0\) with Devi and Devi [63] and Lund et al. [53] in order to validate the results of the current study (refer to Table 3) and found in excellent agreement. The effects of the suction parameter along with solid volume fraction of \({\text{Cu}}\) and \({\text{Fe}}_{{3}} {\text{O}}_{{4}}\) are presented in Figs. 2–5. In Fig. 2, it can be noticed that multiple solutions exist only for the case of suction by the various intensities of copper-type nanoparticle. In this regard, the critical values of suction parameter b for \(\phi_{{{\text{Cu}}}} = 0.005, 0.05, 0.1\), are \(b_{{{\text{c1}}}} = - 3.2064, b_{{{\text{c2}}}} = - 3.0788, \,{\text{and}}\, b_{{{\text{c3}}}} = - 3.0019\), respectively. Moreover, the skin friction coefficient is increased (decreased) by incorporating the copper-type nanoparticles in the base fluid for the first (second) solution. Physically, we can interpret that the velocity of nanofluid near the surface declines as the solid volume fraction rises in the base fluid from 0.5% to 1% only for the case of the first solution.

Table 3 The compression of \(\sqrt {\text{Re}} C_{{\text{f}}}\) with Devi and Devi [63] and Lund et al. [53]
Full size table
Fig. 2
figure 2

Skin frictions plot with b for different \({\phi }_{\mathrm{C}\mathrm{u}}\)

Full size image

In the same manner, the combined effect of the suction parameter and solid volume fraction of \({\text{Fe}}_{{3}} {\text{O}}_{{4}}\) is plotted in Fig. 3. From this profile, it observed that the skin friction coefficient decreases (increases) by the rise in the solid volume fraction of \({\text{Fe}}_{{3}} {\text{O}}_{{4}}\) in the base fluid for the first (second) solution. Therefore, we can conclude that the effect of \({\text{Fe}}_{{3}} {\text{O}}_{{4}}\) nanoparticles on the skin friction coefficient is totally opposite to the effect of copper type nanoparticles. Hence, the velocity near the solid surface increases (decreases) in the first (second) solution. Moreover, it is also observed from this profile that dual solutions exist only for the case of suction and critical values of suction parameter b for \(\phi_{{{\text{Fe}}_{{3}} {\text{O}}_{{4}} { }}} = 0.05, 0.5, 0.1\) are \(b_{{{\text{c1}}}} = - 3.0582\), \(b_{{{\text{c2}}}} = - 3.0788,\) and \(b_{{{\text{c3}}}} = - 3.1249\). Figure 4 shows the effect of heat transfer coefficient \(- \theta^{\prime}\left( 0 \right)\) with variation of \(b\) by variation of \(\phi_{{{\text{Cu}}}}\). It is noticed that there are regions of two solutions \(b \le b_{{\text{c}}}\), and no solution range is \(b > b_{{\text{c}}}\). Here, \(b_{{\text{c}}}\) is the critical value of b (10% volume fraction) where the dual solution exists. Moreover, it is noticed from this profile that the heat transfer coefficient decreases by simultaneously enhancing \(\phi_{{{\text{Cu}}}}\) and \(b\). It is worth to notice that due to the instability of the second solution, singularities exist as shown in the upper half of the graphs. The same scenario can be depicted in Fig. 5 for \(\phi_{{{\text{Fe}}_{{3}} {\text{O}}_{{4}} }}\).

Fig. 3
figure 3

Skin frictions plot with b for different \({\phi }_{\mathrm{F}{\mathrm{e}}_{3}{\mathrm{O}}_{4}}\)

Full size image
Fig. 4
figure 4

Heat transfer rate plot with b for different \({\phi }_{\mathrm{C}\mathrm{u}}\)

Full size image
Fig. 5
figure 5

Heat transfer rate plot with b for different \({\phi }_{\mathrm{F}{\mathrm{e}}_{3}{\mathrm{O}}_{4}}\)

Full size image

Figure 6 presents the effects of various values of \(\phi_{{{\text{Cu}}}}\)- and \(\phi_{{{\text{Fe}}_{{3}} {\text{O}}_{{4}} }}\)-type nanofluids. The effects of magnetic parameter \(M\) on velocity profile \(f^{\prime}\left( \eta \right)\) are shown in Fig. 7. Clearly, it is seen that the velocity of the hybrid nanofluid increases as the intensity of the magnetic parameter rises gradually for the first solution and decreases for the second solution. Generally, we can say that boundary layer thickness inclines monotonically for the first solution and decreases for the second solution due to the Lorentz force which creates the resistivity on the fluid flow inside the boundary layer. Hence, the motion of solid nanoparticles diminishes. Figure 8 presents the effects of permeability coefficient on velocity profile. It is seen that at higher values of permeability the velocity of hybrid nanofluid deaccelerates in the first solution and accelerates for the second solution. The impact of power index \(m\) can be seen in Fig. 9 on velocity profile. It is perceived that as power index \(m \ge 1\), the boundary layer thickness rises gradually and therefore velocity of the hybrid nanoparticles increases for both solutions.

Fig. 6
figure 6

Velocity plot for different values of nanoparticle volume fractions

Full size image
Fig. 7
figure 7

Velocity plot for increasing values of M

Full size image
Fig. 8
figure 8

Velocity plot for increasing values of K

Full size image
Fig. 9
figure 9

Velocity plot for increasing values of m

Full size image

Figure 10 elucidates the effect of \(\phi_{{{\text{Cu}}}}\) and \(\phi_{{{\text{Fe}}_{{3}} {\text{O}}_{{4}} }}\) on temperature profile \(\theta \left( \eta \right)\). It is realized from this graph that for the case of simple viscous fluid where the intensity of \(\phi_{{{\text{Cu}}}}\) and \(\phi_{{{\text{Fe}}_{{3}} {\text{O}}_{{4}} }}\) are negligible (i.e., \(\phi_{{{\text{Cu}}}} = \phi_{{{\text{Fe}}_{{3}} {\text{O}}_{{4}} }} = 0\)), the temperature profile is much lower. In other words, the thermal boundary layer thickness of viscous fluid is lower as compared to hybrid nanofluid. Moreover, it is worthy to notify that the thermal boundary layer becomes thicker for a 5% suspension of nanoparticles of \({\text{Cu}}\) and \({\text{Fe}}_{{3}} {\text{O}}_{{4}}\) in the base fluid. Similarly, the upshot of the magnetic parameter \(M\) on temperature profile is depicted in Fig. 11. In the first solution, the temperature of the hybrid nanofluid increases as the strength of the magnetic parameter \(M\) increases. From the physical aspect, we can say that the rise in the magnetic parameter produces the Lorentz force which contributes to increase in the temperature of the fluid due to the slowdown of the fluid motion. Similar behavior of temperature profile can be seen in Fig. 12 for the variation of permeability parameter \(K\). Outcomes of power index \(m\) and Eckert number \({\text{Ec}}\) on temperature profile are plotted in Figs. 13 and 14, respectively. From these graphs, it is noticed that the temperature profile of hybrid nanofluid is directly proportional to power index \(m\) and Eckert number \({\text{Ec}}{.}\) Physically, the thickness of the thermal layer, as well as the temperature of the fluid increase due to the high intensity of kinetic energy as Eckert number, is directly proportional to the kinetic energy.

Fig. 10
figure 10

Temperature plot for different values of nanoparticle volume fractions

Full size image
Fig. 11
figure 11

Temperature plot for increasing values of M

Full size image
Fig. 12
figure 12

Temperature plot for increasing values of K

Full size image
Fig. 13
figure 13

Temperature plot for increasing values of m

Full size image
Fig. 14
figure 14

Temperature plot for increasing values of Ec

Full size image

Finally, Table 4 gives the values of the smallest eigenvalue for variation of suction parameter. It can be concluded easily that the first solution is the stable one as the sign of the value of the smallest eigenvalue is positive which shows the initial decay, while in the second solution, the sign of the values of the smallest eigenvalue is negative, indicating the existence of the initial growth of disturbance which causes the solution to be unstable.

Table 4 The smallest eigenvalues \(\gamma\) for the several values of suction parameter \(b\) at \(\phi_{{{\text{Cu}}}} = \phi_{{{\text{Al}}_{{2}} {\text{O}}_{{3}} }} = 0.05\) \(m = 5, \Pr = 6.2,\,{\text{Ec}} = M = K = 0.1\) and \(\lambda = - 1\)
Full size table

Conclusions

In the current study, 2D steady MHD flow of \({\text{Cu}} - {\text{Fe}}_{{3}} {\text{O}}_{4} /{\text{H}}_{{2}} {\text{O}}\) hybrid nanofluid over the nonlinear stretching/shrinking surface has been examined. The effects of energy dissipation function and porous term also have been taken into account. Similarity variables are used to change the partial differential equations (PDEs) into ODEs. ODEs are solved by employing the shooting method with the RK fourth-order method. For the stability of solutions, a three-stage Lobatto IIIa formula has been used to find the values of the smallest eigenvalue. In light of the present examination, the following points are the major findings of this study.

  1. 1.

    There is a region of dual solutions that depend upon the suction and stretching/shrinking parameters, respectively.

  2. 2.

    The results of the stability analysis reveal that the first solution is more stable as compared to the second solution.

  3. 3.

    The rate of heat transfer reduces when suction and solid volume fraction of copper are increased.

  4. 4.

    The thickness of the hydrodynamic boundary layer increases for the intensive impact of the magnetic field, permeability, and power index parameter in the first solution, while reverse nature of velocity profiles is noticed in the second solution when the magnetic field and permeability parameters have risen.

  5. 5.

    The temperature of hybrid nanofluid is high in the first solution when the magnetic field, power index parameter, and Eckert number increase.