Profit analysis of a 2-out-of-2 redundant system with single standby and degradation of the units after repair

Abstract

The purpose of this paper is to carry out the profit analysis of a three unit redundant system in which two units work in parallel and one unit is kept as spare in cold standby. Each unit has direct complete failure from normal mode. There is a single repairman (called server) who visits the system immediately to do repair, inspection and replacement of the units. The unit does not work as new after repair and so called a degraded unit. The degraded unit at its further failure undergoes for inspection to see the feasibility of its repair. If the repair is not feasible, it is replaced immediately by new unit. The system is considered in up-state if any two of original and/or degraded units are operative. The time to failure, repair and inspection of the units are taken as arbitrary with different probability density functions. By adopting semi-Markov process and regenerative point technique, the results for some measures of system effectiveness are obtained in steady state.

1 Introduction

It is proved that parallel redundancy is one of the best method to improve the performance and reliability of systems. Therefore, in recent years, reliability and profit analysis aspects of the systems of two or more units have been examined by the researchers including Nakagawa (1980), Gopalan and Naidu (1982), Singh (1989) and Chander (2005). And, most of these systems have been analyzed under a common assumption that unit works as new after repair. Infect, this assumption cannot be considered always true since the working capability and efficiency of a unit after repair depends more or less on the repair mechanism adopted. And, a unit may have increased failure rate if it not repaired by an expert repairman and so called degraded unit after repair. Chander and Mukender (2009) have discussed reliability and economic measures of a 2-out-of-3 redundant system subject to degradation after repair. In that paper, authors also assumed that repair of the degraded unit at its further is always feasible to the system. However, this assumption is not true many times and it is a known fact that degraded unit can be used further failure up to some extent. And, the degraded unit may be replaced by new one in case of its excessive use and high cost of maintenance which can be revealed by inspection.

In view of the above and considering practical importance here we analyzed a reliability model for a system of three identical units in which two units work in parallel and one unit is taken in cold standby and so called a 2-out-of-2 redundant system with single standby. Each unit has two modes of failure—normal (N) and complete failure (F). There is a single repairman (called server) who visits the system immediately whenever needed and he cannot leave the system while performing jobs. The original unit does not work as new after repair and thus called a degraded unit. The degraded unit after repair is considered as degraded. The inspection of the degraded unit at its further failure is carried out by the repairman to see the feasibility of its repair. If repair is not feasible, it is replaced immediately by original unit in order to avoid the unnecessary expanses on repair. The system is considered in up-state if any two of original and/or degraded units are operative. The failure, inspection and repair times of the units are mutually independent and uncorrelated random variables. The time to failure, repair and inspection of the units are taken as arbitrary with different probability density functions. By adopting semi-Markov process and regenerative point technique, the results for some measures of system effectiveness are obtained in steady state. The results for a particular case are obtained to depict the behavior of mean time to system failure (MTSF), availability and profit incurred to the system model.

2 Methodology

The system has been analyzed using well known semi-Markov process and regenerative point technique which are briefly described as:

Markov process: If {X(t), t ∈ T} is a stochastic process such that, given the value of X(s), the value of X(t), t > s do not depend on the values of X(u), u < s Then the process {X(t), t ∈ T} is a Markov process.

Semi-Markov process: A semi-Markov process is a stochastic process in which changes of state occur according to a Markov chain and in which the time interval between two successive transitions is a random variable, whose distribution may depend on the state from which the transition take place as well as on the state to which the next transition take place.

Regenerative process: Regenerative stochastic process was defined by Smith (1955) and has been crucial in the analysis of complex system. In this, we take time points at which the system history prior to the time points is irrelevant to the system conditions. These points are called regenerative points. Let X(t) be the state of the system of epoch. If t₁, t₂, … are the epochs at which the process probabilistically restarts, then these epochs are called regenerative epochs and the process {X(t), t = t₁, t₂, …} is called regenerative process. The state in which regenerative points occur is known as regenerative state.

3 Notations

E:

Set of regenerative states

No/No:

Original unit in normal mode and operative/not working

Do/Do:

Degraded unit is operative/not working

NCs/DCs:

Original/degraded unit in cold standby

p/q:

Probability that repair of degraded unit is feasible/not feasible

a(t)/A(t):

Probability density function (p.d.f.)/cumulative distribution function (c.d.f) of failure rate of original unit

b(t)/B(t):

p.d.f./c.d.f of failure rate of degraded unit

f(t)/F(t):

p.d.f./c.d.f of failure rate of original unit when both are available to use

z(t)/Z(t):

p.d.f./c.d.f of failure rate of degraded unit when both are available to use

g(t)/G(t), g₁(t)/G₁(t):

p.d.f./c.d.f of repair time for original/degraded unit

h(t)/H(t):

p.d.f./c.d.f of inspection time

NF_ur/NF_UR/NF_wr :

Original unit is failed and under repair/under continuous repair from previous state/waiting for repair

DF_ur/DF_UR/DF_wr :

Degraded unit is failed and under repair/under continuous repair from previous state/waiting for repair

DF_ui/DF_wi/DF_UI/DF_WI :

Degraded unit is failed and is under inspection/waiting for inspection/under continuous inspection from the previous state/waiting for inspection continuously from previous state

q_ij(t), Q_ij(t):

p.d.f and c.d.f of first passage time from regenerative state i to a regenerative state j or to a failed state j without visiting any other regenerative state in (0,t]

q_ij.k(t), Q_ij.k(t):

p.d.f and c.d.f of first passage time from regenerative state i to a regenerative state j or to a failed state j visiting state k once in (0,t]

q_ij.kr(t), Q_ij.kr(t):

p.d.f and c.d.f of first passage time from regenerative state i to a regenerative state j or to a failed state j visiting state k, r once in (0,t]

PU_i(t):

Probability that system up initially in state S_i ∈ E is up at time t without visiting to any other regenerative sate]

W_i(t):

Probability that server is busy in the state S_i up to time t without making any transition to any other regenerative state or returning to the same via one or more non-regenerative states]

m_ij :

Contribution to mean sojourn time in state S_i ∈ E and non regenerative state if occurs before transition to S_j ∈ E

®/©:

Symbols for Stieltjes convolution/Laplace convolution

~|*:

Symbols for Laplace Stieltjes transform (LST)/Laplace transform (LT)

′:

Symbol for derivative of the function

The following are the possible transition states of the system model

$$\begin{array}{lll} {{\text{S}}_{0} = \left( {{\text{No}},{\text{No}},{\text{NCs}}} \right),} & {{\text{S}}_{ 1} = \left( {{\text{No}},{\text{No}},{\text{NF}}_{\text{ur}} } \right),} & {{\text{S}}_{ 2} = \left( {\underline{\text{N}} {\text{o}},{\text{NF}}_{\text{wr}} ,{\text{NF}}_{\text{UR}} } \right),} \\ {{\text{S}}_{ 3} = \left( {{\text{No}},{\text{No}},{\text{DCs}}} \right),} & {{\text{S}}_{ 4} = \left( {{\text{No}},{\text{Do}},{\text{NF}}_{\text{ur}} } \right),} & {{\text{S}}_{ 5} = \left( {{\text{NF}}_{\text{wr}} ,\underline{\text{D}} {\text{o}},{\text{NF}}_{\text{UR}} } \right),} \\ {{\text{S}}_{ 6} = \left( {{\text{No}},{\text{Do}},{\text{DCs}}} \right),} & {{\text{S}}_{ 7} = \left( {{\text{Do}},{\text{Do}},{\text{NF}}_{\text{ur}} } \right),} & {{\text{S}}_{ 8} = \left( {{\text{No}},{\text{Do}},{\text{DF}}_{\text{ui}} } \right),} \\ {{\text{S}}_{ 9} = \left( {{\text{No}},{\text{Do}},{\text{NCs}}} \right),} & {{\text{S}}_{ 10} = \left( {{\text{NF}}_{\text{wr}} ,\underline{\text{D}} {\text{o}},{\text{DF}}_{\text{UI}} } \right),} & {{\text{S}}_{ 1 1} = \left( {{\text{NF}}_{\text{WR}} ,\underline{\text{D}} {\text{o}},{\text{ DF}}_{\text{ur}} } \right),} \\ {{\text{S}}_{ 1 2} = \left( {{\text{No}},{\text{Do}},{\text{DF}}_{\text{ur}} } \right),} & {{\text{S}}_{ 1 3} = \left( {\underline{\text{N}} {\text{o}},{\text{ DF}}_{\text{wi}} ,{\text{DF}}_{\text{UI}} } \right),} & {{\text{S}}_{ 1 4} = \left( {{\text{No}},{\text{No}},{\text{DF}}_{\text{ui}} } \right),} \\ {{\text{S}}_{ 1 5} = \left( {\underline{\text{N}} {\text{o}},{\text{DF}}_{\text{wi}} ,{\text{DF}}_{\text{UR}} } \right),} & {{\text{S}}_{ 1 6} = \left( {{\text{NF}}_{\text{wr}} ,\underline{\text{D}} {\text{o}},{\text{DF}}_{\text{UR}} } \right),} & {{\text{S}}_{ 1 7} = \left( {{\text{No}},{\text{No}},{\text{DF}}_{\text{ur}} } \right),} \\ {{\text{S}}_{ 1 8} = \left( {\underline{\text{N}} {\text{o}},{\text{NF}}_{\text{wr}} ,{\text{DF}}_{\text{UR}} } \right),} & {{\text{S}}_{ 1 9} = \left( {\underline{\text{N}} {\text{o}},{\text{NF}}_{\text{wr}} ,{\text{DF}}_{\text{UI}} } \right),} & {{\text{S}}_{ 20} = \left( {\underline{\text{N}} {\text{o}},{\text{NF}}_{\text{WR}} ,{\text{DF}}_{\text{ur}} } \right),} \\ {{\text{S}}_{ 2 1} = \left( {\underline{\text{N}} {\text{o}},{\text{DF}}_{\text{WI}} ,{\text{DF}}_{\text{ur}} } \right),} & {{\text{S}}_{ 2 2} = \left( {\underline{\text{N}} {\text{o}},{\text{DF}}_{\text{wi}} ,{\text{NF}}_{\text{UR}} } \right),} & {{\text{S}}_{ 2 3} = \left( {{\text{Do}},{\text{DF}}_{\text{wi}} ,{\text{DF}}_{\text{UI}} } \right),} \\ {{\text{S}}_{ 2 4} = \left( {\underline{\text{D}} {\text{o}},{\text{DF}}_{\text{WI}} ,{\text{DF}}_{\text{ur}} } \right) ,} & {{\text{S}}_{ 2 5} = \left( {{\text{Do}},{\text{Do}},{\text{DCs}}} \right) ,} & {{\text{S}}_{ 2 6} = \left( {{\text{Do}},{\text{Do}},{\text{DF}}_{\text{ui}} } \right),} \\ {{\text{S}}_{ 2 7} = \left( {{\text{Do}},{\text{Do}},{\text{NCs}}} \right),} & {{\text{S}}_{ 2 8} = \left( {{\text{Do}},{\text{Do}},{\text{DF}}_{\text{ur}} } \right),} & {{\text{S}}_{ 2 9} = \left( {\underline{\text{D}} {\text{o}},{\text{ DF}}_{\text{wi}} ,{\text{NF}}_{\text{UR}} } \right),} \\ {\text{S}}_{ 30} = \left( {\underline{\text{D}} {\text{o}},{\text{ DF}}_{\text{wi}} ,{\text{ DF}}_{\text{UR}} } \right), & & \end{array} $$

(1)

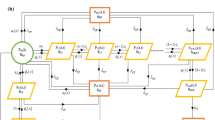
The states S₀, S₁, S₃, S₄, S₆, S₇, S₈, S₉, S₁₂, S₁₄, S₁₇, S₂₅, S₂₆, S₂₇ and S₂₈ are regenerative states while the remaining states are non-regenerative states. Thus E = {S₀, S₁, S₃, S₄, S₆, S₇, S₈, S₉, S₁₂, S₁₄, S₁₇, S₂₅, S₂₆, S₂₇, S₂₈}. The possible transition between states along with transition rates for the model is shown in Fig. 1.

Fig. 1

State transition diagram

4 Probability density function (p.d.f.)

Probability density function (p.d.f.) is defined as the function that gives us the probability per unit interval. This can be illustrated with the following.

$$ f\left( x \right) = \mathop {\lim }\limits_{h \to 0} \frac{{p\left( {x < X < x + h} \right)}}{h} $$

As such, for a continuous random variable X, we define a p.d.f. A function f(x) is said to be a p.d.f. if it satisfies the following properties.

• (i) f(x) ≥ 0, −∞ < x < ∞

• (ii) $\int\limits_{ - \infty }^{\infty } {f\left( x \right)dx} = 1$

5 Transition probabilities and mean sojourn times

Simple probabilistic considerations yield the following expressions for the non-zero elements p_ij = Q_ij (∞) = ∫q_ij(t) dt as (Medhi 1982)

$$ \begin{array}{lll} {p_{01} = \int\limits_{0}^{\infty } {f(t)dt} } & {p_{12} = \int\limits_{0}^{\infty } {f(t)\overline{G(t)} dt} } & {p_{13} = \int\limits_{0}^{\infty } {g(t)\overline{F(t)} dt} } \\ {p_{24} = \int\limits_{0}^{\infty } {g(t)dt} } & {p_{34} = \int\limits_{0}^{\infty } {f(t)dt} } & {p_{4,22} = \int\limits_{0}^{\infty } {b(t){\overline{A(t)}} \,{\overline{G(t)}} dt} } \\ {p_{4,6} = \int\limits_{0}^{\infty } {g(t){\overline{A(t)}}\, {\overline{B(t)}} dt} } & {p_{4,5} = \int\limits_{0}^{\infty } {a(t){\overline{G(t)}} \,{\overline{B(t)}} dt} } & {p_{5,7} = \int\limits_{0}^{\infty } {g(t)dt} } \\ {p_{6,7} = \int\limits_{0}^{\infty } {a(t)\overline{B(t)} dt} } & {p_{6,8} = \int\limits_{0}^{\infty } {b(t)\overline{A(t)} dt} } & {p_{7,29} = \int\limits_{0}^{\infty } {z(t)\overline{G(t)} dt} } \\ {p_{7,25} = \int\limits_{0}^{\infty } {g(t)\overline{Z(t)} dt} } & {p_{8,9} = \int\limits_{0}^{\infty } {qh(t){\overline{B(t)}} \,{\overline{A(t)}} dt} } & {p_{8,12} = \int\limits_{0}^{\infty } {ph(t){\overline{B(t)}} \,{\overline{A(t)}} dt} } \\ {p_{8,10} = \int\limits_{0}^{\infty } {a(t){\overline{B(t)}} \,{\overline{H(t)}} dt} } & {p_{8,13} = \int\limits_{0}^{\infty } {b(t){\overline{A(t)}} \,{\overline{H(t)}} dt} } & {p_{9,14} = \int\limits_{0}^{\infty } {b(t)\overline{A(t)} dt} } \\ {p_{9,4} = \int\limits_{0}^{\infty } {a(t)\overline{B(t)} dt} } & {p_{10,11} = \int\limits_{0}^{\infty } {ph(t)dt} } & {p_{10,4} = \int\limits_{0}^{\infty } {qh(t)dt} } \\ {p_{11,7} = \int\limits_{0}^{\infty } {g_{1} (t)dt} } & {p_{12,16} = \int\limits_{0}^{\infty } {a(t){\overline{B(t)}} \,{\overline{{G_{1} (t)}}} dt} } & {p_{12,15} = \int\limits_{0}^{\infty } {b(t){\overline{A(t)}} \,{\overline{{G_{1} (t)}}} dt} } \\ {p_{12,6} = \int\limits_{0}^{\infty } {g_{1} (t){\overline{A(t)}} \,{\overline{B(t)}} dt} } & {p_{13,14} = \int\limits_{0}^{\infty } {qh(t)dt} } & {p_{13,21} = \int\limits_{0}^{\infty } {ph(t)dt} } \\ {p_{14,17} = \int\limits_{0}^{\infty } {ph(t)\overline{F(t)} dt} } & {p_{14,0} = \int\limits_{0}^{\infty } {qh(t)\overline{F(t)} dt} } & {p_{14,19} = \int\limits_{0}^{\infty } {f(t)\overline{H(t)} dt} }\\ {p_{15,8} = \int\limits_{0}^{\infty } {g_{1} (t)dt} } & {p_{16,7} = \int\limits_{0}^{\infty } {g_{1} (t)dt} } & {p_{17,18} = \int\limits_{0}^{\infty } {f(t)\overline{{G_{1} (t)}} dt} } \\ {p_{17,3} = \int\limits_{0}^{\infty } {g_{1} (t)\overline{F(t)} dt} } & {p_{18,4} = \int\limits_{0}^{\infty } {g_{1} (t)dt} } & {p_{19,1} = \int\limits_{0}^{\infty } {qh(t)dt} } \\ {p_{19,20} = \int\limits_{0}^{\infty } {ph(t)dt} } & {p_{20,4} = \int\limits_{0}^{\infty } {g_{1} (t)dt} } & {p_{21,8} = \int\limits_{0}^{\infty } {g_{1} (t)dt} } \\ {p_{22,8} = \int\limits_{0}^{\infty } {g(t)dt} } & {p_{23,8} = \int\limits_{0}^{\infty } {qh(t)dt} } & {p_{23,24} = \int\limits_{0}^{\infty } {ph(t)dt} } \\ {p_{24,26} = \int\limits_{0}^{\infty } {g_{1} (t)dt} } & {p_{25,26} = \int\limits_{0}^{\infty } {z(t)dt} } & {p_{26,27} = \int\limits_{0}^{\infty } {qh(t)\overline{Z(t)} dt} } \\ {p_{26,28} = \int\limits_{0}^{\infty } {ph(t)\overline{Z(t)} dt} } & {p_{26,23} = \int\limits_{0}^{\infty } {z(t)\overline{H(t)}{dt} } } & {p_{27,28} = \int\limits_{0}^{\infty } {z(t)dt} } \\ {p_{28,25} = \int\limits_{0}^{\infty } {g_{1} (t)\overline{Z(t)} dt} } & {p_{28,30} = \int\limits_{0}^{\infty } {z(t)\overline{{G_{1} (t)}} dt} } & {p_{29,26} = \int\limits_{0}^{\infty } {g(t)dt} } \\ {p_{30,26} = \int\limits_{0}^{\infty } {g_{1} (t)dt} } & {p_{14.2} = p_{12}{}^{\circledR} p_{24} } & {p_{47.5} = p_{45} {}^{\circledR} p_{57} } \\ {p_{4,8.22} = p_{4,22} {}^{\circledR} p_{22,8} } & {p_{7,26.29} = p_{7,29} {}^{\circledR} p_{29,26} } & {p_{8,4.10} = p_{8,10}{}^{\circledR} p_{10,4} } \\ {p_{8,8.13,21} = p_{8,13}{}^{\circledR} p_{13,21} {}^{\circledR} p_{21,8} } & {p_{8,7.10,11} = p_{8,10}{}^{\circledR} p_{10,11} {}^{\circledR} p_{11,7} } & {p_{8,14.13} = p_{8,13} {}^{\circledR} p_{13,14} } \\ {p_{12,8.15} = p_{12,15} {}^{\circledR} p_{15,8} } & {p_{12,7.16} = p_{12,16} {}^{\circledR} p_{16,7} } & {p_{14,1.19} = p_{14,19} {}^{\circledR} p_{19,1} } \\{p_{14,4.19,20} = p_{14,19} {}^{\circledR} p_{19,20} {}^{\circledR} p_{20,4} } & {p_{17,4.18} = p_{17,18} {}^{\circledR} p_{18,4} } & {p_{26,8.23} = p_{26,23} {}^{\circledR} p_{23,8} } \\ {p_{28,26.30} = p_{28,30} {}^{\circledR} p_{30,26} } &{p_{26,26.23,24} = p_{26,23} {}^{\circledR} p_{23,24} {}^{\circledR} p_{24,26} } \\ \end{array}. $$

(2)

For these transition probabilities, it can be verified that

$$ \begin{aligned} & {\text{p}}_{01} = {\text{p}}_{ 34} = {\text{p}}_{ 25, 26} = {\text{p}}_{ 27, 8} = {\text{p}}_{ 12} + {\text{p}}_{ 13} = {\text{p}}_{ 13} + {\text{p}}_{ 1,4. 2} = {\text{p}}_{ 45} + {\text{p}}_{ 46} + {\text{p}}_{ 4, 22} = {\text{p}}_{ 46} + {\text{p}}_{ 4,7. 5} + {\text{p}}_{ 4,8. 22} \\ & = {\text{p}}_{ 67} + {\text{p}}_{ 68} = {\text{p}}_{ 7, 2 5} + {\text{p}}_{ 7, 29} = {\text{p}}_{ 7, 25} + {\text{p}}_{ 7, 2 6. 29} = {\text{p}}_{ 89} + {\text{p}}_{ 8, 12} + {\text{p}}_{ 8, 13} + {\text{p}}_{ 8, 10} = {\text{p}}_{ 89} + {\text{p}}_{ 8, 1 2} + {\text{p}}_{ 8,4. 10} \\ & + {\text{p}}_{ 8,7. 10, 11} + {\text{p}}_{ 8, 14. 13} + {\text{p}}_{ 8,8. 13, 21} = {\text{p}}_{ 9,4} + {\text{p}}_{ 9, 14} = {\text{p}}_{ 12, 6} + {\text{p}}_{ 1 2, 15} + {\text{p}}_{ 12, 16} = {\text{p}}_{ 12, 6} + {\text{p}}_{ 12, 8. 15} + {\text{p}}_{ 12, 7. 16} \\ & = {\text{p}}_{ 14,0} + {\text{p}}_{ 14, 17} + {\text{p}}_{ 14, 19} = {\text{p}}_{ 14,0} + {\text{p}}_{ 14, 17} + {\text{p}}_{ 14, 1. 19} + {\text{p}}_{ 1 4, 4. 19, 20} = {\text{p}}_{ 17, 3} + {\text{p}}_{ 17, 18} = {\text{p}}_{ 17, 3} + {\text{p}}_{ 17, 4. 18} \\ & = {\text{p}}_{ 26, 28} + {\text{p}}_{ 26, 27} + {\text{p}}_{ 26, 23} = {\text{p}}_{ 26, 28} + {\text{p}}_{ 26, 27} + {\text{p}}_{ 26, 8. 23} + {\text{p}}_{ 26, 26. 23, 24} = {\text{p}}_{ 28, 2 5} + {\text{p}}_{ 28, 30} = {\text{p}}_{ 28, 25} + {\text{p}}_{ 28, 26. 30} = 1\\\end{aligned} .$$

(3)

The mean sojourn times μ_i in state S_i are given by:

$$ \begin{array}{lll} {\mu_{0} = \int\limits_{0}^{\infty } {\overline{F(t)} dt} = \mu_{3} ,} & {\mu_{1} = \int\limits_{0}^{\infty } {{\overline{F(t)}} {\overline{G(t)}} dt} ,} & {\mu_{4} = \int\limits_{0}^{\infty } {{\overline{A(t)}} {\overline{G(t)}} {\overline{B(t)}} dt} ,} \\ {\mu_{6} = \int\limits_{0}^{\infty } {{\overline{A(t)}} {\overline{B(t)}} dt} = \mu_{9} ,} & {\mu_{7} = \int\limits_{0}^{\infty } {{\overline{Z(t)}} {\overline{G(t)}} dt} ,} & {\mu_{8} = \int\limits_{0}^{\infty } {{\overline{A(t)}} {\overline{H(t)}} {\overline{B(t)}} dt} ,} \\ {\mu_{12} = \int\limits_{0}^{\infty } {{\overline{A(t)}} {\overline{{G_{1} (t)}}} \overline{B(t)} dt} ,} & {\mu_{14} = \int\limits_{0}^{\infty } {{\overline{F(t)}} {\overline{H(t)}} dt} ,} & {\mu_{17} = \int\limits_{0}^{\infty } {{\overline{F(t)}} {\overline{{G_{1} (t)}}} dt} ,} \\ {\mu_{25} = \int\limits_{0}^{\infty } {\overline{Z(t)} dt} = \mu_{27} ,} & {\mu_{26} = \int\limits_{0}^{\infty } {{\overline{Z(t)}} {\overline{H(t)}} dt} ,} & {\mu_{28} = \int\limits_{0}^{\infty } {{\overline{Z(t)}} {\overline{{G_{1} (t)}}} dt} .} \\ \end{array} $$

(4)

The unconditional mean time taken by the system to transit from any state S_i when time is counted from epoch at entrance into state S_j is stated as (Cox 1962):

$$ {\text{m}}_{\text{ij}} = \int {\text{t}} {\text{dQ}}_{\text{ij}} \left( {\text{t}} \right) = - {\text{q}}_{\text{ij}} *{^ \prime} \left( 0 \right) $$

(5)

and

$$ \begin{aligned} {\text{m}}_{0 1} = \mu_{0} ,\quad {\text{m}}_{ 1 2} + {\text{m}}_{ 1 3} = \mu_{ 1} ,\quad {\text{m}}_{ 1 3} + {\text{m}}_{ 1 4. 2} = \mu_{1}^{1} \;\left( {\text{say}} \right), \\ {\text{m}}_{ 3 4} = \mu_{ 3} ,\quad {\text{m}}_{ 4 5} + {\text{m}}_{ 4 6} + {\text{m}}_{ 4, 2 2} = \mu_{ 4} ,\quad {\text{m}}_{ 4 6} + {\text{m}}_{ 4 7. 5} + {\text{m}}_{ 4 8. 2 2} = \mu_{4}^{1} \;\left( {\text{say}} \right), \\ {\text{m}}_{ 6 7} + {\text{m}}_{ 6 8} = \mu_{ 6} ,\quad {\text{m}}_{ 7, 2 5} + {\text{m}}_{ 7, 2 9} = \mu_{ 7} ,\quad {\text{m}}_{ 7, 2 5} + {\text{m}}_{ 7, 2 6. 2 9} = \mu_{ 7}^{ 1} , \\ {\text{m}}_{ 8 9} + {\text{m}}_{ 8, 1 2} + {\text{m}}_{ 8, 1 3} + {\text{m}}_{ 8, 10} = \mu_{ 8} , \\ {\text{m}}_{ 8 3} + {\text{m}}_{ 8 8. 1 2, 20} + {\text{m}}_{ 8 4. 9} + {\text{m}}_{ 8, 1 1} + {\text{m}}_{ 8 7. 9, 10} + {\text{m}}_{ 8, 1 3. 1 2} = \mu_{ 8}^{ 1} \;\left( {\text{say}} \right), \\ {\text{m}}_{ 1 2, 6} + {\text{m}}_{ 1 2, 1 5} + {\text{m}}_{ 1 2, 1 6} = \mu_{ 1 2,} \quad {\text{m}}_{ 1 2, 6} + {\text{m}}_{ 1 2, 8. 1 5} + {\text{m}}_{ 1 2, 7. 1 6} = \mu_{ 1 2}^{ 1} \;\left( {\text{say}} \right) \\ {\text{m}}_{ 1 4,0} + {\text{m}}_{ 1 4, 1 7} + {\text{m}}_{ 1 4, 1 9} = \mu_{ 1 4,} \quad {\text{m}}_{ 1 4,0} + {\text{m}}_{ 1 4, 1 7} + {\text{m}}_{ 1 4, 1. 1 9} + {\text{m}}_{ 1 4, 4.. 1 9, 20} = \mu_{ 1 4}^{ 1} \;\left( {\text{say}} \right), \\ {\text{m}}_{ 1 7, 3} + {\text{m}}_{ 1 7, 1 8} = \mu_{ 1 7} ,\quad {\text{m}}_{ 1 7, 3} + {\text{m}}_{ 1 7, 4. 1 8} = \mu^{ 1}_{ 1 7} \;\left( {\text{say}} \right),\quad {\text{m}}_{ 2 5, 2 6} = \mu_{ 2 5} , \\ {\text{m}}_{ 2 6, 2 8} + {\text{m}}_{ 2 6, 2 7} + {\text{m}}_{ 2 6, 2 3} = \mu_{ 2 6,} \quad {\text{m}}_{ 2 6, 2 8} + {\text{m}}_{ 2 6, 2 7} + {\text{m}}_{ 2 6, 8. 2 3} + {\text{m}}_{ 2 6, 2 6. 2 3, 2 4} = \mu_{ 2 6}^{ 1} \;\left( {\text{say}} \right), \\ {\text{m}}_{ 2 8, 2 5} + {\text{m}}_{ 2 8, 30} = \mu_{ 2 8,} \quad {\text{m}}_{ 2 8, 2 5} + {\text{m}}_{ 2 8, 2 6. 30} = \mu_{ 2 8}^{ 1} . \\ \end{aligned} $$

(6)

6 Reliability and MTSF

Let ϕ_i(t) be the c.d.f of the first passage time from regenerative state i to a failed state. Regarding the failed state as absorbing state, we have the following recursive relations for ϕ_i(t):

$$ \phi_{i} \left( t \right) = \sum\limits_{j} {Q_{i,j} \left( t \right)\circledR \phi_{j} \left( t \right)} + \sum\limits_{k} {Q_{i,k} \left( t \right)} . $$

(7a)

The system equations given in (7a) can be obtained similar as ϕ₀(t) and ϕ₁(t)

$$ \phi_{0} \left( t \right) = Q_{0,1} (t)\circledR \phi_{1} \left( t \right)\quad \left( {{\text{for}}\;{\text{i}} = 0,\;{\text{j}} = 1} \right) $$

(7b)

$$ \phi_{ 1} \left( {\text{t}} \right) = {\text{Q}}_{ 1 3} \left( {\text{t}} \right)\circledR \phi_{ 3} \left( {\text{t}} \right) + {\text{Q}}_{ 1 2} \left( {\text{t}} \right)\quad \left( {{\text{for}}\;{\text{i}} = 1,\;{\text{j}} = 3,\;{\text{k}} = 2} \right) $$

(7c)

where j is an operative regenerative state to which the given regenerative state i can transit and k is a failed state to which the state i can transit directly

Taking LST of relations (7a) and solving for $\widetilde{\phi }_{0} ({\text{s}})$, we have

$$ {\text{R}}^{*} ({\text{s}}) = {{\left( {1 - \widetilde{\phi }_{0} ({\text{s}})} \right)} \mathord{\left/ {\vphantom {{\left( {1 - \widetilde{\phi }_{0} ({\text{s}})} \right)} {\text{s}}}} \right. \kern-0pt} {\text{s}}} . $$

(8)

The reliability R(t) can be obtained by taking inverse Laplace transition of (8) and MTSF is given by

$$ MTSF = \mathop {\lim }\limits_{s \to 0} R^{*} (s) = \frac{{Numerator\;of\;MTSF\;(M_{11} )}}{{Deno\hbox{Min} ator\;of\;MTSF\;(D_{11} )}} $$

(9)

where

$$ {\text{M}}_{ 1 1} = \left( {\mu_{0} + \mu_{ 1} } \right)[\left( { 1- {\text{p}}_{ 2 6, 2 8} {\text{p}}_{ 2 8, 2 5} } \right)\left\{ { 1- {\text{p}}_{ 6 8} \left( {{\text{p}}_{ 4 6} {\text{p}}_{ 8 9} \left( {{\text{p}}_{ 9 4} + {\text{p}}_{ 9, 1 4} {\text{p}}_{ 1 4, 1 7} {\text{p}}_{ 1 7, 3} } \right) + {\text{p}}_{ 8, 1 2} {\text{p}}_{ 1 2, 6} } \right)} \right\} - \left( {{\text{p}}_{ 6 7} {\text{p}}_{ 7, 2 5} {\text{p}}_{ 2 6, 2 7} } \right)\left\{ {{\text{p}}_{ 4 6} {\text{p}}_{ 8 9} \left( {{\text{p}}_{ 9 4} + {\text{p}}_{ 9, 1 4} {\text{p}}_{ 1 4, 1 7} {\text{p}}_{ 1 7, 3} } \right) + {\text{p}}_{ 8, 1 2} {\text{p}}_{ 1 2, 6} } \right\}] + {\text{p}}_{ 1 3} \mu_{ 3} [\left( { 1- {\text{p}}_{ 2 6, 2 8} {\text{p}}_{ 2 8, 2 5} } \right) \left\{ { 1- \left( {{\text{p}}_{ 8, 1 2} {\text{p}}_{ 1 2, 6} + {\text{p}}_{ 4 6} {\text{p}}_{ 8 9} {\text{p}}_{ 9 4} } \right){\text{p}}_{ 6 8} } \right\} - \left( {{\text{p}}_{ 6 7} {\text{p}}_{ 7, 2 5} {\text{p}}_{ 2 6, 2 7} } \right)\left( {{\text{p}}_{ 8, 1 2} {\text{p}}_{ 1 2, 6} + {\text{p}}_{ 4 6} {\text{p}}_{ 8 9} {\text{p}}_{ 9 4} } \right)] + {\text{p}}_{ 1 3} \mu_{ 4} \left[ {\left( { 1- {\text{p}}_{ 2 6, 2 8} {\text{p}}_{ 2 8, 2 5} } \right)\left( { 1- {\text{p}}_{ 6 8} {\text{p}}_{ 8, 1 2} {\text{p}}_{ 1 2, 6} } \right) - \left( {{\text{p}}_{ 6 7} {\text{p}}_{ 7, 2 5} {\text{p}}_{ 2 6, 2 7} } \right){\text{p}}_{ 8, 1 2} {\text{p}}_{ 1 2, 6} } \right] + {\text{p}}_{ 1 3} {\text{p}}_{ 4 6} \left( { 1- {\text{p}}_{ 2 6, 2 8} {\text{p}}_{ 2 8, 2 5} } \right)\left[ {\mu_{ 6} + {\text{p}}_{ 6 7} \mu_{ 7} } \right] + {\text{p}}_{ 1 3} {\text{p}}_{ 4 6} [ {\text{p}}_{ 6 8} \left( { 1- {\text{p}}_{ 2 6, 2 8} {\text{p}}_{ 2 8, 2 5} } \right) + \left( {{\text{p}}_{ 6 7} {\text{p}}_{ 7, 2 5} {\text{p}}_{ 2 6, 2 7} } \right)][\mu_{ 8} + {\text{p}}_{ 8 9} \mu_{ 9} + {\text{p}}_{ 8, 1 2} \mu_{ 1 2} + {\text{p}}_{ 8 9} {\text{p}}_{ 9, 1 4} \mu_{ 1 4} + {\text{p}}_{ 8 9} {\text{p}}_{ 9, 1 4} {\text{p}}_{ 1 4, 1 7} {\text{p}}\mu_{ 1 7} ] + {\text{p}}_{ 1 3} {\text{p}}_{ 4 6} {\text{p}}_{ 6 7} {\text{p}}_{ 7, 2 5} \left[ {\mu_{ 2 6} + \mu_{ 2 5} + {\text{p}}_{ 2 6, 2 8} \mu_{ 2 8} + {\text{p}}_{ 2 6, 2 7} \mu_{ 2 7} } \right] $$

$${\text{and\;D}}_{ 1 1} = \left( { 1- {\text{p}}_{ 2 6, 2 8} {\text{p}}_{ 2 8, 2 5} } \right)[ 1- {\text{p}}_{ 6 8} \left\{ {{\text{p}}_{ 8, 1 2} {\text{p}}_{ 1 2, 6} + {\text{p}}_{ 4 6} {\text{p}}_{ 8 9} \left( {{\text{p}}_{ 9, 4} + {\text{p}}_{ 9, 1 4} {\text{p}}_{ 1 4, 1 7} {\text{p}}_{ 1 7, 3} } \right)} \right\} - {\text{p}}_{ 6 8} {\text{p}}_{ 4 6} {\text{p}}_{ 8 9} {\text{p}}_{ 9, 1 4} {\text{p}}_{ 1 4,0} {\text{p}}_{ 1 3} - {\text{ p}}_{ 6 7} {\text{p}}_{ 7, 2 5} {\text{p}}_{ 2 6, 2 7} [\{ {\text{p}}_{ 8, 1 2} {\text{p}}_{ 1 2, 6} + {\text{p}}_{ 4 6} {\text{p}}_{ 8 9} ({\text{p}}_{ 9, 4} + {\text{p}}_{ 9, 1 4} {\text{p}}_{ 1 4, 1 7} {\text{p}}_{ 1 7, 3} )\} + {\text{p}}_{ 4 6} {\text{p}}_{ 8 9} {\text{p}}_{ 9, 1 4} {\text{p}}_{ 1 4,0} {\text{p}}_{ 1 3} ]. $$

7 Availability analysis

Let A_i(t) be the probability that the system is in up state at instant t given that the system entered regenerative state i at t = 0. The recursive relations for A_i(t) are given by:

$$ {\text{A}}_{\text{i}} \left( {\text{t}} \right) = {\text{PU}}_{\text{i}} \left( {\text{t}} \right) + \sum\limits_{\text{j}} {{\text{q}}_{{{\text{i}},{\text{j}}}}^{{\left( {\text{n}} \right)}} \left( {\text{t}} \right)\copyright{\text{A}}_{\text{j}} \left( {\text{t}} \right)} $$

(10a)

The system equations given in (10a) can be obtained similar as A₀(t) and A₁(t)

$$ {\text{A}}_{0} \left( {\text{t}} \right) = {\text{PU}}_{0} ({\text{t}}) + {\text{q}}_{0,1} ({\text{t}}) \, \copyright{\text{A}}_{1} \left( {\text{t}} \right)\quad \left( {{\text{for}}\;{\text{i}} = 0,\;{\text{j}} = 1} \right) $$

(10b)

$$ {\text{A}}_{ 1} \left( {\text{t}} \right) = {\text{PU}}_{ 1} \left( {\text{t}} \right) + {\text{q}}_{ 1 3} \left( {\text{t}} \right)\copyright{\text{A}}_{ 3} \left( {\text{t}} \right) + {\text{q}}_{ 1 4. 2} \left( {\text{t}} \right)\copyright{\text{A}}_{ 4} \left( {\text{t}} \right)\quad \left( {{\text{for}}\;{\text{i}} = 1,\;{\text{j}} = 3, 4} \right) $$

(10c)

where j is any successive regenerative state to which the regenerative state i can transit through n ≥ 1 (natural number) transitions, and

$$ \begin{array}{lll} {{\text{PU}}_{0} \left( {\text{t}} \right) = {\text{e}}^{{ - 2\lambda {\text{t}}}} = {\text{PU}}_{ 3} \left( {\text{t}} \right),} & {{\text{PU}}_{ 1} \left( {\text{t}} \right) = {\text{e}}^{{ - 2\lambda {\text{t}}}} \bar{G}(t),} & {{\text{PU}}_{ 4} \left( {\text{t}} \right) = e^{{ - (\lambda + \lambda_{1} )t}} \bar{G}(t),} \\ {{\text{PU}}_{ 6} \left( {\text{t}} \right) = e^{{ - (\lambda + \lambda_{1} )t}} ,} & {{\text{PU}}_{ 7} \left( {\text{t}} \right) = e^{{ - 2\lambda_{1} t}} \bar{G}(t),} & {{\text{PU}}_{ 8} \left( {\text{t}} \right) = e^{{ - (\lambda + \lambda_{1} )t}} \overline{H} (t),} \\ {{\text{PU}}_{ 9} \left( {\text{t}} \right) = e^{{ - (\lambda + \lambda_{1} )t}} } & {{\text{PU}}_{ 1 2} \left( {\text{t}} \right) = e^{{ - (\lambda + \lambda_{1} )t}} \bar{G}_{1} (t),} & {{\text{PU}}_{ 1 4} \left( {\text{t}} \right) = {\text{e}}^{{ - 2\lambda {\text{t}}}} \overline{H} (t),} \\ {{\text{PU}}_{ 1 7} \left( {\text{t}} \right) = {\text{e}}^{{ - 2\lambda {\text{t}}}} \bar{G}_{1} (t),} & {{\text{PU}}_{ 2 5} \left( {\text{t}} \right) = e^{{ - 2\lambda_{1} t}} ,} & {{\text{PU}}_{ 2 6} \left( {\text{t}} \right) = e^{{ - 2\lambda_{1} t}} \overline{H} (t),} \\ {{\text{PU}}_{ 2 7} \left( {\text{t}} \right) = e^{{ - 2\lambda_{1} t}} ,} & {{\text{PU}}_{ 2 8} \left( {\text{t}} \right) = e^{{ - 2\lambda_{1} t}} \bar{G}_{1} (t).} & {} \\ \end{array} $$

(11)

Now taking LT of relations (10a) and solving for A₀*(s) the steady-state availability can be obtained as

$$ {\text{A}}_{0} \left( \infty \right) \,=\,\mathop {\lim }\limits_{s \to 0} {\text{sA}}_{0}^{*} \left( {\text{s}} \right)=\frac{{{\text{Numerator}}\;{\text{of}}\;{\text{Steady}}\;{\text{State}}\;{\text{Availability}}\; ( {\text{A}}_{ 1 1} )}}{{{\text{Denoinator}}\;{\text{of}}\;{\text{Steady}}\;{\text{State}}\;{\text{Availability}}\; ( {\text{D}}_{ 1 2} )}} $$

(12)

where

$$ \begin{aligned} {\text{A}}_{ 1 1} =\, & \left( {{\text{p}}_{ 2 6, 8. 2 3} + {\text{p}}_{ 2 6, 2 7} } \right)\left( {{\text{p}}_{ 8, 1 4. 1 3} + {\text{p}}_{ 8 9} {\text{p}}_{ 9, 1 4} } \right)[(\mu_{0} {\text{p}}_{ 1 4,0} + \mu_{ 1} \left( {{\text{p}}_{ 1 4,0} + {\text{p}}_{ 1 4, 1. 1 9} } \right) + \mu_{ 3} \{ {\text{p}}_{ 1 3} \left( {{\text{p}}_{ 1 4,0} + {\text{p}}_{ 1 4, 1. 1 9} } \right) \\ & +\, {\text{p}}_{ 1 4, 1 7} {\text{p}}_{ 1 7, 3} \} + \mu_{ 1 4} + \mu_{ 1 7} {\text{p}}_{ 1 4, 1 7} ] + \left( {{\text{p}}_{ 2 6, 8. 2 3} + {\text{p}}_{ 2 6, 2 7} } \right)[\mu_{ 4} \left( {{\text{p}}_{ 8 9} + {\text{p}}_{ 8 4. 10} + {\text{p}}_{ 8, 1 4. 1 3} } \right) + \mu_{ 6} \{ ({\text{p}}_{ 8 9} + {\text{p}}_{ 8 4. 10} \\ & +\, {\text{p}}_{ 8, 1 4. 1 3} ){\text{p}}_{ 4 6} + {\text{p}}_{ 8, 1 2} {\text{p}}_{ 1 2, 6} \} + \mu_{ 7} \{ 1- \left( {{\text{p}}_{ 4 8. 2 2} + {\text{p}}_{ 4 6} {\text{p}}_{ 6 8} } \right)\left( {{\text{p}}_{ 8 9} + {\text{p}}_{ 8 4. 10} + {\text{p}}_{ 8, 1 4. 1 3} } \right) - {\text{p}}_{ 8 8. 1 3, 2 1} \\ & -\, {\text{p}}_{ 8, 1 2} \left( {{\text{p}}_{ 1 2, 8. 1 5} + {\text{p}}_{ 1 2, 6} {\text{p}}_{ 6 8} } \right)\} + \mu_{ 8} + {\text{p}}_{ 8, 9} \mu_{ 9} + {\text{p}}_{ 8, 1 2} \mu_{ 1 2} ] + \{ 1- \left( {{\text{p}}_{ 4 8. 2 2} + {\text{p}}_{ 4 6} {\text{p}}_{ 6 8} } \right)\left( {{\text{p}}_{ 8 9} + {\text{p}}_{ 8 4. 10} + {\text{p}}_{ 8, 1 4. 1 3} } \right) \\ & -\, {\text{p}}_{ 8 8. 1 3, 2 1} - {\text{p}}_{ 8, 1 2} \left( {{\text{p}}_{ 1 2, 8. 1 5} + {\text{p}}_{ 1 2, 6} {\text{p}}_{ 6 8} } \right)\} [\mu_{ 2 5} \left\{ {{\text{p}}_{ 7, 2 5} \left( {{\text{p}}_{ 2 6, 8. 2 3} + {\text{p}}_{ 2 6, 2 7} } \right) + {\text{p}}_{ 2 6, 2 8} {\text{p}}_{ 2 8, 2 5} } \right\} + \mu_{ 2 6} \\ & +\, \mu_{ 2 7} {\text{p}}_{ 2 6, 2 7} + \mu_{ 2 8} {\text{p}}_{ 2 6, 2 8} ] \\ {\text{D}}_{ 1 2} =\, & \left( {{\text{p}}_{ 2 6, 8. 2 3} + {\text{p}}_{ 2 6, 2 7} } \right)\left( {{\text{p}}_{ 8, 1 4. 1 3} + {\text{p}}_{ 8 9} {\text{p}}_{ 9, 1 4} } \right)[(\mu_{0} {\text{p}}_{ 1 4,0} + \mu^{\prime }_{ 1} \left( {{\text{p}}_{ 1 4,0} + {\text{p}}_{ 1 4, 1. 1 9} } \right) + \mu_{ 3} \{ {\text{p}}_{ 1 3} \left( {{\text{p}}_{ 1 4,0} + {\text{ p}}_{ 1 4, 1. 1 9} } \right) \\ & +\, {\text{p}}_{ 1 4, 1 7} {\text{p}}_{ 1 7, 3} \} + \mu^{\prime }_{ 1 4} + \mu^{\prime }_{ 1 7} {\text{p}}_{ 1 4, 1 7} ] + \left( {{\text{p}}_{ 2 6, 8. 2 3} + {\text{p}}_{ 2 6, 2 7} } \right)[\mu^{\prime }_{ 4} \left( {{\text{p}}_{ 8 9} + {\text{p}}_{ 8 4. 10} + {\text{p}}_{ 8, 1 4. 1 3} } \right) + \mu_{ 6} \{ ({\text{p}}_{ 8 9} + {\text{p}}_{ 8 4. 10} \\ & +\, {\text{p}}_{ 8, 1 4. 1 3} ){\text{p}}_{ 4 6} + {\text{p}}_{ 8, 1 2} {\text{p}}_{ 1 2, 6} \} + \mu^{\prime }_{ 7} \{ 1- \left( {{\text{p}}_{ 4 8. 2 2} + {\text{p}}_{ 4 6} {\text{p}}_{ 6 8} } \right)\left( {{\text{p}}_{ 8 9} + {\text{p}}_{ 8 4. 10} + {\text{p}}_{ 8, 1 4. 1 3} } \right) - {\text{p}}_{ 8 8. 1 3, 2 1} \\ & -\, {\text{p}}_{ 8, 1 2} \left( {{\text{p}}_{ 1 2, 8. 1 5} + {\text{p}}_{ 1 2, 6} {\text{p}}_{ 6 8} } \right)\} + \mu^{\prime }_{ 8} + {\text{p}}_{ 8, 9} \mu_{ 9} + {\text{p}}_{ 8, 1 2} \mu^{\prime }_{ 1 2} ] + \{ 1- {\text{p}}_{ 4 8. 2 2} + {\text{p}}_{ 4 6} {\text{p}}_{ 6 8} )\left( {{\text{p}}_{ 8 9} + {\text{p}}_{ 8 4. 10} + {\text{p}}_{ 8, 1 4. 1 3} } \right) \\ & -\, {\text{p}}_{ 8 8. 1 3, 2 1} - {\text{p}}_{ 8, 1 2} \left( {{\text{p}}_{ 1 2, 8. 1 5} + {\text{p}}_{ 1 2, 6} {\text{p}}_{ 6 8} } \right)\} [\mu_{ 2 5} \left\{ {{\text{p}}_{ 7, 2 5} \left( {{\text{p}}_{ 2 6, 8. 2 3} + {\text{p}}_{ 2 6, 2 7} } \right) + {\text{p}}_{ 2 6, 2 8} {\text{p}}_{ 2 8, 2 5} } \right\} + \mu^{\prime }_{ 2 6} \\ & +\, \mu_{ 2 7} {\text{p}}_{ 2 6, 2 7} + \mu^{\prime }_{ 2 8} {\text{p}}_{ 2 6, 2 8} ] \\ \end{aligned} $$

8 Busy period analysis

Let B_i(t) be the probability that the server is busy at an instant t given that the system entered regenerative state i at t = 0. The following are the recursive relations for B_i(t)

$$ {\text{B}}_{\text{i}} \left( {\text{t}} \right) = {\text{W}}_{\text{i}} \left( {\text{t}} \right) + \sum\limits_{\text{j}} {{\text{q}}_{\text{i,j}}^{{\left( {\text{n}} \right)}} \left( {\text{t}} \right){\text{\copyright B}}_{\text{j}} \left( {\text{t}} \right)} $$

(13a)

The system equations given in (13a) can be obtained similar as B₀(t) and B₁(t)

$$ {\text{B}}_{0} \left( {\text{t}} \right) = {\text{q}}_{0,1} ({\text{t}}) \, \copyright{\text{B}}_{1} \left( {\text{t}} \right)\quad \left( {{\text{for}}\;{\text{i}} = 0,\;{\text{j}} = 1} \right) $$

(13b)

$$ {\text{B}}_{ 1} \left( {\text{t}} \right) = {\text{W}}_{ 1} \left( {\text{t}} \right) + {\text{q}}_{ 1 3} \left( {\text{t}} \right)\copyright{\text{B}}_{ 3} \left( {\text{t}} \right) + {\text{q}}_{ 1 4. 2} \left( {\text{t}} \right)\copyright{\text{B}}_{ 4} \left( {\text{t}} \right)\quad \left( {{\text{for}}\;{\text{i}} = 1,\;{\text{j}} = 3, 4} \right) $$

(14)

where j is a subsequent regenerative state to which state i transits through n ≥ 1 (natural number) transitions.

Taking LT of relations (13a) and solving for B₀*(s). Using this, we can obtain the fraction of time for which the server is busy in steady state as

$$ B_{0} \left( \infty \right) = \mathop {\lim }\limits_{s \to 0} sB_{0}^{*} \left( s \right) = \frac{{Numerator\;of\;Busy\;Period\;of\;Server\;(B_{11} )}}{{Denoinator\;of\;Busy\;Period\;of\;Server\;(D_{12} )}} $$

(15)

$$ {\text{B}}_{ 1 1} = \left( {{\text{p}}_{ 2 6, 8. 2 3} + {\text{p}}_{ 2 6, 2 7} } \right)\left( {{\text{p}}_{ 8, 1 4. 1 3} + {\text{p}}_{ 8 9} {\text{p}}_{ 9, 1 4} } \right)[{\text{W}}_{ 1}^{*} \left( 0 \right)\left\{ {{\text{p}}_{ 1 4,0} + {\text{p}}_{ 1 4, 1. 1 9} } \right\} + {\text{W}}_{ 1 4}^{*} \left( 0 \right) + {\text{W}}_{ 1 7}^{*} \left( 0 \right){\text{p}}_{ 1 4, 1 7} ] + \left( {{\text{p}}_{ 2 6, 8. 2 3} + {\text{p}}_{ 2 6, 2 7} } \right)[{\text{W}}_{ 4}^{*} \left( 0 \right)\left\{ {{\text{p}}_{ 1 4,0} + {\text{p}}_{ 1 4, 1. 1 9} } \right\} + {\text{W}}_{ 7}^{*} \left( 0 \right)\left\{ { 1- \left( {{\text{p}}_{ 4 8. 2 2} + {\text{p}}_{ 4 6} {\text{p}}_{ 6 8} } \right)\left( {{\text{p}}_{ 8 9} + {\text{p}}_{ 8 4. 10} + {\text{p}}_{ 8, 1 4. 1 3} } \right) - {\text{p}}_{ 8 8. 1 3, 2 1} - {\text{p}}_{ 8, 1 2} \left( {{\text{p}}_{ 1 2, 8. 1 5} + {\text{p}}_{ 1 2, 6} {\text{p}}_{ 6 8} } \right)} \right\} + {\text{W}}_{ 8}^{*} \left( 0 \right) + {\text{W}}_{ 1 2}^{*} \left( 0 \right){\text{p}}_{ 8, 1 2} ] + \{ 1- \left( {{\text{p}}_{ 4 8. 2 2} + {\text{p}}_{ 4 6} {\text{p}}_{ 6 8} } \right)\left( {{\text{p}}_{ 8 9} + {\text{p}}_{ 8 4. 10} + {\text{p}}_{ 8, 1 4. 1 3} } \right) - {\text{p}}_{ 8 8. 1 3, 2 1} - {\text{ p}}_{ 8, 1 2} \left( {{\text{p}}_{ 1 2, 8. 1 5} + {\text{p}}_{ 1 2, 6} {\text{p}}_{ 6 8} } \right)\} \left[ {{\text{ W}}_{ 2 6}^{*} \left( 0 \right) + {\text{ W}}_{ 2 8}^{*} \left( 0 \right){\text{ p}}_{ 2 6, 2 8} } \right] $$

and D₁₂ is already mentioned.

9 Expected number of visits by the server

Let N_i(t) be the expected number of visits by the server in (0,t] given that the system entered the regenerative state i at t = 0. We have the following recursive relations for N_i(t):

$$ {\text{N}}_{\text{i}} \left( {\text{t}} \right) = \sum\limits_{\text{j}} {{\text{Q}}_{\text{i,j}} \left( {\text{t}} \right)\circledR \left[ {\delta_{\text{j}} + {\text{N}}_{\text{j}} \left( {\text{t}} \right)} \right]} $$

(16a)

The system equations given in (16a) can be obtained similar as N₀(t) and N₁(t)

$$ {\text{N}}_{0} \left( {\text{t}} \right) = Q_{0,1} \left( {\text{t}} \right)\circledR \left[ {1 + {\text{N}}_{1} \left( {\text{t}} \right)} \right] \quad \left( {{\text{for}}\;{\text{i}} = 0,\;{\text{j}} = 1} \right) $$

(16b)

$$ {\text{N}}_{ 1} \left( {\text{t}} \right) = {\text{Q}}_{ 1 3} \left( {\text{t}} \right)\circledR {\text{N}}_{ 3} \left( {\text{t}} \right) + {\text{Q}}_{ 1 4. 2} \left( {\text{t}} \right)\circledR {\text{N}}_{ 4} \left( {\text{t}} \right)\quad \left( {{\text{for}}\;{\text{i}} = 1,\;{\text{j}} = 3, 4} \right) $$

(16c)

where j is any regenerative state to which the given regenerative state i transits and δ _i  = 1, if j is the regenerative state where the server does job afresh otherwise δ _i  = 0.

Taking LST of relations (16a) and solving for ${\tilde{\text{N}}}_{0} ({\text{s}})$.

The expected number of visits per unit time as

$$ N_{0} \left( \infty \right) = \mathop {\lim }\limits_{s \to 0} s\tilde{N}_{0} \left( s \right) = \frac{{Numerator\;of\;Expected\;Number\;of\;Visits\;By\;Server\;(N_{11} )}}{{Denoinator\;of\;Expected\;Number\;of\;Visits\;By\;Server\;(D_{12} )}} $$

(17)

where

$$ {\text{N}}_{ 1 1} = \left( {{\text{p}}_{ 2 6, 8. 2 3} + {\text{p}}_{ 2 6, 2 7} } \right)\left( {{\text{p}}_{ 8, 1 4. 1 3} + {\text{p}}_{ 8 9} {\text{p}}_{ 9, 1 4} } \right)\times\left[ {{\text{p}}_{ 1 4,0} + \{ {\text{p}}_{ 1 3} \left( {{\text{p}}_{ 1 4,0} + {\text{p}}_{ 1 4, 1. 1 9} } \right) + {\text{p}}_{ 1 4, 1 7} {\text{p}}_{ 1 7, 3} \} } \right] + \left( {{\text{p}}_{ 2 6, 8. 2 3} + {\text{p}}_{ 2 6, 2 7} } \right)\left[ {\left\{ {\left( {{\text{p}}_{ 8 9} + {\text{ p}}_{ 8 4. 10} + {\text{ p}}_{ 8, 1 4. 1 3} } \right){\text{p}}_{ 4 6} + {\text{p}}_{ 8, 1 2} {\text{p}}_{ 1 2, 6} } \right\} + {\text{p}}_{ 8 9} } \right] + \{ 1- \left( {{\text{p}}_{ 4 8. 2 2} + {\text{p}}_{ 4 6} {\text{p}}_{ 6 8} } \right)\times\left( {{\text{p}}_{ 8 9} + {\text{p}}_{ 8 4. 10} + {\text{p}}_{ 8, 1 4. 1 3} } \right) - {\text{p}}_{ 8 8. 1 3, 2 1} - {\text{p}}_{ 8, 1 2} \left( {{\text{p}}_{ 1 2, 8. 1 5} + {\text{p}}_{ 1 2, 6} {\text{p}}_{ 6 8} } \right)\} \left[ {\left\{ {{\text{p}}_{ 7, 2 5} \left( {{\text{p}}_{ 2 6, 8. 2 3} + {\text{p}}_{ 2 6, 2 7} } \right) + {\text{p}}_{ 2 6, 2 7 8} {\text{p}}_{ 2 8, 2 5} } \right\} + {\text{p}}_{ 2 6, 2 7} } \right] $$

and D₁₂ is already specified.

10 Profit analysis

Any manufacturing industry is basically a profit making organization and no organization can survive for long without minimum financial returns for its investment. There must be an optimal balance between the reliability aspect of a product and its cost. The major factors contributing to the total cost are availability, busy period of server and expected number of visits by the server. The cost of these individual items varies with reliability or mean time to system failure. In order to increase the reliability of the products, we would require a correspondingly high investment in the research and development activities. The production cost also would increase with the requirement of greater reliability.

The revenue and cost function lead to the profit function of a firm, as the profit is excess of revenue over the cost of production. The profit function in time t is given by:

$$ {\text{P}}\left( {\text{t}} \right) = {\text{Expected}}\;{\text{revenue}}\;{\text{in}}\;\left( {0,{\text{t}}} \right]-{\text{Expected}}\;{\text{total}}\;{\text{cost}}\;{\text{in}}\;\left( {0,{\text{t}}} \right]. $$

In general, the optimal policies can more easily be derived for an infinite time span or compared to a finite time span. The profit per unit time, in infinite time span is expressed as

$$ \mathop {\lim }\limits_{t \to \infty } \frac{\text{P(t)}}{\text{t}} $$

i.e. profit per unit time = total revenue per unit time − total cost per unit time. Considering the various costs, the profit equation is given as

$$ {\text{P}} = {\text{K}}_{0} {\text{A}}_{0} -{\text{K}}_{ 1} {\text{B}}_{0} -{\text{K}}_{ 2} {\text{N}}_{0} $$

where P is the profit per unit time incurred to the system, K₀ the revenue per unit up time of the system, A₀ the total fraction of time for which the system is up, K₁ the cost per unit time for which server is busy, B₀ the total fraction of time for which the server is busy, K₂ the cost per visit by the server, and N₀ is the expected number of visits per unit time for the server.

11 Application of the study

The application of the present study can be visualized in various practical situations in different areas. The communication system with three transmitters can be cited as a good example of such systems where the average messages load may be such that at least two transmitters must be operational at all times otherwise critical messages will be lost. The system of communication amplifier in which redundancy is used as means of increasing the reliability may also be considered as an important application area of the present study.

12 Results and discussion

The time to failure, repair and inspection are Weibull distributed with two parameters. Probability density function of Weibull distribution with two parameters is given by

$$ f(t) = 2\lambda \exp \left[ { - 2\lambda t^{b + 1} /b + 1} \right]. $$

From the Weibull distribution, If b = 0, it become the exponential distribution and when b = 1, it become the Rayleigh distribution.

Let

$$ \begin{array}{ll} {z(t) = 2\lambda_{1} \exp \left[ { - 2\lambda_{1} t^{b + 1} /b + 1} \right]} & {a(t) = \lambda \exp \left[ { - \lambda t^{b + 1} /b + 1} \right]} \\ {b(t) = \lambda {}_{1}\exp \left[ { - \lambda {}_{1}t^{b + 1} /b + 1} \right]} & {h(t) = \alpha \exp \left[ { - \alpha t^{b + 1} /b + 1} \right]} \\ {g(t) = \theta \exp \left[ { - \theta t^{b + 1} /b + 1} \right]} & {g_{1} (t) = \theta_{1} \exp \left[ { - \theta_{1} t^{b + 1} /b + 1} \right]} \\ \end{array} $$

The results for a particular case are obtained to depict the behavior of MTSF, availability and profit of the system as shown in Tables 1, 2, 3, 4 and 5. From Table 1, it is observed that MTSF, availability and profit decrease with the increase of failure rate of new unit (λ). A declining trend of MTSF, availability and profit with respect to increase in failure rate of degraded unit (λ₁) is noted in Table 2. From Tables 3 and 4, it can be seen that, MTSF, availability and profit of the system increase with increase of repair rate of degraded unit (θ₁) and inspection rate (α). It is also observed that system becomes more available to use and profitable if the degraded unit at its failure is replaced by new one. In Table 5, there is a substantial positive change in MTSF, availability and profit when we interchange values of p and q. From Tables 1, 2, 3, 4 and 5, we have the comparison between two distributions and it is observed that the exponential distribution is better than the Rayleigh distribution in system under stated conditions.

Table 1 Comparison between the effects of the exponential and Rayleigh distributions with respect to failure rate of new unit (λ) and other parameters (λ₁ = 0.08, θ = 1.2, θ₁ = 2.1, p = 0.7, q = 0.3, α = 15, K₀ = 5000, K₁ = 450, K₂ = 50) on the system

Table 2 Comparison between the effects of the exponential and Rayleigh distributions with respect to failure rate of new unit (λ) and other parameters (λ₁ = 0.28, θ = 1.2, θ₁ = 2.1, p = 0.7, q = 0.3, α = 15, K₀ = 5000, K₁ = 450, K₂ = 50) on the system

Table 3 Comparison between the effects of the exponential and Rayleigh distributions with respect to failure rate of new unit (λ) and other parameters (λ₁ = 0.08, θ = 1.2, θ₁ = 3.1, p = 0.7, q = 0.3, α = 15, K₀ = 5000, K₁ = 450, K₂ = 50) on the system

Table 4 Comparison between the effects of the exponential and Rayleigh distributions with respect to failure rate of new unit (λ) and other parameters (λ₁ = 0.08, θ = 1.2, θ₁ = 2.1, p = 0.7, q = 0.3, α = 25, K₀ = 5000, K₁ = 450, K₂ = 50) on the system

Table 5 Comparison between the effects of the exponential and Rayleigh distributions with respect to failure rate of new unit (λ) and other parameters (λ₁ = 0.08, θ = 1.2, θ₁ = 2.1, p = 0.3, q = 0.7, α = 15, K₀ = 5000, K₁ = 450, K₂ = 50) on the system

13 Conclusion

On the basis of the results obtained for a particular case it is concluded that a 2-out-of-2 redundant system with single standby in which unit becomes degraded after repair can be made more reliable and profitable to use by the following ways:

• (1) By making immediate replacement of the degraded unit at its further failure if inspection reveals that repair is not feasible to the system.

• (2) By increasing the repair rate of the degraded unit at its failure.