1 Introduction

Since 1983, Cohen–Grossberg neural networks (CGNNs) have attracted considerable attention due to their potential applications in pattern recognition, parallel computing, signal and image processing, associative memory, combinatorial optimization, etc (see [1]). Many interesting results on the dynamical behaviors of CGNNs have been obtained (see, for example, [2–5, 26–28]). However, most of the previous results on CGNNs did not consider the jump discontinuities of neuron activations. As far as we know, discontinuous or non-Lipschitz activation functions of neural networks are significant and can be used to solve programming problems and various control problems (see [6–8]). Nowadays, the study of dynamical behaviors for neural networks with discontinuous activations has become a hot research topic. For instance, the paper [29] gave global stability analysis of a general class of discontinuous neural networks with linear growth activation functions. In [30], the authors discussed the existence and stability of periodic solution for BAM neural networks with discontinuous neuron activations and impulses. The paper [31] investigated the exponential state estimation for Markovian jumping neural networks with discontinuous activation functions and mixed time-varying delays. In recent years, under the Filippov differential inclusion framework, some attempts have been made to investigate the existence and convergence of periodic solutions or almost periodic solutions or even equilibrium points for CGNNs possessing discontinuous neuron activations (see [9–11]). Nevertheless, there is still not much research on finite-time synchronization issues of CGNNs with discontinuous activation functions.

Actually, finite-time synchronization requires that the system trajectories of error states converge to the desired aim over the finite time and to keep them there then after. As a powerful tool, finite-time synchronization control plays an important role in the field of artificial neural networks. On the one hand, we can understand an unknown dynamical neuron system from the well-known dynamical neuron system via finite-time synchronization. On the other hand, by using finite-time synchronization control, the convergence time of error states can be shortened. This means that finite-time synchronization possesses faster convergence speed than asymptotic synchronization and exponential synchronization (see [12]). Note that the dynamical neuron system with discontinuous neuron activation may also exhibit some unstable behaviors such as periodic oscillation and chaos. Especially, if time-delays between neuron signals occur in a discontinuous neuron system, the behaviors of oscillation or chaos will become more apparent. Therefore, it is of great necessity for us to realize the finite-time synchronization control of CGNNs with discontinuous activations and time-delays. In addition, the finite-time synchronization of drive-response system is more easy to be achieved by utilizing non-smooth controllers such as sliding mode controller and switching controller. However, the classical continuous linear controllers are usually difficult to realize the finite-time synchronization of discontinuous neural network systems. The main reasons include two aspects: (1) the classical continuous linear controllers are difficult to deal with the uncertain differences between the Filippov solutions of the drive system and response system with discontinuous factors. (2) The classical continuous linear controllers are difficult to eliminate the influence of time-delays on the error states of discontinuous neuron systems. It should be emphasized that, different from classical continuous linear controllers, the switching state-feedback controllers usually include a discontinuous function sign \((\cdot )\) which can effectively overcome the above two difficulties.

Up to now, some theoretical results on the synchronization issues of neural networks with discontinuous activations have already been obtained. For example, the authors of [13] dealt with the quasi-synchronization problem of neural networks with discontinuous neuron activations, but the state error of drive-response system can only be controlled within a small region around zero. In [32] the adaptive exponential synchronization problem of delayed Cohen–Grossberg neural networks with discontinuous activations was considered. In [14, 39], by constructing suitable Lyapunov functionals, the exponential synchronization of time-delayed neural networks with discontinuous activations were investigated. Also in [15], the periodic synchronization problem of time-delayed neural networks with discontinuous activations was discussed via switching control approach. However, the convergence time of the state error for synchronization in [13–15, 32, 39] is sufficiently large. The paper [16] handled the finite-time synchronization issue of complex networks with discontinuous node dynamics, but the discrete and distributed time-delays between neuron signal are not considered. To the best of the authors’ knowledge, only a few papers have studied finite-time synchronization problems of neural networks with time-delays and discontinuous neuron activations.

Inspired by the above discussions, this paper consider a class of discontinuous Cohen–Grossberg neural network model with both discrete time-delays and distributed time-delays as follows:

$$\begin{aligned} \frac{\mathrm{d}x_{i}(t)}{\mathrm{d}t} =&-d_{i}(x_{i}(t))\left[ a_{i}(x_{i}(t))-\sum \limits _{j=1}^{n}b_{ij}f_{j}(x_{j}(t))\right. \nonumber \\&-\sum \limits _{j=1}^{n}c_{ij}f_{j}(x_{j}(t-\tau _{j}(t)))\nonumber \\&\left. -\sum \limits _{j=1}^{n}w_{ij}\int _{t-\delta _{j}(t)}^{t}f_{j}(x_{j}(s))\mathrm{d}s-J_{i}\right] , \end{aligned}$$
(1)

where \(i\in \mathbb {N}\doteq \{1,2,\ldots ,n\},\) n corresponds to the number of units in the delayed network system (1); \(x_{i}(t)\) denotes the state variable of the ith unit at time t; \(f_{j}(\cdot )\) represents the activation function of jth neuron; \(d_{i}(x_{i}(t))>0\) represents the amplification function of the ith neuron; \(a_{i}(x_{i}(t))\) denotes appropriately behaved function; \(b_{ij}\) represents the connection strength of jth neuron on the ith neuron; \(c_{ij}\) denotes the discrete time-delayed connection strength of jth neuron on the ith neuron; \(w_{ij}\) denotes the distributed time-delayed connection strength of jth neuron on the ith neuron; \(J_{i}\) is the neuron input on the ith unit; \(\tau _{j}(t)\) corresponds to the discrete time-varying delay at time t and is a continuous function satisfying \(0\le \tau _{j}(t)\le \tau ^{M},\) \(\dot{\tau }_{j}(t)\le \tau _{j}^{D}<1,\) where \(\tau ^{M}=\max \limits _{j\in \mathbb {N}}\{\sup \limits _{t\ge 0}\tau _{j}(t)\}\) and \(\tau _{j}^{D}\) are nonnegative constants; \(\delta _{j}(t)\) denotes the distributed time-varying delay at time t and is a continuous function satisfying \(0\le \delta _{j}(t)\le \delta ^{M}\), \(\dot{\delta }_{j}(t)\le \delta _{j}^{D}<1\), where \(\delta ^{M}=\max \limits _{j\in \mathbb {N}}\{\sup \limits _{t\ge 0}\delta _{j}(t)\}\) and \(\delta _{j}^{D}\) are nonnegative constants.

Throughout this paper, we always make the following fundamental assumptions:

  • (\(\mathscr {H}\)1) For each \(i\in \mathbb {N}\), the amplification function \(d_{i}(u)\) is continuous and there exist positive numbers \(d_{i}^{*}\) and \(d_{i}^{**}\) such that \(0<d_{i}^{*}\le d_{i}(u)\le d_{i}^{**}\) for \(u\in \mathbb {R}\).

  • (\(\mathscr {H}\)2) The neuron activation \(f(x)=(f_{1}(x_{1}),f_{2}(x_{2}),\ldots ,f_{n}(x_{n}))^\mathrm{T}\) is allowed to be discontinuous and satisfies the following conditions:

    1. (i)

      For each \(i\in \mathbb {N}\), \(f_{i}:\mathbb {R}\rightarrow \mathbb {R}\) is piecewise continuous, i.e., \(f_{i}\) is continuous except on a countable set of isolate points \(\{\rho _{k}^{i}\}\), where there exist finite right and left limits, \(f_{i}^{+}(\rho _{k}^{i})\) and \(f_{i}^{-}(\rho _{k}^{i})\), respectively. Moreover, \(f_{i}\) has at most a finite number of discontinuities on any compact interval of \(\mathbb {R}\).

    2. (ii)

      For each \(i\in \mathbb {N}\), there exist nonnegative constants \(L_{i}\) and \(p_{i}\) such that for any \(u,v\in \mathbb {R}\),

      $$\begin{aligned} \sup \limits _{\xi _{i}\in \overline{\mathrm{co}}[f_{i}(u)],\eta _{i}\in \overline{\mathrm{co}}[f_{i}(v)]}|\xi _{i}-\eta _{i}|\le L_{i}|u-v|+p_{i}, \end{aligned}$$
      (2)

      where, for \(\theta \in \mathbb {R},\)

      $$\begin{aligned} \overline{\mathrm{co}}[f_{i}(\theta )]=\left[ \min \{f_{i}^{-}(\theta ) ,f_{i}^{+}(\theta )\},\max \{f_{i}^{-}(\theta ) ,f_{i}^{+}(\theta )\}\right] . \end{aligned}$$

  • (\(\mathscr {H}\)3) For any \(i\in \mathbb {N}\), there exists a positive constant \(\dot{a}_{i}(u)\ge \beta _{i}\), where \(\dot{a}_{i}(u)\) denotes the derivative of \(a_{i}(u)\) for \(u\in \mathbb {R}\) and \(a_{i}(0)=0\).

The structure of this paper is organized as follows. Section 2 presents some preliminary knowledge. Our main results and their proofs are contained in Sect. 3. Section 4 gives two numerical examples to verify the theoretical results. Finally, we conclude this paper in Sect. 5.

Notations Let \(\varsigma =\max \{\tau ^{M},\delta ^{M}\}\). \(\mathbb {R}\) denotes the space of real number and \(\mathbb {R}^{n}\) represents the n-dimensional Euclidean space. Given column vectors \(x=(x_{1},x_{2},\ldots ,x_{n})^{\mathrm{T}}\in \mathbb {R}^{n}\) and \(y=(y_{1},y_{2},\ldots ,y_{n})^{\mathrm{T}}\in \mathbb {R}^{n}\), \(\langle x,y\rangle =x^{\mathrm{T}}y=\sum \nolimits _{i=1}^{n}x_{i}y_{i}\) denotes the scalar product of x and y, where the superscript \(\mathrm{T}\) represents the transpose operator. Given \(x=(x_{1},x_{2},\ldots ,x_{n})^{\mathrm{T}}\in \mathbb {R}^{n}\), let \(\parallel x\parallel\) denote any vector norm of x. Finally, let \(\mathrm {sign}(\cdot )\) be the sign function and \(2^{\mathbb {R}^{n}}\) denote the family of all nonempty subsets of \(\mathbb {R}^{n}\).

2 Preliminaries

In this section, we give some preliminary knowledge about set-valued analysis, differential inclusion theory, non-smooth Lyapunov approach and an important inequality. The readers may refer to [17–25] for more details.

Definition 1

(see [17, 18]) Suppose \(X\subseteq \mathbb {R}^{n}\), then \(x\mapsto F(x)\) is said to be a set-valued map from \(X\rightarrow 2^{\mathbb {R}^{n}},\) if for every point x of the set \(X\subset \mathbb {R}^{n},\) there corresponds a nonempty set \(F(x)\subset \mathbb {R}^{n}.\) A set-valued map F with nonempty values is said to be upper semi-continuous (USC) at \(x_{0}\in X,\) if for any open set N containing \(F(x_{0}),\) there exists a neighborhood M of \(x_{0}\) such that \(F(M)\subset N.\)

Now let us introduce extended Filippov-framework (see [18, 19]). Let \(\varsigma\) be a given nonnegative real number and \(C=C([-\varsigma ,0],\mathbb {R}^{n})\) denote the Banach space of continuous functions \(\phi\) mapping the interval \([-\varsigma ,0]\) into \(\mathbb {R}^{n}\) with the norm \(\Vert \phi \Vert _{C}=\sup \limits _{-\varsigma \le s\le 0}\Vert \phi (s)\Vert .\) If for \(\mathcal {T}\in (0,+\infty ],\) \(x(t):[-\varsigma ,\mathcal {T})\rightarrow \mathbb {R}^{n}\) is continuous, then \(x_{t}\in C\) is defined by \(x_{t}(\theta )=x(t+\theta ),\) \(-\varsigma \le \theta \le 0\) for any \(t\in [0,\mathcal {T}).\) Consider the following time-delayed differential equation:

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}=f(t,x_{t}), \end{aligned}$$
(3)

where \(x_{t}(\cdot )\) represents the history of the state from time \(t-\varsigma\), up to the present time t; \(\mathrm{d}x/\mathrm{d}t\) is the time derivative of x and \(f:\mathbb {R}\times C\rightarrow \mathbb {R}^{n}\) denotes measurable and essentially locally bounded function. In this case, \(f(t,x_{t})\) is allowed to be discontinuous in \(x_{t}\).

Let us construct the following Filippov set-valued map \(F:\mathbb {R}\times C\rightarrow 2^{\mathbb {R}^{n}}\)

$$\begin{aligned} F(t,x_{t})=\bigcap \limits _{\rho>0}\bigcap \limits _{\mathrm{meas} (\mathcal {N})=0}\overline{\mathrm{co}}[f(t,\mathcal {B}(x_{t},\rho) {\setminus} \mathcal {N})]. \end{aligned}$$
(4)

Here \(\mathrm{meas}(\mathcal {N})\) denotes the Lebesgue measure of set \(\mathcal {N}\); intersection is taken over all sets \(\mathcal {N}\) of Lebesgue measure zero and over all \(\rho>0\); \(\mathcal {B}(x_{t},\rho )=\{x^{*}_{t}\in C\mid \Vert x^{*}_{t}-x_{t}\Vert _{C}<\rho \}\); \(\overline{\mathrm{co}}[\mathbb {E}]\) represents the closure of the convex hull of some set \(\mathbb {E}\).

Definition 2

We say a vector-valued function x(t) defined on a non-degenerate interval \(\mathbb {I}\subseteq \mathbb {R}\) is a Filippov solution for time-delayed differential equation (4), if it is absolutely continuous on any compact subinterval \([t_{1},t_{2}]\) of \(\mathbb {I}\), and for a.e. \(t\in \mathbb {I}\), x(t) satisfies the following time-delayed differential inclusion

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}\in F(t,x_{t}). \end{aligned}$$
(5)

In the following, we apply the extended Filippov differential inclusion framework in discussing the solution of CGNNs with mixed time-delays and discontinuous activations.

Definition 3

A function \(x(t)=(x_{1}(t),x_{2}(t),\ldots ,x_{n}(t))^{\mathrm{T}}:[-\varsigma ,\mathcal {T})\rightarrow \mathbb {R}^{n},\mathcal {T}\in (0,+\infty ],\) is a state solution of the delayed and discontinuous system (1) on \([-\varsigma ,\mathcal {T})\) if

  1. (i)

    x is continuous on \([-\varsigma ,\mathcal {T})\) and absolutely continuous on any compact subinterval of \([0,\mathcal {T})\);

  2. (ii)

    there exists a measurable function \(\gamma =(\gamma _{1},\gamma _{2},\ldots ,\gamma _{n})^\mathrm{T}:[-\varsigma ,\mathcal {T})\rightarrow \mathbb {R}^{n}\) such that \(\gamma _{j}(t)\in \overline{\mathrm{co}}[f_{j}(x_{j}(t))]\) for a.e. \(t\in [-\varsigma ,\mathcal {T})\) and for a.e. \(t\in [0,\mathcal {T}),~i\in \mathbb {N}\),

    $$\begin{aligned} \frac{\mathrm{d}x_{i}(t)}{\mathrm{d}t}& =-d_{i}(x_{i}(t))[a_{i}(x_{i}(t))-\sum \limits _{j=1}^{n}b_{ij}\gamma _{j}(t)\nonumber \\& \quad -\sum \limits _{j=1}^{n}c_{ij}\gamma _{j}(t-\tau _{j}(t))-\sum \limits _{j=1}^{n}w_{ij}\int _{t-\delta _{j}(t)}^{t}\gamma _{j}(s)\mathrm{d}s-J_{i}]. \end{aligned}$$
    (6)

Any function \(\gamma =(\gamma _{1},\gamma _{2},\ldots ,\gamma _{n})^\mathrm{T}\) satisfying (6) is called an output solution associated with the state x. With this definition it turns out that the state \(x(t)=(x_{1}(t),x_{2}(t),\ldots ,x_{n}(t))^\mathrm{T}\) is a solution of (1) in the sense of Filippov since for a.e. \(t\in [0,\mathcal {T})\) and \(i\in \mathbb {N}\), it satisfies

$$\begin{aligned} \begin{array}{ll} \frac{\mathrm{d}x_{i}(t)}{\mathrm{d}t} \in & -d_{i}(x_{i}(t))\left[ a_{i}(x_{i}(t))-\sum \limits _{j=1}^{n}b_{ij}\overline{\mathrm{co}}[f_{j}(x_{j}(t))]\right. \\ & -\sum \limits _{j=1}^{n}c_{ij}\overline{\mathrm{co}}[f_{j}(x_{j}(t-\tau _{j}(t)))]\\ & \left. -\sum \limits _{j=1}^{n}w_{ij}\int _{t-\delta _{j}(t)}^{t}\overline{\mathrm{co}}[f_{j}(x_{j}(s))]\mathrm{d}s-J_{i}\right] . \end{array} \end{aligned}$$

The next definition is the initial value problem associated with CGNNs (1) as follows.

Definition 4

Let \(\phi =(\phi _{1},\phi _{2},\ldots ,\phi _{n})^\mathrm{T}:[-\varsigma ,0]\rightarrow \mathbb {R}^{n}\) be any continuous function and \(\psi =(\psi _{1},\psi _{2},\ldots ,\psi _{n})^\mathrm{T}:[-\varsigma ,0]\rightarrow \mathbb {R}^{n}\) be any measurable selection, such that \(\psi _{j}(s)\in \overline{\mathrm{co}}[f_{j}(\phi _{j}(s))]\) \((j\in \mathbb {N})\) for a.e. \(s\in [-\varsigma ,0]\), an absolute continuous function \(x(t)=x(t,\phi ,\psi )\) associated with a measurable function \(\gamma\) is said to be a solution of the Cauchy problem for system (1) on \([-\varsigma ,\mathcal {T})\) (\(\mathcal {T}\) might be \(+\infty\)) with initial value \((\phi (s),\psi (s)), s\in [-\varsigma ,0]\), if

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\mathrm{d}x_{i}(t)}{\mathrm{d}t} & =-d_{i}(x_{i}(t)) [a_{i}(x_{i}(t))-\sum \limits _{j=1}^{n}b_{ij}\gamma _{j}(t) \\ & \quad -\sum \limits _{j=1}^{n}c_{ij}\gamma _{j}(t-\tau _{j}(t)) -\sum \limits _{j=1}^{n}w_{ij}\int _{t-\delta _{j}(t)}^{t}\gamma _{j}(s)\mathrm{d}s \\ & \quad -J_{i}],\quad \mathrm{for~ a.e.} ~t\in [0,\mathcal {T}), \\ \gamma _{j}(t)&\in \overline{\mathrm{co}}[f_{j}(x_{j}(t))], \mathrm{for ~a.e.} ~t\in [0,\mathcal {T}), \\ x(s)&=\phi (s), \quad \forall s\in [-\varsigma ,0], \\ \gamma (s)&=\psi (s), \quad \mathrm{for\; a.e.} s\in [-\varsigma ,0]. \end{array}\right. } \end{aligned}$$
(7)

Consider the neural network model (1) as the drive system, the controlled response system is given as follows:

$$\begin{aligned} \frac{\mathrm{d}y_{i}(t)}{\mathrm{d}t} =&-d_{i}(y_{i}(t))\left[ a_{i}(y_{i}(t))-\sum \limits _{j=1}^{n}b_{ij}f_{j}(y_{j}(t)) \right. \nonumber \\& -\sum \limits _{j=1}^{n}c_{ij}f_{j}(y_{j}(t-\tau _{j}(t)))\nonumber \\&\left. -\sum \limits _{j=1}^{n}w_{ij}\int _{t-\delta _{j}(t)}^{t}f_{j}(y_{j}(s))\mathrm{d}s-J_{i}-u_{i}(t)\right] , \end{aligned}$$
(8)

where \(i\in \mathbb {N}\), \(u_{i}(t)\) is the controller to be designed for realizing synchronization of the drive-response system. The other parameters are the same as those defined in system (1)

Similar to Definition 4, we can give the initial value problem (IVP) of response system (8) as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\mathrm{d}y_{i}(t)}{\mathrm{d}t} &= -d_{i}(y_{i}(t))[a_{i}(y_{i}(t))-\sum \limits _{j=1}^{n}b_{ij}\xi _{j}(t) \\ & \quad -\sum \limits _{j=1}^{n}c_{ij}\xi _{j}(t-\tau _{j}(t)) -\sum \limits _{j=1}^{n}w_{ij}\int _{t-\delta _{j}(t)}^{t}\xi _{j}(s)\mathrm{d}s \\ & \quad -J_{i}-u_{i}(t)],\mathrm{for~ a.e.} ~t\in [0,\mathcal {T}), \\ \xi _{j}(t) & \in \overline{\mathrm{co}}[f_{j}(y_{j}(t))],~ \mathrm{for ~a.e.} ~t\in [0,\mathcal {T}), \\ y(s)& =\varphi (s),~\forall s\in [-\varsigma ,0], \\ \xi (s)&=\omega (s),~\mathrm{for ~a.e.}~s\in [-\varsigma ,0]. \end{array}\right. } \end{aligned}$$
(9)

Lemma 1

(Chain Rule [20, 21]) Assume that \(V(z):\mathbb {R}^{n}\rightarrow \mathbb {R}\) is C-regular, and \(z(t):[0,+\infty )\rightarrow \mathbb {R}^{n}\) is absolutely continuous on any compact subinterval of \([0,+\infty )\). Then, z(t) and \(V(z(t)):[0,+\infty )\rightarrow \mathbb {R}\) are differential for a.e. \(t\in [0,+\infty )\) and

$$\begin{aligned} \frac{\mathrm{d}V(z(t))}{\mathrm{d}t}=\left\langle \zeta (t),\frac{\mathrm{d}z(t)}{\mathrm{d}t}\right\rangle , \forall \zeta (t)\in \partial V(z(t)), \end{aligned}$$

where \(\partial V(z)\) denotes the Clarke’s generalized gradient of V at point \(z\in \mathbb {R}^{n}\).

Lemma 2

(see [21]) Assume that \(V(z(t)):\mathbb {R}^{n}\rightarrow \mathbb {R}\) is C-regular, and that \(z(t):[0,+\infty )\rightarrow \mathbb {R}^{n}\) is absolutely continuous on any compact subinterval of \([0,+\infty )\). If there exists a continuous function \(\Upsilon :(0,+\infty )\rightarrow \mathbb {R}\), with \(\Upsilon (\varrho )>0\) for \(\varrho \in (0,+\infty )\), such that

$$\begin{aligned} \frac{\mathrm{d}V(t)}{\mathrm{d}t}\le -\Upsilon (V(t)),~\mathrm{for~a.e.}~t\ge 0, \end{aligned}$$

and

$$\begin{aligned} \int _{0}^{V(0)}\frac{1}{\Upsilon (\varrho )}\mathrm{d}\varrho =t^{*}<+\infty , \end{aligned}$$
(10)

then we have \(V(t)=0\) for \(t\ge t^{*}\). Especially, we have following conclusions.

  1. (i)

    If \(\Upsilon (\varrho )=K_{1}\varrho +K_{2}\varrho ^{\mu }\), for all \(\varrho \in (0,+\infty )\), where \(\mu \in (0,1)\) and \(K_{1},K_{2}>0\), then the settling time can be estimated by

    $$\begin{aligned} t^{*}=\frac{1}{K_{1}(1-\mu )}\ln \frac{K_{1}V^{1-\mu }(0)+K_{2}}{K_{2}}. \end{aligned}$$
    (11)
  2. (ii)

    If \(\Upsilon (\varrho )=K\varrho ^{\mu }\) and \(K>0\), then the settling time can be estimated by

    $$\begin{aligned} t^{*}=\frac{V^{1-\mu }(0)}{K(1-\mu )}. \end{aligned}$$
    (12)

Definition 5

Discontinuous drive-response systems (1) and (8) are said to be finite-time synchronized if, for a suitable controller, there exists a time \(t^{*}\) such that \(\lim \limits _{t\rightarrow t^{*}}\Vert e(t)\Vert =0,\) and \(\Vert e(t)\Vert =\Vert y(t)-x(t)\Vert \equiv 0\) for \(t>t^{*}\), where x(t) and y(t) are the solutions of drive system (1) and response system (8) with initial conditions \(\phi\) and \(\varphi\), respectively.

Lemma 3

(Jensen Inequality [25]) If \(a_{1},a_{2},\ldots ,a_{n}\) are positive numbers and \(0<r<p\), then

$$\begin{aligned} \left( \sum \limits _{i=1}^{n}a_{i}^{p}\right) ^{1/p}\le \left( \sum \limits _{i=1}^{n}a_{i}^{r}\right) ^{1/r}. \end{aligned}$$

3 Main results

In this section, we consider the possibility to implement finite-time synchronization control of time-delayed neural networks with discontinuous activations. Different from previous works, we design two classes of novel switching state-feedback controllers which involve time-delays and discontinuous factors. Based on extended Filippov differential inclusion framework and famous finite-time stability theory, we will provide some new basic results about finite-time synchronization of drive-response neural networks with time-delays and discontinuous activations. Now let us define the synchronization error between the drive system (1) and the response system (8) as follows

$$\begin{aligned} e_{i}(t)=y_{i}(t)-x_{i}(t),i\in \mathbb {N}. \end{aligned}$$

In order to realized finite-time synchronization goal, we design the following two classes of switching state-feedback controllers:

Case (1) The switching state-feedback controller \(u(t)=(u_{1}(t),u_{2}(t),\ldots ,u_{n}(t))^\mathrm{T}\) is given by

$$\begin{aligned}&u_{i}(t)= {\left\{ \begin{array}{ll} -k_{i}\mathrm{sign}(e_{i}(t))-\frac{r_{i}|e_{i}(t)|^{\sigma }}{\mathrm{sign}(e_{i}(t))}\\ -\sum \limits _{j=1}^{n}\pi _{ij}\mathrm{sign}(e_{i}(t))|e_{j}(t-\tau _{j}(t))|\\ -\sum \limits _{j=1}^{n}\varpi _{ij}\mathrm{sign}(e_{i}(t))\int _{t-\delta _{j}(t)}^{t}|e_{j}(s)|\mathrm{d}s,\mathrm{if} e_{i}(t)\ne 0, \\ 0, \quad \mathrm{if} e_{i}(t)=0, \end{array}\right. } \end{aligned}$$
(13)

where \(i\in \mathbb {N}\), the constants \(k_{i}, r_{i},\pi _{ij},\varpi _{ij}\) are the gain coefficients to be determined, and the real number \(\sigma\) satisfies \(0<\sigma <1\).

Case (2) The switching state-feedback controller \(u(t)=(u_{1}(t),u_{2}(t),\ldots ,u_{n}(t))^\mathrm{T}\) is given by

$$\begin{aligned} u_{i}(t)={\left\{ \begin{array}{ll} -\ell _{i}\mathrm{sign}(e_{i}(t))-\frac{\eta _{i}|e_{i}(t)|^{\sigma }}{\mathrm{sign}(e_{i}(t))}\\ ~-\frac{q}{\mathrm{sign}(e_{i}(t))}\left( \int _{-\delta _{i}(t)}^{0}\int _{t+\theta }^{t}\vartheta _{i}|e_{i}(s)|\mathrm{d}s\mathrm{d}\theta \right) ^{\sigma }\\ ~~~-\frac{\hbar }{\mathrm{sign}(e_{i}(t))}\left( \int _{t-\tau _{i}(t)}^{t}\zeta _{i}|e_{i}(s)|\mathrm{d}s\right) ^{\sigma },~\mathrm{if}~ e_{i}(t)\ne 0,\\ 0, \quad \text{if}~e_{i}(t)=0. \end{array}\right. } \end{aligned}$$
(14)

Here \(i\in \mathbb {N}\), the constants \(\ell _{i},\eta _{i},\zeta _{i},\vartheta _{i}\) are the gain coefficients to be determined, \(\hbar>0\) and \(q>0\) are tunable constants, and the real number \(\sigma\) satisfies \(0<\sigma <1\).

Remark 1

Different from conventional continuous linear controllers and adaptive controllers, the switching state-feedback controllers (13) and (14) include the discontinuous term \(\mathrm{sign}(e_{i}(t))\) which can switch the system state and makes the error state converge to zero in a finite-time. Such switching state-feedback controllers possess some merits. One of merits is that they can well handle the uncertain differences of the Filippov solutions for neural networks with discontinuous activations. Another merit is that such switching state-feedback controllers can eliminate the influence of time-delay on the states of neuron system with especial state-dependent nonlinear discontinuous properties.

3.1 State-feedback control design in Case (1)

Theorem 1

Suppose that the conditions (\(\mathscr {H}\)1)-(\(\mathscr {H}\)3) are satisfied, assume further that

  • (\(\mathscr {H}\)4) \(k_{i}\ge \sum \limits _{j=1}^{n}\left( |b_{ij}|+|c_{ij}|+\delta ^{M}|w_{ij}|\right) p_{j}\) for each \(i\in \mathbb {N}\), \(\mathscr {B}>\mathscr {A}\), \(\min \limits _{1\le i,j\le n}\left\{ \pi _{ij}\right\} \ge \max \limits _{1\le i,j\le n}\left\{ |c_{ij}|L_{j}\right\}\) and \(\min \limits _{1\le i,j\le n}\left\{ \varpi _{ij}\right\} \ge \max \limits _{1\le i,j\le n}\left\{ |w_{ij}|L_{j}\right\}\), where

    $$\begin{aligned} \mathscr {B}=\min \limits _{1\le i\le n}\left\{ \beta _{i}\right\} ,~\mathscr {A}=\max \limits _{1\le j\le n}\left\{ \sum \limits _{i=1}^{n}|b_{ij}|L_{j}\right\} . \end{aligned}$$

If the drive-response system is controlled with the control law (13), then the response system (8) can be synchronized with the drive system (1) in a finite time, and the settling time for finite-time synchronization is given by

$$\begin{aligned} t_{1}^{*} =\, &\frac{1}{(1-\sigma )(\mathscr {B}-\mathscr {A})d_{\min }^{*}}\nonumber \\&\times \ln \left( \frac{(\mathscr {B}-\mathscr {A})d_{\min }^{*}V^{1-\sigma }(0) +\mathscr {D}(d_{\min }^{*})^{\sigma }}{\mathscr {D}(d_{\min }^{*})^{\sigma }}\right) . \end{aligned}$$
(15)

Proof

Consider the following Lyapunov functional for the drive-response system with switching state-feedback controller (13):

$$\begin{aligned} V(t)=\sum \limits _{i=1}^{n}\mathrm{sign}(e_{i}(t))\int _{x_{i}(t)}^{y_{i}(t)}\frac{1}{d_{i}(s)}\mathrm{d}s. \end{aligned}$$
(16)

Obviously, V(t) is C-regular and the following inequality holds:

$$\begin{aligned} \frac{1}{d_{\max }^{**}}\sum \limits _{i=1}^{n}|e_{i}(t)|\le V(t)\le \frac{1}{d_{\min }^{*}}\sum \limits _{i=1}^{n}|e_{i}(t)|, \end{aligned}$$
(17)

where \(d_{\min }^{*}=\min \nolimits _{i\in \mathbb {N}}\{d_{i}^{*}\}\) and \(d_{\max }^{**}=\max \nolimits _{i\in \mathbb {N}}\{d_{i}^{**}\}\). By the chain rule in Lemma 1, calculate the time derivative of V(t) along the trajectories of the drive-response system, we can obtain

$$\begin{aligned} \frac{\mathrm{d}V(t)}{\mathrm{d}t}& =\sum \limits _{i=1}^{n}\mathrm{sign}(e_{i}(t))[-(a_{i}(y_{i}(t))-a_{i}(x_{i}(t)))\nonumber \\& \quad + \sum \limits _{j=1}^{n}b_{ij}(\xi _{j}(t)-\gamma _{j}(t))\nonumber \\& \quad +\sum \limits _{j=1}^{n}c_{ij}(\xi _{j}(t-\tau _{j}(t))-\gamma _{j}(t-\tau _{j}(t)))\nonumber \\& \quad +\sum \limits _{j=1}^{n}w_{ij}\int _{t-\delta _{j}(t)}^{t}(\xi _{j}(s)-\gamma _{j}(s))\mathrm{d}s+u_{i}(t)]\nonumber \\& \le -\sum \limits _{i=1}^{n}(a_{i}(y_{i}(t))-a_{i}(x_{i}(t)))\mathrm{sign}(e_{i}(t))\nonumber \\& \quad +\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}|b_{ij}||\xi _{j}(t)-\gamma _{j}(t)||\mathrm{sign}(e_{i}(t))|\nonumber \\& \quad +\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}|c_{ij}||\xi _{j}(t-\tau _{j}(t))-\gamma _{j}(t-\tau _{j}(t))||\mathrm{sign}(e_{i}(t))|\nonumber \\& \quad +\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}|w_{ij}|\int _{t-\delta _{j}(t)}^{t}|\xi _{j}(s)-\gamma _{j}(s)|\mathrm{d}s\cdot |\mathrm{sign}(e_{i}(t))|\nonumber \\& \quad +\sum \limits _{i=1}^{n}u_{i}(t)\mathrm{sign}(e_{i}(t)), ~\mathrm{for~a.e.}~t\ge 0. \end{aligned}$$
(18)

Recalling the assumptions (\(\mathscr {H}\)1) and (\(\mathscr {H}\)3), we can get from (18) that

$$\begin{aligned} \frac{\mathrm{d}V(t)}{\mathrm{d}t}& \le -\sum \limits _{i=1}^{n}\beta _{i} |e_{i}(t)|\nonumber \\& \quad +\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}|b_{ij}|(L_{j}|e_{j}(t)|+p_{j})|\mathrm{sign}(e_{i}(t))|\nonumber \\& \quad +\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}|c_{ij}|(L_{j}|e_{j}(t-\tau _{j}(t))|+p_{j})|\mathrm{sign}(e_{i}(t))|\nonumber \\& \quad +\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}|w_{ij}|\int _{t-\delta _{j}(t)}^{t}(L_{j}|e_{j}(s)|+p_{j})\mathrm{d}s\cdot |\mathrm{sign}(e_{i}(t))|\nonumber \\& \quad +\sum \limits _{i=1}^{n}u_{i}(t)\mathrm{sign}(e_{i}(t)), ~\mathrm{for~a.e.}~t\ge 0. \end{aligned}$$
(19)

Multiplying both sides of switching state-feedback controller (13) by \(\mathrm{sign}(e_{i}(t))\), we have

$$\begin{aligned}&u_{i}(t)\mathrm{sign}(e_{i}(t))\nonumber \\&= {\left\{ \begin{array}{ll} -k_{i}|\mathrm{sign}(e_{i}(t))|-\frac{r_{i}|e_{i}(t)|^{\sigma }}{\mathrm{sign}(e_{i}(t))}\mathrm{sign}(e_{i}(t))\\ ~~-\sum \limits _{j=1}^{n}\pi _{ij}|\mathrm{sign}(e_{i}(t))||e_{j}(t-\tau _{j}(t))| \\ ~~~-\sum \limits _{j=1}^{n}\varpi _{ij}|\mathrm{sign}(e_{i}(t))|\int _{t-\delta _{j}(t)}^{t}|e_{j}(s)|\mathrm{d}s,~ \mathrm{if}~e_{i}(t)\ne 0, \\ 0, \quad \mathrm{if}~e_{i}(t)=0, \end{array}\right. }\nonumber \\&=-k_{i}|\mathrm{sign}(e_{i}(t))|-\sum \limits _{j=1}^{n}\pi _{ij}|\mathrm{sign}(e_{i}(t))||e_{j}(t-\tau _{j}(t))|\nonumber \\&\qquad -r_{i}|e_{i}(t)|^{\sigma }-\sum \limits _{j=1}^{n}\varpi _{ij}|\mathrm{sign}(e_{i}(t))|\int _{t-\delta _{j}(t)}^{t}|e_{j}(s)|\mathrm{d}s. \end{aligned}$$
(20)

Substituting the formula (20) into Eq. (19) and using the assumption (\(\mathscr {H}\)4), we can deduce that

$$\begin{aligned} \frac{\mathrm{d}V(t)}{\mathrm{d}t}& \le -\sum \limits _{i=1}^{n}\beta _{i} |e_{i}(t)|+\sum \limits _{j=1}^{n}\sum \limits _{i=1}^{n}|b_{ij}|L_{j}|e_{j}(t)|\nonumber \\& \quad -\sum \limits _{i=1}^{n}\left( k_{i}-\sum \limits _{j=1}^{n}(|b_{ij}|+|c_{ij}|+\delta ^{M}|w_{ij}|)p_{j}\right) \nonumber \\& \quad \quad \times |\mathrm{sign}(e_{i}(t))|-\sum \limits _{i=1}^{n}r_{i}|e_{i}(t)|^{\sigma }\nonumber \\& \quad -\left( \min \limits _{1\le i,j\le n}\left\{ \varpi _{ij}\right\} -\max \limits _{1\le i,j\le n}\left\{ |w_{ij}|L_{j}\right\} \right) \nonumber \\& \quad \quad \times \sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}|\mathrm{sign}(e_{i}(t))|\int _{t-\delta _{j}(t)}^{t}|e_{j}(s)|\mathrm{d}s\nonumber \\ & \le -\min \limits _{1\le i\le n}\left\{ \beta _{i}\right\} \sum \limits _{i=1}^{n}|e_{i}(t)|-\min \limits _{1\le i\le n}\left\{ r_{i}\right\} \sum \limits _{i=1}^{n}|e_{i}(t)|^{\sigma }\nonumber \\& \quad +\max \limits _{1\le j\le n}\left\{ \sum \limits _{i=1}^{n}|b_{ij}|L_{j}\right\} \sum \limits _{j=1}^{n}|e_{j}(t)|\nonumber \\& =-(\mathscr {B}-\mathscr {A})\sum \limits _{i=1}^{n}|e_{i}(t)|-\mathscr {D}\sum \limits _{i=1}^{n}|e_{i}(t)|^{\sigma }, ~\mathrm{a.e.}~t\ge 0, \end{aligned}$$
(21)

where \(\mathscr {B}=\min \limits _{1\le i\le n}\left\{ \beta _{i}\right\}\), \(\mathscr {A}=\max \limits _{1\le j\le n}\left\{ \sum \limits _{i=1}^{n}|b_{ij}|L_{j}\right\}\) and \(\mathscr {D}=\min \limits _{1\le i\le n}\left\{ r_{i}\right\}\). From \(0<\sigma <1\) and Lemma 3, we can get

$$\begin{aligned} \left( \sum \limits _{i=1}^{n}|e_{i}(t)|^{\sigma }\right) ^{\frac{1}{\sigma }}\ge \sum \limits _{i=1}^{n}|e_{i}(t)|, \end{aligned}$$
(22)

which implies

$$\begin{aligned} \sum \limits _{i=1}^{n}|e_{i}(t)|^{\sigma }\ge \left( \sum \limits _{i=1}^{n}|e_{i}(t)|\right) ^{\sigma }. \end{aligned}$$
(23)

Combining (17) and (23), it follows from (21) that

$$\begin{aligned} \frac{\mathrm{d}V(t)}{\mathrm{d}t} \le -(\mathscr {B}-\mathscr {A})d_{\min }^{*}V(t)-\mathscr {D}(d_{\min }^{*})^{\sigma }V^{\sigma }(t),~\mathrm{a.e.} ~t\ge 0. \end{aligned}$$

According to the special case (i) in Lemma 2, the response system (1) and the drive system (8) can achieve the finite-time synchronization under the switching state-feedback controller (13). Obviously, \(\Upsilon (\varrho )=K_{1}\varrho +K_{2}\varrho ^{\sigma }\), where \(K_{1}=(\mathscr {B}-\mathscr {A})d_{\min }^{*}>0\) and \(K_{2}=\mathscr {D}(d_{\min }^{*})^{\sigma }>0\). Therefore, the settling time can be given by

$$\begin{aligned} t_{1}^{*}=&\int _{0}^{V(0)}\frac{1}{\Upsilon (\varrho )}\mathrm{d}\varrho =\frac{1}{(1-\sigma )(\mathscr {B}-\mathscr {A})d_{\min }^{*}}\nonumber \\&\times \ln \left( \frac{(\mathscr {B}-\mathscr {A})d_{\min }^{*}V^{1-\sigma }(0)+\mathscr {D}(d_{\min }^{*})^{\sigma }}{\mathscr {D}(d_{\min }^{*})^{\sigma }}\right) . \end{aligned}$$
(24)

The proof is complete. \(\square\)

3.2 State-feedback control design in Case (2)

Theorem 2

Under the assumptions (\(\mathscr {H}\)1)-(\(\mathscr {H}\)3) and \(0<\sigma <1\), assume further that the following inequalities hold.

  • (\(\mathscr {H}\)5) For each \(i\in \mathbb {N}\), \(\beta _{i}-\sum \limits _{j=1}^{n}|b_{ji}|L_{i} -\frac{\zeta _{i}}{1-\tau _{i}^{D}}-\frac{\vartheta _{i}\delta ^{M}}{1-\delta _{i}^{D}}\ge 0\), \(\ell _{i}\ge \sum \limits _{j=1}^{n}\left( |b_{ij}|+|c_{ij}|+\delta ^{M}|w_{ij}|\right) p_{j}\), \(\zeta _{i}\ge \sum \limits _{j=1}^{n}|c_{ji}|L_{i}\) and \(\vartheta _{i}\ge \sum \limits _{j=1}^{n}|w_{ji}|L_{i}\).

If the drive-response system is controlled with the control law (14), then the response system (8) can be synchronized with the drive system (1) in a finite time, and the settling time forfinite-time synchronization is given by

$$\begin{aligned} t_{2}^{*}=\frac{V^{1-\sigma }(0)}{\mathscr {G}(1-\sigma )}. \end{aligned}$$
(25)

Proof

Consider the following Lyapunov functional for the drive-response system with switching state-feedback controller (14):

$$\begin{aligned} V(t)=&\sum \limits _{i=1}^{n}\mathrm{sign}(e_{i}(t))\int _{x_{i}(t)}^{y_{i}(t)}\frac{1}{d_{i}(s)}\mathrm{d}s\nonumber \\&+\sum \limits _{i=1}^{n}\frac{1}{1-\tau _{i}^{D}}\int _{t-\tau _{i}(t)}^{t}\zeta _{i}|e_{i}(s)|\mathrm{d}s\nonumber \\&+\sum \limits _{i=1}^{n}\frac{1}{1-\delta _{i}^{D}}\int _{-\delta _{i}(t)}^{0}\int _{t+\theta }^{t}\vartheta _{i}|e_{i}(s)|\mathrm{d}s\mathrm{d}\theta . \end{aligned}$$
(26)

Obviously, V(t) is C-regular. By the chain rule in Lemma 1, calculate the time derivative of V(t) along the trajectories of the drive-response system, we have

$$\begin{aligned} \frac{\mathrm{d}V(t)}{\mathrm{d}t}& =\sum \limits _{i=1}^{n}\mathrm{sign}(e_{i}(t))[-(a_{i}(y_{i}(t))-a_{i}(x_{i}(t)))\nonumber \\& \quad +\sum \limits _{j=1}^{n}b_{ij}(\xi _{j}(t)-\gamma _{j}(t))\nonumber \\& \quad +\sum \limits _{j=1}^{n}c_{ij}(\xi _{j}(t-\tau _{j}(t))-\gamma _{j}(t-\tau _{j}(t)))\nonumber \\& \quad +\sum \limits _{j=1}^{n}w_{ij}\int _{t-\delta _{j}(t)}^{t}(\xi _{j}(s)-\gamma _{j}(s))\mathrm{d}s+u_{i}(t)]\nonumber \\& \quad +\sum \limits _{i=1}^{n}\frac{\zeta _{i}}{1-\tau _{i}^{D}}|e_{i}(t)| +\sum \limits _{i=1}^{n}\frac{\vartheta _{i}}{1-\delta _{i}^{D}}\delta _{i}(t)|e_{i}(t)|\nonumber \\& \quad -\sum \limits _{i=1}^{n}\frac{\zeta _{i}}{1-\tau _{i}^{D}}(1-\dot{\tau }_{i}(t))|e_{i}(t-\tau _{i}(t))|\nonumber \\& \quad -\sum \limits _{i=1}^{n}\frac{\vartheta _{i}}{1-\delta _{i}^{D}}(1-\dot{\delta }_{i}(t))\int _{t-\delta _{i}(t)}^{t}|e_{i}(s)|\mathrm{d}s\nonumber \\& \le -\sum \limits _{i=1}^{n}(a_{i}(y_{i}(t))-a_{i}(x_{i}(t)))\mathrm{sign}(e_{i}(t))\nonumber \\& \quad +\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}|b_{ij}||\xi _{j}(t)-\gamma _{j}(t)||\mathrm{sign}(e_{i}(t))|\nonumber \\& \quad +\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}|c_{ij}||\xi _{j}(t-\tau _{j}(t))-\gamma _{j}(t-\tau _{j}(t))||\mathrm{sign}(e_{i}(t))|\nonumber \\& \quad +\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}|w_{ij}|\int _{t-\delta _{j}(t)}^{t}|\xi _{j}(s)-\gamma _{j}(s)|\mathrm{d}s\cdot |\mathrm{sign}(e_{i}(t))|\nonumber \\& \quad +\sum \limits _{i=1}^{n}u_{i}(t)\mathrm{sign}(e_{i}(t)) +\sum \limits _{i=1}^{n}\frac{\zeta _{i}}{1-\tau _{i}^{D}}|e_{i}(t)|\nonumber \\& \quad -\sum \limits _{i=1}^{n}\frac{\zeta _{i}}{1-\tau _{i}^{D}}(1-\tau _{i}^{D})|e_{i}(t-\tau _{i}(t))|\nonumber \\& \quad -\sum \limits _{i=1}^{n}\frac{\vartheta _{i}}{1-\delta _{i}^{D}}(1-\delta _{i}^{D})\int _{t-\delta _{i}(t)}^{t}|e_{i}(s)|\mathrm{d}s\nonumber \\& \quad +\sum \limits _{i=1}^{n}\frac{\vartheta _{i}\delta ^{M}}{1-\delta _{i}^{D}}|e_{i}(t)|,~\mathrm{for~a.e.}~t\ge 0. \end{aligned}$$
(27)

Multiplying both sides of controller (14) by \(\mathrm{sign}(e_{i}(t))\), we have

$$\begin{aligned}&u_{i}(t)\mathrm{sign}(e_{i}(t))\nonumber \\&= {\left\{ \begin{array}{ll} -\ell _{i}|\mathrm{sign}(e_{i}(t))|-\frac{\eta _{i}|e_{i}(t)|^{\sigma }}{\mathrm{sign}(e_{i}(t))}\mathrm{sign}(e_{i}(t))\\ ~-\frac{\hbar }{\mathrm{sign}(e_{i}(t))}\mathrm{sign}(e_{i}(t))\left( \int _{t-\tau _{i}(t)}^{t}\zeta _{i}|e_{i}(s)|\mathrm{d}s\right) ^{\sigma } \\ ~~-\frac{q}{\mathrm{sign}(e_{i}(t))}\mathrm{sign}(e_{i}(t))\left( \int _{-\delta _{i}(t)}^{0}\int _{t+\theta }^{t}\vartheta _{i}|e_{i}(s)|\mathrm{d}s\mathrm{d}\theta \right) ^{\sigma }, \\ \quad \mathrm{if}~e_{i}(t)\ne 0, \\ 0,\quad \mathrm{if}~e_{i}(t)=0, \end{array}\right. }\nonumber \\&=-\ell _{i}|\mathrm{sign}(e_{i}(t))|-\eta _{i}|e_{i}(t)|^{\sigma }-\hbar \left( \int _{t-\tau _{i}(t)}^{t}\zeta _{i}|e_{i}(s)|\mathrm{d}s\right) ^{\sigma }\nonumber \\&\quad -q\left( \int _{-\delta _{i}(t)}^{0}\int _{t+\theta }^{t}\vartheta _{i}|e_{i}(s)|\mathrm{d}s\mathrm{d}\theta \right) ^{\sigma }. \end{aligned}$$
(28)

Recalling the assumption (\(\mathscr {H}\)3), we can obtain that

$$\begin{aligned} \sum \limits _{i=1}^{n}(a_{i}(y_{i}(t))-a_{i}(x_{i}(t)))\mathrm{sign}(e_{i}(t))\ge \sum \limits _{i=1}^{n}\beta _{i}|e_{i}(t)|. \end{aligned}$$
(29)

By using the assumption (\(\mathscr {H}\)2), we can get

$$\begin{aligned}&\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}|b_{ij}||\xi _{j}(t)-\gamma _{j}(t)||\mathrm{sign}(e_{i}(t))|\nonumber \\&\quad \le \sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}|b_{ij}|(L_{j}|e_{j}(t)|+p_{j})|\mathrm{sign}(e_{i}(t))|\nonumber \\& \quad \le \sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}|b_{ji}|L_{i}|e_{i}(t)|+\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}|b_{ij}|p_{j}|\mathrm{sign}(e_{i}(t))|. \end{aligned}$$
(30)

Similarly, we have

$$\begin{aligned}&\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}|c_{ij}||\xi _{j}(t-\tau _{j}(t))-\gamma _{j}(t-\tau _{j}(t))||\mathrm{sign}(e_{i}(t))|\nonumber \\& \quad \le \sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}|c_{ij}|(L_{j}|e_{j}(t-\tau _{j}(t))|+p_{j})|\mathrm{sign}(e_{i}(t))|\nonumber \\& \quad \le \sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}|c_{ji}|L_{i}|e_{i}(t-\tau _{i}(t))|+\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}|c_{ij}|p_{j}|\mathrm{sign}(e_{i}(t))|, \end{aligned}$$
(31)

and

$$\begin{aligned}& \sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}|w_{ij}|\int _{t-\delta _{j}(t)}^{t}|\xi _{j}(s)-\gamma _{j}(s)|\mathrm{d}s\cdot |\mathrm{sign}(e_{i}(t))|\nonumber \\& \quad \le \sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}|w_{ij}|\int _{t-\delta _{j}(t)}^{t}(L_{j}|e_{j}(s)|+p_{j})\mathrm{d}s\cdot |\mathrm{sign}(e_{i}(t))|\nonumber \\& \quad \le\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}|w_{ji}|L_{i}\int _{t-\delta _{i}(t)}^{t}|e_{i}(s)|\mathrm{d}s\nonumber \\& \qquad +\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}\delta ^{M}|w_{ij}|p_{j}|\mathrm{sign}(e_{i}(t))|. \end{aligned}$$
(32)

It follows from (27)–(32) that

$$\begin{aligned} \frac{\mathrm{d}V(t)}{\mathrm{d}t}& \quad \le -\sum \limits _{i=1}^{n}|e_{i}(t)|\left( \beta _{i}-\sum \limits _{j=1}^{n}|b_{ji}|L_{i} -\frac{\zeta _{i}}{1-\tau _{i}^{D}}-\frac{\vartheta _{i}\delta ^{M}}{1-\delta _{i}^{D}}\right) \nonumber \\& \qquad -\sum \limits _{i=1}^{n}[\ell _{i}-\sum \limits _{j=1}^{n}(|b_{ij}|+|c_{ij}|+\delta ^{M}|w_{ij}|)p_{j}]|\mathrm{sign}(e_{i}(t))|\nonumber \\& \qquad -\sum \limits _{i=1}^{n}\left( \zeta _{i}-\sum \limits _{j=1}^{n}|c_{ji}|L_{i}\right) |e_{i}(t-\tau _{i}(t))|\nonumber \\& \qquad -\sum \limits _{i=1}^{n}\left( \vartheta _{i}-\sum \limits _{j=1}^{n}|w_{ji}|L_{i}\right) \int _{t-\delta _{i}(t)}^{t}|e_{i}(s)|\mathrm{d}s\nonumber \\& \qquad -\sum \limits _{i=1}^{n}\eta _{i}|e_{i}(t)|^{\sigma }-\hbar \sum \limits _{i=1}^{n}\left( \int _{t-\tau _{i}(t)}^{t}\zeta _{i}|e_{i}(s)|\mathrm{d}s\right) ^{\sigma }\nonumber \\& \qquad -q\sum \limits _{i=1}^{n}\left( \int _{-\delta _{i}(t)}^{0}\int _{t+\theta }^{t}\vartheta _{i}|e_{i}(s)|\mathrm{d}s\mathrm{d}\theta \right) ^{\sigma }, ~\mathrm{for~a.e.}~t\ge 0. \end{aligned}$$
(33)

According to the assumption (\(\mathscr {H}\)5), we can obtain from (33) that

$$\begin{aligned} \frac{\mathrm{d}V(t)}{\mathrm{d}t}&\le -\sum \limits _{i=1}^{n}\eta _{i}|e_{i}(t)|^{\sigma }-\hbar \sum \limits _{i=1}^{n}\left( \int _{t-\tau _{i}(t)}^{t}\zeta _{i}|e_{i}(s)|\mathrm{d}s\right) ^{\sigma }\nonumber \\&~~-q\sum \limits _{i=1}^{n}\left( \int _{-\delta _{i}(t)}^{0}\int _{t+\theta }^{t}\vartheta _{i}|e_{i}(s)|\mathrm{d}s\mathrm{d}\theta \right) ^{\sigma },\mathrm{for~a.e.}~t\ge 0. \end{aligned}$$
(34)

By using the assumptions (\(\mathscr {H}\)1), we have

$$\begin{aligned} \left( \mathrm{sign}(e_{i}(t))\int _{x_{i}(t)}^{y_{i}(t)}\frac{1}{d_{i}(s)}\mathrm{d}s\right) ^{\sigma }\le \left( \frac{1}{d_{i}^{*}}|e_{i}(t)|\right) ^{\sigma }. \end{aligned}$$
(35)

It follows from Eqs. (34) and (35) that

$$\begin{aligned}\frac{\mathrm{d}V(t)}{\mathrm{d}t} & \le -\sum \limits _{i=1}^{n}\eta _{i}(d_{i}^{*})^{\sigma }\left( \mathrm{sign}(e_{i}(t))\int _{x_{i}(t)}^{y_{i}(t)}\frac{1}{d_{i}(s)}\mathrm{d}s\right) ^{\sigma }\nonumber \\& \quad -\sum \limits _{i=1}^{n}\hbar \left( 1-\tau _{i}^{D}\right) ^{\sigma }\left( \frac{1}{1-\tau _{i}^{D}}\int _{t-\tau _{i}(t)}^{t}\zeta _{i}|e_{i}(s)|\mathrm{d}s\right) ^{\sigma }\nonumber \\& \quad -\sum \limits _{i=1}^{n}q\left( 1-\delta _{i}^{D}\right) ^{\sigma }\left( \frac{1}{1-\delta _{i}^{D}}\int _{-\delta _{i}(t)}^{0}\int _{t+\theta }^{t}\vartheta _{i}|e_{i}(s)|\mathrm{d}s\mathrm{d}\theta \right) ^{\sigma }\nonumber \\& \le -\mathscr {G}\left[ \sum \limits _{i=1}^{n}\left( \mathrm{sign}(e_{i}(t))\int _{x_{i}(t)}^{y_{i}(t)}\frac{1}{d_{i}(s)}\mathrm{d}s\right) ^{\sigma } \right. \nonumber \\& \quad +\sum \limits _{i=1}^{n}\left( \frac{1}{1-\tau _{i}^{D}}\int _{t-\tau _{i}(t)}^{t}\zeta _{i}|e_{i}(s)|\mathrm{d}s\right) ^{\sigma }\nonumber \\ & \left. \quad +\sum \limits _{i=1}^{n}\left( \frac{1}{1-\delta _{i}^{D}}\int _{-\delta _{i}(t)}^{0}\int _{t+\theta }^{t}\vartheta _{i}|e_{i}(s)|\mathrm{d}s\mathrm{d}\theta \right) ^{\sigma }\right] , \mathrm{for~a.e.}~t\ge 0, \end{aligned}$$
(36)

where

$$\begin{aligned} \mathscr {G}=\min \{\mathscr {G}_{1},\mathscr {G}_{2},\mathscr {G}_{3}\},~ \mathscr {G}_{1}=\min \limits _{1\le i\le n}\{\eta _{i}(d_{i}^{*})^{\sigma }\}, \end{aligned}$$
$$\begin{aligned} \mathscr {G}_{2}=\min \limits _{1\le i\le n}\left\{ \hbar \left( 1-\tau _{i}^{D}\right) ^{\sigma }\right\} ,~ \mathscr {G}_{3}=\min \limits _{1\le i\le n}\left\{ q\left( 1-\delta _{i}^{D}\right) ^{\sigma }\right\} . \end{aligned}$$

Since \(0<\sigma <1\), based on Lemma 3, we have

$$\begin{aligned}& \left[ \sum \limits _{i=1}^{n}\left( \mathrm{sign}(e_{i}(t))\int _{x_{i}(t)}^{y_{i}(t)}\frac{1}{d_{i}(s)}\mathrm{d}s\right) ^{\sigma }\right. \nonumber \\& \qquad +\sum \limits _{i=1}^{n}\left( \frac{1}{1-\tau _{i}^{D}}\int _{t-\tau _{i}(t)}^{t}\zeta _{i}|e_{i}(s)|\mathrm{d}s\right) ^{\sigma }\nonumber \\& \qquad \left. +\sum \limits _{i=1}^{n}\left( \frac{1}{1-\delta _{i}^{D}}\int _{-\delta _{i}(t)}^{0}\int _{t+\theta }^{t}\vartheta _{i}|e_{i}(s)|\mathrm{d}s\mathrm{d}\theta \right) ^{\sigma }\right] ^{\frac{1}{\sigma }}\nonumber \\& \quad \ge \sum \limits _{i=1}^{n}\mathrm{sign}(e_{i}(t))\int _{x_{i}(t)}^{y_{i}(t)}\frac{1}{d_{i}(s)}\mathrm{d}s\nonumber \\& \qquad +\sum \limits _{i=1}^{n}\frac{1}{1-\tau _{i}^{D}}\int _{t-\tau _{i}(t)}^{t}\zeta _{i}|e_{i}(s)|\mathrm{d}s\nonumber \\& \qquad +\sum \limits _{i=1}^{n}\frac{1}{1-\delta _{i}^{D}}\int _{-\delta _{i}(t)}^{0}\int _{t+\theta }^{t}\vartheta _{i}|e_{i}(s)|\mathrm{d}s\mathrm{d}\theta , \end{aligned}$$
(37)

which yields

$$\begin{aligned}& \sum \limits _{i=1}^{n}\left( \mathrm{sign}(e_{i}(t))\int _{x_{i}(t)}^{y_{i}(t)}\frac{1}{d_{i}(s)}\mathrm{d}s\right) ^{\sigma }\nonumber \\& \qquad +\sum \limits _{i=1}^{n}\left( \frac{1}{1-\tau _{i}^{D}}\int _{t-\tau _{i}(t)}^{t}\zeta _{i}|e_{i}(s)|\mathrm{d}s\right) ^{\sigma }\nonumber \\& \qquad +\sum \limits _{i=1}^{n}\left( \frac{1}{1-\delta _{i}^{D}}\int _{-\delta _{i}(t)}^{0}\int _{t+\theta }^{t}\vartheta _{i}|e_{i}(s)|\mathrm{d}s\mathrm{d}\theta \right) ^{\sigma }\nonumber \\& \quad \ge \left[ \sum \limits _{i=1}^{n}\mathrm{sign}(e_{i}(t))\int _{x_{i}(t)}^{y_{i}(t)}\frac{1}{d_{i}(s)}\mathrm{d}s\right. \nonumber \\& \qquad +\sum \limits _{i=1}^{n}\frac{1}{1-\tau _{i}^{D}}\int _{t-\tau _{i}(t)}^{t}\zeta _{i}|e_{i}(s)|\mathrm{d}s\nonumber \\& \qquad \left. +\sum \limits _{i=1}^{n}\frac{1}{1-\delta _{i}^{D}}\int _{-\delta _{i}(t)}^{0}\int _{t+\theta }^{t}\vartheta _{i}|e_{i}(s)|\mathrm{d}s\mathrm{d}\theta \right] ^{\sigma }=V^{\sigma }(t). \end{aligned}$$
(38)

From (36) and (38), we derive that

$$\begin{aligned} \frac{\mathrm{d}V(t)}{\mathrm{d}t} \le -\mathscr {G}V^{\sigma }(t),~\mathrm{for~ a.e.} ~t\ge 0. \end{aligned}$$

By the special case (ii) in Lemma 2, the response system (1) and the drive system (8) can realize the finite-time synchronization under the switching state-feedback controller (14). Clearly, \(\Upsilon (\varrho )=K\varrho ^{\mu }\), where \(K=\mathscr {G}>0\). Hence, the settling time can be given by

$$\begin{aligned} t_{2}^{*}=\int _{0}^{V(0)}\frac{1}{\Upsilon (\varrho )}\mathrm{d}\varrho =\frac{V^{1-\sigma }(0)}{\mathscr {G}(1-\sigma )}. \end{aligned}$$
(39)

The proof is complete. \(\square\)

Remark 2

By using the finite-time stability theorem given by Forti et al., this paper has studied the finite-time synchronization problem of CGNNs with discontinuous activation functions. In [33], Wang and Zhu dealt with the problem of finite-time stabilization for a class of high-order stochastic nonlinear systems in strict-feedback form. However, the finite-time stability theorem of [33] is invalid to handle the discontinuous dynamical systems.

Remark 3

In the existing literature [34–38], there are some results on synchronization for neural networks. However, the neural network models of [34–38] did not consider the discontinuities of neuron activations. Moreover, the finite-time synchronization results of this paper are more better than the synchronization results of [34–38]. That is because finite-time synchronization possesses faster convergence speed than asymptotic or exponential synchronization.

Remark 4

Different from the classical state-feedback methods, our state-feedback methods (13) and (14) include switching term, time-delayed term and integral term. From Theorems 1 and 2, we can see that the two state-feedback control methods are effective in realizing the finite-time synchronization of CGNNs with discontinuous activations and mixed time-delays. However, the classical controllers are difficult to deal with the uncertain differences of the Filippov solutions of differential equation with discontinuous right-hand side. In [14], the authors used adaptive control method to study the exponential synchronization problem of time-delayed neural networks with discontinuous activations. Nevertheless, the adaptive control method of [14] is difficult to realize the finite-time synchronization of neural network model (1) due to the emergence of mixed time-delays and discontinuities of activations.

4 Numerical simulations

In this section, two numerical examples are given to illustrate the effectiveness of main results.

Example 1

Consider the following 2-dimensional CGNNs (1) with \(d_{i}(x_{i}(t))=0.6+\frac{0.1}{1+x_{i}^{2}(t)}(i=1,2)\), \(a_{1}(x_{1}(t))=1.9x_{1}(t)\), \(a_{2}(x_{2}(t))=2x_{2}(t)\), \(b_{11}=2\), \(b_{12}=-0.2\), \(b_{21}=-1\), \(b_{22}=0.5\), \(c_{11}=-1.5\), \(c_{12}=c_{21}=-0.5\), \(c_{22}=-3,\) \(w_{11}=w_{22}=-0.01\), \(w_{21}=w_{12}=0\), \(J_{1}=J_{2}=0\) and \(\tau _{j}(t)=\delta _{j}(t)=1(j=1,2).\) The discontinuous activation functions are described by

$$\begin{aligned} f_{i}(\theta )={\left\{ \begin{array}{ll} 0.6\tanh (\theta )-0.1,~\theta \ge 0,\\ 0.6\tanh (\theta )+0.1,~\theta <0, \end{array}\right. }~i=1,2. \end{aligned}$$

It is obvious that the discontinuous activation function \(f_{i}(\theta )\) is non-monotonic and satisfies the assumption (\(\mathscr {H}\)2). Actually, the activation function \(f_{i}(\theta )\) possesses a discontinuous point \(\theta =0\) and \(\overline{\mathrm{co}}[f_{i}(0)]=[f_{i}^{+}(0),f_{i}^{-}(0)]=[-0.1,0.1].\) We can choose \(L_{1}=L_{2}=0.6\) and \(p_{1}=p_{2}=0.2\) such that the inequality (2) holds. Under the switching state-feedback controller (13), let us select the control gains \(k_{1}=k_{2}=12,\) \(r_{1}=r_{2}=6,\) \(\pi _{ij}=2\), \(\varpi _{ij}=0.02\) and \(\sigma =0.5\). By simple computation, we can get

$$\begin{aligned} 12=k_{1}\ge \sum \limits _{j=1}^{n}\left( |b_{1j}|+|c_{1j}|+\delta ^{M}|w_{1j}|\right) p_{j}=0.842,~ \end{aligned}$$
$$\begin{aligned} 12=k_{2}\ge \sum \limits _{j=1}^{n}\left( |b_{2j}|+|c_{2j}|+\delta ^{M}|w_{2j}|\right) p_{j}=1.002,~ \end{aligned}$$
$$\begin{aligned} 2=\min \limits _{1\le i,j\le n}\left\{ \pi _{ij}\right\} \ge \max \limits _{1\le i,j\le n}\left\{ |c_{ij}|L_{j}\right\} =1.8, \end{aligned}$$
$$\begin{aligned} 0.02=\min \limits _{1\le i,j\le n}\left\{ \varpi _{ij}\right\} \ge \max \limits _{1\le i,j\le n}\left\{ |w_{ij}|L_{j}\right\} =0.006, \end{aligned}$$
$$\begin{aligned} 1.9=\mathscr {B}>\mathscr {A}=1.8. \end{aligned}$$

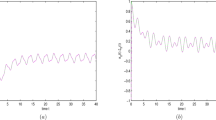
This shows that the conditions of Theorem 1 are satisfied. Thus, the discontinuous and time-delayed CGNNs can realize the finite-time synchronization with the corresponding response system under the switching state-feedback controller (13). Consider the drive-response neural network system with initial conditions \([\phi (t),\psi (t)]=[(2.5,-1.2)^\mathrm{T},(f_{1}(2.5),f_{2}(-1.2))^\mathrm{T}]\), for \(t\in [-1,0]\) and \([\varphi (t),\omega (t)]=[(-1,2)^\mathrm{T},(f_{1}(-1),f_{2}(2))^\mathrm{T}]\) for \(t\in [-1,0]\). Figure 1 presents the trajectory of each error state which approaches to zero in a finite time. Figure 2 describes the state trajectories of drive system and its corresponding response system. The numerical simulations fit the theoretical results perfectly.

Fig. 1
figure 1

Synchronization error state trajectories between drive system and corresponding response system under the switching state-feedback controller (13) for Example 1

Full size image
Fig. 2
figure 2

a Time evolution of variables \(x_{1}(t)\) and \(y_{1}(t)\) of drive neural network and corresponding response system for Example 1; b time evolution of variables \(x_{2}(t)\) and \(y_{2}(t)\) of drive neural network and corresponding response system for Example 1

Full size image

Example 2

Consider the following 2-dimensional CGNNs (1) with \(d_{i}(x_{i}(t))=0.7+\frac{0.2}{1+x_{i}^{2}(t)}(i=1,2)\), \(a_{1}(x_{1}(t))=4x_{1}(t)\), \(a_{2}(x_{2}(t))=3x_{2}(t)\), \(b_{11}=-1\), \(b_{12}=-0.1\), \(b_{21}=-1.5\), \(b_{22}=0.8\), \(c_{11}=-1\), \(c_{12}=-0.2\), \(c_{21}=0.8\), \(c_{22}=-2.5\), \(w_{11}=w_{22}=0.02\), \(w_{21}=w_{12}=0\), \(J_{1}=J_{2}=0\) and \(\tau _{j}(t)=\delta _{j}(t)=1(j=1,2)\). The discontinuous activation functions are given as

$$\begin{aligned} f_{i}(\theta )={\left\{ \begin{array}{ll} 0.3\theta +0.1,~\theta \ge 0,\\ 0.3\theta -0.1,~\theta <0, \end{array}\right. }~i=1,2. \end{aligned}$$

It is not difficult to check that the discontinuous activation function \(f_{i}(\theta )\) satisfies the assumption (\(\mathscr {H}\)2)with \(L_{1}=L_{2}=0.3\) and \(p_{1}=p_{2}=0.2\). Under the switching state-feedback controller (14), let us choose the control gains \(\ell _{1}=\ell _{2}=6\), \(\eta _{1}=\eta _{2}=5\), \(\hbar =q=0.01\), \(\zeta _{i}=\vartheta _{i}=1\) and \(\sigma =0.5\). It is easy to calculate that

$$\begin{aligned} 1.1=\beta _{1}-\sum \limits _{j=1}^{n}|b_{j1}|L_{1} -\frac{\zeta _{1}}{1-\tau _{1}^{D}}-\frac{\vartheta _{1}\delta ^{M}}{1-\delta _{1}^{D}}\ge 0,~ \end{aligned}$$
$$\begin{aligned} 0.79=\beta _{2}-\sum \limits _{j=1}^{n}|b_{j2}|L_{2} -\frac{\zeta _{2}}{1-\tau _{2}^{D}}-\frac{\vartheta _{2}\delta ^{M}}{1-\delta _{2}^{D}}\ge 0,~ \end{aligned}$$
$$\begin{aligned} 6=\ell _{1}\ge \sum \limits _{j=1}^{n}\left( |b_{1j}|+|c_{1j}|+\delta ^{M}|w_{1j}|\right) p_{j}=0.564, \end{aligned}$$
$$\begin{aligned} 6=\ell _{2}\ge \sum \limits _{j=1}^{n}\left( |b_{2j}|+|c_{2j}|+\delta ^{M}|w_{2j}|\right) p_{j}=1.124, \end{aligned}$$
$$\begin{aligned} 1=\vartheta _{i}\ge \sum \limits _{j=1}^{n}|w_{ji}|L_{i}=0.006(i=1,2), \end{aligned}$$
$$\begin{aligned} 1=\zeta _{1}\ge \sum \limits _{j=1}^{n}|c_{j1}|L_{1}=0.54,~1=\zeta _{2}\ge \sum \limits _{j=1}^{n}|c_{j2}|L_{2}=0.81. \end{aligned}$$

Hence, all the conditions of Theorem 2 are satisfied. Then, the discontinuous and time-delayed CGNNs can realize the finite-time synchronization with the corresponding response system under the switching state-feedback controller (14). Consider the initial conditions of drive-response neural network system: \([\phi (t),\psi (t)]=[(3,-2)^\mathrm{T},(f_{1}(3),f_{2}(-2))^\mathrm{T}]\), for \(t\in [-1,0]\) and \([\varphi (t),\omega (t)]=[(-2,3)^\mathrm{T},(f_{1}(-2),f_{2}(3))^\mathrm{T}]\) for \(t\in [-1,0]\). Figures 3 and 4 also show the theoretical results are correct.

Fig. 3
figure 3

Synchronization error state trajectories between drive system and corresponding response system under the switching state-feedback controller (14) for Example 2

Full size image
Fig. 4
figure 4

a Time evolution of variables \(x_{1}(t)\) and \(y_{1}(t)\) of drive neural network and corresponding response system for Example 2; b time evolution of variables \(x_{2}(t)\) and \(y_{2}(t)\) of drive neural network and corresponding response system for Example 2

Full size image

Remark 5

Comparing with the control methods of [34–38], only the asymptotic or exponential synchronization can be realized for neural networks. From Example 1 and 2, it can be seen that the proposed finite-time synchronization control method here in this paper has better convergence property for neural networks. On the other hand, different from the existing control methods used in studying finite-time synchronization of [16, 43, 47], our switching state-feedback control method can be used to deal with more general neural networks with time-delay and discontinuous factors. Example 1 and 2 can also illustrate that our control method is effective and the conditions are easy to be verified.

5 Conclusions

In this paper, we have dealt with the finite-time synchronization issue of a class of CGNNs with discontinuous activations and mixed time-delays. Firstly, we have designed two classes of novel switching state-feedback controllers. Such switching state-feedback controllers play an important role in handling the uncertain differences of the Filippov solutions for discontinuous CGNNs and can eliminate the influence of time-delay on the states of CGNNs. Then, some easily testable conditions have been established to check the finite-time synchronization control of drive-response system. The main tools of this paper involve the differential inclusion theory, non-smooth analysis theory, the famous finite-time stability theorem, inequality techniques and the generalized Lyapunov functional method. Finally, the designed control method and theoretical results have been illustrated by numerical examples. We think that it would be interesting to extend the theory and control method of this paper to other classes of discontinuous neural networks such as stochastic neural networks, Markovian jump switched neural networks, reaction-diffusion neural networks, memristor-based neural networks, bidirectional associative memory (BAM) neural networks, and so on. There are some papers [40–45] related to this topic. In addition, it is also expected to explore some other complex dynamical behaviors of discontinuous neural networks such as homoclinic orbits, cluster synchronization, exponential \(H_{\infty }\) filtering problem, finite-time boundedness and passivity [46–49].