Synchronization of reaction–diffusion neural networks with time-varying delays via stochastic sampled-data controller

Abstract

This paper discusses the synchronization problem for a class of reaction–diffusion neural networks with Dirichlet boundary conditions. Unlike other studies, a sampled-data controller with stochastic sampling is designed in order to synchronize the concerned neural networks with reaction–diffusion terms and time-varying delays, where $m$ sampling periods are considered whose occurrence probabilities are given constants and satisfy the Bernoulli distribution. A novel discontinuous Lyapunov–Krasovskii functional with triple integral terms is introduced based on the extended Wirtinger’s inequality. Using Jensen’s inequality and reciprocally convex technique in deriving the upper bound for the derivative of the Lyapunov–Krasovskii functional, some new synchronization criteria are obtained in terms of linear matrix inequalities. Numerical examples are provided in order to show the effectiveness of the proposed theoretical results.

1 Introduction

During the past decades, different types of neural network models have been investigated extensively and have been implemented widely in different areas such as combinatorial optimization, signal processing, pattern recognition, speed detection of moving objects, optimization and associative memories, see [1–4]. Such potential applications strongly depend on the dynamical behaviors of neural networks. Therefore, the study of dynamical behaviors of neural networks is an essential step in the practical design of neural networks. Since neural networks can exhibit some complicated dynamics and even chaotic behavior, the synchronization of neural networks has also become an important area of study and there have been many investigations, see [5–10], for instance.

It is well known that in the course of studying neural networks, time delays are unavoidable, which is an inherent phenomena due to the finite processing speed of information, for example, the finite axonal propagation speed from soma to synapses, the diffusion of chemical across the synapses, the postsynaptic potential integration of membrane potential at the neuronal cell body and dendrites. Moreover, in the electronic implementation of analog neural networks, time delays inevitably occur in the communication and response of neurons due to the finite switching speed of amplifiers [11] and transmission of signals in hardware implementation. In addition, the process of moving images requires the introduction of delays in signals transmitted among the cells [12]. Time delays may lead to undesirable dynamical network behaviors such as oscillation, divergence or instability and thus to manufacture high-quality neural networks that it is necessary to study the dynamics of neural networks with delays. However, there are few results in the literature for the synchronization issue of neural networks with time-varying delays, see [13–16] and references therein. All the aforementioned works do not take diffusion effects into consideration.

It is common to describe the neural network models by ordinary differential equations. But in the real world, the diffusion effects cannot be ignored in the neural network model when electrons are moving in an uneven electromagnetic field. For instance, it is well known that the multilayer cellular neural networks which are arrays of nonlinear and simple computing elements characterized by local interactions between cells will well suit to describe locally interconnected simple dynamical systems showing a lattice-like structure. In other words, the whole structure and dynamic behavior of multilayer cellular neural networks not only heavily depend on the evolution time of each variable and its position but also on its interactions deriving from the space-distributed structure of the whole networks. Therefore, it essential to consider the state variables varying with time and space variables. On the other side, there are a large number of reaction–diffusion phenomena in nature and many discipline fields, particularly in chemistry and biology. When such phenomena exist in chemical reactions, the interaction between chemicals and spatial diffusion on the chemical media can be seen until a steady-state spatial concentration pattern has completely developed. Thus, it is of great importance to model both biological and man-made neural networks with reaction–diffusion effects. In [17–21], the authors have investigated the globally exponential stability and periodicity of reaction–diffusion recurrent neural networks with Dirichlet boundary conditions. The globally exponential stability and synchronization of delayed reaction–diffusion neural networks with Dirichlet boundary conditions under the impulsive controller have been studied in [22]. In [23], the authors have formulated and solved the feedback stabilization problem for unstable nonuniform spatial pattern in reaction–diffusion systems. Boundary control to stabilize a system of coupled linear plant and reaction–diffusion process has been considered in [24], and backstepping transformations with a kernel function and a vector-valued function were introduced to design control laws. Adaptive synchronization in an array of linearly coupled neural networks with reaction–diffusion terms and time delays has been discussed in [25]. Very recently, the authors in [26] have studied the synchronization problem for coupled reaction–diffusion neural networks with time-varying delays via pinning-impulsive controller, and some novel synchronization criteria have been proposed. Both theoretically and practically the models with time delays and reaction–diffusion terms provide a good approximation for neural networks, and this effect leads to poor performance of the networks. Therefore, it becomes a challenging problem for the researchers to design a controller that completely makes use of their advantages and also that completely ignores their disadvantages.

In recent years, the sampled-data-based discrete control approach has experienced a wide range of applications than other type of control approaches such as state feedback control, sliding mode control, fuzzy logic control and intermittent control. Since the signals which we use in real world are analog, such as our voices, in order to process these signals in computers, it is necessary to convert them into digital signals, which are discrete in both time and amplitude. Employing the sampling process in which the values of the signals are measured at certain interval of time, the continuous signals are converted into discrete ones and this measurement is referred to as a sample signal. Then, these signals are fed into the digital controller, which processes and finally transformed into continuous signals from the zero-order hold device. An application of this technique is in the radio broadcasts of the live musical program. Therefore, due to the wide range of applications in the real world, the controller design problem using the sampled-data has attracted much attention and corresponding results have been published in the literature, see [27–34].

Selecting proper sampling period is the most important task in sampled-data control systems for designing suitable controllers. In the last decades, a considerable attention has been paid for constant sampling but in recent years it is seen that variable sampling periods are applied to various practical systems [35] due to their ability in dealing effectively with the problems such as change in network situation and limitation of the calculating speed of hardware. The stability problem of feedback control systems with time-varying sampling periods was discussed in [36, 37]. Further extension to the time-varying sampling periods is the stochastically varying sampling periods, and it has been used in the control of sampled-data systems in most recent works. In [38], the problem of robust $H_\infty$ control for sampled-data systems with uncertainties and probabilistic sampling has been investigated. More recently, robust synchronization of uncertain nonlinear chaotic systems has been investigated in [39] using stochastic sampled-data control, where $m$ sampling periods are taken into consideration. To the best of authors’ knowledge, there has been no results found in the literature regarding the synchronization problem for reaction–diffusion neural networks with time-varying delays via a stochastic sampled-data controller.

Motivated by the above discussions, in the present work, we have studied the synchronization problem for reaction–diffusion neural networks with time-varying delays by designing a suitable sampled-data controller with stochastic sampling. We have considered $m$ sampling periods, whose occurrence probabilities are given constants and satisfy Bernoulli distribution. By constructing a new discontinuous Lyapunov–Krasovskii functional with triple integral terms and by employing Jensen’s inequality and reciprocally convex technique, some novel and easily verified synchronization criteria are derived in terms of LMIs, which can be solved using any of the available standard softwares. Numerical simulations are provided in order to show the efficiency of our theoretical results.

The rest of the paper is organized as follows: Notations that we carry out throughout this paper and some necessary lemmas are given in Sect. 2. In Sect. 3, the considered model of reaction–diffusion neural networks with time-varying delays is presented. In Sect. 4, asymptotic synchronization of the proposed model in mean-square sense is studied by designing a sampled-data controller with stochastic sampling. Numerical simulations are presented in Sect. 4, and conclusions are drawn in Sect. 5.

2 Notations and preliminaries

Let $R^n$ denotes the $n$-dimensional Euclidean space and $R^{n\times m}$ denotes the set of all real $n\times m$ matrices. $P>0$ ($P\ge 0$) means that the $P$ is symmetric and positive definite (positive semi-definite). In symmetric matrices, the notation $(\star )$ represents a term that is induced by symmetry. Let $\text{ Prob }\{\alpha \}$ denotes the occurrence probability of an event $\alpha .$ The conditional probability of $\alpha \,\text{ and }\,\ \beta$ is denoted by $\text{ Prob }\{\alpha | \beta \}. \mathbb {E}\{x\} \,\text{ and }\, \mathbb {E}\{x| y\}$ are the expectation of a stochastic variable $x$ and the expectation of the stochastic variable $x$ conditional on the stochastic variable $y,$ respectively. $\varXi (i,j)$ denotes the $i$th row, $j$th column element of a matrix $\varXi .\,A=(a_{ij})_{N\times N}$ denotes a matrix of $N$-dimension. T denotes the transposition of a matrix. $C=\mathrm{diag}(c_1,c_2,\ldots ,c_n)$ means that $C$ is a diagonal matrix.

Before proceeding further, it is necessary to introduce the following Lemmas.

Lemma 1

[40, 41] For any constant matrix $X\in R^{n\times n}, X=X^T>0,$ two scalars $h_1>0,h_2\ge 0$ such that the integrations concerned are well defined, then

$$\begin{aligned}&-\frac{h_2^2-h_1^2}{2} \int _{t-h_2}^{t-h_1}\int _{t+\theta }^{t} x^T(s)X(s)x(s) \mathrm {d}s\mathrm {d}\theta \nonumber \\&\quad \!\le \! \!-\left( \int _{t-h_2}^{t\!-\!h_1}\int _{t\!+\!\theta }^{t}x(s) \mathrm {d}s\mathrm {d}\theta \right) ^T X\left( \int _{t-h_2}^{t-h_1}\int _{t+\theta }^{t}x(s) \mathrm {d}s\mathrm {d}\theta \right) , \end{aligned}$$

(1)

$$\begin{aligned}&-\,(h_2-h_1)\int _{t-h_2}^{t-h_1}x^T(x)Xx(s)\mathrm {d}s \nonumber \\&\quad \le -\left( \int _{t-h_2}^{t-h_1}x(s)\mathrm {d}s\right) ^TX \left( \int _{t-h_2}^{t-h_1}x(s)\mathrm {d}s\right) \!. \end{aligned}$$

(2)

Lemma 2

[42] For any vectors $\delta _{1}, \delta _{2}$, constant matrices $R,S$ and real scalars $\alpha \ge 0, \beta \ge 0$ satisfying that $\left[ \begin{array}{ll} R &{} S \\ \star &{} R\end{array} \right] \ge 0$, and $\alpha +\beta =1$, then the following inequality holds:

$$\begin{aligned} -\frac{1}{\alpha }\delta _{1}^{T}R\delta _{1}\!-\!\frac{1}{\beta } \delta _{2}^{T}R\delta _{2}\!\le \! \!-\!\left[ \begin{array}{c}\delta _{1} \\ \delta _{2} \end{array}\right] ^{T}\left[ \begin{array}{cc} R &{} S \\ \star &{} R\end{array}\right] \left[ \begin{array}{c}\delta _{1} \\ \delta _{2} \end{array}\right] . \end{aligned}$$

(3)

3 Problem formulation

Generally, neural network models are described by ordinary differential equations. But in the real world, diffusion effect cannot be avoided in the neural network model when electrons are moving in asymmetric electromagnetic field. Due to this phenomenon, we introduce a single neural network with reaction–diffusion terms and time-varying delays as follows:

$$\begin{aligned} \frac{\partial y_m(t,x)}{\partial t}&= \sum _{k=1}^q\frac{\partial }{\partial x_k}\left( d_{mk}\frac{\partial y_m(t,x)}{\partial x_k}\right) -c_my_m(t,x)\nonumber \\&\quad \!+\!\sum _{j=1}^n a_{mj}f_j(y_j(t,x))\nonumber \\&\quad \!+\!\sum _{j=1}^n b_{mj}f_j(y_j(t\!-\!d(t),x))\nonumber \\&\quad +\,J_m, \quad m=1,2,\ldots ,n, \end{aligned}$$

(4)

where $x=(x_1,x_2,\ldots ,x_q)^T\in \varOmega \subset R^q$, where $\varOmega =\{x||x_k|\le l_k, k=1,2,\ldots ,q\}$ and $l_k$ is a positive constant. $d_{mk}\ge 0$ means the transmission diffusion coefficient along the $m$th neuron, $y_m(t,x) (m=1,2,\ldots ,n)$ is the state of the $m$th unit at time $t$ and in space $x$. $n$ corresponds to the number of neurons. $f_j(y_j(t,x))$ denotes the neuron activation function of the $j$th unit at time $t$ and in space $x$. $c_m>0 (m=1,2,\ldots ,n)$ represents the rate with which the $m$th unit will reset its potential to the resting state in isolation when disconnected from the network and external inputs. $a_{mj}$ and $b_{mj}$ denotes the strength of the $j$th unit on the $m$th unit at time $t$ and in space $x$ and the strength of the $j$th unit on the $m$th unit at time $t-d(t)$ and in space $x$, respectively. $d(t)$ denotes the time-varying transmission delay along the axon of the $j$th unit from the $m$th unit and satisfies $d_1\le d(t)\le d_2, \dot{d}(t)\le \mu ,$ where $d_2>d_1>0, \mu$ are real constants. $J_m$ is the external input.

Assumption 1

For any $u,v \in R,$ the neuron activation function $g_i(\cdot )$ is continuously bounded and satisfy

$$\begin{aligned} F_i^-\le \frac{g_i(u)-g_i(v)}{u-v}\le F_i^+, \quad i=1,2,\ldots ,n. \end{aligned}$$

(5)

where $F_i^-$ and $F_i^+$ are some real constants and may be positive, zero or negative.

System (4) is supplemented with the following Dirichlet boundary condition

$$\begin{aligned} y_m(t,x)=0, \quad (t,x)\in [-d_2,+\infty ]\times \partial \varOmega . \end{aligned}$$

(6)

Also, system (4) has a unique continuous solution for any initial condition of the form

$$\begin{aligned} y_m(s,x)&= \phi _m(s,x), \quad (s,x)\in [-d_2,0]\times \varOmega , \nonumber \\&m=1,2,\ldots ,n, \end{aligned}$$

(7)

where $\phi _m(s,x)\!=\!(\phi _1(s,x),\phi _2(s,x),\ldots ,\phi _n(s,x))^T\!\in C([-d_2,0]\times \varOmega ,R^n),$ in which $C([-d_2,0]\times \varOmega ,R^n)$ stands for the Banach space of all continuous functions from $[-d_2,0] \times \varOmega$ to $R^n$ with the norm

$$\begin{aligned} \Vert \phi (s,x)\Vert =\left[ \int _{\varOmega }\phi ^T(s,x)\phi (s,x) \mathrm {d}x\right] ^{1/2}. \end{aligned}$$

(8)

Rewriting system (4) in a compact form, we obtain

$$\begin{aligned} \frac{\partial y(t,x)}{\partial t}&= \sum _{k=1}^q\frac{\partial }{\partial x_k}\left( D_k\frac{\partial y(t,x)}{\partial x_k}\right) -Cy(t,x)\nonumber \\&\quad +\,Af(y(t,x))+Bf(y(t-d(t),x))+J, \end{aligned}$$

(9)

where $y(t,x)=(y_1(t,x),y_2(t,x),\ldots ,y_n(t,x))^T\!, D_k=\mathrm{diag}(d_{1k},d_{2k},\ldots ,d_{nk}), f(y(t,x))\!=\!(f_1(y_1(t,x)),$

$f_2(y_2(t,x)),\ldots ,f_n(y_n(t,x)))^T\!, C\!\!=\!\mathrm{diag}(c_1,c_2,\ldots ,c_n), A\!=\!(a_{mj})_{n\times n}$, and $B\!=\!(b_{mj})_{n\times n}, J\!=\!(J_1,J_2,\ldots ,J_n)^T.$ It is a common fact that neural networks may lead to bifurcation, oscillation, divergence or instability if the networks’ parameters and time delays are appropriately chosen. In this case, those networks become unstable. Thus, in order to control the dynamic behaviors of system (9), we introduce the control model of system (9) as

$$\begin{aligned} \frac{\partial u_i(t,x)}{\partial t}&= \sum _{k=1}^q\frac{\partial }{\partial x_k}\left( D_k\frac{\partial u_i(t,x)}{\partial x_k}\right) -Cu_i(t,x)\nonumber \\&\quad +\,Af(u_i(t,x)) +Bf(u_i(t-d(t),x)) \nonumber \\&\quad +\,J+U_i(t,x),\quad i=1,2,\ldots ,N, \end{aligned}$$

(10)

where $u_i(t,x)=(u_{i1}(t,x),u_{i2}(t,x),\ldots ,u_{in}(t,x))^T\in R^n$ is the state vector of the $i$th node at time $t$ and space $x, U_i(t,x)$ is the controller of the $i$th node at time $t$ and space $x.$ Define the error vector as $e_i(t,x)=u_i(t,x)-y(t,x), i=1,2,\ldots ,N.$ Thus, we get the error dynamical system from (9) and (10) as

$$\begin{aligned} \frac{\partial e_i(t,x)}{\partial t}&= \sum _{k=1}^q\frac{\partial }{\partial x_k}\left( D_k\frac{\partial e_i(t,x)}{\partial x_k}\right) -Ce_i(t,x)\nonumber \\&\quad +\,Ag(e_i(t,x))+Bg(e_i(t-d(t),x))\nonumber \\&\quad +\,U_i(t,x), \quad i=1,2,\ldots ,N, \end{aligned}$$

(11)

where $g(e_i(t,x))=f(u_i(t,x))-f(y(t,x)).$ It is obvious that (11) satisfies the Dirichlet boundary condition and its initial condition is given by

$$\begin{aligned} e_i(s,x)&= \varphi _i(s,x)-\phi (s,x) \\&:= \bar{\varphi }_i(s,x)\in C([-d_2,0]\times \partial \varOmega ,R^n),\\&i=1,2,\ldots ,N. \end{aligned}$$

Controllers which we use nowadays are mostly digital controllers or networked to the system. These control systems can be modeled by sampled-data control systems. Thus, the sampled-data control approach has received much attention, and in this paper, the controller design using sampled-data signal with stochastic sampling is investigated. For this purpose, assume the control input to be in the form,

$$\begin{aligned} U_i(t,x)&= K_i e_i(t_k,x),\quad t_k\le t <t_{k+1}, \nonumber \\&k=0,1,2,\ldots , \end{aligned}$$

(12)

where $K_i$ is the gain matrix, $t_k$ is the updating instant time and the sampling interval is defined as $h=t_{k+1}-t_k.$ Under the controller (12), system (11) can be represented as

$$\begin{aligned} \frac{\partial e_i(t,x)}{\partial t}&= \sum _{k=1}^q\frac{\partial }{\partial x_k}\left( D_k\frac{\partial e_i(t,x)}{\partial x_k}\right) -Ce_i(t,x)\nonumber \\&\quad +\,Ag(e_i(t,x))+Bg(e_i(t-d(t),x))\nonumber \\&\quad +\,K_ie_i(t_k,x), \quad i=1,2,\ldots ,N. \end{aligned}$$

(13)

The sampling period is denoted by $h$ and is assumed to take $m$ values such that $t_{k+1}-t_k = h_p,$ where the integer $p$ take values randomly in a set $\{1,2,\ldots ,m\}.$ The occurrence probability of each sampling period is given by

$$\begin{aligned} \text{ Prob }\{h=h_p\}=\beta _p, \quad p=1,2,\ldots ,m \end{aligned}$$

where $\beta _p\in [0,1] ,p=1,2,\ldots ,m$ are known constants and such that $\sum _{p=1}^m \beta _p=1.$ Also, $0=h_0<h_1<\cdots <h_m.$

Further, time delays in the control input are often encountered in many real-world problems, which may cause poor performance or instability of the system, and hence, the presence of time delays should be considered in control input. Moreover, it should be mentioned that time delays in the control input may be variable due to the complex disturbance or other conditions. Motivated by this fact, in this paper, we introduce the time-varying delay in the control input, and thus, the controller (12) takes the form

$$\begin{aligned} U_i(t,x)&= K_ie_i(t_k,x) \nonumber \\&= K_ie_i(t-\tau (t),x), \quad t_k\le t\le t_{k+1}, \end{aligned}$$

(14)

where we write $t_k=t-(t-t_k)=t-\tau (t).$ Here, $\tau (t)$ is the time-varying delay and satisfies $\dot{\tau }(t)=1.$ The probability of the time-varying delay is defined as follows:

$$\begin{aligned}&\text{ Prob }\{0\le \tau (t)<h_1\} = \frac{h_1}{h_m}, \\&\text{ Prob }\{h_1\le \tau (t)<h_2\} = \frac{h_2-h_1}{h_m}, \\&\qquad \qquad \qquad \vdots \\&\text{ Prob }\{h_{m-1}\le \tau (t)<h_m\} = \frac{h_m-h_{m-1}}{h_m}. \end{aligned}$$

The stochastic variables $\alpha _p(t)\,\text{ and }\, \beta _p(t)$ are defined as

$$\begin{aligned} \alpha _p(t)&= \left\{ \begin{array}{ll} 1, &{} h_{p-1}\le \tau (t)<h_p \\ 0, &{} \text{ otherwise } \end{array},\quad p=1,2,\ldots ,m,\right. \\ \beta _p(t)&= \left\{ \begin{array}{ll} 1, &{} h=h_p \\ 0, &{} \text{ otherwise } \end{array}, \quad p=1,2,\ldots ,m.\right. \end{aligned}$$

The probability of these stochastic variables are given by,

$$\begin{aligned} \text{ Prob }\{\alpha _p(t)=1\}&= \text{ Prob }\{h_{p-1}\le \tau (t)<h_p\} \nonumber \\&= \sum _{r=p}^m \beta _r \frac{h_p-h_{p-1}}{h_r} = \alpha _p, \end{aligned}$$

(15)

$$\begin{aligned} \text{ Prob }\{\beta _p(t)=1\}&= \text{ Prob }\{h=h_p\} =\beta _p, \end{aligned}$$

(16)

where $p=1,2,\ldots ,m$ and $\sum _{p=1}^m \alpha _p=1.$ Since $\alpha _p(t)$ satisfies the Bernoulli distribution as reported in [38], we have

$$\begin{aligned} \mathbb {E}\{\alpha _p(t)\}=\alpha _p \quad \text{ and } \quad \mathbb {E}\{(\alpha _p(t)-\alpha _p)^2\}=\alpha _p(1-\alpha _p). \end{aligned}$$

Therefore, system (11) with $m$ sampling intervals can be expressed as

$$\begin{aligned} \frac{\partial e_i(t,x)}{\partial t}&= \sum _{k=1}^q\frac{\partial }{\partial x_k}\left( D_k\frac{\partial e_i(t,x)}{\partial x_k}\right) -Ce_i(t,x)\nonumber \\&\quad +\,Ag(e_i(t,x))+Bg(e_i(t-d(t),x))\nonumber \\&\quad +\,\sum _{p=1}^m \alpha _p(t)K_ie_i(t-\tau _p(t),x), \end{aligned}$$

(17)

where $i=1,2,\ldots ,N$ and $h_{p-1}\le \tau _p(t)<h_p.$

Definition 1

[38] The error system (17) is said to be mean-square stable if for any $\epsilon >0, \sigma (\epsilon ) >0$ such that $\mathbb {E}\{\Vert e_i(t,x)\Vert ^2\}<\epsilon , t>0$ when $\mathbb {E}\{\Vert e_i(0,x)\Vert ^2\ < \sigma (\epsilon ).$ In addition, if $\lim _{t\rightarrow \infty } \mathbb {E}\{\Vert e_i(t,x)\Vert ^2\}=0,$ for any initial condition, the system (17) is said to be globally mean-square asymptotically stable.

In the following theorem, asymptotic stability of the error system (17) in the sense of mean square is investigated based on a novel Lyapunov–Krasovskii functional, and sufficient conditions that ensure the system stability are derived by employing some inequality techniques. We establish our main result based on the LMI approach.

For representation convenience, the following notations are introduced:

$$\begin{aligned} F_1&= \mathrm{diag}\{F_1^-F_1^+,F_2^-F_2^+,\ldots ,F_n^-F_n^+\}, \\ F_2&= \mathrm{diag}\left\{ \frac{F_1^-+F_1^+}{2}, \frac{F_2^-+F_2^+}{2},\ldots ,\frac{F_n^-+F_n^+}{2}\right\} . \end{aligned}$$

Theorem 1

For given positive constants $\alpha _p, \lambda _p, h_p (p=1,2,\ldots ,m), \mu$, system (17) is globally mean-square asymptotically stable, if there exist matrices $P>0, Q>0, G>0, W>0, H>0, S\!>\!0, X\!>\!0, \tilde{T}>0, G_1>0, G_2>0, Z_p>0, \ U_p>0, X_p>0, Y_p>0, M_p>0, S_p>0 (p=1,2,\ldots ,m),$ symmetric matrices $T_p>0, W_p>0 (p=1,2,\ldots ,m),$ diagonal matrices $\varLambda _{1}>0, \varLambda _{2}>0, \varLambda _{3}>0, \varLambda _{4}>0,$ and any matrices $H, V_p (p=1,2,\ldots ,m)$ with appropriate dimensions satisfying the following LMIs:

(18)

$$\begin{aligned}&\quad \left[ \begin{array}{cc} U_p &{} V_p \\ \star &{} U_p \end{array} \right] \ge 0, \end{aligned}$$

(19)

$$\begin{aligned}&\quad \left[ \begin{array}{cc} X_p &{} T_p \\ \star &{} Y_p \end{array} \right] > 0, \end{aligned}$$

(20)

$$\begin{aligned}&\quad \left[ \begin{array}{cc} X_p &{} W_p \\ \star &{} Y_p \end{array} \right] > 0, \end{aligned}$$

(21)

$$\begin{aligned} \varSigma _1&= \left[ \begin{array}{ccccccccccc} 0&0&0&\varPhi _2&\varPhi _3&0&BG&0&0&d_1G_1&0 \end{array}\right] \\ \varSigma _2&= \left[ \begin{array}{ccccccccccc} \varPhi _4 &{} 0 &{} 0 &{} 0 &{} 0 &{} F_2\varLambda _{3} &{} 0 &{} 0 &{} 0 &{} 0 &{} \varPhi _5 \\ \star &{} \varPhi _6 &{} 0 &{} 0 &{} 0 &{} 0 &{} F_2\varLambda _{2} &{} 0 &{} 0 &{} 0 &{} 0 \\ \star &{} \star &{} \varPhi _7 &{} 0 &{} 0 &{} 0 &{} 0 &{} F_2\varLambda _{4} &{} 0 &{} 0 &{} 0 \\ \star &{} \star &{} \star &{} \varPhi _8 &{} GA &{} 0 &{} GB &{} 0 &{} 0 &{} 0 &{} 0 \\ \star &{} \star &{} \star &{} \star &{} -\varLambda _{1} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \star &{} \star &{} \star &{} \star &{} \star &{} -\varLambda _{3} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \star &{} \star &{} \star &{} \star &{} \star &{} \star &{} -\varLambda _{2} &{} 0 &{} 0 &{} 0 &{} 0 \\ \star &{} \star &{} \star &{} \star &{} \star &{} \star &{} \star &{} -\varLambda _{4} &{} 0 &{} 0 &{} 0 \\ \star &{} \star &{} \star &{} \star &{} \star &{} \star &{} \star &{} \star &{} \varPhi _9 &{} 0 &{} 0 \\ \star &{} \star &{} \star &{} \star &{} \star &{} \star &{} \star &{} \star &{} \star &{} \varPhi _{10} &{} 0 \\ \star &{} \star &{} \star &{} \star &{} \star &{} \star &{} \star &{} \star &{} \star &{} \star &{} \varPhi _{11} \end{array}\right] \end{aligned}$$

where

$$\begin{aligned} \varPhi _1&= Q+W+d_1^2X+\alpha _1Z_1-\alpha _1U_1+\alpha _1T_1\nonumber \\&\quad -\,\bar{S}_1 +2CG -2\tilde{D}-F_1\varLambda _{1i}-\alpha _1c_1^2M_1\nonumber \\&\quad -\,\alpha _2c_2^2M_2 + \sum _{i=1}^m \alpha _pc_pX_p, \nonumber \\ \varPhi _2&= P-G-CG, \nonumber \\ \varPhi _3&= AG+F_2\varLambda _{1i}, \nonumber \\ \varPhi _4&= -Q+H+\frac{d_{12}^3}{2}\tilde{T}-\,(-d_1+d_2)^2G_2-F_1\varLambda _{3i}, \nonumber \\ \varPhi _5&= (-d_1+d_2)G_2, \nonumber \\ \varPhi _6&= -(1-\mu )W-F_1\varLambda _{2i}, \nonumber \\ \varPhi _7&= -H-F_1\varLambda _{4i}, \nonumber \\ \varPhi _8&= S+\left( \frac{d_1^2}{2}\right) ^2G_1\nonumber \\&\quad +\sum _{p=1}^m \left( \alpha _pc_p^2U_p+\alpha _pc_pY_p+\beta _ph_p^2S_p \right) , \nonumber \\ \bar{S}_i&= \sum _{r=1}^m \left( \beta _r \frac{\pi ^2}{4}\frac{c_p}{c_r} S_r \right) , \nonumber \\ c_p&= h_p-h_{p-1}, \nonumber \\ \kappa&= \left( -d_1-\frac{d_1^2}{2}-\frac{d_2^2}{2}\right) , \nonumber \\ \varXi _1&= \left\{ \begin{array}{l} (1,1) = \alpha _1U_1-\alpha _1V_1+\bar{S}_1+\alpha _1\tilde{H}, \\ (1,2) = \alpha _1V_1, \\ (1,p) = \alpha _{\frac{p}{3}}c_{\frac{p}{3}}M_{\frac{p}{3}},\quad p=3,6,\ldots ,3m \\ (1,p) = \alpha _{\frac{p+2}{3}}\tilde{H},\quad p=4,7,\ldots ,3m-2, \\ \mathrm{otherwise} = 0, \end{array}\right. \nonumber \\ \varXi _2 \!&= \! \left\{ \begin{array}{l} (p,p) \!=\! \alpha _{\frac{p+2}{3}}\Big (\!\!-\!2U_{\frac{p+2}{3}}\!+\!V_{\frac{p+2}{3}} \!+\!V_{\frac{p+2}{3}}^T\!+\!W_{\frac{p+2}{3}}\\ \left. \quad \!-\!\,T_{\frac{p+2}{3}} \right) \!-\!\bar{S}_{\frac{p+2}{3}},\quad p\!=\!1,4,7,\ldots ,3m\!-\!2 \\ (p,p) = -\alpha _{\frac{p+1}{3}}\left( Z_{\frac{p+1}{3}}+U_{\frac{p+1}{3}}+W_{\frac{p+1}{3}}\right) \\ \quad +\,\alpha _{\frac{p+4}{3}}\left( Z_{\frac{p+4}{3}}-U_{\frac{p+4}{3}}+T_{\frac{p+4}{3}} \right) \!-\! \bar{S}_{\frac{p+4}{3}}, \\ \quad p=2,5,\ldots ,3m-1 \\ (p,p) = -\alpha _{\frac{p}{3}} M_{\frac{p}{3}}, \quad p=3,6,\ldots ,3m \\ (p,p+1) = \alpha _{\frac{p+2}{3}}\left( U_{\frac{p+2}{3}} -V_{\frac{p+2}{3}}\right) , \\ \quad p=1,4,\ldots ,3m-2 \\ (p,p+2) = \alpha _{\frac{p+4}{3}} \left( U_{\frac{p+4}{3}} -V_{\frac{p+4}{3}} \right) + \bar{S}_{\frac{p+4}{3}}, \\ \quad p=2,5,\ldots ,3m-1 \\ (p,p+3) = \alpha _{\frac{p+4}{3}}V_{\frac{p+4}{3}}, \\ \quad p=2,5,\ldots ,3m-1 \\ \mathrm{otherwise}= 0, \end{array} \right. \end{aligned}$$

$$\begin{aligned} \varXi _3(p,1)&= \alpha _\frac{p+2}{3}\tilde{H},\quad p=1,4,\ldots , 3m-2 \end{aligned}$$

(22)

and other entries of $\varXi _1, \varXi _2, \varXi _3$ are zero, $h_0=0$ and $\alpha _p,Z_p,U_p,\bar{S}_p=0,\,\text{ for }\,p>m.$ Then, the desired gain is given by $K=G^{-1}\tilde{H}.$

Proof

Consider the following discontinuous Lyapunov functional for the error system (17):

$$\begin{aligned} V(t)=\sum _{\nu =1}^{10}V_{\nu }(t), \end{aligned}$$

(23)

where

$$\begin{aligned} V_1(t)&= \int _\varOmega \sum _{i=1}^N e_i^T(t,x)Pe_i(t,x)\mathrm {d}x\!+\!\int _\varOmega \sum _{i=1}^N \sum _{k=1}^q D_k\nonumber \\&\quad \times \,\left( \frac{\partial e_i(t,x)}{\partial x_k}\right) ^TG\left( \frac{\partial e_i(t,x)}{\partial x_k}\right) \mathrm {d}x, \end{aligned}$$

(24)

$$\begin{aligned} V_2(t)&= \int _\varOmega \sum _{i=1}^N \int _{t-d_1}^t e_i^T(s,x)Qe_i(s,x)\mathrm {d}s \mathrm {d}x\nonumber \\&\quad +\,\int _\varOmega \sum _{i=1}^N \int _{t-d(t)}^t e_i^T(s,x)We_i(s,x)\mathrm {d}s \mathrm {d}x\nonumber \\&\quad +\,\int _\varOmega \sum _{i=1}^N \int _{t-d_2}^{t-d_1} e_i^T(s,x)He_i(s,x)\mathrm {d}s \mathrm {d}x\nonumber \\&\quad +\,\int _\varOmega \sum _{i=1}^N \int _{t-d_1}^t \dot{e}_i^T(s,x)S\dot{e}_i(s,x)\mathrm {d}s \mathrm {d}x, \end{aligned}$$

(25)

$$\begin{aligned} V_3(t) \!\!\!&=\!&d_1\!\!\int _\varOmega \!\!\sum _{i=1}^N \int _{-d_1}^0\int _{t+\theta }^t e_i^T(s,x)Xe_i(s,x) \mathrm {d}s\mathrm {d}\theta \mathrm {d}x, \end{aligned}$$

(26)

$$\begin{aligned} V_4(t)&= \frac{d_{12}^2}{2}\int _\varOmega \sum _{i=1}^N \int _{-d_2}^{-d_1}\int _{t+\theta }^{t-d_1} e_i^T(s,x)\nonumber \\&\quad \times \,\tilde{T}e_i(s,x) \mathrm {d}s\mathrm {d}\theta \mathrm {d}x, \end{aligned}$$

(27)

$$\begin{aligned} V_5(t)&= \frac{d_1^2}{2} \int _\varOmega \sum _{i=1}^N \int _{-d_1}^0\int _{\theta }^0\int _{t+\lambda }^t \dot{e}_i^T(s,x)\nonumber \\&\quad \times \,G_1\dot{e}_i(s,x) \mathrm {d}s\mathrm {d}\lambda \mathrm {d}\theta \mathrm {d}x, \end{aligned}$$

(28)

$$\begin{aligned} V_6(t)&= \frac{d_2^2-d_1^2}{2} \int _\varOmega \sum _{i=1}^N \int _{-d_2}^{-d_1}\int _{\theta }^{-d_1}\int _{t+\lambda }^{t-d_1} \dot{e}_i^T(s,x)\nonumber \\&\quad \times \,G_2\dot{e}_i(s,x) \mathrm {d}s\mathrm {d}\lambda \mathrm {d}\theta \mathrm {d}x, \end{aligned}$$

(29)

$$\begin{aligned} V_7(t)&\!\!=\!\! \!\!\int _\varOmega \!\!\sum _{i=1}^N\sum _{p=1}^m \alpha _p(t)\!\!\left( \int _{t-h_p}^{t-h_{p-1}}e_i^T(s,x)Z_pe_i(s,x) \mathrm {d}s \right. \nonumber \\&\quad \left. \!+\!\,c_p \!\!\int _{\!-h_p}^{\!-h_{p-1}}\!\!\int _{t\!+\!\theta }^t\dot{e}_i^T(s,x)U_p\dot{e}_i(s,x)\mathrm {d}s \mathrm {d}\theta \right) \mathrm {d}x, \nonumber \\ \end{aligned}$$

(30)

$$\begin{aligned} V_8(t)&= \int _\varOmega \sum _{i=1}^N\sum _{p=1}^m \alpha _p(t)\left( \int _{-h_p}^{-h_{p-1}} \int _{t+\theta }^t \left( e_i^T(s,x)X_p\right. \right. \nonumber \\&{\quad } \left. \left. \times \, e_i(s,x)+e_i^T(s,x)Y_pe_i(s,x) \right) \mathrm {d}s \mathrm {d}\theta \right) \mathrm {d}x, \nonumber \\ \end{aligned}$$

(31)

$$\begin{aligned}&V_9(t) = \int _\varOmega \sum _{i=1}^N\sum _{p=1}^m \alpha _p(t) \left( \frac{h_p^2-h_{p-1}^2}{2}\right) \nonumber \\&\times \int _{-h_p}^{-h_{p-1}}\int _{\theta }^0\int _{t+\lambda }^{t} \dot{e}_i^T(s,x)M\dot{e}_i(s,x) \mathrm {d}s\mathrm {d}\lambda \mathrm {d}\theta \mathrm {d}x, \end{aligned}$$

(32)

$$\begin{aligned}&V_{10}(t) = \int _\varOmega \sum _{i=1}^N\sum _{p=1}^m V_{10p}(t)\mathrm {d}x, \end{aligned}$$

(33)

$$\begin{aligned} V_{10p}(t)&= \beta _p(t)\left( h_p^2 \int _{t_k}^t \dot{e}_i^T(s,x)S_p\dot{e}_i(s,x)\mathrm {d}s\right. \nonumber \\&\left. -\,\frac{\pi ^2}{4}\int _{t_k}^t \left( e_i(s,x)-e_i(t_k,x)\right) ^T\right. \nonumber \\&\left. \times \, S_p(e_i(s,x)-e_i(t_k,x))\mathrm {d}s\right) . \end{aligned}$$

(34)

Obviously, $V_{10p}(t)$ can be easily computed by Wirtinger’s inequality. Also, since $V_{10p}(t)$ will disappear at $t=t_k,$ we obtain $\lim _{t\rightarrow t_k^-}V(t)\ge V(t_k).$

Define the infinitesimal operator $L$ of $V(t)$ as follows:

$$\begin{aligned} LV(t)=\lim _{h\rightarrow 0^+}\frac{1}{h}\{\mathbb {E}\{V(e_{t+h})|e_t\}-V(e_t)\}. \end{aligned}$$

(35)

It can be derived that

$$\begin{aligned} \mathbb {E}\{LV(t)\}= \sum _{\nu =1}^{10}\mathbb {E}\{LV_{\nu }(t)\}, \end{aligned}$$

(36)

where

$$\begin{aligned}&\mathbb {E}\{LV_1(t)\}\! \!=\!\! \int _\varOmega \sum _{i=1}^N\mathbb {E}\bigg \{2e_i^T(t,x)P\dot{e}_i(t,x)\nonumber \\&{\quad }\!+\!\,2\!\sum _{k=1}^q\!D_k \frac{\partial e_i^T(t,x)}{\partial x_k}G{\partial \dot{e}_i(t,x)}{\partial x_k}\bigg \}\mathrm {d}x, \end{aligned}$$

(37)

$$\begin{aligned}&\mathbb {E}\{LV_2(t)\}\!\!=\!\! \!\int _\varOmega \sum _{i=1}^N\mathbb {E}\!\bigg \{e_i^T(t,x)Qe_i(t,x)\!-\!e_i^T(t\!-\!d_1,x)\nonumber \\&{\quad }\times \!\, Qe_i(t\!-\!d_1,x)\!+\!e_i^T(t,x)We_i(t,x)\nonumber \\&{\quad }-\!\,(1\!-\!\dot{d}(t))e_i^T(t\!-\!d(t),x)We_i(t\!-\!d(t),x)\nonumber \\&{\quad }+\!\,e_i^T(t\!-\!d_1,x) He_i(t\!-\!d_1,x)\!-\!e_i^T(t\!-\!d_2,x)\nonumber \\&{\quad }\times \,He_i(t\!-\!d_2,x)\!+\!\dot{e}_i^T(t,x)S\dot{e}_i(t,x)\nonumber \\&{\quad }-\!\,\dot{e}_i^T(t\!-\!d_1,x) S\dot{e}_i(t\!-\!d_1,x)\bigg \}\mathrm {d}x, \end{aligned}$$

(38)

$$\begin{aligned} \mathbb {E}\{LV_3(t)\}&= \int _\varOmega \sum _{i=1}^N\mathbb {E}\bigg \{d_1^2e_i^T(t,x)Xe_i(t,x)\nonumber \\&-\,\left( \int _{t-d_1}^te_i(s,x)\mathrm {d}s\right) ^T\nonumber \\&\times \left( \int _{t-d_1}^te_i(s,x)\mathrm {d}s\right) \mathrm {d}s\bigg \}\mathrm {d}x, \end{aligned}$$

(39)

$$\begin{aligned} \mathbb {E}\{LV_4(t)\}&= \int _\varOmega \sum _{i=1}^N\mathbb {E}\bigg \{\frac{d_{12}^3}{2}e_i^T(t\!-\!d_1,x)\tilde{T}e_i(t\!-\!d_1,x)\nonumber \\&-\,\frac{d_{12}}{2} \times \left( \int _{t-d_2}^{t-d_1}e_i(s,x)\mathrm {d}s\right) ^T\nonumber \\&\times \,\tilde{T} \left( \int _{t-d_2}^{t-d_1}e_i(s,x)\mathrm {d}s\right) \mathrm {d}s\bigg \}\mathrm {d}x, \end{aligned}$$

(40)

$$\begin{aligned} \mathbb {E}\{LV_5(t)\}&= \int _\varOmega \sum _{i=1}^N\mathbb {E}\bigg \{\left( \frac{d_1^2}{2}\right) ^2\dot{e}_i^T(t,x)G_1\dot{e}_i(t,x)\nonumber \\&-\,d_1^2e_i^T(t,x)G_1e_i(t,x)\nonumber \\&+\,d_1\int _{t-d_1}^te_i^T(s,x)\mathrm {d}sG_1e_i(t,x)\nonumber \\&+\,d_1\int _{t-d_1}^te_i^T(s,x)\mathrm {d}sG_1e_i(t,x)\nonumber \\&-\,\int _{t-d_1}^te_i^T(s,x)\mathrm {d}s\nonumber \\&\times \, G_1\int _{t-d_1}^te_i(s,x)\mathrm {d}s \bigg \}\mathrm {d}x, \end{aligned}$$

(41)

$$\begin{aligned}&\mathbb {E}\{LV_6(t)\}\nonumber \\&\quad = \int _\varOmega \sum _{i=1}^N\mathbb {E}\bigg \{\frac{{d_2^2}\!-\!d_1^2}{2}\kappa \dot{e}_i^T(t\!-\!d_1,x)G_2\dot{e}_i(t-d_1,x)\nonumber \\&\qquad -\!\,(\!-d_1\!+\!d_2)^2e_i^T(t\!-\!d_1,x)G_2e_i(t\!-\!d_1,x)\nonumber \\&\qquad +\!\,2(\!-d_1\!+\!d_2)\int _{t-d_2}^{t-d_1}e_i^T(s,x)\mathrm {d}s G_2e_i(t\!-\!d_1,x)\nonumber \\&\qquad -\,\int _{t-d_2}^{t-d_1}e_i^T(s,x)\mathrm {d}sG_2\int _{t-d_2}^{t-d_1}e_i(s,x)\mathrm {d}s \bigg \}\mathrm {d}x, \nonumber \\ \end{aligned}$$

(42)

$$\begin{aligned}&\mathbb {E}\{LV_7(t)\} = \int _\varOmega \sum _{i=1}^N\mathbb {E}\bigg \{\!\sum _{p=1}^m\alpha _p\left( e_i^T(t-h_{p-1},x)\right. \nonumber \\&\qquad \times \,\left. Z_pe_i(t-h_{p-1},x)\right. \nonumber \\&\qquad -\,\left. e_i^T(t-h_p,x)Z_pe_i(t-h_p,x)\right. \nonumber \\&\qquad +\,\left. c_p^2\dot{e}_i^T(t,x)U_p\dot{e}_i(t,x)\right. \nonumber \\&\qquad -\,\left. c_p\int _{t-h_p}^{t-h_{p-1}}\dot{e}_i^T(s,x)U_p\dot{e}_i(s,x)\mathrm {d}\theta \right) \bigg \}\mathrm {d}x,\nonumber \\ \end{aligned}$$

(43)

Applying Lemma 1 to the last integration term, it follows that

$$\begin{aligned}&-\alpha _pc_p\int _{t-h_p}^{t-h_{p-1}} \dot{e}_i^T(s,x)U_p\dot{e}_i(s,x)\mathrm {d}s \nonumber \\&\quad = -\alpha _p \left[ \left( 1+ \frac{h_p-\tau _p(t)}{\tau _p(t)-h_{p-1}} \right) \delta _{1p}^T(t)U_p\delta _{1p}(t)\right. \nonumber \\&\quad \quad \left. +\,\left( 1+\frac{\tau _p(t)-h_{p-1}}{h_p(t)-\tau _p(t)}\right) \delta _{2p}^T(t)U_p\delta _{2p}(t)\right] , \end{aligned}$$

(44)

$\delta _{1p}(t)\!=\!\int _{t-\tau _p(t)}^{t-h_{p-1}} \dot{e}_i(s,x)\mathrm {d}s,\ \delta _{2p}(t)\!=\!\int _{t-h_p}^{t-\tau _p(t)}\dot{e}_i(s,x) \mathrm {d}s.$ Combining (19) and Lemma 2, we obtain

$$\begin{aligned}&\frac{h_p-\tau _p(t)}{\tau _p(t)-h_{p-1}} \delta _{1p}^T(t)U_p\delta _{1p}(t)\nonumber \\&\qquad +\frac{\tau _p(t)-h_{p-1}}{h_p-\tau _p(t)}\delta _{2p}^T(t)U_p \delta _{2p}(t) \nonumber \\&\quad \ge \delta _{1p}(t)V_p\delta _{2p}(t)+\delta _{2p}(t)V_p^T\delta _{1p}(t). \end{aligned}$$

(45)

Substituting (45) into (44) yields

$$\begin{aligned}&-\alpha _pc_p\int _{t-h_p}^{t-h_{p-1}}\dot{e}_i^T(s,x)U_p\dot{e}_i(s,x) \mathrm {d}s \nonumber \\&\quad \le -\alpha _p\bigg (\delta _{1p}^T(t)U_p\delta _{1p}(t)+\delta _{2p}^T(t)U_p\delta _{2p}(t)\nonumber \\&\quad \quad +\,\delta _{1p}^T(t)V_p\delta _{2p}(t)+\delta _{2p}(t)V_p^T\delta _{1p}(t)\bigg ) \nonumber \\&\quad = \alpha _p\left( \left[ \begin{array}{c} e_i(t-h_{p-1},x) \\ e_i(t-\tau _p(t),x) \\ e_i(t-h_p,x) \end{array} \right] ^T \right. \nonumber \\&\quad \quad \left. \times \, \left[ \begin{array}{ccc} -U_p &{} U_p-V_p &{} V_p \\ \star &{} -2U_p+V_p+V_p^T &{} U_p-V_p \\ \star &{} \star &{} -U_p \end{array}\right] \right. \nonumber \\&\quad \quad \left. \times \, \left[ \begin{array}{c} e_i(t-h_{p-1},x) \\ e_i(t-\tau _p(t),x) \\ e_i(t-h_p,x) \end{array} \right] \right) . \end{aligned}$$

(46)

Furthermore,

$$\begin{aligned} \mathbb {E}\{LV_8(t)\}&\!=\! \int _\varOmega \!\sum _{i=1}^N\mathbb {E}\!\bigg \{\sum _{p=1}^m\alpha _p\left( c_pe_i^T(t,x)X_pe_i(t,x)\right. \nonumber \\&\quad -\,\left. \int _{t-h_p}^{t-h_{p-1}}e_i^T(s,x)X_pe_i(s,x)\right. \nonumber \\&\quad +\,c_p\dot{e}_i^T(t,x)Y_p\dot{e}_i(t,x)\nonumber \\&\quad -\,\left. \int _{t-h_p}^{t-h_{p-1}}\dot{e}_i^T(s,x)Y_p\dot{e}_i(s,x)\mathrm {d}s\right) \bigg \}\mathrm {d}x, \end{aligned}$$

(47)

Consider the following two zero equalities,

$$\begin{aligned} 0&\!=\!\alpha _p\!\left( e_i^T(t\!-\!h_{p-1},x)T_pe_i(t\!-\!h_{p-1},x)\right. \\&\quad \,\!\left. -\!e_i^T(t\!-\!\tau _p(t),x) \times \, T_pe_i(t\!-\!\tau _p(t),x)\right. \\&\quad \,\left. -2\int _{t-\tau _p(t)}^{t-h_{p-1}}\!e_i^T(s,x)T_p\dot{e}_i(s,x)\mathrm {d}s\!\right) ,\\ 0&\!=\alpha _p\left( e_i^T(t\!-\!\tau _p(t),x)W_pe_i(t\!-\!\tau _p(t),x)\right. \\&\quad -\,\left. \!e_i^T(t\!-\!h_p,x) \times \, \!W_pe_i(t\!-\!h_p,x)\!\right. \\&\quad \,\left. -\!2\int _{t-h_p}^{t-\tau _p(t)}e_i^T(s,x)W_p\dot{e}_i(s,x)\mathrm {d}s\!\right) , \end{aligned}$$

where $T_p\,\text{ and }\,W_p$ are any symmetric matrices. By adding the above zero equalities to the left-hand side of $LV_8(t),$ we get

$$\begin{aligned}&\mathbb {E}\{LV_8(t)\} \nonumber \\&\quad =\int _\varOmega \mathbb {E}\left\{ \sum _{p=1}^m\alpha _p \left[ c_pe_i^T(t,x)X_pe_i(t,x)\right. \right. \nonumber \\&{\qquad }+\left. \left. c_p\dot{e}_i^T(t,x) \times Y_p\dot{e}_i(t,x)\right. \right. \nonumber \\&{\qquad }+\left. \left. e_i^T(t-h_{p-1},x)T_pe_i(t-h_{p-1},x) \right. \right. \nonumber \\&{\qquad }+\left. \left. e_i^T(t-\tau _p(t),x)(W_p-T_p)e_i(t-\tau _p(t),x)\right. \right. \nonumber \\&{\qquad }-\left. \left. e_i^T(t-h_p,x)W_pe_i(t-h_p,x) \right. \right. \nonumber \\&{\qquad }- \left. \left. \int _{t-\tau _p(t)}^{t-h_{p-1}} \left[ \begin{array}{c} e_i(s,x) \\ \dot{e}_i(s,x) \end{array}\right] ^T\left[ \begin{array}{cc} X_p &{} T_p \\ \star &{} Y_p \end{array} \right] \left[ \begin{array}{c} e_i(s,x) \\ \dot{e}_i(s,x) \end{array}\right] \mathrm {d}s \right. \right. \nonumber \\&\qquad -\,\left. \left. \int _{t-h_p}^{t-\tau _p(t)} \!\left[ \begin{array}{c} e_i(s,x) \\ \dot{e}_i(s,x) \end{array}\right] ^T\! \!\left[ \begin{array}{cc} X_p&{} W_p \\ \star &{} Y_p \end{array} \right] \right. \right. \nonumber \\&\qquad -\,\left. \left. \,\left[ \begin{array}{c} e_i(s,x) \\ \dot{e}_i(s,x) \end{array}\right] \! \mathrm {d}s \right] \right\} \mathrm {d}x \nonumber \\&\quad \le \int _\varOmega \mathbb {E}\left\{ \sum _{p=1}^m\alpha _p\left[ c_p e_i^T(t,x)X_pe_i(t,x)\right. \right. \nonumber \\&{\qquad }+\left. \left. \,c_p\dot{e}_i^T(t,x)\right. \right. \nonumber \\&{\qquad }\times \, \left. \left. Y_p\dot{e}_i(t,x)\right. \right. \nonumber \\&{\qquad }+\left. \left. \,e_i^T(t-h_{p-1},x)T_p e_i(t-h_{p-1},x) \right. \right. \nonumber \\&{\qquad }+\,\left. \left. e_i^T(t-\tau _p(t),x)(W_p-T_p)e_i(t-\tau _p(t),x) \right. \right. \nonumber \\&{\qquad }-\,\left. \left. e_i^T(t-h_p,x)W_pe_i(t-h_p,x) \right] \right\} \mathrm {d}x. \end{aligned}$$

(48)

Also, we have

$$\begin{aligned}&\mathbb {E}\{LV_9(t)\} \nonumber \\&\quad = \int _\varOmega \sum _{i=1}^N\mathbb {E}\left\{ \sum _{p=1}^m\alpha _p\left[ \left( \frac{h_p^2-h_{p-1}^2}{2}\right) ^2 \left( -\dot{e}_i^T(t,x)\right. \right. \right. \nonumber \\&{\qquad }\times \left. \left. \left. M_p\dot{e}_i(t,x)\right) -c_p^2e_i^T(t,x)M_pe_i(t,x)\right. \right. \nonumber \\&{\qquad }+\left. \left. c_p\int _{t-h_p}^{t-h_{p-1}}e_i^T(s,x)M_pe_i(t,x)+c_pe_i^T(t,x)\right. \right. \nonumber \\&{\qquad }\times \left. \left. M_p\int _{t-h_p}^{t-h_{p-1}}e_i(s,x)\mathrm {d}s -\int _{t-h_p}^{t-h_{p-1}}e_i^T(s,x)\mathrm {d}s\right. \right. \nonumber \\&{\qquad }\times \left. \left. M_p\int _{t-h_p}^{t-h_{p-1}}e_i(s,x)\mathrm {d}s \right] \right\} \mathrm {d}x, \end{aligned}$$

(49)

In order to obtain $LV_{10p}(t)$, we do the following to the last integration term of $V_{10p}(t):$

The definition of $\tau _p(t)=t-t_k$ shows that the last integration term of $V_{10p}(t)$ is

$$\begin{aligned}&\!-\!\frac{\pi ^2}{4}\int _{t_k}^t\left( e_i(s,x)\!-\!e_i(t_k,x)\right) ^T\nonumber \\&\qquad \times \,S_p\left( e_i(s,x)\!-\!e_i(t_k,x)\right) \mathrm {d}s\nonumber \\&\quad \!=\!-\!\sum _{r=1}^p\alpha _r(t)\frac{\pi ^2}{4}\!\!\int _{t-\tau _r(t)}^{t-h_{r-1}}\left( e_i(s,x)\! -\!e_i(t\!-\!\tau _r(t),x)\right) ^T\nonumber \\&\qquad \times \, S_p\left( e_i(s,x)-e_i(t-\tau _r(t),x)\right) \mathrm {d}s. \end{aligned}$$

(50)

Using fully the information of stochastically varying interval delay $\tau (t)$, the stochastic variables $\rho _{pr}(t)\,(r\le p=1,2,\ldots ,m)$ are introduced and such that

$$\begin{aligned} \rho _{pr}(t) = \left\{ \begin{array}{llll} 1, &{} \beta _p(t)\alpha _r(t)=1 &{} \\ 0, &{} \text{ otherwise } &{} \ r\le p=1,2,\ldots ,m \end{array} \right. \end{aligned}$$

with the probability,

$$\begin{aligned} \text{ Prob }\{\rho _{pr}(t)=1\} = \beta _p \frac{h_r-h_{r-1}}{h_p} = \rho _{pr}, \end{aligned}$$

where $\sum \nolimits _{p=1}^{m} \sum _{r=1}^p \rho _{pr}=1.$ Then, $V_{10p}(t)$ can be rewritten as the following:

$$\begin{aligned} V_{10p}(t)&= \int _\varOmega \left\{ \beta _p(t) h_p^2 \dot{e}_i^T(t,x) S_p\dot{e}_i(t,x)\right. \nonumber \\&{\quad }-\,\left. \sum _{r=1}^p\left( \rho _{pr}\frac{\pi ^2}{4}\int _{t-\tau (t)}^{t-h_{r-1}}(e_i(s,x)\right. \right. \nonumber \\&{\quad }-\,\left. \left. e_i(t-\tau (t),x))^T\right. \right. \nonumber \\&{\quad }\times \,\left. \left. S_p(e_i(s,x)-e_i(t-\tau (t),x))\mathrm {d}s\right) \right\} dx. \nonumber \\ \end{aligned}$$

(51)

By (51), we can easily get

$$\begin{aligned}&\mathbb {E}\{{L}V_{10p}(t)\} =\int _\varOmega \mathbb {E}\left\{ \beta _ph_p^2 \dot{e}_i^T(t,x) S_p\dot{e}_i(t,x)\right. \nonumber \\&{\quad }-\,\left. \sum _{r=1}^p\left( \rho _{pr}\frac{\pi ^2}{4}\left[ \begin{array}{c} e_i(t-h_{r-1},x)\\ e_i(t-\tau _r(t),x) \end{array} \right] ^T \right. \right. \nonumber \\&{\quad }\times \, \left. \left. \left[ \begin{array}{cc} S_p &{} -S_p \\ \star &{} S_p \end{array} \right] \left[ \begin{array}{c} e_i(t-h_{r-1},x)\\ e_i(t-\tau _r(t),x) \end{array} \right] \right) \right\} \mathrm {d}x,\nonumber \\&{\quad } p=1,2,\ldots ,m. \end{aligned}$$

(52)

According to the error system (17), we can have

$$\begin{aligned}&\int _\varOmega \sum _{i=1}^N\mathbb {E}\left\{ 2[e_i^T(t,x)G+\dot{e}_i^T(t,x)G]\left[ -\dot{e}_i(t,x)\right. \right. \nonumber \\&\quad \left. \left. \!+\!\,\sum _{k=1}^q\!\frac{\partial }{\partial x_k}\!\left( D_k\frac{\partial e_i(t,x)}{\partial x_k}\!\right) \!-\!Ce_i(t,x)\!+\!Ag(e_i(t,x))\right. \right. \nonumber \\&\quad \left. \left. +\,Bg(e_i(t-d(t),x))\right. \right. \nonumber \\&\quad \left. \left. +\sum _{p=1}^m \alpha _p(t)K_ie_i(t-\tau _p(t),x)\right] \right\} =0, \end{aligned}$$

(53)

with $\tilde{H}=GK_i.$

For positive diagonal matrices $\varLambda _{1},\varLambda _{2},\varLambda _{3}\,\text{ and }\,\varLambda _{4}$, we can get from Assumption 1 that

$$\begin{aligned}&\left[ \begin{array}{c} e_i(t,x) \\ g(e_i(t,x)) \end{array}\right] ^T \left[ \begin{array}{cc} F_1\varLambda _{1} &{} -F_2\varLambda _{1} \\ \star &{} \varLambda _{1} \end{array}\right] \nonumber \\&\quad \left[ \begin{array}{c} e_i(t,x) \\ g(e_i(t,x)) \end{array}\right] \le 0, \end{aligned}$$

(54)

$$\begin{aligned}&\left[ \begin{array}{c} e_i(t-d(t),x) \\ g(e_i(t-d(t),x)) \end{array}\right] ^T \left[ \begin{array}{cc} F_1\varLambda _{2} &{} -F_2\varLambda _{2} \\ \star &{} \varLambda _{2} \end{array}\right] \nonumber \\&\quad \left[ \begin{array}{c} e_i(t-d(t),x) \\ g(e_i(t-d(t),x)) \end{array}\right] \le x 0, \end{aligned}$$

(55)

$$\begin{aligned}&\left[ \begin{array}{c} e_i(t-d_1,x) \\ g(e_i(t-d_1,x)) \end{array}\right] ^T \left[ \begin{array}{cc} F_1\varLambda _{3} &{} -F_2\varLambda _{3} \\ \star &{} \varLambda _{3} \end{array}\right] \nonumber \\&\quad \left[ \begin{array}{c} e_i(t-d_1,x) \\ g(e_i(t-d_1,x)) \end{array}\right] \le 0, \end{aligned}$$

(56)

$$\begin{aligned}&\left[ \begin{array}{c} e_i(t-d_2,x) \\ g(e_i(t-d_2,x)) \end{array}\right] ^T \left[ \begin{array}{cc} F_1\varLambda _{4} &{} -F_2\varLambda _{4} \\ \star &{} \varLambda _{4} \end{array}\right] \nonumber \\&\quad \left[ \begin{array}{c} e_i(t-d_2,x) \\ g(e_i(t-d_2,x)) \end{array}\right] \le 0. \end{aligned}$$

(57)

From Eqs. (37)–(48) and adding (53)–(57) to $LV(t)$, we obtain

$$\begin{aligned} \int _\varOmega \sum _{i=1}^N\mathbb {E}\{LV(t)\}\le \int _\varOmega \sum _{i=1}^N\mathbb {E}\{\zeta _i^T(t,x)\varPhi \zeta _i(t,x)\}, \end{aligned}$$

(58)

where the matrix $\varPhi$ is defined in Theorem 1 and $\zeta _i(t,x)=[e_i^T(t,x) e_{im}^T(t,x) e_i^T(t-d_1,x) e_i^T(t-d(t),x) e_i^T(t-d_2,x) \dot{e}_i^T(t,x) g^T(e_i(t,x)) g^T(e_i(t-d_1,x)) g^T(e_i(t-d(t),x)) g^T(e_i(t-d_2,x)) \dot{e}_i^T(t-d_1,x) \int _{t-d_1}^t e_i^T(s,x)\mathrm {d}s \int _{t-d_2}^{t-d_1}e_i^T(s,x)\mathrm {d}s]^T$ with $e_{im}(t,x) = [e_i^T(t-\tau _1(t),x) e_i^T(t-h_1,x) \int _{t-h_1}^{t-h_0}e_i^T(s,x)\mathrm {d}s \cdots e_i^T(t-\tau _m(t),x) e_i^T(t-h_m,x) \int _{t-h_m}^{t-h_{m-1}}e_i^T(s,x)\mathrm {d}s]^T.$

By (58) and (18)–(21), we obtain

$$\begin{aligned} \int _\varOmega \sum _{i=1}^N\mathbb {E}\{LV(t)\}\le 0, \end{aligned}$$

which together with Definition 1 implies that the error system (17) is mean-square stable. This completes the proof.

Remark 1

In Theorem 1 taking $m=2,$ we obtain the matrix $\varPhi$ as

$$\begin{aligned} \varPhi = \left[ \begin{array}{cccccc} \varGamma _1 &{} \varGamma _2 &{} \varGamma _3 &{} \varGamma _4 &{} \varGamma _5 &{} \varGamma _6 \\ \star &{} \varGamma _7 &{} \varGamma _8 &{} \varGamma _9 &{} \varGamma _{10} &{} \varGamma _{11} \\ \star &{} \star &{} \varGamma _{12} &{} \varGamma _{13} &{} \varGamma _{14} &{} \varGamma _{15} \\ \star &{} \star &{} \star &{} \varGamma _{16} &{} \varGamma _{17} &{} \varGamma _{18} \\ \star &{} \star &{} \star &{} \star &{} \varGamma _{19} &{} \varGamma _{20} \\ \star &{} \star &{} \star &{} \star &{} \star &{} \varGamma _{21} \end{array} \right] <0 \end{aligned}$$

(59)

where

$$\begin{aligned} \varGamma _1&=\left[ \begin{array}{ccc} \varPhi _1 &{} \varXi _{11}^1 &{} \varXi _{12}^1 \\ \star &{} \varXi _{11}^2 &{} \varXi _{12}^2 \\ \star &{} \star &{} \varXi _{22}^2 \end{array}\right] \quad \varGamma _2 =\left[ \begin{array}{ccc} \varXi _{13}^1 &{} \varXi _{14}^1 &{} 0 \\ 0 &{} 0 &{} 0 \\ \varXi _{23}^2 &{} \varXi _{24}^2 &{} \varXi _{25}^2 \end{array}\right] \\ \varGamma _3&=\left[ \begin{array}{ccc} \varXi _{16}^1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{array}\right] \quad \varGamma _4 =\left[ \begin{array}{ccc} 0 &{} \varPhi _2 &{}\varPhi _3 \\ 0 &{} \varXi _{11}^3 &{} 0 \\ 0 &{} 0 &{} 0 \end{array}\right] \\ \varGamma _5&=\left[ \begin{array}{ccc} 0 &{} GB &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{array}\right] \quad \varGamma _6 =\left[ \begin{array}{ccc} 0 &{} d_1G_1 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{array}\right] \\ \varGamma _7&=\left[ \begin{array}{ccc} \varXi _{33}^2 &{} 0 &{} 0 \\ \star &{} \varXi _{44}^2 &{} \varXi _{45}^2 \\ \star &{} \star &{} \varXi _{55}^2 \end{array}\right] \quad \varGamma _8 =\left[ \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{array}\right] \\ \varGamma _9&=\left[ \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} \varXi _{14}^3 &{} 0 \\ 0 &{} 0 &{} 0 \end{array}\right] \quad \varGamma _{10} =\left[ \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{array}\right] \\ \varGamma _{11}&=\left[ \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{array}\right] \quad \varGamma _{12} =\left[ \begin{array}{ccc} \varXi _{66}^2 &{} 0 &{} 0 \\ \star &{} \varPhi _4 &{} 0 \\ \star &{} \star &{} \varPhi _7 \end{array}\right] \\ \varGamma _{13}&=\left[ \begin{array}{ccc} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 \end{array}\right] \quad \varGamma _{14} =\left[ \begin{array}{ccc} 0 &{} 0 &{} 0\\ \varPhi _5 &{} 0 &{} 0\\ 0 &{} \varPhi _8 &{} 0 \end{array}\right] \end{aligned}$$

$$\begin{aligned} \varGamma _{15}&=\left[ \begin{array}{ccc} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} \varPhi _6\\ 0 &{} 0 &{} 0 \end{array}\right] \quad \varGamma _{16} =\left[ \begin{array}{ccc} \varPhi _9 &{} 0 &{} 0\\ \star &{} \varPhi _{11} &{} GA\\ \star &{} \star &{} -\varLambda _{1} \end{array}\right] \\ \varGamma _{17}&=\left[ \begin{array}{ccc} 0 &{} 0 &{} \varPhi _{10}\\ 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 \end{array}\right] \quad \varGamma _{18} =\left[ \begin{array}{ccc} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 \end{array}\right] \\ \varGamma _{19}&=\left[ \begin{array}{ccc} -\varLambda _{3} &{} 0 &{} 0\\ \star &{} -\varLambda _{2} &{} 0\\ \star &{} \star &{} -\varLambda _{4} \end{array}\right] \quad \varGamma _{20} =\left[ \begin{array}{ccc} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 \end{array}\right] \\ \varGamma _{21}&=\left[ \begin{array}{ccc} \varPhi _{12} &{} 0 &{} 0\\ \star &{} \varPhi _{13} &{} 0\\ \star &{} \star &{} \varPhi _{14} \end{array}\right] \end{aligned}$$

The Lyapunov functional (23) is discontinuous due to the presence of the Lyapunov functional $V_{10}(t)$. If $S_p=0$ in (23), the Lyapunov functional becomes continuous and the following can be obtained as a consequence of the above theorem.

Corollary 1

For given positive constants $\alpha _p, \lambda _p, h_p (p=1,2,\ldots ,m), \mu$, the system (17) is globally mean-square asymptotically stable, if there exist matrices, $P>0, Q>0, G>0, W>0, H>0, S>0, X>0, \tilde{T}>0, G_1>0, G_2>0, Z_p>0, U_p>0, X_p>0, Y_p>0, M_p>0 (p=1,2,\ldots ,m),$ symmetric matrices $T_p>0, W_p>0 (p=1,2,\ldots ,m),$ diagonal matrices $\varLambda _1>0, \varLambda _2>0, \varLambda _3>0, \varLambda _4>0,$ and any matrices $H, V_p (p=1,2,\ldots ,m)$ with appropriate dimensions satisfying the LMIs (18) such that (18) $|_{S_p=0} (\forall p=1,2,\ldots ,m)$ and (19)–(21). Moreover, the desired control gain matrix is given by $K_i=G^{-1}\tilde{H}.$

Proof

The proof of this corollary is similar to that of Theorem 1 without considering the discontinuous Lyapunov functional.

Fig. 1

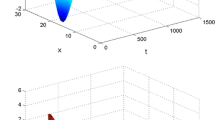
Chaotic behavior of the states $y_1(t,x)$ and $y_2(t,x)$ in system (60)

Remark 2

In this paper, the discontinuous Lyapunov functional approach, which makes full use of the sawtooth characteristic of the sampling input delay, has been handled, and for this purpose, the stochastic variables $\beta _p(t)$ and $\rho _{pr}(t)$ are introduced. This gives the significance of this present work. To the best of authors’ knowledge, this procedure for the synchronization of reaction–diffusion neural networks with time-varying delays has not yet been studied in the literature.

Remark 3

The effects of time delays and diffusion in the real world cannot be avoided in modeling neural networks, and thus, the neural networks with reaction–diffusion terms and time-varying delays have been considered rigorously, and numerous results have been proposed in the existing literature, see for example [17, 22, 25, 26, 43, 44]. In [43], the authors have discussed the synchronization scheme for a class of delayed neural networks with reaction–diffusion terms using inequality techniques and Lyapunov method.

In [44], the problem of asymptotic synchronization for a class of neural networks with reaction–diffusion terms and time-varying delays has been investigated. Very recently, in [26], the synchronization problem for coupled reaction–diffusion neural networks with time-varying delays has been proposed and a pinning-impulsive control strategy has been developed. However, the problem of synchronization for reaction–diffusion neural networks with time-varying delays through sampled-data controller with stochastic sampling has not yet been investigated in the literature. A discontinuous Lyapunov approach, that uses the sawtooth structure characteristic of the sampling input delay, has been employed, and the synchronization criterion depending on the lower and upper delay bounds has been derived in terms of LMIs using some inequality techniques. Numerical simulations were provided to illustrate the effectiveness of the proposed synchronization criteria.

Remark 4

We can easily see that the results and research method obtained in this paper can be easily extended to many other types of neural networks with reaction–diffusion effects and the Dirichlet boundary conditions, for example, chaotic continuous-time neural networks [45], recurrent neural networks [46] and fuzzy cellular neural networks [47].

4 Numerical examples

In this section, two numerical examples are provided to demonstrate the effectiveness of the proposed results. For convenience, let us choose the number of sampling periods to be two, i.e., $m=2$.

Example 1

Consider the following reaction–diffusion neural network with the time-varying delay

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\partial y(t,x)}{\partial t}\! =\! \frac{\partial }{\partial x}\left( \!D \frac{\partial y(t,x)}{\partial x}\!\right) \!-\!Cy(t,x)\!+\!A \!\tanh (y(t,x))\\ +B\tanh (y(t-d(t),x))+J, \\ y(t,0)= y(t,20)=0, \quad t\ge 0, \\ y(s,x)= \sin (0.2\pi x), \ ( s,x)\in [-1,0]\times [0,20], \end{array}\right. \end{aligned}$$

(60)

where $y(t,x) = (y_1(t,x),y_2(t,x))^T, \tanh (y(t,x))=(\tanh (y_1(t,x)), \tanh (y_2(t,x)))^T, D\!=\!\mathrm{diag}(0.1,0.1), J=0$ and with

$$\begin{aligned} C&=\left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} 0.95 \end{array}\right) , \quad A=\left( \begin{array}{cc} -2.8 &{} 0.9 \\ 2.7 &{} -4.3 \end{array}\right) , \\ B&=\left( \begin{array}{cc} -4.5 &{} -0.7 \\ -4.4 &{} -0.5 \end{array}\right) . \end{aligned}$$

Also the activation function satisfies Assumption 1 with $F_1^-=F_2^-=0$ and $F_1^+=F_2^+=0.5.$ Thus,

$$\begin{aligned} F_1=\left( \begin{array}{cc} 0 &{} 0 \\ 0 &{} 0 \end{array}\right) , \quad F_2=\left( \begin{array}{cc} 0.25 &{} 0 \\ 0 &{} 0.25 \end{array}\right) . \end{aligned}$$

The neural network (60) exhibits chaotic behavior as shown in Fig. 1. Under the stochastic sampled-data controller $U$, the system (60) can be rewritten as

$$\begin{aligned} \frac{\partial u_i(t,x)}{\partial t}&= \frac{\partial }{\partial x}\left( D \frac{\partial u_i(t,x)}{\partial x}\right) -Cu_i(t,x)\nonumber \\&\quad \!\!+\,A \tanh (u_i(t,x))\!+\!\!B\tanh (u_i(t\!\!-\!\!d(t),x))\nonumber \\&\quad \!\!+\,J+U_i, \end{aligned}$$

(61)

Then, the error system can be obtained as

$$\begin{aligned} \frac{\partial e_i(t,x)}{\partial t}&= \frac{\partial }{\partial x}\left( D \frac{\partial e_i(t,x)}{\partial x}\right) -Ce_i(t,x)\nonumber \\&\quad +\!\!A \tanh (e_i(t,x))\!+\!\!B\tanh (e_i(t\!-\!d(t),x))\nonumber \\&\quad +\,\sum _{p=1}^2\alpha _p(t)K_ie_i(t-\tau _p(t),x), \end{aligned}$$

(62)

Let $h_0=0, h_1=0.2, h_2=0.4, \beta _1=0.25$ and the time-varying delay $d(t)=e^t/(1+e^t).$ With these parameters, using the Matlab LMI toolbox, sufficient conditions in terms of LMIs in Theorem 1 are found to be feasible for the given values of $d_1=0.5, d_2=1$, and the control gain matrix is obtained as

$$\begin{aligned} K_i=\left[ \begin{array}{cc} -0.2129 &{} -0.3399 \\ -0.0159 &{} -1.0633 \end{array}\right] . \end{aligned}$$

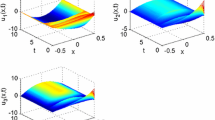
The simulation results are shown in Fig. 2, where $e_1(t,x)$ and $e_2(t,x)$ are very close to zero when time increases gradually to 0.5 under the stochastic sampled-data controller (14) and those states are maintained along with the increasing of t, which imply that system (62) is globally asymptotically stable under the stochastic sampled-data controller (14).

Fig. 2

Dynamical behavior of synchronization errors $e_{i1}(t,x)$ and $e_{i2}(t,x)$ between (61) and (60)

Example 2

Consider the same reaction–diffusion neural network (60) with the time-varying delay and with the parameters

$$\begin{aligned}&C=\left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} 1 \end{array}\right) , A=\left( \begin{array}{cc} 2.1 &{} -0.12 \\ -5.1 &{} 3.2 \end{array}\right) ,\\&\quad B=\left( \begin{array}{cc} -1.6 &{} -0.1 \\ -0.2 &{} -2.4 \end{array}\right) . \end{aligned}$$

and correspondingly the same error system (62). Obviously, Assumption 1 holds with $F_1^-=F_2^-=0$ and $F_1^+=F_2^+=0.5.$ Thus, we have

$$\begin{aligned} F_1=\left[ \begin{array}{cc} 0 &{} 0 \\ 0 &{} 0 \end{array}\right] , F_2=\left[ \begin{array}{cc} 0.25 &{} 0 \\ 0 &{} 0.25 \end{array}\right] . \end{aligned}$$

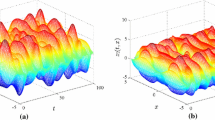
For the aforementioned parameters, system (60) behaves chaotically and it is shown in Fig. 3.

Fig. 3

Chaotic behavior of states $y_1(t,x)$ and $y_2(t,x)$ of system (60)

Let $h_0=0, h_1=0.2, h_2=0.4\,\text{ and }\,\beta _1=0.8.$ Using the Matlab LMI toolbox, sufficient conditions of Theorem 1 are verified and found to be feasible for the given values of $d_1=0.7, d_2=1.3.$ In this case, the controller gain is obtained as

$$\begin{aligned} K_i=\left[ \begin{array}{cc} -1.2005 &{} 0.9574 \\ -0.2745 &{} -1.7610 \end{array}\right] . \end{aligned}$$

Fig. 4

Dynamical behavior of synchronization errors $e_{i1}(t,x)$ and $e_{i2}(t,x)$ between (61) and (60)

Thus, we conclude that the error system (62) is asymptotically stable in the sense of mean square for the aforementioned parameters. The simulation results that show the chaotic behavior of system (60) is given in Figs. 3 and 4 describes that the error system with aforementioned gain of stochastic sampled-data controller (14) is asymptotically stable as time increases gradually.

The numerical simulations clearly verify the effectiveness of the developed stochastic sampled-data controller with $m$ sampling intervals to the asymptotical synchronization of neural networks with time-varying delays and reaction–diffusion effects.

5 Conclusions

In contrast to the studies on design of controllers for synchronization of reaction–diffusion neural networks with time-varying delays, in this paper, we have used the sampled-data controller with stochastic sampling for the synchronization process. The sampling periods are assumed to be $m$ in number, whose occurrence probabilities are given constants and satisfy Bernoulli distribution. The discontinuous Lyapunov functional with triple integral terms that capture the information on the upper and lower bounds of time-varying delays has been constructed based on the extended Wirtinger’s inequality to fully use the sawtooth characteristic of the sampling delay. Sufficient conditions have been derived in terms of LMIs and have been proved to be less conservative due to the use of the discontinuous type Lyapunov functional. The obtained LMIs were easily verified for their feasibility using the Matlab LMI toolbox and the corresponding results are presented with two numerical examples.