1 Introduction

Recently, neural networks with discontinuous (or non-Lipschitz, or non-smooth) neuron activations have been found useful to address a number of interesting engineering tasks, such as dry friction, impacting machines, systems oscillating under the effect of an earthquake, power circuits, switching in electronic circuits, linear complimentarily systems, and therefore have received a great deal of attention in the literature [1–7]. It is well known that, in the paper [1], under the framework of the theory of Filippov differential inclusions, Forti and Nistri were the first who dealt with the global stability of a neural network modeled by a differential equation with a discontinuous right-hand side. As Forti and Nistri pointed out, neural networks with discontinuous neuron activations are important and do frequently arise in the applications. For example, consider the classical Hopfield neural networks with graded response neurons [7, 8]. Under the standard hypothesis of high-gain amplifiers, the sigmoidal neuron activations would closely approach a discontinuous hard comparator function. Moreover, the analysis of discontinuous neural networks can reveal many specially interesting and important traits of the dynamics such as the phenomenon of convergence in finite time toward the equilibrium point or limit cycle. Thus, it is of practical importance to explore the dynamical behaviors of discontinuous neural networks.

Note that the properties of periodic solutions are of great interest, which have been successfully applied in many neural networks, such as many biological and cognitive activities (for example heartbeat, respiration, mastication, and locomotion, and memorization) require repetition. Moreover, an equilibrium point can be regarded as a special case of periodic solution for neural networks with arbitrary period. Therefore, the analysis of periodic solutions for neural networks is more general and interesting. In [9], the authors studied the global exponential stability of the periodic solution for a delayed neural network with discontinuous neuron activations. In [10–18], by using the theory of fixed point in differential inclusion and Lyapunov approach, the authors analyzed the problems of periodic solutions for various neural networks with discontinuous neuron activations.

However, the discontinuous neuron activations considered in these papers are bounded or satisfy the growth condition. As pointed out by Gonzalez [19], to truly exploit the potential of neural networks, a nonlinear activation function must be used. Virtually, all neural networks use nonlinear activation functions at some point within the network. This permits the network to reproduce nonlinear patterns in complex data sets. There are several types of nonlinear activation functions, such as the log-sigmoid transfer function and the tan-sigmoid transfer function. When dealing with a dependent variable that is not bounded, we could choose an unbounded nonlinear activation function such as \(f(x)=x^3\). Thus, it is interesting and practical to investigate neural networks with discontinuous neuron activations which are unbounded or satisfy nonlinear growth condition.

As pointed out by [20], the coexistence of multiple equilibria is necessary in the applications of neural networks for associative memory storage, pattern recognition, decision making, digital selection, and analogy application. In [21–30], some methods guaranteeing the existence of many equilibria or multiple periodic solutions of neural networks have been derived. However, all of the above works were based on the assumption that the activation functions are continuous, even piecewise linear functions. To the existence of many equilibria or multiple periodic solutions of neural networks with general activation functions, even discontinuous activations, the methods used in [21–30] will be invalid. Therefore, it is very difficult to obtain the existence of many equilibria or multiple periodic solutions of neural networks with discontinuous activations. And a few results have been obtained on the existence of many equilibria or multiple periodic solutions of neural networks with discontinuous activations. Motivated by the above discussion, one of the main contributions of this paper is to investigate the existence of one and multiple periodic solutions of neural networks with discontinuous neuron activations.

Because of finite switching speed of amplifiers and communication time, in many practical applications of neural networks like communication systems, electric power systems with lossless transmission lines, control, image processing, pattern recognition, signal processing and associative memory, time delays are often inevitable. Moreover, as Forti et al. pointed out, it is interesting and important to investigate discontinuous neural networks with more general delays, such as time-varying or distributed ones. In fact, in electronic implementation of analog neural networks, the delays between neurons are usually time-varying and sometimes vary violently with time due to the finite switching speed of amplifiers and faults in the electrical circuit [31, 32]. On the other hand, although the models with discrete delays is a good approximation in simple circuits consisting of only a small number of cells, neural networks usually have a spatial extent due to the presence of a multitude of parallel pathways with a variety of axon sizes and lengths. Thus it is common to have a distribution of propagation delays. In these circumstances, the signal propagation is not instantaneous, and it cannot be modeled by discrete delays. A more appropriate approach is to incorporate continuously distributed delays [33, 34]. It is worthy to pointed out that, time delays can affect the stability of the neural network systems and may lead to some complex dynamic behaviors such as oscillation, chaos, and instability. Thus, it is of great importance to explore the dynamical behaviors of neural networks with mixed delays. Hence, we consider the more general type of delays, such as time-varying and distributed ones, which are general more complex, and therefore, they are more difficult to deal with.

On the other hand, Cohen–Grossberg neural network (CGNN) model is an important recurrent neural network model, which was first described by Cohen and Grossberg in 1983 [35]. It is easy to see that CGNN include a range of well-known ecological models and neural networks such as the Lotka–Volterra system, the bidirectional associative memory (BAM) neural networks [36, 37], and the Hopfield neural networks [7, 8]. In recent years, CGNNs with or without delays have been extensively studied due to the potential for applications in classification, parallel computing, associative memory, especially in solving some optimization problems. Such applications depend on the existence and uniqueness of equilibrium points and the qualitative properties of stability, so the qualitative analysis of these dynamical behaviors is important in the practical design and applications of neural networks. Many researchers have investigated the delayed or without delayed Cohen–Grossberg neural networks [25, 38].

There are also some works on CGNN discontinuous neuron activations with time delays [39–45]. In [39, 40], the authors studied the stability of delayed CGNN with discontinuous neuron activation. Some sufficient conditions were obtained to ensure the existence, uniqueness, and global stability of the equilibrium point of the neural network, respectively. In [41], the authors investigated the nonnegative periodic dynamics of delayed Cohen–Grossberg neural networks with discontinuous activations. In [42], based on the Mawhin-like coincidence theorem, the authors studied the periodic dynamics of delayed Cohen–Grossberg neural networks with discontinuous activations. In [43], the authors investigated the existence, uniqueness, and global stability of periodic solution in view of fixed-point theorem of set-valued maps and non-smooth analysis theory. However, there are no results on multiple periodic solutions for delayed CGNN with discontinuous neuron activations.

Motivated by the above works, in this paper, we consider the following general CGNN model with discontinuous activations:

(1.1)

or equivalently in the vector form

$$\begin{aligned} \dfrac{\hbox {d}x(t)}{\hbox {d}t}&=Q(x(t))[-D(t)x(t)+A(t)f(x(t)) \nonumber \\&+B(t)f(x(t-\tau (t))) \nonumber \\&+C(t)\int _0^{+\infty }f(x(t-s))l(s)\hbox {d}s+I(t)], \end{aligned}$$
(1.2)

where \(x(t)=(x_1(t),x_2(t),\ldots ,x_n(t))^T\in \mathbb {R}^n\) and \(x_i(t)\) represents the state of the ith unit at time t; \(Q(x(t))=\hbox {diag}(q_1(x_1(t)),q_2(x_2(t)),\ldots ,q_n(x_n(t)))\) and \(q_i(x_i(t))\) denotes amplification function of the ith neuron; \(D(t)=\hbox {diag}(d_1(t),d_2(t),\ldots ,d_n(t))\) and \(d_i(t)>0\) is the self-inhibition of the ith neuron; \(A(t)=(a_{ij}(t))_{n\times n}\) and \(a_{ij}(t)\) is the connection strength of the jth neuron on the ith neuron; \(B(t)=(b_{ij}(t))_{n\times n}\), \(C(t)=(C_{ij}(t))_{n\times n}\), \(b_{ij}(t)\) and \(c_{ij}(t)\) are the delayed feedbacks of the jth neuron on the ith neuron, with time-varying and distributed delay, respectively; \(\tau (t)\) is the time-varying delay; \(l(s)=(l_1(s),l_2(s),\ldots ,l_n(s))^T\) and \(l_i(t)\) is the probability kernel of the distributed delay; \(f(x(t))=(f_1(x_1(t)),f_2(x_2(t)),\ldots ,f_n(x_n(t)))^T{:}\mathbb {R}^n{\rightarrow } \mathbb {R}^n\) and \(f_i(x_i(t))\) denotes the neuron input-output activation of the ith neuron; \(I(t)=(I_1(t),I_2(t),\ldots ,I_n(t))^T\in \mathbb {R}^n\) and \(I_i(t)\) denotes the external input to the ith neuron.

The neuron activation functions in (1.1) are assumed to satisfy the following properties:

(H1) For every \(i=1,2,\ldots ,n\), \(f_i\) is continuous except on a countable set of isolate points \(\rho _k^i\), where there exist finite right limits \(\lim _{x_i\rightarrow {(\rho _k^i)}^+}f_i(x_i)\triangleq f_i^+(\rho _k^i)\) and left limits \(\lim _{x_i\rightarrow {(\rho _k^i)}^-}f_i(x_i)\triangleq f_i^-(\rho _k^i)\), respectively. Moreover, \(f_i\) has a finite number of discontinuous points on any compact interval of \(\mathbb {R}\).

(H2) For each \(i=1,2,\ldots ,n\), there exist nonnegative continuous functions \(W_i\) such that

$$\begin{aligned} \sup _{\gamma _i\in \overline{co}[f_i(x_i)]}|\gamma _i|&\leqslant W_i(x_i),\ \ \forall x_i\in \mathbb {R}, \end{aligned}$$

where \(\overline{co}[f_i(x_i)]=[\min \{f_i^-(x_i),f_i^+(x_i)\},\max \{f_i^-(x_i),f_i^+(x_i)\}]\).

Throughout this paper, we always assume that \(d_i(t), a_{ij}(t), b_{ij}(t), \tau (t), I_i(t)\) are continuous \(\omega \)-periodic functions, where \(i,j=1,2,\ldots ,n\); \(\tau (t)\geqslant 0\), \(d_i(t)>0\) for each \(i=1,2,\ldots ,n\) and \(t>0\). \(q_i(x)\) are all positive, continuous and bounded functions, there exist positive constants \(q_i^l, q_i^M\) such that \(0<q_i^l\leqslant q_i(x)\leqslant q_i^M\), for \(\forall x\in \mathbb {R}\) and \(i,j=1,2,\ldots ,n\). The delay kernels \(l_{j}:[0,+\infty )\rightarrow \mathbb {R}\) are continuous, integrable, and there exist constants \(L_{j}\) such that \(\int _0^{+\infty }|l_{j}(s)|ds\leqslant L_{j}\), \(j=1,2,\ldots ,n\).

For convenience, we shall introduce the notations

$$\begin{aligned} g^l=\min _{s\in [0,\omega ]}g(s),\qquad g^M=\max _{s\in [0,\omega ]}g(s), \end{aligned}$$

where g(t) is an \(\omega \)-periodic function.

The main contributions of this paper include three aspects. First, for the delayed differential equations with discontinuous right-hand sides, we obtain the existence of global solution. Second, by using the fixed-point theorem of multi-valued maps, we study the periodicity and multiperiodicity of the neural networks with discontinuous neuron activations. Third, in terms of non-smooth analysis theory and Lyapunov-like approach, we discuss the global exponential stability of the neural networks with discontinuous neuron activations.

2 Preliminaries

Note that CGNN model (1.1) is defined as a piecewise continuous vector function, and the classical definition of solutions has been shown to be invalid. To deal with the differential equation with discontinuous right-hand side, a solution in the sense of Filippov [46, 47] is particularly useful because Filippov solutions are good approximation of solutions of actual systems that possess nonlinearities with very high slop. To specify what is meant by a solution of the delayed differential equation (1.1) with a discontinuous right-hand side, we extend the concept of the Filippov solutions with the delayed differential equation (1.1) as follows:

Definition 2.1

A vector function \(x\!=\!(x_1,x_2,\ldots ,x_n)^T:({-}\infty ,\mathcal {T}){\rightarrow } \mathbb {R}^n, \mathcal {T}\in (0,{+}\infty ]\), is a state solution of the discontinuous system (1.1) on \((-\infty ,\mathcal {T})\) if

  1. (1)

    x is continuous on \((-\infty ,\mathcal {T})\) and absolutely continuous on any compact interval of \([0,\mathcal {T})\);

  2. (2)

    there exists a measurable function \(\gamma =(\gamma _1,\gamma _2,\ldots ,\gamma _n)^T:(-\infty ,\mathcal {T})\rightarrow \mathbb {R}^n\) such that \(\gamma _j(t)\in \overline{co}[f_j(x_j(t))]\) for a.e. \(t\in (-\infty ,\mathcal {T})\) and

    $$\begin{aligned} \dfrac{\hbox {d}x_i(t)}{\hbox {d}t}&= q_i(x_i(t))\mathcal {F}_i(t,\gamma ),\ \ \hbox {for a.e.}\ t\in [0,\mathcal {T}), \nonumber \\ i&=1,2,\ldots ,n \end{aligned}$$
    (2.1)

    where

    $$\begin{aligned} \mathcal {F}_i(t,\gamma )= & {} -d_i(t)x_i(t)+\sum _{j=1}^na_{ij}(t)\gamma _j(t) \\&+\sum _{j=1}^nb_{ij}(t)\gamma _j(t-\tau (t)) +\sum _{j=1}^nc_{ij}(t) \\&\times \int _0^{+\infty }\gamma _j(t-s)l_{j}(s)\hbox {d}s+I_i(t). \end{aligned}$$

    Any function \(\gamma =(\gamma _1,\gamma _2,\ldots ,\gamma _n)^T\) satisfying (2.1) is called an output solution associated with the state \(x=(x_1,x_2,\ldots ,x_n)^T\). With this definition, it turns out that the state \(x=(x_1,x_2,\ldots ,x_n)^T\) is a solution of (1.1) in the sense of Filippov since it satisfies

    $$\begin{aligned}&\dfrac{\hbox {d}x_i(t)}{\hbox {d}t}\in q_i(x_i(t))\mathcal {F}_i(t,f),\ \ \hbox {for a.e.}\ t\in [0,\mathcal {T}), \nonumber \\&\quad i=1,2,\ldots ,n \end{aligned}$$
    (2.2)

    where

    $$\begin{aligned}&\mathcal {F}_i(t,f)=-d_i(t)x_i(t)+\sum _{j=1}^na_{ij}(t)\overline{co}[f_j(x_j(t))] \\&\quad +\sum _{j=1}^nb_{ij}(t)\overline{co}[f_j(x_j(t-\tau (t)))]+\sum _{j=1}^nc_{ij}(t) \\&\quad \times \int _0^{+\infty }\overline{co}[f_j(x_j(t-s))]l_{j}(s)\hbox {d}s+I_i(t). \end{aligned}$$

For an initial value problem (IVP) associated with the CGNN neural network (1.1), we follow the definition introduced by Forti et al. in [1, 9].

Definition 2.2

(IVP). For any continuous function \(\phi \,{=}\,(\phi _1,\phi _2,\ldots ,\phi _n)^T\,{:}\,(-\infty ,0]\rightarrow \mathbb {R}^n\) and any measurable selection \(\psi \,{=}\,(\psi _1,\psi _2,\ldots ,\psi _n)^T\,{:}\,(-\infty ,0]\!\rightarrow \!\mathbb {R}^n\), such that \(\psi _j(s)\in \overline{co}[f_j(\phi _j(s))] (j=1,2,\ldots ,n)\) for a.e. \(s\in (-\infty ,0]\) by an initial value problem associated with (1.1) with initial condition \([\phi ,\psi ]\), we mean the following problem: find a couple of functions \([x,\gamma ]\,{:}\,(-\infty ,\mathcal {T})\rightarrow \mathbb {R}^n\times \mathbb {R}^n\), such that x is a solution of (1.1) on \((-\infty ,\mathcal {T})\) for some \(\mathcal {T}>0\), \(\gamma \) is an output solution associated with x, and

$$\begin{aligned} \left\{ {{\begin{array}{ll} \frac{\hbox {d}x_i(t)}{\hbox {d}t}\\ = q_i(x_i(t))\mathcal {F}_i(t,\gamma ), &{} \hbox {for} \quad \hbox {a.e. }\, t\in [0,\mathcal {T}), \\ \quad i=1,2,\ldots ,n, \\ \gamma _j(t)\in \overline{co}[f_j(x_j(t))], &{} \hbox {for} \quad \hbox {a.e.}\ t\in [0,\mathcal {T}), \\ x(s)=\phi (s), &{} \forall s\in (-\infty ,0], \\ \gamma (s)=\psi (s), &{} \hbox {for} \quad \hbox {a.e.}\ s\in (-\infty ,0]. \end{array}}} \right. \end{aligned}$$
(2.3)

Throughout this paper, the initial functions \(\phi \) and \(\psi \) (as described in Definition 2.2) satisfy the following: \(\phi \) is a bounded continuous function from \((-\infty ,0]\) to \(\mathbb {R}^{n}\) and \(\psi \) is an essentially bounded measurable function from \((-\infty ,0]\) to \(\mathbb {R}^{n}\).

The following proposition shows that the solutions in the sense of Filippov of system (1.1) exist globally.

Proposition 2.1

(See Appendix A for a Proof). Suppose that the conditions (H1), (H2) and (H3) there exists a nonnegative and monotonically nondecreasing function W(x), such that

$$\begin{aligned}&\max _{1\leqslant i\leqslant n}W_i(x)\leqslant W(x)\ \ \hbox {and}\\&\quad \int _0^{+\infty }\dfrac{1}{1+r+W(r)}\mathrm {d}r=+\infty ; \end{aligned}$$

be satisfied. Then each solution x(t) of the system (1.1) in the sense of Filippov exists on the interval \([0,+\infty )\), i.e., the solution x(t) of the functional differential inclusions (2.2) with the initial condition \([\phi ,\psi ]\) exists on the interval \([0,+\infty )\).

Remark 1

If W(x) is bounded or satisfies \(W(x)=\,a|x|^{\alpha }+b (\alpha \in (0,1], a,b\,{\geqslant }\,0)\), then the condition (H3) holds. That is to say, Proposition 2.1 generalizes and improves the corresponding results of some earlier literature, such as Theorem 1 of [4], Property 2 of [6], Lemma 2 of [17], Theorem 3.1 of [18], and Lemma 2 of [41]. Moreover, for a class of more general functional differential inclusions, such as \(x^\prime (t)\in F(t,x(t),x(t-\tau ))\), \(x^\prime (t)\in F(t,x(t),x(t-\tau (t)),x(t-\sigma (t)))\), the global existence of solutions can be similarly dealt with.

Next, let us introduce some basic concepts and facts from multi-valued analysis which will be used throughout this paper [48–56].

Let \(([0,\omega ],\mathfrak {L})\) denote the Lebesgue measurable space and \(\mathbb {R}^n(n\geqslant 1)\) be an n-dimensional real Euclidean space with inner product \(\langle \cdot ,\cdot \rangle \) and induced norm \(||\cdot ||\). Suppose \(E\subset \mathbb {R}^n\), then \(x\mapsto F(x)\) is called a multi-valued map from \(E\hookrightarrow \mathbb {R}^n\), if for each point x of a set \(E\subset \mathbb {R}^n\), there corresponds a non-empty set \(F(x)\subset \mathbb {R}^n\). F is said to have a fixed point if there is \(x\in E\) such that \(x\in F(x)\). For the sake of convenience, we introduce the following notations:

$$\begin{aligned}&P_{cl(cb)}(\mathbb {R}^n)\\&\quad =\{A\subset \mathbb {R}^n:\hbox {non-empty and closed (bounded)}\}, \\&P_{cp(cv)}(\mathbb {R}^n)\\ {}&\quad =\{A\subset \mathbb {R}^n:\hbox {non-empty and compact (convex) }\}. \end{aligned}$$

Let \(A\subset P_{cl}(\mathbb {R}^n)\), then the distance from x to A is given by dist\((x,A)=\inf \{||x-a||:a\in A\}\). On \(P_{cl}(\mathbb {R}^n)\) we can define a generalized metric known in the literatures as “Hausdorff metric,” by setting

$$\begin{aligned} \rho (A,B)=\max \{\beta (A,B),\beta (B,A)\}, A,B\subset P_{cl}(\mathbb {R}^n), \end{aligned}$$

where

$$\begin{aligned} \beta (A,B)= & {} \sup \{\hbox {dist}(x,B):x\in A\},\\ \beta (B,A)= & {} \sup \{\hbox {dist}(y,A):y\in B\}. \end{aligned}$$

It is well known that \(P_{cl}(\mathbb {R}^n)\) is a complete metric space with the Hausdorff metric \(\rho \) and \(P_{cl,cv}(\mathbb {R}^n)\) is a closed subset of it.

Definition 2.3

A multi-valued map F with non-empty values is said to be upper semi-continuous (USC) at \(x_0\in E\), if \(\beta (F(x),F(x_0))\rightarrow 0\) as \(x\rightarrow x_0\). F(x) is said to have a closed (convex, compact) image if for each \(x\in E\), F(x) is closed (convex, compact). A multi-valued map \(F:[0,\omega ]\rightarrow P_{cl}(\mathbb {R}^n)\) is said to be measurable, if for each \(x\in \mathbb {R}^n\), the \(\mathbb {R}_+\) valued function \(t\mapsto \hbox {dist}(x,F(t))=\inf \{||x-v||:v\in F(t)\}\) is measurable. This definition of measurability is equivalent to saying that

$$\begin{aligned}&\hbox {Graph}(F)=\{(t,v)\in [0,\omega ]\times \mathbb {R}^n,v\in F(t)\}\\&\quad \in \mathfrak {L}\times \mathfrak {B}(\mathbb {R}^n) \end{aligned}$$

(graph measurability), where \(\mathfrak {L}([0,\omega ])\) is the Lebesgue \(\sigma \)-field of \([0,\omega ]\), \(\mathfrak {B}(\mathbb {R}^n)\) is the Borel \(\sigma \)-field of \(\mathbb {R}^n\).

For notational purposes, for \(\varrho >0\) let

$$\begin{aligned} \Omega _{\varrho }= & {} \{x\in X:||x||_{X}<\varrho \},\\ \partial \Omega _{\varrho }= & {} \{x\in X:||x||_{X}=\varrho \},\\ \overline{\Omega }_{\varrho }= & {} \{x\in X:||x||_{X}\leqslant \varrho \}. \end{aligned}$$

As a matter of convenience, we recall the fixed-point theorem of multi-valued maps due to Agarwal and O’Regan. (see [50] Theorems 2.3 and 2.7).

Lemma 2.1

Let \(X=(X,||\cdot ||_{X})\) be a Banach space and \(E\subseteq X\) a closed, convex, non-empty set with \(\alpha u+\beta v\in E\) for all \(\alpha \geqslant 0, \beta \geqslant 0\) and \(u,v\in E\). And let r, R be positive constants with \(0<r<R\). Suppose \(F:\overline{\Omega }_R\rightarrow P_{cp,cv}(E)\) (here \(P_{cp,cv}(E)\) denotes the family of non-empty, compact, convex subset of E) is a USC, k-set-contractive (here \(0\leqslant k<1\)) map and assume the following conditions hold:

  1. (1)

    \(x\not \in \lambda F(x)\ \ \ \hbox {for}\ \ \lambda \in [0,1)\ \ \hbox {and}\ \ x\in \partial \Omega _{R}\),

  2. (2)

    \(\hbox {there exist a}\ v\,{\in }\, E\backslash \{\theta \}\ \hbox {with}\ x\,{\not \in }\, F(x)+\delta v\ \ \delta \,{>}\,0 \hbox {and}\ \ x\in \partial \Omega _{r}\).

Then F has a fixed point in \(\{x:x\in E\) and \(r\leqslant ||x||_X\leqslant R\}\).

Lemma 2.2

Let \(X=(X,||\cdot ||_{X})\) be a Banach space and \(E\subseteq X\) a closed, convex, non-empty set with \(\alpha u+\beta v\in E\) for all \(\alpha \geqslant 0, \beta \geqslant 0\) and \(u,v\in E\). And let r, R be positive constants with \(0<r<R\). Suppose \(F:\overline{\Omega }_R\rightarrow P_{cp,cv}(E)\) (here \(P_{cp,cv}(E)\) denotes the family of non-empty, compact, convex subset of E) is a USC, k-set-contractive (here \(0\leqslant k<1\)) map and assume the following conditions hold:

  1. (1)

    \(x\not \in \lambda F(x)\ \ \ \hbox {for}\ \ \lambda \in [0,1)\ \ \hbox {and}\ \ x\in \partial \Omega _{r}\),

  2. (2)

    \(\hbox {there exist a}\ v\in E\backslash \{\theta \}\ \hbox {with}\ x\not \in F(x)+\delta v\ \ \delta >0\ \ \hbox {and}\ \ x\in \partial \Omega _{R}\).

Then F has a fixed point in \(\{x:x\in E\) and \(r\leqslant ||x||_X\leqslant R\}\).

Definition 2.4

[52]. A multi-valued map \(F:[0,\omega ]\times E\rightarrow P(E)\) is called \(L^1\)-Carathéodory if

  1. (1)

    \(t\rightarrow F(t,u)\) is measurable with respect to t for every \(u\in E\);

  2. (2)

    \(t\rightarrow F(t,u)\) is USC with respect to u for a.e. \(t\in [0,\omega ]\);

  3. (3)

    for each \(q>0\), there exists \(h_q\in L^1([0,\omega ], [0,\infty ))\) such that \(|||F(t,u)|||\triangleq \sup \{|v|:v\in F(t,u)\}\leqslant h_q(t)\) for all \(||u||\leqslant q\) and for a.e. \(t\in [0,\omega ]\).

The following lemma will be used in the proof.

Lemma 2.3

[53]. Let J be a compact real interval, \(F:J\times E\rightarrow P_{cb,cl,cv}(E)\), \((t,x)\rightarrow F(t,x)\ (\)here \(P_{cb,cl,cv}(E)\) denote the set of all bounded, closed, convex and non-empty subsets of E) a \(L^1\)-Carathéodory multi-valued map, \(S_{F,x}\ (\)here \(S_{F,x}=\{f_x\in L^1(J,E):f_x(t)\in F(t,x)\) for a.e. \(t\in J\})\) be non-empty for each fixed \(x\in E\) and let \(\Gamma \) be a linear continuous mapping from \(L^1(J,E)\) to C(J, E). Then the map \(\Gamma \circ S_{F}:C(J,E)\rightarrow P_{cb,cl,cv}(C(J,E))\), \(y\rightarrow (\Gamma \circ S_{F})(y)=\Gamma (S_{F,y})\) is a closed graph map in \(C(J,E)\times C(J,E)\).

Definition 2.5

A solution x(t) of the given IVP of system (1.1) on \([0,+\infty )\) is a periodic solution with period \(\omega \) if \(x(t+\omega )=x(t)\) for all \(t\geqslant 0\).

Definition 2.6

Let \(x^{*}(t)=(x_1^{*}(t),x_2^{*}(t),\ldots ,x_n^{*}(t))^T\) be a solution of the given IVP of system (1.1), \(x^{*}(t)\) is said to be globally exponentially stable, if for any solution \(x(t)=(x_1(t),x_2(t),\ldots ,x_n(t))^T\) of (1.1), there exist constants \(M>0\) and \(\delta >0\) such that

$$\begin{aligned} ||x(t)-x^{*}(t)||\leqslant M\hbox {e}^{-\delta t},\ \ \ \hbox {for}\ \ t\geqslant t_0\geqslant 0. \end{aligned}$$

Suppose that \(x(t):[0,+\infty )\rightarrow \mathbb {R}^n\) is absolutely continuous on any compact interval of \([0,+\infty )\). We give a chain rule for computing the time derivative of the composed function \(V(x(t)):[0,+\infty )\rightarrow \mathbb {R}\) as follows.

Lemma 2.4

(Chain Rule) [47, 56]. Suppose that \(V(x):\mathbb {R}^n\rightarrow \mathbb {R}\) is C-regular and that \(x(t):[0,+\infty )\rightarrow \mathbb {R}^n\) is absolutely continuous on any compact interval of \([0,+\infty )\). Then, x(t) and \(V(x(t)):[0,+\infty )\rightarrow \mathbb {R}\) are differential for a.e. \(t\in [0,+\infty )\), and we have

$$\begin{aligned} \dfrac{\mathrm{d}V(x(t))}{\mathrm{d}t}=\langle \xi (t),\dfrac{\mathrm{d}x(t)}{\mathrm{d}t}\rangle ,\ \ \forall \xi (t)\in \partial V(x(t)), \end{aligned}$$

where \(\partial V(x(t))\) is the Clark generalized gradient of V at x(t).

3 Periodicity and multiperiodicity

In this section, under some conditions, we investigate the periodicity and multiperiodicity of IVP for the system (1.1) with discontinuous neuron activations. Our approaches are based on the application of fixed-point theorem of multi-valued maps due to Agarwal and O’Regan [50] and the functional differential inclusions theory.

Lemma 3.1

(See Appendix B for a Proof) Vector function \(x(t)=(x_1(t),x_2(t),\ldots ,x_n(t))^T\) is a \(\omega \)-periodic solution of the system (1.1) in the sense of Filippov if and only if \(x(t)=(x_1(t),x_2(t),\ldots ,x_n(t))^T\) is a \(\omega \)-periodic solution the following integral inclusions

$$\begin{aligned}&x_i(t)\in \int _t^{t+\omega }G_i(t,v)q_i(x_i(v))\mathfrak {F}_i(v,f)\mathrm{d}v, \nonumber \\&\quad \hbox {for}\quad \ t\in [0,\omega ], \ i=1,2,\ldots ,n, \end{aligned}$$
(3.1)

where

$$\begin{aligned}&\mathfrak {F}_i(v,f)=\sum _{j=1}^na_{ij}(v)\overline{co}[f_j(x_j(v))] \\&\quad +\sum _{j=1}^nb_{ij}(v)\overline{co}[f_j(x_j(v-\tau (v)))] \\&\quad +\sum _{j=1}^nc_{ij}(v)\int _0^{+\infty }\overline{co}[f_j(x_j(v{-}s))]l_{j}(s)\mathrm{d}s{+}I_i(v), \\&G_i(t,v)=\dfrac{\mathrm{e}^{\int _t^vq_i(x_i(s))d_i(s)\mathrm{d}s}}{\mathrm{e}^{\int _t^{t+\omega }q_i(x_i(s))d_i(s)\mathrm{d}s}-1}, \quad i=1,2,\ldots ,n. \end{aligned}$$

Let us define

$$\begin{aligned}&X=\{x(t)=(x_1(t),x_2(t),\ldots ,x_n(t))^T \\&\qquad \quad \in C(\mathbb {R},\mathbb {R}^n):x(t+\omega )=x(t)\}, \\&||x||_{X}=\max _{1\leqslant i\leqslant n}|x_i|_{\infty },\ \ |x_i|_{\infty }=\max _{t\in [0,\omega ]}|x_i(t)|, \\&\quad i=1,2,\ldots ,n. \end{aligned}$$

Then X is a Banach space with the above norm \(||\cdot ||_X\). Define a cone \(\mathbb {P}\) in X by

$$\begin{aligned} \mathbb {P}&=\{x(t)=(x_1(t),x_2(t),\ldots ,x_n(t))^T\in X:x_i(t) \\&\geqslant \kappa _i|x_i|_{\infty },\ i=1,2,\ldots ,n\}, \end{aligned}$$

where \(\kappa _i=\dfrac{g_i}{G_i}\) and \(g_i=\dfrac{1}{e^{q_i^Md_i^M}-1}\), \(G_i=\dfrac{\hbox {e}^{q_i^Ld_i^L}}{\hbox {e}^{q_i^Ld_i^L}-1}\).

Define the multi-valued map \(\varphi :X\rightarrow P(X)\) by

$$\begin{aligned} \varphi (x)=(\varphi _1(x),\varphi _2(x),\ldots ,\varphi _n(x))^T, \end{aligned}$$

where

$$\begin{aligned}&\varphi _i(x)(t)=\int _t^{t+\omega }G_i(t,v)q_i(x_i(v))\mathfrak {F}_i(v,f)\hbox {d}v, \\&\quad i=1,2,\ldots ,n. \end{aligned}$$

It follows from Lemma 3.1 that, the existence problem of \(\omega \)-periodic solutions to the system (1.1) is equivalent to the existence problem of \(\omega \)-periodic solutions to the integral inclusions (3.1). Hence, if \(x^*(t)=(x_1^*(t),x_2^*(t),\ldots ,x_n^*(t))^T\in X\) is a fixed point of the multi-valued map \(\varphi (x)\), then \(x^*(t)\) is a positive \(\omega \)-periodic solution of the system (1.1). In the following discussion, we will solve the fixed-point problem by virtue of Lemmas 2.1 and 2.2. For the multi-valued map \(\varphi :X\rightarrow P(X)\), we have the following Lemmas.

Lemma 3.2

(See Appendix C for a Proof). If the conditions (H1), (H2) and (H4) for \(i=1,2,\ldots ,n\) and \(x(t)\in \overline{\Omega }_R\cap \mathbb {P}\), we have

$$\begin{aligned} \inf _{\gamma _j(t)\in \overline{co}[f_j(x_j(t))]}\{\mathfrak {F}_i(v,\gamma )\}>0 \end{aligned}$$

where

$$\begin{aligned}&\mathfrak {F}_i(t,\gamma )=\sum _{j=1}^na_{ij}(t)\gamma _j(t)+\sum _{j=1}^nb_{ij}(t)\gamma _j(t-\tau _{ij}(t)) \\&\quad +\sum _{j=1}^nc_{ij}(t)\int _0^{+\infty }\gamma _j(t-s)l_j(s)\mathrm{d}s+I_i(t), \end{aligned}$$

hold, then the multi-valued map \(\varphi :\overline{\Omega }_R\cap \mathbb {P}\rightarrow P_{cp,cv}(\mathbb {P})\), i.e., \(\varphi (x)\in P_{cp,cv}(\mathbb {P})\) for each fixed \(x(t)\in \overline{\Omega }_R\cap \mathbb {P}\).

Lemma 3.3

(See Appendix D for a Proof). Assume that the conditions (H1), (H2), and (H4) hold. Then the multi-valued map \(\varphi :\overline{\Omega }_R\cap \mathbb {P}\rightarrow P_{cp,cv}(\mathbb {P})\) is a k-set-contractive map with \(k=0\).

Lemma 3.4

(See Appendix E for a Proof). Assume that the conditions (H1), (H2), and (H4) hold. Then the multi-valued map \(\varphi :\overline{\Omega }_R\cap \mathbb {P}\rightarrow P_{cp,cv}(\mathbb {P})\) is an upper semi-continuous(USC) map.

Denote

$$\begin{aligned} \Phi _i(r)= & {} \max _{t\in [0,\omega ]}\sup _{x\in \partial \Omega _r\bigcap \mathbb {P}}\int _t^{t+\omega }G_i(t,v)q_i(x_i(v)) \\&\times \, \mathfrak {F}_i(v,\gamma )\mathrm{d}v, \\ \Psi _i(r)= & {} \min _{t\in [0,\omega ]}\inf _{x\in \partial \Omega _r\bigcap \mathbb {P}}\int _t^{t+\omega }G_i(t,v)q_i(x_i(v)) \\&\times \, \mathfrak {F}_i(v,\gamma )\mathrm{d}v, \end{aligned}$$

where \(\mathfrak {F}_i(v,\gamma )\) is defined as above and \(\gamma _j(v)\in \overline{co}[f_j(x_j(v))]\).

(H5) There exists two positive constants \(R_0, R_1\) with \(0<R_0<R_1\), such that

$$\begin{aligned} \Phi (R_1)= & {} \max _{1\leqslant i\leqslant n}\Phi _i(R_1)\leqslant R_1\ \ \hbox {and}\ \ \\ \Psi (R_0)= & {} \min _{1\leqslant i\leqslant n}\Psi _i(R_0)\geqslant R_0. \end{aligned}$$

(H5*) There exists two positive constants \(R_0, R_1\) with \(0<R_0<R_1\), such that

$$\begin{aligned} \Phi (R_0)= & {} \max _{1\leqslant i\leqslant n}\Phi _i(R_0)\leqslant R_0\ \ \hbox {and}\ \ \\ \Psi (R_1)= & {} \min _{1\leqslant i\leqslant n}\Psi _i(R_1)\geqslant R_1. \end{aligned}$$

(H6) There exists four positive constants \(R_0, R_1, R_2, R_3\) with \(0<R_0<R_1<R_2<R_3\), such that

$$\begin{aligned} \Phi (R_1)&=\max _{1\leqslant i\leqslant n}\Phi _i(R_1)\leqslant R_1, \ \\ \Psi (R_0)&= \min _{1\leqslant i\leqslant n}\Psi _i(R_0)\geqslant R_0, \\ \Phi (R_3)&=\max _{1\leqslant i\leqslant n}\Phi _i(R_3)\leqslant R_3, \ \\ \Psi (R_2)&= \min _{1\leqslant i\leqslant n}\Psi _i(R_2)\geqslant R_2. \end{aligned}$$

(H6*) There exists four positive constants \(R_0, R_1, R_2, R_3\) with \(0<R_0<R_1<R_2<R_3\), such that

$$\begin{aligned} \Phi (R_0)&=\max _{1\leqslant i\leqslant n}\Phi _i(R_0)\leqslant R_0, \ \\ \Psi (R_1)&=\min _{1\leqslant i\leqslant n}\Psi _i(R_1)\geqslant R_1, \\ \Phi (R_2)&=\max _{1\leqslant i\leqslant n}\Phi _i(R_2)\leqslant R_2, \ \\ \Psi (R_3)&=\min _{1\leqslant i\leqslant n}\Psi _i(R_3)\geqslant R_3. \end{aligned}$$

(H7) There exists 2m positive constants \(R_0, R_1, \ldots , R_{2m-1}\) with \(0<R_0<R_1<\cdots <R_{2m}\), such that

$$\begin{aligned}&\Phi (R_{2k+1})=\max _{1\leqslant i\leqslant n}\Phi _i(R_{2k+1})\leqslant R_{2k+1}\ \ \hbox {and}\\&\Psi (R_{2k}){=} \min _{1\leqslant i\leqslant n}\Psi _i(R_{2k})\geqslant R_{2k},k{=}0,1,\ldots ,m-1. \end{aligned}$$

(H7*) There exists 2m positive constants \(R_0, R_1, \ldots , R_{2m}\) with \(0<R_0<R_1<\cdots <R_{2m-1}\), such that

$$\begin{aligned}&\Phi (R_{2k+1})=\min _{1\leqslant i\leqslant n}\Phi _i(R_{2k+1})\geqslant R_{2k+1}\ \ \hbox {and}\ \ \Psi (R_{2k}) \\&= \max _{1\leqslant i\leqslant n}\Psi _i(R_{2k})\leqslant R_{2k},\ \ k=0,1,\ldots ,m-1. \end{aligned}$$

Theorem 3.1

Assume that the conditions (H1), (H2), (H4), and (H5) hold. Then the system (1.1) has at least one positive \(\omega \)-periodic solution.

Proof

To prove that the result of Theorem 3.1 is true, it is enough to show that \(\varphi \) has least one fixed point in \(\{x:x\in \mathbb {P}\) and \(R_0\leqslant ||x||_X\leqslant R_1\}\). In view of Lemmas 3.1–3.4, it remains to verify whether the conditions (1) and (2) of Lemma 2.1 hold. \(\square \)

First, for any \(x(t)=(x_1(t),x_2(t),\ldots ,x_n(t))^T\in \overline{\Omega }_R\cap \mathbb {P}\), \(\kappa _i|x_i|_{\infty }\leqslant x_i(t)\leqslant |x_i|_{\infty }\) and \(y(t)=(y_1(t),y_2(t),\ldots ,\) \(y_n(t))^T\in \varphi (x)\). There exists a measurable function \(\gamma =(\gamma _1,\gamma _2,\ldots ,\gamma _n)^T:[0,\mathcal {T})\rightarrow \mathbb {R}^n\) such that \(\gamma _i(t)\in \overline{co}[f_i(x_i(t))]\) with \( |\gamma _i(t)|\leqslant \max _{0\leqslant s\leqslant R}\{W_i(s)\}\ (i=1,2,\ldots ,n)\) for \(t\in [0, \mathcal {T})\) and

$$\begin{aligned} y_i(t)&=\int _t^{t+\omega }G_i(t,v)q_i(x_i(v))\mathfrak {F}_i(v,\gamma )\hbox {d}v>0, \\ i&=1,2,\ldots ,n. \end{aligned}$$

Then, we have

$$\begin{aligned} |y_i(t)|_{\infty }&=\max _{t\in [0,\omega ]}\left\{ |\int _t^{t+\omega }G_i(t,v)q_i(x_i(v))\mathfrak {F}_i(v,\gamma )\hbox {d}v|\right\} \\&=\max _{t\in [0,\omega ]}\left\{ \int _t^{t+\omega }G_i(t,v)q_i(x_i(v))\mathfrak {F}_i(v,\gamma )\hbox {d}v\right\} \\&\leqslant \Phi _i(R_1)\leqslant \Phi (R_1)\leqslant R_1. \end{aligned}$$

Hence, for any \(x=(x_1,x_2,\ldots ,x_n)^T\in \partial \Omega _{R_1}\cap \mathbb {P}\),

$$\begin{aligned} ||y||_X= & {} \max _{1\leqslant i\leqslant n}|y_i(t)|_{\infty }\leqslant \max _{1\leqslant i\leqslant n}\Phi _i(R_1)\\= & {} \Phi (R_1)\leqslant R_1. \end{aligned}$$

Thus, we claim that the condition (1) in Lemma 2.1 is true. Otherwise, there exists \(x^0\in \partial \Omega _{R_1}\cap \mathbb {P}\) and some constant \(\lambda _0\in [0,1)\) such that

$$\begin{aligned} x^0\in \lambda _0\varphi (x^0)\ \ \ \hbox {for}\ \ x^0\in \partial \Omega _{R_1}\cap \mathbb {P}. \end{aligned}$$

Then there exists \(y^0\in \varphi (x^0)\) with \(x^0=\lambda _0y^0\). Therefore,

$$\begin{aligned} R_1= & {} ||x^0||_X=||\lambda _0y^0||_X=|\lambda _0|\cdot ||y^0||_X<||y^0||_X \\&\leqslant ||y||_X\leqslant R_1, \end{aligned}$$

which is a contradiction. That is, the condition (1) in Lemma 2.1 is satisfied.

Next, we will prove that the condition (2) in Lemma 2.1 hold. Suppose \(\eta =(\eta _1,\eta _2,\ldots ,\eta _n)^T\in \mathbb {P}\backslash \{\theta \}\). We will show that for any \(x=(x_1,x_2,\ldots ,x_n)^T\in \partial \Omega _{R_0}\cap \mathbb {P}\) and any \(\mu >0\), such that \(x\not \in \varphi (x)+\mu \eta \). Otherwise, there exist some \(x^{00}=(x^{00}_1,x^{00}_2,\ldots ,x^{00}_n)^T\in \partial \Omega _{R_0}\cap \mathbb {P}\) and some \(\mu _{00}>0\), such that

$$\begin{aligned} x^{00}\in \varphi (x^{00})+\mu _{00}\eta . \end{aligned}$$

Then there exists \(y^{00}=(y_1^{00},y_2^{00},\ldots ,y_n^{00})^T\in \varphi (x^{00})\) with \(x^{00}=y^{00}+\mu _{00}\eta \). Let \(\eta _{i_0}\ne 0\) for some \(i_0\in \{1,2,\ldots ,n\}\). Thus

$$\begin{aligned} x_{i_0}^{00}=y_{i_0}^{00}+\mu _{00}\eta _{i_0}. \end{aligned}$$

Note that \(x^{00}=(x^{00}_1,x^{00}_2,\ldots ,x^{00}_n)^T\in \partial \Omega _{R_0}\cap \mathbb {P}\), then we have \(\kappa _{i_0}|x^{00}_{i_0}|_{\infty }\leqslant x^{00}_{i_0}(t)\leqslant |x_{i_0}^{00}|_{\infty }\). Since

$$\begin{aligned}&\varphi _{i_0}(x^{00})=\int _t^{t+\omega }G_{i_0}(t,v)a_{i_0}(x^{00}_{i_0}(v)) \\&\quad \,\times \,\left\{ \sum _{j=1}^na_{{i_0}j}(v)\overline{co}[f_j(x^{00}_j(v))] \right. \\&\quad \, +\sum _{j=1}^nb_{{i_0}j}(v)\overline{co}[f_j(x^{00}_j(v-\tau (v)))] \\&\quad \, +\sum _{j=1}^nc_{{i_0}j}(v)\int _0^{+\infty }\overline{co}[f_j(x^{00}_j(v-s))]l_{j}(s)\hbox {d}s \\&\quad \, \left. +\,I_{i_0}(v) \right\} \hbox {d}v, \end{aligned}$$

that is

$$\begin{aligned} y^{00}_{i_0}&=\int _t^{t+\omega }G_{i_0}(t,v)a_{i_0}(x^{00}_{i_0}(v)) \\&\quad \,\times \, \left\{ \sum _{j=1}^na_{{i_0}j}(v)\gamma _j^{00}(v)+\sum _{j=1}^nb_{{i_0}j}(v)\gamma _j^{00}(v-\tau (v)) \right. \\&\quad \, \left. +\sum _{j=1}^nc_{{i_0}j}(v)\int _0^{+\infty }\gamma _j^{00}(v-s)l_{j}(s)ds+I_{i_0}(v)\right\} \hbox {d}v \\&\geqslant \Psi _{i_0}(R_0)\geqslant \Psi (R_0)\geqslant R_0, \end{aligned}$$

where \(\gamma _j^{00}(t)\in \overline{co}[f_j(x^{00}_j(t))]\ (j=1,2,\ldots ,n)\).

Hence,

$$\begin{aligned} R_0\geqslant |x_{i_0}^{00}|_{\infty }=|y_{i_0}^{00}+\mu _{00}\eta _{i_0}|_{\infty }\geqslant R_0+\mu _{00}\eta _{i_0}>R_0, \end{aligned}$$

which is a contradiction. This proves the condition (2) in Lemma 2.1 is also satisfied.

By Lemma 2.1, the system (1.1) has at least one positive \(\omega \)-periodic solution.

Applying Lemma 2.2 and similar to the proof of Theorem 3.1, we also have the following Theorem 3.2.

Theorem 3.2

Assume that the conditions (H1), (H2), (H4) and (H5*) hold. Then the system (1.1) has at least one positive \(\omega \)-periodic solution.

Remark 2

Based on fixed-point theorem of multi-valued maps due to Agarwal and O’Regan[50], we apply a new method to investigate the existence of positive periodic solutions for the neural networks (1.1) with discontinuous neuron activations and mixed delays. Compared with the corresponding results in the earlier literature [1, 2, 7, 9–18, 39–44], Theorems 3.1 and 3.2 obtained in this section are essentially new. In addition, note that the control function \(W_i(x_i)\) (see assumption (H2)) may be unbounded, may be super linear, even to be exponential. Thus, the discontinuous neuron activations \(f_i(i=1,2,\ldots ,n)\) are allowed to be unbounded, to be super linear, even to be exponential. Meanwhile, the restriction condition \(f_i^+(\rho ^i_k)>f_i^-(\rho ^i_k)\) (where \(f_i\) is discontinuous at \(\rho ^i_k\)) in the existing papers has also been eliminated successfully. Therefore, the activation functions of this paper are more general and more practical. Hence, Theorems 3.1 and 3.2 generalize and improve the corresponding results of the earlier literature [9, 10, 12, 13, 15–18, 41, 42].

Next, we discuss the multiplicity of positive \(\omega \)-periodic solutions for the neural networks (1.1) with discontinuous neuron activations.

Theorem 3.3

Assume that the conditions (H1), (H2), (H4) and (H6) hold. Then the system (1.1) has at least two positive \(\omega \)-periodic solutions.

Proof

It follows from Theorem 3.1 that \(\varphi \) has at least one fixed point in \(\{x^{(1)}:x^{(1)}\in \mathbb {P}\) and \(R_0\leqslant ||x^{(1)}||_X\leqslant R_1\}\). Meanwhile, Theorem 3.2 implies that \(\varphi \) has at least one fixed point in \(\{x^{(2)}:x^{(2)}\in \mathbb {P}\) and \(R_2\leqslant ||x^{(2)}||_X\leqslant R_3\}\). That is, \(\varphi \) has at least two fixed points in \(x^{(1)}, x^{(2)}\) \((x^{(1)}, x^{(2)}\in \mathbb {P})\) with \(R_0\leqslant ||x^{(1)}||_X\leqslant R_1<R_2\leqslant ||x^{(2)}||_X\leqslant R_3\). Thus the system (1.1) has at least two positive \(\omega \)-periodic solutions. \(\square \)

From the proof of Theorems 3.1–3.3, it is easy to obtain the following result.

Theorem 3.4

Assume that the conditions (H1), (H2), (H4) and (H6*) hold. Then the system (1.1) has at least two positive \(\omega \)-periodic solutions.

Theorem 3.5

Assume that the conditions (H1), (H2), (H4) and (H7) hold. Then the system (1.1) has at least m positive \(\omega \)-periodic solutions.

Theorem 3.6

Assume that the conditions (H1), (H2), (H4) and (H7*) hold. Then the system (1.1) has at least m positive \(\omega \)-periodic solutions.

Remark 3

In the earlier papers, such as [23, 24, 27, 28], the authors investigated the multiperiodicity for neuron networks with continuous neuron activations. However, for neuron networks with discontinuous neuron activations, there are few papers studied the multiperiodicity of it. In [29, 30], the authors studied the multiperiodicity of neuron networks with r-level discontinuous neuron activation functions. For neuron networks with more general discontinuous neuron activation functions, the methods used in [29, 30] will be invalid. Hence, to study the multiperiodicity of neuron networks with discontinuous neuron activations, a new method should be introduced. By means of functional differential inclusions theory and fixed-point theorem of multi-valued maps due to Agarwal and O’Regan [50], we obtain the existence of multiple positive periodic solutions for the neural networks with more general discontinuous neuron activations. In this sense, Theorems 3.3–3.6 are completely new.

4 Uniqueness and global exponential stability

For most practical applications, it is of prime importance to make sure that the designed neural networks are stable. By applying Theorems 3.3 and 3.4, under appropriate conditions, there exist multiple periodic solutions of system (1.1). Thus, it is interesting to obtain the uniqueness of \(\omega \)-periodic solution to the system (1.1). And so, in this section, we shall explore the uniqueness and global exponential stability of the \(\omega \)-periodic solution for the time-varying and distributed delayed Cohen–Grossberg neural networks (1.1) with discontinuous neuron activations. For convenience, we state some assumptions.

(H8) For each \(i=1,2,\ldots ,n\), \(f_i(x_i)\) is monotonically decreasing in \(\mathbb {R}\).

(H8*) For each \(i=1,2,\ldots ,n\), \(f_i(x_i)\) is monotonically nondecreasing in \(\mathbb {R}\).

(H9) The time-varying delay \(\tau (t)\) is continuously differentiable function and satisfying \(\tau ^\prime (t)<1\). Moreover, there exist positive constants \(\xi _1,\xi _2,\ldots ,\xi _n\) and \(\delta >0\) such that

$$\begin{aligned}&d_i^lq_i^l>\delta \ \ \hbox {and}\ \ \limsup _{t\rightarrow +\infty }\Upsilon _i(t)<0,\ \ i=1,2,\ldots ,n, \\&\quad \Upsilon _i(t) =-\xi _ia_{ii}(t) \\&\quad +\sum _{j=1,j\ne i}^n\xi _j|a_{ji}(t)|+\sum _{j=1}^n\dfrac{\xi _j\hbox {e}^{\delta \tau ^M}|b_{ji}(\varphi ^{-1}(t))|}{1-\tau ^\prime (\varphi ^{-1}(t))} \\&\quad +\sum _{j=1}^n\xi _j\int _0^{+\infty }|c_{ji}(s+t)||l_j(s)|\hbox {e}^{\delta s}\hbox {d}s. \end{aligned}$$

and \(\varphi ^{-1}\) is the inverse function of \(\varphi =t-\tau (t)\).

(H9*) The time-varying delay \(\tau (t)\) is continuously differentiable function and satisfying \(\tau ^\prime (t)<1\). Moreover, there exist positive constants \(\xi _1,\xi _2,\ldots ,\xi _n\) and \(\delta >0\) such that

$$\begin{aligned} d_i^lq_i^l>\delta \ \ \hbox {and}\ \ \limsup _{t\rightarrow +\infty }\widehat{\Upsilon }_i(t)<0,\ \ i=1,2,\ldots ,n, \end{aligned}$$

where

$$\begin{aligned} \widehat{\Upsilon }_i(t)&=\xi _ia_{ii}(t)+\sum _{j=1,j\ne i}^n\xi _j|a_{ji}(t)| \\&\quad +\sum _{j=1}^n\dfrac{\xi _j\hbox {e}^{\delta \tau ^M}|b_{ji}(\varphi ^{-1}(t))|}{1-\tau ^\prime (\varphi ^{-1}(t))} \\&\quad +\sum _{j=1}^n\xi _j\int _0^{+\infty }|c_{ji}(s+t)||l_j(s)|\hbox {e}^{\delta s}\hbox {d}s. \end{aligned}$$

and \(\varphi ^{-1}\) is the inverse function of \(\varphi =t-\tau (t)\).

Theorem 4.1

Assume that the conditions (H1), (H2), (H4), (H5), (H8) and (H9) hold. Then the system (1.1) has a uniqueness positive \(\omega \)-periodic solution which is globally exponentially stable.

Proof

It follows from Theorem 3.1 that the existence of the \(\omega \)-periodic solution for the system (1.1) is obvious. Assume that \(x^*(t)=(x_1^*(t),x_2^*(t),\ldots ,x_n^*(t))^T\) is a positive \(\omega \)-periodic solution of (1.1), \(\gamma ^*(t)=(\gamma _1^*(t),\gamma _2^*(t),\ldots ,\gamma _n^*(t))^T\) \((\gamma _i^*(t)\in \overline{co}[f_i(x_i^*(t))])\) is an output solution associated with the state \(x^*(t)=(x_1^*(t),x_2^*(t),\ldots ,x_n^*(t))^T\). And that \(x(t)=(x_1(t),x_2(t),\ldots ,x_n(t))^T\) is any solution of (1.1), \(\gamma (t)=(\gamma _1(t),\gamma _2(t),\ldots ,\gamma _n(t))^T\) \((\gamma _i(t)\in \overline{co}[f_i(x_i(t))])\) is an output solution corresponding to the state \(x(t)=(x_1(t),x_2(t),\ldots ,x_n(t))^T\).

Now, we consider the following Lyapunov function as follows:

$$\begin{aligned}&V(t)=\sum _{i=1}^n\xi _i\hbox {e}^{\delta t}|\int _{x_i^*(t)}^{x_i(t)}\dfrac{\hbox {d}\rho }{q_i(\rho )}| \\&\quad \qquad +\sum _{i=1}^n\sum _{j=1}^n\xi _i\int _{t-\tau (t)}^{t}\dfrac{|b_{ij}(\varphi ^{-1}(\rho ))|}{1-\tau ^\prime (\varphi ^{-1}(\rho ))}|\gamma _j(\rho ) \\&\quad \qquad -\gamma _j^*(\rho )|\hbox {e}^{\delta (\rho +\tau ^M)}\hbox {d}\rho , \\&\quad \qquad +\sum _{i=1}^n\sum _{j=1}^n\xi _i\int _0^{+\infty }\int _{t-s}^t|c_{ij}(s+\rho )||\gamma _j(\rho ) \\&\quad \qquad -\gamma _j^*(\rho )||l_j(s)|\hbox {e}^{\delta (s+\rho )}\hbox {d}\rho \hbox {d}s. \end{aligned}$$

Obviously, V(t) is regular. Meanwhile, the \(\omega \)-periodic solution \(x^*(t)\) and any solution x(t) of the system (1.1) are all absolutely continuous. Then, V(t) is differential for a.e. \(t\geqslant 0\), and the time derivative can be evaluated by Lemma 2.4.

Moreover,

$$\begin{aligned}&\dfrac{\hbox {d}}{\hbox {d}t}|\int _{x_i^*(t)}^{x_i(t)}\dfrac{\hbox {d}\rho }{q_i(\rho )}|{=} \partial |\int _{x_i^*(t)}^{x_i(t)}\dfrac{\hbox {d}\rho }{q_i(\rho )}|\times \dfrac{\hbox {d}}{\hbox {d}t}\int _{x_i^*(t)}^{x_i(t)}\dfrac{\hbox {d}\rho }{q_i(\rho )} \\&\quad =\nu _i(t)\left\{ \dfrac{1}{q_i(x_i(t))}\dfrac{\hbox {d} x_i(t)}{\hbox {d}t}-\dfrac{1}{q_i(x^*_i(t))}\dfrac{\hbox {d} x^*_i(t)}{\hbox {d}t}\right\} , \end{aligned}$$

where \(\nu _i(t)=\hbox {sign}\{\int _{x_i^*(t)}^{x_i(t)}\dfrac{\hbox {d}\rho }{q_i(\rho )}\}=\hbox {sign}\{x_i(t)-x^*_i(t)\}\), if \(x_i(t)\ne x_i^*(t)\), while \(\nu _i(t)\) can be arbitrarily choosen in \([-1,1]\), if \(x_i(t)=x_i^*(t)\). In particular, we choose \(\nu _i(t)\) as follows

$$\begin{aligned} \nu _i(t)=\left\{ {{\begin{array}{ll} 0, &{}\hbox {if} \quad \ x_i(t)-x^*_i(t)\\ {} &{}\quad =\gamma _i(t)-\gamma ^*_i(t)=0, \\ -\hbox {sign}\{\gamma _i(t)-\gamma ^*_i(t)\}, &{}\hbox {if}\quad x_i(t)=x^*_i(t)\\ &{}\quad \hbox {and}\ \gamma _i(t)\ne \gamma ^*_i(t), \\ \hbox {sign}\{x_i(t)-x^*_i(t)\}, &{}\hbox {if}\quad \ x_i(t)\ne x^*_i(t). \end{array}}} \right. \end{aligned}$$

It is easy to see that

$$\begin{aligned}&\nu _i(t)\{x_i(t)-x^*_i(t)\}=|x_i(t)-x^*_i(t)|,\ \nu _i(t) \\&\quad \{\gamma _i(t)-\gamma ^*_i(t)\}=-|\gamma _i(t)-\gamma ^*_i(t)|,\ i=1,2,\ldots ,n. \end{aligned}$$

In view of the chain rule in Lemma 2.4, calculate the time derivative of V(t) along the solution trajectories of the system (1.1) in the sense of equation (2.2), then we can get

$$\begin{aligned}&\dfrac{\hbox {d}V(t)}{\hbox {d}t}=\sum _{i=1}^n\delta \xi _i\hbox {e}^{\delta t}|\int _{x_i^*(t)}^{x_i(t)}\dfrac{\hbox {d}\rho }{q_i(\rho )}| +\sum _{i=1}^n\xi _i\hbox {e}^{\delta t}\nu _i(t)\\&\quad \times \,\left\{ \dfrac{1}{q_i(x_i(t))}\dfrac{\hbox {d} x_i(t)}{\hbox {d}t}-\dfrac{1}{q_i(x^*_i(t))}\dfrac{\hbox {d} x^*_i(t)}{\hbox {d}t}\right\} \\&\quad +\sum _{i=1}^n\sum _{j=1}^n\xi _i\dfrac{|b_{ij}(\varphi ^{-1}(t))|}{1-\tau ^\prime (\varphi ^{-1}(t))}|\gamma _j(t)-\gamma _j^*(t)|\hbox {e}^{\delta (t+\tau ^M)} \\&\quad -\sum _{i=1}^n\sum _{j=1}^n\xi _i|b_{ij}(t)||\gamma _j(t-\tau (t)) \\&\quad -\gamma _j^*(t-\tau (t))|\hbox {e}^{\delta [t-\tau (t)+\tau ^M]} \\&\quad +\sum _{i=1}^n\sum _{j=1}^n\xi _i\int _0^{+\infty }|c_{ij}(s+t)||\gamma _j(t) \\&\quad -\gamma _j^*(t)||l_{j}(s)|\hbox {e}^{\delta (s+t)}\hbox {d}s \\&\quad -\sum _{i=1}^n\sum _{j=1}^n\xi _i\int _0^{+\infty }|c_{ij}(t)||\gamma _j(t-s) \\&\quad -\gamma _j^*(t-s)||l_{j}(s)|\hbox {e}^{\delta t}\hbox {d}s \\&\quad \leqslant -\hbox {e}^{\delta t}\sum _{i=1}^n\xi _i\left( d_i^L-\dfrac{\delta }{q_i^L}\right) |{x_i(t)}-{x^*_i(t)}| \\&\quad +\hbox {e}^{\delta t}\sum _{i=1}^n\Upsilon _i(t)|{\gamma _i(t)}-{\gamma ^*_i(t)}|. \end{aligned}$$

It follows from the condition (H9) that, there exists nonnegative constants \(\varsigma _i (i=1,2,\ldots ,n)\) and \(t_0\geqslant 0\) such that for \(t\geqslant t_0\), we have

$$\begin{aligned} \Upsilon _i(t)\leqslant -\varsigma _i\leqslant 0. \end{aligned}$$

Thus

$$\begin{aligned} \dfrac{\hbox {d}V(t)}{\hbox {d}t}\leqslant -\Lambda _0\hbox {e}^{\delta t}\sum _{i=1}^n\xi _i\left( d_i^L-\dfrac{\delta }{q_i^L}\right) |{x_i(t)}-{x^*_i(t)}|, \end{aligned}$$

where \(\Lambda _0=\min _{0\leqslant i\leqslant n}\xi _i\left( d_i^L-\dfrac{\delta }{q_i^L}\right) >0\). Notice that

$$\begin{aligned} \sum _{i=1}^n\hbox {e}^{\delta t}\dfrac{\xi _i}{q_i^M}|{x_i(t)}-{x^*_i(t)}|\leqslant V(t). \end{aligned}$$

Hence

$$\begin{aligned} \sum _{i=1}^n|{x_i(t)}-{x^*_i(t)}|\leqslant \dfrac{V(t)}{\xi }\hbox {e}^{-\delta t}\leqslant \dfrac{V(t_0)}{\xi }\hbox {e}^{-\delta t}, \end{aligned}$$

where \(\xi =\min \{\xi _1,\xi _2,\ldots ,\xi _n\}>0\). Therefore, the positive \(\omega \)-periodic solution \(x^*(t)\) of the system (1.1) is globally exponentially stable. Consequently, the periodic solution \(x^*(t)\) of the system (1.1) is unique. The proof is complete. \(\square \)

From the proof of the Theorem 4.1, it is easy get the following theorems.

Theorem 4.2

Assume that the conditions (H1), (H2), (H4), (H5), (H8*) and (H9*) hold. Then the system (1.1) has a uniqueness positive \(\omega \)-periodic solution which is globally exponentially stable.

Theorem 4.3

Assume that the conditions (H1), (H2), (H4), (H5*), (H8) and (H9) hold. Then the system (1.1) has a uniqueness positive \(\omega \)-periodic solution which is globally exponentially stable.

Theorem 4.4

Assume that the conditions (H1), (H2), (H4), (H5*), (H8*) and (H9*) hold. Then the system (1.1) has a uniqueness positive \(\omega \)-periodic solution which is globally exponentially stable.

Remark 4

By construct suitable Lyapunov-like functions, we study the global exponential stability of the periodic solution for the neural network dynamic system (1.1) with discontinuous neuron activations and mixed time delayed. However, by comparison we find that Theorems 4.1–4.4 obtained in this section make the following improvements:

  1. (1)

    It is well known that most of the existing results concerning the delayed neural network dynamical systems with discontinuous neuron activations have not considered the time-varying delays and distributed delays situation. It is easy to see that the systems in the papers [1, 2, 6, 7, 9–18, 39, 40, 44] are just special cases of our system.

  2. (2)

    It is well known that, in the papers [1, 2, 6, 7, 9–18, 39, 40, 44], many results on the stability (or global exponential stability) analysis of periodic solution or equilibrium point for neural networks with discontinuous activation functions are conducted under the following assumptions:

    • For each \(i=1,2,\ldots ,n\), \(f_i(x_i)\) is monotonically non-decreasing in \(\mathbb {R}\).

    • For each \(i=1,2,\ldots ,n\), there exists a constant \(L_i\), such that for any two different numbers \(u,v\in \mathbb {R}\), \(\forall \gamma _i\in \overline{co}[f_i(u)]\), \(\forall \eta _i\in \overline{co}[f_i(v)]\),

      $$\begin{aligned} \dfrac{\gamma _i-\eta _i}{u-v}\geqslant -L_i. \end{aligned}$$

      It is easy to see that these conditions are not required in this paper.

In addition, the restriction condition \(f_i^+(\rho ^i_k)>f_i^-(\rho ^i_k)\) (where \(f_i\) is discontinuous at \(\rho ^i_k\)) in the papers [1, 2, 6, 7, 9–18, 39, 40, 44] has also been eliminated successfully. Therefore, the results on global exponential stability of periodic solution in this paper are more general and more practical.

5 Numerical examples

In this section, we consider three numerical examples, with which the time-varying and distributed delayed neural networks have different discontinuous neuron activation functions, to show the effectiveness of the theoretical results given in the previous sections.

Example 5.1

Consider the following general Cohen–Grossberg neural networks:

$$\begin{aligned} \dfrac{\hbox {d}x_1(t)}{\hbox {d}t}= & {} [0.4+0.1\tanh (x_1(t))][-2x_1(t) \nonumber \\&+\,(2+0.01\hbox {e}^{\sin 2 t})f_1(x_1(t))+0.1f_2(x_2(t)) \nonumber \\&+\,(0.1+0.1\sin (\sin 2 t))f_1(x_1(t-\tau (t))) \nonumber \\&+\,0.1f_2(x_2(t-\tau (t)))+0.2+0.01\sin (\sin 2 t)] \nonumber \\&\dfrac{\hbox {d}x_2(t)}{\hbox {d}t} =[0.4+0.1\tanh (x_2(t))][-2x_2(t) \nonumber \\&+\,0.1f_1(x_1(t))+(2+0.01\hbox {e}^{\cos 2 t})f_2(x_2(t)) \nonumber \\&+\,0.1f_1(x_1(t-\tau (t)))+(0.1+0.1\sin (\cos 2 t)) \nonumber \\&\times \, f_2(x_2(t-\tau (t)))+0.2+0.01\cos (\cos 2 t)],\nonumber \\ \end{aligned}$$
(5.1)

where \(f_1(s)=f_2(s)=\left\{ {{\begin{array}{ll} 0.01, &{} \quad |s|\leqslant 2, \\ s^2+40, &{} \quad |s|>2, \end{array}}} \right. \) and \(\tau (t)\equiv 1\).

Fig. 1
figure 1

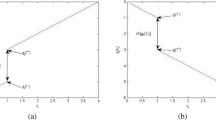
Trajectory of the system (5.1) with initial value \(x(t)=(0.111,0.115)^T, t\in [-1,0]\)

Full size image
Fig. 2
figure 2

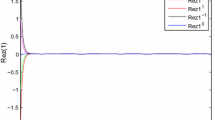
Trajectory of the system (5.2) with 5 random initial conditions

Full size image

Consider the IVP of the system (5.1) with the initial condition \(\phi (s)=(0.111,0.115)^T\) for \(s\in [-1,0]\), and \(\psi (s)=(0.01,0.01)^T\) for \(s\in [-1,0]\). It is not difficult to verify that the coefficients of the system (5.1) satisfy all the conditions in Theorem 3.1. Therefore, it follows from Theorem 3.1 that the non-autonomous system (5.1) has at least one \(\pi \)-periodic solution. As shown in Figure 1, numerical simulations also confirm that there exists a \(\pi \)-periodic solution of the system (5.1) by MATLAB.

Remark 5

It is easy to see that the activation functions \(f_1(s)\) and \(f_2(s)\) of Example 5.1 are discontinuous, unbounded, non-monotonic, and satisfy the super linear growth condition(in fact, \(|f_i(s)|\leqslant s^2+40, i=1,2\)). Therefore, the results in [9, 10, 12, 13, 15–18, 41, 42] cannot be applied to discuss the existence of periodic solution for the system (5.1). Moreover, the activation functions \(f_i(s)(i=1,2)\) are discontinuous at \(s=\pm 2\) and \(f_i^-(-2)=44>0.01=f_i^+(-2)(i=1,2)\). It is obviously from this example that the assumption (H2) in this paper is much less conservative than that in [9, 10, 12, 13, 15–18, 41, 42] since the functions \(W_i(s)\) may be a class of general functions and the restriction condition \(f_i^+(\rho ^i_k)>f_i^-(\rho ^i_k)\)(where \(f_i\) is discontinuous at \(\rho ^i_k\)) in [9, 10, 16, 18, 41, 42] has also been eliminated successfully.

Example 5.2

Consider the following general Cohen–Grossberg neural networks:

$$\begin{aligned}&\dfrac{\hbox {d}x_1(t)}{\hbox {d}t}=[0.3+0.1\arctan (x_1(t))][-0.3x_1(t) \nonumber \\&\quad +(1.5+0.2\cos (\sin t+1))f_1(x_1(t))+0.1f_2(x_2(t)) \nonumber \\&\quad +(0.2+0.1\sin (2\sin t+1))f_1(x_1(t-\tau (t))) \nonumber \\&\quad +0.1f_2(x_2(t-\tau (t)))+0.3+0.1\tanh (\sin t+1)] \nonumber \\&\quad \dfrac{\hbox {d}x_2(t)}{\hbox {d}t}=[0.3-0.1\arctan (x_2(t))][-0.3x_2(t) \nonumber \\&\quad +0.1f_1(x_1(t))+(1.5-0.2\sin (\cos t+1))f_2(x_2(t)) \nonumber \\&\quad +0.1f_1(x_1(t-\tau (t)))+(0.2-0.1\cos (2\cos t+1)) \nonumber \\&\quad \times f_2(x_2(t-\tau (t)))+0.3+0.1\tanh (\cos t+1)], \end{aligned}$$
(5.2)

where \( f_1(s)=f_2(s)=\left\{ {{\begin{array}{ll} s^2+100, &{} \quad s\leqslant 0, \\ 0.1, &{} \quad 0<s<2, \\ 0.001, &{} \quad s\geqslant 2,\end{array}}} \right. \hbox { and} \tau (t)=1\).

Fig. 3
figure 3

Trajectory of the system (5.3) with 9 random initial conditions

Full size image

Consider the IVP of the system (5.2) with 5 random initial conditions \(\phi (s)=(1.5,1.5)^T\), \((1.75,1.75)^T\), \((2.0,2.0)^T\), \((2.25,2.25)^T\) and \((2.5,2.5)^T\) for \(s\in [-1,0]\). It is not difficult to verify that the coefficients of the system (5.2) satisfy all the conditions in Theorem 4.1. Therefore, it follows from Theorem 4.1 that the non-autonomous system (5.2) has a unique \(2\pi \)-periodic solution which is globally exponentially stable. As shown in Figure 2, numerical simulations also confirm that all the solutions converge to the unique \(2\pi \)-periodic solution of the system (5.2) by MATLAB.

Remark 6

It is easy to see that the activation functions \(f_1(s)\) and \(f_2(s)\) of Example 5.2 are discontinuous, unbounded, monotonic decreasing, and satisfy the super linear growth condition(in fact, \(|f_i(s)|\leqslant s^2+100, i=1,2\)). Therefore, the results in [9, 10, 12, 13, 15–18, 41, 42] cannot be applied to discuss the stability (or global exponential stability) of periodic solution for the system (5.2). Meanwhile, the activation functions \(f_i(s)(i=1,2)\) are discontinuous at \(s=2\) and \(s=0\). In addition, for \(i=1,2\), we have \(f_i^-(0)=10>0.1=f_i^+(0)\) and \(f_i^-(2)=0.1>0.01=f_i^+(2)\). Thus, the restriction condition \(f_i^+(\rho ^i_k)>f_i^-(\rho ^i_k)\)(where \(f_i\) is discontinuous at \(\rho ^i_k\)) in the papers [9, 10, 12, 13, 15–18, 41, 42] has also been eliminated successfully. Therefore, the results of this paper are more general and more practical.

Example 5.3

Consider the following general Cohen–Grossberg neural networks:

$$\begin{aligned}&\dfrac{\hbox {d}x_1(t)}{\hbox {d}t}=[1+0.01\arctan (x_1(t))] \nonumber \\&\quad \times \left[ -2x_1(t)+(1.5+0.1\tanh (\sin t+1)) \right. \nonumber \\&\quad \times f_1(x_1(t))+0.01f_2(x_2(t)) \nonumber \\&\quad +\,(0.1+0.1\sin (2\sin t+t))f_1(x_1(t-\tau (t))) \nonumber \\&\quad \left. +\,0.1f_2(x_2(t-\tau (t)))+0.5+0.1\arctan (\sin t+1)\right] \nonumber \\&\quad \dfrac{\hbox {d}x_2(t)}{\hbox {d}t} =[1-0.01\arctan (x_2(t))][-2x_2(t) \nonumber \\&\quad +\,0.01f_1(x_1(t)) {+}(1.5{-}0.1\tanh (\cos t{+}1))f_2(x_2(t)) \nonumber \\&\quad +\,0.1f_1(x_1(t{-}\tau (t))){+}(0.1{-}0.1\cos (2\cos t{+}t)) \nonumber \\&\quad \times f_2(x_2(t-\tau (t)))+0.5-0.1\arctan (\cos t+1)], \end{aligned}$$
(5.3)

where \(f_1(s)=f_2(s)=\left\{ {{\begin{array}{ll} 0.1s^2+0.4, &{} \quad s\leqslant 0.5, \\ 0.01, &{} \quad 0.5<s<1, \\ 0.1s^2+1, &{} \quad s\geqslant 1, \end{array}}} \right. \hbox { and } \tau (t)=0.5\).

Consider the IVP of the system (5.3) with 9 random initial conditions \(\phi (s)=(0,0)^T\), \((0.25,0.25)^T\), \((0.5,0.5)^T\), \((0.75,0.75)^T\), \((1.0,1.0)^T\), \((1.25,1.25)^T\), \((1.5,1.5)^T\), \((1.75,1.75)^T\) and \((2.0,2.0)^T\) for \(s\in [-1,0]\). Take \(R_0=0.1\), \(R_1=0.5\), \(R_2=1\) and \(R_3=2\). It is not difficult to verify that the coefficients of the system (5.3) satisfy all the conditions in Theorem 3.3. Therefore, it follows from Theorem 3.3 that the non-autonomous system (5.3) has at least two positive \(2\pi \)-periodic solutions. As shown in Figure 3, numerical simulations also confirm that there exists two \(2\pi \)-periodic solutions of the system (5.3) by MATLAB.

Remark 7

It is easy to see that the activation functions \(f_1(s)\) and \(f_2(s)\) of Example 5.3 are discontinuous, unbounded, and satisfy the super linear growth condition(in fact, \(|f_i(s)|\leqslant 0.1 s^2+1, i=1,2\)). Therefore, the results in [23, 24, 27–30] cannot be applied to discuss the existence of multiple periodic solutions for the system (5.3). In addition, from Figure 3, there exist at least two stable periodic solutions. Now, another problem arising in discontinuous neural networks: the multistability of periodic solutions(or equilibria), we left it for future research.

6 Conclusion

In this paper, a class of general Cohen–Grossberg neural networks with discontinuous neuron activations and mixed delays has been investigated. Under the framework of the theory of Filippov functional differential inclusions, the existence of the global solutions is given. Based on fixed-point theorem of multi-valued analysis due to Agarwal and O’Regan, the existence of one and multiple periodic solutions for the neural network systems have been obtained. It is worthy to point out that, without assuming the boundedness or under linear growth condition of the discontinuous neuron activation functions, our results on the existence of one and multiple positive periodic solutions will also be valid. After that, in terms of non-smooth analysis theory with generalized Lyapunov approach, we have got some sufficient conditions for the global exponential stability of the neural network systems. It is interesting that, under the hypnosis of the discontinuous neuron activations to be monotonically decreasing, the results of the global exponential stability also hold. Moreover, our results extend previous works not only on time-varying and distributed delayed neural networks with continuous or even Lipschitz continuous activations, but also on time-varying and distributed delayed neural networks with discontinuous activations. Finally, we gave some numerical examples to show the applicability and effectiveness of our main results. We think it would be interesting to investigate the possibility of extending the results to more complex discontinuous neural network systems with time-varying and distributed delays, such as multistability of multiple periodic solutions, uncertain network systems and stochastic neural network systems. These issues will be the topic of our future research.