Parameters optimization of polygonal fuzzy neural networks based on GA-BP hybrid algorithm

Abstract

Based on the extensive operations of polygonal fuzzy numbers, a GA-BP hybrid algorithm for polygonal fuzzy neural network is designed. Firstly, an optimal solution is obtained by the global searching ability of GA algorithm for the untrained polygonal fuzzy neural network. Secondly, some parameters for connection weights and threshold values are appropriately optimized by using an improved BP algorithm. Finally, through a simulation example, we demonstrate that the GA-BP hybrid algorithm based on the polygonal fuzzy neural network can not only avoid the initial values’ dependence and local convergence of the original BP algorithm, but also overcome a blindness problem of the traditional GA algorithm.

1 Introduction

In recent years, it is an increasing interest that is combing artificial neural networks with fuzzy system. Fuzzy neural networks (FNN), which is made up of artificial neural networks and fuzzy system, can learn, identify and process fuzzy information. So FNN is one of the most successful examples to bring the artificial networks and fuzzy system together [1, 2]. But FNN based on Zadeh’s extension principle has not satisfied linearity so that some extensive applications of FNN can be greatly restricted. Consequently, in order to realize a nonlinear operation between fuzzy numbers and improve the ability of universal approximation of fuzzy neural networks, polygonal FNN is introduced. The polygonal FNN is a new network which depends on polygonal fuzzy numbers and artificial neural networks. The connection weights and threshold of polygonal FNN both take values of polygonal fuzzy numbers. Furthermore, the topology of polygonal FNN is intuitive and clear, and operations of polygonal FNN are simple and satisfy the linearity. So, the polygonal FNN has a stronger approximation ability than fuzzy neural network based on Zadeh’s extensive principle [3, 4]. Generally, when the network is fixed, its performance is determined by parameters of the network. However, parameters optimization of polygonal FNNs mainly embody in networks’ learning algorithms. Therefore, how to optimize parameters of polygonal FNNs is an important goal of the networks’ learning algorithms.

In 2002, Liu [3] first developed a concept of n-symmetric polygonal fuzzy numbers and established a polygonal fuzzy neural network. Because the polygonal FNNs rely on the linear operations of polygonal fuzzy numbers to design a learning algorithm, learning algorithms of the polygonal FNNs are more convenient to compute than those of the FNNs. Next, according to the above characteristic, through presenting a traditional Back Propagation (BP) algorithm for polygonal FNNs to realize parameters optimization, Liu [4] verified the polygonal FNNs had a better performance in the application than FNNs. But initial values’ dependence and local convergence of the traditional BP algorithm has not been resolved. Thus, it is necessary to design some new and effective learning algorithms for polygonal FNNs. In 2011, a traditional genetic algorithm (GA), which is based on natural selection and genetic principles, was used for optimizing parameters of polygonal FNNs [5]. However, the traditional GA which is a kind of global searching algorithm has a blindness problem to make the optimization ineffective. Besides, recently, although some learning algorithms were proposed to optimize the polygonal FNNs [6–9], there were many aspects to be improved. In fact, through analyzing feature of the BP and GA algorithms, we can find that the global searching capability of GA can resolve the traditional BP algorithm’ deficiencies. And, feasibility and local searching ability of BP algorithm can make the traditional GA get rid of blindness problem. Thus, now, we present parameters optimization of polygonal FNNs based on GA-BP hybrid algorithm.

In this paper, we introduce the polygonal FNN based on the extensive operations of polygonal fuzzy numbers. And then, according to their extensive operations, we improve the traditional BP [3, 4] and GA algorithm [5] based on the polygonal FNN. At the same time, using the improved GA to search a global optimal solution for the untrained polygonal FNN, and combining the improved BP algorithm to optimize the connection weights and threshold values, we design a GA-BP hybrid algorithm for polygonal FNN. Finally, through a simulation example, the results show that a GA-BP hybrid algorithm doesn’t only overcome the initial values’ dependence and local convergence of the BP algorithms and blindness problem of the traditional GA, but also improves the convergence rate of the polygonal FNN.

In addition, the paper is organized as follows: After the introduction, some basic notations for polygonal fuzzy numbers and its graphical explanation are briefly summarized in Sect. 2. In Sect. 3, the structural model and the error function of the polygonal fuzzy neural network are given. Section 4 shows that a new GA-BP hybrid algorithm and its parameters optimization are designed. In Sect. 5, a simulation example for the polygonal FNN is realized. Some conclusions are indicated in the final section.

2 Polygonal fuzzy numbers

It is well known that one of the simplest fuzzy numbers, even the triangular fuzzy numbers, doesn’t satisfy linear operation, so the application of fuzzy numbers is a difficult problem. This also raises an important issue that how to approximately achieve a nonlinear operation between fuzzy numbers. And how to construct the appropriate FNN to approximate a given nonlinear function can be very significant. For this, Liu [3] was the first to put forward the concept of n-symmetric polygonal fuzzy number, and its operations can be linearized. But this polygonal fuzzy numbers are a little shortage, and he [6] revised and improved it.

Throughout this paper, we always let ${\mathbf{\mathbb{R}}}$denote the set of all real numbers, ${\mathbf{\mathbb{R}}}^{ + }$the set of non-negative real numbers and ${\mathbb{N}}$ the family of all natural numbers. Let sign $\left\| {\, \cdot \,} \right\|$ be a Euclid norm, $F_{0} ({\mathbf{\mathbb{R}}})$ the family of all of fuzzy numbers on ${\mathbf{{\mathbb{R}} }}.$

Definition 1

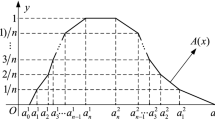
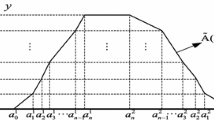
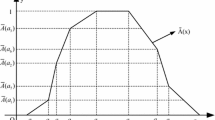
[3, 6] Let $\tilde{A} \in F_{0} ({\mathbf{\mathbb{R}}}),$for given $n \in {\mathbf{\mathbb{N}}}$, divide the closed interval $[0,1]$ along the $y$-axis into $n$ equal-sized closed intervals bounded by points $x_{i} = {i \mathord{\left/ {\vphantom {i n}} \right. \kern-0pt} n},\,i = 1,2, \cdots ,n - 1.$ If there exists a set of ordered real numbers: $a_{0}^{1} ,a_{1}^{1} , \cdots ,a_{n}^{1} ,a_{n}^{2} , \cdots ,a_{1}^{2} ,a_{0}^{2} \in {\mathbf{\mathbb{R}}}$ with $a_{0}^{1} \le a_{1}^{1} \le \cdots \le a_{n}^{1}$ $\le a_{n}^{2} \le \cdots \, \le a_{1}^{2} \le a_{0}^{2}$ such that $\tilde A(a_i^q)={i\mathord{\left/{\vphantom{i n}}\right.\kern-\nulldelimiterspace}n}$, where $q=1,2$ and membership function $\tilde{A}(x)$ takes straight lines in $[a^1_{i-1},\,\,a^1_i]$ and $[a^2_i,\,\,a^2_{i-1}]$, where $i = 1,2,\, \ldots ,n$ (see Figs. 1, 2).

Fig. 1

Image of $n-$ polygonal fuzzy number $\widetilde{A}$

Fig. 2

Mixed image of $\widetilde{A}$ and its 2- polygonal fuzzy number

Then $\tilde{A}$ is called an $n -$polygonal fuzzy number, for simplicity, it is always denoted as follows

$$\tilde{A} = (a_{0}^{1} ,a_{1}^{1} , \cdots ,a_{n}^{1} ,a_{n}^{2} , \cdots ,a_{1}^{2} ,a_{0}^{2} ).$$

Obviously, an $n -$polygonal fuzzy number $\tilde{A}$ can be completely determined by the finite ordered points $a_{0}^{1} ,a_{1}^{1} , \cdots ,a_{n}^{1} ,a_{n}^{2} , \cdots ,a_{1}^{2} ,a_{0}^{2}$ on $x -$axis, where the coordinate of each vertex is$(a_{\,i}^{q} ,\,{i \mathord{\left/ {\vphantom {i n}} \right. \kern-0pt} n})$, $q = 1,2$; $i = 0,1, \cdots ,n.$

Generally, the value of $n$ determines the size of nodes on the polyline. Specially, if $n = 1$, a $1 -$polygonal fuzzy number reduces to a trapezoidal or triangle fuzzy number. For any given fuzzy number and $n \in {\mathbf{\mathbb{N}}}$, we can get only one $n -$polygonal fuzzy number by method in Fig. 1, to replace the original fuzzy number (see Fig. 2).

Let $F_{0}^{{t{\kern 1pt} n}}( {\mathbf{\mathbb{R}}})$ denote the set of all $n-$ polygonal fuzzy numbers on ${\mathbf{\mathbb{R}}}$, and $\tilde{A} \in F_{0}^{{t{\kern 1pt} n}} ({\mathbf{\mathbb{R}}}^{ + } )$ $\Leftrightarrow$ $\tilde{A}(x) = 0,$ $\forall x < 0$. In addition, extended linear operators of polygonal fuzzy numbers can be described in papers [6–8], This article will do not repeat.

3 Polygonal FNN

Polygonal FNN is a kind of new network system, its connection weights and threshold are polygonal fuzzy numbers, so its internal processing are based on the extension operations of polygonal fuzzy numbers. In fact, the network’s expression is a system that contains the arithmetics of polygonal fuzzy numbers, and the network can process information by a finite number of real numbers. The research object of this article is a single input single output (for short SISO) three-layer forward polygonal FNN.

If the input variable $\tilde{X}$, the connection weights $\tilde{U}_{j}$ and $\tilde{V}_{j}$, the threshold $\tilde{\varTheta }_{j}$ of the hidden layer are taken values in $F_{0}^{{t{\kern 1pt} n}} ({\mathbf{\mathbb{R}}})$, and let an activation function $\sigma$ be a continuous monotonic Sigmoidal function, then SISO three-layer forward polygonal FNN can be denoted as follow

$$\tilde{Y} = \tilde{F}_{nn} (\tilde{X}) = \sum\nolimits_{j = 1}^{p} {\tilde{V}_{j} \cdot \sigma (\tilde{U}_{j} \cdot \tilde{X} + \tilde{\varTheta }_{j} )}.$$

For given untrained polygonal fuzzy pattern pairs $(\tilde{X}(1),\tilde{O}(1)),(\tilde{X}(2),\tilde{O}(2)), \ldots ,(\tilde{X}(L),\tilde{O}(L))$, where $\tilde{X}(l),$ $\tilde{O}(l) \in F_{0}^{{t{\kern 1pt} n}} ({\mathbf{\mathbb{R}}}^{ + } )$, and $\tilde{X}(l)$ denote network’s input, $\tilde{O}(l)$ denote network’s expected output. If the network’s actual output can be denoted as $\tilde{Y}(l)$, then $\tilde{Y}(l) = \tilde{F}_{nn} (\tilde{X}(l))$, $l = 1,2, \cdots ,L$. This moment, let

$$\tilde{X}(l) = (x_{0}^{1} (l),x_{1}^{1} (l), \cdots ,x_{n}^{1} (l),x_{n}^{2} (l), \cdots ,x_{1}^{2} (l),x_{0}^{2} (l)),$$

$$\tilde{Y}(l) = (y_{0}^{1} (l),y_{1}^{1} (l), \cdots ,y_{n}^{1} (l),y_{n}^{2} (l), \cdots ,y_{1}^{2} (l),y_{0}^{2} (l)) ,$$

$$\tilde{O}(l) = (o_{0}^{1} (l),o_{1}^{1} (l), \cdots ,o_{n}^{1} (l),o_{n}^{2} (l), \cdots ,o_{1}^{2} (l),o_{0}^{2} (l)).$$

According to the metric $D$ of polygonal fuzzy number [3], we may define the error function $\,\,E$ of polygonal FNN as follows

$$E = \frac{1}{2}\sum\limits_{l = 1}^{L} {D(\tilde{O}(l),\tilde{Y}(l))^{2} } = \frac{1}{2}\sum\limits_{l = 1}^{L} {\left(\sum\limits_{i = 0}^{n} {((o_{i}^{1} (l) - y_{i}^{1} (l))^{2} + (o_{i}^{2} (l) - y_{i}^{2} (l))^{2} )}\right )} .$$

(1)

In terms of input variable $\tilde{X}$, the network can gradually optimized connection weights $\tilde{U}_{j}$, $\tilde{V}_{j}$ and threshold $\tilde{\varTheta }_{j}$ by learning. And this optimization can make $\tilde{O}(l)$ approximate or equal $\tilde{Y}(l)$. In addition, we can also put all of adjustable parameters $u_{i}^{q} (j)$, $v_{i}^{q} (j)$, $\theta_{i}^{q} (j)$ $(i = 0,1, \cdots ,n;\,\,j =$ $1,2, \cdots ,p;$ $q = 1,2)$ together to express a form of parameters vector, denoted as $w$, that is

$$w = (w_{1} ,w_{2} , \cdots w_{N} ) = (u_{0}^{1} (1), \cdots ,u_{0}^{2} (1), \cdots ,u_{0}^{1} (p), \cdots ,u_{0}^{2} (p),v_{0}^{1} (1), \cdots ,v_{0}^{2} (1), \cdots ,v_{0}^{1} (p), \cdots ,v_{0}^{2} (p),\theta_{0}^{1} (1), \cdots ,\theta_{0}^{2} (1), \cdots ,\theta_{0}^{1} (p), \cdots ,\theta_{0}^{2} (p))$$

(2)

Aim at $(1)$, the error function $E$ can be denoted as $E(w)$, and its gradient vector can be denoted as

$$\nabla E(w{\kern 1pt} {\kern 1pt} [t]) = (\partial E(w)/\partial w_{1} ,\partial E(w)/\partial w_{2} , \cdots ,\partial E(w)/\partial w_{N} ).$$

Lemma 1

[4] Let $E(w)$ denote the error function defined by formula $(1)$, then for $i = 0,1, \cdots ,n;\,j = 1,2,\, \cdots ,p;q = 1,2,\,E(w)$ is almost everywhere differentiable in ${\mathbf{\mathbb{R}}}^{N}$, and its partial derivate formula $\partial E/\partial u_{i}^{q} (j),\,\partial E/\partial v_{i}^{q} (j),\partial E/\partial \theta_{i}^{q} (j)$ can exist. (Detailed expressions of several partial derivative can be found.(see [4]))

4 GA-BP hybrid algorithm

An original BP algorithm is one of the common learning algorithms in neural networks, and it is not only simple and easy to implement, but also has a strong local search ability. However, BP algorithm has slower convergence speed and is easy to fall into minimum. For example, when there are many extreme points in solution space, and the initial parameters are not appropriate, BP algorithm can be easy to fall into local convergence point to result in a bad situation surely. In addition, a GA algorithm is a global optimization algorithm. It combines natural selection in biology with population evolution. The GA algorithm can code parameters into a space of the individual, and it also can select the optimal individual in groups by genetic manipulation, then decode the optimal individual to restore parameters to achieve optimization. But a traditional GA algorithm’s iterative process is based on the same original group, so it maybe can’t select the optimal gene in the original group. Hence, the traditional GA algorithm can search for the sub-optimal solution, sometimes it happens “inbreeding” phenomenon (see [10–12]).

Accordingly, this paper combines the advantages of BP and GA algorithm, and proposes a GA-BP hybrid algorithm based on parameters optimization for polygonal FNN (see Fig. 3).

Fig. 3

Schematic diagram of GA-BP hybrid algorithm

From Fig. 3, with GA and BP interacting each other, we can see that many parameters can be optimized by BP algorithm (see [13, 14]). In addition, according to gradient vector $\nabla E(w)$ from the partial derivative formula of Lemma 1, we can design the GA-BP hybrid algorithm based on polygonal FNN as follows.

Algorithm 1 (BP algorithm part): Based on polygonal FNN, we improve the original BP algorithm to make arithmetics of its neurons meet extensive operations of polygonal fuzzy numbers. At the same time, we can introduce dynamic learning constant and momentum constant to accelerate searching rate. Then, parameters of the network can be optimized to design the following algorithm.

Step 1. For $j = 1,2, \cdots ,p$, let connection weights $\tilde{U}_{j} [t_{ 1} ]$, $\tilde{V}_{j} [t_{ 1} ]$ and threshold $\tilde{\varTheta }_{j} [t_{ 1} ]$ $\in F_{0}^{{t{\kern 1pt} n}} ({\mathbf{\mathbb{R}}}^{ + } )$ denote

$$\tilde{U}_{j} [t_{ 1} ] = (u_{0}^{1} (j)[t_{ 1} ],u_{1}^{1} (j)[t_{ 1} ], \cdots ,u_{n}^{1} (j)[t_{ 1} ],u_{n}^{2} (j)[t_{ 1} ], \cdots ,u_{1}^{2} (j)[t_{ 1} ],u_{0}^{2} (j)[t_{ 1} ]),$$

$$\tilde{V}_{j} [t_{ 1} ] = (v_{0}^{1} (j)[t_{ 1} ],v_{1}^{1} (j)[t_{ 1} ], \cdots ,v_{n}^{1} (j)[t_{ 1} ],v_{n}^{2} (j)[t_{ 1} ], \cdots ,v_{1}^{2} (j)[t_{ 1} ],v_{0}^{2} (j)[t_{ 1} ]),$$

$$\tilde{\varTheta }_{j} [t_{ 1} ] = (\theta_{0}^{1} (j)[t_{ 1} ],\theta_{1}^{1} (j)[t_{ 1} ], \cdots ,\theta_{n}^{1} (j)[t_{ 1} ],\theta_{n}^{2} (j)[t_{ 1} ], \cdots ,\theta_{1}^{2} (j)[t_{ 1} ],\theta_{0}^{2} (j)[t_{ 1} ]).$$

We make the number of iteration step $t_{ 1} = 0$, and randomly select initial values $\tilde{U}_{j} [0],\tilde{V}_{j} [0],\tilde{\varTheta }_{j} [0]\,(j = 1,2, \cdots ,\,p)$, and for given error accuracy $\varepsilon > 0.$

Step 2. For $l = 1,2, \cdots ,L;j = 1,2, \cdots ,p;i = 0,1, \cdots ,n;q = 1,2$, according to Lemma 1, we calculate the partial derivatives $\partial E/\partial u_{i}^{q} (j),\,\partial E/\partial v_{i}^{q} (j),\partial E/\partial \theta_{i}^{q} (j)$, where the iterative formula of the connection weights’ component $u_{i}^{q} (j),\,v_{i}^{q} (j)$ and threshold’s component $\theta_{i}^{q} (j)$ can be denoted as

$$\left\{ \begin{gathered} \,u_{i}^{q} (j)[t + 1] = u_{i}^{q} (j)[t] + \eta \cdot \frac{\partial E}{{\partial u_{i}^{q} (j)[t]}} + \alpha \cdot \varDelta u_{i}^{q} (j)[t]; \hfill \\ \,v_{i}^{q} (j)[t + 1] = v_{i}^{q} (j)[t] + \eta \cdot \frac{\partial E}{{\partial v_{i}^{q} (j)[t]}} + \alpha \cdot \varDelta v_{i}^{q} (j)[t]; \hfill \\ \,\theta_{i}^{q} (j)[t + 1] = \theta_{i}^{q} (j)[t] + \eta \cdot \frac{\partial E}{{\partial \theta_{i}^{q} (j)[t]}} + \alpha \cdot \varDelta \theta_{i}^{q} (j)[t]. \hfill \\ \end{gathered} \right.$$

where differentials $\varDelta u_{i}^{q} (j)[t_{ 1} ] = u_{i}^{q} (j)[t_{ 1} ] - u_{i}^{q} (j)[t_{ 1} - 1],\,\varDelta v_{i}^{q} (j)[t_{1} ] = \,v_{i}^{q} (j)[t_{ 1} ] - v_{i}^{q} (j)\,[t_{ 1} - 1],\,\varDelta \theta_{i}^{q} (j)[t_{ 1} ] = \,\theta_{i}^{q} (j)[t_{ 1} ] - \theta_{i}^{q} (j)[t_{ 1} - 1]$, this $\eta ,\alpha$ denote learning constant and momentum constant.

Step 3. Through the above iteration formulas, we can calculate components $u_{i}^{q} (j)[t_{ 1} + 1],v_{i}^{q} (j)[t_{ 1} + 1],\,\theta_{i}^{q} (j)\,\,[t_{ 1} + 1]\,(q = 1,2;i = 0,1, \cdots ,n;j = 1,2, \cdots ,p).$ According to incrementally reorder, the new order relation of polygonal fuzzy numbers are obtained as follows:

$$u_{1}^{\prime 0} (j)[t_{1} + 1] \le u_{1}^{\prime 1} (j)[t_{1} + 1] \le \cdots \le u_{n}^{\prime 1} (j)[t_{1} + 1] \le u_{n}^{\prime 2} (j)[t_{1} + 1] \le \cdots \le u_{1}^{\prime 2} (j)[t_{1} + 1] \le u_{0}^{\prime 2} (j)[t_{1} + 1];$$

$$v_{0}^{\prime 1} (j)[t_{ 1} + 1] \le v_{1}^{\prime 1} (j)[t_{ 1} + 1] \le \cdots \le v_{n}^{\prime 1} (j)[t_{ 1} + 1] \le v_{n}^{\prime 2} (j)[t_{ 1} + 1] \le \cdots \le v_{1}^{\prime 2} (j)[t_{ 1} + 1] \le v_{0}^{\prime 2} (j)[t_{ 1} + 1];$$

$$\theta_{0}^{\prime 1} (j)[t_{ 1} + 1] \le \theta_{1}^{\prime 1} (j)[t_{ 1} + 1] \le \cdots \le \theta_{n}^{\prime 1} (j)[t_{ 1} + 1] \le \theta_{n}^{\prime 2} (j)[t_{ 1} + 1] \le \cdots \le \theta_{1}^{\prime 2} (j)[t_{ 1} + 1] \le \theta_{0}^{\prime 2} (j)[t_{ 1} + 1].$$

Step 4. For $\varepsilon > 0$ and $l = 1,2, \cdots ,L$, whether $D(\tilde{Y}(l),\tilde{O}(l)) < \varepsilon .$ If they fulfill, then output $\tilde{U}_{j} [t_{ 1} ],\,\tilde{V}_{j} [t_{ 1} ],\,\tilde{\varTheta }_{j} [t_{ 1} ]\,(j = 1,\,2, \cdots ,p)$ and $\tilde{O}(l)\,{\kern 1pt} (l = 1,2, \cdots ,L)$; otherwise, let $t_{ 1} = t_{ 1} + 1$, and turn to Algorithm 2.

Note 1. According to [15–17], based on extensive operations of polygonal fuzzy numbers, we can improve learning constant $\eta$ and momentum constant $\alpha$ in Step 3 to make them become functions about iteration step $t_{ 1} .$ Let

$$\eta = \eta [t_{ 1} ] = \frac{{\rho_{0} \cdot E(w\,[t_{ 1} ])}}{{\left\| {\nabla E(w\,[t_{ 1} ])} \right\|^{2} }};\quad \alpha = \alpha [t_{ 1} ] = \frac{{\left| {\varDelta E(w\,[t_{ 1} ])} \right|}}{{\sum\nolimits_{k = 1}^{{t_{ 1} - 1}} {\left| {\varDelta E(w\,[k])} \right|} }},$$

where, $\varDelta E(w\,[t_{ 1} ]) = E(w\,[t_{ 1} ]) - E(w\,[t_{ 1} - 1]),\,w\,[t_{ 1} ]$ denote the parameter’s vector of $t_{ 1}$ step. Clearly, when $t_{ 1} = 0$, $E(w\,[0])$ is usually a large number, i.e. $E(w\,[0]) = 100$. And $\rho_{0}$is a small constant, i.e. $0.01$.$\nabla E(w\,[t_{ 1} ])$ can be denoted as gradient vector of $E$ in step $t_{ 1}$, so we can get that

$$\nabla E(w[t_{ 1} ]) = \,(\partial E(w)/\partial w_{1} ,\partial E(w)/\partial w_{2} , \ldots ,\partial E(w)/\partial w_{N} ).$$

Algorithm 2 (GA algorithm part): Based on polygonal FNN, we can use network’s parameters as an initial group of GA algorithm. The original single group can be denoted as multiple groups, and we can also adjust crossover and mutation probability dynamically. This improved GA algorithm is not only easy to combine with BP algorithm, but also avoids the above disadvantages. And it can search for the global optimal solution to optimize parameters better than the traditional GA algorithm.

Step 1. Given searching accuracy $\gamma > 0$, and the number of iteration step $t_{2} = 0$, for $j = 1,2, \cdots ,p$, let

$$\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\;\;a_{j} [t_{2} ] = \mathop {\hbox{min} }\limits_{{0 \le \,{\kern 1pt} i\,{\kern 1pt} \le n;\;q = 1,2}} u_{i}^{q} (j)[t_{1} ]} \\ {a_{j + p} [t_{2} ] = \mathop {\hbox{min} }\limits_{{0 \le \,{\kern 1pt} i\,{\kern 1pt} \le n;\;q = 1,2}} v_{i}^{q} (j)[t_{1} ]} \\ \end{array} } \\ {a_{j + 2p} [t_{2} ] = \mathop {\hbox{min} }\limits_{{0 \le \,{\kern 1pt} i\,{\kern 1pt} \le n;\;q = 1,2}} \theta_{i}^{q} (j)[t_{1} ]} \\ \end{array} ;} \right.\quad \quad \quad \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\;\;b_{j} [t_{2} ] = \mathop {\hbox{max} }\limits_{{0 \le \,{\kern 1pt} i\,{\kern 1pt} \le n;\;q = 1,2}} u_{i}^{q} (j)[t_{1} ]} \\ {b_{j + p} [t_{2} ] = \mathop {\hbox{max} }\limits_{{0 \le \,{\kern 1pt} i\,{\kern 1pt} \le n;\;q = 1,2}} v_{i}^{q} (j)[t_{1} ]} \\ \end{array} } \\ {b_{j + 2p} [t_{2} ] = \mathop {\hbox{max} }\limits_{{0 \le \,{\kern 1pt} i\,{\kern 1pt} \le n;\;q = 1,2}} \theta_{i}^{q} (j)[t_{1} ]} \\ \end{array} } \right.,$$

Step 2. For each$j = 1,2, \cdots ,3p$, let each parameter’s vector of binary string length denote $l_{j} = \log_{2} ((a_{j} [t_{2} ] - b_{j} [t_{2} ])/\gamma )$ In addition, $l$ denotes a group’s gene pool of binary string length, i.e. $l = \hbox{max} \{ l_{1} ,l_{2} , \ldots ,l_{3p} \}$. According to (2), we let $w\,[t_{2} ] = (w_{1} [t_{2} ],w_{2} [t_{2} ], \ldots ,w_{N} [t_{2} ])$, and for all $i = 1,2, \ldots ,N$, and approximately, each parameter’s component can be expressed as a binary number $\beta_{i} [t_{2} ] \in \varpi_{nn}$ $(w_{i} [t_{2} ] \to \beta_{i} [t_{2} ])$.

Step 3. Based on Algorithm 1, we randomly generate $m_{0}$ groups of $N$ individuals. (Total of groups expands as $m_{0} .$) To calculate easily, we introduce fitness function $J(w) = 1/(1 + E(w))$, and for $\beta_{i} (k)[t_{2} ](i = 1,2, \ldots ,N$; $k = 1,2, \ldots ,m_{0} )$, decode to transform $w'(k)[t_{2} ] = (w'_{1} (k)[t_{2} ],w'_{2} (k)[t_{2} ], \ldots ,w'_{N} (k)[t_{2} ])$, then calculate $J(w'(k)[t_{2} ]).$

Step 4. According to the roulette wheel selection (see [9]), for $k = 1,2, \ldots ,m_{0}$, let survival probability of each individual $\beta_{i} (k)[t_{2} ]$ denote $p_{k} =$ $J(w'(k)[t_{2} ])/\sum\nolimits_{k' = 1}^{{m_{0} }} {J(w'(k')[t_{2} ])} .$ Let single-point crossover operator $p:\varpi_{nn}^{2} \to \varpi_{nn}^{2}$, randomly select two-to-two individuals $(\beta_{i} (k_{1} )[t_{2} ],\beta_{i} (k_{2} )[t_{2} ])$ from $m_{0}$ groups, then based on crossover probability $p(\beta_{i} (k_{1} )[t_{2} ],\beta_{i} (k_{2} )[t_{2} ])$, we can get two new individuals $(\beta_{i} (k_{1}^{'} )[t_{2} + 1],\beta_{i} (k_{2}^{'} )[t_{2} + 1]).$ In addition, the group of new individuals can be denoted as $\beta '_{i} (k)[t_{2} + 1](i =$ $1,2, \ldots ,N;k = 1,2, \ldots ,m_{0} ).$

Step 5. For all $i = 1,2, \ldots ,N;k = 1,2, \ldots ,m_{0}$, decode component $\beta '_{i} (k)[t_{2} ]$, then transform $w'(k)[t_{2} + 1] = (w'_{1} (k)[t_{2} + 1],w'_{2} (k)[t_{2} + 1], \ldots ,w'_{N} (k)[t_{2} + 1])$, so we need to recalculate $J(w'(k)[t_{2} + 1])$, and let

$$w_{best} [t_{2} + 1] = \hbox{max} \{ J(w'(k)[t_{2} + 1])\;|\,\,k = 1,2, \ldots ,m_{0} \} .$$

Step 6. Judge $k = k_{0}$, for each $i = 0,1,2, \ldots ,n;\,\,j = 1,2, \ldots ,p$, whether $w_{best} [t_{2} + 1]$ satisfies the following formula.

$$w_{i}^{'1} (j)(k_{0} )[t_{2} + 1] \le w_{i + 1}^{'1} (j)(k_{0} )[t_{2} + 1] \le w_{i + 1}^{'2} (j)(k_{0} )[t_{2} + 1] \le w_{i}^{'2} (j)(k_{0} )[t_{2} + 1].$$

If the above expression is established, then turn to step 7; otherwise, for all $j = 1,2, \ldots ,p$, sort with selection method from small to big, and turn to step 7.

Step 7. Judge whether $J(w'(k_{0} )[t_{2} + 1]) \ge J(w'(k_{0} )[t_{2} ])$. If they fulfill, let $t_{1} = t_{1} + 1$, and turn to step 2 in Algorithm 1; otherwise, let $t_{2} = t_{2} + 1$, and turn to step 1 in Algorithm 2.

Note 2. The problem in this paper is a discrete optimization problem, so in the section of GA algorithm, we can use the binary to represent each individual’s gene. This method can make encoding and decoding operations easy, and simplify crossover and mutation evolutionary processes.

Note 3. In Algorithm 2, to maintain the diversity of population and parameters optimization, and prevent premature phenomenon, we can use dynamic crossover and mutation probability. Let the number of evolution step $\lambda { = 100}$, for $k = 1,2, \ldots ,$ $m_{0}$, and crossover probability denotes $\xi_{k} [t_{2} ]$, mutation probability denotes $\zeta_{k} [t_{2} ]$, then their formulas are that

$$\xi_{k} [t_{2} ] = \left\{ {\begin{array}{*{20}c} {\frac{{\xi_{\hbox{max} } }}{{1 + t_{2} /\lambda }},\,\,\xi_{k} [t_{2} ] > \xi_{\hbox{min} } } \\ {\xi_{\hbox{min} } ,\quad \quad \xi_{k} [t_{2} ] \le \xi_{\hbox{min} } } \\ \end{array} ;} \right.\quad \quad \quad \quad \zeta_{k} [t_{2} ] = \left\{ {\begin{array}{*{20}c} {\zeta_{\hbox{max} } \cdot e^{{ - \mu t_{2} /\lambda }} ,\,\,\zeta_{k} [t_{2} ] > \zeta_{\hbox{min} } } \\ {\zeta_{\hbox{min} } ,\quad \quad \quad \zeta_{k} [t_{2} ] \le \zeta_{\hbox{min} } } \\ \end{array} } \right..$$

Generally, crossover probability $\xi_{k} [t_{2} ]$ is taken values in 0.4–0.99, and mutation probability $\zeta_{k} [t_{2} ]$ is taken values in 0.001–0.1. So we can let minimum of crossover probability $\xi_{\hbox{min} } = 0.4$, maximum of crossover probability $\xi_{\hbox{max} } = 0.99$, minimum of mutation probability $\zeta_{\hbox{min} } = 0.001$, and maximum of mutation probability $\zeta_{\hbox{max} } =$ $0.1$, and $\mu = 0.1.$

Note 4.The decoding process in step 3 and step 5 of Algorithm 2 is the following process. Firstly, we can calculate the decimal number $d_{i} (j)$ based on the corresponding binary number. Then, according to the following formula, we can get the actual network’s parameters $w_{i} (j)[t_{2} ]:w_{i} (j)[t_{2} ] = d_{i} (j) \cdot \gamma ' + a_{j} [t_{2} ]\,(i = 1,2, \ldots ,2n + 2;j = 1,2, \ldots ,p)$, where $\gamma '$ denotes actual searching accuracy after encoding, and the computing formula of $\gamma '$ is that $\gamma ' = (b_{j} [t_{2} ] - a_{j} [t_{2} ])/(2^{l} - 1).$

5 A simulation example

To discuss parameters optimization’s influence of polygonal FNN based on a GA-BP hybrid algorithm, this paper can apply the optimization to the simulation model of boiler drum water level control (see [18, 19]). We can see the structure of model system as follows (see Fig. 4).

Fig. 4

Structure of boiler drums water level control system

Generally, boiler drum water level control model can be expressed as $G(s) = {k \mathord{\left/ {\vphantom {k {s(Ts + 1)}}} \right. \kern-0pt} {s(Ts + 1)}}$, where $s$ denotes level, $k$ denotes rate of water level, and $T$ denotes time (see [20, 21]). According to the actual parameters of the boiler drum water level, the transfer function of the water flow about water level can be denoted as $G(s) = {{0.0037} \mathord{\left/ {\vphantom {{0.0037} {(30s^{2} }}} \right. \kern-0pt} {(30s^{2} }}$ $+ s).$ Based on a SISO network, traditional PID controller can be denoted as $u[t] = K \cdot \varDelta h[t] + C.$ In fact, when a boiler is working, the rating of water level must be maintained between $- 0.08\;$ and $0.08\;{\text{m}} .$ So, to the error of water level $\varDelta h$, the range should be $[ - 0.08\;{\text{m}}, + 0.08\;{\text{m}}].$ This paper takes the interval $[ - 3,3]$ as range of the level’s error $\varDelta h$ and the direct voltage $u$, then the coefficient $K = 3/0.08 = 37.5.$

Then we can design the controller of polygonal FNN, and the number of fuzzy inference rules $L = 7.$ Antecedent polygonal number $\tilde{X}(l)$ can be denoted as water level’s error, and consequent polygonal number $\tilde{O}(l)$ can be denoted as direct voltage. We can use the single–input–single–output relationship as the above polygonal numbers, then we can get fuzzy pattern pairs of polygonal FNN $(\tilde{X}(l),\tilde{O}(l)),\,l = 1,2, \ldots ,7.$ To simplify, let $n = 4$, and randomly select actual input $\tilde{X}(l)$ and expected output $\tilde{O}(l)$ corresponding to 4-polygonal fuzzy pattern pairs (see Tables 1, 2).

Table 1 Trained 4-polygonal fuzzy pattern pairs

Table 2 Trained 4-polygonal fuzzy pattern pairs

From the above Tables 1, 2 showed two 4-polygonal fuzzy pattern pairs, we can draw the membership functions’ curves of the actual input $\tilde{X}(l)$ and expected output $\tilde{O}(l)\,(l = 1,2, \ldots ,7)$ with Mathematica software in Figs. 5, 6.

Fig. 5

Antecedent 4-polygonal fuzzy numbers

Fig. 6

Consequent 2-polygonal fuzzy numbers

We can apply the original BP algorithm, the traditional GA algorithm and the GA-BP hybrid algorithm to parameters optimization based on polygonal FNN. Let transfer function $\sigma (x) = 0,x < 0;\,\sigma (x) = x/(1 + x^{2} ),\,\,x \ge 0$, and error accuracy $\varepsilon = 10^{ - 3}$, searching accuracy $\gamma = 10^{ - 6}$, total of groups $m_{0} = 40$, where the number of hidden layers is 14. If error function $E(w)$ satisfies the condition or the algorithm’s iteration is stopped, we can get the following optimization results (see Table 3).

Table 3 Comparison of parameters optimization results among three algorithms

From Table 3, we can see that the GA-BP hybrid algorithm can reduce the number of iterations to 174, and greatly reduce the number of local minimum. This algorithm doesn’t only overcome slow convergence of the original BP algorithm which is easy to fall into local minimum, but also enhances the ability of the GA algorithm’s global searching to improve the rate of polygonal FNN’s parameters optimization. The optimized parameters of the above three algorithms are applied to polygonal FNN’s controller in the boiler drum water level control system, and we can get the system’s simulation results by comparing PID controller (see Fig. 7).

Fig. 7

The simulation curve of boiler drum water level control system

Clearly, from Fig. 7, we can get that the system of the simulation curve’s amplitude is small, and the system responses fast, control accuracy is high, and it has the best optimization result by parameters optimization of the GA-BP hybrid algorithm based on the polygonal FNN’s controller. In addition, comparing with the original BP and the traditional GA algorithm, parameters optimization is improved, and reduces the system’s overshoot and responding time greatly by the GA-BP hybrid algorithm. Then the system can be adjusted to a steady state in short period of time, and also improved its stability. The result shows that parameters optimization of the GA-BP hybrid algorithm for polygonal FNN is better than others. And the optimization doesn’t only get rid of the dependence of the original BP algorithm’s initial points and local convergence, but also overcomes the random and probabilistic problem of the traditional GA algorithm. Therefore, the optimization can lay the foundation to study the good performance of polygonal FNN in the future.

6 Conclusion

In this article, based on the expansive operations of polygonal fuzzy numbers, we combine the BP algorithm with the GA algorithm, and design a GA-BP hybrid learning algorithm for polygonal FNN. Finally, we prove the effectiveness of the GA-BP hybrid algorithm by simulation examples. In fact, because the algorithm is complex, it results in its convergence’s time to be slightly longer than the BP algorithm. In addition, we don’t add the other convergence criteria to solve the global optimal value, and the GA algorithm has blindness and probabilistic problem. Hence, the algorithm maybe doesn’t reach the optimal solution, but just approximate the optimal value. So how to design simple and practical algorithm for polygonal FNN is a further research. For example, join A-G criteria of the dynamic convergence condition to solve the global optimal value. In addition, it is worth studying further to improve the parameters’ iteration formula of the BP algorithm appropriately.