A robust self-learning PID control system design for nonlinear systems using a particle swarm optimization algorithm

Abstract

This study presents a robust self-learning proportional-integral-derivative (RSPID) control system design for nonlinear systems. This RSPID control system comprises a self-learning PID (SPID) controller and a robust controller. The gradient descent method is utilized to derive the on-line tuning laws of SPID controller; and the $\, H_{\infty } \,$ control technique is applied for the robust controller design so as to achieve robust tracking performance. Moreover, in order to achieve fast learning of PID controller, a particle swarm optimization (PSO) algorithm is adopted to search the optimal learning-rates of PID adaptive gains. Finally, two nonlinear systems, a two-link manipulator and a chaotic system are examined to illustrate the effectiveness of the proposed control algorithm. Simulation results show that the proposed control system can achieve favorable control performance for these nonlinear systems.

1 Introduction

The proportional-integral-derivative (PID) controller has been practically applied in industries for 60 years due to its simple architecture and easy design properties. Until today, the PID controller is still used in different control applications, even though lots of new control techniques have been proposed. However, the traditional PID controller needs some manual tuning before it is used to practical application in industries. When the PID controllers are applied to complicated systems such as nonlinear systems, different tuning algorithms of PID controllers have been proposed [1–5]. In recent decade, several intelligent tuning algorithms have been applied to tune the PID controllers. The PID controller automatic tuning methods have been proposed by using a genetic algorithm [6], an immune algorithm [7] and a fuzzy-genetic algorithm [8]. However, the learning speed of these algorithms is slow; thus, they are not suitable for real time control systems. Harinath and Mann [9] proposed a fuzzy PID controller for multivariable process systems. However, it takes a two-level tuning algorithm; thus, it also takes too much computation time. Therefore, in this paper, another simple optimization algorithm called particle swam optimization (PSO) algorithm will be used for the optimal parameter search of the PID controller.

The PSO algorithm, a new evolutionary computation technique, is proposed by Kennedy and Eberhart [10]. It was developed by the research of the social behavior of animals, e.g., bird flocking. Unlike a typical GA, PSO algorithms have memorial capability without complicated evolutionary process such as crossover and mutation in GA, and each particle can memorize its best solution. In addition, if another particle discovers a better solution, it will be shared among other particles. The best solution is thus memorized and every particle will move toward this best solution. In past decade, PSO algorithms have been widely used to solve the modeling and control problems of application systems [11–14]. Moreover, the PID control based on PSO algorithms have been proposed in [15, 16]. However, it is difficult to solve the inequality for the optimal solution in [15]; and it has not given the stability analysis in [16].

In this paper, a robust self-learning PID (RSPID) control system is proposed for nonlinear systems. This RSPID control system comprises a self-learning PID (SPID) controller and a robust controller. The SPID controller is utilized to approximate an ideal controller, and the robust controller is designed to recover the residual approximation error between the ideal controller and SPID controller. The gradient descent method and $\, H_{\infty } \,$ control technique are utilized to derive the on-line tuning laws of SPID controller and robust controller, so that the robust stability of the system can be obtained. Furthermore, the PSO algorithm is adopted to auto-search the optimal learning-rates of PID controller to increase the learning speed. Finally, two nonlinear systems are presented to support the validity of the proposed control method.

This study is organized as follows. Problem formulation is described in Sect. 2. The PSO algorithm is briefly reviewed in Sect. 3. The design procedure of the proposed RSPID control system is constructed in Sect. 4. In Sect. 5, simulations are performed to verify the effectiveness of the proposed control method. Finally, conclusions are drawn in Sect. 6.

2 Problem formulation

Consider a class of nth-order multi-input multi-output (MIMO) nonlinear systems expressed in the following form:

$$ \begin{aligned} \user2{x}^{(n)} (t) & = \user2{f}(\underline{\user2{x}} (t)) + \user2{G}(\underline{\user2{x}} )(t)\user2{u}(t) + \user2{d}(t) \\ \user2{y} & = \user2{x}(t) \\ \end{aligned} $$

(1)

where

$\user2{u}(t) = [u_{1} (t),u_{2} (t), \ldots , \, u_{m} (t)]^{T} \in \Re^{m} \,$ :

the control input vector of the system

$\user2{y} = \user2{x}(t) = [x_{1} (t),x_{2} (t), \ldots , \, x_{m} (t)]^{T} \in \Re^{m}$ :

the system output vector

$\underline{\user2{x}} (t) = [\user2{x}^{T} (t),\dot{\user2{x}}^{T} (t), \ldots ,\user2{x}^{(n - 1)T} (t)]^{T} \in \Re^{mn}$ :

the state vector of the system

$\user2{f}(\underline{\user2{x}} (t)) \in \Re^{m} \,$ :

unknown bounded nonlinear function

$\user2{G}(\underline{\user2{x}} (t)) \in \Re^{m \times m} \,$ :

unknown bounded nonlinear matrix

$\user2{d}(t) = [d_{ 1} (t) ,d_{2} (t) ,\ldots , { }d_{m} (t)]^{T} \in \Re^{m}$ :

unknown bounded external disturbance.

When neglecting the modeling uncertainty and external disturbance, the nominal system of Eq. 1 can be obtained as

$$ \user2{x}^{(n)} (t) = \user2{f}_{n} (\underline{\user2{x}} (t)) + \user2{G}_{n} \user2{u}(t) $$

(2)

where $\, \user2{f}_{n} (\underline{\user2{x}} (t)) \in \Re^{\text{m}}$ is the nominal function of $\user2{f}(\underline{\user2{x}} (t))$, and the constant matrix $\user2{G}_{n} = diag(g_{n1} , \, g_{n2} , \ldots , \, g_{nm} ) \in \Re^{m \times m} \,$ is the nominal functions of $\user2{G}(\underline{\user2{x}} (t))$. Without losing generality, assume the constant $g_{ni} \ge 0$ for $i = 1 \ldots m$. Assume that the nonlinear system of Eq. 2 is controllable and $\user2{G}_{n}^{ - 1}$ exists for all $\underline{\user2{x}} (t)$. If the external disturbance and modeling uncertainty exist, the MIMO nonlinear systems Eq. 1 can be reformulated as

$$ \user2{x}^{(n)} (t) = \user2{f}_{n} (\underline{\user2{x}} (t)) + \user2{G}_{n} \user2{u}(t) + \user2{l}(\underline{\user2{x}} (t),t) $$

(3)

where $\user2{l}(\underline{\user2{x}} (t),t)$ is referred to as the lumped uncertainty, including system’s uncertainty and external disturbance.

The control problem is to find a suitable controller for the MIMO nonlinear systems Eq. 1 so that the system output vector $\user2{x}(t)$ can track desired reference trajectory vector $\user2{x}{}_{d}(t) = [x_{d1} (t),x_{d2} (t), \ldots , \, x_{dm} (t)]^{T} \in \Re^{m}$ closely.

A lot of control techniques have been presented to achieve reference trajectory tracking. However, in this paper, a simple adaptive PID control scheme will be proposed to deal with the uncertain MIMO nonlinear system. Moreover, the $\, H_{\infty } \,$ control technique will be used to guarantee the robust tracking performance.

Define the tracking error as

$$ \user2{e}(t)\underline{\underline{\Updelta }} \user2{x}_{d} (t) - \user2{x}(t) \in \Re^{m} $$

(4)

then the system tracking error vector is defined as

$$ \underline{\user2{e}} \underline{\underline{\Updelta }} [\user2{e}^{T} (t),\dot{\user2{e}}^{T} (t), \ldots ,\user2{e}^{(n - 1)T} (t)]^{T} \in \Re^{mn} $$

(5)

If the system dynamics $\user2{f}_{n} (\underline{\user2{x}} (t))$ and $\user2{G}_{n}$, and the lumped uncertainty $\user2{l}(\underline{\user2{x}} ,t)$ are exactly known, an ideal controller can be designed as

$$ \user2{u}^{*} (t) = \user2{G}_{n}^{ - 1} [\user2{x}_{d}^{(n)} (t) - \user2{f}_{n} (\underline{\user2{x}} (t)) - \user2{l}(\underline{\user2{x}} (t),t) + \underline{\user2{H}}^{T} \underline{\user2{e}} (t)] $$

(6)

where $\underline{\user2{H}} = [\user2{H}_{n} , \ldots ,\user2{H}_{2} ,\user2{H}_{1} ]^{T} \in \Re^{mn \times m}$ is the feedback gain matrix which contains real numbers. $\user2{H}_{i} = diag(h_{i1} ,h_{i2} , \ldots ,h_{im} ) \in \Re^{m \times m} \,$ is a nonzero positive constant diagonal matrix. Substituting the ideal controller Eq. 6 into Eq. 3, gives the error dynamic equation

$$ \user2{e}^{(n)} + \underline{\user2{H}}^{T} \underline{\user2{e}} = 0 $$

(7)

In Eq. 7, if H is chosen to correspond to the coefficients of a Hurwitz polynomial, it implies $\mathop {\lim }\limits_{t \to \infty } ||\underline{\user2{e}} (t)|| = 0$. However, in practical application, the system uncertainties and external disturbance of nonlinear systems are generally unknown, so that the idea controller $\user2{u}^{*}$ in Eq. 6 is always unobtainable. Thus, a SPID controller is designed to mimic the idea controller. And then, based on the $H_{\infty }$ control technique, the robust controller is developed to attenuate the effect of the approximation error between SPID controller and the ideal controller so that the robust tracking performance can be achieved.

3 Robust self-learning PID (RSPID) control system design

The block diagram of the nonlinear control system is shown in Fig. 1. The RSPID control system is assumed to take the following form:

$$ \user2{u}_{RSPID} (t) = \user2{u}_{SPID} (t) + \user2{u}_{R} (t) $$

(8)

where $\user2{u}_{SPID} (t)$ is a self-learning PID controller utilized to approximate the ideal controller $\user2{u}^{*}$, and $\user2{u}_{R} (t)$ is the robust controller designed to suppress the influence of residual approximation error between the ideal controller and SPID controller.

Fig. 1

The block diagram of RSPID control system

3.1 SPID controller design

The SPID controller can be described as

$$ \user2{u}_{SPID} (t) = \hat{\user2{K}}_{P} \user2{e}(t) + \hat{\user2{K}}_{I} \int\limits_{0}^{t} {\user2{e}(\tau )d\tau } + \hat{\user2{K}}_{D} \frac{{d\user2{e}(t)}}{dt} $$

(9)

where $\hat{\user2{K}}_{P} ,\; \, \hat{\user2{K}}_{I}$ and $\hat{\user2{K}}_{D}$ are the adaptive parameters of proportional gain, integral gain and derivative gain matrices, respectively; and $\hat{\user2{K}}_{P} = diag(\hat{k}_{P1} ,\hat{k}_{P2} , \ldots ,\hat{k}_{Pm} ) \in \Re^{m \times m} ,$ $\hat{\user2{K}}_{I} = diag(\hat{k}_{I1} ,\hat{k}_{I2} , \ldots ,\hat{k}_{Im} ) \in \Re^{m \times m} ,$ $\hat{\user2{K}}_{D} = diag(\hat{k}_{D1} ,\hat{k}_{D2} , \ldots \hat{k}_{Dm} ) \in \Re^{m \times m} .$

An integrated error function is defined as

$$ \user2{s}(\underline{\user2{e}} ,t) \equiv \user2{e}^{(n - 1)} + \user2{H}_{1} \user2{e}^{(n - 2)} + \cdots + \user2{H}_{n} \int\limits_{0}^{t} {\user2{e}(\tau )d\tau } $$

(10)

where $\user2{s}(\underline{\user2{e}} ,t) = [s_{1} (t),s_{2} (t), \ldots ,s_{m} (t)]^{T}$. From Eq. 9, the control law Eq. 8 can be rewritten as

$$ \user2{u}_{RSPID} (t) = \user2{u}_{SPID} (\hat{\user2{K}}_{P} ,\hat{\user2{K}}_{I} ,\hat{\user2{K}}_{D} ,t) + \user2{u}_{R} (t) $$

(11)

Taking the time derivative of both sides of Eq. 10 and using Eq. 3, it can be obtained that

$$ \dot{\user2{s}}(\underline{\user2{e}} ,t) = \user2{e}^{(n)} + \underline{\user2{H}}^{T} \underline{\user2{e}} = - \user2{f}_{n} (\underline{\user2{x}} (t)) - \user2{G}_{n} \, \user2{u}(t) + \user2{x}_{d}^{(n)} - \user2{l}(\underline{\user2{x}} (t),t) + \underline{\user2{H}}^{T} \underline{\user2{e}} $$

(12)

Substituting Eq. 9 into Eq. 12 and multiplying both sides by $\user2{s}^{T} (\underline{\user2{e}} ,t)$, yields

$$ \begin{aligned} \user2{s}^{T} ({{\underline{\user2{e}} }} ,t)\dot{\user2{s}}(\underline{\user2{e}} ,t) & = - \user2{s}^{T} (\underline{\user2{e}} ,t)\user2{f}_{n} (\underline{\user2{x}} (t)) - \user2{s}^{T} ({{\underline{\user2{e}} }} ,t)\user2{G}_{n} [\user2{u}_{SPID} (\hat{\user2{K}}_{P} ,\hat{\user2{K}}_{I} ,\hat{\user2{K}}_{D} ,t) + \user2{u}_{R} (t)] \\ & \quad + \user2{s}^{T} (\underline{\user2{e}} ,t)\;(\user2{x}_{d}^{(n)} - \user2{l} (\underline{\user2{x}} (t),t )+ \underline{\user2{H}}^{T} \underline{\user2{e}} ) \\ \end{aligned} $$

(13)

By defining $\frac{1}{2}\user2{s}^{T} (\underline{\user2{e}} ,t)\user2{s}(\underline{\user2{e}} ,t)$ as a cost function, then its derivative is $\user2{s}^{T} (\underline{\user2{e}} ,t)\dot{\user2{s}}(\underline{\user2{e}} ,t)$. According to the gradient descent method, the gains of $\hat{\user2{K}}_{P} ,\,\hat{\user2{K}}_{I}$ and $\hat{\user2{K}}_{D}$ are updated by the following tuning laws

$$ \dot{\hat{k}}_{Pi} = - \eta_{p} \frac{{\partial \user2{s}^{T} (\underline{\user2{e}} ,t)\dot{\user2{s}}(\underline{\user2{e}} ,t)}}{{\partial \, u_{{SPID_{i} }} (t)}}\frac{{\partial u_{{SPID_{i} }} (t)}}{{\partial \hat{k}_{Pi} }} = \eta_{P} \, s_{i} (t)g_{ni} \, e_{i} (t) $$

(14)

$$ \dot{\hat{k}}_{Ii} = - \eta_{I} \frac{{\partial \user2{s}^{T} (\underline{\user2{e}} ,t)\dot{\user2{s}}(\underline{\user2{e}} ,t)}}{{\partial u_{{SPID_{i} }} (t)}}\frac{{\partial u_{{SPID_{i} }} (t)}}{{\partial \hat{k}_{Ii} }} = \eta_{I} \, s_{i} (t)g_{ni} \, \int\limits_{0}^{t} {e_{i} (t)d\tau } $$

(15)

$$ \dot{\hat{k}}_{Di} = - \eta_{D} \frac{{\partial \user2{s}^{T} (\underline{\user2{e}} ,t)\dot{\user2{s}}(\underline{\user2{e}} ,t)}}{{\partial u_{{SPID_{i} }} (t)}}\frac{{\partial u_{{SPID_{i} }} (t)}}{{\partial \hat{k}_{Di} }} = \eta_{D} \, s_{i} (t)g_{ni} \, \frac{{de_{i} (t)}}{dt} $$

(16)

where $u_{{SPID_{i} }}$ is the ith element of $\user2{u}_{SPID}$; $\eta_{P} ,\,\eta_{I}$ and $\eta_{D}$ are the learning-rates, which will be auto-searched by PSO algorithm.

3.2 Robust controller design

In case of the existence of an approximation error, the ideal controller can be reformulated as the summation of SPID controller and the approximation error:

$$ \user2{u}^{*} (t) = \user2{u}_{SPID} (\hat{\user2{K}}_{P} ,\hat{\user2{K}}_{I} ,\hat{\user2{K}}_{D} ,t) + \varepsilon (t) $$

(17)

where $\varepsilon (t) = [\varepsilon_{1} (t),\varepsilon_{2} (t), \ldots , \, \varepsilon_{m} (t)]^{T} \in \Re^{m}$ denotes the approximation error.

Substituting Eq. 8 into Eq. 3, yields

$$ \user2{x}^{(n)} (t) = \user2{f}_{n} (\underline{\user2{x}} (t)) + \user2{G}_{n} [\user2{u}_{SPID} (t) + \user2{u}_{R} (t)] + \user2{l}(\underline{\user2{x}} (t),t) $$

(18)

From Eqs. 6, 10, 18 and after some straightforward manipulation, it can be obtained that

$$ \user2{e}^{(n)} + \underline{\user2{H}}^{T} \underline{\user2{e}} = \user2{G}_{n} [\user2{u}^{*} (t) - \user2{u}_{SPID} (t) - \user2{u}_{R} (t)] = \dot{\user2{s}}(\underline{\user2{e}} ,t) $$

(19)

Now, the robust controller can be developed to attenuate the effect of the approximation error between the ideal controller and SPID controller so that the $\, H_{\infty } \,$ tracking performance can be achieved. In case of the existence of $\, {\mathbf{\varepsilon }}(t) ,$ consider a specified $\, H_{\infty } \,$ tracking performance [17]

$$ \sum\limits_{i = 1}^{m} {\int\limits_{0}^{T} {s_{i}^{ 2} (t ) { }dt} \le } \sum\limits_{i = 1}^{m} {[s_{i}^{ 2} ( 0 ) /g_{ni} ] + } \sum\limits_{i = 1}^{m} {r_{i}^{ 2} \int\limits_{0}^{T} {\varepsilon_{i}^{ 2} (t ) { }dt} } $$

(20)

where $r_{i} \,$ is a prescribed attenuation constant. The robust controller is designed as

$$ \user2{u}_{R} (t )= { (2}\user2{R}^{ 2} )^{ - 1} (\user2{R}^{ 2} + \user2{I} ) { }\user2{s}(\underline{\user2{e}} ,t) $$

(21)

where $\, \user2{R} = diag (r_{ 1} ,r_{2} ,\ldots ,r_{m} )\in \Re^{m \times m} . { }$ Then the following theorem can be stated and proven.

Theorem 1: Consider the nth-order MIMO nonlinear systems represented by Eq. 1 . The RSPID control law is designed as Eq. 11 , where $\user2{u}_{SPID} (t)$ is given in Eq. 9 with the on-line parameter tuning algorithms given as Eqs. 14–16, and the robust controller is designed as Eq. 21 . Then the desired $H_{\infty }$ tracking performance in Eq. 20 can be achieved for the specified attenuation levels $\, r_{i} ,i = 1,2, \ldots ,m.$

Proof: The Lyapunov function is given by

$$ V(\user2{s}(\underline{\user2{e}} ,t)) = \frac{1}{2}\user2{s}^{T} (\underline{\user2{e}} ,t)\user2{s}(\underline{\user2{e}} ,t) $$

(22)

Taking the derivative of the Lyapunov function and using Eqs. 17, 19 and 21, yields

$$ \begin{aligned} \dot{V}(\user2{s}(\underline{\user2{e}} ,t)) & = \user2{s}^{T} (\underline{\user2{e}} ,t)\dot{\user2{s}}(\underline{\user2{e}} ,t) \\ & = \user2{s}^{T} (\underline{\user2{e}} ,t)\user2{G}_{n} [\varepsilon (t) - (2\user2{R}^{2} )^{ - 1} (\user2{R}^{2} + \user2{I}) \, \user2{s}(\underline{\user2{e}} ,t)] \\ & = \sum\limits_{i = 1}^{m} {g_{ni} \left[ {s_{i} (t)\varepsilon_{i} (t) - s_{i}^{2} (t)\frac{{r_{i}^{2} + 1}}{{2r_{i}^{2} }}} \right]} \\ & = \sum\limits_{i = 1}^{m} {g_{ni} \left[ { {s_{i} (t)\varepsilon_{i} (t) - \frac{{s_{i}^{2} (t)}}{2 \, } - \frac{{s_{i}^{2} (t)}}{{2 \, r_{i}^{2} }}} } \right]} \\ & = \sum\limits_{i = 1}^{m} {g_{ni} \left[ { - \frac{{s_{i}^{2} (t)}}{2 \, } - \frac{1}{2}\left( {\frac{{s_{i} (t)}}{{ \, r_{i} }} - r_{i} \varepsilon_{i} (t)} \right)^{2} + \frac{{r_{i}^{2} \varepsilon_{i}^{2} (t)}}{2 \, }} \right]} \le \sum\limits_{i = 1}^{m} {g_{ni} \left[ { - \frac{{s_{i}^{2} (t)}}{2 \, } + \frac{{r_{i}^{2} \varepsilon_{i}^{2} (t)}}{2 \, }} \right]} \\ \end{aligned} $$

(23)

Assuming $\, \varepsilon_{i} (t) \in L_{2} [0,T], \, \forall T \in [0,\infty ),$ integrating the above equation from t = 0 to t = T, yields

$$ V(T) - V(0) \le \sum\limits_{i = 1}^{m} {g_{ni} \left[ { - \frac{1}{2}\int\limits_{0}^{T} {s_{i}^{2} (t)\left( t \right) \, dt} + \frac{{r_{i}^{2} }}{2 \, }\int\limits_{0}^{T} {\varepsilon_{i}^{2} (t)dt} } \right]} $$

(24)

Since $V(T) \ge 0$, the above inequality implies the following inequality

$$ \frac{1}{2}\sum\limits_{i = 1}^{m} {g_{ni} \int\limits_{0}^{T} {s_{i}^{2} (t)dt} \le \, } V(0) + \frac{1}{2}\sum\limits_{i = 1}^{m} {g_{ni} r_{i}^{2} \int\limits_{0}^{T} {\varepsilon_{i}^{2} (t)dt} } $$

(25)

Using Eq. 22, the above inequality is equivalent to the following

$$ \sum\limits_{i = 1}^{m} {\int\limits_{0}^{T} {s_{i}^{2} (t)dt} \le } \, \sum\limits_{i = 1}^{m} {[s_{i}^{2} (0)/g_{ni} ]} + \sum\limits_{i = 1}^{m} {r_{i}^{2} \int\limits_{0}^{T} {\varepsilon_{i}^{2} (t)dt} } $$

(26)

Thus the proof is completed.

4 Particle swarm optimization (PSO) algorithm

The learning-rates of the tuning laws in SPID controller are usually selected by trial-and-error process. In order to achieve the best learning speed, the PSO algorithm is adopted to search the optimal learning-rates $\eta_{P} ,\,\eta_{I}$ and $\eta_{D}$ in the SPID controller.

In 1995, Kennedy and Eberhart [10] initially proposed the particle swarm concept and PSO algorithm; this algorithm is one of optimization methods. It has been proven to be efficient in solving optimization problem. In the PSO algorithm, each particle represents a candidate solution to the optimization problem. The particle keeps track of its coordinates in the problem space which are associated with the personal best solution. Another is the global best value that is tracked by the global version of the particle swarm optimizer. At each time step, the PSO algorithm consists of changing the velocity that accelerates each particle toward its personal best and global best locations. Acceleration is weighted by a random term with separate random numbers being generated for acceleration toward personal best and global best locations, respectively [11]. From then on, several PSO algorithms have been proposed with slightly different versions [12–16].

The flowchart of the utilized PSO algorithm is drawn in Fig. 2.

Fig. 2

The flowchart of PSO algorithm

4.1 Fitness function

In order to maintain the control characteristic of SPID controller, a fitness function is chosen as

$$ fit = \frac{1}{{0.1 + ||\underline{\user2{e}} (t)||}} $$

(27)

It means that if the error states $\underline{\user2{e}} (t)$ is forced to zero then the expected value of fitness will be $fit = 10$.

4.2 Velocity and position update law

In PSO algorithm, a population of particles is randomly generated initially; each particle adjusts self-position with velocity according to its own experience and the experiences of other particles. The particle velocity and position update law is adopted as [16]

$$ \begin{aligned} v_{q}^{l} (n + 1) & = v_{q}^{l} (n) \times iw + \xi_{1} \times rand_{1} ( \cdot ) \times [L_{{best_{q} }}^{l} - p_{q}^{l} (n)] \\ & \quad + \xi_{2} \times rand_{2} ( \cdot ) \times [G_{{best_{q} }}^{l} - p_{q}^{l} (n)] \\ & \quad + \xi_{3} \times rand_{3} ( \cdot ) \times [S_{{best_{q} }}^{l} - p_{q}^{l} (n)] \\ \end{aligned} $$

(28)

$$ p_{q}^{l} (n + 1) = p_{q}^{l} (n) + v_{q}^{l} (n + 1) $$

where iw is called the inertia weight which balances the global and local search, $v_{q}^{l} (n)$ and $p_{q}^{l} (n)$ denote current velocity and current position, respectively; $rand_{1} ( \cdot )$, $rand_{2} ( \cdot )$ and $rand_{3} ( \cdot )$ denote random variables between 0 and 1; ξ ₁, ξ ₂, and ξ ₃ denote acceleration factor_1, acceleration factor_2 and acceleration factor_3, respectively; $L_{{best_{q} }}^{l}$, $G_{{best_{q} }}^{l}$, and $S_{{best_{q} }}^{l}$ are the personal best index, the global best index, and the sub-population best index of the qth particle, respectively. Additionally, $q = 1,2, \ldots ,n_{p}$, in which $n_{p}$ is the population size and $\ell = 1,2, \ldots ,n_{d}$, in which n _d is the dimension of each particle and iw is given by

$$ iw = iw_{\max } - \frac{{iw_{\max } - iw_{\min } }}{{N_{\max } }} \times N_{n} $$

(29)

where iw _max, iw _min, N _max and N _n are iteration maximum value, iteration minimum value, total iteration number and current iteration number of inertia weight.

This PSO algorithm is used to on-line tune the learning-rates η _P , η _I and η _D in Eqs. 14–16 to achieve fast learning speed of PID gains.

5 Simulation results

Two uncertain nonlinear systems, a two-link manipulator control system and a unified chaotic system are examined to illustrate the effectiveness of the proposed design method. The parameters of PSO are set as: the population size z = 20, the dimension of the particle h = 2, the acceleration factors ξ ₁ = 0.75, ξ ₂ = 3.25, ξ ₃ = 0.1, the total iteration number N _max = 10, the iteration maximum value iw _max = 0.9, the iteration minimum value iw _min = 0.4, the initial states of velocity $v_{q}^{l} (n)$ and position $p_{q}^{l} (n)$ of each particle are randomly generated.

Example 1. Two-link manipulator system

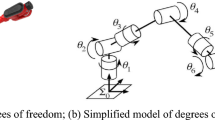
In this example, the proposed control system is applied to control a two-link robot manipulator. Figure 3 depicts this two-link manipulator, the angles of the second and the third links were considered to be θ ₁ and θ ₂, respectively [18]. In addition, the numerical values of parameters of the robot model were specified as that in [19]. The dynamic equation is given as follows

Fig. 3

The two-link manipulator system

$$ \user2{M} ({\varvec{\theta}} )\ddot{{\varvec{\theta}} } + \user2{A}_{m} ({\varvec{\theta}} ,\dot{{\varvec{\theta}} } )\dot{{\varvec{\theta}} } + \user2{B} ({\varvec{\theta}} )+ \user2{Z}\dot{{\varvec{\theta}} } + \tau_{d} = \tau $$

(30)

where ${\varvec{\theta}} \in \Re^{n}$ is the joint position vector; $\user2{M} ({\varvec{\theta}} )\in \Re^{n \times n}$ is a symmetric positive definite inertia matrix; $\user2{A}_{m} ({\varvec{\theta}} ,\dot{{\varvec{\theta}} })$ is a vector of Coriolos and centripetal torques; $\user2{B}({\varvec{\uptheta}}) \in \Re^{n}$ representing the gravitational torques; $\user2{Z} = \user2{K}_{\omega } + \user2{V}_{f} \in \Re^{n \times n}$ is a diagonal matrix consisting of the back emf coefficient matrix $\user2{K}_{\omega }$ and the viscous friction coefficient matrix $\user2{V}_{f}$; $\tau_{d} \in \Re^{n}$ is the unmodeled disturbances vector; $\tau \in \Re^{n}$ is the vector of control input torques. By defining the state vector $\underline{x} (t) = [x_{1} (t),x_{2} (t)]^{T} = [\theta_{1} ,\theta_{2} ]^{T}$, the dynamic Eq. 30 can be expressed as

$$ {\ddot{\user2{x}}} (t )= \user2{f} (\user2{x} (t ) )+ \user2{G} (\user2{x} (t ) )\;\user2{u} (t )+ \user2{d} (t ) $$

(31)

where the unknown nonlinear function $\user2{G} (\user2{x} (t ) )= \user2{M}^{ - 1} ({\varvec{\theta}} ),$ and $\user2{f} (\underline{\user2{x}} (t) )= \user2{M}^{ - 1} ({\varvec{\theta}} ) - \left[ {\user2{A}_{m} ({\varvec{\theta}} ,\dot{{\varvec{\theta}} })\dot{{\varvec{\theta}} } - \user2{B}(\dot{{\varvec{\theta}} }) - \user2{Z}\dot{{\varvec{\theta}} } - \tau_{d} } \right],$ where $\user2{A}_{m} ({\varvec{\theta}} ,\dot{{\varvec{\theta}} }) = \sin (\theta_{2} )(a_{2} + p_{2} a_{9} )\left[ {\begin{array}{*{20}c} { - \dot{\theta }_{2} } & { - (\dot{\theta }_{1} + \dot{\theta }_{2} )} \\ {\dot{\theta }_{1} } & 0 \\ \end{array} } \right],\quad \user2{B}({\varvec{\theta}} ) = \left[ {\begin{array}{*{20}c} {a_{2} } & 0 \\ 0 & {a_{8} } \\ \end{array} } \right],$ $\user2{Z} = \left[ {\begin{array}{*{20}c} {a_{5} \cos (\theta_{1} ) + a_{6} \cos (\theta_{1} + \theta_{2} ) + p_{4} \cos (\theta_{1} ) + p_{5} \cos (\theta_{1} + \theta_{2} )a_{9} } \\ {a_{6} \cos (\theta_{1} + \theta_{2} ) + p_{5} \cos (\theta_{1} + \theta_{2} )a_{9} } \\ \end{array} } \right],M = \left[ {\begin{array}{*{20}c} {M_{11} } & {M_{12} } \\ {M_{21} } & {M_{22} } \\ \end{array} } \right]$

where $\begin{aligned} M_{11} & = a_{1} + 2a_{2} \cos (\theta_{2} ) + (p_{1} + 2p_{2} \cos (\theta_{2} )a_{9} ),M_{12} = (a_{3} + a_{2} \cos (\theta_{2} )) + (p_{3} + p_{2} \cos (\theta_{2} )a_{9}), \\ M_{21} & = (a_{3} + a_{2} \cos (\theta_{2} )) + (p_{3} + p_{2} \cos (\theta_{2} )a_{9} ),\,M_{22} = a_{1} + p_{3} a_{9} \\ \end{aligned}$ [19].

In this example, the initial conditions of the states are given as $a_{1} = 6.33,a_{2} = 0.14,a_{3} = 0.11,a_{4} = 27.6,a_{5} = 31.9,a_{6} = 3.3,a_{7} = 0.94,a_{8} = 4.54,a_{9} = 1.25,$ $p_{1} = 0.37,p_{2} = 0.18,p_{3} = 0.18,p_{4} = 4.23,p_{5} = 4.15,\theta_{1} = 50{\varvec{\pi}} /180,\theta_{2} = 10{\varvec{\pi}} /180,$ $\dot{\theta }_{1} = 0,\dot{\theta }_{2} = 0.$

For demonstrating the tracking performance of the proposed control system, the desired trajectories for $x_{d1} (t)$ and $x_{d2} (t)$ are set as

$$ \underline{x}_{d} (t) = \left[ {\begin{array}{*{20}c} {x_{d1} (t)} \\ {x_{d2} (t)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {0.5 + 0.2\;(\sin (t) + \sin \,(2t))} \\ {1.3 - 0.1\;(\sin (t) + \sin \,(2t))} \\ \end{array} } \right] $$

(32)

where $\underline{\user2{x}}_{d} (t) = \left[ {x_{d1} (t),x_{d2} (t)} \right]^{T} = \left[ {\theta_{d1} ,\theta_{d2} } \right]^{T}$ is the reference trajectory vector.

For the proposed RSPID control system, the feedback gain matrix is designed as $\underline{\user2{H}} = diag(40,4)$; the initial conditions of the learning-rates are chosen as η _P  = 400, η _I  = 300 and η _D  = 400, respectively; all the PID gains are set as zero initially; the initial states of two-link manipulator are specified as $x_{1} (0) = 20\pi /180,x_{2} (0) = 10\pi /180,\dot{x}_{1} (0) = 0{\text{ and }}\dot{x}_{2} (0) = 0,$ and the initial states of desired trajectories $x_{d1} (0) = 0,x_{d2} (0) = 0,\dot{x}_{d1} (0) = 0{\text{ and }}\dot{x}_{d2} (0) = 0.$ In order to study the robustness of the proposed control system, assume that the two-link manipulator control system has external disturbance $\tau_{d} = [40,25]$ at $t = 5\,\text{s}$. Besides, the attenuation level is chosen as $\user2{R} = diag(0.5,0.5)$

In order to compare the control performance, the adaptive fuzzy control (AFC) presented in [18] is also applied to this manipulator system. Using this control system, the tracking trajectories are shown in Fig. 4a, b, respectively. The simulation results of the proposed RSPID control system for this two-link manipulator control system are shown in Figs. 4, 5, 6, 7. Figure 4c, d represents the tracking responses of $x_{1} (t)$ and $x_{2} (t)$ by the proposed RSPID control scheme, respectively. Moreover, the control inputs and tracking errors of $x_{1} (t)$ and $\, x_{2} (t)$ are plotted in Fig. 5a–d, respectively. In addition, the fitness function and learning-rates are shown in Fig. 6a–d, respectively. The PID gains $\user2{K}_{P} ,\;\user2{K}_{I}$ and $\user2{K}_{D}$ are shown in Fig. 7a–c, respectively. Comparing Fig. 4c, d with Fig. 4a, b, it can be seen the tracking error have been much reduced by using the RSPID controller. Moreover, from Fig. 6, it is also seen that the learning-rates of PID controller converge after the 5th second. The simulation results also show that the proposed RSPID control system can effectively achieve parameter tuning and favorable control for the two-link manipulator control system.

Fig. 4

The state responses of AFC and RSPID. a state response 1 of AFC, b state response 2 of AFC, c state response 1 of RSPID, d state response 2 of RSPID (dashed line desired trajectory, continuous line state trajectory)

Fig. 5

The control inputs and tracking errors of the two-link manipulator system a control input 1, b control input 2, c tracking error 1, d tracking error 2

Fig. 6

The fitness function and learning-rates of SPID a fitness function, b learning rate η _P , c learning rate η _I , d learning rate η _D

Fig. 7

K _P , K _I and K _D gains of SPID controller for the two-link manipulator system

Example 2 . Unified chaotic system

Consider a general master–slave unified chaotic systems; the master system and slave system are given as [20].

$$ \begin{aligned} & \dot{x}_{d1} (t) = (25\theta_{c} + 10)(x_{d2} (t) - x_{d1} (t)) \\ {\text{Master}}\, & \dot{x}_{d2} (t) = (28 - 35\theta_{c} )x_{d1} (t) - x_{d1} (t)x_{d3} (t) + (29\theta_{c} - 1)x_{d2} (t) \\ & \dot{x}_{d3} (t) = x_{d1} (t)x_{d2} (t) - \left( {\frac{{8 + \theta_{c} }}{3}} \right)x_{d3} (t) \\ \end{aligned} $$

(33)

$$ \begin{aligned} & \dot{x}_{1} (t) = (25\theta_{c} + 10)(x_{2} (t) - x_{1} (t)) + d_{1} (t) + u_{1} (t) \\ {\text{Slave}}\; & \dot{x}_{2} (t) = (28 - 35\theta_{c} )x_{1} (t) - x_{1} (t)x_{3} (t) + (29\theta_{c} - 1)x_{2} (t) + d_{2} (t) + u_{2} (t) \\ & \dot{x}_{3} (t) = x_{1} (t)x_{2} (t) - \left( {\frac{{8 + \theta_{c} }}{3}} \right)x_{3} (t) + d_{3} (t) + u_{3} (t) \\ \end{aligned} $$

(34)

where x _di (t) and x _i (t) are the system states variables of master system and slave system, respectively; d _i , i = 1, 2, 3 denote the disturbances and u _i , i = 1, 2, 3 are the control inputs. Assume $\alpha_{1} = (25\theta_{c} + 10),\alpha_{2} = (28 - 35\theta_{c} ),\alpha_{3} = (29\theta_{c} - 1)$ and $\alpha_{4} = \left( {\frac{{8 + \theta_{c} }}{3}} \right)$; then the master system Eq. 33 and the slave system Eq. 34 can be rewritten as

$$ \begin{gathered} \dot{x}_{d1} (t) = \alpha_{1} (x_{d2} (t) - x_{d1} (t)) \hfill \\ \dot{x}_{d2} (t) = \alpha_{2} x_{d1} (t) - x_{d1} (t)x_{d3} (t) + \alpha_{3} x_{d2} (t) \hfill \\ \dot{x}_{d3} (t) = x_{d1} (t)x_{d2} (t) - \alpha_{4} x_{d3} (t) \hfill \\ \end{gathered} $$

(35)

$$ \begin{gathered} \dot{x}_{1} (t) = \alpha_{1} (x_{2} (t) - x_{1} (t)) + d_{1} (t) + u_{1} (t) \hfill \\ \dot{x}_{2} (t) = \alpha_{2} x_{1} (t) - x_{1} (t)x_{3} (t) + \alpha_{3} x_{2} (t) + d_{2} (t) + u_{2} (t) \hfill \\ \dot{x}_{3} (t) = x_{1} (t)x_{2} (t) - \alpha_{4} x_{3} (t) + d_{3} (t) + u_{3} (t) \hfill \\ \end{gathered} $$

(36)

the master–slave system can be expressed as

$$ \dot{\user2{x}}{}_{d}(t) = \user2{f}(\user2{x}_{d} (t)) $$

(37)

and

$$ \dot{\user2{x}}(t) = \user2{f}(\user2{x}(t)) + \user2{G} (\user2{x}(t) )\user2{u}(t) + \user2{d}(t) $$

(38)

where $\user2{x}{}_{d}(t) = [x_{d1} (t),x_{d2} (t),x_{d3} (t)]^{T} ,\user2{x}(t) = [x_{1} (t),x_{2} (t),x_{3} (t)]^{T} ,$ $\user2{f} (\user2{x}{}_{d}(t) )= [\alpha_{1} (x_{d2} (t) - x_{d1} (t)),\alpha_{2} x_{d1} (t) - x_{d1} (t)x_{d3} (t) + \alpha_{3} x_{d2} (t),x_{d1} (t)x_{d2} (t) - \alpha_{4} x_{d3} (t)]^{T}$, $\user2{f} (\user2{x}(t) )= [\alpha_{1} (x_{2} (t) - x_{1} (t)),\alpha_{2} x_{1} (t) - x_{1} (t)x_{3} (t) + \alpha_{3} x_{2} (t),x_{1} (t)x_{2} (t) - \alpha_{4} x_{3} (t)]^{T} ,$ $\user2{G} (\user2{x}(t) )= diag[1,1,1]$, $\user2{d}(t) = [d_{1} (t),d_{2} (t),d_{3} (t)]^{T}$ and $\user2{u}(t) = [u_{1} (t),u_{2} (t),u_{3} (t)]^{T}$.

The control objective is to find a suitable control law $\user2{u}(t)$, so that the state trajectories of slave chaotic system $\user2{x}(t)$ can follow the master chaotic system $\user2{x}{}_{d}(t)$ under different initial conditions and subject to disturbances.

When $\theta_{c} = [0\sim 0.8)$ the system is known to be the generalized Lorenz system; when $\theta_{c} = 0.8$ the system is called the Lu system; and when $\theta_{c} = (0.8\sim 1]$ the system is called the Chen system. It is supposed that the initial conditions of the states are $x_{d1} (0) = 3, \, x_{d2} (0) = 5, \, x_{d3} (0) = 7$ for the master system, and $x_{1} (0) = - 2, \, x_{2} (0) = 2, \, x_{2} (0) = 3$ for the salve system. In addition, $\theta_{c} = 1$and the external disturbance $\user2{d}(t) = [0.2\cos (\pi t),0.1\cos (t),0.3\cos (2t)]^{T}$ are used. The attenuation level is chosen as $\user2{R} = diag(0.6,0.6,0.6)$ and the gains of integrated error function are selected as $\underline{\user2{H}} = diag(0.1,0.1,0.1). \,$In addition, the initial values of the learning-rates of PID gains are set as $\eta_{P} = 80,\eta_{I} = 20,$ and $\eta_{D} = 0,$ respectively; all the PID gains are set as zero initially.

For comparison, an adaptive fuzzy sliding model control (AFSMC) [21] is also applied to this system, the tracking trajectories are shown in Fig. 8a–c, respectively. The simulation results of the proposed RSPID control are shown in Figs. 8, 9, 10, 11. Synchronization responses of $x_{d1} (t),x_{1} (t),x_{d2} (t),x_{2} (t),x_{d3} (t)$ and $x_{3} (t)$ are depicted in Figs. 8d–f, respectively. Figure 9 shows the synchronization errors and control efforts of chaotic system. The fitness function and learning-rates are shown in Fig. 10, it is shown when error state $\underline{\user2{e}} (t)$ converges to zero, the fitness function also approximates to $fit = 10$. Figure 11 illustrates the $\user2{K}_{P} ,\;\user2{K}_{I}$ and $\user2{K}_{D}$ gains. Since this system is a first order system (i.e. PI controller is used); thus, $\user2{K}_{D}$ gains approach to zero.

Fig. 8

The synchronization responses of a chaotic system. (dashed line drive system trajectory, continuous line response system trajectory)

Fig. 9

The synchronization errors and control efforts of unified chaotic system

Fig. 10

The fitness function and learning-rates of SPID

Fig. 11

K _P , K _I and K _D gains of SPID controller for unified chaotic system

From Figs. 4 and 8, it’s easy to find that the proposed control system can achieve control performance better than AFSMC scheme, even under disturbance. By using the proposed design method, the tracking error can converge to zero quickly even in the presence of disturbance for different initial conditions.

6 Conclusion

This paper proposes a nonlinear system control scheme by using a robust self-learning PID (RSPID) control system. In the proposed control system, the self-learning PID (SPID) controller is the main controller used to mimic an ideal controller, and the robust controller is designed to compensate for the difference between the ideal controller and the SPID controller based on H _∞ control technology. In addition, a PSO algorithm has been adopted to search the optimal learning-rates of the tuning law in SPID controller. Simulation results have demonstrated that the proposed RSPID control system can achieve favorable control performance for the nonlinear systems. The major contributions of this study are: (1) The successful development of a self-learning PID controller. (2) The SPID controller with PSO algorithm and the robust controller are successful combined for MIMO nonlinear systems.