1 Introduction

Fluctuations always exist in actual systems. For example, the temperature and humidity under which a system operates can lead to the occurrence of heat noise. The variety of electromagnetic field environment and inhomogeneity of semiconductor medium will cause the change in an inductor or a resistor. In general, the introduction of noise will reduce the output performance of a system. Yet, under certain conditions, noise can play a constructive role in the improvement in a system output signal. Stochastic resonance (SR) is such a nonlinear phenomenon appearing in a noisy dynamic system, which means the maximum output response by virtue of the cooperation between the system, the input signal and the dynamic system [1, 2].

Since its discovery, SR phenomenon has been paid much attention. For a first-order bistable system, the SR at the subharmonic frequency [1] and the SR with Poisson white noise [2] and with multiplicative and additive trichotomous noise [3] have been investigated. The SR with time-delayed feedback and three types of asymmetries [4] and the SR driven by non-Gaussian colored noise [5] have also been studied. In addition, the SR for partnership systems with an asymmetric bistable Cobb–Douglas utility [6], the SR for two kinds of asymmetric nonlinear systems [7], the SR for an overdamped system with a fractional power nonlinearity [8], as well as the SR for a noisy confined overdamped bistable system [9], have been studied. At the same time, the SR for a time polo-delayed asymmetry bistable system [10], logical SR for a two-well potential system [11], as well as the inverse SR for a minimal bistable spiking neural circuit [12], have also been researched.

The SR for other first-order systems has also been considered [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41]. The SR for a nonsmooth system [13] and for anterior cruciate ligament reconstructed patients [14], as well as the SR for a financial market with stock crashes [15] and for a forced van der Pol-type birhythmic system [16], has been investigated. The SR for cortical networks [22] and for Hopfield neural networks [23], the SR for energy market Prices [24] and for a gene transcriptional regulatory model [25], as well as the SR for a stochastic insect outbreak system [26] and for a metapopulation system [27], have been researched. Meanwhile, the SR for a tristable system with colored noise [28, 29] and the SR for a symmetry tristable system induced by levy noise background [30, 31] have been studied. The SR for a high-order time-delayed feedback tristable dynamic system [32] and the SR for an asymmetric tristable system driven by correlated noises [33] have been investigated. At the same time, the SR for noisy monostable systems has also been investigated [36,37,38,39,40]. The SR for a bias monostable system with frequency mixing force [37] and the SR for a time-delayed exponential monostable system [38] have been investigated. The SR for bilateral partnership systems with a bias monostable Cobb–Douglas utility [39] and Levy noise-driven SR for a coupled monostable system [40] have been studied.

For a second-order system, due to the damping coefficient being a finity value, the system should be regarded as an underdamped one. Impact fault detection of gearbox based on variational mode decomposition for a coupled underdamped system [41], the SR for an underdamped asymmetric bistable system [42], and the SR for a coupled bistable system with Poisson white noises [2] have been investigated. The SR for an underdamped bistable system driven by harmonic mixing signals [43], the SR for an underdamped triple-well potential system [44], as well as the SR for an underdamped bistable system driven by weak asymmetric dichotomous noise [45], have also been studied.

On the other hand, dichotomous noise is a common noise model used in various fields [46,47,48,49], generated by a two-state Poisson process and formed by quasiparticles (defects, impurities, spins, etc.). In actual systems, dichotomous noise and white noise maybe exist simultaneously. The synchronization and the SR enhanced by dichotomous noise and by white noise have been studied [50, 51]. For a communication system, a digital circuit may be perturbed by Gaussian white noise induced by the background noise around the circuit. This circuit can also be perturbed by dichotomous noise induced by other digital circuits close to it. It can be seen that the study of the effect of both dichotomous noise and white noise on a dynamic system is of important engineering significance. For a practical application, the enhancement of SR in comparison with standard stochastic systems is of great importance. By the enhancement of SR, one means that the system output spectral power amplification and (or) the signal-to-noise ratio can reach larger values. It has been shown that SR can be enhanced in a first-order bistable system driven additionally by a dichotomic noise [52]. Thus, motivated by this, we study the effect of dichotomous noise for a second-order system to investigate its enhancement of SR for the system.

We note that, although the SR phenomenon has been considered for a first-order monostable system with multiplicative noise [37,38,39,40, 49, 53] or for a second-order system [2, 29, 41,42,43,44,45] with additive noise, few attention has been paid on the SR phenomenon for a second-order (underdamped) monostable system with multiplicative noise and additive dichotomous noise. Thus, in this work, we aim to investigate the nonlinear SR phenomenon for an underdamped monostable system with multiplicative noise and additive dichotomous noise.

2 The underdamped monostable system and its output signal-to-noise ratio

Consider the movement of a particle described by the following stochastic second-order differential equation

$$\ddot{x} + \gamma \dot{x} = - \frac{{{\text{d}}V(x)}}{{{\text{d}}x}} + x\xi (t) + f(t) + \eta (t),\;f(t) = B\Gamma (t) + A\cos (\Omega t),$$
(1)

where x is the displacement of the particle and \(\ddot{x} = \frac{{{\text{d}}^{2} x}}{{{\text{d}}t^{2} }}\) and \(\dot{x} = \frac{{{\text{d}}x}}{{{\text{d}}t}}\) denote the acceleration and velocity of the moving particle, respectively. \(V(x){ = }bx^{4} /4\) is the potential function of system (1). \(\gamma\) is the damping coefficient for the underdamped system (1). \(\Gamma (t)\) is the dichotomous noise with unit amplitude and transition rate \(\lambda\). We introduce the dichotomous noise into \(f(t)\) to study the effect of dichotomous noise on the improvement in the system output performance. \(\xi (t)\) and \(\eta (t)\) are the uncorrelated multiplicative and additive Gaussian white noises with zero means and characterized by their variances

$$\left\langle {\left[ {\begin{array}{*{20}c} {\xi (t_{1} )} \\ {\eta (t_{1} )} \\ \end{array} } \right]\left[ {\xi (t_{2} )\begin{array}{*{20}c} {} \\ \end{array} \eta (t_{2} )} \right]} \right\rangle = \delta (t_{1} - t_{2} )\left[ {\begin{array}{*{20}c} {2D} & 0 \\ 0 & {2P} \\ \end{array} } \right],$$
(2)

where D and P are the strengths of the multiplicative and additive noise, respectively.

One can see that, for the absence of driving force, i.e., \(\xi (t) = \eta (t) = f(t) = 0\), system (1) has a monostable potential function with one stable state \(x = 0\). Let \(y = \dot{x}\), this state can be expressed as a two-dimensional coordinate \(G(x,y) = (0,0)\). Equation (1) can be rewritten as

$$\left\{ {\begin{array}{*{20}l} {\dot{x} = y} \hfill \\ {\dot{y} = - \gamma y - bx^{3} + x\xi (t) + f(t) + \eta (t)} \hfill \\ \end{array} } \right.,$$
(3)

and the Fokker–Planck equation for the probability density corresponding to Eq. (3) can be written as

$$\begin{aligned} \frac{\partial \rho (x,y,t)}{{\partial t}} & = - \frac{\partial }{\partial x}[y\rho (x,y,t)] - \frac{\partial }{\partial y}\{ [ - \gamma y + Dx - bx^{3} + f(t)]\rho (x,y,t)\} \\ & \quad + \;\frac{{\partial^{2} }}{{\partial y^{2} }}[(Dx^{2} + P)\rho (x,y,t)]. \\ \end{aligned}$$
(4)

Let \(\partial \rho (x,y,t)/\partial t = 0\), under the detailed balance condition [52, 54], the solution for the stationary probability density \(\rho_{st} (x,y)\) should meet the following condition, i.e.,

$$\left\{ {\begin{array}{*{20}l} {\frac{\partial }{\partial x}[y\rho_{st} (x,y)]{ + }\frac{\partial }{\partial y}\{ [Dx - bx^{3} + f(t)]\rho_{st} (x,y)\} = 0} \hfill \\ {\frac{\partial }{\partial y}[\gamma y\rho_{st} (x,y)] + \frac{{\partial^{2} }}{{\partial y^{2} }}[(Dx^{2} + P)\rho_{st} (x,y)] = 0} \hfill \\ \end{array} } \right..$$
(5)

Substituting \(\rho_{st} (x,y) = M\exp ( - ay^{2} )\Phi (x)\) into Eq. (5), for the case of weak noise, i.e.,\(D \ll 1,P \ll 1\), one can obtain

$$\rho_{st} (x,y) = N\exp \left[ { - \frac{U(x,y)}{P}} \right],$$
(6)

where N is the normalization constant and

$$U(x,y) = \frac{\gamma P}{2}\left[ {\frac{{y^{2} }}{{Dx^{2} + P}} - 2\int {\frac{{Dx - bx^{3} + f(t)}}{{Dx^{2} + P}}} {\text{d}}x} \right]$$
(7)

is the potential function for system (1). From Eq. (7), one can see that for the presence of the multiplicative noise, i.e., \(D \ne 0\), the system thus becomes a two-dimension bistable system with two stable states \(G_{{s{ + }}} (x,y) = (\sqrt {D/b} ,0)\),\(G_{s - } (x,y) = ( - \sqrt {D/b} ,0)\) and one unstable state \(G_{uo} (x,y) = (0,0)\). The eigenvalues of linearized matrix for the autonomous deterministic model of the bistable system at points \(G_{{s{ + }}}\) and \(G_{{s{ - }}}\) are \(\beta_{1,2} = \frac{{ - \gamma \pm \sqrt {\gamma^{2} - 8D} }}{2}\). The eigenvalues of linearized matrix at points \(G_{uo}\) are \(\beta_{3,4} = \frac{{ - \gamma \pm \sqrt {\gamma^{2} + 4D} }}{2}\). Based on two-state theory [55], with the presence of dichotomous noise, the general modified transition rate for the particle out of \(G_{i}\) (\(i = {\text{s}} + ,s -\)) can be expressed as

$$W_{0} (G_{s \pm } ,\Gamma_{ \pm } ) = \frac{1}{2\pi }\sqrt { - \frac{{\beta_{1} \beta_{2} \beta_{3} }}{{\beta_{4} }}} \exp \left( { - \frac{\Delta U \pm \gamma PkB/2}{P}} \right),$$
(8)

with

$$\Delta U = [U(G_{s \pm } ) - U(G_{uo} )]|_{f(t) = 0} .$$
(9)

The master equation for system (1) can be described as [50, 51, 53, 55]

$$\begin{aligned} \frac{{\text{d}}}{{{\text{d}}t}}p(G,\Gamma ) & = - W_{0} (G_{s + } ,\Gamma_{ + } )p(G_{s + } ,\Gamma_{ + } ) + W_{0} (G_{s - } ,\Gamma_{ + } )p(G_{s - } ,\Gamma_{ + } ) \\ & \quad + \;\lambda [p(G_{s + } ,\Gamma_{ - } ) - p(G_{s + } ,\Gamma_{ - } )]. \\ \end{aligned}$$
(10)

The mean switching frequency of the system output can be obtained by [50, 51, 54, 55]

$$\left\langle W \right\rangle_{out} = \frac{\pi }{2}\left[ {a_{1} + a_{2} - \frac{{(a_{2} - a_{1} )^{2} }}{{a_{1} + a_{2} + 2\gamma }}} \right],$$
(11)

with

$$a_{1,2} = \frac{{\sqrt {\gamma^{2} + 4D} - \gamma }}{2\sqrt 2 \pi }\exp \left( { - \frac{\Delta U \pm \gamma PkB/2}{P}} \right)$$
(12)
$$k = \arctan (D/\sqrt {bP} )/\sqrt {DP} .$$
(13)

With the presence of weak (\(A \ll 1\)) and slow (\(\Omega \ll 1\)) periodic force, the modified transition rate can be obtained by

$$W(G,\Gamma ) = W_{0} (G,\Gamma )\exp \left[ { - \frac{\gamma k}{2}A\cos (\Omega t)} \right] \approx W_{0} (G,\Gamma )\left[ {1 - \frac{\gamma k}{2}A\cos (\Omega t)} \right].$$
(14)

The autocorrelation function for the system output can be derived from Eqs. (10) and (14), which can be given by

$$\begin{aligned} \frac{{\text{d}}}{{{\text{d}}t}}\left\langle {x(t)x(t_{1} )} \right\rangle & = - (a_{1} + a_{2} )\left\langle {x(t)x(t_{1} )} \right\rangle + (a_{2} - a_{1} )\left\langle {\Gamma (t)x(t_{1} )} \right\rangle \\ & \quad + \;[(a_{1} + a_{2} )\left\langle {x(t_{1} )} \right\rangle - (a_{2} - a_{1} )\left\langle {x(t)\Gamma (t)x(t_{1} )} \right\rangle ]\frac{\gamma k}{2}A\cos (\Omega t). \\ \end{aligned}$$
(15)

The cross-correlation function meets the following equation

$$\frac{{\text{d}}}{{{\text{d}}t}}\left\langle {\Gamma (t)x(t_{1} )} \right\rangle = - 2\lambda \left\langle {\Gamma (t)x(t_{1} )} \right\rangle .$$
(16)

Applying Fourier transform on both sides of Eq. (15), one can get the output power spectrum for the system, i.e.,

$$S(\omega ) = S_{n} (\omega ) + A^{2} \pi S_{{\text{s}}} (\omega )\delta (\omega - \Omega ),$$
(17)

where \(S_{n} (\omega )\) denotes the power density of the background

$$S_{n} (\omega ) = \frac{{4(a_{1} + a_{2} )}}{{(a_{1} + a_{2} )^{2} + \omega^{2} }}\left[ {1 + \frac{{(a_{2} - a_{1} )^{2} }}{{4\gamma^{2} + \omega^{2} }}} \right] - \frac{{4(a_{2} - a_{1} )^{2} }}{{(a_{1} + a_{2} + 2\gamma )(4\gamma^{2} + \omega^{2} )}},$$
(18)

and \(S_{{\text{s}}} (\omega )\) is the spectral power amplification

$$S_{{\text{s}}} (\Omega ) = \frac{{\left( {\gamma k/2} \right)^{2} }}{{(a_{1} + a_{2} )^{2} + \Omega^{2} }}\left[ {a_{1} + a_{2} - \frac{{(a_{2} - a_{1} )^{2} }}{{a_{1} + a_{2} + 2\gamma }}} \right]^{2} .$$
(19)

On the basis of linear response theory, the signal-to-noise ratio (SNR) defined as the ratio between the noise power density and the signal spectral power can be given by

$${\text{SNR}} = \frac{{\pi S_{{\text{s}}} (\Omega )}}{{S_{n} (\Omega )}}.$$
(20)

3 Discussion

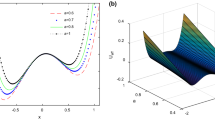
Multiplicative noise is a fluctuation associated with a system, which can be expressed as a product of the noise and the system state variables. Because multiplicative noise always results from the perturbation of system parameters, it may change the output response of the noisy system. In this paper, by virtue of the dependence of the multiplicative noise \(\xi (t)\) on the state variable x of the system, the multiplicative noise can affect the structure of the system. From Eq. (7), one can see that, with the presence of multiplicative noise \(\xi (t)\), the potential function of system (1) becomes a bistable one, i.e., the multiplicative noise has an effect on the system’s potential function.

Based on two-state theory, by virtue of Eqs. (18)–(20), we now analyze the nonmonotonic dependence of the system SNR on the parameters of the noises and those of the system. From Figs. 1 and 2, one can conclude that the SNR depends nonmonotonically on the multiplicative noise strength. With the increase in the multiplicative noise intensity D, the curve of SNR shows a resonance peak, i.e., the SR phenomenon occurs, a similar phenomenon taken place in first-order systems [37, 49, 52, 54] with multiplicative noise. Meanwhile, the values of SNR for the two figures are much greater than those obtained in Refs. [37, 49, 52, 54], where the dichotomous noise is absent. This phenomenon means that the introduction of dichotomous noise has greatly improved the system SNR.

Fig. 1
figure 1

The signal-to-noise ratio (SNR) versus the multiplicative noise intensity D for \(P = 0.5\), \(\gamma = 5\), \(B = 3\), \(\Omega = 0.1\) for different values of the system parameter b. The lines with no markers are the theoretical results, and the lines with markers are numerical simulation results

Full size image
Fig. 2
figure 2

The signal-to-noise ratio (SNR) versus the multiplicative noise intensity D for \(b = 1\), \(P = 0.5\), \(B = 3\), \(\Omega = 0.1\) for different values of the damping coefficient \(\gamma\)

Full size image

This resonance behavior can be explained in the view of the system potential function. The potential function \(V(x,0)\) is shown in Fig. 3. From this figure, one can see that for relatively small values of D, the system is almost a monostable one. The particle moves around the stable state, and the output signal is very small; but for relatively large values of D, the potential barrier is too high for the particle to jump over, which also suppresses the system output signal. We point that although \(y = 0\) in Fig. 3, for any other values of y, the trend of the variation for the potential \(V(x,y)\) is the same as that for \(V(x,0)\). Moreover, the peak value moves in the direction of large values of D with the increase in the parameter b, while it shifts to small values of noise strength D with the increase in the damping coefficient \(\gamma\), as shown in Figs. 1 and 2, respectively. This suggests that in order to maximize the system output signal, for small values of multiplicative noise intensity, relatively small values of b and large value of \(\gamma\) should be chosen.

Fig. 3
figure 3

The potential function V(x,0) for \(\gamma = 0.6\), \(b = 0.5\), \(P = 0.3\), \(A = 0\), \(B = 0\) for different values of multiplicative noise strength D

Full size image

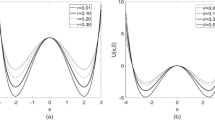
We analyze the effect of the additive noise strength P on the SNR from Figs. 4 and 5. From these two figures, one can easily find that the SNR obtains one maximum value with the variety of the additive noise intensity. Therefore, we observe again the SR phenomenon from these figures, similar effects occurred in first-order systems [37, 38, 49,50,51, 53,54,55] and second-order systems Refs. [42,43,44], while it is somewhat different from that appeared in second-order tristable system [29]. The SNR curve for Ref. [29] firstly obtained one minimum value and then reached its maximum value. The occurrence of the resonance peak can also be interpreted applying the stable states and barrier of potential function \(V(x,0)\) shown in Fig. 6. The peak value of SNR moves in the direction of small amount of additive noise with the increase in the parameter b, while it shifts to large values of noise strength P with the increase in the damping coefficient \(\gamma\), as shown in Figs. 4 and 5, respectively. This suggests that in order to enhance the system performance, for small values of multiplicative noise intensity, one should select relatively large values of b and small values of \(\gamma\), respectively. The comparison between Figs. 1, 2 and Figs. 4, 5 indicates that, for small (or large) values of parameter b and \(\gamma\), the effect of the multiplicative noise on the SNR is different from that of the additive noise.

Fig. 4
figure 4

The signal-to-noise ratio (SNR) versus the additive noise intensity P for \(D = 0.3\), \(\gamma = 4\), \(B = 2\), \(\Omega = 0.1\) for different values of the system parameter b. The lines with no markers are the theoretical results, and the lines with markers are numerical simulation results

Full size image
Fig. 5
figure 5

The signal-to-noise ratio (SNR) versus the additive noise intensity P for \(b = 1\),\(D = 0.3\), \(B = 2\), \(\Omega = 0.1\) for different values of the damping coefficient \(\gamma\)

Full size image
Fig. 6
figure 6

The potential function V(x,0) for \(\gamma = 0.6\), \(b = 0.5\), \(D = 0.3\), \(A = 0\), \(B = 0\) for different values of multiplicative noise strength D

Full size image

We investigate the effect of the amplitude B of the dichotomous noise on the system SNR from Figs. 7 and 8. It can be seen from these figures that the SNR obtains one maximum value with the variety of the amplitude B, i.e., a typical SR phenomenon appears, similar to those occurred in Ref. [54] and [55]. In addition, the peak value shifts to large values of B with the increase in the system parameter b or with the decrease in the damping coefficient \(\gamma\), which means that for large values of B, large values of b or small values of \(\gamma\) should be chosen to optimize the system SNR.

Fig. 7
figure 7

The signal-to-noise ratio (SNR) versus the amplitude B of the dichotomous noise for \(D = 0.9\), \(P = 0.1\), \(\gamma = 5\), \(\Omega = 0.1\) for different values of the system parameter b. The lines with no markers are the theoretical results, and the lines with markers are numerical simulation results

Full size image
Fig. 8
figure 8

The signal-to-noise ratio (SNR) versus the amplitude B of the dichotomous noise for \(b = 4\), \(D = 0.9\), \(P = 0.1\), \(\Omega = 0.1\) for different values of the damping coefficient \(\gamma\)

Full size image

The nonlinear dependence of the SNR on the damping coefficient \(\gamma\) can be discussed using Figs. 9 and 10. With the increase in \(\gamma\), the SNR increases until it reaches a maximum value and then it decreases monotonically. Thus, the SR in a broad sense occurs; a similar phenomenon appeared in a second-order system [44]. It can be seen that the system output no longer decreases monotonically with the damping coefficient resulting from the nonlinear effect between the noise and the nonlinear system. With the increase in the amplitude B and the system parameter b, the resonance peak shifts to large and small values of \(\gamma\), respectively. Moreover, the SNR depends nonmonotonically on the system parameter b, as shown in Figs. 11 and 12. At the same time, to maximize the SNR, small values of amplitude B and damping coefficient \(\gamma\) should be selected for small parameter b.

Fig. 9
figure 9

The signal-to-noise ratio (SNR) versus the damping coefficient \(\gamma\) for \(b = 2\), \(D = 0.1\), \(P = 0.1\), \(\Omega = 0.1\) for different values of the amplitude B of the dichotomous noise. The lines with no markers are the theoretical results, and the lines with markers are numerical simulation results

Full size image
Fig. 10
figure 10

The signal-to-noise ratio (SNR) versus the damping coefficient \(\gamma\) for \(D = 0.1\), \(P = 0.1\), \(B = 0.5\), \(\Omega = 0.1\) for different values of the system parameter b

Full size image
Fig. 11
figure 11

The signal-to-noise ratio (SNR) versus the system parameter b for \(D = 0.2\), \(P = 0.3\), \(\gamma = 2\), \(\Omega = 0.1\) for different values of the amplitude B of the dichotomous noise

Full size image
Fig. 12
figure 12

The signal-to-noise ratio (SNR) versus the system parameter b for \(D = 0.2\), \(P = 0.2\), \(B = 1\), \(\Omega = 0.1\) for different values of the damping coefficient \(\gamma\)

Full size image

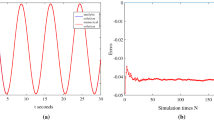
In order to examine the validity of theoretical results, numerical simulations are performed by directly integrating Eq. (1). The numerical data for the time series are obtained by using the forward Euler procedure. The power spectra were calculated by virtue of a fast Fourier transform of the auto-correlation function, and the output signal-to-noise ratio is defined as the height of the peak in the power spectrum at the input frequency divided by the height of the noisy background in the power spectrum around the input frequency. Figures 13, 14, 15, 16 and 17 show the system output time-domain signal \(x(t)\). From these five figures, one can easily find that as the increase in multiplicative noise strength D, the noise component in the output signal \(x(t)\) first is small for relatively small amount of noise (\(D = 0.05\), 0.1) and then it becomes larger for relatively more amount of noise (\(D = 0.2\), 0.3), which results in the resonance behavior of the system SNR with the variety of the multiplicative noise. Some simulation results are also shown in Figs. 1, 4, 7 and 9. From these figures, one can conclude that the theoretical results are consistent with the numerical simulations.

Fig. 13
figure 13

The simulation results of the system output time-domain signal \(x(t)\) for \(D = 0.05\), \(\gamma = 5\), \(b = 1\), \(P = 0.5\), \(B = 3\), \(A = 0.2\), \(\Omega = 0.1\)

Full size image
Fig. 14
figure 14

The simulation results of the system output time-domain signal \(x(t)\) for \(D = 0.10\), \(\gamma = 5\), \(b = 1\), \(P = 0.5\), \(B = 3\), \(A = 0.2\), \(\Omega = 0.1\)

Full size image
Fig. 15
figure 15

The simulation results of the system output time-domain signal \(x(t)\) for \(D = 0.15\), \(\gamma = 5\), \(b = 1\), \(P = 0.5\), \(B = 3\), \(A = 0.2\), \(\Omega = 0.1\)

Full size image
Fig. 16
figure 16

The simulation results of the system output time-domain signal \(x(t)\) for \(D = 0.20\), \(\gamma = 5\), \(b = 1\), \(P = 0.5\), \(B = 3\), \(A = 0.2\), \(\Omega = 0.1\)

Full size image
Fig. 17
figure 17

The simulation results of the system output time-domain signal \(x(t)\) for \(D = 0.30\), \(\gamma = 5\), \(b = 1\), \(P = 0.5\), \(B = 3\), \(A = 0.2\), \(\Omega = 0.1\)

Full size image

4 Conclusions

In conclusion, in this work, we have investigated the SR phenomenon for an underdamped monostable system with multiplicative and additive noise. Under the detailed balance condition and weak noise limit, the stationary probability density for the system is obtained. For the presence of multiplicative noise, the equivalent potential function is then regarded as a bistable one. Based on two-state theory, the system output SNR is derived. Traditional SR has been observed on the curves of SNR versus the intensities of the multiplicative and additive noises and on the curves of SNR versus the amplitude of the dichotomous noise. The SR in a broad sense has been occurred on the curves of SNR versus the damping coefficient and versus the system parameter b.