1 Introduction

The response of the random system is a noteworthy issue in the engineering and scientific fields. If the nonlinear system is excited by the combination of a noise and a weak low-frequency harmonic signal, the response at the driving frequency can be enhanced by the noise with an appropriate intensity. This constitutes the well-known phenomenon of the stochastic resonance [1]. When the stochastic resonance occurs, the energy of the noise is transferred to the weak signal, and the input–output achieves optimal synchronization [2]. The stochastic resonance theory was originally proposed and developed by Benzi et al. [3–5] and Nicolis et al. [6–8] in the context of the study of the climatic change. Stochastic resonance has been a rather hot topic in the last 30 years [9–11]. It has been investigated in various disciplines, such as optics [12], chemistry [13–15], biology [16–18], neuroscience [19–21], medicine [22, 23], mechanical engineering [24, 25]. In general, there are three basic ingredients for the stochastic resonance to occur, i.e., a nonlinear term, a noise and a weak input signal. The nonlinearity may arise from a nonlinear term in the system, e.g., a cubic term in a simple bistable system. It may be also originated from the coupling of the noise and the signal [26, 27], or a parametric excitation [28, 29]. The weak input signal may be in a periodic or aperiodic form. When the signal is aperiodic, the aperiodic stochastic resonance may occur in a nonlinear system when tuning the noise which is included in the excitations [30, 31], even in absence of a weak input signal. The stochastic resonance may also occur at the natural frequency of the system. This constitutes the stochastic coherence phenomenon [32, 33].

According to nonlinear dynamics, there are many other subharmonic and superharmonic frequencies in the response besides the driving frequency [34–36]. Although the stochastic resonance is a typical nonlinear phenomenon, most of the former works on stochastic resonance are studied based on the linear response theory [1, 37]. Specifically, when the weak input signal is periodic, most of the works are always concentrated on the response at the frequency of the input signal. In other words, only the driving frequency is considered in these studies. Moreover, there are also a few works that have considered the nonlinear contributions to the stochastic resonance in the nonlinear response theory framework [38, 39]. They have found that the noise can induce the resonance at the higher-order harmonics which are odd multiples of the driving frequency. However, to our knowledge, there are few references considering the noise-induced resonance at the subharmonic frequency which is smaller than the driving frequency. In many situations, the subharmonic components in the response might have a profound impact on the system [40–43]. Hence, it is necessary to study the response at the subharmonic frequency in the noise excited system. In particular, the effect of the noise on the response at the subharmonic frequency should be investigated. If the noise can induce the resonance at the subharmonic frequency, this would be a complement to the stochastic dynamics theory. This constitutes the main goal and motivation of this paper.

In the present work, we pay much attention to the noise-induced resonance at the subharmonic frequency which equals 1/3 multiple of the driving frequency. The outline of the paper is organized as follows. In Sect. 2, we study the noise-induced resonance at the subharmonic frequency in an overdamped bistable system which is subjected to a weak low-frequency signal and a white noise. In Sect. 3, the noise-induced resonance at the subharmonic frequency is investigated in the underdamped bistable system. The noise-induced classical stochastic resonance at the driving frequency will be compared with the noise-induced resonance at the subharmonic resonance in Sects. 2 and 3. We will find that the noise-induced resonance at the subharmonic frequency may be stronger than the classical stochastic resonance which indicates the importance of the subharmonic component in the response. Finally, some discussions and the main conclusions will be given in Sect. 4.

2 The overdamped bistable system

The overdamped bistable system is a typical system for the study of stochastic resonance, and we take it here as an example. The system is described by the following equation, i.e.,

$$\begin{aligned} \frac{{\hbox {d}x}}{{\hbox {d}t}} = ax - b{x^3} + f\cos (\omega t) + \xi (t), \end{aligned}$$
(1)

where a and b are positive parameters. \(\xi (t)\) is the Gaussian white noise satisfying the statistical properties \(\left\langle {\xi (t)} \right\rangle = 0\) and \(\left\langle {\xi (t)\xi (t')} \right\rangle = \sigma \delta (t - t')\). The frequency components in the response should contain the driving frequency \(\omega \), the subharmonic frequency which is smaller than \(\omega \), and the superharmonic frequency which is larger than \(\omega \) [25, 27]. The subharmonic frequencies and the superharmonic frequencies are induced by the nonlinear terms in the system. Beside these frequencies, there are many other combined frequencies which are generated by the combination of the driving, subharmonic and superharmonic frequencies. In general, when the response is periodic or quasi-periodic, only the driving frequency and a few subharmonic and superharmonic frequencies are dominant in the response. The response amplitudes at other frequencies are small and can be ignored. For a long enough time t, the mean value of the asymptotic solution of Eq. (1) can be written in the form

$$\begin{aligned} \left\langle {x(t)} \right\rangle _\mathrm{as} = \sum {{x_\mathrm{m}}} (k\omega )\cos \left[ {k\omega - {\varphi _\mathrm{m}}(k\omega )} \right] , \end{aligned}$$
(2)

where k is nonnegative and it can be an integer or a fraction. When \(k=0\), it presents the constant component in the response. \(x_\mathrm{m}(k\omega )\) and \(\varphi _\mathrm{m}(k\omega )\) are the mean response amplitude and the phase lag, respectively, at the frequency \(k\omega \). They are obtained by averaging the inhomogeneous process x(t) with arbitrary initial conditions \(x_0=x(t_0)\) over the ensemble of different random path realizations. In the former references [1, 37], in Eq. (2), k is chosen as nonnegative integers only. It may miss the subharmonic and the combined components in the response. For a single path, the response amplitude and the phase lag at the frequency \(k\omega \) are computed by

$$\begin{aligned} \bar{x} = \sqrt{B_\mathrm{s}^2 + B_\mathrm{c}^2} \end{aligned}$$
(3)

and

$$\begin{aligned} \bar{\varphi }= {\tan ^{ - 1}}({{{B_\mathrm{s}}}/{{B_\mathrm{c}}}}), \end{aligned}$$
(4)

where \(B_\mathrm{s}\) and \(B_\mathrm{c}\) are the sine and cosine components of the Fourier transform, specifically

$$\begin{aligned} {B_\mathrm{s}}= & {} \frac{2}{{nT}}\int _0^{nT} {x(t)\sin (k\omega t)\hbox {d}t},\nonumber \\ {B_\mathrm{c}}= & {} \frac{2}{{nT}}\int _0^{nT} {x(t)\cos (k\omega t)\hbox {d}t}. \end{aligned}$$
(5)

In Eq. (5), \(T=2\pi /\omega \) and n is a large enough integer number, what means that the effect of the initial condition on the response can be ignored. If only the driving frequency \(\omega \) in the response is considered, it is the classical stochastic resonance problem based on the linear response theory [1, 37]. Else, if the higher-order harmonics are considered in the response, the nonlinear contributions to the stochastic resonance are observed [38, 39]. According to Eq. (2), the response of the system (1) at the subharmonic frequency can be analyzed in the framework of the nonlinear response theory. To make the problem simpler, we only consider the subharmonic frequency \(\omega /3\) in the following analysis and choose the mean amplitude at the driving frequency \(\omega \) as a comparison. When the noise induces the resonance at the driving frequency \(\omega \), it is simply the well-known stochastic resonance. When the noise induces the resonance at the subharmonic frequency \(\omega /3\), it constitutes another noise-induced resonance phenomenon.

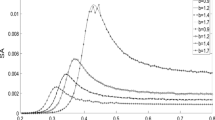
The subharmonic frequency \(\omega /3\) is induced by the cubic term \(x^3\) in system (1). For different values of the driving frequency \(\omega \), we plot the mean response amplitude \(x_\mathrm{m} (\omega )\) and \(x_\mathrm{m}(\omega /3)\) versus the noise intensity \(\sigma \) in Fig. 1. The stochastic resonance is shown clearly in this figure. It coincides with the result shown in previous references. We give the curve of the stochastic resonance only to compare with the noise-induced resonance at the subharmonic frequency \(\omega /3\). Now we pay more attention to the mean amplitude \(x_\mathrm{m}(\omega /3)\). With the increase in the noise intensity, the mean amplitude \(x_\mathrm{m}(\omega /3)\) increases at first and then it decreases. There is a particular noise intensity for the mean amplitude \(x_\mathrm{m}(\omega /3)\) to achieve the resonance peak. This is precisely a noise-induced resonance phenomenon, which is similar to the classical stochastic resonance. In Fig. 1a, b, \(\omega =0.09\) and \(\omega =0.15\), respectively, the peak value of the mean value amplitude \(x_\mathrm{m}(\omega /3)\) is smaller than the peak value of \(x_\mathrm{m}(\omega )\). The frequency component \(\omega \) in the response is predominant in the response for these two cases. When we take \(\omega =0.30\) and \(\omega =0.45\), as shown in Fig. 1c, d, the peak value of the mean amplitude \(x_\mathrm{m}(\omega /3)\) is larger than that of \(x_\mathrm{m}(\omega )\). This is an important phenomenon, and it indicates that we cannot breezily ignore the subharmonic components in the response, since the strength of the subharmonic component could be stronger than the strength at the driving frequency in some cases. Also in this figure, we find that the noise intensity which induces the resonance at the subharmonic frequency \(\omega /3\) is weaker than the resonance induced at the driving frequency \(\omega \). With the increase in the driving frequency \(\omega \), the subharmonic frequency \(\omega /3\) may be much more evident in a noise excited nonlinear system. It leads to the noise-induced resonance at the subharmonic frequency to be stronger than the classical stochastic resonance.

Fig. 1
figure 1

Mean amplitude \(x_\mathrm{m}(\omega )\) and \(x_\mathrm{m}(\omega /3)\) versus the noise intensity \(\sigma \) for different values of \(\omega \) in the overdamped bistable system. The simulation parameters are \(a=1, b=1, f=0.05\)

Full size image

In Fig. 2, the effect of the amplitude of the weak input signal on the classical stochastic resonance and the noise-induced resonance at the subharmonic frequency \(\omega /3\) is clearly shown. For the very weak input signal, e.g., \(f=0.01\) in Fig. 2a, the peak value on the curve \(x_\mathrm{m}(\omega )-\sigma \) is smaller than the peak value on the curve \(x_\mathrm{m}(\omega /3)-\sigma \). In other words, the noise-induced resonance at the subharmonic frequency \(\omega /3\) is stronger than the classical stochastic resonance in this subplot. With the increase of f, the peak value on the curve \(x_\mathrm{m}(\omega )-\sigma \) will be larger than the peak value on the curve \(x_\mathrm{m}(\omega /3)-\sigma \). It indicates that the classical stochastic resonance turns stronger than the noise-induced resonance at the subharmonic frequency with the increase in the amplitude of the low-frequency input.

Fig. 2
figure 2

Mean amplitude \(x_\mathrm{m}(\omega )\) and \(x_\mathrm{m}(\omega /3)\) versus the noise intensity \(\sigma \) for different values of f in the overdamped bistable system. The simulation parameters are \(a=1, b=1, \omega =0.6\)

Full size image

In order to clarify the problem further, we investigate the two kinds of the noise-induced resonance in Fig. 3. From Fig. 3a–d, we find that we need a stronger noise to make two kinds of noise-induced resonance to occur when we increase the value of a gradually. This is because the potential barrier is given by \(\Delta V = {{{a^2}}/{(4b}})\). It needs a stronger noise to make the output across the two potential wells regularly for the higher potential barrier. With the increase in the parameter a, the curve \(x_\mathrm{m}(\omega )-\sigma \) turns faintly. There is no obvious peak on the \(x_\mathrm{m}(\omega )-\sigma \) curve in Fig. 3c, d. Another fact in this figure, for a larger value of a, the noise-induced resonance at the subharmonic frequency may be much more distinct than the classical stochastic resonance, such as the curves in Fig. 3c, d. This indicates the importance of the subharmonic component in the response of a stochastic nonlinear system once again.

Fig. 3
figure 3

Mean amplitude \(x_\mathrm{m}(\omega )\) and \(x_\mathrm{m}(\omega /3)\) versus the noise intensity \(\sigma \) for different values of a in the overdamped bistable system. The simulation parameters are \(b=1, f=0.05, \omega =0.5\)

Full size image

In Fig. 4, the effect of the parameter b on two kinds of noise-induced resonance is shown. For larger values of b, we need a weaker noise to make the noise-induced resonance at the subharmonic frequency or the classic stochastic resonance to occur. It is because the barrier height of the adjacent potential well turns to be lower with the increase of b. On the \(x_\mathrm{m}(\omega )-\sigma \) and \(x_\mathrm{m}(\omega /3)-\sigma \) curves, the noise-induced resonance at the subharmonic frequency appears before the classical stochastic resonance. The maximal value of the \(x_\mathrm{m}(\omega /3)\) is larger for the smaller value of b.

Fig. 4
figure 4

Mean amplitude \(x_\mathrm{m}(\omega )\) and \(x_\mathrm{m}(\omega /3)\) versus the noise intensity \(\sigma \) for different values of b in the overdamped bistable system. The simulation parameters are \(a=1, f=0.05, \omega =0.5\)

Full size image

From Figs. 1, 2, 3 and 4, the noise-induced resonance at the subharmonic frequency \(\omega /3\) is compared with the classical stochastic resonance in the overdamped bistable system. More importantly, the noise-induced resonance at the subharmonic frequency may be stronger than the classical stochastic resonance for some cases. This is the reason why the study of the noise-induced resonance at the subharmonic frequency is important.

3 The underdamped bistable system

The stochastic resonance not only occurs in the overdamped bistable system. It also occurs in the bistable system for the underdamped case [44–48]. For some engineering systems, we need the underdamped dynamical model to describe the response of the system. For example, in an energy harvesting system, the stochastic resonance usually is used in the underdamped bistable system to enhance the harvesting efficiency [49, 50]. Herein, the underdamped bistable system considered is governed by the equation

$$\begin{aligned} \frac{{{\hbox {d}^2}x}}{{\hbox {d}{t^2}}} + \delta \frac{{\hbox {d}x}}{{\hbox {d}t}} - x + {x^3} = f\cos (\omega t) + \xi (t), \end{aligned}$$
(6)

where \(\delta >0\) is the damping parameter and \(\xi (t)\) is the noise which is the same as the one used in Eq. (1). According to the nonlinear dynamics theory [34, 36, 51], the subharmonic frequency \(\omega /3\) exists in the response of Eq. (6). The effect of the noise on the response at the subharmonic frequency \(\omega /3\) should be investigated further. In this section, we compare the classical stochastic resonance and noise-induced resonance at the subharmonic frequency in the underdamped bistable system.

In Fig. 5, the noise-induced resonance at the driving frequency \(\omega \) and at the subharmonic frequency \(\omega /3\) is plotted for different values of the driving frequency \(\omega \). The classical stochastic resonance and the noise-induced resonance at the subharmonic frequency do appear in this figure. By varying the frequency, the noise-induced resonance at the subharmonic frequency may be stronger than the classical stochastic resonance. The noise-induced resonance at the subharmonic frequency in the underdamped bistable system is similar to the one found for the overdamped bistable system.

Fig. 5
figure 5

Mean amplitude \(x_\mathrm{m}(\omega )\) and \(x_\mathrm{m}(\omega /3)\) versus the noise intensity \(\sigma \) for different values of \(\omega \) in the underdamped bistable system. The simulation parameters are \(f=0.05, \delta =0.5\)

Full size image

In Fig. 6, the effect of the damping coefficient on the noise-induced resonance at the subharmonic frequency is investigated. For the chosen simulation parameters, we find that the noise-induced resonance at the subharmonic frequency turns to be much stronger than the classical stochastic resonance with the increase in the damping coefficient. However, for small damping coefficients, the resonance phenomenon is much more apparent. For large damping coefficients, the mean amplitude curves versus the noise intensity turns flat when the curve passes through the resonance peak. From Figs. 5 and 6, we know that the noise-induced resonance at the subharmonic frequency also appear in the underdamped bistable system.

Fig. 6
figure 6

Mean amplitude \(x_\mathrm{m}(\omega )\) and \(x_\mathrm{m}(\omega /3)\) versus the noise intensity \(\sigma \) for different values of \(\delta \) in the underdamped bistable system. The simulation parameters are \(f=0.05, \omega =0.42\)

Full size image

4 Discussions and conclusions

At first, we give a discussion on the difference between the classical stochastic resonance and the noise-induced resonance on the subharmonic frequency. Besides the mean amplitude, there are some other indexes to quantify the classical stochastic resonance, such as the signal-to-noise ratio, the spectral amplification, the residence time distribution. Among them, the residence time distribution which describes to a good approximation the first-passage time between the potential wells is an important index for the classical stochastic resonance. According to the former work, the classical stochastic resonance achieves the optimal state when the residence time distribution shows the first peak at \(T_\omega /2\), where \(T_\omega \) is the period of the input signal. In the residence time distribution plot, the second peak may locate at \(3T_\omega /2\). However, we cannot confirm the existence of the subharmonic frequency \(\omega /3\) according to the second peak in the residence time distribution plot because the second peak only indicates that the system needs to wait another full period to achieve the optimal synchronization. This fact has been specially pointed out in Refs. [1, 2]. Hence, the residence time distribution or the first-passage time cannot be used as an index to quantify the noise-induced resonance at the subharmonic frequency.

Then, we give a discussion on the difference between the noise-induced resonance and the traditional nonlinear resonance in mechanics. As we know, the mechanism of the stochastic resonance is different from the traditional resonance theory. The stochastic resonance occurs as a cooperation of the noise and the weak low-frequency signal. The optimal input–output synchronization is achieved when the stochastic resonance occurs. It is different from the traditional primary resonance in the field of mechanics. Specifically, when the primary resonance occurs, the driving frequency is reached at approximately the natural frequency of the linear system which is obtained from the linearization of the corresponding nonlinear system. However, when the stochastic resonance occurs, the driving frequency may be far away from the natural frequency of the considered system. On the same principle, we cannot confound the noise-induced resonance at the subharmonic frequency with the traditional subharmonic resonance. In a nonlinear system, when the driving frequency approximately equals 1/3 multiple the natural frequency of the system, the subharmonic resonance may occur. However, when the noise induces the resonance at the subharmonic frequency, the driving frequency may also be far away from 1/3 multiple the natural frequency. Due to these reasons, we cannot name the noise-induced resonance at the subharmonic resonance as the noise-induced 1/3 subharmonic resonance.

Finally, we provide some conclusions of this paper. In most of the previous works, for a nonlinear system excited by the combination of a weak low-frequency signal and the noise, the noise-induced resonance is mainly focused on the driving frequency and only a few works consider the superharmonic frequency. They correspond to the classical stochastic resonance in the linear response theory and the stochastic resonance in the nonlinear response regime, respectively. In this paper, we consider the response amplitude of a random bistable system at the subharmonic frequency. We find that the noise can induce a resonance at the subharmonic frequency. The noise-induced resonance at the subharmonic frequency may be stronger than the classical stochastic resonance. We show this new kind of nonlinear resonance in the overdamped bistable system and the underdamped bistable system, respectively, by using numerical methods. We make the bold forecast, besides the two systems studied in this paper, that the noise-induced resonance at the subharmonic frequency should also be found in other nonlinear systems. As a consequence, the results under the nonlinear stochastic theory may be very different from the results obtained from the linear response theory. If we only consider the driving frequency in the response, we may miss some important information. Hence, we believe that it is necessary to consider the noise-induced resonance at the subharmonic frequency in random systems.