1 Introduction

The vibration phenomena widely exist in our daily life as well as in various types of engineering systems [1,2,3]. Among them, the simple harmonic vibration plays a critical role in the study of the vibration phenomena. So far, the dynamic behavior of harmonic oscillators without noise has been widely studied [4]. However, in natural science, especially in the study of vibration phenomena, stochastic forces exist almost everywhere. Thus, in order to describe the phenomenon more realistically, it is crucial to consider the effect of the stochastic forces on natural phenomena. More precisely, the stochastic forces, according to their origins, can be divided into internal noise and external noise [5, 6]. The internal noise, which usually appears as additive noise, is caused by the irregular collisions of the internal molecules within the system. On the other hand, the external noise, which usually appears as multiplicative noise, originates from the fluctuation of external input signal or parameters. By the way, compared with the external noise, the influence of the internal thermal fluctuation noise is generally small; therefore, the internal noise can be ignored [5].

However, when considering the external noise of the system, many researchers only focus on the multiplicative fluctuation of the system intrinsic parameters [7,8,9,10], while we consider the multiplicative fluctuation in the input signal as well. Moreover, the study on the fluctuation of the system affected by multiplicative noise mainly focused on the multiplicative dichotomous or trichotomous noise, and few studies analyze the systems fluctuated by multiplicative white noise. As a result, we take Gaussian white noise as multiplicative fluctuation of frequency and input signal of the system.

As for a harmonic oscillator, the system can be described by the Langevin equation. Thus, if we take Gaussian white noise into account, the solution of the equation can be described as a Wiener process. Bernt Øksendal introduced Brownian motion and stochastic calculus in 2003 [11]; thus, the solution of the system is itô process precisely. And with the theory of stochastic differential equation, that a function of an itô process \(X_t\) and time t which is twice continuously differentiable in \(X_t\) and once continuously differentiable in t satisfies the conditions of itô formula [12], we can derive the analytic expression of the displacement of the system.

In this paper, we study the phenomenon of stochastic resonance (SR). The concept of SR was first introduced by Benzi [13] to explain the periodic recurrence of ice ages on Earth in 1981. And the term SR is a nonlinear synergistic effect of non-monotonicity among system parameters, noise and periodic input signals of a physical system [14]. The phenomenon of SR shows that, under certain conditions, when appropriately increasing the input noise, the ordered component of the system output will greatly increase instead of decreasing. The phenomenon of SR has attracted considerable interest due to many applications in biology [15,16,17,18], physics [19, 20], chemistry [21], signal detection and recovery [22, 23], circuit [24], molecular motor [25]. Thus, the mathematical modeling and parameter analysis of SR will be of great importance, which can potentially provide theoretical support for applications. Li et al. [26] hold the view that SR takes place only for multiplicative colored noise, but disappears for white noise, which is verified by us. However, we find that SR occurs in the second-order moment solution. As we change the parameters of the system, the phenomenon of inverse stochastic resonance (ISR) [27, 28] appears instead of SR. The term ISR is similar to SR but consists of an unexpected depression in the response of a system under external noise [27]. Though we mainly focus on SR instead of ISR, we hope our work could be helpful in the research of ISR.

Before us, Zhang et al. [29] use Taylor series to approximate the nonlinear expression of Gaussian white noise to analyze the damped linear oscillator model. Though their results go against that SR disappears for white noise, they built a constructed role in the study of linear system with Gaussian white noise. Furthermore, Cao et al. [30] studied a linear system driven by correlated Gaussian colored noise instead of Gaussian white noise. And they focused on signal-modulated noise, while we are going further, focusing on frequency and input signal fluctuation of the system. Thus, we would like to explore the SR phenomenon in a linear oscillator subjected to multiplicative Gaussian white noise in both frequency and input signal fluctuation.

At last, the structure of this paper is as follows. In Sect. 2, we provide the analytic expressions of both the first-order and the second-order moment of output signal amplitude. Furthermore, we obtain the analytic expression of the SNR. In Sect. 3, we propose the numerical simulations based on analytic expressions. At last, some discussions conclude this paper in Sect. 4.

2 System model

2.1 The expression of the first-order moment

We consider the generalized Langevin equation with Gaussian white noise as follows

$$\begin{aligned} \frac{\mathop {}\!\mathrm {d}}{\mathop {}\!\mathrm {d}t}X_t+(\omega ^2+\xi _t)X_t=(A_0+\eta _t)\cos (\Omega t) , \end{aligned}$$
(1)

where X(t) is the oscillator displacement, \(\omega \) is the frequency constant of the system, and \(A_0\) and \(\Omega \) are the amplitude and the frequency of the periodic cosine wave input signal, respectively. \(\xi _t\) and \(\eta _t\) are Gaussian white noise, satisfying

$$\begin{aligned}&\langle \xi _t \rangle =0,\langle \xi _t \xi _s \rangle =D_1^2\delta (t-s) ,\nonumber \\&\langle \eta _t \rangle =0,\langle \eta _t \eta _s \rangle =D_2^2\delta (t-s) ,\nonumber \\&\langle \xi _t \eta _s \rangle =D_1D_2\delta (t-s), \end{aligned}$$
(2)

where \(D_1\) and \(D_2\) are the variances of the \(\xi _t\) and \(\eta _t\), respectively. And we can learn from the theory of stochastic differential equation (SDE) [11] that \(\mathop {}\!\mathrm {d}G_t\), which is the differentiation of a Brownian motion \(G_t\), can be written as

$$\begin{aligned} \mathop {}\!\mathrm {d}G_t =\gamma _t\cdot \mathop {}\!\mathrm {d}t, \end{aligned}$$
(3)

where \(\gamma _t\) is Gaussian white noise. Thus, we can rewrite Eq. (1) as follows

$$\begin{aligned} \mathop {}\!\mathrm {d}X_t=&-\omega ^2X_t\mathop {}\!\mathrm {d}t+A_0\cos (\Omega t) \mathop {}\!\mathrm {d}t-X_t\mathop {}\!\mathrm {d}B_t\nonumber \\&+\cos (\Omega t) \mathop {}\!\mathrm {d}W_t , \end{aligned}$$
(4)

where \(B_t\) and \(W_t\) are Brownian motions satisfying Eq. (3). In particular, \(\mathop {}\!\mathrm {d}B_t=\xi _t\cdot \mathop {}\!\mathrm {d}t\) and \(\mathop {}\!\mathrm {d}W_t=\eta _t\cdot \mathop {}\!\mathrm {d}t\). Then, we simply multiply both sides of Eq. (4) by \(e^{\omega ^2t}\) to obtain

$$\begin{aligned}&e^{\omega ^{2} t}(\mathop {}\!\mathrm {d}X_{t}+\omega ^{2} X_{t} \mathop {}\!\mathrm {d}t)=\mathop {}\!\mathrm {d}(e^{\omega ^{2} t} X_{t})\nonumber \\&\quad =e^{\omega ^{2} t}(A_{0} \cos \Omega t \mathop {}\!\mathrm {d}t-X_{t} \mathop {}\!\mathrm {d}B_{t}+\cos (\Omega t) \mathop {}\!\mathrm {d}W_{t}),\nonumber \\ \end{aligned}$$
(5)

and the integration of both sides of the above equation is as follows,

$$\begin{aligned} e^{\omega ^{2} t} X_{t}-X_{0}=&\int _{0}^{t} e^{\omega ^{2} s}(-X_{s} \mathop {}\!\mathrm {d}B_{s}\nonumber \\&+A_{0} \cos \Omega s \mathop {}\!\mathrm {d}s+\cos (\Omega s) \mathop {}\!\mathrm {d}W_{s}).\nonumber \\ \end{aligned}$$
(6)

In fact, since \(\omega ^2 > 0\), the initial displacement has little effect on the stable displacement of the system, as time t grows. Therefore, we obtain the following equation, assuming that \(X_0=0\),

$$\begin{aligned} e^{\omega ^2t}X_t=&- \int _{0}^{t}e^{\omega ^2s}X_s\mathop {}\!\mathrm {d}B_s \nonumber \\&+A_0\int _{0}^{t}e^{\omega ^2s}\cos (\Omega s) \mathop {}\!\mathrm {d}s\nonumber \\&+\int _0^te^{\omega ^2s}\cos (\Omega s)\mathop {}\!\mathrm {d}W_s ,&\end{aligned}$$
(7)

and then, take average of Eq. (7), and we acquire

$$\begin{aligned} \langle X_t \rangle&=A_0e^{-\omega ^2t}\int _{0}^{t}e^{\omega ^2s}\cos (\Omega s) \mathop {}\!\mathrm {d}s \nonumber \\&=A_1\cos (\Omega t-\phi _0)-A_1\cos \phi _0e^{-\omega ^2t},&\end{aligned}$$
(8)

where \(A_1/A_0=\frac{1}{\sqrt{\omega ^4+\Omega ^2}}\) and \(tan\phi _0 =\Omega /\omega ^2\). And the stationary solution \(\langle X_t \rangle _{as}\) satisfies

$$\begin{aligned}&\langle X_t \rangle _{as}=A_1\cos (\Omega t-\phi _0).&\end{aligned}$$
(9)

From Eq. (9), we find that the amplitude of the response is monotone with both \(\Omega \) and \(\omega \). Thus, we deduce that there is no SR phenomenon in the first-order moment of the response, which is one of our main results in this paper.

2.2 The expression of the second-order moment

Assume there exists a function \(f(t,x_t)=x_t^2\), and obviously \(f(t,x_t)\) is twice continuously differentiable in \(x_t\) which is an itô process and once continuously differentiable in time t. Then by itô formula [12], we have

$$\begin{aligned} x_t^2=&\int _0^t\frac{\partial f}{\partial u}\mathop {}\!\mathrm {d}u+\int _0^t\frac{\partial f}{\partial x_u}\mathop {}\!\mathrm {d}x_u\nonumber \\&+\frac{1}{2}\int _0^t\frac{\partial ^2f}{\partial x_u^2}(\mathop {}\!\mathrm {d}x_u\cdot \mathop {}\!\mathrm {d}x_u), \end{aligned}$$
(10)

and

$$\begin{aligned}&\mathop {}\!\mathrm {d}t\cdot \mathop {}\!\mathrm {d}t = \mathop {}\!\mathrm {d}t \cdot \mathop {}\!\mathrm {d}B_t= \mathop {}\!\mathrm {d}t \cdot \mathop {}\!\mathrm {d}W_t = 0,\nonumber \\&\mathop {}\!\mathrm {d}B_t \cdot \mathop {}\!\mathrm {d}B_t = D_1^2 \mathop {}\!\mathrm {d}t, \mathop {}\!\mathrm {d}W_t \cdot \mathop {}\!\mathrm {d}W_t = D_2^2\mathop {}\!\mathrm {d}t,\\&\mathop {}\!\mathrm {d}B_t \cdot \mathop {}\!\mathrm {d}W_t = D_1D_2\mathop {}\!\mathrm {d}t.\nonumber \end{aligned}$$
(11)

Thus, it can be obtained by Eqs. (4) and (11) that

$$\begin{aligned} \mathop {}\!\mathrm {d}X_{t} \cdot \mathop {}\!\mathrm {d}X_{t}=&D_{1}^{2} X_{t}^{2} \mathop {}\!\mathrm {d}t+D_{2}^{2} \cos ^{2}(\Omega t) \mathop {}\!\mathrm {d}t\nonumber \\&-2 D_{1} D_{2} X_{t} \cos (\Omega t) \mathop {}\!\mathrm {d}t, \end{aligned}$$
(12)

Inserting Eqs. (4) and (12) into Eq. (10) by substituting \(\mathop {}\!\mathrm {d}x_t\) with \(\mathop {}\!\mathrm {d}X_t\), and \(\mathop {}\!\mathrm {d}x_t \cdot \mathop {}\!\mathrm {d}x_t\) with \(\mathop {}\!\mathrm {d}X_t \cdot \mathop {}\!\mathrm {d}X_t\), respectively, Eq. (10) can be rewritten as

$$\begin{aligned} X_{t}^{2}=&2 \int _{0}^{t}( -\omega ^{2} X_{s}^{2}\mathop {}\!\mathrm {d}s+A_{0} \cos (\Omega s)X_s \mathop {}\!\mathrm {d}s \nonumber \\&-X_{s}^{2} \mathop {}\!\mathrm {d}B_{s}+\cos (\Omega s) X_{s}\mathop {}\!\mathrm {d}W_{s}) \nonumber \\ {}&+\int _{0}^{t} (D_{1} ^{2} X_{s}^{2} \mathop {}\!\mathrm {d}s+D_{2} ^{2} \cos ^{2}(\Omega s) \mathop {}\!\mathrm {d}s\nonumber \\ {}&-2 D_{1} D_{2} X_{s} \cos (\Omega s) \mathop {}\! \mathrm {d}s). \end{aligned}$$
(13)

After taking average of the above equation, we have

$$\begin{aligned} \langle X_t^2 \rangle =&(-2\omega ^2+D_1^2)\int _0^t\langle X_s^2\rangle \mathop {}\!\mathrm {d}s\nonumber \\&+2A_0\int _0^t\langle X_s\rangle \cos (\Omega s) \mathop {}\!\mathrm {d}s\nonumber \\&+D_2^2 \int _0^t \cos ^2(\Omega s) \mathop {}\!\mathrm {d}s\nonumber \\ {}&-2D_1D_2\int _0^t\langle X_s\rangle \cos (\Omega s)\mathop {}\!\mathrm {d}s. \end{aligned}$$
(14)

Since \(\langle X_t^2 \rangle \) and \(\langle X_t \rangle \) are functions of t, then we can take the differential of Eq. (14) by t and acquire

$$\begin{aligned} \frac{\mathop {}\!\mathrm {d}}{\mathop {}\!\mathrm {d}t} \langle X_t^2\rangle =&(-2\omega ^2+D_1^2)\langle X_t^2\rangle \nonumber \\&+D_2^2\cos ^2(\Omega t)\nonumber \\&+2(A_0-D_1D_2)\langle X_t\rangle cos(\Omega t). \end{aligned}$$
(15)

The solution of Eq. (15) is convergent if and only if \(2\omega ^2>D_1^2\). In the long-time limit(\(t \rightarrow +\infty \)), we then obtain the expression of the stationary second-order moment

$$\begin{aligned} \langle X_t^2 \rangle _{as}=A_2\sqrt{R_1^2+R_2^2}cos(2\Omega t-\phi _1-\phi _2)+\alpha _s, \end{aligned}$$
(16)

where

$$\begin{aligned}&R_1=A_1^2\omega ^2(1-D_1D_2)+\frac{1}{2}D_2^2,\nonumber \\&R_2=A_1^2\Omega (1-D_1D_2),\nonumber \\&A_2=1/\sqrt{(2\omega ^2-D_1^2)^2+4\Omega ^2},\\&tan\phi _1=2\Omega /(2\omega ^2-D_1^2), tan\phi _2=R_2/R_1,\nonumber \\&\alpha _s=R_1/(2\omega ^2-D_1^2).\nonumber&\end{aligned}$$
(17)

Additionally, Eq. (15) shows that the system is stable if and only if

$$\begin{aligned} D_1^2<2\omega ^2. \end{aligned}$$
(18)

2.3 SNR

The influence of the external signal on the system reflects on SNR. Then, the effect of frequency and input signal fluctuation is going to be considered. It is crucial that correlation function should be calculated, in order to obtain the analytic expression of SNR. In Eq. (7), replace t by \(t+\tau (\tau \ge 0)\); we obtain the time-delay model of Eq. (7)

$$\begin{aligned} e^{\omega ^2(t+\tau )}X_{t+\tau }=&e^{\omega ^2t}X_t- \int _{t}^{t+\tau }e^{\omega ^2s}X_s\mathop {}\!\mathrm {d}B_s \nonumber \\&+A_0\int _{t}^{t+\tau }e^{\omega ^2s}cos (\Omega s) \mathop {}\!\mathrm {d}s\nonumber \\&+\int _t^{t+\tau }e^{\omega ^2s}cos(\Omega s)\mathop {}\!\mathrm {d}W_s \end{aligned}$$
(19)

and take average of Eq. (19) to obtain

$$\begin{aligned} \langle e^{\omega ^{2}(t+\tau )} X_{t+\tau }\rangle&=e^{\omega ^{2}(t+\tau )}\langle X_{t+\tau }\rangle \nonumber \\&=e^{\omega ^{2} t}\langle X_{t}\rangle \nonumber \\&\quad +A_{0}\int _{t}^{t+\tau } e^{\omega ^{2} s} \cos (\Omega s) \mathop {}\!\mathrm {d}s. \end{aligned}$$
(20)

On the other hand, let \(E[X\mid {\mathcal {F}}]\) represent the conditional expectation of random variable X with a given \(\sigma \)-algebra \({\mathcal {F}}\), then

$$\begin{aligned}&\langle e^{\omega ^{2}(t+\tau )} X_{t+\tau } X_{t}\rangle =E[e^{\omega ^{2}(2 t+\tau )} X_{t+\tau } X_{t}]\nonumber \\&\quad =E[E[e^{\omega ^{2}(2 t+\tau )} X_{t+\tau } X_{t} \mid {\mathcal {F}}_{t}]] \nonumber \\&\quad =E[e^{\omega ^{2} t} X_{t} E[e^{\omega ^{2}(t+\tau )} X_{t+\tau } \mid {\mathcal {F}}_{t}]], \end{aligned}$$
(21)

where \({\mathcal {F}}_t=\{e^{\omega ^2s}X_s,s\le t\}\) is a \(\sigma \)-algebra [11], and since

$$\begin{aligned} e^{\omega ^{2} t}\left( X_{t}-\left\langle X_{t}\right\rangle \right) =&e^{\omega ^{2} t} X_{t}-A_{0} \int _{0}^{t} e^{\omega ^{2} s} \cos (\Omega s) \mathop {}\!\mathrm {d}s\nonumber \\ =&-\int _{0}^{t} e^{\omega ^{2} s} X_{s} \mathop {}\!\mathrm {d}B_{s}\nonumber \\&+\int _{0}^{t} e^{\omega ^{2} s} \cos (\Omega s) \mathop {}\!\mathrm {d}W_{s}, \end{aligned}$$
(22)

is a martingale [11],

$$\begin{aligned}&e^{\omega ^{2}(2 t+\tau )}\langle X_{t+\tau } X_{t}\rangle =\langle e^{\omega ^{2} (2 t+\tau )} X_{t+\tau } X_{t}\rangle \nonumber \\ {}&\quad =E[e^{\omega ^{2} t} X_{t} E[e^{\omega ^{2}(t+\tau )}(X_{t+\tau }-\langle X_{t+\tau }\rangle \nonumber \\ {}&\qquad +\langle X_{t+\tau }\rangle ) \mid {\mathcal {F}}_{t}]] \nonumber \\ {}&\quad =E[e^{\omega ^{2} t} X_{t} (E[e^{\omega ^{2} (t+\tau )}(X_{t+\tau }- \langle X_{t+\tau }\rangle ) \mid {\mathcal {F}}_{t}]\nonumber \\ {}&\qquad +e^{\omega ^{2}(t+\tau )}\langle X_{t+\tau }\rangle )] \nonumber \\ {}&\quad =E[e^{\omega ^{2} t} X_{t}(e^{\omega ^{2} t} (X_{t}-\langle X_{t}\rangle )+e^{\omega ^{2}(t+\tau )}\langle X_{t+\tau }\rangle )] \nonumber \\ {}&\quad =E[e^{\omega ^{2} t} X_{t}(e^{\omega ^{2} t} X_{t}+e^{\omega ^{2} (t+\tau )}\langle X_{t+\tau }\rangle - e^{\omega ^{2} t}\langle X_{t}\rangle )] \nonumber \\ {}&\quad =E[e^{\omega ^{2} t} X_{t}(e^{\omega ^{2} t} X_{t}+A_{0} \int _{t} ^{t+\tau } e^{\omega ^{2} s} \cos (\Omega s) \mathop {}\!\mathrm {d} s)] \nonumber \\ {}&\quad =e^{2 \omega ^{2} t}\langle X_{t} ^{2}\rangle +A_{0} e^{\omega ^{2} t}\langle X_{t}\rangle \int ^{t+\tau }_t e^{\omega ^{2} s} \cos (\Omega s) \mathop {}\!\mathrm {d}s. \end{aligned}$$
(23)

Divide both sides of Eq. (23) by \(e^{\omega ^2(2t+\tau )}\)

$$\begin{aligned} \langle X_{t+\tau }X_t\rangle&=e^{-\omega ^2\tau }\langle X_t^2\rangle \nonumber \\&\quad + A_0e^{-\omega ^2(t+\tau )}\langle X_t\rangle \int ^{t+\tau }_t e^{\omega ^s}cos(\Omega s)\mathop {}\!\mathrm {d}s\nonumber \\ \quad&=e^{-\omega ^2\tau }\langle X_t^2\rangle + \langle X_t\rangle (\langle X_{t+\tau }\rangle -e^{-\omega ^2\tau }\langle X_t\rangle )\nonumber \\ \quad&=\frac{A_1^2}{2}\{cos[\Omega (2t+\tau )-2\phi _0]+cos(\Omega \tau )\} \nonumber \\&\quad + e^{-\omega ^2\tau }(\langle X_t^2\rangle -\langle X_t\rangle ^2). \end{aligned}$$
(24)

Therefore, we derive the correlation function from Eq. (24)

$$\begin{aligned} C(\tau )&=\frac{\Omega }{\pi }\int _0^{\pi /\Omega }\langle X_{t+\tau }X_t\rangle \mathop {}\!\mathrm {d}t\nonumber \\&=e^{-\omega ^2\tau }\frac{D_2^2+A_1^2D_1(D_1-2D_2\omega ^2)}{2(2\omega ^2-D_1^2)}\nonumber \\ {}&\quad +\frac{A_1^2}{2}cos(\Omega \tau ). \end{aligned}$$
(25)

On the other hand, when \(\tau <0\), we can easily obtain

$$\begin{aligned} C(\tau )&=\frac{\Omega }{\pi }\int _0^{\pi /\Omega }\langle X_{t+\tau }X_t\rangle \mathop {}\!\mathrm {d}t\nonumber \\&=e^{\omega ^2\tau }\frac{D_2^2+A_1^2D_1(D_1-2D_2\omega ^2)}{2(2\omega ^2-D_1^2)}\nonumber \\ {}&\quad +\frac{A_1^2}{2}cos(\Omega \tau ).&\end{aligned}$$
(26)

Thus, for any \(\tau \) we have

$$\begin{aligned} C(\tau )&=\frac{\Omega }{\pi }\int _0^{\pi /\Omega }\langle X_{t+\tau }X_t\rangle \mathop {}\!\mathrm {d}t\nonumber \nonumber \\&=e^{-\omega ^2|\tau |}\frac{D_2^2+A_1^2D_1(D_1-2D_2\omega ^2)}{2(2\omega ^2-D_1^2)}\nonumber \\&\quad +\frac{A_1^2}{2}cos(\Omega \tau ).&\end{aligned}$$
(27)

The power spectrum \(S(\omega _0)\) is calculated as the Fourier transform of the correlation function. Then in order to calculate the output SNR we break up \(S(\omega _0)\) into two parts:

$$\begin{aligned}&S(\omega )=S_0(\omega _0)+N(\omega _0),&\end{aligned}$$
(28)

where

$$\begin{aligned} S_0(\omega _0)&=\frac{A_1^2}{2}\int _{-\infty }^{+\infty }cos(\Omega \tau ) e^{-i\omega _0 \tau }\mathop {}\!\mathrm {d}\tau \nonumber \\&=\frac{A_1^2}{2}\delta (\omega _0-\Omega ), \end{aligned}$$
(29)

and

$$\begin{aligned} N(\omega _0)&=\frac{D_2^2+A_1^2D_1(D_1-2D_2\omega ^2)}{2(2\omega ^2-D_1^2)}\nonumber \\&\quad \times \int _{-\infty } ^{+\infty }e^{-\omega ^2|\tau |}e^{-i\omega _0\tau }\mathop {}\!\mathrm {d}\tau \nonumber \\&=\frac{D_2^2+A_1^2D_1(D_1-2D_2\omega ^2)}{(2\omega ^2-D_1^2)}\frac{\omega ^2}{\omega _0^2+\omega ^4}.&\end{aligned}$$
(30)

Finally, the expression of the SNR is derived

$$\begin{aligned} SNR&=\frac{A_1^2}{2N(\omega _0=\Omega )}\nonumber \\&=\frac{1}{2\omega ^2}\frac{2\omega ^2-D_1^2}{D_2^2+A_1^2(D_1^2-2D_1D_2\omega ^2)}, \end{aligned}$$
(31)

where the parameters in Eq. (31) are introduced above.

3 Simulation

In order to verify the expression of the first-order moment in Eq. (9) and the second-order moment in Eq. (16), we use numerical simulation to approximate the system model Eq. (1) and compare the simulation results with the analytic results. The existence of noise makes the output of the system unpredictable, and the amplitude of the response is a random variable. Thus, the Monte Carlo method is used under the same parameter conditions taking simulation times \(N=200\), simulation time \(t=30s\) and time interval \(\Delta t=1e-3s\). The average value of simulation times N is taken as the steady-state response of the system.

Fig. 1
figure 1

When fixing parameters to \(\Omega =0.8, D_1=1.1, D_2=0.9, \omega =1\), a the relationship between first-order moment analytic solution and numerical solution, and b errors between first-order moment analytic solution and numerical solution

Full size image
Fig. 2
figure 2

When fixing parameters to \(\Omega =0.8, D_1=1.1, D_2=0.9, \omega =1\), a the relationship between second-order moment analytic solution and numerical solution, and b errors between first-order moment analytic solution and numerical solution

Full size image

When we do simulations on the numerical solution, we set the initial value to zero regardless of the initial value of the analytic solution. The first-order moment analytic solution and the numerical solution of Eq. (1) are shown in Fig. 1, which shows that the numerical first-order moment solution is statistically consistent to the analytic solution meaning that the initial value does not affect our analysis of the results. Thus, it is certain that the first-order moment of the analytic expression is reliable.

Fig. 3
figure 3

When fixing parameters to \(\Omega =0.8, D_2=0.9, \omega =1\), a the region of stability of the system versus \(D_1\) and \(\omega \), and b the numerical solution of the second-order moment with \(D_1=2\)

Full size image
Fig. 4
figure 4

The amplitude versus \(\omega \) while fixing, a \(\Omega = 0.8\) and \(D_1=0.5\); b \(\Omega =0.8\) and \(D_2=0.9\). Specifically, the green points in both a and b are the lower bounds of \(\omega \) with different \(D_1\) satisfying Eq. (18)

Full size image

Similarly, the initial value of second-order moment of numerical solution is also set to zero. Then, we can learn from Fig. 2 that the numerical solution of the second-order moment expression is statistically consistent to the analytic one. Thus, we can say that the second-order moment of the analytic expression is reliable.

According to Eq. (18), we obtain the stable region of the system in Fig. 3a. Take \(D_1=2\) and Fig. 3b shows that the output is unstable. And comparing to Fig. 2a in which the parameters are identical to Fig.3a except that \(D_1=1.1\), we verify the condition of stability of the system.

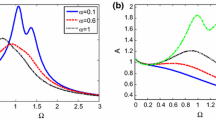
However, it is difficult for us to tell if there is any SR phenomenon directly in Eq. (16). Thus, we figure out the parameters which influence the amplitude through simulation. For some \(D_1\) and \(\omega \) satisfying Eq. (18), the peak appears. In particular, in Fig. 4, the green points are lower bounds of \(\omega \) satisfying \(D_1^2=2\omega ^2\). In other words, the figure is valid when \(\omega \) is over the lower bound.

Fig. 5
figure 5

The amplitude versus \(D_2\) while fixing, a \(\Omega =0.8\) and \(\omega =0.9\); b \(\Omega =0.8\) and \(D_1=1.1\)

Full size image
Fig. 6
figure 6

When fixing parameters to \(D_1=1.1, \Omega =0.8\), a the SNR versus \(\omega \) and \(D_2\); b the projection of a to \(\omega \)-SNR plane

Full size image

From Eqs. (9) and (16), we obtain the first-order and second-order moment response of the system model Eq. (1). Equation (9) shows that the expression of amplitude is monotone with \(\Omega \) and \(\omega \), resulting in the lack of SR phenomenon in the first-order moment expression of the response. On the other hand, from Figs. 4 and 5, we obtain both SR and ISR phenomenon.

From Eq. (31), we obtain the analytical expression of SNR. In Fig. 6, we investigate that SNR versus both \(\omega \) and \(D_2\) has a peak, while \(\Omega \) and \(D_1\) are fixed. In other words, as \(D_2\) or \(\omega \) increase, the SNR rises at first and then falls. Since the system is under the synergy between each parameter, the noise does not only restrain the system, but enhances the system under some conditions.

4 Conclusion

In this paper, we investigate the phenomenon of stochastic resonance(SR), inverse stochastic resonance(ISR) and signal-to-noise ratio (SNR) in generalized Langevin equation (GLE) subjected to a multiplicative Gaussian white noise in both frequency and input signal fluctuation. We obtain the analytic response, which is in both the first- and second-order moment of the system. Then, we verify the analytic responses by comparison with the numerical stationary ones. Then, we find that SR phenomenon does not exist in the first-order moment response in theory, while there are both SR and ISR phenomenon existing in the second-order moment response. Specifically, the output amplitude versus \(\omega \) presents one-peak oscillation. Since \(D_1\) has strong relationships with \(\omega \), when fixing \(\omega \), the amplitude versus \(D_1\) also presents one-peak oscillation. On the other hand, while fixing \(D_1\) and \(\omega \), the parameter \(D_2\) causes one-valley in the amplitude. Finally, in Fig. 6 we investigate the graphic of SNR versus \(\omega \) and \(D_2\) with fixed \(D_1=1.1\) and \(\Omega =0.8\).

In summary, by adjusting the parameters properly, we can control SR and ISR of the system. Additionally, we expect that the model of Gaussian white noise in both frequency and input signal fluctuation will find ways to fit in applications of modern science.