Rogue-wave solutions of a higher-order nonlinear Schrödinger equation for inhomogeneous Heisenberg ferromagnetic system

Abstract

In this paper, a higher-order nonlinear Schrödinger equation for the inhomogeneous Heisenberg ferromagnetic spin system is studied. By virtue of the generalized Darboux transformation, higher-order rogue-wave solutions are derived. Rogue-wave propagation and interaction are analyzed. We have observed that perturbation parameter and inhomogeneities in the medium affect the propagation speed and direction of first-order rogue waves and interaction of second-order rogue waves.

1 Introduction

In recent years, Heisenberg magnetic spin chains are subject of several investigations [1–5]. One of the main reasons, is that, one-dimensional array of spins can store quantum information [2]. During the study of those characters, it is found that Heisenberg ferromagnets models with different magnetic interactions in semiclassical and continuum limits are equivalent to a class of the nonlinear evolution equations (NLEEs) [6, 7].

Moreover, an inhomogeneous Heisenberg ferromagnetic spin system with the prolongation structure has been attained [8–10]:

$$\begin{aligned} \overrightarrow{\Gamma }_t = & \,\,\frac{1}{2}\overrightarrow{\Gamma }\times \overrightarrow{\Gamma }_{xx}+h\overrightarrow{\Gamma }_x+\frac{5}{2}\epsilon (\overrightarrow{\Gamma }_x\cdot \overrightarrow{\Gamma }_x) \overrightarrow{\Gamma }_{xxx}+\epsilon \overrightarrow{\Gamma }_{xxxxx}+\epsilon \Big [\frac{35}{2}(\overrightarrow{\Gamma }_x\cdot \overrightarrow{\Gamma }_x)(\overrightarrow{\Gamma }_x\cdot \overrightarrow{\Gamma }_{xx}) \\ &\quad+10\overrightarrow{\Gamma }_{xx}\overrightarrow{\Gamma }_{xxx}+5\overrightarrow{\Gamma }_x\cdot \overrightarrow{\Gamma }_{xxxx}\Big ]\overrightarrow{\Gamma }+\epsilon \Big [\frac{35}{8}(\overrightarrow{\Gamma }_x\cdot \overrightarrow{\Gamma }_x)^2 +10\overrightarrow{\Gamma }_x\cdot \overrightarrow{\Gamma }_{xxx}+\frac{15}{2}\overrightarrow{\Gamma }_{xx}\cdot \overrightarrow{\Gamma }_{xx}\Big ]\overrightarrow{\Gamma }_x \\ &\quad+10\epsilon (\overrightarrow{\Gamma }_x\cdot \overrightarrow{\Gamma }_{xx})\overrightarrow{\Gamma }_{xx}, \end{aligned}$$

(1)

where $\epsilon$ is a perturbation parameter, $h$ represents inhomogeneities of the medium, $\overrightarrow{\Gamma }$ is spin vector in respect of the scaled temporal $t$ and spatial coordinate $x$. It can be found that Eq. (1) can degenerate into the Heisenberg ferromagnetic spin system, when $h=\epsilon =0$.

On the other hand, some NLEEs have Rogue-wave solutions, such as the nonlinear Schrödinger (NLS) equation [11–15]:

$$\begin{aligned} i Q_{\tau }+ Q^2 Q^*+\frac{1}{2} Q_{\iota \iota }=0, \end{aligned}$$

(2)

where $*$ represents the complex conjugation and $Q$ is a function of $\tau$ and $\iota.$ Solli et al. [12] have attained rogue waves governed by Eq. (2) in an optical system. Chabchoub et al. [13] have observed rogue waves governed by Eq. (2) in a water tank. Akhmediev et al. [14] and Guo et al. [15] have obtained exact rogue-wave solutions of Eq. (2) via the modified Darboux transformation (DT) and generalized DT respectively. A rogue-wave is assumed as an isolated “huge” wave with an amplitude “much larger” than the average wave crests around it in the ocean [11] and also relevant in other physical contexts such as the Bose–Einstein condensates, optics and superfluids [11–16].

In this paper, we work on a higher-order NLS equation, which is equivalent to Eq. (1) via mapping of the spin vector function $\overrightarrow{\Gamma }$ onto a unit tangent vector of a moving helical space curve [6], as follows [10]:

$$\begin{aligned}&i q_{t}+ q^2 q^*-30 i \epsilon q_{x} q^2 (q^*)^2-10 i \epsilon q_{xx} q q^*_{x}-10 i \epsilon q_{x} q q^*_{xx}-10 i \epsilon q_{xxx} q q^*-10 i \epsilon q_{x}^2 q^*_{x} \\ &\quad -20 i \epsilon q_{x} q_{xx} q^*+\frac{1}{2} q_{xx}-i h q_{x}-i \epsilon q_{}=0, \end{aligned}$$

(3)

where $q$ is a complex function of $t$ and $x$. We note that Eq. (3) can degenerate into Eq. (2), when $\epsilon =h=0.$ Lax pairs for Eq. (3) have been obtained [10, 17].

However, to our knowledge, rogue-wave solutions and generalized DT of Eq. (3) have not been obtained. With the aid of symbolic computation [18, 19], generalized DT, higher-order rogue-wave solutions and interaction for Eq. (3) is obtained.

2 Generalized Darboux transformation for Eq. (3)

In order to be self-contained, we recall the DT of Eq. (3) briefly. Lax pairs of Eq. (3) are [10, 17]

$$\begin{aligned} \overrightarrow{\Psi }_t&= U\overrightarrow{\Psi },\end{aligned}$$

(4)

$$\begin{aligned} \overrightarrow{\Psi }_x&= V\overrightarrow{\Psi }, \end{aligned}$$

(5)

where $\overrightarrow{\Psi }=(\psi _1,\,\psi _2)^T$ is a vector function of $x$ and $t$, $T$ denotes the transpose of a matrix and the matrices $U$ and $V$ have the forms

$$\begin{aligned} U=&\left[ \begin{array}{cc} -i \lambda &{} q \\ -q^* &{} i \lambda \\ \end{array} \right] ,\\ V=&\left[ \begin{array}{cc} V_{11} &{} V_{12} \\ V_{21} &{} -V_{11} \\ \end{array} \right] ,\\ V_{11}=&\frac{1}{2} \big (-2 i h \lambda -2 i \lambda ^2-32 i \epsilon \lambda ^5+i qq^*+16 i \epsilon \lambda ^3 qq^*-12 i \epsilon \lambda q^2(q^*)^2-8 \epsilon \lambda ^2q^* q_{x}\\&+12 \epsilon q(q^*)^2 q_{x}+8 \epsilon \lambda ^2 qq^*_{x}-12 \epsilon q^2q^*q^*_{x}+4 i \epsilon \lambda q_{x}q^*_{x} -4 i \epsilon \lambda q^* q_{xx}-2 \epsilon q^*_{x} q_{xx}\\&-4 i \epsilon \lambda qq^*_{xx}+2 \epsilon q_{x} q^*_{xx}+2 \epsilon q^* q_{xxx}-2 \epsilon qq^*_{xxx}\big ),\\ V_{12}=&\frac{1}{2} \big (2 h q+2 \lambda q+32 \epsilon \lambda ^4 q-16 \epsilon \lambda ^2 q^2q^*+12 \epsilon q^3(q^*)^2+i q_{x}+16 i \epsilon \lambda ^3 q_{x}\\&-24 i \epsilon \lambda qq^* q_{x}+12 \epsilon q^* q_{x}^2+8 \epsilon q q_{x}q^*_{x}-8 \epsilon \lambda ^2 q_{xx}+16 \epsilon qq^* q_{xx}+4 \epsilon q^2q^*_{xx}\\&-4 i \epsilon \lambda q_{xxx}+2 \epsilon q_{xxxx}\big ),\\ V_{21}=&\frac{1}{2} \big (-2 hq^*-2 \lambda q^*-32 \epsilon \lambda ^4q^*+16 \epsilon \lambda ^2 q(q^*)^2-12 \epsilon q^2(q^*)^3+iq^*_{x}+16 i \epsilon \lambda ^3q^*_{x}\\&-24 i \epsilon \lambda qq^*q^*_{x}-8 \epsilon q^* q_{x}q^*_{x}-12 \epsilon q(q^*_{x})^2-4 \epsilon (q^*)^2 q_{xx}+8 \epsilon \lambda ^2q^*_{xx}-16 \epsilon qq^*q^*_{xx}\\&-4 i \epsilon \lambda q^*_{xxx}-2 \epsilon q^*_{xxxx}\big ), \end{aligned}$$

where $\lambda$ is a parameter independent of $x$ and $t$. The compatibility condition $U_t-V_x+UV-VU=0$ leads to Eq. (3) [10, 17].

By virtue of Lax Pairs given by Eqs. (4) and (5), DT matrix $M^{[1]}$ has the form as [10, 17]

$$\begin{aligned}&M^{[1]}=\left[\begin{array}{cc} \lambda&0\\ 0&\lambda \end{array}\right]-S^{[1]}, \quad S^{[1]}=H^{[1]}\Lambda ^{[1]} (H^{[1]})^{-1},\end{aligned}$$

(6)

$$\begin{aligned}&H^{[1]}=\left[\begin{array}{cc} \phi _{11}&-\phi _{12}^*\\ \phi _{12}&\phi _{11}^* \end{array}\right], \quad \Lambda ^{[1]}=\left[\begin{array}{cc} \lambda _1&0\\ 0&\lambda _1^* \end{array}\right], \end{aligned}$$

(7)

where ${(\phi _{11},\,\phi _{12})}^{\text{T}}$ is a solution of Lax Pairs given in Eqs. (4) and (5) at $\lambda =\lambda _1$ and $q$, $\lambda _1$ is a parameter independent of $x$ and $t$, $(H^{[1]})^{-1}$ is inverse matrix of $H^{[1]}$. Sign $^{[1]}$ on the upper right corner of a function/matrix, means that function/matrix is engendered from the first DT. Sign $^{[k]}(k=2,3,\ldots )$ means that those functions/matrices are engendered from the $k$-th DTs. Therefore, the first-order solutions of Eq. (3) can be given as

$$\begin{aligned} q^{[1]}=q-\frac{2i(\lambda _1-\lambda _1^*)\phi _{11}\phi ^*_{12}}{\phi _{11} \phi ^*_{11}+\phi _{12}\phi ^*_{12}}. \end{aligned}$$

(8)

If we continue such process, $N$-th $(N=2,3,\ldots )$ DTs and $N$-th order solutions for Eq. (3) can be obtained.

By virtue of DT given by Eq. (6), the generalized DT for Eq. (3) can be obtained as shown below. We assume that $\widetilde{q}$ is a solution of Eq. (3) [15]

$$\begin{aligned} \overrightarrow{\Theta }(\zeta _1+\varepsilon ) \end{aligned}$$

(9)

is a solution for Lax Pairs given by Eqs. (4) and (5) at $q=\widetilde{q}$ and $\lambda =\zeta _1+\varepsilon$, where $\zeta _1$ and $\varepsilon$ are both parameters independent of $x$ and $t$. Expanding $\overrightarrow{\Theta }$ at $\zeta _1$, we have

$$\begin{aligned} \overrightarrow{\Theta }(\zeta _1+\varepsilon )=\overrightarrow{\Xi }_0+\overrightarrow{\Xi }_1\varepsilon +\overrightarrow{\Xi }_2\varepsilon ^2+ \cdots, \end{aligned}$$

(10)

where $\overrightarrow{\Xi }_k=\frac{1}{k!}\frac{\partial ^k}{\partial \zeta ^k}\overrightarrow{\Theta }(\zeta )| _{\zeta =\zeta _1}\,\,(k=0,1,2,\ldots )$ are all the functions of $x$ and $t$. It can be shown that $\overrightarrow{\Xi }_0$ is a solution of Lax Pairs given by Eqs. (4) and (5) at $q=\widetilde{q}$ and $\lambda =\zeta _1$ [15].

By virtue of DT given by Eq. (6), generalized DT matrix $\mathcal{M}^{[1]}$ of the first-step generalized DT for Eq. (3) is

$$\begin{aligned}&\mathcal{M}^{[1]}=\left[\begin{array}{cc} \lambda&0\\ 0&\lambda \end{array}\right] -\mathcal{S}_1, \quad \mathcal{S}_1=\mathcal{H}^{[1]}\mathcal{L} (\mathcal{H}^{[1]})^{-1},\end{aligned}$$

(11)

$$\begin{aligned}&\mathcal{H}^{[1]}=\left[\begin{array}{cc}\varphi _{11}&-(\varphi _{12})^* \\ \varphi _{12}&(\varphi _{11})^* \end{array}\right], \quad \mathcal{L}=\left[\begin{array}{cc} \zeta _1&0\\ 0&\zeta ^*_1 \end{array}\right], \end{aligned}$$

(12)

where $(\varphi _{11},\,\varphi _{12})^T=\overrightarrow{\Xi }_0.$ Thus, the first-order solutions $\widetilde{q}^{[1]}$ for Eq. (3) are

$$\begin{aligned} \widetilde{q}^{[1]}=\widetilde{q}-\frac{2i(\zeta _1-\zeta _1^*) \varphi _{11}(\varphi _{12})^*}{\varphi _{11} (\varphi _{11})^*+\varphi _{12}(\varphi _{12})^*}. \end{aligned}$$

(13)

As the second-step generalized DT, using Eq. (11) in Eq. (10) and taking the limit process [15], we have

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}\frac{\big (\mathcal{M}^{[1]}|_{\lambda =\zeta _1+\varepsilon }\big )\overrightarrow{\Theta }}{\varepsilon }&= \lim _{\varepsilon \rightarrow 0}\frac{\big (\varepsilon +\mathcal{M}^{[1]}|_{\lambda =\zeta _1}\big )\overrightarrow{\Theta }}{\varepsilon } \\ &= \overrightarrow{\Xi }_0+\mathcal{M}^{[1]}|_{\lambda =\zeta _1}\overrightarrow{\Xi }_1=(\varphi _{21},\,\varphi _{22})^T. \end{aligned}$$

(14)

We find a solution $(\varphi _{21},\,\varphi _{22})^T$ for Lax Pairs given by Eqs. (4) and (5) at $q=\widetilde{q}^{[1]}$ and $\lambda =\zeta _1$. Thus, we can obtain the second-step generalized DT matrix $\mathcal{M}^{[2]}$ as follows,

$$\begin{aligned}&\mathcal{M}^{[2]}=\left[\begin{array}{cc} \lambda&0\\ 0&\lambda \end{array}\right] -\mathcal{S}_2, \quad \mathcal{S}_2=\mathcal{H}^{[2]}\mathcal{L} (\mathcal{H}^{[2]})^{-1},\end{aligned}$$

(15)

$$\begin{aligned}&\mathcal{H}^{[2]}=\left[\begin{array}{cc}\varphi _{21}&-(\varphi _{22})^*\\ \varphi _{22}&(\varphi _{21})^* \end{array}\right]. \end{aligned}$$

(16)

This allows us to find the second-order solutions $\widetilde{q}^{[2]}$ of Eq. (3) as

$$\begin{aligned} \widetilde{q}^{[2]}=\widetilde{q}^{[1]}-\frac{2i(\zeta _1-\zeta _1^*) \varphi _{21}(\varphi _{22})^*}{\varphi _{21} (\varphi _{21})^*+\varphi _{22}(\varphi _{22})^*}. \end{aligned}$$

(17)

For the third-step generalized DT, using the same method as above, we have

$$\begin{aligned}&\lim _{\varepsilon \rightarrow 0}\frac{\big (\mathcal{M}^{[2]}|_{\lambda =\zeta _1+\varepsilon }\big )\big (\mathcal{M}^{[1]}|_{\lambda =\zeta _1+\varepsilon }\big )\overrightarrow{\Theta }}{\varepsilon }\, \\ &\quad =\lim _{\varepsilon \rightarrow 0}\frac{\big (\varepsilon +\mathcal{M}^{[2]}|_{\lambda =\zeta _1}\big )\big (\varepsilon +\mathcal{M}^{[1]}|_{\lambda =\zeta _1}\big )\overrightarrow{\Theta }}{\varepsilon }\, \\ &\quad =\overrightarrow{\Xi }_0+(\mathcal{M}^{[2]}|_{\lambda =\zeta _1}+\mathcal{M}^{[1]}|_{\lambda =\zeta _1})\overrightarrow{\Xi }_1+\mathcal{M}^{[2]}|_{\lambda =\zeta _1}\mathcal{M}^{[1]}|_{\lambda =\zeta _1}\overrightarrow{\Xi }_2\, \\ &\quad =(\varphi _{31},\,\varphi _{32})^T. \end{aligned}$$

(18)

Thus, we find a solution $(\varphi _{31},\,\varphi _{32})^T$ for Lax Pairs given by Eqs. (4) and (5) at $q=\widetilde{q}^{[2]}$ and $\lambda =\zeta _1$ [15]. This allows us to find the third-order solutions $\widetilde{q}^{[3]}$ of Eq. (3) as

$$\begin{aligned} \widetilde{q}^{[3]}=\widetilde{q}^{[2]}-\frac{2i(\zeta _1-\zeta _1^*) \varphi _{31}(\varphi _{32})^*}{\varphi _{31} (\varphi _{31})^*+\varphi _{32}(\varphi _{32})^*}. \end{aligned}$$

(19)

If we continue such process, the 4th- and 5th-step generalized DTs for Eq. (3) might be obtained.

3 Results and discussion

In this section, the rogue-wave solutions, interaction and propagation for Eq. (3) have been discussed.

3.1 Rogue-wave solutions for Eq. (3)

We take the plane waves as the seed solutions for Eq. (3)

$$\begin{aligned} q=ie^{it}. \end{aligned}$$

(20)

Then, the solution $\overrightarrow{\Theta }(x,t;s)$ for Lax Pairs given by Eqs. (4) and (5) at $\lambda =-is$ and $q=ie^{it}$ is

$$\begin{aligned} \overrightarrow{\Theta }(x,t;s)=\left[\begin{array}{c} i(a_1e^\eta -a_2e^{-\eta })e^{\frac{it}{2}}\\ (a_2e^\eta -a_1e^{-\eta })e^{-\frac{it}{2}}\end{array}\right], \end{aligned}$$

(21)

where

$$\begin{aligned}&a_1=\frac{\sqrt{s+\sqrt{-1+s^2}}}{\sqrt{-1+s^2}}, \quad a_2=\frac{\sqrt{s-\sqrt{-1+s^2}}}{\sqrt{-1+s^2}},\\&\eta =\mu (x+\omega t), \quad \mu =-\sqrt{-1+s^2}, \quad \omega =h-i s+6 \epsilon +8 s^2 \epsilon +16 s^4 \epsilon , \end{aligned}$$

and $s$ is a parameter independent of $x$ and $t$. Taking $s=1+\tau ^2$ and expanding the vector function $\overrightarrow{\Theta }(x,t;\tau )$ at $\tau =0$, where $\tau$ is a parameter independent of $x$ and $t$, we have

$$\begin{aligned} \overrightarrow{\Theta }(x,t;\tau )=\overrightarrow{\Xi }_0+\overrightarrow{\Xi }_1\tau ^2+\overrightarrow{\Xi }_2\tau ^4\cdots, \end{aligned}$$

(22)

where

$$\begin{aligned}&\overrightarrow{\Xi }_0=\left[\begin{array}{c} -i e^{\frac{i t}{2}} (-1+2 x+2 t (-i+h+30 \epsilon ))\\ e^{-\frac{i t}{2}} (-1-2 x-2 t (-i+h+30 \epsilon )) \end{array}\right],\end{aligned}$$

(23)

$$\begin{aligned}& \overrightarrow{\Xi }_1=\left[ {\begin{array}{c} \widehat{\widehat{\theta }}_1{[1]} \\ \widehat{\theta }_1{[1]}\end{array}}\right], \overrightarrow{\Xi }_2=\left[{\begin{array}{c} \widehat{\widehat{\theta }}_1{[2]} \\ \widehat{\theta }_1{[2]} \end{array}}\right], \end{aligned}$$

(24)

with

$$\begin{aligned}\widehat{\widehat{\theta }}_1{[1]} &=-\frac{1}{12} i e^{\frac{i t}{2}} \big (3+6 x-12 x^2+8 x^3+12 t^2 (-1+2 x) (-i+h+30 \epsilon )^2\\ &\quad+8 t^3 (-i+h+30 \epsilon )^3+6 t \big (-5 i+h (1-2 x)^2+x (4 i-120 \epsilon )+350 \epsilon \\ &\quad+4 x^2 (-i+30 \epsilon )\big )\big ),\\ \widehat{\theta }_1{[1]}&=\frac{1}{12} e^{-\frac{i t}{2}} \big (3-6 x-12 x^2-8 x^3-12 t^2 (1+2 x) (-i+h+30 \epsilon )^2-\\ &\quad 8 t^3 (-i+h+30 \epsilon )^3-6 t \big (-5 i+h (1+2 x)^2+350 \epsilon +4 x (-i+30 \epsilon )\\ &\quad +4 x^2 (-i+30 \epsilon )\big )\big ), \end{aligned}$$

and $\widehat{\widehat{\theta }}_1{[2]},\,\widehat{\theta }_1{[2]}$ are presented in Appendix 1.

By virtue of Eqs. (13) and (23), we can obtain the first-order rogue-wave solutions of Eq. (3) as

$$\begin{aligned} q^{[1]}=-\frac{i e^{i t} \big (-3-8 i t+4 t^2+4 h^2 t^2+8 h t x+4 x^2+240 h t^2 \epsilon +240 t x \epsilon +3600 t^2 \epsilon ^2\big )}{1+4 t^2+4 h^2 t^2+8 h t x+4 x^2+240 h t^2 \epsilon +240 t x \epsilon +3600 t^2 \epsilon ^2}. \end{aligned}$$

(25)

We can confirm by direct validation that Eq. (25) is a solution of Eq. (3) via the Mathematica/Matlab.

By virtue of Eqs. (17) and (24), we can obtain the second-order rogue-wave solutions of Eq. (3) as

$$\begin{aligned} q^{[2]}=\frac{\widehat{\widehat{q}}^{[2]}}{\widehat{q}^{[2]}}e^{it}, \end{aligned}$$

(26)

where $\widehat{\widehat{q}}^{[2]}$ and $\widehat{q}^{[2]}$ are exhibited in Appendix 2. The characteristic parameters of rogue waves presented in this manuscript is the same as NLS in [14].

By virtue of Eqs. (18), (19) and (24), we can obtain the third-order rogue-wave solutions. For simplicity, we omit the tedious expression of the third-order rogue waves and exhibit the dynamical behavior of those in Fig. 7.

Fig. 1

(a) First-order rogue-wave solutions via Eq. (25) with parameters $h=5$ and $\epsilon = 0.9$; (b) is the wave profile in (a) with $t=-0.4, 0$ and $0.4$, where $t$ and x are the scaled time and spatial coordinate respectively

Fig. 2

(a) First-order rogue-wave solutions via Eq. (25) with parameters $h=-5$ and $\epsilon = 0.9$; (b) is the wave profile in (a) with $t=-0.4, 0$ and $0.4$, where $t$ and x are the scaled time and spatial coordinate respectively

Fig. 3

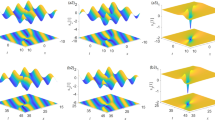
(a) First-order rogue-wave solutions via Eq. (25) with parameters $h=5$ and $\epsilon = -0.9$; (b) is the wave profile in (a) with $t=-0.4, 0$ and $0.4$, where $t$ and x are the scaled time and spatial coordinate respectively

If we continue such process, the fourth- and fifth-order rogue-wave solutions for Eq. (3) might be obtained.

3.2 Rogue-wave interaction and propagation

By virtue of the graphical illustrations of rogue waves, rogue-wave propagation and interaction are analyzed as follows:

Figures 1(a), 1(b) and 2(a), 2(b) show that inhomogeneity in the medium, which is represented by $h$, has an effect on the propagation speed of first-order rogue waves. Propagation distance of first-order rogue waves, as displayed in Fig. 1(a) (with $h=5$ and $\epsilon = 0.9$), is longer than that exhibited in Fig. 2(a) (with $h=-5$ and $\epsilon = 0.9$) during the same time, this phenomenon also can be found from Figs. 1(b) and 2(b). We note that the coefficient $h$ of Eq. (3) can be removed by using suitable transformation, but it can affect the propagation speed of first-order rogue waves.

Figures 1, 2 and 3 display that the perturbation parameter $\epsilon$ has an effect on the propagation direction of first-order rogue waves. Propagation direction of first-order rogue waves in Figs. 1(a), 1(b) and 2(a), 2(b) are all consistent with the negative $x$ axis, when $\epsilon =0.9$ and $h=\pm 5$ accordingly; Propagation direction of first-order rogue waves in Fig. 3(a), 3(b) are both consistent with the positive $x$ axis, when $\epsilon =-0.9$ and $h=5$. In addition, Figs. 1, 2 and 3 show that $q$ is a bright-rogue wave.

Figures 4(a), 4(b) and 5(a), 5(b) show that $h$ has an effect on interaction of second-order rogue waves. Propagation distance of second-order rogue waves, as exhibited in Fig. 4(a), 4(b), is longer than those displayed in Fig. 5(a), 5(b) during the same time, when $h=5$ and $\epsilon = 0.9$ in Fig. 4(a), 4(b) while $h=-5$ and $\epsilon = 0.9$ in Fig. 5(a), 5(b).

Fig. 4

(a) Second-order rogue-wave interaction via Eq. (26) with parameters $h=5$ and $\epsilon = 0.9$; (b) is the wave profile in (a) with $t=-0.3, 0$ and $0.3$, where $t$ and x are the scaled time and spatial coordinate respectively

Fig. 5

(a) Second-order rogue-wave interaction via Eq. (26) with parameters $h=-5$ and $\epsilon = 0.9$; (b) is the wave profile in (a) with $t=-0.3, 0$ and $0.3$, where $t$ and x are the scaled time and spatial coordinate respectively

Figures 4, 5 and 6 display that $\epsilon$ has an effect on interaction of second-order rogue waves. Propagation direction of second-order rogue waves in Figs. 4(a), 4(b) and 5(a), 5(b) are all consistent with the negative $x$ axis, when $\epsilon =0.9$ and $h=\pm 5$. Accordingly propagation direction of second-order rogue waves in Fig. 6(a), 6(b) are both consistent with the positive $x$ axis, when $\epsilon =-0.9$ and $h=5$.

Fig. 6

(a) Second-order rogue-wave interaction via Eq. (26) with parameters $h=5$ and $\epsilon = -0.9$; (b) is the wave profile in (a) with $t=-0.3, 0$ and $0.3$, where $t$ and x are the scaled time and spatial coordinate respectively

Figure 7(a)–7(c) exhibit interaction of third-order rogue waves, behaviors of which are similar to those of second-order rogue waves in Figs. 4, 5 and 6, i.e., behavior of Fig. 7(a) is similar to Fig. 4(a), behavior of Fig. 7(b) is similar to Fig. 5(a) and behavior of Fig. 7(c) is similar to Fig. 6(a).

Fig. 7

Third-order rogue-wave interaction with parameters: (a) of $h=5, \epsilon =0.9$; (b) of $h=-5, \epsilon =0.9$; (c) of $h=5, \epsilon =-0.9$

4 Conclusions

In this paper, a higher order inhomogeneous NLS equation [i.e. Eq. (3)] for inhomogeneous Heisenberg ferromagnetic spin system has been investigated. Our results state that Higher-Order Generalized DT given by Eq. (18) and Higher-Order Rogue-Wave solutions given by Eq. (26) have been attained. Rogue-wave propagation and interaction have been analyzed. For first-order rogue waves, relation between the inhomogeneities of medium is characterized by $h$ and propagation speed of first-order rogue waves has been discussed. Relation of the perturbation parameter $\epsilon$ and propagation direction of first-order rogue waves has been discussed. For second-order rogue waves, coefficients $h$ and $\epsilon$ both have an effect on interaction of second-order rogue waves. For third-order rogue waves, the behaviors are similar to those of second-order rogue waves.

Appendices

Appendix 1

$\widehat{\widehat{\theta }}_1{[2]}=-\frac{1}{480} i e^{\frac{i t}{2}} \big (-45-30 x-120 x^2+240 x^3-80 x^4+32 x^5+80 t^4 (-1+2 x) (-i+h+30 \epsilon )^4+32 t^5 (-i+h+30 \epsilon )^5+80 t^3 (-i+h+30 \epsilon )^2 \big (h \big (3-4 x+4 x^2\big )+x (4 i-120 \epsilon )+4 x^2 (-i+30 \epsilon )+15 (-i+70 \epsilon )\big )+10 t \big (h \big (-3-24 x+72 x^2-32 x^3+16 x^4\big )+x^3 (32 i-960 \epsilon )+16 x^4 (-i+30 \epsilon )-120 x (-i+70 \epsilon )+24 x^2 (-7 i+410 \epsilon )+3 (-7 i+3938 \epsilon )\big )+40 t^2 \big (27+h^2 \big (-3+18 x-12 x^2+8 x^3\big )-12 x^2 (i-30 \epsilon )^2+8 x^3 (i-30 \epsilon )^2+2820 i \epsilon -60300 \epsilon ^2+6 x \big (-11-1060 i \epsilon +21900 \epsilon ^2\big )+2 h \big (15 i+x^2 (12 i-360 \epsilon )-1050 \epsilon +8 x^3 (-i+30 \epsilon )+6 x (-7 i+410 \epsilon )\big )\big )\big ).$

$\widehat{\theta }_1{[2]}=\frac{1}{480} e^{-\frac{i t}{2}} \big (-45+30 x-120 x^2-240 x^3-80 x^4-32 x^5-80 t^4 (1+2 x) (-i+h+30 \epsilon )^4-32 t^5 (-i+h+30 \epsilon )^5-80 t^3 (-i+h+30 \epsilon )^2 \big (h \big (3+4 x+4 x^2\big )+4 x (-i+30 \epsilon )+4 x^2 (-i+30 \epsilon )+15 (-i+70 \epsilon )\big )-10 t \big (h \big (-3+24 x+72 x^2+32 x^3+16 x^4\big )+32 x^3 (-i+30 \epsilon )+16 x^4 (-i+30 \epsilon )+120 x (-i+70 \epsilon )+24 x^2 (-7 i+410 \epsilon )+3 (-7 i+3938 \epsilon )\big )-40 t^2 \big (h^2 \big (3+18 x+12 x^2+8 x^3\big )+12 x^2 (i-30 \epsilon )^2+8 x^3 (i-30 \epsilon )^2+3 \big (-9-940 i \epsilon +20100 \epsilon ^2\big )+6 x \big (-11-1060 i \epsilon +21900 \epsilon ^2\big )+2 h \big (12 x^2 (-i+30 \epsilon )+8 x^3 (-i+30 \epsilon )+15 (-i+70 \epsilon )+6 x (-7 i+410 \epsilon )\big )\big )\big ).$

Appendix 2

$\widehat{\widehat{q}}^{[2]}=45 i-360 t-468 i t^2-180 i h^2 t^2+192 t^3-576 h^2 t^3-528 i t^4-1440 i h^2 t^4-144 i h^4 t^4+384 t^5+768 h^2 t^5+384 h^4 t^5+64 i t^6+192 i h^2 t^6+192 i h^4 t^6+64 i h^6 t^6-360 i h t x-1152 h t^2 x-2880 i h t^3 x-576 i h^3 t^3 x+1536 h t^4 x+1536 h^3 t^4 x+384 i h t^5 x+768 i h^3 t^5 x+384 i h^5 t^5 x-180 i x^2-576 t x^2-1440 i t^2 x^2-864 i h^2 t^2 x^2+768 t^3 x^2+2304 h^2 t^3 x^2+192 i t^4 x^2+1152 i h^2 t^4 x^2+960 i h^4 t^4 x^2-576 i h t x^3+1536 h t^2 x^3+768 i h t^3 x^3+1280 i h^3 t^3 x^3-144 i x^4+384 t x^4+192 i t^2 x^4+960 i h^2 t^2 x^4+384 i h t x^5+64 i x^6-45360 i h t^2 \epsilon +57600 h t^3 \epsilon -40320 i h t^4 \epsilon -32640 i h^3 t^4 \epsilon +46080 h t^5 \epsilon +46080 h^3 t^5 \epsilon +11520 i h t^6 \epsilon +23040 i h^3 t^6 \epsilon +11520 i h^5 t^6 \epsilon -45360 i t x \epsilon +57600 t^2 x \epsilon -40320 i t^3 x \epsilon -97920 i h^2 t^3 x \epsilon +46080 t^4 x \epsilon +138240 h^2 t^4 x \epsilon +11520 i t^5 x \epsilon +69120 i h^2 t^5 x \epsilon +57600 i h^4 t^5 x \epsilon -97920 i h t^2 x^2 \epsilon +138240 h t^3 x^2 \epsilon +69120 i h t^4 x^2 \epsilon +115200 i h^3 t^4 x^2 \epsilon -32640 i t x^3 \epsilon +46080 t^2 x^3 \epsilon +23040 i t^3 x^3 \epsilon +115200 i h^2 t^3 x^3 \epsilon +57600 i h t^2 x^4 \epsilon +11520 i t x^5 \epsilon -277200 i t^2 \epsilon ^2+2246400 t^3 \epsilon ^2+86400 i t^4 \epsilon ^2-2160000 i h^2 t^4 \epsilon ^2+691200 t^5 \epsilon ^2+2073600 h^2 t^5 \epsilon ^2+172800 i t^6 \epsilon ^2+1036800 i h^2 t^6 \epsilon ^2+864000 i h^4 t^6 \epsilon ^2-4320000 i h t^3 x \epsilon ^2+4147200 h t^4 x \epsilon ^2+2073600 i h t^5 x \epsilon ^2+3456000 i h^3 t^5 x \epsilon ^2-2160000 i t^2 x^2 \epsilon ^2+2073600 t^3 x^2 \epsilon ^2+1036800 i t^4 x^2 \epsilon ^2+5184000 i h^2 t^4 x^2 \epsilon ^2+3456000 i h t^3 x^3 \epsilon ^2+864000 i t^2 x^4 \epsilon ^2-57024000 i h t^4 \epsilon ^3+41472000 h t^5 \epsilon ^3+20736000 i h t^6 \epsilon ^3+34560000 i h^3 t^6 \epsilon ^3-57024000 i t^3 x \epsilon ^3+41472000 t^4 x \epsilon ^3+20736000 i t^5 x \epsilon ^3+103680000 i h^2 t^5 x \epsilon ^3+103680000 i h t^4 x^2 \epsilon ^3+34560000 i t^3 x^3 \epsilon ^3-531360000 i t^4 \epsilon ^4+311040000 t^5 \epsilon ^4+155520000 i t^6 \epsilon ^4+777600000 i h^2 t^6 \epsilon ^4+1555200000 i h t^5 x \epsilon ^4+777600000 i t^4 x^2 \epsilon ^4+9331200000 i h t^6 \epsilon ^5+9331200000 i t^5 x \epsilon ^5+46656000000 i t^6 \epsilon ^6.$

$\widehat{q}^{[2]}=9+396 t^2+108 h^2 t^2+432 t^4-288 h^2 t^4+48 h^4 t^4+64 t^6+192 h^2 t^6+192 h^4 t^6+64 h^6 t^6+216 h t x-576 h t^3 x+192 h^3 t^3 x+384 h t^5 x+768 h^3 t^5 x+384 h^5 t^5 x+108 x^2-288 t^2 x^2+288 h^2 t^2 x^2+192 t^4 x^2+1152 h^2 t^4 x^2+960 h^4 t^4 x^2+192 h t x^3+768 h t^3 x^3+1280 h^3 t^3 x^3+48 x^4+192 t^2 x^4+960 h^2 t^2 x^4+384 h t x^5+64 x^6+18000 h t^2 \epsilon +28800 h t^4 \epsilon -9600 h^3 t^4 \epsilon +11520 h t^6 \epsilon +23040 h^3 t^6 \epsilon +11520 h^5 t^6 \epsilon +18000 t x \epsilon +28800 t^3 x \epsilon -28800 h^2 t^3 x \epsilon +11520 t^5 x \epsilon +69120 h^2 t^5 x \epsilon +57600 h^4 t^5 x \epsilon -28800 h t^2 x^2 \epsilon +69120 h t^4 x^2 \epsilon +115200 h^3 t^4 x^2 \epsilon -9600 t x^3 \epsilon +23040 t^3 x^3 \epsilon +115200 h^2 t^3 x^3 \epsilon +57600 h t^2 x^4 \epsilon +11520 t x^5 \epsilon +1364400 t^2 \epsilon ^2+1123200 t^4 \epsilon ^2-1123200 h^2 t^4 \epsilon ^2+172800 t^6 \epsilon ^2+1036800 h^2 t^6 \epsilon ^2+864000 h^4 t^6 \epsilon ^2-2246400 h t^3 x \epsilon ^2+2073600 h t^5 x \epsilon ^2+3456000 h^3 t^5 x \epsilon ^2-1123200 t^2 x^2 \epsilon ^2+1036800 t^4 x^2 \epsilon ^2+5184000 h^2 t^4 x^2 \epsilon ^2+3456000 h t^3 x^3 \epsilon ^2+864000 t^2 x^4 \epsilon ^2-36288000 h t^4 \epsilon ^3+20736000 h t^6 \epsilon ^3+34560000 h^3 t^6 \epsilon ^3-36288000 t^3 x \epsilon ^3+20736000 t^5 x \epsilon ^3+103680000 h^2 t^5 x \epsilon ^3+103680000 h t^4 x^2 \epsilon ^3+34560000 t^3 x^3 \epsilon ^3-375840000 t^4 \epsilon ^4+155520000 t^6 \epsilon ^4+777600000 h^2 t^6 \epsilon ^4+1555200000 h t^5 x \epsilon ^4+777600000 t^4 x^2 \epsilon ^4+9331200000 h t^6 \epsilon ^5+9331200000 t^5 x \epsilon ^5+46656000000 t^6 \epsilon ^6.$