1 Introduction

Recently, the studies on the propagation of electron-acoustic (EA) waves have been attracted significant attentions because of their potential importance in interpreting the electrostatic component of the broad-band electrostatic noise observed in the cusp region of the terrestrial magnetosphere [1, 2], geomagnetic tail [3] and in the dayside auroral acceleration region [4, 5], beside the other situations. EA waves may occur in plasmas characterized by a co-existence of two distinct electron populations, here referred to as cool and hot electrons. These are electrostatic waves of high frequency (in comparison with the ion plasma frequency), propagating at a phase speed which lies between the hot and cool electron thermal velocities. On such a fast (high frequency) dynamical scale, the positive ions may safely be assumed to create a uniform background stationary charge simply providing charge neutrality. Therefore this part of plasma has no essential role in the plasma dynamics. The cool electrons provide the inertia necessary to maintain the electrostatic oscillations, while the restoring force comes from the hot electron pressure. Singh et al. [6] examined electron acoustic solitary waves in four-component plasma and applied their results to explain the Viking satellite observations in the dayside auroral zone. Verheest et al. [7, 8] showed that inclusion of hot electron inertia can lead to positive potential electron-acoustic solitons. Lakhina et al. [9, 10] investigated large amplitude ion- and electron-acoustic solitary waves in an unmagnetized multi-fluid plasmas. The propagation of EASWs in a plasma system has been studied by several investigators in unmagnetized two-electron plasmas [11–13] as well as in magnetized plasmas [14–18]. The nonlinear propagation of the EA waves in magnetized plasma has been considered by Dubouloz et al. [14] who reported that the electric field spectrum produced by an EASW is not significantly modified at the presence of the magnetic field. Mace and Hellberg [17] studied the properties of obliquely propagating EASWs in magnetized plasmas. They showed the existence of negative potential EASWs corresponding to compression of the cold electron density. The properties of obliquely propagating EAWs in magnetized plasmas were studied by Mamun et al. [18]. Their model supports EAWs with a positive potential, which corresponds to a hole (hump) in the cold (hot) electron number density. Ergun et al. [19, 20] observed that BEN bursts in the dayside auroral zone have three-dimensional wave structure with the inclusion of the magnetic field effects. The external magnetic field and the wave obliqueness are found to change significantly the properties of the EAWs. On the other side, space plasma observations indicate clearly the presence of electron populations which are far away from their thermodynamic equilibrium [21–29]. Numerous observations of space plasmas [30–33] clearly prove the presence of superthermal electron and ion structures as ubiquitous in a variety of astrophysical plasma environments. Ghosh et al. [34] demonstrated that both negative as well as positive nonplanar ion acoustic solitons are formed in the plasmas with superthermal electrons and positrons. More recently, the properties of dust acoustic solitary waves with superthermal electrons in cylindrical and spherical geometry have been investigated in [35]. Superthermal particles may arise due to the effect of external forces acting on the natural space environment plasmas or because of wave–particle interactions. Plasmas with an excess of superthermal (non-Maxwellian) electrons are generally characterized by a long tail in the high energy region. It has been found that generalized Lorentzian of κ distribution can be modeled such space plasmas, better than the Maxwellian distribution [36–40]. Kappa distribution has been used by several authors [41–47] in studying the effect of Landau damping on the various plasma modes. “Superthermal” plasma behavior was observed in several experimental plasma contexts, such as laser matter interactions or plasma turbulence [48]. At very large values of the spectral index κ, the velocity distribution function approaches a Maxwellian distribution, while for low values of κ, they represent a “hard” spectrum with a strong non-Maxwellian tail having a power-law form at high speeds. The motivation of the presented paper is therefore to study the existence of EASWs in magnetized plasmas having stationary ions, cold inertial electrons and hot superthermal electrons. Because of nonlinear nature of the system it is expected to find new results different from the other situations.

2 Basic equations

Consider a homogeneous plasma consisting of a cold electron fluid, hot electrons obeying a superthermal distribution and stationary ions in the presence of an external magnetic field \( {\text{B}} = {\text{B}}_{0} {\hat{\text{z}}} \). The nonlinear dynamics of the electron acoustic solitary waves is governed by the continuity and motion equations for cold electrons, and the Poisson’s equation [18]

$$ \frac{{\partial n_{c} }}{\partial t} + \nabla \cdot(n_{c} u_{c} ) = 0 $$
$$ \frac{{\partial u_{c} }}{\partial t} + (u_{c} \cdot\nabla )u_{c} = \alpha \nabla \phi - \omega_{cc} (u_{c} \times \hat{z}) $$
(1)
$$ \nabla^{2} \phi = \frac{1}{\alpha }n_{c} + n_{h} - \left( {1 + \frac{1}{\alpha }} \right) $$

In the above equations, \( n_{c} \;(n_{h} ) \) is the cold (hot) electron number density normalized by its equilibrium value \( n_{c0} (n_{h0} ),\;u_{c} \) is the cold electron fluid velocity normalized by \( C_{e} = (k_{B} T_{h} /\alpha \,m_{e} )^{1/2} ,\;\;\omega_{cc} = (eB_{0} /mc)/\omega_{pc} \) is the cold electron cyclotron frequency normalized by the cold electron plasma frequency \( \omega_{pc} ,\;\phi \) is the electrostatic wave potential normalized by \( k_{B} T_{h} /e \) while \( k_{B} \) is the Boltzmann’s constant. “e” is the electron charge, \( m_{e} \) is electron mass and \( \alpha = n_{h0} /n_{c0} \). The time and space variables are in units of the cold electron plasma period \( \omega_{pc}^{ - 1} \) and the hot electron Debye radius \( \lambda_{Dh} \), respectively. The \( n_{h} \) is superthermal hot electron density and it is given by [24]

$$ n_{h} = (1 - \frac{\phi }{\kappa - 1/2})^{{ - \kappa - \frac{1}{2}}} $$
(2)

The parameter κ shapes predominantly the superthermal tail of the distribution [49] and the normalization is provided for any value of the spectral index κ > 1/2 [50]. In the limit \( \kappa \to \infty \), (2) reduces to the well known Maxwell–Boltzmann density. Low values of \( \kappa \) represent distributions with a relatively large component of particles where their velocity is greater than the thermal speed (“superthermal particles”) and an associated reduction in “thermal” particles, as one observes in a “hard” spectrum. Such a very hard spectrum, with an extreme accelerated superthermal component, may be found near very strong shocks associated with Fermi acceleration [40].

3 Solitary structure

In order to study electron acoustic solitary waves in the plasma model under consideration, we construct a weakly nonlinear theory of the electrostatic waves with small but finite amplitude which leads to a scaling of the independent variables through the stretched coordinates \( \xi = \varepsilon^{1/2\,\,\,} (l_{x} x + l_{z} z - \lambda t), \; \tau = \varepsilon^{3/2} t \) [51]; where ε is a small dimensionless parameter measuring the weakness of the dispersion and nonlinearity, λ is the unknown phase velocity (to be determined later) normalized by \( C_{e} \), and \( l_{x} ,\;l_{y} \) and \( l_{z} \) are the directional cosines of the wave vector k along the x, y and z axes, respectively, so that \( l_{x}^{2} + l_{y}^{2} + l_{z}^{2} = 1 \).

We also expand \( n_{c} ,\;u_{cx} ,\;u_{cy} ,\;u_{cz} \) and \( \phi \) in a power series of ε

$$ \left[ \begin{array}{l} n_{c} = 1 + \varepsilon n_{1c} + \varepsilon^{2} n_{2c} + \cdots \\ u_{cx} = 0 + \varepsilon^{3/2} u_{1cx} + \varepsilon^{2} u_{2cx} + \cdots \\ u_{cy} = 0 + \varepsilon^{3/2} u_{1cy} + \varepsilon^{2} u_{2cy} + \cdots \\ u_{cz} = 0 + \varepsilon u_{1cz} + \varepsilon^{2} u_{2cz} + \cdots \\ \phi = 0 + \varepsilon \phi_{1} + \varepsilon^{2} \phi_{2} + \cdots \\\end{array} \right. $$
(3)

One can write Eq. (1) in various powers of ε after inserting Eq. (3) in these equations. The lowest order of ε from the continuity equation, the z component of the momentum equation and Poisson’s equation give \( n_{1c} = \,\,\frac{{ - \alpha l_{z}^{2} }}{{\lambda^{2} }}\phi_{1} ,\:u_{1cz} = \,\frac{{ - \alpha l_{z}^{{}} }}{\lambda }\phi_{1} \) and \( \lambda = \sqrt {\frac{2\kappa - 1}{2\kappa + 1}} l_{z} \). We can also obtain the lower and next leading orders of x and y components of the momentum equation as

$$ \left\{ \begin{array}{l} u_{1cx} = \,\frac{{ - \alpha l_{y} }}{{\omega_{cc} }}\frac{{\partial \phi_{1} }}{\partial \xi };\quad u_{1cy} = \,\frac{{\alpha l_{x} }}{{\omega_{cc} }}\frac{{\partial \phi_{1} }}{\partial \xi }_{1} \\ u_{2cx} = \,\frac{{ - \alpha l_{x} \lambda }}{{\omega_{cc}^{2} }}\frac{{\partial^{2} \phi_{1} }}{{\partial \xi^{2} }};\quad u_{2cy} = \,\frac{{ - \alpha l_{y} \lambda }}{{\omega_{cc}^{2} }}\frac{{\partial^{2} \phi_{1} }}{{\partial \xi^{2} }} \\ \end{array} \right. $$
(4)

Using the next orders of ε from the continuity equation, the z-component of the momentum equation and Poisson’s equation one can find the following relations

$$ \left| \begin{aligned} \frac{{\partial n_{1c} }}{\partial \tau } & - \lambda \frac{{\partial n_{2c} }}{\partial \xi } + l_{x} \frac{{\partial u_{2cx} }}{\partial \xi } + l_{y} \frac{{\partial u_{2cy} }}{\partial \xi } + l_{z} \frac{{\partial u_{2cz} }}{\partial \xi } = 0 \\ \frac{{\partial u_{1cz} }}{\partial \tau } & - \lambda \frac{{\partial u_{2cz} }}{\partial \xi } + u_{1cz} l_{z} \frac{{\partial u_{1cz} }}{\partial \xi } - \alpha l_{z} \frac{{\partial \phi_{2} }}{\partial \xi } = 0 \\ \frac{{\partial^{2} \phi_{1} }}{{\partial \xi^{2} }} & - \frac{{n_{2c} }}{\alpha } - \left[ {\frac{2\kappa + 1}{2\kappa - 1}\phi_{2} + \frac{(2\kappa + 1)(2\kappa + 3)}{{(2\kappa - 1)^{2} }}\phi_{1}^{2} } \right] = 0 \\ \end{aligned} \right. $$
(5)

Finally from Eqs. (4) and (5) the KdV equation yields

$$ \frac{{\partial \phi_{1} }}{\partial \tau }\,\, + \,\,A\phi_{1} \frac{{\partial \phi_{1} }}{\partial \xi } + B\frac{{\partial^{3} \phi_{1} }}{{\partial \xi^{3} }} = 0 $$
(6)

where the coefficients are

$$ A = - \frac{1}{2}\sqrt {\frac{2\kappa - 1}{2\kappa + 1}} l_{z} \left\{ {\frac{2\kappa + 3}{2\kappa - 1} + 3\,\left( {\frac{2\kappa + 1}{2\kappa - 1}} \right)\alpha } \right\},\;\;B = \left( {\frac{2\kappa - 1}{2\kappa + 1}} \right)\,\frac{\lambda }{2}\,\,\left\{ {1 + \frac{{1 - l_{z}^{2} }}{{\omega_{cc}^{2} }}} \right\}\, $$
(7)

The above results can be compared with the results reported [52, 53] for unmagnetized plasmas with planar and nonplanar geometries, respectively. In order to study a stationary solitary wave solution of Eq. (6), we assume that the stationary solution can be expressed as \( \phi_{1} = \phi_{1} (\chi ) \), where \( \chi = \xi - u\tau \). Substituting this expression into Eq. (6), we can obtained the stationary solitary wave solution as

$$ \phi_{1} = \phi_{m} \sec h^{2} \left( {\frac{\chi }{w}} \right) $$
(8)

where \( \phi_{m}\, = {{3u} \mathord{\left/ {\vphantom {{3u} A}} \right. \kern-0pt} A} \) is the soliton amplitude and \( w = 2\sqrt {B/u} \) is its width.

The electron-acoustic soliton, Eq. (8) which is obtained in the small amplitude approximation, clearly indicates the existence of solitary waves with negative amplitude. Note that Eq. (7) shows that “A” is negative for all the values of the parameters. Therefore only the rarefactive solitons are able to propagate in this plasma. The soliton maximum amplitude is independent of the magnitude of the external magnetic field as can be observed in other such plasma systems [18, 21]. It is obvious that the magnetic field cannot change the energy of a physical system. Eq. (8) shows that the parameter “A” is proportional to \( l_{z} \) (\( l_{z} = \cos \gamma , \) where γ is the angle between the directions of the wave propagation vector k and the external magnetic field \( B_{0} \)). Therefore \( \phi_{m} \) is inversely proportional to \( l_{z} \). In plasmas with nonisothermal distributions of electrons the soliton maximum amplitude is inversely proportional to \( l_{z}^{2} \) [18]. On the other hand the soliton amplitude is also inversely proportional to α. \( \phi_{m} \) is a complicated function of κ and one can find the effect of this parameter on the soliton amplitude using numerical analysis.

For \( 1 - l_{z}^{2} \ll \omega_{cc}^{2} \) the soliton width is almost independent of \( \omega_{cc} \) and directly proportional to \( \sqrt {l_{z} } \). For \( 1 - l_{z}^{2} \gg\omega_{cc}^{2} \) he soliton width is very sensitive to \( \omega_{cc} \). These results are in agreement with the results reported in ref. [18].

4 Results and discussion

Numerical analysis has been employed to study the effects of superthermal hot electrons κ, the density ratio between hot and cold electrons (α) and external magnetic field on the features of solitary waves.

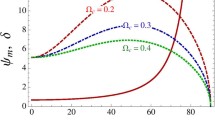
Figure 1 shows how the amplitude \( \phi_{m} \) changes respect to the propagation angle for different values of superthermal parameter. Absolute value of the soliton amplitude \( \phi_{m} \) increases when “κ” increases. Increasing in the soliton amplitude is more sensible for the larger values of γ (smaller values of \( l_{z} \)). This figure also shows that the soliton amplitude is an increasing function of γ. Thus the soliton amplitude finds its maximum value in smaller values of \( l_{z} \).

Fig. 1
figure 1

Soliton amplitude \( \phi_{m} \) respect to γ with different values for the parameter “κ”

Full size image

Figure 2 presents \( \phi_{m} \) as a function of γ with different values of α. This figure clearly shows that the absolute value of the soliton peak decreases with an increasing α. Therefore the soliton energy decreases when the population of hot electrons (relative to the cold electrons) increases.

Fig. 2
figure 2

Maximum amplitude \( \phi_{m} \) respect to \( l_{z} \) with different values for the parameter α

Full size image

Variation of the soliton width respect to γ is shown in Fig. 3. In general, the soliton width has a maximum value in the range of variation of γ. The maximum value of the soliton width increases as “κ” increases. It is mentioned that superthermal distribution reduces to Maxwellian distribution for large values of “κ”. This means that the effect of superthermality is noticeable with smaller values of “κ”. Therefore one can conclude that the presence of superthermal electrons decreases the width of the soliton. Variation of the κ value does not change the angle in which the maximum soliton width appears.

Fig. 3
figure 3

Soliton width as functions of \( l_{z} \) with different values for the parameter “κ”

Full size image

Figure 4 demonstrates the width of the soliton respect to γ with different values of the parameter \( \omega_{cc} \). Soliton width decreases with an increasing \( \omega_{cc} \). It is obvious that for \( \gamma = 0 \) the soliton width is not depending on the \( \omega_{cc} \) as also presented in Fig. 4.

Fig. 4
figure 4

Soliton width respect to \( l_{z} \) with different values for the parameter \( \omega_{cc} \)

Full size image

The above results in general are agreement with the results reported earlier [18, 21].

5 Conclusions

Properties of electron acoustic solitary waves propagating in magnetized plasmas of cold fluid ions and electrons with a superthermal distribution have been investigated in this paper. It may be noted that Landau damping of electrostatic plasma waves is often enhanced in the presence of a superthermal electron population, as compared with Maxwellian plasmas. It is found that only rarefactive solitons can be propagated in this plasma. The absolute value of the soliton amplitude increases with an increasing value of the superthermal parameter “κ” and also angle γ. Therefore the soliton energy is reduced in the presence of superthermal electrons. Solitons in plasmas with lower values of “κ” have steeper profiles. On the other hand, solitons in plasmas with greater values of α have smaller maximum amplitude and therefore smaller energy. Also it is shown that the soliton profile becomes narrower in stronger magnetic fields.