Complex nonlinearities of rogue waves in generalized inhomogeneous higher-order nonlinear Schrödinger equation

Abstract

In this paper, the Nth-order rogue waves are investigated for an inhomogeneous higher-order nonlinear Schrödinger equation. Based on the Heisenberg ferromagnetic spin system, the higher-order nonlinear Schrödinger equation is generated. The generalized Darboux transformation is constructed by the Darboux matrix. The solutions of the Nth-order rogue waves are given in terms of a recursive formula. There are complex nonlinear phenomena in the rogue waves, add the first-order to the fourth-order rogue waves are discussed in some figures obtained by analytical solutions. It is shown that the general Nth-order rogue waves contain $2n-1$ free parameters. The free parameters play a crucial role to affect the dynamic distributions of the rogue waves. The results obtained in this paper will be useful to understand the generation mechanism of the rogue wave.

1 Introduction

The rogue wave is the giant single wave, which was firstly found in the ocean [1]. The single rogue wave is referred to the fundamental form of the hierarchy for the rogue wave. The amplitude of the rogue wave is two to three times higher than those of the surrounding waves. One of the features of the rogue wave is that it appears from nowhere and disappears without a trace [2]. In the nature, the rogue wave is very dangerous, which can appear unexpectedly and forms the larger amplitude in 1 min to shred a boat. Beyond oceanic expanses, the rogue wave has also been found experimentally in optical fibers [3], Bose–Einstein condensates (BECs) [4], superfluids [5] and so on. In a word, the rogue waves have the characteristic of the burst, the localization, the short time and the dramatic concentration of the energy. The phenomenon in the rogue waves has nonlinear characteristic. Thus, the linear wave theories based on the superposition principle are not used to explain the complex phenomenon of the rogue wave in the ocean, the optical fibers and the engineering field. The nonlinear theories [6–8] are being applied to analyze these nonlinear phenomena of the rogue waves. The rogue wave has been an important issue in the fields of the nonlinear science.

One of the important known models for the rogue wave is the nonlinear Schrödinger (NLS) equation. Many research results have been obtained for the NLS equation. For example, the first-order rational solutions [9, 10], the control of the rogue waves [11], the soliton solutions [12] and Darboux transformation (DT) [13] of the NLS equation are studied in detail. Apart from the NLS equation, researchers have also investigated the solution of the rogue wave for the generalized nonlinear Schrödinger (GNLS) equation [14], (3+1)-dimensional GNLS equation [15], the higher-order NLS equation [16], the dissipative NLS equation with a variable coefficient [17], the two-component NLS equations [18] and the general two-coupled NLS equation [19].

The stability of solutions is also an important problem for waves. There are a few achievements of this aspect; for example, Dai et al. [20, 21] investigated the stability of analytical spatial soliton solutions for a two-dimensional NLS equation with power-law nonlinearity in PT-symmetric potentials. They used the linear stability theory and the direct numerical simulations to analyze the stability of the solutions.

Motivated by the aforementioned works, in this paper, an inhomogeneous higher-order NLS equation is considered as follows [22]

$$\begin{aligned}&i\frac{\partial q}{\partial t}+\varepsilon \frac{\partial ^{4}q}{\partial x^{4}}+8\varepsilon \left| {q} \right| ^{2}\frac{\partial ^{2}q}{\partial x^{2}}+2\varepsilon q^{2}\frac{\partial ^{2}q^{*}}{\partial x^{2}}\nonumber \\&\quad +\,4\varepsilon \left| {\frac{\partial q}{\partial x}} \right| ^{2}q+6\varepsilon q^{*}\left( \frac{\partial ^{2}q}{\partial x^{2}}\right) ^{2}+6\varepsilon \left| {q} \right| ^{4}q+\frac{\partial ^{2}(fq)}{\partial x^{2}}\nonumber \\&\quad +2q\left[ {f\left| {q} \right| ^{2}+\int _{-\infty }^{x} {\frac{\partial f}{\partial s}\left| {q(s,t)} \right| ^{2}\hbox {d}s} } \right] -i\frac{\partial (hq)}{\partial x}=0, \end{aligned}$$

(1)

where q(x, t) is a complex function, t and x denote the scaled time and spatial coordinate, respectively, f and h represent the inhomogeneousness present in the medium and are the linear functions of spatial variable x, which are of the form

$$\begin{aligned} f=f_1 x+f_2, \quad h=h_1 x+h_2, \end{aligned}$$

(2)

$f_{j}$ and $h_{j} (j=1,2)$ are real constants, $\varepsilon$ is a perturbation parameter, and the asterisk represents the complex conjugation.

Equation (1) is generated by deforming the inhomogeneous Heisenberg ferromagnetic spin system with the prolongation structure [22] and the space curve formalism, which describes the dynamics of a site-dependent Heisenberg ferromagnetic spin chain in the highly idealized physical situations. In fact, we also take into account the inhomogeneity or nonuniformity of the realistic physical medium [23, 24] in Eq. (1). The inhomogeneous equation has a wide range of applications in the propagation of radio waves in the ionosphere, waves in the ocean, optical pulses in glass fibers, laser radiations in plasma and impurities in magnetic systems [25, 26].

Radha [22] used the gauge transformation to construct the multi-solitary solutions of Eq. (1) and discussed the interaction of the soliton. On the basis of the associated linear eigenvalue problems, Zhong et al. [27] gave the bright soliton solutions of Eq. (1) using the prolongation structure theory. However, to the best of our knowledge, there are no reports about the solution of the rogue wave related to Eq. (1), and the construction of the higher-order NLS equation is regarded as a challenging work.

The aim of this paper is to construct the Nth-order solutions of the rogue wave for Eq. (1) using the generalized Darboux transformation, which is an effective approach to derive the solution of the rogue wave [28]. Based on the DT matrix, the generalized Darboux transformation is obtained and the formula for generating the Nth-order solutions of the rogue wave is given.

2 Generalized Darboux transformation for Eq. (1)

Equation (1) is the compatibility condition of the linear spectral problems [22]

$$\begin{aligned} \Phi _x= & {} U\Phi =\left( {{\begin{array}{c@{\quad }c} {-i\lambda }&{} q \\ {-q^{*}}&{} {i\lambda } \\ \end{array} }} \right) \Phi , \end{aligned}$$

(3a)

$$\begin{aligned} \Phi _t= & {} V\Phi =\left( {{\begin{array}{c@{\quad }c} A&{} B \\ {-B^{*}}&{} {-A} \\ \end{array} }} \right) \Phi , \end{aligned}$$

(3b)

with

$$\begin{aligned} A= & {} i\varepsilon \left( q\frac{\partial ^{2}q^*}{\partial x^{2}}+q^{*}\frac{\partial ^{2}q}{\partial x^{2}}-\left| {\frac{\partial q}{\partial x}} \right| ^{2}\right) \nonumber \\&+\,3i\varepsilon \left| q \right| ^{4}-2\lambda \varepsilon \left( q^{*}\frac{\partial q}{\partial x}-q\frac{\partial q^{*}}{\partial x}\right) \nonumber \\&-\,4i\lambda ^{2}\varepsilon \left| q \right| ^{2}+8i\varepsilon \lambda ^{4}\nonumber \\&+\,if\left| {q} \right| ^{2}+\int _{-\infty }^{x} {\frac{\partial f}{\partial s}\left| {q(s,t)} \right| ^{2}\hbox {d}s} \nonumber \\&-2if\lambda ^{2}-ih\lambda , \end{aligned}$$

(4)

$$\begin{aligned} B= & {} i\varepsilon \frac{\partial ^{3}q}{\partial x^{3}} +2\varepsilon \lambda \frac{\partial ^{2}q}{\partial x^{2}}+6i\varepsilon \left| q \right| ^{2}\frac{\partial q}{\partial x}\nonumber \\&-\,4i\varepsilon \lambda ^{2}\frac{\partial q}{\partial x}+4\varepsilon \lambda \left| q \right| ^{2}q-8\varepsilon \lambda ^{3}q\nonumber \\&+\,i\frac{\partial ^{2}(fq)}{\partial x^{2}}+2f\lambda q+hq, \end{aligned}$$

(5)

where $\Phi =(\varphi ,\phi )^\mathrm{T}$ is the vector eigenfunction of the Lax pair (3a) and (3b), q is a potential function, and $\lambda$ is a constant spectral parameter.

It is easy to verify that the zero-curvature equation

$$\begin{aligned} U_t -V_x +[U,V]=0 \end{aligned}$$

(6)

gives rise to Eq. (1).

The Darboux matrix T is defined as [22]

$$\begin{aligned} T=\lambda I-S,\quad S=H\Lambda H^{-1}, \end{aligned}$$

(7)

where

$$\begin{aligned} I=\left( {{\begin{array}{c@{\quad }c} 1&{} 0 \\ 0&{} 1 \\ \end{array} }} \right) ,\quad H=\left( {{\begin{array}{c@{\quad }c} {\varphi _1 }&{} {{\phi }_1^*} \\ {{\phi }_1 }&{} {-\varphi _1^*} \\ \end{array} }} \right) ,\quad \Lambda =\left( {{\begin{array}{c@{\quad }c} {\lambda _1 }&{} 0 \\ 0&{} {\lambda _1^*} \\ \end{array} }} \right) . \end{aligned}$$

(8)

Let $\Phi _1 =(\varphi _1 ,{\phi }_1 )^\mathrm{T}$ be an eigenfunction of the Lax pair (3a) and (3b) with a seeding solution $q=q[0]$ and $\lambda =\lambda _1$. It is seen that $({\phi }_1^*,-\varphi _1^*)^\mathrm{T}$ also satisfies equation (3) with $\lambda =\lambda _1^*$. Choosing different eigenfunctions $\Phi _k =(\varphi _k ,{\phi }_k )^\mathrm{T}$ at $\lambda _k$, respectively, the aforementioned DT procedure can be easily iterated.

Based on the Darboux matrix T of Eq. (7), the elementary DT of Eq. (1) is given as

$$\begin{aligned} \Phi _1 [0]= & {} T[0]\Phi _1 , q[1]=q[0]\nonumber \\&-\,2i(\lambda _1 -\lambda _1^*)\frac{\varphi _1 [0]{\phi }_1^*[0]}{\left| {\varphi _1 [0]} \right| ^{2}+\left| {{\phi }_1 [0]} \right| ^{2}}, \end{aligned}$$

(9)

where

$$\begin{aligned}&T[1] = \lambda _2 I-H[0]\Lambda [1]H[0]^{-1},\end{aligned}$$

(10a)

$$\begin{aligned}&T[0] = I, H[0]=\left( {{\begin{array}{c@{\quad }c} {\varphi _1 [0]}&{} {{\phi }_1^*[0]} \\ {{\phi }_1 [0]}&{} {-\varphi _1^*[0]} \\ \end{array} }} \right) , \nonumber \\&\Lambda [1]=\left( {{\begin{array}{c@{\quad }c} {\lambda _1 }&{} 0 \\ 0&{} {\lambda _1^*} \\ \end{array} }} \right) , \end{aligned}$$

(10b)

$$\begin{aligned} \Phi _1 [0]= & {} (\varphi _1 [0],{\phi }_1 [0])^\mathrm{T}\nonumber \\= & {} (\varphi _1 ,{\phi }_1 )^\mathrm{T}=\Phi _1 , q[0]=q. \end{aligned}$$

(10c)

If N different basic solutions $\Phi _k =(\varphi _k ,{\phi }_k )^\mathrm{T}(k=1 ,\;2 ,\;\ldots ,\;N)$ of the Lax pair (3a) and (3b) at $\lambda =\lambda _k (k=1 ,\;2 ,\;\ldots ,\;N)$ are given, the elementary DT is repeated N times. Then, the N th-step DT of Eq. (1) is

$$\begin{aligned}&\Phi _N [N-1]=T[N-1]T[N-2]\cdots T[1]T[0]\Phi _N , \end{aligned}$$

(11a)

$$\begin{aligned} q[N]= & {} q[0]-2i\sum _{k=1}^N (\lambda _1 -\lambda _1^*)\nonumber \\&\times \frac{\varphi _k [k-1]{\phi }_k^*[k-1]}{\left| {\varphi _k [k-1]} \right| ^{2}+\left| {{\phi }_k [k-1]} \right| ^{2}}, \end{aligned}$$

(11b)

where

$$\begin{aligned}&T[k]=\lambda _{k+1} I-H[k-1]\Lambda [k]H[k-1]^{-1}, \end{aligned}$$

(12a)

$$\begin{aligned}&H[k-1]=\left( {{\begin{array}{c@{\quad }c} {\varphi _k [k-1]}&{} {{\phi }_k^*[k-1]}\\ {{\phi }_k [k-1]}&{} {-\varphi _k^*[k-1]}\\ \end{array} }} \right) , \nonumber \\&\Lambda [k]=\left( {{\begin{array}{cc} {\lambda _k }&{} 0 \\ 0&{} {\lambda _k^*} \\ \end{array} }} \right) , \end{aligned}$$

(12b)

$$\begin{aligned} \Phi _k [k-1]= & {} \left. {(T[k-1]T[k-2]\cdots T[1]T[0])} \right| _{\lambda =\lambda _k } \nonumber \\&\Phi _k , (k=1 ,\;2 ,\;\ldots ,\;N). \end{aligned}$$

(12c)

The initial value is $\Phi _1 [0]=(\varphi _1 [0],{\phi }_1 [0])^\mathrm{T}=(\varphi _1 ,{\phi }_1 )^\mathrm{T}=\Phi _1$. Based on the aforementioned elementary DT, a generalized DT is obtained for Eq. (1). We assume that

$$\begin{aligned} \Psi =\Phi _1 (\lambda _1 ,\eta ) \end{aligned}$$

(13)

is a special solution of the Lax pair (3a) and (3b), and $\eta$ is a small parameter.

With the aid of the Taylor series, $\Psi$ can be expanded at $\eta =0$

$$\begin{aligned} \Psi= & {} \Phi _1^{[0]} +\Phi _1^{[1]} \eta +\Phi _1^{[2]} \eta ^{2}+\cdots \nonumber \\&+\,\Phi _1^{[m]} \eta ^{m}+o(\eta ^{m}), \end{aligned}$$

(14)

where $\Phi _1^{[j]} =\frac{1}{j!}\frac{\partial ^{j}}{\partial \lambda ^{j}}\left. {\Phi _1 (\lambda )} \right| _{\lambda =\lambda _1 } (j=1 , 2, \ldots ,m)$.

From the above assumption, it is easily found that $\Phi _1^{[0]} =\Phi _1 [0]$ is a particular solution of the Lax pair (3a) and (3b) with $q=q[0]$ and $\lambda =\lambda _1$. Therefore, the Nth-step generalized DT is constructed as follows

$$\begin{aligned}&\Phi _1 [N-1]\nonumber \\&\quad =\Phi _1^{[0]} +\left[ {\sum _{l=1}^{N-1} {T_1 [l]} } \right] \Phi _1^{[1]}\nonumber \\&\qquad +\left[ {\sum _{l=1}^{N-1} {\sum _{k>l}^{N-1} {T_1 [k]} T_1 [l]} } \right] \Phi _1^{[2]} +\cdots \nonumber \\&\qquad +\left[ {T_1 [N-1]T_1 [N-2]\cdots T_1 [1]} \right] \Phi _1^{[N-1]}, \end{aligned}$$

(15)

$$\begin{aligned}&q[N]=q[N-1]\nonumber \\&\quad -\,2i(\lambda _1 -\lambda _1^*)\frac{\varphi _1 [N-1]{\phi }_1 [N-1]^{*}}{\left| {\varphi _1 [N-1]} \right| ^{2}+\left| {{\phi }_1 [N-1]} \right| ^{2}}, \end{aligned}$$

(16)

where

$$\begin{aligned}&T_1 [k] = \lambda _1 I-H_1 [k-1]\Lambda [1]H_1 [k-1]^{-1},\end{aligned}$$

(17a)

$$\begin{aligned}&H_1 [k-1]=\left( {{\begin{array}{c@{\quad }c} {\varphi _k [k-1]}&{} {{\phi }_k^*[k-1]} \\ {{\phi }_k [k-1]}&{} {-\varphi _k^*[k-1]} \\ \end{array} }} \right) , \end{aligned}$$

(17b)

$$\begin{aligned}&\Phi _1 [k-1]=\left( {{\begin{array}{l} {\varphi _k [k-1]} \\ {{\phi }_k [k-1]} \\ \end{array} }} \right) , (k=1 ,\;2 ,\;\ldots ,\;N).\nonumber \\ \end{aligned}$$

(17c)

Equations (15)–(17) are the recursive formulae of the Nth-step generalized DT for Eq. (1), which can be converted into the $2n\times 2n$ determinant representation using the Crum theorem [29, 30]. The recursive formulae are easily used to construct the higher-order solutions of the rogue wave. Based on these solutions of Eq. (1), some figures of interesting higher-order rogue waves will be obtained in the next section.

3 Solutions of rogue waves

For simplicity, the solutions of the rogue waves are calculated when the inhomogeneous parameters are independent of x, namely $f_1 =h_1 =0$. We choose the parameters $f_2 =\frac{1}{2}$ and $h_2 =\frac{1}{4}$.

We take a periodic plane seed solution $q[0]=a\hbox {e}^{i\theta }$ with $\theta =kx+\omega t$. Here, a and k are both real constants, and the frequency $\omega$ satisfies the nonlinear dispersion relation

$$\begin{aligned} \upomega =k^{4}\varepsilon -k^{2}(12\varepsilon a^{2}+f)+hk+2fa^{2}+6\varepsilon a^{4}. \end{aligned}$$

(18)

Using the Maple program, the corresponding solution of the linear spectral problem at $\lambda =\frac{k}{2}-ia+\eta ^{2}$ is obtained

$$\begin{aligned} \Phi _1 (\eta )=\left( {{\begin{array}{l} {(C_{1} \hbox {e}^{\rho }+C_{2} \hbox {e}^{-\rho })\hbox {e}^{\frac{i\theta }{2}}} \\ {(C_{2} \hbox {e}^{\rho }+C_{1} \hbox {e}^{-\rho })\hbox {e}^{-\frac{i\theta }{2}}} \\ \end{array} }} \right) , \end{aligned}$$

(19)

where

$$\begin{aligned} C_1= & {} \sqrt{-\mu +\frac{i}{2}k+i\lambda },C_2 \nonumber \\= & {} \sqrt{\mu +\frac{i}{2}k+i\lambda }, \rho =\mu (x+\delta t+\Omega (\eta )), \end{aligned}$$

(20a)

$$\begin{aligned} \mu= & {} \sqrt{k\lambda -\frac{k^{2}}{4}-\lambda ^{2}-a^{2}}, \Omega (\eta )\nonumber \\= & {} \sum _{j=1}^N {(a_{j} +i} b_{j} )\eta ^{2j}\;(a_{j} ,b_{j} \in R), \end{aligned}$$

(20b)

$$\begin{aligned} \delta= & {} \varepsilon k^{3}-2\varepsilon \lambda k^{2}-6\varepsilon ka^{2}+4\varepsilon k\lambda ^{2}\nonumber \\&+\,4\varepsilon \lambda a^{2}-8\varepsilon \lambda ^{3}-fk+2f\lambda +h, \end{aligned}$$

(20c)

where $\Omega (\eta )$ is a separating function and $a_{j}$, $b_{j}$ are real constants.

Letting $\lambda =\frac{k}{2}-ia+\eta ^{2}$ and expanding the vector function $\Phi _1 (\eta )$ at $\eta =0$, we have

$$\begin{aligned} \Phi _1 (\eta )= & {} \Phi _1^{[0]} +\Phi _1^{[1]} \eta ^{2}+\Phi _1^{[2]} \eta ^{4}+\Phi _1^{[3]} \eta ^{6}\nonumber \\&+\,\Phi _1^{[4]} \eta ^{8}\ldots +\Phi _1^{[m]} \eta ^{2m}+\cdots , \end{aligned}$$

(21)

with

$$\begin{aligned}&\Phi _1^{[0]} =\left( {{\begin{array}{l} {\varphi _1^{[0]} } \\ {{\phi }_1^{[0]} } \\ \end{array} }} \right) , \Phi _1^{[1]} =\left( {{\begin{array}{l} {\varphi _1^{[1]} } \\ {{\phi }_1^{[1]} } \\ \end{array} }} \right) ,\nonumber \\&\quad \Phi _1^{[2]} =\left( {{\begin{array}{l} {\varphi _1^{[2]} } \\ {{\phi }_1^{[2]} } \\ \end{array} }} \right) ,\ldots , \end{aligned}$$

(22)

where

$$\begin{aligned} \varphi _1^{[0]}= & {} 2\sqrt{a}\hbox {e}^{\frac{i}{2}\theta }, \quad {\phi }_{1}^{[0]} =2\sqrt{a}\hbox {e}^{-\frac{i}{2}\theta },\end{aligned}$$

(23a)

$$\begin{aligned} \varphi _1^{[1]}= & {} \left( \frac{i}{8}a^{\frac{2}{3}}\left( {-4x+48it\varepsilon a^{3}+4ita-t} \right) ^{2}\right. \nonumber \\&+\left. \frac{i}{2}\sqrt{a}\left( {-4x+48it\varepsilon a^{3}+4ita-t} \right) +\frac{\frac{i}{2}}{\sqrt{a}} \right) \hbox {e}^{\frac{i}{2}\theta },\nonumber \\\end{aligned}$$

(23b)

$$\begin{aligned} {\phi }_1^{[1]}= & {} \left( \frac{i}{8}a^{\frac{2}{3}}\left( {-4x+48it\varepsilon a^{3}+4ita-t} \right) ^{2}\right. \nonumber \\&\left. -\frac{i}{2}\sqrt{a}\left( {-4x+48it\varepsilon a^{3}+4ita-t} \right) +\frac{\frac{i}{2}}{\sqrt{a}} \right) \hbox {e}^{-\frac{i}{2}\theta }. \end{aligned}$$

(23c)

$\varphi _1^{[2]}$ and ${\phi }_1^{[2]}$ are given in the “Appendix.”

Other expressions are too cumbersome to write them down. In the following discussions, we set $a=1$ and $k=0$ to simplify the calculation process. Then, we have $q[0]=\hbox {e}^{i\theta }$with $\theta =(1+6\varepsilon )t$ and $\lambda =-i$.

It is clearly seen that $\Phi _1^{[0]}$ is a solution of the Lax pair (3a) and (3b) at $q[0]=\hbox {e}^{i\theta }$ and $\lambda =-i$. Hence, substituting $\Phi _1^{[0]}, q[0]=\hbox {e}^{i\theta }$ and $\lambda =-i$ into Eq. (16), we obtain a trivial solution of Eq. (1)

$$\begin{aligned} q[1]=-\hbox {e}^{i\theta }, \end{aligned}$$

(24)

and

$$\begin{aligned} T_1 [1]=\left( {{\begin{array}{c@{\quad }c} {-i}&{} {i\hbox {e}^{i\theta }} \\ {i\hbox {e}^{-i\theta }}&{} {-i} \\ \end{array} }} \right) . \end{aligned}$$

(25)

Consider the following limit

$$\begin{aligned} \mathop {\lim }\limits _{\eta \rightarrow 0} \frac{\left. {[T_1 [1]} \right| _{\lambda =\lambda _1 +\eta } ]\Psi }{\eta }= & {} \mathop {\lim }\limits _{\eta \rightarrow 0} \frac{\left. {[\eta +T_1 [1]} \right| _{\lambda =\lambda _1 } ]\Psi }{\eta } \nonumber \\= & {} \Phi _1^{[0]} +T_1 [1](\lambda _1)\Phi _1^{[1]}\nonumber \\= & {} \Phi _1 [1], \end{aligned}$$

(26a)

$$\begin{aligned} \Phi _1 [1]= & {} \left( {{\begin{array}{l} {\varphi _1 [1]} \\ {{\phi }_1 [1]} \\ \end{array} }} \right) , \end{aligned}$$

(26b)

where

$$\begin{aligned} \varphi _1 [1]= & {} \left( {-4x+48it\varepsilon +4it-t+2} \right) \hbox {e}^{\frac{i}{2}\theta }, \end{aligned}$$

(27a)

$$\begin{aligned} {\phi }_1 [1]= & {} -\left( {-4x+48it\varepsilon +4it-t-2} \right) \hbox {e}^{-\frac{i}{2}\theta }. \end{aligned}$$

(27b)

Substituting $\Phi _1^{[0]}$, $\Phi _1^{[1]}$ and $\lambda =-i$ into Eq. (16), we obtain the first-order solution of the rogue wave for Eq. (1)

$$\begin{aligned} q[2]=\left( {-1-\frac{2(4-2304t^{2}\varepsilon ^{2}-384t^{2}\varepsilon -16x^{2}-8xt-17t^{2}+192it\varepsilon +16it)}{4+2304t^{2}\varepsilon ^{2}+384t^{2}\varepsilon +16x^{2}+8xt+17t^{2}}} \right) \hbox {e}^{i\theta }, \end{aligned}$$

(28)

and

$$\begin{aligned} T_1 [2]=\left( {{\begin{array}{l@{\quad }l} {-i-\frac{4i(t+4x)}{\Delta }}&{} {\frac{i\hbox {e}^{i\theta }\Delta _1 }{\Delta }} \\ {\frac{i\hbox {e}^{-i\theta }\Delta _2 }{\Delta }}&{} {-i+\frac{4i(t+4x)}{\Delta }} \\ \end{array} }} \right) , \end{aligned}$$

(29)

where

$$\begin{aligned} \Delta= & {} 4+2304t^{2}\varepsilon ^{2}+384t^{2}\varepsilon \nonumber \\&+16x^{2}+8xt+17t^{2}, \end{aligned}$$

(30a)

$$\begin{aligned} \Delta _1= & {} 4-2304t^{2}\varepsilon ^{2}-384t^{2}\varepsilon \nonumber \\&-16x^{2}-8xt-17t^{2}+192it\varepsilon +16it, \end{aligned}$$

(30b)

$$\begin{aligned} \Delta _2= & {} 4-2304t^{2}\varepsilon ^{2}-384t^{2}\varepsilon \nonumber \\&-16x^{2}-8xt-17t^{2}-192it\varepsilon -16it. \end{aligned}$$

(30c)

Next, consider the following limit

$$\begin{aligned}&\mathop {\lim }\limits _{\eta \rightarrow 0} \frac{\left. {[\eta +T_1 [2]} \right| _{\lambda =\lambda _1 } ]\left. {[\eta +T_1 [1]} \right| _{\lambda =\lambda _1 } ]\Psi }{\eta ^{2}} \nonumber \\&\quad =\Phi _1^{[0]} +\left( {T_1 [1](\lambda _1 )+T_1 [2](\lambda _1 )} \right) \Phi _1^{[1]}\nonumber \\&\qquad +\,T_1 [2](\lambda _1 )T_1 [1](\lambda _1 )\Phi _1^{[2]} =\Phi _1 [2], \end{aligned}$$

(31a)

$$\begin{aligned}&\Phi _1 [2]=\left( {{\begin{array}{l} {\varphi _1 [2]} \\ {{\phi }_1 [2]} \\ \end{array} }} \right) , \end{aligned}$$

(31b)

where $T_1 [2]$ and $\Phi _1 [2]$ can be calculated by the Maple program.

We do not give the expression of $\Phi _1 [2]$ since it is rather cumbersome to write down. Substituting $\Phi _1^{[0]} , \Phi _1^{[1]} , \Phi _1^{[2]}$ and $\lambda =-i$ into Eq. (16), we obtain the second-order solution of the rogue wave for Eq. (1)

$$\begin{aligned} q[3]=q[2]-4\frac{\varphi _1 [2]\cdot {\phi }_1 [2]^{*}}{\left| {\varphi _1 [2]} \right| ^{2}+\left| {{\phi }_1 [2]} \right| ^{2}}. \end{aligned}$$

(32)

Furthermore, we focus on the third-order solution q[4] of Eq. (1). Consider the following limitation

$$\begin{aligned}&\mathop {\lim }\limits _{\eta \rightarrow 0} \frac{\left. {[\eta +T_1 [3]} \right| _{\lambda =\lambda _1 } ]\left. {[\eta +T_1 [2]} \right| _{\lambda =\lambda _1 } ]\left. {[\eta +T_1 [1]} \right| _{\lambda =\lambda _1 } ]\Psi }{\eta ^{3}}\nonumber \\&\quad =\Phi _1^{[0]} +\left( {T_1 [1](\lambda _1 )+T_1 [2](\lambda _1 )+T_1 [3](\lambda _1 )} \right) \Phi _1^{[1]}\nonumber \\&\qquad +\,(T_1 [2](\lambda _1 )T_1 [1](\lambda _1 )+T_1 [3](\lambda _1 )T_1 [1](\lambda _1 )\nonumber \\&\qquad +\,T_1 [3](\lambda _1 )T_1 [2](\lambda _1 ))\Phi _1^{[2]} \nonumber \\&\qquad +\,T_1 [3](\lambda _1 )T_1 [2](\lambda _1 )T_1 [1](\lambda _1 )\Phi _1^{[3]} =\Phi _1 [3], \end{aligned}$$

(33)

$$\begin{aligned}&\Phi _1 [3]=\left( {{\begin{array}{l} {\varphi _1 [3]} \\ {{\phi }_1 [3]} \\ \end{array} }} \right) , \end{aligned}$$

(34)

where $T_1 [3]$ and $\Phi _1 [3]$ are calculated by the Maple program.

It is also seen that the expression of $\Phi _1 [3]$ is rather tedious to write them down in this paper. Substituting $\Phi _1^{[0]} , \Phi _1^{[1]}, \Phi _1^{[2]}, \Phi _1^{[3]}$ and $\lambda =-i$ into Eq. (16), we obtain the third-order rogue waves of Eq. (1)

$$\begin{aligned} q[4]=q[3]-4\frac{\varphi _1 [3]\cdot {\phi }_1 [3]^{*}}{\left| {\varphi _1 [3]} \right| ^{2}+\left| {{\phi }_1 [3]} \right| ^{2}}. \end{aligned}$$

(35)

Lastly, consider the following limit

$$\begin{aligned}&\mathop {\lim }\limits _{\eta \rightarrow 0} \frac{\left. {\left. {[\eta +T_1 [4]} \right| _{\lambda =\lambda _1 } ][\eta +T_1 [3]} \right| _{\lambda =\lambda _1 } ]\left. {[\eta +T_1 [2]} \right| _{\lambda =\lambda _1 } ]\left. {[\eta +T_1 [1]} \right| _{\lambda =\lambda _1 } ]\Psi }{\eta ^{4}}\nonumber \\&\quad =\Phi _1^{[0]} +(T_1 [1](\lambda _1 )+T_1 [2](\lambda _1 )+T_1[3](\lambda _1 )\nonumber \\&\qquad +T_1 [4](\lambda _1 ))\Phi _1^{[1]} +(T_1 [2](\lambda _1 )T_1 [1](\lambda _1 )\nonumber \\&\qquad +T_1 [3](\lambda _1 )T_1 [1](\lambda _1 )+T_1 [4](\lambda _1 )T_1 [1](\lambda _1 )\nonumber \\&\qquad +T_1 [3](\lambda _1 )T_1 [2](\lambda _1 )+T_1 [4](\lambda _1 )T_1 [2](\lambda _1 )\nonumber \\&\qquad +T_1 [4](\lambda _1 )T_1 [3](\lambda _1 ))\Phi _1^{[2]} +(T_1 [3](\lambda _1 )T_1 [2](\lambda _1 )T_1 [1](\lambda _1 )\nonumber \\&\qquad +T_1 [4](\lambda _1 )T_1 [3](\lambda _1 )T_1 [2](\lambda _1 )\nonumber \\&\qquad +T_1 [4](\lambda _1 )T_1 [3](\lambda _1 )T_1 [1](\lambda _1 )\nonumber \\&\qquad +T_1 [4](\lambda _1 )T_1 [2](\lambda _1 )T_1 [1](\lambda _1 ))\Phi _1^{[3]} =\Phi _1 [4], \end{aligned}$$

(36a)

$$\begin{aligned}&\Phi _1 [4]=\left( {{\begin{array}{l} {\varphi _1 [4]} \\ {{\phi }_1 [4]} \\ \end{array} }} \right) . \end{aligned}$$

(36b)

where $T_1 [4]$ and $\Phi _1 [4]$ are calculated by the Maple program.

Substituting $\Phi _1^{[0]} , \Phi _1^{[1]}, \Phi _1^{[2]}, \Phi _1^{[3]} , \Phi _1^{[4]}$ and $\lambda =-i$ into Eq. (16), we obtain the fourth-order rogue waves of Eq. (1)

$$\begin{aligned} q[5]=q[4]-4\frac{\varphi _1 [4]\cdot {\phi }_1 [4]^{*}}{\left| {\varphi _1 [4]} \right| ^{2}+\left| {{\phi }_1 [4]} \right| ^{2}}. \end{aligned}$$

(37)

4 Numerical results

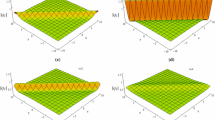
In this section, we use numerical results to investigate the nonlinear dynamic properties of the rogue waves for the inhomogeneous higher-order nonlinear Schrödinger equation. The plot of the first-order rogue wave is depicted, as shown in Fig. 1. Figure 1a represents the amplitude in the space (t, x, q[2]), and Fig. 1b is the density plot in the plane (t, x). In Fig. 1a, b, we have $\varepsilon =0$. In Fig. 1c, d, there is $\varepsilon =0.1$. As $\varepsilon$ increases, it is found that the temporal range for the appearance of the rogue wave shortens.

Fig. 1

First-order rogue wave $\left| {q[2]} \right|$ and the density picture are plotted, a, b with parameter $\varepsilon =0$; c, d with parameter $\varepsilon =0.1$

In Eq. (32), there are three free parameters $\varepsilon$, $a_1$ and $b_1$. We will take different values to display different second-order rogue waves. For the general case $\varepsilon =0$ and $a_1 =b_1 =0$, the corresponding plot of the second-order rogue wave is depicted, as shown in Fig. 2a, b. Figure 2a is a fundamental pattern in which a single maximum appears at the center. By slightly adjusting the parameter $\varepsilon =0.1$ and keeping other parameters constant, the rogue waves are also depicted, as shown in Fig. 2c, d. In Figure 2d, the spatial range extends a little toward both sides, but the temporal range for the appearance of the rogue wave shortens.

Fig. 2

Second-order rogue waves $\left| {q[3]} \right|$ and the density picture are plotted, a, b with parameters $\varepsilon =0$ and $a_1 =b_1 =0$; c, d with parameters $\varepsilon =0.1$ and $a_1 =b_1 =0$

Then, we study the influence of the separating function $\Omega (\eta )$ on the second-order rogue wave. The plots of the second-order rogue waves are depicted, as shown in Fig. 3. In Fig. 3a, b, we have $\varepsilon =0$ and $a_1 =b_{1} =5$. In Fig. 3a, b, the solution q[2] splits into three first-order rogue waves, but are connected each other. Three first-order rogue waves have a structure of the equilateral triangle. In Fig. 3c, d, there are $\varepsilon =0.2$ and $a_1 =b_{1} =60$. The solution q[3] is also composed of three first-order rogue waves and forms a structure of the triangle, but is separated completely.

Fig. 3

Second-order rogue waves $\left| {q[3]} \right|$ and the density picture are plotted, a, b with parameters $\varepsilon =0$ and $a_1 =b_1 =5$; c, d with parameters $\varepsilon =0.2$ and $a_1 =b_1 =60$

There are five parameters $\varepsilon , a_1 , b_1, a_2$ and $b_2$ in the third-order solution q[4]. The corresponding plots of this solution are depicted, as shown in Fig. 4. In Fig. 4a, b, we have $\varepsilon =0$, $a_1 =b_1 =0$ and $a_2 =b_2 =0$. There is a single maximum peak at the center, and six small peaks lie around the maximum one. In this case, the maximum amplitude of q[4] is 7. Changing the parameter $\varepsilon =0.1$ and keeping other parameters same, the solution q[4] is depicted, as shown in Fig. 4c, d. In this case, the temporal range for the appearance of the rogue wave shortens with the increase in the parameter $\varepsilon$.

Fig. 4

Third-order the rogue waves $\left| {q[4]} \right|$ and the density picture are plotted, a, b with parameters $\varepsilon =0$, $a_1 =b_1 =0$ and $a_2 =b_2 =0$; c, d with parameters $\varepsilon =0.1, \quad a_1 =b_1 =0$ and $a_2 =b_2 =0$

When we select the parameters as $\varepsilon =0.1$ and $b_{1} =50$, the corresponding plots of the solution q[4] are depicted, as shown in Fig. 5a, b. When we only change the parameter $b_{2} =1000$, the corresponding plots of the solution q[4] are given in Fig. 5c, d. Comparing Fig. 5a with 5c, it is found that the third-order rogue waves consist of six first-order rogue waves. Meanwhile, it is observed from Fig. 5b that six first-order rogue waves form an equilateral triangle. However, it is obviously seen from Fig. 5d that these waves also form a pentagon. One wave is located in the center, and other waves are put on the vertices of the pentagon.

Fig. 5

Third-order rogue waves $\left| {q[4]} \right|$ and the density picture are plotted, a, b with parameters $\varepsilon =0.1$ and $b_1 =50$; c, d with parameters $\varepsilon =0.1$ and $b_2 =1000$

There are seven parameters $\varepsilon , a_1 , b_1 , a_2 , b_2 , a_3$ and $b_3$ in the fourth-order solution q[5]. The corresponding plots of this solution are depicted, as shown in Fig. 6. In Fig. 6a, b, we have $\varepsilon =0, a_1 =b_1 =0, a_2 =b_2 =0$ and $a_3 =b_3 =0$. It is a fundamental pattern of the fourth-order rogue wave and is a single maximum at the center, and eight small peaks lie around the maximum one. In this case, the maximum amplitude of q[5] is 9. Changing the parameter $\varepsilon =0.02$ and keeping other parameters same, the solution q[5] is depicted, as shown in Fig. 6c, d. In this case, the temporal range for the appearance of the rogue wave shortens with the increase in the parameter $\varepsilon$.

Fig. 6

Fourth-order rogue waves $\left| {q[5]} \right|$ and the density picture are plotted, a, b with parameters $\varepsilon =0$, $a_1 =b_1 =0$, $a_2 =b_2 =0$ and $a_3 =b_3 =0$; c, d with parameters $\varepsilon =0.02$, $a_1 =b_1 =0$, $a_2 =b_2 =0$ and $a_3 =b_3 =0$

Setting $\varepsilon =0.02$ and $b_{3} =35{,}000$, the corresponding plots of the solution q[5] are depicted, as shown in Fig. 7a, b. In Fig. 7a, the fourth-order rogue waves are composed of seven first-order rogue waves and one second-order rogue wave. In Fig. 7b, seven first-order rogue waves form a ring structure and the second-order rogue wave lie in the center of the ring.

Fig. 7

Fourth-order rogue wave $\left| {q[5]} \right|$ and the density picture are plotted with parameters $\varepsilon =0.02$ and $b_{3} =35{,}000$

With the increase in the order of the solution q[N], the solutions of the rogue wave contain more free parameters and display more interesting spatial–temporal structures. It is guessed that these new structures could be a polygon which could be extended to the general N th-order systems.

5 Conclusions

In this paper, the first-order to the fourth-order rogue waves are investigated using the generalized Darboux transformation for the inhomogeneous higher-order nonlinear Schrödinger equation for the first time. A brief introduction of the DT is given, and the generalized DT is studied using the Taylor series expansion of a special solution to the linear spectral problem and a limit procedure. Some different types of figures are explicitly obtained to illustrate the nonlinear dynamic properties of the rogue waves for the inhomogeneous higher-order nonlinear Schrödinger equation by changing the free parameters. Generally speaking, the Nth-order rogue waves contain $2n-1$ free parameters and the total number of the peaks is $\frac{n(n+1)}{2}$ in terms of a complete decomposition pattern. The structures of the Nth-order rogue waves depend on the choice of the free parameters. If we continue to use the generalized DT procedure, it will be found that there exist the solutions of the more complicated rogue waves. We are looking forward to see that the theoretical results may be verified by the experiments in the future.

Appendix

Analytical expressions of the coefficients in Eq. (21) are given as

$$\begin{aligned} \varphi _1^{[2]}= & {} \left( \frac{1}{\sqrt{a}}\left( \frac{i}{96}\left( 27648a^{9}t^{3}{\varepsilon }^{2}+2304a^{7}t^{3}{\varepsilon }\right. \right. \right. \nonumber \\&-\,96a^{3}xt^{2}-192a^{3}x^{2}t+64a^{5}t^{3}-240ta\nonumber \\&-\,12t^{3}a^{3}1152ia^{6}t^{3}{\varepsilon }+27648ia^{8}xt^{2}{\varepsilon }^{2}\nonumber \\&+\,4608ia^{6}xt^{2}{\varepsilon }-1152a^{5}xt^{2}{\varepsilon }-2304a^{5}x^{2}t{\varepsilon }\nonumber \\&\times \,110592a^{11}t^{3}{\varepsilon }^{3}+192ia^{4}xt^{2}+6912ia^{8}t^{3}{\varepsilon }^{2}\nonumber \\&-\,48ia^{2}x^{2}t-12ia^{2}xt^{2}-5952t{\varepsilon }a^{3}-192aa_1\nonumber \\&-\,48 i x-12it-144a^{5}t^{3}{\varepsilon }-192iab_1 \nonumber \\&\left. -\,64ia^{2}x^{3}-ia^{2}t^{3}+48ia^{4}t^{3}\right) \nonumber \\&-\,\frac{1}{32}\sqrt{a}\left( {-4x+48it{\varepsilon }a^{3}-t+4ita} \right) ^{2}\nonumber \\&+\,1/16a^{-3/2}+\frac{1}{768}\sqrt{a}\big ( -4x+48it{\varepsilon }a^{3}\nonumber \\&-\,t+4ita \big )\big (-1152a^{6}t^{3}{\varepsilon }-192a^{4}xt^{2}\nonumber \\&+\,192x+48t-48a^{4}t^{3}-4608a^{6}xt^{2}{\varepsilon }\nonumber \\&-\,1152ia^{5}xt^{2}{\varepsilon }-2304ia^{5}x^{2}t{\varepsilon }\nonumber \\&-\,27648a^{8}xt^{2}{\varepsilon }^{2}+64a^{2}x^{3}+a^{2}t^{3}-6912a^{8}t^{3}{\varepsilon }^{2}\nonumber \\&+\,48a^{2}x^{2}t+12a^{2}xt^{2}-960ita-12ia^{3}t^{3}\nonumber \\&\times \,64ia^{5}t^{3}-768iaa_1 +768ab_1 -23808it{\varepsilon }a^{3}\nonumber \\&-\,144ia^{5}t^{3}{\varepsilon }-96ia^{3}xt^{2}+27648ia^{9}t^{3}{\varepsilon }^{2}\nonumber \\&\times \,2304ia^{7}t^{3}{\varepsilon }-192ia^{3}x^{2}t\nonumber \\&\left. \left. +\,110592ia^{11}t^{3}{\varepsilon }^{3}\big )\right) \right) e^{\frac{i}{2}\theta },\nonumber \\ \end{aligned}$$

$$\begin{aligned} \varphi _1^{[2]}= & {} \left( {-\frac{1}{\sqrt{a}}\left( \frac{i}{96}\right. \left( 110592a^{11}t^{3}{\varepsilon }^{3}+27648a^{9}t^{3}\right. {\varepsilon }^{2}} \right. \nonumber \\&+\,2304a^{7}t^{3}{\varepsilon }-96a^{3}xt^{2}+192a^{3}x^{2}t\nonumber \\&+\,27648ia^{8}xt^{2}{\varepsilon }^{2}-48ia^{2}x^{2}t+64a^{5}t^{3}\nonumber \\&-240ta-12t^{3}a^{3}+1152ia^{6}t^{3}{\varepsilon } 12ia^{2}xt^{2}\nonumber \\&+\,6912ia^{8}t^{3}{\varepsilon }^{2}+192ia^{4}xt^{2}-48ix-12it\nonumber \\&-\,ia^{2}t^{3}-192iab_1+48ia^{4}t^{3}-64ia^{2}x^{3}\nonumber \\&-\,1152a^{5}xt^{2}{\varepsilon }-2304a^{5}x^{2}t{\varepsilon }-192aa_1 \nonumber \\&\left. \left. -\,5952t{\varepsilon }a^{3}-144a^{5}t^{3}{\varepsilon }4608ia^{6}xt^{2}{\varepsilon } \right) \right) \nonumber \\&-\frac{1}{32}\sqrt{a}\Big ( {-4x+48it{\varepsilon }a^{3}-t+4ita} \Big )^{2}\nonumber \\&+\,1/16a^{-3/2}+ \frac{1}{768}\sqrt{a}\Big ( -4x+48it{\varepsilon }a^{3}\nonumber \\&-\,t+4ita\Big )\Big (-96ia^{3}xt^{2}-192ia^{3}x^{2}t\nonumber \\&+\,192x+48t+64ia^{5}t^{3}+110592ia^{11}t^{3}{\varepsilon }^{3}\nonumber \\&+\,27648ia^{9}t^{3}{\varepsilon }^{2}-768iaa_1-12ia^{3}t^{3}\nonumber \\&-\,960ita+12a^{2}xt^{2}+48a^{2}x^{2}t-192a^{4}xt^{2}\nonumber \\&+\,768ab_1 -144ia^{5}t^{3}{\varepsilon }+2304ia^{7}t^{3}{\varepsilon }\nonumber \\&-23808it{\varepsilon }a^{3}-4608a^{6}xt^{2}{\varepsilon }-27648a^{8}xt^{2}{\varepsilon }^{2}\nonumber \\&-48a^{4}t^{3}+a^{2}t^{3}+64a^{2}x^{3}-6912a^{8}t^{3}{\varepsilon }^{2}\nonumber \\&-1152t^{3}a^{6}{\varepsilon } \quad -1152ia^{5}xt^{2}{\varepsilon }\nonumber \\&\left. -\,2304ia^{5}x^{2}t{\varepsilon } \Big ) \right) e^{-\frac{i}{2}\theta }. \end{aligned}$$

(38)