Novel applications of bipolar fuzzy graphs to decision making problems

Abstract

Zhang introduced the concept of bipolar fuzzy sets as a generalization of fuzzy sets. Bipolar fuzzy sets have shown advantages in solving decision making problems than fuzzy sets. In this research paper, we study several different types of domination, including equitable domination, k-domination and restrained domination in bipolar fuzzy graphs. We present novel applications of bipolar fuzzy graphs to decision making problems. We also present an algorithm for computing dominating number in our applications.

1 Introduction

In 1965, Zadeh [32] introduced the notion of fuzzy sets. In 1994, Zhang [34] initiated the concept of bipolar fuzzy sets. Bipolar fuzzy sets are extension of fuzzy sets whose membership degree range is [$-1$, 1]. In a bipolar fuzzy set, the membership degree 0 of an element means that the element is irrelevant to the corresponding property, the membership degree (0, 1] of an element indicates that the element somewhat satisfies the property, and the membership degree [$-1$, 0) of an element indicates that the element somewhat satisfies the implicit counter-property. The idea which lies behind such description is connected with the existence of “bipolar information” (e.g., positive information and negative information) about the given set. Positive information represents what is granted to be possible, while negative information represents what is considered to be impossible. Actually, a wide variety of human decision making is based on double-sided or bipolar judgemental thinking on a positive side and a negative side. For instance, cooperation and competition, friendship and hostility, common interests and conflict of interests, effect and side effect, likelihood and unlikelihood, feedforward and feedback, and so forth are often the two sides in decision and coordination. Thus, bipolar fuzzy sets indeed have potential impacts on many fields, including artificial intelligence, computer science, information science, cognitive science, decision science, management science, economics, neural science, quantum computing, medical science, and social science. In recent years bipolar fuzzy sets seem to have been studied and applied a bit enthusiastically and a bit increasingly.

Based on Zadeh’s [33] fuzzy relations Kaufmann defined in [15] a fuzzy graph. The fuzzy relations between fuzzy sets were also considered by Rosenfeld [27] and he developed the structure of fuzzy graphs, obtaining analogs of several graph theoretical concepts. Later on, Bhattacharya [6] gave some remarks on fuzzy graphs, and several concepts were introduced by Mordeson and Peng [16]. Somasundaram and Somasundaram [28] introduced several new ideas including, dominating sets, total dominating sets and independent sets in fuzzy graph theory. Nagoorgani and Ahamed presented [20] the idea of strong and weak domination in fuzzy graphs. Several researchers published their work on domination in fuzzy graphs (see [21–26, 29–31]). Talebi and Eslami [31] introduced the concept of restrained and global restrained domination in fuzzy graphs. Akram [1] introduced the concept of bipolar fuzzy graphs. In this article, we study several different types of domination, including equitable domination(ED), k-domination and restrained domination(RD) in bipolar fuzzy graphs. We present novel applications of bipolar fuzzy graphs to decision making problems. We also present an algorithm for computing dominating number in our applications. We have used standard definitions and terminologies in this paper. For other notations, terminologies and applications not mentioned in the paper, the readers are referred to [2–5, 7–14, 16–19].

2 Certain types of domination in bipolar fuzzy graphs

Definition 2.1

[1] A bipolar fuzzy graph (BFG, in short) on a non-empty V is a pair $G=(X,Y)$ where, $X=(\tau ^{P}_{X}, \tau ^{N}_{X})$ is a bipolar fuzzy set on V and $Y =(\tau ^{P}_{Y}, \tau ^{N}_{Y})$ is a bipolar fuzzy relation on V such that

$$\begin{aligned} \tau _{Y}^{P}(xy)\le \min ( \tau _{X}^{P}(x) ,\tau _{X}^{P}(y)) \text { and } \tau _{Y}^{N}(xy)\ge \max (\tau _{X}^{N}(x), \tau _{X}^{N}(y)), \quad \text {for all } x, y\in V. \end{aligned}$$

y is called relations on x.

Definition 2.2

Let $G=(X,Y)$ be a BFG on a non-empty set V. The equitable neighborhood (EN, in short) of a vertex $v\in V$, denoted by EN(v), is defined as, $EN(v)=(EN^P(v),EN^N(v))$, where $EN^P(v)=\{u\in V:u\in N(v),|deg^P(u)-deg^P(v)|\le 1, \tau _Y^P(uv)=\min \{\tau _X^P(u),\tau _X^P(v)\}$ and $EN^N(v)=\{u\in V:u\in N(v),|deg^N(u)-deg^N(v)|\ge 1, \tau _Y^N(uv)=\max \{\tau _X^N(u),\tau _X^N(v)\}.$

Definition 2.3

The EN degree of a vertex $v\in V$, denoted by $deg_{EN}(v),$ is defined as, $deg_{EN}(v)=(deg_{EN}^P(v),deg_{EN}^N(v))$, where $deg_{EN}^P(v)=\sum _{u\in EN(v)}\tau _Y^P(vu)$ and $deg_{EN}^N(v)$=$\sum _{u\in EN(v)}\tau _Y^N(vu).$

The minimum EN degree, denoted by $\delta _{EN}(G),$ is defined as, $\delta _{EN}(G)=(\delta _{EN}^P(G), \delta _{EN}^N(G)),$ where $\delta _{EN}^P(G)=\min \{deg_{EN}^P(v):v\in V\}$ and $\delta _{EN}^N(G)=\min \{deg_{EN}^P(v):v\in V\}.$

The maximum EN degree, denoted by $\Delta _{EN}(G),$ is defined as, $\Delta _{EN}(G)=(\Delta _{EN}^P(G), \Delta _{EN}^N(G)),$ where $\Delta _{EN}^P(G)=\max \{deg_{EN}^P(v):v\in V\}$ and $\Delta _{EN}^N(G)=\max \{deg_{EN}^N(v):v\in V\}.$

Example 2.4

Let $G^*$ be a crisp graph such that $V=\{u, v, w,x, y, z\}, E=\{uv, uw, wx, xv, vy, wz \}.$ Let $X=(\tau _X^P,\tau _X^N)$ be a bipolar fuzzy subset of V and let $Y=(\tau _Y^P,\tau _Y^N)$ be a bipolar fuzzy subset of $E\subseteq \widetilde{V^2}$ defined by Fig. 1.

Fig. 1

Bipolar fuzzy graph

By routine verification, it is clear from Fig. 1, that $EN(u)=\{v,w\}, EN(v)=\{u,x,y\}, EN(w)=\{u,x,z\},$ $EN(x)=\{w,v\}, EN(y)=\{v\}$ and $EN(z)=\{w\}.$ The EN degrees of vertices is as follows: $deg_{EN}(u)=(0.4,-1.4)$, $deg_{EN}(v)=(0.5,-2.1)$, $deg_{EN}(w)=(0.5,-1.9), deg_{EN}(x)=(0.2,-1.5)$, $deg_{EN}(y)=(0.2,-0.6)$ and $deg_{EN}(z)=(0.2,-0.5).$ The minimum EN degree of a BFG G is $\delta _{EN}(G)=(0.2,-2.1)$ and the maximum EN degree of a BFG G is $\Delta _{EN}(G)=(0.5,-0.5).$

Definition 2.5

Let $G=(X,Y)$ be a BFG on non-empty set V. A vertex $v\in V$ is called an equitable isolated vertex in G, if for every $u\in V, |deg^P(u)-deg^P(v)|>1$, $\tau ^P_Y(uv)<\min \{\tau ^P_X(u),\tau ^P_X(v)\},$ and $|deg^N(u)-deg^N(v)|<1$, $\tau ^N_Y(uv)>\max \{\tau ^N_X(u),\tau ^N_X(v)\},$ i.e., $EN(v)=\phi .$

Example 2.6

Consider a BFG $G=(X,Y)$ on $V=\{u,v,w,x,y\},$ as shown in Fig. 2.

Fig. 2

Equitable isolated vertex

From Fig. 2, it is clear that $deg(u)=(1.5,-0.5)$, $deg(y)=(0.2,-0.1), deg(w)=(1.4,-0.5)$ and $deg(x)=(0.2,-0.1).$ Since $|deg^P(u)-deg^P(y)|>1$, $\tau ^P_Y(uy)<\min \{\tau ^P_X(u),\tau ^P_X(y)\}$ and $|deg^N(u)-deg^N(y)|<1$, $\tau ^P_Y(uy)>\max \{\tau ^P_X(u),\tau ^P_X(y)\},$ i.e., $EN(y)=\phi .$ Also, $|deg^P(w)-deg^P(x)|>1$, $\tau ^P_Y(wx)<\min \{\tau ^P_X(w),\tau ^P_X(x)\}$ and $|deg^N(w)-deg^N(x)|<1$,

$\tau ^N_Y(wx)>\max \{\tau ^N_X(w),\tau ^N_X(x)\},$ i.e., $EN(x)=\phi .$ Therefore, y and x are equitable isolated vertices in G.

Definition 2.7

Let $G=(X,Y)$ be a BFG on non-empty set V. A set $S\subseteq V$ is called an equitable dominating set (EDS, in short) of G if for every vertex $v\in V-S$, there exists a vertex $u\in V$ such that $uv\in E,$ $|deg^P(u)-deg^P(v)|\le 1$, $\tau ^P_Y(uv)=\min \{\tau ^P_X(u), \tau ^P_X(v)\}$ and $|deg^N(u)-deg^N(v)|\ge 1$, $\tau ^N_Y(uv)=\max \{\tau ^N_X(u), \tau ^N_X(v)\}.$ The ED number of G, denoted by $\gamma _{e}(G)$, is defined as the minimum cardinality of an EDS S.

Definition 2.8

An EDS S is called minimal EDS of G if for every vertex $v\in S$, the set $S-\{v\}$ is not an EDS, i.e., no proper subset of S is an EDS of G.

Example 2.9

Consider a BFG $G=(X,Y)$ on $V=\{u,v,w,x\}$, as shown in Fig. 3.

Fig. 3

Equitable dominating set of G

By definition 2.7, it is easy to see from Fig. 3, that the minimal EDS of a BFG G is $S=\{u\}$. The ED number of G is $\gamma _{e}(G)=0.4.$

Definition 2.10

Let $G=(X,Y)$ be a BFG on a non-empty set V. G is called a degree equitable, if for every vertex $v\in V,$ there exists a vertex $u\in V$ such that $uv\in E,$ $|deg^P(u)-deg^P(v)|\le 1$, $\tau ^P_Y(uv)=\min \{\tau ^P_X(u), \tau ^P_X(v)\}$ and $|deg^N(u)-deg^N(v)|\ge 1$, $\tau ^N_Y(uv)=\max \{\tau ^N_X(u), \tau ^N_X(v)\}.$

Example 2.11

Consider a BFG $G=(X,Y)$ on $V=\{u,v,w,x\}$, as shown in Fig. 4.

Fig. 4

Degree equitable BFG

Routine computations show that G is a degree equitable BFG.

Definition 2.12

A set $I\subseteq V$ is called an equitable independent set (EIS, in short) of G if $|deg^P(u)-deg^P(v)|>1$, $\tau ^P_Y(uv)<\min \{\tau ^P_X(u), \tau ^P_X(v)\}$ and $|deg^N(u)-deg^N(v)|<1$, $\tau ^N_Y(uv)>\max \{\tau ^N_X(u), \tau ^N_X(v)\}$ for all $u,v\in I.$ The EI number of G, denoted by $\gamma _{ie}(G)$, is defined as the minimum cardinality of an EIS of G.

Definition 2.13

An EIS I is called a maximal EIS of G, if for every vertex $u\in V-I$, the set $I\cup \{u\}$ is not EI.

Example 2.14

Consider a BFG $G=(X,Y)$ on $V=\{u,v,w,x,y,z\},$ as shown in Fig. 5.

Fig. 5

Equitable independent set of G

By routine verifications, it is easy to see from Fig. 5, that $S_1=\{u,x\}$ and $S_2=\{v,w\}$ are maximal EIS sets of G. The equitable independent number of G is $\gamma _{ie}(G)=1.25.$

Definition 2.15

Let $G=(X,Y)$ be a BFG on V. For any two vertices u, $v \in V$, we call u strongly dominates v in G if $\tau ^P_Y(uv)=\min \{\tau ^P_X(u), \tau ^P_X(v)\}$, $\tau ^N_Y(uv)=\max \{\tau ^N_X(u), \tau ^N_X(v)\}$ $d^P_G(u)\ge d^P_G(v)$ and $d^N_G(u)\le d^N_G(v).$

Similarly, u weakly dominates v if $\tau ^P_Y(uv)=\min \{\tau ^P_X(u), \tau ^P_X(v)\},$ $\tau ^N_Y(uv)=\max \{\tau ^N_X(u), \tau ^N_X(v)\}$, $d^P_G(v)\ge d^P_G(u)$ and $d^N_G(v)\le d^N_G(u).$

Definition 2.16

An EDS $S\subseteq V$ is called a strong (weak) EDS of G, if for every vertex $v\in V-S$, there exists a vertex $u\in S$ such that v is strongly (weakly) dominated by u. The strong (weak) ED number of G, denoted by $\gamma _{se} (G)$ ($\gamma _{we} (G)$), is defined as the minimum cardinality of a strong (weak) EDS of G.

Example 2.17

An exam of a strong EDS of G is shown in Fig. 6.

Fig. 6

Strong equitable dominating set of G

By routine computations, it is easy to see from Fig. 6, that the strong EDS of G is $S=\{u,v\}.$ The strong equitable domination number of G is $\gamma _{se} (G)=0.5.$

Definition 2.18

Let $G=(X,Y)$ be a connected BFG on V. A set $V'\subseteq V$ of G is called a connected EDS if

• (i) For every $v\in V-V'$, there exists a vertex $u\in V'$ such that $vu\in E$, $|deg^P(u)-deg^P(v)|\le 1,$ $\tau ^P_Y(uv)=\min \{\tau ^P_X(u),\tau ^P_X(v)\}$ and $|deg^N(u)-deg^N(v)|\ge 1,$ $\tau ^N_Y(uv)=\max \{\tau ^N_X(u),\tau ^N_X(v)\}.$

• (ii) The subgraph $H=(X',Y')$ of $G=(X,Y)$ induced by $V'$ is connected.

Theorem 2.19

Let $G=(X,Y)$ be a BFG of order O(G),  then

• (i) $\gamma _e (G)\le \gamma _{se} (G)\le O(G)-\Delta _{EN}^P(G),$

• (ii) $\gamma _e (G)\le \gamma _{we} (G)\le O(G)-\delta _{EN}^P(G).$

Theorem 2.20

Let $G=(X,Y)$ be a BFG without isolated vertices and let S be a minimal EDS of G. Then $V-S$ is an EDS of G.

Definition 2.21

A set $S\subseteq V$ of G is called a total EDS of G if for every vertex $v\in V$, there exists a vertex $u\in S$ such that $uv\in E(G)$, $|deg^P(u)-deg^P(v)|\le 1$, $\tau ^P_Y(uv)=\min \{\tau ^P_X(u),\tau ^P_X(v)\}$ and $|deg^N(u)-deg^N(v)|\ge 1$, $\tau ^N_Y(uv)=\max \{\tau ^N_X(u),\tau ^N_X(v)\}$. The total equitable domination number of G, denoted by $\gamma _{te}(G)$, is defined as the minimum cardinality of a total EDS S.

Definition 2.22

A total EDS S of G is called minimal total EDS if for every vertex $v\in S$, the set $S-\{v\}$ is not a total EDS, i.e., no proper subset of S is a total EDS of G.

Example 2.23

Consider a BFG $G=(X,Y)$ on crisp set $V=\{u,v,w,x,y\}$, as shown in Fig. 7.

Fig. 7

Total equitable dominating set of G

By Definition 2.21, it is easy to see from Fig. 7, that $S=\{w,y\}$ is a total EDS of G.

Remark 2.1

If G has an equitable isolated vertex, then $\gamma _{te}(G)=\infty .$

Theorem 2.24

Let $G=(X,Y)$ be a BFG on non-empty set V. A total EDS S of G is called minimal total EDS if and only if for each $v\in S$ one of the following conditions is satisfied:

• (i) There exists a vertex $u\in V-S$ such that $N(u)\cup S=\{v\},$

• (ii) $\langle S-\{v\} \rangle$ contains an isolated vertex.

Proof

Proof is obvious. $\square$

Theorem 2.25

If G is a BFG without isolated vertices, then $\gamma _{t}(G)\le \gamma _{te}(G).$

Definition 2.26

Let $G=(X,Y)$ be a BFG on non-empty set V and let $k\ge 1$ be an integer. A set $S\subseteq V$ is called a k-dominating set of G, if for every vertex $u\in V-S$, there exists a (u, v) path which contains at least k effective edges for $v\in S$. The k-domination number of G, denoted by $\gamma _{k}(G)$, is defined as the minimum cardinality of a k-dominating set in G.

Definition 2.27

Let $G=(X,Y)$ be a BFG on non-empty set V and let $k\ge 1$ be an integer. A set $S\subseteq V$ is called a total k-dominating set of G, if for every vertex $u\in V$, there exists a (u, v) path which contains at least k effective edges for $v\in S$. The total k-domination number of G, denoted by $\gamma _{tk}(G)$, is defined as the minimum cardinality of a total k-dominating set in G.

Example 2.28

Consider an exam of a total 2-dominating set of G as shown in Fig. 8.

Fig. 8

Total 2-dominating set of G

By definition 2.27, it is clear from Fig. 8, that $S=\{u,z\}$ is a minimal total 2-dominating set of a BFG G. The total 2-domination number of G is $\gamma _k(G)=0.95.$

Definition 2.29

Let $G=(X,Y)$ be a BFG on V. A set $S\subseteq V$ is called a k-independent dominating set of G,  if for every vertex $u\in V-S$, there exists a (u, v) path which contains at least $k+1$ effective edges for $v\in S$. The k-independent domination number of G, denoted by $\gamma _{ik}(G)$, is defined as the minimum cardinality of a k-independent dominating set in G.

Definition 2.30

Let $G=(X,Y)$ be a BFG on V. A set $S\subseteq V$ is called a restrained dominating set (RDS, in short) of G if every vertex in $V-S$ dominates a vertex in S and also a vertex in $V-S.$ The restrained domination number of G, denoted by $\gamma _r(G)$, is defined as the minimum cardinality of a restrained dominating set in G.

Example 2.31

Consider a BFG $G=(X,Y)$ on $V=\{u,v,w,x\}$, as shown in Fig. 9.

Fig. 9

Restrained dominating set of G

From Fig. 9, it is clear that $S=\{w,x\}$ is a RDS of G. The restrained domination number of G is $\gamma _r(G)=0.95.$

Definition 2.32

Let $G=(X,Y)$ be a BFG on V. A set $S\subseteq V$ is called a global restrained dominating set of G if it is a RDS of both G and $\overline{G}.$ The global restrained domination number of G, denoted by $\gamma _{gr}(G)$, is defined as the minimum cardinality of a GRDS in G.

Example 2.33

Consider G and $\overline{G}$ on $V=\{u,v,w,x,y,z\}$, as shown in Fig. 10.

Fig. 10

Global restrained dominating set of G

By direct calculations, it is easy to see that $S_1=\{v,y\}$, $S_2=\{u,x\}$ and $S_3=\{w,z\}$ are GRDSs of G. The global restrained domination number of G is $\gamma _{gr} (G)=1.15.$

Theorem 2.34

Let $G=(X, Y)$ be a complete BFG. Then

$$\begin{aligned} \gamma _r (G)=\min \left\{ \sum _{v\in V}\left( \frac{1+\tau ^P_X(v)+\tau ^N_X(v)}{2}\right) \right\} \end{aligned}$$

for all $v\in G.$

Note 2.1

For a complete bipartite BFG, the restrained domination number is,

$$\begin{aligned} \gamma _r (G)=\min _{v\in V_1}\left( \frac{1+\tau ^P_X(v)+\tau ^N_X(v)}{2}\right) +\min _{u\in V_2}\left( \frac{1+\tau ^P_X(u)+\tau ^N_X(u)}{2}\right) . \end{aligned}$$

Definition 2.35

[1] The Cartesian product of two bipolar fuzzy graphs $G_1=( X_1, Y_1)$ and $G_2=( X_2, Y_2)$ of the graphs $G^*_1=(V_1,{E}_1)$ and $G^*_2=(V_2,{E}_2)$, denoted by $G_1 \times G_2=( X_1 \square X_2, Y_1 \square Y_2)$, is defined as follows:

• (i) $(\tau ^P_{ X_1} \square \tau ^P_{ X_2})(u, v)=\min \{\tau ^P_{ X_1}(u), \tau ^P_{ X_2}(v)\}$

  $(\tau ^N_{ X_1} \square \tau ^N_{ X_2})(u, v)=\max \{\tau ^N_{ X_1}(u), \tau ^N_{ X_2}(v)\}$ for all $(u, v) \in V$,

• (ii) $(\tau ^P_{ Y_1} \square \tau ^P_{ Y_2})((u,u_1)(u, v_1))=\min \{\tau ^P_{ X_1}(u), \tau ^P_{ Y_2}(u_1v_1)\}$

  $(\tau ^N_{ Y_1} \square \tau ^N_{ Y_2})((u,u_1)(u, v_1))=\max \{\tau ^N_{ X_1}(u), \tau ^N_{ Y_2}(u_1v_1)\}$ for all $u\in V_1,~ u_1v_1 \in {E}_2$,

• (iii) $(\tau ^P_{ Y_1} \square \tau ^P_{ Y_2})((u,u_1)(v, u_1))=\min \{\tau ^P_{ Y_1}(uv), \tau ^P_{ X_2}(u_1)\}$

  $(\tau ^N_{ Y_1} \square \tau ^N_{ Y_2})((u,u_1)(v, u_1))=\max \{\tau ^N_{ Y_1}(uv), \tau ^N_{ X_2}(u_1)\}$ for all $u_1\in V_2,~ uv \in {E}_1$.

Definition 2.36

The Strong product of two bipolar fuzzy graphs $G_1=( X_1, Y_1)$ and $G_2=( X_2, Y_2)$ of the graphs $G^*_1=(V_1,{E}_1)$ and $G^*_2=(V_2,{E}_2)$, where $V_1\cap V_2=\phi$, denoted by $G_1 \boxtimes G_2=( X_1 \boxtimes X_2, Y_1 \boxtimes Y_2),$ is defined as follows:

• (i) $(\tau ^P_{ X_1} \boxtimes \tau ^P_{ X_2})(u, v)=\min \{\tau ^P_{ X_1}(u), \tau ^P_{ X_2}(v)\}$

  $(\tau ^N_{ X_1} \boxtimes \tau ^N_{ X_2})(u, v)=\max \{\tau ^N_{ X_1}(u), \tau ^N_{ X_2}(v)\}$ for all $(u, v) \in V$,

• (ii) $(\tau ^P_{ Y_1} \boxtimes \tau ^P_{ Y_2})((u,u_1)(u, v_1))=\min \{\tau ^P_{ X_1}(u), \tau ^P_{ Y_2}(u_1v_1)\}$

  $(\tau ^N_{B_1} \boxtimes \tau ^N_{ Y_2})((u,u_1)(u, v_1))=\max \{\tau ^N_{ X_1}(u), \tau ^N_{ Y_2}(u_1v_1)\}$ for all $u\in V_1,~ u_1v_1 \in {E}_2$,

• (iii) $(\tau ^P_{ Y_1} \boxtimes \tau ^P_{ Y_2})((u,u_1)(v, u_1))=\min \{\tau ^P_{ Y_1}(uv), \tau ^P_{ X_2}(u_1)\}$

  $(\tau ^N_{ Y_1} \boxtimes \tau ^N_{ Y_2})((u,u_1)(v, u_1))=\max \{\tau ^N_{ Y_1}(uv), \tau ^N_{ X_2}(u_1)\}$ for all $u_1\in V_2,~ uv \in {E}_1$,

• (iv) $(\tau ^P_{ Y_1} \boxtimes \tau ^P_{ Y_2})((u,u_1)(v, v_1))=\min \{\tau ^P_{ Y_1}(uv), \tau ^P_{ Y_2}(u_1v_1)\}$

  $(\tau ^N_{ Y_1} \boxtimes \tau ^N_{ Y_2})((u,u_1)(v, v_1))=\max \{\tau ^N_{ Y_1}(uv), \tau ^N_{ Y_2}(u_1v_1)\}$ for all $uv\in {E}_1, ~u_1v_1 \in {E}_2$.

Theorem 2.37

Let $G_1=( X_1, Y_1)$ and $G_2=( X_2, Y_2)$ be two bipolar fuzzy graphs with $V_1\cap V_2=\phi .$ Then strong product $G= G_1\boxtimes G_2$ remains connected even after removal of all non-effective edges in it.

Proof

Suppose that $G= G_1\boxtimes G_2$ is a strong product of two bipolar fuzzy graphs $G_1$ and $G_2$. Let $e=((u,u_1),(v,v_1))$ be a non-effective edge in G, i.e., $\tau ^P_Y((u,u_1),(v,v_1))<\min \{\tau ^P_X(u,u_1),\tau ^P_X(v,v_1)\}$ and $\tau ^N_Y((u,u_1),(v,v_1))>\max \{\tau ^N_X(u,u_1),\tau ^N_X(v,v_1)\}.$ Let $G'=G-e,$ and assume $G'$ is disconnected. The edge e disconnects the graph in to more than one components. Thus there does not exist any path between $(u,u_1)$ and $(v,v_1)$ except the edge $e=((u,u_1),(v,v_1))$ in $G'.$ This implies that $\tau ^P_Y((u,u_1),(v,v_1))=\min \{\tau ^P_X(u,u_1),\tau ^P_X(v,v_1)\}$ and $\tau ^N_Y((u,u_1),(v,v_1))=\max \{\tau ^N_X(u,u_1),\tau ^N_X(v,v_1)\},$ which is a contradiction. Hence $G'=G-e$ is connected. $\square$

Theorem 2.38

The strong product $G_1\boxtimes G_2$ of two complete bipolar fuzzy graphs is a complete BFG.

Proof

If $(\tau ^P_{ Y_1} \boxtimes \tau ^P_{ Y_2})((u,u_1)(u, v_1))\in E$, then since $G_2$ is complete,

$$\begin{aligned} (\tau ^P_{ Y_1} \boxtimes \tau ^P_{ Y_2})((u,u_1)(u, v_1))= & {} \min \{\tau ^P_{ X_1}(u), \tau ^P_{ Y_2}(u_1v_1)\}\\= & {} \min \{\tau ^P_{ X_1}(u),\min \{\tau ^P_{ X_2}(u_1),\tau ^P_{ X_2}(v_1)\}\\= & {} \min \{(\tau ^P_{ Y_1} \boxtimes \tau ^P_{ Y_2})(u,u_1),(\tau ^P_{ Y_1} \boxtimes \tau ^P_{ Y_2})(u,v_1)\}. \end{aligned}$$

If $(\tau ^P_{ Y_1} \boxtimes \tau ^P_{ Y_2})((u,u_1)(v, u_1))\in E$, then since $G_1$ is complete,

$$\begin{aligned} (\tau ^P_{ Y_1} \boxtimes \tau ^P_{ Y_2})((u,u_1)(v, u_1))= & {} \min \{\tau ^P_{ Y_1}(u,v), \tau ^P_{ X_2}(u_1)\}\\= & {} \min \{\min \{\tau ^P_{ X_1}(u),\tau ^P_{ X_1}(v)\},\tau ^P_{ X_2}(u_1)\}\\= & {} \min \{(\tau ^P_{ Y_1} \boxtimes \tau ^P_{ Y_2})(u,u_1),(\tau ^P_{ Y_1} \boxtimes \tau ^P_{ Y_2})(v,u_1)\}. \end{aligned}$$

If $(\tau ^P_{ Y_1} \boxtimes \tau ^P_{ Y_2})((u,u_1)(v, v_1))\in E$, then since $G_1$ and $G_2$ are complete,

$$\begin{aligned} (\tau ^P_{ Y_1} \boxtimes \tau ^P_{ Y_2})((u,u_1)(v, v_1))= & {} \min \{\tau ^P_{ Y_1}(u,v), \tau ^P_{ Y_2}(u_1v_1)\}\\= & {} \min \{\min \{\tau ^P_{ X_1}(u),\tau ^P_{ X_1}(v)\},\min \{\tau ^P_{ X_2}(u_1),\tau ^P_{ X_2}(v_1)\}\\= & {} \min \{(\tau ^P_{ Y_1} \boxtimes \tau ^P_{ Y_2})(u,u_1),(\tau ^P_{ Y_1} \boxtimes \tau ^P_{ Y_2})(v,v_1)\}. \end{aligned}$$

Similarly, others can be proved. Hence $G_1\boxtimes G_2$ is a complete BFG. $\square$

Fig. 11

Direct product of $G_1$ and $G_2$

Definition 2.39

The direct product of two bipolar fuzzy graphs $G_1=( X_1, Y_1)$ and $G_2=( X_2, Y_2)$ of the graphs $G^*_1=(V_1,{E}_1)$ and $G^*_2=(V_2,{E}_2)$, where $V_1\cap V_2=\phi$, denoted by $G_1 \otimes G_2=( X_1 \otimes X_2, Y_1 \otimes Y_2),$ is defined as follows:

• (i) $(\tau ^P_{ X_1} \otimes \tau ^P_{ X_2})(u, v)=\min \{\tau ^P_{ X_1}(u), \tau ^P_{ X_2}(v)\}$

  $(\tau ^N_{ X_1} \otimes \tau ^N_{ X_2})(u, v)=\max \{\tau ^N_{ X_1}(u), \tau ^N_{ X_2}(v)\}$ for all $(u, v) \in V$,

• (ii) $(\tau ^P_{ Y_1} \otimes \tau ^P_{ Y_2})((u,u_1)(v, v_1))=\min \{\tau ^P_{ Y_1}(uv), \tau ^P_{ Y_2}(u_1v_1)\}$

  $(\tau ^N_{ Y_1} \otimes \tau ^N_{ Y_2})((u,u_1)(v, v_1))=\max \{\tau ^N_{ Y_1}(uv), \tau ^N_{ Y_2}(u_1v_1)\}$ for all $uv\in {E}_1,~ u_1v_1 \in {E}_2$.

Theorem 2.40

If a vertex u dominates a vertex v in $G_1$ and the vertex $u_1$ dominates a vertex $v_1$ in $G_2.$ Then the vertex uv does not dominate the vertex $u_1v_1$ in $G_1\square G_2.$

Proof

Assume that u dominates v in $G_1$. Then there exists an effective edge uv in $G_1$, i.e., $\tau ^P_Y(uv)=\min \{\tau ^P_X(u),\tau ^P_X(v)\}$ and $\tau ^N_Y(uv)=\max \{\tau ^N_X(u),\tau ^N_X(v)\}$. Similarly, suppose that a vertex $u_1$ dominates a vertex $v_1$ in $G_2$ such that $\tau ^P_Y(u_1v_1)=\min \{\tau ^P_X(u_1),\tau ^P_X(v_1)\}$ and $\tau ^N_Y(u_1v_1)=\max \{\tau ^N_X(u_1),\tau ^N_X(v_1)\}$. Now by definition 2.35, there does not exist any edge between the vertices $(u,u_1)$ and $(v,v_1)$ in $G_1\square G_2,$ i.e., $\tau ^P_Y((u,u_1),(v,v_1))=0$ and $\tau ^N_Y((u,u_1),(v,v_1))=0$. Thus $(u,u_1)$ does not dominate $(v,v_1)$ in $G_1\square G_2.$ $\square$

Note 2.2

If a vertex u dominates a vertex v in $G_1$ and a vertex $u_1$ dominates a vertex $v_1$ in $G_2,$ then the vertex $(u,u_1)$ dominates the vertex $(v,v_1)$ in $G_1\otimes G_2.$ It can be seen in Fig. 11

Example 2.41

Consider a BFG as shown in Fig. 11.

From the Fig. 11, it is clear that the vertex u dominates v in $G_1$ and $v_1$ dominates $w_1$ in $G_2.$ Also, the vertex $(u,v_1)$ dominates the vertex $(v,w_1)$ in $G_1\otimes G_2.$

Theorem 2.42

Let $G_1$ and $G_2$ be BFGs on non-empty sets $V_1$ and $V_2$, respectively. Then

$$\begin{aligned} \gamma _{e}( G_1\otimes G_2)\le \min (|S_1\times V_1|,|S_2\times V_2|). \end{aligned}$$

Proof

Suppose $S_1$ and $S_2$ are EDS sets of minimum cardinality, of $G_1$ and $G_2$, respectively. Then for every vertex $v\in V-S_1$, there exists a vertex $u\in S_1$ such that $|deg^P(v)-deg^P(u)|\le 1$, $\tau ^P_Y(uv)=\min \{\tau ^P_X(u),\tau ^P_X(v)\}$ and $|deg^N(v)-deg^N(u)|\ge 1$, $\tau ^N_B(uv)=\max \{\tau ^N_X(u),\tau ^N_X(v)\}$ Similarly for every vertex $x\in V-S_2$, there exists a vertex $w\in S_2$ such that $|deg^P(w)-deg^P(x)|\le 1$, $\tau ^P_B(wx)=\min \{\tau ^P_A(w),\tau ^P_A(x)\}$ and $|deg^N(w)-deg^N(x)|\ge 1$, $\tau ^N_B(wx)=\max \{\tau ^N_A(w),\tau ^N_A(x)\}.$ That is, u dominates v in $G_1$ and w dominates x in $G_2$. Thus by Note 2.2, the vertex (u, w) dominates the vertex (v, x) in $G_1\otimes G_2$. So, $|deg^P((u,w))-deg^P((v,x))|\le 1$, $\tau ^P_{D}((u,w),(v,x))=\min \{\tau ^P_X(u,w),\tau ^P_X(v,x)\}$ and $|deg^N((u,w))-deg^N((v,x))|\ge 1$, $\tau ^N_{D}((u,w),(v,x))=\max \{\tau ^N_X(u,w),\tau ^N_X(v,x)\}$. Hence $\gamma _{e}(G_1\otimes G_2)\le \min (|S_1\times V_1|,|S_2\times V_2|).$ $\square$

Theorem 2.43

Let $S_1$ and $S_2$ be k-dominating sets of connected bipolar fuzzy graphs $G_1=( X_1, Y_1)$ and $G_2=( X_2, Y_2)$, respectively. Then

• (i) $G_1\square G_2$ is connected,

• (ii) If $S_1$ is connected, then $S_1\times V_2$ is a connected k-dominating set of $G_1\square G_2,$

• (ii) If $S_2$ is connected, then $V_1\times S_2$ is a connected k-dominating set of $G_1\square G_2.$

Proof

To prove $G_1\square G_2$ is connected. Consider any two arbitrary distinct vertices (u, w), (v, x) of $V_1\times V_2.$ Then by Definition 2.35, there exists a path between these two vertices in the following cases.

• Case (i) $u=v.$ Since $G_2$ is a connected BFG. Then there exists a path $P:w,w_1,w_2,\cdots ,x$ such that $\tau ^P_{ Y_2}(rs)>0$ and $\tau ^N_{ Y_2}(rs)<0$ for any two vertices r, s of path P. Thus $\tau ^P_{Y}((u,w),(u,x))=\min \{\tau ^P_{ X_1}(u),\tau ^P_{ Y_2}(wx)\}$ and $\tau ^N_{Y}((u,w),(u,x))=\max \{\tau ^N_{ X_1}(u),\tau ^N_{ Y_2}(wx)\}$. Therefore $P':(u,w),(u,w_1),(u,w_2),\cdots ,(u,x)$ is the path between (u, w), (v, x) in $G_1\square G_2.$

• Case (ii) $w=x.$ Since $G_1$ is a connected BFG. Then there exists a path $Q:u,u_1,u_2,\cdots ,v$ such that $\tau ^P_{ Y_1}(uv)>0$ and $\tau ^N_{ Y_1}(uv)<0$ for any two vertices r, s of path Q. Thus $\tau ^P_{Y}((u,w),(v,w))=\min \{\tau ^P_{ Y_1}(u,v),\tau ^P_{ X_2}(w)\}$ and $\tau ^N_{Y}((u,w),(v,w))=\max \{\tau ^N_{ Y_1}(u,v),\tau ^N_{ X_2}(w)\}$. Therefore $Q':(u,w),(u_1,w),(u_2,w),\cdots ,(v,w)$ is the path between (u, w), (v, x) in $G_1\square G_2.$

• Case (iii) $u\ne v$, $w\ne x.$ By Case (i), there exists a path between the vertices (u, w) and (u, x) in $G_1\square G_2.$ Also by Case (ii), there exists a path between the vertices (u, w) and (v, w) in $G_1\square G_2.$ Thus, the union of these two disjoint paths is a path between the vertices (u, w) and (v, x) in $G_1\square G_2.$

Now, if $S_1$ and $S_2$ are k-dominating sets of $G_1$ and $G_2$, respectively, then $\gamma _k(G_1\square G_2)=\min \{|S_1\times V_2|,|S_1\times V_2|\}.$ Hence $X_1\times S_2$ and $S_1\times X_2$ are k-dominating sets of $G_1\square G_2$ and the connectivity of them can be proved similarly. $\square$

Theorem 2.44

Let $G_1$ and $G_2$ be BFGs on non-empty sets $V_1$ and $V_2$, respectively. Let $S_1$ and $S_2$ be k-dominating sets of $G_1$ and $G_2$, respectively. Then,

• (1) $S_1\times V_2$ is an independent k-dominating set of $G_1\square G_2$ if and only if $S_1$ is k-independent and

  • (i) $\tau ^P_{ Y_1}(uv)<\tau ^P_{ X_2}(w)$ and $\tau ^N_{ Y_1}(uv)>\tau ^N_{ X_2}(w)$ for $u,v\in S_1, w\in V_2,$

  • (ii) $\tau ^P_{ Y_2}(wx)<\tau ^P_{ X_1}(u)$ and $\tau ^N_{ Y_2}(wx)>\tau ^N_{ X_1}(u)$ for $u\in S_1, w,x\in V_2,$

  • (iii) $\tau ^P_{ Y_2}(wx)<\min \{\tau ^P_{ X_2}(w),\tau ^P_{ X_2}(x)\}$ and $\tau ^N_{ Y_2}(wx)>\max \{\tau ^N_{ X_2}(w),\tau ^N_{ X_2}(x)\}$ for $w,x\in V_2.$

• (2) $V_1\times S_2$ is an independent k-dominating set of $G_1\square G_2$ if and only if $S_2$ is k-independent and

  • (i) $\tau ^P_{ Y_1}(uv)<\tau ^P_{ X_2}(w)$ and $\tau ^N_{ Y_1}(uv)>\tau ^N_{ X_2}(w)$ for $u,v\in V_1, w\in S_2,$

  • (ii) $\tau ^P_{ Y_2}(wx)<\tau ^P_{ X_1}(u)$ and $\tau ^N_{ Y_2}(wx)>\tau ^N_{ X_1}(u)$ for $u\in V_1, w,x\in S_2,$

  • (iii) $\tau ^P_{ Y_1}(uv)<\min \{\tau ^P_{ X_1}(u),\tau ^P_{ X_1}(v)\}$ and $\tau ^N_{ Y_1}(uv)>\max \{\tau ^N_{ X_1}(u),\tau ^N_{ X_1}(v)\}$ for $u,v\in V_1.$

Proof

To prove that every two distinct vertices (u, w), (v, x) in $S_1\times V_2$ are not adjacent. If $u=v$, then

$$\begin{aligned} \tau ^P_{Y}((u,w)(u,x))= & {} \min \{\tau ^P_{ X_1}(u),\tau ^P_{ Y_2}(wx)\}\\<&\min \{\tau ^P_{ X_1}(u),\min \{\tau ^P_{ X_2}(w),\tau ^P_{ X_2}(x)\}\}\\< & {} \min \{\tau ^P_{X}(u,w),\tau ^P_{X}(u,x)\},\\ \tau ^N_{Y}((u,w)(u,x))= & {} \max \{\tau ^N_{X_1}(u),\tau ^N_{Y_2}(wx)\}\\>&\max \{\tau ^N_{X_1}(u),\max \{\tau ^N_{X_2}(w),\tau ^N_{X_2}(x)\}\}\\> & {} \max \{\tau ^N_{X}(u,w),\tau ^N_{X}(u,x)\}. \end{aligned}$$

If $w=x$, the result is obtained by independence of u, v of $S_1.$

If $u\ne v$, $w\ne x$, then by definition we have $\tau ^P_{Y}((u,w)(v,x))=0$ and $\tau ^N_{Y}((u,w)(v,x))=0.$ Hence (u, w), (v, x) are not adjacent in $G_1\square G_2.$

Conversely, suppose (1)(iii) is false. That is, there exists vertices $y,z\in V_2$ such that $\tau ^P_{ Y_2}(yz)=\min \{\tau ^P_{ X_2}(y),\tau ^P_{ X_2}(z)\}$ and $\tau ^N_{ Y_2}(yz)=\max \{\tau ^N_{ X_2}(y),\tau ^N_{ X_2}(z)\}.$ Let $u\in S_1,$ then

$$\begin{aligned} \tau ^P_{Y}((u,y)(u,z))= & {} \min \{\tau ^P_{ X_1}(u),\tau ^P_{ Y_2}(yz)\}\\= & {} \min \{\tau ^P_{ X_1}(u),\min \{\tau ^P_{ X_2}(y),\tau ^P_{ X_2}(z)\}\}\\= & {} \min \{\tau ^P_{X}(u,y),\tau ^P_{X}(u,z)\},\\ \tau ^N_{Y}((u,y)(u,z))= & {} \max \{\tau ^N_{ X_1}(u),\tau ^N_{ Y_2}(yz)\}\\= & {} \max \{\tau ^N_{ X_1}(u),\max \{\tau ^N_{ X_2}(y),\tau ^N_{ X_2}(z)\}\}\\= & {} \max \{\tau ^N_{X}(u,y),\tau ^N_{X}(u,z)\}. \end{aligned}$$

Thus $S_1\times V_2$ is not independent. Hence (1)(iii) is true, i.e., $\tau ^P_{ Y_2}(yz)<\min \{\tau ^P_{ X_2}(y),\tau ^P_{ X_2}(z)\}$ and $\tau ^N_{ Y_2}(yz)>\max \{\tau ^N_{ X_2}(y),\tau ^N_{ X_2}(z)\}.$ Similarly (2) can be proved. $\square$

3 Applications

A graph theory is one of the most developing branch of modern mathematics. It has witnessed a magnificent growth due to a variety of applications in linguistics, combinatorial problems, optimization problems, physics, chemistry and biological sciences. Domination in graph theory has a wide range of applications in different fields, including, school bus routing, facility location problem, finding set of representatives, land surveying, coding theory and monitoring communication and electrical networks. In this section, we discuss applications of domination in BFG in a facility location problem, in the problem of finding the set of representatives and in transmission tower location problem (Fig. 12).

Fig. 12

Bipolar fuzzy graph of towns

Fig. 13

Bipolar fuzzy graph of representatives

• (1) Domination in a facility location problem

  Suppose that a provincial government has decided to build some colleges, which must serve all the towns in a province. In order to decide the location of college in a town, it is very important to analyze the educational situation in a town. The educational situation depends on many factors including availability of skilled teachers, availability of transportation, urbanization, rate of literacy, flow rate and drop out rate of students. Now the government want to locate a college in such a way that every town has a college or is a neighbor of a town which has a college, i.e., the government wants to build minimum number of colleges to save money. We can present this problem as a BFG $G=(T,R)$, where T is the bipolar fuzzy set of towns presenting the literacy rate and rate of drop out as positive and negative membership degree and R is a bipolar fuzzy set of roads between the towns. The positive degree of membership and the negative degree of membership is calculated as

  $$\begin{aligned} \tau ^P_Y(uv)\le \min \{\tau ^P_X(u), \tau ^P_X(v)\}, ~~ \tau ^N_Y(uv)\ge \max \{\tau ^N_X(u), \tau ^N_X(v)\} \end{aligned}$$

  By direct computations, it is easy to check that the minimum dominating set of a BFG is $S=\{Tonopah, Beatty, Oasis\}$. Thus the government need to build the colleges in three towns to save money and provide college facility to all towns of the province.

• (2) Domination in finding the set of representatives

  We present here a BFG model in the problem of finding the set of representatives for a youth development council in a university. We consider a group of students who wants to become a member of youth development council. Each student has some good and some bad leadership qualities. Bad leadership is characterized by lack of enthusiasm, poor communication skills, incompetency, inflexibility and poor decision making skills. A member of youth development council must be a good listener, honest and fair, good communicator and approachable. All these qualities are fuzzy. We want to form a council with as few members as possible. We seek to form a council in such a way that every member not in the council has something in common with the member in the council. Thus we have to find a minimum dominating set. This concept can be defined more precisely by using bipolar fuzzy graphs. We apply here the concept of domination in a BFG.

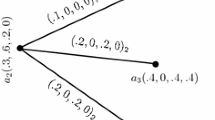
  The nodes of BFG represent the students and their leadership qualities in terms of the positive membership degree and its counter property bad leadership by a negative membership degree, e.g., Usama has 60 % leadership qualities and lacks 20 % leadership qualities. The edges of a BFG represent the common qualities between the students. The positive and negative degree of membership can be interpreted as the percentage of common leadership qualities and the qualities which are not common between the students, e.g., Usama and Aiza has 60 % qualities in common but 10 % qualities are different. From Fig. 13, it is clear that the dominating set of a BFG G is $S=\{Taha, Moez, Aiza, Mifra \}$ and it is also the minimal dominating set of G. The domination number of a BFG G is $\gamma (G)=3.05.$ Thus Taha, Aiza, Moez and Mifra are the members of a youth development council.

  We write general procedure of our method that is used in our application.

  • Step 1 Input the bipolar fuzzy vertex set X defined on V and the bipolar fuzzy edge set Y defined on E.

  • Step 2 Compute the BFG $G=(X,Y).$

  • Step 3 Find the vertices $u_i$ such that $\tau _Y^P(u_i,u_j)=\min \{\tau _X^P(u_i),\tau _X^P(u_j)\}$ and

    $\tau _Y^N(u_i,u_j)=\max \{\tau _X^N(u_i),\tau _X^N(u_j)\}$, $i\ne j.$

  • Step 4 Form the set $S_i\subseteq V$ of vertices $u_i.$

  • Step 5 If $\cup _{j}\{u_j\}=V-S_i$ then $S_i$ is a dominating set otherwise, $S_i$ is not a dominating set.

  • Step 6 Repeat the steps from 3 to 5 and find all the dominating sets $S_i$ of V.

  • Step 7 The decision is $S_i$ if $S_i$ is a minimal dominating set.

• (3) Transmission tower location problem

  Suppose that we have a collection of cities. We want to locate transmission towers in some of the cities so that the transmission can be broadcast to all cities. The selection of location of transmission tower depends on many factors including the availability of electrical power and telecommunication network connectivity, etc. Also, for the better transmission signals, it is necessary to avoid electromagnetic interferences. The strength of the transmission signal decreases as the distance between two towers increases. Since each transmission tower has a limited transmission range, so we have to locate several transmission towers so that the transmission can reach to each city. But transmission towers are costly. Therefore we want to locate as few transmission towers as possible (Fig. 14).

Fig. 14

Bipolar fuzzy graph of cities

This problem can be modeled by using a BFG. Let the vertices of a BFG represent the cities. The positive and the negative membership degree of the vertices can be interpreted as the availability of electrical power and electromagnetic interferences respectively, e.g., Washington has 50 % availability of electrical power and 40 % electromagnetic interferences. The edge between two cities indicates that a transmission from a tower at one of these cities reach the other. The positive and the negative membership degree of the edges represent the transmission strength and transmission range respectively. Now, we want to find minimum number of towers so that each city either has a tower or is a neighbor of a city that has a tower. This is equivalent to find a minimum dominating set of locations that covers all the cities. By routine calculations, it is easy to see that the minimum dominating set is $S=\{Flemington, Newark, Millville, Camden\}$. Thus it is sufficient to place the transmission towers at these four cities for better transmission coverage and minimum cost.

We present our method as an algorithm that is used in our applications.

4 Conclusion

A bipolar fuzzy graph, a generalization of a fuzzy graph, is useful for handling bipolar information and uncertainty. In this paper, we have presented the concept of certain domination in bipolar fuzzy graphs. We have also discussed the applications of domination in bipolar fuzzy graphs in facility location problem and in the problem of finding the set of representatives. We are extending our work to (i) Domination in bipolar fuzzy hypergraphs, (ii) Bipolar fuzzy soft hypergraphs and (iii) Roughness in bipolar fuzzy graphs.