Certain types of fuzzy sets in a fuzzy graph

Abstract

In this paper, we introduce certain types of fuzzy sets in a fuzzy graph including fuzzy dominating set, fuzzy minimal dominating set, fuzzy independent dominating set and fuzzy irredundant set. We describe these concepts with examples and develop the relationship between them. We also describe some interesting properties of fuzzy dominating set, fuzzy minimal dominating set, fuzzy independent dominating set and fuzzy irredundant set.

1 Introduction

Graph theory has numerous applications to problems in computer science, electrical engineering, system analysis, operations research, economics, networking routing, and transportation. However, in many cases, some aspects of a graph-theoretic problem may be uncertain. For example, the vehicle travel time or vehicle capacity on a road network may not be known exactly. In such cases, it is natural to deal with the uncertainty using the methods of fuzzy sets and fuzzy logic. A (crisp) set $A$ in a universe $X$ can be defined in the form of its characteristic function $\mu _A : X \rightarrow \{0, 1\}$ yielding the value 1 for elements belonging to the set $A$ and the value 0 for elements excluded from the set $A$. The most of the generalization of the crisp set have been introduced on the unit interval $[0,1]$ and they are consistent with the asymmetry observation. In other words, the generalization of the crisp set to fuzzy sets [26] relied on spreading positive information that fit the crisp point $\{1 \}$ into the interval $[0, 1]$. The theory of fuzzy sets has become a vigorous area of research in different disciplines including medical and life sciences, management sciences, social sciences, engineering, statistics, graph theory, artificial intelligence, signal processing, multiagent systems, pattern recognition, robotics, computer networks, expert systems, decision making and automata theory. There have been several generalizations of this fundamental concept including intuitionistic fuzzy sets, soft sets, rough sets, and interval-valued fuzzy sets. Applications of these generalizations have been discussed in [22–25].

Fuzzy graph theory is finding an increasing number of applications in modeling real time systems where the level of information inherent in the system varies with different levels of precision. Fuzzy models are becoming useful because of their aim in reducing the differences between the traditional numerical models used in engineering and sciences and the symbolic models used in expert systems. In 1975, Rosenfeld [20] discussed the concept of fuzzy graphs whose basic idea was introduced by Kauffmann [11] in 1973. The fuzzy relations between fuzzy sets were also considered by Rosenfeld and he developed the structure of fuzzy graphs, obtaining analogs of several graph theoretical concepts. Bhattacharya [7] gave some remarks on fuzzy graphs, and some operations on fuzzy graphs were introduced by Mordeson and Peng [12]. Bollobas and Cocakyne [6] generalized the properties of dominating and independent dominating sets in graphs. Somasundram and Somasundaram [21] discussed domination in fuzzy graph. They defined domination using effective edges in fuzzy graph. Nagoorgani and Chandrasekaran [13] discussed domination in fuzzy graph using strong arcs. Nagoorgani and Vadivel [14, 15] discussed fuzzy independent dominating sets and irredundant sets. Akram et al. [1–4] introduced many new concepts, including bipolar fuzzy graphs, complete interval-valued fuzzy graphs, strong intuitionistic fuzzy graphs and intuitionistic fuzzy hypergraphs. Rashmanlou et al. [17–19] studied certain types of interval-valued fuzzy graphs. In this paper, we concern with relations between the parameters fuzzy minimum dominating set, fuzzy independent dominating set and fuzzy irredundant set briefly. We have used standard definitions and terminologies in this paper.

2 Preliminaries

A fuzzy subset of a nonempty set $V$ is a mapping $\sigma : V \rightarrow [0,1]$. A fuzzy relation on $V$ is a fuzzy subset of $V \times V$. A fuzzy graph $G (\sigma , \mu )$ is a pair of function $\sigma : V \rightarrow [0,1]$ and $\mu : V \times V \rightarrow [0,1]$, where $\mu (u, v) \le \sigma (u) \wedge \sigma (v)$ for all $u$, $v \in V$. The underlying crisp graph of $G(\sigma ,\mu )$ is denoted by $G^*(V,E)$, where $V= \{u \in V: \sigma (u) > 0 \}$ and $E = \{(u, v)\in V \times V: \mu (u, v)>0 \}$. The order $p$ and size $q$ of fuzzy graph $G(\sigma ,\mu )$ are defined by $p = \sum _{v\in V} \sigma (v)$ and q = $\sum _{(u,v) \in E} \mu (u, v)$. The graph $G(\sigma , \mu )$ is denoted by $G$, if unless otherwise mentioned. The strength of connectedness between two nodes $u$, $v$ in a fuzzy graph $G$ is $u^\infty (u, v) = \sup \{\mu ^k k(u, v): k= 1, 2, 3, \ldots \}$ where $\{\mu ^k(u, v) = \sup \{ (u,u_1) \wedge \mu (u_1, u_2) \wedge \cdots \wedge (u_{k-1}, v)\}$. An arc $(u, v)$ is said to be a strong arc if $\mu (u, v) \ge \mu ^\infty (u, v)$ and the node $v$ is said to be a strong neighbor of $u$. If $\mu$(u, v) = 0 for every $v\in V$, then $u$ is called isolated node.

Let u be a node in fuzzy graph G then N (u) = {v: (u, v) is a strong arc} is called neighborhood of u and N[u] = N(u)$\cup$ {u} is called closed neighborhood of u. Neighborhood degree of the node is defined by the sum of the weights of the strong neighbor node of u and is denoted by $d_N$ (u) = $\sum _{v \in N(u)} \sigma$ (v). Minimum neighborhood degree of a fuzzy graph G is defined by $\delta _N(G)$= min$d_N$(u) : u $\in$ V(G) and maximum neighborhood degree of G is by $\Delta _N$(G) = max{$d_N$(u) : $u \in V$(G)}.

Notations used

$G(\sigma , \mu)$ :

Fuzzy graph

$G*(V,E)$ :

Crisp graph

$\wedge$ :

Minimum cardinality

$p$ :

Order of G

q :

Size of G

$\mu ^\infty (u, v)$ :

Strength of connectedness between u and v

$N(u)$ :

Neighborhood of u

$N[u]$ :

Closed neighborhood of u

$d_N(u)$ :

Neighborhood degree of u

$\delta _N(G)$ :

Minimum neighborhood degree of G

$\Delta _N(G)$ :

Maximum degree neighborhood of G

$D$ :

Fuzzy dominating set G

$y(G)$ :

Domination number

$i(G)$ :

Independent domination number

$p_n [u,S]$ :

Private neighborhood of $u \epsilon S$

ir(G):

Irredundant set of G

$y^+$ :

Critical node on deletion increase the domination number

3 Fuzzy dominating set

We recollect some necessary definitions.

Definition 3.1

Let $G$ be a fuzzy graph and Let $u$, $v\in V(G^*)$ then $u$ dominates $v$ if $(u,v)$ is a strong arc.

Definition 3.2

Let $G =( \sigma , \mu )$ be a fuzzy graph. A subset $D$ of $V$ is said to be fuzzy dominating set of $G$, if for every $v \in V - D$ there exists $u\in D$ such that $u$ dominates $v$.

Definition 3.3

A fuzzy dominating set $D$ of a fuzzy graph $G$ is called minimal fuzzy dominating set of $G$, if for every node $v \in D$, $D-\{v\}$ is not a fuzzy dominating set.

Minimum cardinalities taken over all dominating set is the minimum dominating set and its domination number is $y(G)$.

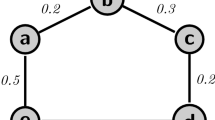
Example 3.4

Consider a fuzzy graph. From Fig. 1, we have $D = \{v, y\}$; $\gamma (G)$ = 0.5.

Fig. 1

Fuzzy graph

4 Fuzzy independent set

We review here some basic definitions of fuzzy independent sets.

Definition 4.1

Let $G(\sigma , \mu )$ be a fuzzy graph. Two nodes in a fuzzy graph $G$ are said to be fuzzy independent if there is no strong arc between them. A subset $S$ of $V$ is said to be fuzzy independent set for $G$ if every two nodes of $S$ are fuzzy independent. Minimum cardinalities taken over all fuzzy independent set is called independence number denoted by $i (G)$.

Example 4.2

In Fig.1 , $S = \{ v, z\}$ and its cardinality is 0.6.

Definition 4.3

Let $G(\sigma , \mu )$ be a fuzzy graph. A fuzzy independent set $S$ of $G$ is said to be maximal fuzzy independent set if there is no fuzzy independent set whose cardinality is greater than the cardinality of $S$. The maximum cardinality among all maximal fuzzy independent set is called fuzzy independence number of $G$ and it is denoted by $\beta$(G).

5 Fuzzy graphs with equal domination number and independent number

In this section, it has been discussed briefly when the minimum domination number and independent domination number will be equal for different types of fuzzy graphs and some comparison with crisp graph also discussed.

Proposition 5.1

Let $G(\sigma , \mu$) be a fuzzy graph. Let $D$ be a dominating set with the domination number $y(G)$ and $i(G)$ denote the independent domination number. Then clearly $y(G) \le i(G)$.

Example 5.2

Consider a fuzzy graph.

From Fig. 2, we see that $\sigma (G) =\sigma (v_3) + \sigma (v_2)$ = 0.3 + 0.2 = 0.5; $i(G)$ = 0.4 + 0.2 = 0.6 and $y(G) \le i ( G)$.

Fig. 2

Fuzzy tree

Definition 5.3

The maximum strength of all he paths in $G$ from $(x,y)$ is called $\mathrm{CONN}_G (x,y)$. A fuzzy graph G is connected if $\mathrm{CONN}_G (x,y) > 0$ for every $x$, $y \in V(G^*)$.

Definition 5.4

A node $z \in V(G)$ is called a fuzzy cut node in $G$ if in the fuzzy graph $G-Z$ obtained from $G$ by replacing $\sigma (Z)$ by 0, we have $\mathrm{CONN}_{G--Z} (x,y) < \mathrm{CONN}_{G}(x,y)$ for every $x$, $y\in V(G^*)$.

Definition 5.5

Let $G(\sigma , \mu )$ be a fuzzy graph such that $G^*(V,E)$ is a cycle. Then $G$ is a fuzzy cycle if and only if there does not exist a unique arc $(x,y)$ such that $\mu (x,y) = \wedge \{ \mu (u,v):(u,v) > 0 \}.$

Theorem 5.6

Let $G =(\sigma , \mu )$ be a fuzzy graph. Let $D$ be a minimum dominating set with the domination number $y(G)$. The subgraph $<D>$ induced by $D$ has isolated nodes, i.e., $\mu (u, v)$ = 0 for all $u$, $v \in D$ then $y(G) = i(G)$ where $i(G)$ denotes the independent domination number.

Proof

It is clear from the definition that the minimum dominating set $D$ is the smallest dominating set among all minimal dominating sets. Since the subgraph induced with the nodes of $D$ are isolated implies that they are independent. Hence $y(G) = i(G)$. In comparing to the crisp case, $y(G) = i(G)$ if the graph $G$ is claw free but that is not required for fuzzy graph. $\square$

Example 5.7

The concept of the above theorem is explained in the following Fig. 3.

From Fig. 3, we have $\gamma (G)$= $U_1 +U_3 +U_5$ = 0.2 + 0.1 + 0.1 = 0.4 = $i(G)$. But in crisp case $y (G)$ = 2 and $i(G)$ =3.

Fig. 3

Simple fuzzy graph

Corollary 5.8

If $G(\sigma , \mu )$ is a complete fuzzy graph then $i(G) < y(G)$.

Proof

Since $G$ is a complete fuzzy graph every arc in $G$ is a strong arc. Hence $i(G)$ = 0 and $y(G) = \wedge \{\sigma (v);$ for all $v \in V\}$ and $i(G)$=0. It is clear that $i(G)< y(G)$. $\square$

Theorem 5.9

Let $G(\sigma , \mu )$ be a fuzzy graph. Let $D$ be a fuzzy dominating set with domination number $y(G)$ and $i(G)$ is the independent dominating set. If the subgraph $<D>$ induced by $D$ has some arcs between the nodes in $D$. Then $y(G) = i(G)$ if the arcs between any two nodes in $D$ must have a fuzzy cycle with nodes in $V-D$ containing a fuzzy cut node.

Proof

Given that all the nodes in the subgraph induced by $<D>$ does not have isolated nodes. Some nodes in $D$ are connected. Assume the contrary that if the arcs between any two nodes in $D$ do not have a fuzzy cycle with nodes in $V-D$ containing fuzzy cut node. Then the arcs between those two nodes will be a strong arc and they cannot be independent. Therefore we get $y(G) \ne i(G)$. Hence it is proved. $\square$

Definition 5.10

Let $G(\sigma , \mu )$ be a fuzzy graph. The fuzzy graph $G$ is fuzzy domination perfect if $y(H) = i(H)$ for every induced subgraph $H$ of $G$.

Theorem 5.11

Let $G(\sigma , \mu )$ be fuzzy graph. Let $D$ be be a dominating set with domination number $y(G)$ and $i(G)$ is the independent dominating set. Then $G$ is said to be fuzzy domination perfect if it satisfies the following conditions

• (i) The subgraph $<D>$ induced by $D$ has isolated nodes,i.e., $\mu (u, v)$ = 0 for all $u$,$v \in D$.

• (ii) $G$ does not have a fuzzy cycle containing fuzzy cut node in it.

Proof

If the condition (i) is true then by theorem 5.3 we know $y(G)$= $i(G)$, i.e., the domination number and independent domination number are equal. To prove $G$ is fuzzy domination perfect we have to prove the condition (ii). Assume the contrary that G has a fuzzy cycle having fuzzy cut node in it. Then $y(G)$ and $i(G)$ differs for the induced subgraph containing the fuzzy cycle. Hence it cannot be domination perfect. So $G$ cannot have a fuzzy cycle. $\square$

Example 5.12

Consider a fuzzy graph.

In this Fig. 4, we note that $y(G)$= 0.3 + 0.2 = 0.5; $i (G)$ = 0.3 + 0.2 = 0.5. Since the arc between 0.3 and 0.2 is not strong arc.

Fig. 4

Connected fuzzy graph

Definition 5.13

Let $u$ be a node in fuzzy graph $G$ then $N (u) = \{v : (u, v)$ is a strong arc $\}$ is called neighborhood of $u$ and $N[u] =N(u)\cup \{u\}$ is called closed neighborhood of $u$. Neighborhood degree of the node is defined by the sum of the weights of the strong neighbor node of $u$ and is denoted by $d_N (u) = \sum _{V \in N(u)} \sigma (v).$

Theorem 5.14

Let $G(\sigma , \mu )$ be connected fuzzy graph which does not have an induced fuzzy cycle subgraph. Let $D$ be a minimum dominating set with domination number $y(G)$ . Then $i(G) = \beta (Y) + \sum _{u \in D - Y} d (N(U))$ where $Y$ is maximal independent set of $D$.

Example 5.15

Consider a fuzzy graph.

From this Fig. 5, we have $y(G)$ = 0.2 + 0.3 + 0.1 = 0.6 ; $i(G)$ = 0.2 + 0.1 + 0.4 = 0.7.

Fig. 5

Fuzzy graph

6 Fuzzy irredundant set

Definition 6.1

Let $G(\sigma , \mu )$ be a fuzzy graph and $S$ be a set of nodes. A node $v$ is said to be fuzzy private neighbor of $u \in S$ with respect to $S$, if $N[v]\cap S = \{u\}$. Further more, we define fuzzy private neighborhood of $u\in S$ with respect to $S$ to be $p_n$ $[u,S] = \{v:N[v] \cap S= \{u\}\}.$

In other words, $p_n [u,S] = N [u] - N [S- \{u\}].$

Note 6.1

If $u \in p_n[u,S]$, then $u$ is an isolated node in $< S >.$

Definition 6.2

Let $G(\sigma , \mu )$ be a fuzzy graph. A node $u$ in $S$ is a subset of $V$ is said to be fuzzy redundant node if $p_n [u,S] = \psi$ . Equivalently, $u$ is redundant in $S$ if $N[V] \subseteq N [S \{u\}].$ otherwise, $u$ is said to be fuzzy irredundant node.

Example 6.3

Consider a fuzzy graph.

From Fig. 6, we see that if $S = \{Y_3, Y_6, Y_5\}; N[Y_3] = \{Y_3, Y_1, Y_2, Y_4, Y_5\}$

Fig. 6

Fuzzy graph

$N[Y_5] = \{Y_5, Y_3, Y_7\}$ ; $N[Y_6] = \{Y_7, Y_4\}.$

Also, $p_n [Y_i , S] = \psi$ ; i=3, 6, 5; Hence $S$ is a redundant set.

Definition 6.4

Let $G(\sigma , \mu )$ be a fuzzy graph. A set $S$ is said to be fuzzy irredundant set if $p_n [u,S] \ne \phi$ for every node in $S$.

Definition 6.5

A fuzzy irredundant set $S$ is maximal fuzzy irredundant set if for every node $v \in V-S$ the set $S\cup \{v\}$ is not fuzzy irredundant set which means that there exists at least one node $w\in S \cup \{u\}$ which does not have a private neighbor.

Example 6.6

consider a fuzzy graph.

By Routine calculation, we have from Fig. 7 $ir (G)$ = 0.1 + 0.2 + 0.3 + 0.4 =1.0.

Fig. 7

Connected fuzzy graph

7 Relations between fuzzy dominating set and fuzzy irredundant set

In this section we introduce the theorems relating $y(G)$ and $ir(G)$.

Definition 7.1

Let $G(\sigma , \mu )$ be a fuzzy graph. A node $v \in D$, i.e., the dominating set is called a $Y^+$ critical node if the deletion of the node in $G$ increases the domination number.

Corollary 7.2

Let $G(\sigma , \mu )$ be a fuzzy graph. Every fuzzy minimal dominating set is a fuzzy dominating set but the converse is not true.

Theorem 7.3

Let $G(\sigma , \mu )$ be a fuzzy graph. A fuzzy dominating set in $G$ is a minimal dominating set if and only if it is fuzzy dominating and fuzzy irredundant set.

Proof

Assume $S$ is a fuzzy minimal dominating set in $G$. Clearly, it is dominating, so we have to prove it is irredundant. By definition 3.3 it implies for every node $v \in S$ there exists a node $y V-(S-\{v\})$ which is not dominated by $S-\{v\}$ that is $y$ is a private neighbor of node $u$. Hence for every node $v \in S$, $p_n[v, S] \ne \phi$ hat is every node in $S$ has at least one private neighbor. Hence $S$ is irredundant.

Conversely, $S$ is fuzzy dominating and irredundant set. Suppose that $S$ is not minimal dominating then there exists a node $v \in S$ such that $S-\{v\}$ is dominating. Since $S$ is irredundant $p_n[v,S]\ne \phi$. Let $w \in p_n [v,S]$ by private neighborhod definition $w$ is not adjacent to any node in $S-\{v\}$, that is, $S-\{v\}$ is not fuzzy dominating set which contradicts. $\square$

Example 7.4

Consider a fuzzy graph.

The cardinality of minimal dominating set from Fig. 8 is 0.4 + 0.2 + 0.3 = 0.9 = $ir (G).$

Fig. 8

Simple fuzzy graph

Theorem 7.5

Let $G(\sigma , \mu )$ be a fuzzy graph. Every minimal dominating set in $G$ is a maximal irredundant set.

Proof

By theorem 7.3 every minimal dominating set $S$ in $G$ is both dominating and irredundant. It remains to show that $S$ is maximal irredundant. Assume the contrary $S$ is not maximal irredundant set. By definition 6.5 there exists a node $u \in V-S$ for which $S \cup \{u\}$ is irredundant. It implies that $p_n[u, S \cup \{u\}] \ne$ that is there exists at least one node $w$ which is a private neighbor of $u$ with respect to $S \cup \{u\}$. This means that no node in $S$ is adjacent to $w$, showing that $S$ is not a dominating set contradicts our assumption. $\square$

In the following theorem we exhibit that on what condition in a fuzzy graph the set of nodes $\cup$ not dominated by a maximal irredundant set $S$.

Theorem 7.6

Let $G(\sigma , \mu$) be a fuzzy graph. Suppose that a node $u$ is not dominated by the maximal irredundant set $S$. Then for some $v\in S$.

• (i) $p_n[v, S] \subseteq N(u)$ and

• (ii) for $v_1, v_2 \in p_n[v, S]$ such that $v_1 \ne v_2$, then either $v_1 v_2 \mu (v_1, v_2)$ or for i= 1, 2 there exists $y_i \in S - \{v\}$ such that $x_i$ is adjacent to each node of $p_n [y_i, S]$.

Proof

Let $G(\sigma , \mu )$ be a fuzzy graph. Let $S\subseteq V$ is maximal fuzzy irredundant set. Then by definition 6.5 for some node $u \in V -S$, $S \cup \{u\}$ is a redundant set. Since $u$ is not dominated by $S$, $u \in p_n[u, S \cup \{u\}]$. Hence some $v \in S$ is redundant in $S \cup \{u\}$. Therefore, $N[v] \subseteq N[S-v] \cup N[u]$ and therefore,$p_n[v, S]$ = $N[v]-N[S-v]\subseteq N[u]$. Hence result (i) follows since $u$ does not belongs to $p_n[v,S]$.

Let $v_1, v_2$ be elements of $p_n[v,S]$ such that $e = v_1 v_2$ is not an arc and without loss of generality for all $w_i \in S - \{v\}$, there exists $Z_i \in p_n [w_i , S]$ such that $v_1 z_i$ is not an arc. $\square$

Consider the {$v_1$} $\cup S$, then we infer that $v_2 \in p_n [v, \{v_1\} \cup S]$ $u \in p_n [v_1, \{v_1\} \cup S ].$ And $z \in p_n [w_i, \{v_1\} S ]$ for each $w_i$ $S - \{v\}$.

Theorem 7.7

For any fuzzy graph $G(\sigma , \mu )$, $y(G)$ and $ir(G)$ denote the minimum domination number and irredundant number, respectively. Then $y(G) \le ir(G)$.

Proof

By corollary 7.2, it means minimum dominating set need not be a minimal dominating set. That is it need not be a maximal irredundant by corollary 7.2. Due to its minimum property the cardinality of minimum dominating set is less than the irredundant set. Hence $y(G) \le ir(G)$. $\square$

We now impose some condition on the dominating set to equal the maximal irredundant set.

Theorem 7.8

Let $G(\sigma , \mu$) be a fuzzy graph. Let $D$ be a minimum dominating set with domination number $y(G)$. Let $S$ be fuzzy maximal irredundant set with irredundant number $ir(G)$. If every node in $D$ is a $y^{+}$ critical node, then $y (G) = ir(G)$.

Proof

Let $G(\sigma , \mu )$ be a fuzzy graph and let $D$ be a minimum dominating set with domination number $y(G)$. If every node in $D$ is a $y^+$ critical node by it has at least one private neighborhood. Then by definition 6.4 every irredundant set has at least one private neighbor. Since $D$ is minimum the domination number and irredundant number are equal. It means $y(G) = ir(G)$. $\square$

Example 7.9

Consider a fuzzy graph.

From Fig. 9, we have $y(G) = ir(G)$ = 0.4 + 0.5 = 0.9.

Fig. 9

Connected fuzzy graph

Finally, we arrive at the relations between the parameters regarding the domination number, independence number and irredundance number. We infer that how the graph theoretical concepts are applied in fuzzy graphs and further its application can be extended.

8 Conclusions

Theoretical concepts of graphs are highly utilized by computer science applications. Especially in research areas of computer science such as data mining, image segmentation, clustering, image capturing and networking. The concept of fuzzy graph finds a lot of application in mathematical modeling. Domination has a wide range of application in every field. In this paper it has been discussed how to manage the domination number for several types of fuzzy graph. Later, the comparisons of the domination number with independent and irredundant fuzzy graphs are also discussed. The concept of fuzzy graphs can be applied in various areas of engineering and computer science. We plan to extend our research work to (1) domination in soft graphs, (2) domination in rough graphs, (3) domination in fuzzy hypergraphs, and (4) domination in fuzzy soft graphs.