Keywords

1 Introduction

In the design of decision making system, to evaluate objectives comprehensively and objectively, we need to evaluate and assess each attribute of the objective. When making decisions between different objectives, it is necessary to compare the similar attributes, and to clarify the correlation between multiple attributes. The decision-making problem that considers multiple attributes at the same time is called the multiple attribute decision making (MADM) problem, which is a hot issue in the current decision support system research.

When the target thing has uncertain properties, fuzzy mathematics is used as a tool to describe the uncertainty of things, where any attribute has positive and negative effects on things. In fuzzy set theory, positive and negative membership functions are used to characterize positive and negative uncertainties, respectively. When it is necessary to describe the uncertain relationship between things, then the bipolar fuzzy graphs are introduced into fuzzy theory to deal with structured data with double-sided uncertainty information. The so-called structured data means that there is a certain connection between the data, and the graph model just describes this interrelated nature (see [1,2,3,4,5,6,7,8]).

The main contribution of this paper is to propose the bipolar picture fuzzy graph based multiple attribute decision making algorithm. The organization of the reminder paper is listed as follows. We first give some basic concepts and notations, then we present the main algorithm and an example is obtained to explain how to deal with a specific MADM problem using bipolar picture fuzzy graph model.

2 Preliminary

ThE main purpose of this section is to present the terminologies and notations in bipolar picture fuzzy graph setting.

Let V be a universal set. The set

$$ A = \{ (v,\mu_{A}^{P} (v),\nu_{A}^{P} (v),\iota_{A}^{P} (v),\mu_{A}^{N} (v),\nu_{A}^{N} (v),\iota_{A}^{N} (v)):v \in V\} $$

is a bipolar picture fuzzy set on V if maps \(\mu_{A}^{P} :V \to [0,1]\), \(\nu_{A}^{P} :V \to [0,1]\), \(\iota_{A}^{P} :V \to [0,1]\), \(\mu_{A}^{N} :V \to [ - 1,0]\), \(\nu_{A}^{N} :V \to [ - 1,0]\) and \(\iota_{A}^{N} :V \to [ - 1,0]\) satisfy that \(\mu_{A}^{P} (v) + \nu_{A}^{P} (v) + \iota_{A}^{P} (v) \le 1\) and \(\mu_{A}^{N} (v) + \nu_{A}^{N} (v) + \iota_{A}^{N} (v) \ge - 1\) for any \(v \in V\).

Let \(A_{1} = \{ (v,\mu_{{A_{1} }}^{P} (v),\nu_{{A_{1} }}^{P} (v),\iota_{{A_{1} }}^{P} (v),\mu_{{A_{1} }}^{N} (v),\nu_{{A_{1} }}^{N} (v),\iota_{{A_{1} }}^{N} (v)):v \in V\}\) and \(A_{2} =\) \(\{ (v,\mu_{{A_{2} }}^{P} (v),\nu_{{A_{2} }}^{P} (v),\iota_{{A_{2} }}^{P} (v),\mu_{{A_{2} }}^{N} (v),\nu_{{A_{2} }}^{N} (v),\iota_{{A_{2} }}^{N} (v)):v \in V\}\) be two bipolar picture fuzzy sets on V. Then, the union and intersection of \(A_{1}\) and \(A_{2}\) are denoted by

$$ \begin{aligned} A_{1} \cup A_{2} = & \{ (v,\mu_{{A_{1} }}^{P} (v) \vee \mu_{{A_{2} }}^{P} (v),\nu_{{A_{1} }}^{P} (v) \vee \nu_{{A_{2} }}^{P} (v),\iota_{{A_{1} }}^{P} (v) \vee \iota_{{A_{2} }}^{P} (v), \\ & \mu_{{A_{1} }}^{N} (v) \wedge \mu_{{A_{2} }}^{N} (v),\nu_{{A_{1} }}^{N} (v) \wedge \nu_{{A_{2} }}^{N} (v),\iota_{{A_{1} }}^{N} (v) \wedge \iota_{{A_{2} }}^{N} (v)):v \in V\} , \\ \end{aligned} $$
$$ \begin{aligned} A_{1} \cap A_{2} = & \{ (v,\mu_{{A_{1} }}^{P} (v) \wedge \mu_{{A_{2} }}^{P} (v),\nu_{{A_{1} }}^{P} (v) \wedge \nu_{{A_{2} }}^{P} (v),\iota_{{A_{1} }}^{P} (v) \wedge \iota_{{A_{2} }}^{P} (v), \\ & \mu_{{A_{1} }}^{N} (v) \vee \mu_{{A_{2} }}^{N} (v),\nu_{{A_{1} }}^{N} (v) \vee \nu_{{A_{2} }}^{N} (v),\iota_{{A_{1} }}^{N} (v) \vee \iota_{{A_{2} }}^{N} (v)):v \in V\} . \\ \end{aligned} $$

A mapping \(B = (\mu_{B}^{P} (v,v^{\prime}),\nu_{B}^{P} (v,v^{\prime}),\iota_{B}^{P} (v,v^{\prime}),\mu_{B}^{N} (v,v^{\prime}),\nu_{B}^{N} (v,v^{\prime}),\iota_{B}^{N} (v,v^{\prime}))\) is a bipolar picture fuzzy relation on \(V \times V\) if \(\nu_{B}^{P} (v,v^{\prime}) \in [0,1]\),\(\mu_{B}^{P} (v,v^{\prime}) \in [0,1]\), \(\iota_{B}^{P} (v,v^{\prime}) \in [0,1]\),\(\mu_{B}^{N} (v,v^{\prime}) \in [ - 1,0]\), \(\nu_{B}^{N} (v,v^{\prime}) \in [ - 1,0]\),\(\iota_{B}^{N} (v,v^{\prime}) \in [ - 1,0]\), and \(\mu_{B}^{P} (v,v^{\prime}) + \nu_{B}^{P} (v,v^{\prime}) + \iota_{B}^{P} (v,v^{\prime}) \le 1\), \(\mu_{B}^{N} (v,v^{\prime}) + \nu_{B}^{N} (v,v^{\prime}) + \iota_{B}^{N} (v,v^{\prime}) \ge - 1\) for any \((v,v^{\prime}) \in V \times V\).

The bipolar picture fuzzy graphs are defined as follows. If \(A = \{ (v,\mu_{A}^{P} (v),\) \(\nu_{A}^{P} (v),\iota_{A}^{P} (v),\mu_{A}^{N} (v),\nu_{A}^{N} (v),\iota_{A}^{N} (v)):v \in V\}\) is a bipolar picture fuzzy set on an underlying set V and \(B = (\mu_{B}^{P} (v,v^{\prime}),\nu_{B}^{P} (v,v^{\prime}),\iota_{B}^{P} (v,v^{\prime}),\mu_{B}^{N} (v,v^{\prime}),\nu_{B}^{N} (v,v^{\prime}),\) \(\iota_{B}^{N} (v,v^{\prime}))\) is a bipolar picture fuzzy set on \(\tilde{V}^{2}\) where

$$ \begin{array}{*{20}l} {\mu_{B}^{P} (v,v^{\prime}) \le min\{ \mu_{A}^{P} (v),\mu_{A}^{P} (v^{\prime})\} ,} \hfill \\ {\nu_{B}^{P} (v,v^{\prime}) \ge \max \{ \nu_{A}^{P} (v),\nu_{A}^{P} (v^{\prime})\} ,} \hfill \\ {\iota_{B}^{P} (v,v^{\prime}) \ge \max \{ \iota_{A}^{P} (v),\iota_{A}^{P} (v^{\prime})\} ,} \hfill \\ {\mu_{B}^{N} (v,v^{\prime}) \ge \max \{ \mu_{A}^{N} (v),\mu_{A}^{N} (v^{\prime})\} ,} \hfill \\ {\nu_{B}^{N} (v,v^{\prime}) \le \min \{ \nu_{A}^{N} (v),\nu_{A}^{N} (v^{\prime})\} ,} \hfill \\ {\iota_{B}^{N} (v,v^{\prime}) \le \min \{ \iota_{A}^{N} (v),\iota_{A}^{N} (v^{\prime})\} ,} \hfill \\ \end{array} $$

for any \((v,v^{\prime}) \in \tilde{V}^{2}\), and \(\mu_{B}^{P} (v,v^{\prime}) = \nu_{B}^{P} (v,v^{\prime}) = \iota_{B}^{P} (v,v^{\prime}) = \mu_{B}^{N} (v,v^{\prime}) = \nu_{B}^{N} (v,v^{\prime})\) \(= \iota_{B}^{N} (v,v^{\prime}) = 0\) for any \((v,v^{\prime}) \in \tilde{V}^{2} - E\), then \(G = (V,A,B)\) is a bipolar picture fuzzy graph (in short, is called BPFG) of the graph \(G* = (V,E)\).

3 Bipolar Picture Fuzzy Graph-Based MADM Algorithm

The main purpose of this section is to present the bipolar picture fuzzy graph-based multiple attribute decision making algorithm.

Let \(A = \{ A_{1} , \cdots ,A_{m} \}\) be the set of alternatives, \(C = \{ C_{1} , \cdots ,C_{n} \}\) be the set of attributes, and \(w^{P} = \{ w_{1}^{P} , \cdots ,w_{n}^{P} \}\) and \(w^{N} = \{ w_{1}^{N} , \cdots ,w_{n}^{N} \}\) be the set of positive weight vector and negative weight vector for the attributes \(C_{i}\) (\(i \in \{ 1, \cdots ,n\}\)) respectively, where \(w_{i}^{P} \ge 0\), \(w_{i}^{N} \le 0\), \(\sum\limits_{i = 1}^{n} {w_{i}^{P} } = 1\) and \(\sum\limits_{i = 1}^{n} {w_{i}^{N} } = - 1\). Let \(M = [b_{ij} ]_{m \times n}\) \(= [\mu_{ij}^{P} ,\nu_{ij}^{P} ,\iota_{ij}^{P} ,\mu_{ij}^{N} ,\nu_{ij}^{N} ,\iota_{ij}^{N} ]_{m \times n}\) be a bipolar picture fuzzy decision matrix, where \(\mu_{ij}^{P} \in [0,1]\), \(\nu_{ij}^{P} \in [0,1]\), \(\iota_{ij}^{P} \in [0,1]\), \(\mu_{ij}^{N} \in [ - 1,0]\), \(\nu_{ij}^{N} \in [ - 1,0]\), \(\iota_{ij}^{N} \in [ - 1,0]\) are for alternative \(A_{i}\) and attribute \(C_{j}\), and \(0 \le \mu_{ij}^{P} + \nu_{ij}^{P} + \iota_{ij}^{P} \le 1\), \(- 1 \le \mu_{ij}^{N} + \nu_{ij}^{N} + \iota_{ij}^{N} \le 0\) for \(i \in \{ 1, \cdots ,m\}\). The bipolar picture fuzzy relation between two attributes \(C_{i} = (\mu_{i}^{P} ,\nu_{i}^{P} ,\iota_{i}^{P} ,\mu_{i}^{N} ,\nu_{i}^{N} ,\iota_{i}^{N} )\) and \(C_{j} = (\mu_{j}^{P} ,\nu_{j}^{P} ,\iota_{j}^{P} ,\mu_{j}^{N} ,\nu_{j}^{N} ,\iota_{j}^{N} )\) is defined by \(f_{ij} = (\mu_{ij}^{P} ,\nu_{ij}^{P} ,\iota_{ij}^{P} ,\mu_{ij}^{N} ,\nu_{ij}^{N} ,\iota_{ij}^{N} )\), where \(\mu_{ij}^{P} \le \mu_{j}^{P} \wedge \mu_{j}^{P}\), \(\nu_{ij}^{P} \ge \nu_{j}^{P} \vee \nu_{j}^{P}\), \(\iota_{ij}^{P} \ge \iota_{j}^{P} \vee \iota_{j}^{P}\), \(\mu_{ij}^{N} \ge \mu_{j}^{N} \vee \mu_{j}^{N}\),\(\nu_{ij}^{N} \le \nu_{j}^{N} \wedge \nu_{j}^{N}\) and \(\iota_{ij}^{N} \le \iota_{j}^{N} \wedge \iota_{j}^{N}\) for \(i,j \in \{ 1, \cdots ,n\}\). Otherwise, \(f_{ij} = (0,0,1,0,0, - 1)\).

We raise two bipolar picture fuzzy graph based algorithm for multiple attribute decision making problem below.

Algorithm A.

Calculate the optimal alternative

A1: Determine the bipolar impact coefficient between attributes \(C_{i} = (\mu_{i}^{P} ,\nu_{i}^{P} ,\iota_{i}^{P} ,\mu_{i}^{N} ,\nu_{i}^{N} ,\iota_{i}^{N} )\) and \(C_{j} = (\mu_{j}^{P} ,\nu_{j}^{P} ,\iota_{j}^{P} ,\mu_{j}^{N} ,\nu_{j}^{N} ,\iota_{j}^{N} )\) by

$$ \eta_{ij}^{P} = \frac{{\mu_{ij}^{P} + (1 - \nu_{ij}^{P} )(1 - \iota_{ij}^{P} )}}{3}, $$
$$ \eta_{ij}^{N} = \frac{{\mu_{ij}^{N} - ( - 1 - \nu_{ij}^{N} )( - 1 - \iota_{ij}^{N} )}}{3}, $$

for \(i,j \in \{ 1, \cdots ,n\}\), where \(\eta_{ij} = (\mu_{ij}^{P} ,\nu_{ij}^{P} ,\iota_{ij}^{P} ,\mu_{ij}^{N} ,\nu_{ij}^{N} ,\iota_{ij}^{N} )\) is the bipolar picture fuzzy edge between vertices \(C_{i}\) and \(C_{i}\) for \(i,j \in \{ 1, \cdots ,n\}\). We have \(\eta_{ij}^{P} = \eta_{ji}^{P} = 1\) and \(\eta_{ij}^{N} = \eta_{ji}^{N} = - 1\) if \(i = j\).

A2: Determine the attribute of alternative \(A_{k}\) by

$$ \tilde{A}_{k} = (\tilde{\mu }_{k}^{P} ,\tilde{\nu }_{k}^{P} ,\tilde{\iota }_{k}^{P} ,\tilde{\mu }_{k}^{N} ,\tilde{\nu }_{k}^{N} ,\tilde{\iota }_{k}^{N} ) = \left( {\frac{{\sum\limits_{j = 1}^{n} {w_{j}^{P} (\sum\limits_{t = 1}^{n} {\eta_{tj}^{P} b_{kt}^{P} } )} }}{3},\frac{{\sum\limits_{j = 1}^{n} {w_{j}^{N} (\sum\limits_{t = 1}^{n} {\eta_{tj}^{N} b_{kt}^{N} )} } }}{3}} \right), $$

where \(b_{kt}^{P}\) and \(b_{kt}^{N}\) denote the positive and negative parts of element \(b_{kt}\), and \(f_{tj} = (\mu_{tj}^{P} ,\nu_{tj}^{P} ,\iota_{tj}^{P} ,\mu_{tj}^{N} ,\nu_{tj}^{N} ,\iota_{tj}^{N} )\).

A3: Compute the score function of alternative \(\tilde{A}_{k}\) by

$$ S(\tilde{A}_{k} ) = \frac{{\tilde{\mu }_{k}^{P} - 2\tilde{\nu }_{k}^{P} - \tilde{\iota }_{k}^{P} + \tilde{\mu }_{k}^{N} - 2\tilde{\nu }_{k}^{N} - \tilde{\iota }_{k}^{N} }}{2}. $$

A4: Rank all the alternative \(A_{k}\) by means of \(S(\tilde{A}_{k} )\) and select the optimal alternative.

A5: Output

The next algorithm is another strategy to get the best alternative.

Algorithm B.

Calculate the optimal alternative based on similarity computation.

B1: Determine the bipolar impact coefficient between attributes \(C_{i} = (\mu_{i}^{P} ,\)\(\nu_{i}^{P} ,\iota_{i}^{P} ,\mu_{i}^{N} ,\nu_{i}^{N} ,\iota_{i}^{N} )\) and \(C_{j} = (\mu_{j}^{P} ,\nu_{j}^{P} ,\iota_{j}^{P} ,\mu_{j}^{N} ,\nu_{j}^{N} ,\iota_{j}^{N} )\) by

$$ \eta_{ij}^{P} = \frac{{\mu_{ij}^{P} + (1 - \nu_{ij}^{P} )(1 - \iota_{ij}^{P} )}}{3}, $$
$$ \eta_{ij}^{N} = \frac{{\mu_{ij}^{N} - ( - 1 - \nu_{ij}^{N} )( - 1 - \iota_{ij}^{N} )}}{3}, $$

for \(i,j \in \{ 1, \cdots ,n\}\), where \(\eta_{ij} = (\mu_{ij}^{P} ,\nu_{ij}^{P} ,\iota_{ij}^{P} ,\mu_{ij}^{N} ,\nu_{ij}^{N} ,\iota_{ij}^{N} )\) is the bipolar picture fuzzy edge between vertices \(C_{i}\) and \(C_{i}\) for \(i,j \in \{ 1, \cdots ,n\}\). We have \(\eta_{ij}^{P} = \eta_{ji}^{P} = 1\) and \(\eta_{ij}^{N} = \eta_{ji}^{N} = - 1\) if \(i = j\).

B2: Determine the associated weighted value of attribute \(C_{j}\) (\(j \in \{ 1, \cdots ,n\}\)) over the other criteria by

$$ \tilde{b}_{kj} = (\tilde{\mu }_{kj}^{P} ,\tilde{\nu }_{kj}^{P} ,\tilde{\iota }_{kj}^{P} ,\tilde{\mu }_{kj}^{N} ,\tilde{\nu }_{kj}^{N} ,\tilde{\iota }_{kj}^{N} ) = \left( {\frac{{w_{j}^{P} \sum\limits_{t = 1}^{n} {\eta_{tj}^{P} b_{kt}^{P} } }}{3},\frac{{w_{j}^{N} \sum\limits_{t = 1}^{n} {\eta_{tj}^{N} b_{kt}^{N} } }}{3}} \right), $$

where \(b_{kt}^{P}\) and \(b_{kt}^{N}\) denote the positive and negative parts of element \(b_{kt}\).

B3: Compute the similarity measure between the decision solution \(A = (\mu_{j}^{P} ,\nu_{j}^{P} ,\iota_{j}^{P} ,\mu_{j}^{N} ,\nu_{j}^{N} ,\iota_{j}^{N} )\), \(j \in \{ 1, \cdots ,n\}\), and each alternative \(A_{k}\),\(k \in \{ 1, \cdots ,m\}\), by

$$ \begin{aligned} S(A,A_{k} ) = & 1 - \frac{1}{6n}\sum\limits_{j = 1}^{n} {(\left| {\mu_{j}^{P} - \tilde{\mu }_{kj}^{P} } \right| + \left| {\nu_{j}^{P} - \tilde{\nu }_{kj}^{P} } \right| + \left| {\iota_{j}^{P} - \tilde{\iota }_{kj}^{P} } \right|} \\ & + \left| {\mu_{j}^{N} - \tilde{\mu }_{kj}^{N} } \right| + \left| {\nu_{j}^{N} - \tilde{\nu }_{kj}^{N} } \right| + \left| {\iota_{j}^{P} - \tilde{\iota }_{kj}^{N} } \right|). \\ \end{aligned} $$

B4: Rank all the alternative \(A_{k}\) by means of \(S(A,A_{k} )\) for \(k \in \{ 1, \cdots ,m\}\) and select the optimal alternative.

B5: Output.

4 Numerical Example for Algorithm A

IN this section, we explain how to implement the Algorithm A by showing the following instance. It is noted that the implement of Algorithm B will be explained in “Bipolar Picture Fuzzy Graph Based Multiple Attribute Decision Making Approach-Part II”. The data of the simulation experiments in this paper are mainly adapted from Ashraf et al. [9] and Amanathulla et al. [10].

The investment company has to make decisions on several alternative companies and choose the best investment object. There are four alternatives:

  • \(A_{1}\): a car company;

  • \(A_{2}\): a food company;

  • \(A_{3}\): a computer company;

  • \(A_{4}\): an energy company.

There are three attributes for these four companies with positive weight vector \(w^{P} = \{ 0.3,0.2,0.5\}\) and negative weight vector \(w^{N} = \{ - 0.2, - 0.2, - 0.6\}\):

  • \(C_{1}\): risk analysis;

  • \(C_{2}\): growth analysis;

  • \(C_{3}\): environmental impact analysis.

The four candidate alternatives are to be considered under the three attributes and are shown by means of bipolar picture fuzzy information by decision-making according to three attributes \(C_{1}\), \(C_{2}\) and \(C_{3}\) and the evaluation information on the alternative \(A_{1}\), \(A_{2}\), \(A_{3}\) and \(A_{4}\) under the factors \(C_{1}\), \(C_{2}\) and \(C_{3}\) can be shown in the following \(4 \times 3\) bipolar picture fuzzy decision matrix \(M\):

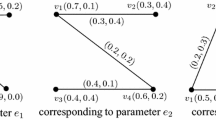
$$ M = \left[ {\begin{array}{*{20}c} \begin{gathered} (0.5,0.2,0.3, \hfill \\ - 0.4, - 0.3, - 0.3) \hfill \\ \end{gathered} & \begin{gathered} (0.8,0.1,0.1, \hfill \\ - 0.2, - 0.4, - 0.4) \hfill \\ \end{gathered} & \begin{gathered} (0.6,0.2,0.2, \hfill \\ - 0.5, - 0.2, - 0.3) \hfill \\ \end{gathered} \\ \begin{gathered} (0.6,0.2,0.2, \hfill \\ - 0.5, - 0.2, - 0.3) \hfill \\ \end{gathered} & \begin{gathered} (0.5,0.3,0.2, \hfill \\ - 0.5, - 0.2, - 0.3) \hfill \\ \end{gathered} & \begin{gathered} (0.8,0.1,0.1, \hfill \\ - 0.1, - 0.4, - 0.5) \hfill \\ \end{gathered} \\ \begin{gathered} (0.4,0.3,0.3, \hfill \\ - 0.5, - 0.3, - 0.2) \hfill \\ \end{gathered} & \begin{gathered} (0.7,0.1,0.2, \hfill \\ - 0.4, - 0.3, - 0.3) \hfill \\ \end{gathered} & \begin{gathered} (0.4,0.4,0.2, \hfill \\ - 0.5, - 0.2, - 0.3) \hfill \\ \end{gathered} \\ \begin{gathered} (0.3,0.2,0.5, \hfill \\ - 0.2, - 0.3, - 0.5) \hfill \\ \end{gathered} & \begin{gathered} (0.7,0.2,0.1, \hfill \\ - 0.1, - 0.3, - 0.6) \hfill \\ \end{gathered} & \begin{gathered} (0.4,0.2,0.4, \hfill \\ - 0.1, - 0.8, - 0.1) \hfill \\ \end{gathered} \\ \end{array} } \right]. $$

The relationship among the attributes \(C_{1}\), \(C_{2}\) and \(C_{3}\) is assumed to be a complete graph \(G = (V,E)\) with vertex set \(V = \{ C_{1} ,C_{2} ,C_{3} \}\) and edge set \(E = \{ C_{1} C_{2} ,\) \(C_{2} C_{3} ,C_{1} C_{3} \}\), see Fig. 1. This graph is a bipolar fuzzy graph corresponding to the relationship between attribute for all alternatives.

Fig. 1.
figure 1

A graph of relationship between attributes.

Full size image

The bipolar membership functions on the edge set of G which feature the relative among the attributes are defined as follows:

$$ f_{12} = (\mu_{12}^{P} ,\nu_{12}^{P} ,\iota_{12}^{P} ,\mu_{12}^{N} ,\nu_{12}^{N} ,\iota_{12}^{N} ) = (0.3,0.3,0.6, - 0.1, - 0.4, - 0.7), $$
$$ f_{13} = (\mu_{13}^{P} ,\nu_{13}^{P} ,\iota_{13}^{P} ,\mu_{13}^{N} ,\nu_{13}^{N} ,\iota_{13}^{N} ) = (0.1,0.4,0.6, - 0.1, - 0.8, - 0.5), $$
$$ f_{23} = (\mu_{23}^{P} ,\nu_{23}^{P} ,\iota_{23}^{P} ,\mu_{23}^{N} ,\nu_{23}^{N} ,\iota_{23}^{N} ) = (0.4,0.4,0.4, - 0.4, - 0.5, - 0.2). $$

To search for the optimal alternative, the following steps are implemented.

Step 1: Compute the bipolar impact coefficient between attributes \(C_{1}\), \(C_{2}\) and \(C_{3}\).

$$ \eta_{12}^{P} = \frac{{\mu_{12}^{P} + (1 - \nu_{12}^{P} )(1 - \iota_{12}^{P} )}}{3} = \frac{0.3 + (1 - 0.3)(1 - 0.6)}{3} = \frac{19}{{150}}, $$
$$ \eta_{12}^{N} = \frac{{\mu_{12}^{N} + ( - 1 - \nu_{12}^{N} )( - 1 - \iota_{12}^{N} )}}{3} = \frac{ - 0.1 - ( - 1 + 0.4)( - 1 + 0.7)}{3} = - \frac{7}{75}, $$
$$ \eta_{13}^{P} = \frac{{\mu_{13}^{P} + (1 - \nu_{13}^{P} )(1 - \iota_{13}^{P} )}}{3} = \frac{0.1 + (1 - 0.4)(1 - 0.6)}{3} = \frac{17}{{150}}, $$
$$ \eta_{13}^{N} = \frac{{\mu_{13}^{N} + ( - 1 - \nu_{13}^{N} )( - 1 - \iota_{13}^{N} )}}{3} = \frac{ - 0.1 - ( - 1 + 0.8)( - 1 + 0.5)}{3} = - \frac{1}{15}, $$
$$ \eta_{23}^{P} = \frac{{\mu_{23}^{P} + (1 - \nu_{23}^{P} )(1 - \iota_{23}^{P} )}}{3} = \frac{0.4 + (1 - 0.4)(1 - 0.4)}{3} = \frac{19}{{75}}, $$
$$ \eta_{23}^{N} = \frac{{\mu_{23}^{N} + ( - 1 - \nu_{23}^{N} )( - 1 - \iota_{23}^{N} )}}{3} = \frac{ - 0.4 - ( - 1 + 0.5)( - 1 + 0.2)}{3} = - \frac{4}{15}. $$

Step 2: determine the alternatives \(A_{k}\) as follows:

$$ \begin{aligned} \tilde{A}_{1} = & \frac{1}{3}[w_{1}^{P} (\eta_{11}^{P} b_{11}^{P} + \eta_{21}^{P} b_{12}^{P} + \eta_{31}^{P} b_{13}^{P} ) + w_{2}^{P} (\eta_{12}^{P} b_{11}^{P} + \eta_{22}^{P} b_{12}^{P} + \eta_{32}^{P} b_{13}^{P} ) \\ & + \left| {\mu_{j}^{N} - \tilde{\mu }_{kj}^{N} } \right| + \left| {\nu_{j}^{N} - \tilde{\nu }_{kj}^{N} } \right| + \left| {\iota_{j}^{P} - \tilde{\iota }_{kj}^{N} } \right|) \\ & + w_{2}^{N} (\eta_{12}^{N} b_{11}^{N} + \eta_{22}^{N} b_{12}^{N} + \eta_{32}^{N} b_{13}^{N} ) + w_{3}^{N} (\eta_{13}^{N} b_{11}^{N} + \eta_{23}^{N} b_{12}^{N} + \eta_{33}^{N} b_{13}^{N} )] \\ \end{aligned} $$
$$ \begin{aligned} = & \frac{1}{3}[0.3\{ 1 \times (0.5,0.2,0.3) + \frac{19}{{150}} \times (0.8,0.1,0.1) + \frac{17}{{150}} \times (0.6,0.2,0.2)\} \\ & + 0.2\{ \frac{19}{{150}} \times (0.5,0.2,0.3) + 1 \times (0.8,0.1,0.1) + \frac{19}{{75}} \times (0.6,0.2,0.2)\} \\ & + 0.5\{ \frac{17}{{150}} \times (0.5,0.2,0.3) + \frac{19}{{75}} \times (0.8,0.1,0.1) + 1 \times (0.6,0.2,0.2)\} ], \\ \end{aligned} $$
$$ \begin{gathered} \frac{1}{3}[ - 0.2\{ - 1 \times ( - 0.4, - 0.3, - 0.3) - \frac{7}{{75}} \times ( - 0.2, - 0.4, - 0.4) - \frac{1}{{15}} \hfill \\ \times ( - 0.5, - 0.2, - 0.3)\} \hfill \\ - 0.2\{ - \frac{7}{{75}} \times ( - 0.4, - 0.3, - 0.3) - 1 \times ( - 0.2, - 0.4, - 0.4) - \frac{4}{{15}} \hfill \\ \times ( - 0.5, - 0.2, - 0.3)\} \hfill \\ - 0.6\{ - \frac{1}{{15}} \times ( - 0.4, - 0.3, - 0.3) - \frac{4}{{15}} \times ( - 0.2, - 0.4, - 0.4) - 1 \hfill \\ \times ( - 0.5, - 0.2, - 0.3)\} ] \hfill \\ = (0.28,0.11,0.09, - 0.171, - 0.121, - 0.143), \hfill \\ \end{gathered} $$
$$ \begin{aligned} \tilde{A}_{2} = & \frac{1}{3}[w_{1}^{P} (\eta_{11}^{P} b_{21}^{P} + \eta_{21}^{P} b_{22}^{P} + \eta_{31}^{P} b_{23}^{P} ) + w_{2}^{P} (\eta_{12}^{P} b_{21}^{P} + \eta_{22}^{P} b_{22}^{P} + \eta_{32}^{P} b_{23}^{P} ) \\ & + w_{3}^{P} (\eta_{13}^{P} b_{21}^{P} + \eta_{23}^{P} b_{22}^{P} + \eta_{33}^{P} b_{23}^{P} )],\frac{1}{3}[w_{1}^{N} (\eta_{11}^{N} b_{21}^{N} + \eta_{21}^{N} b_{22}^{N} + \eta_{31}^{N} b_{23}^{N} ) \\ & + w_{2}^{N} (\eta_{12}^{N} b_{21}^{N} + \eta_{22}^{N} b_{22}^{N} + \eta_{32}^{N} b_{23}^{N} ) + w_{3}^{N} (\eta_{13}^{N} b_{21}^{N} + \eta_{23}^{N} b_{22}^{N} + \eta_{33}^{N} b_{23}^{N} )] \\ \end{aligned} $$
$$ \begin{aligned} = & \frac{1}{3}[0.3\{ 1 \times (0.6,0.2,0.2) + \frac{19}{{150}} \times (0.5,0.3,0.2) + \frac{17}{{150}} \times (0.8,0.1,0.1)\} \\ & + 0.2\{ \frac{19}{{150}} \times (0.6,0.2,0.2) + 1 \times (0.5,0.3,0.2) + \frac{19}{{75}} \times (0.8,0.1,0.1)\} \\ & + 0.5\{ \frac{17}{{150}} \times (0.6,0.2,0.2) + \frac{19}{{75}} \times (0.5,0.3,0.2) + 1 \times (0.8,0.1,0.1)\} ], \\ \end{aligned} $$
$$ \begin{gathered} \frac{1}{3}[ - 0.2\{ - 1 \times ( - 0.5, - 0.2, - 0.3) - \frac{7}{{75}} \times ( - 0.5, - 0.2, - 0.3) - \frac{1}{{15}} \hfill \\ \times ( - 0.1, - 0.4, - 0.5)\} \hfill \\ - 0.2\{ - \frac{7}{{75}} \times ( - 0.5, - 0.2, - 0.3) - 1 \times ( - 0.5, - 0.2, - 0.3) - \frac{4}{{15}} \hfill \\ \times ( - 0.1, - 0.4, - 0.5)\} \hfill \\ - 0.2\{ - \frac{7}{{75}} \times ( - 0.5, - 0.2, - 0.3) - 1 \times ( - 0.5, - 0.2, - 0.3) - \frac{4}{{15}} \hfill \\ \times ( - 0.1, - 0.4, - 0.5)\} \hfill \\ = (0.293,0.081,0.069, - 0.068, - 0.059, - 0.085), \hfill \\ \end{gathered} $$
$$ \begin{aligned} \tilde{A}_{3} = & \frac{1}{3}[w_{1}^{P} (\eta_{11}^{P} b_{31}^{P} + \eta_{21}^{P} b_{32}^{P} + \eta_{31}^{P} b_{33}^{P} ) + w_{2}^{P} (\eta_{12}^{P} b_{31}^{P} + \eta_{22}^{P} b_{32}^{P} + \eta_{32}^{P} b_{33}^{P} ) \\ & + w_{3}^{P} (\eta_{13}^{P} b_{31}^{P} + \eta_{23}^{P} b_{32}^{P} + \eta_{33}^{P} b_{33}^{P} )],\frac{1}{3}[w_{1}^{N} (\eta_{11}^{N} b_{31}^{N} + \eta_{21}^{N} b_{32}^{N} + \eta_{31}^{N} b_{33}^{N} ) \\ & + w_{2}^{N} (\eta_{12}^{N} b_{31}^{N} + \eta_{22}^{N} b_{32}^{N} + \eta_{32}^{N} b_{33}^{N} ) + w_{3}^{N} (\eta_{13}^{N} b_{31}^{N} + \eta_{23}^{N} b_{32}^{N} + \eta_{33}^{N} b_{33}^{N} )] \\ \end{aligned} $$
$$ \begin{aligned} = & \frac{1}{3}[0.3\{ 1 \times (0.4,0.3,0.3) + \frac{19}{{150}} \times (0.7,0.1,0.2) + \frac{17}{{150}} \times (0.4,0.4,0.2)\} \\ & + 0.2\{ \frac{19}{{150}} \times (0.4,0.3,0.3) + 1 \times (0.7,0.1,0.2) + \frac{19}{{75}} \times (0.4,0.4,0.2)\} \\ & + 0.5\{ \frac{17}{{150}} \times (0.4,0.3,0.3) + \frac{19}{{75}} \times (0.7,0.1,0.2) + 1 \times (0.4,0.4,0.2)\} ], \\ \end{aligned} $$
$$ \begin{gathered} \frac{1}{3}[ - 0.2\{ - 1 \times ( - 0.5, - 0.3, - 0.2) - \frac{7}{{75}} \times ( - 0.4, - 0.3, - 0.3) - \frac{1}{{15}} \hfill \\ \times ( - 0.5, - 0.2, - 0.3)\} \hfill \\ - 0.2\{ - \frac{7}{{75}} \times ( - 0.5, - 0.3, - 0.2) - 1 \times ( - 0.4, - 0.3, - 0.3) - \frac{4}{{15}} \hfill \\ \times ( - 0.5, - 0.2, - 0.3)\} \hfill \\ - 0.6\{ - \frac{1}{{15}} \times ( - 0.5, - 0.3, - 0.2) - \frac{4}{{15}} \times ( - 0.4, - 0.3, - 0.3) - 1 \hfill \\ \times ( - 0.5, - 0.2, - 0.3)\} ] \hfill \\ = (0.275,0.128,0.101, - 0.205, - 0.108, - 0.068), \hfill \\ \end{gathered} $$
$$ \begin{aligned} \tilde{A}_{4} = & \frac{1}{3}[w_{1}^{P} (\eta_{11}^{P} b_{41}^{P} + \eta_{21}^{P} b_{42}^{P} + \eta_{31}^{P} b_{43}^{P} ) + w_{2}^{P} (\eta_{12}^{P} b_{41}^{P} + \eta_{22}^{P} b_{42}^{P} + \eta_{32}^{P} b_{43}^{P} ) \\ & + w_{3}^{P} (\eta_{13}^{P} b_{41}^{P} + \eta_{23}^{P} b_{42}^{P} + \eta_{33}^{P} b_{43}^{P} )],\frac{1}{3}[w_{1}^{N} (\eta_{11}^{N} b_{41}^{N} + \eta_{21}^{N} b_{42}^{N} + \eta_{31}^{N} b_{43}^{N} ) \\ & + w_{2}^{N} (\eta_{12}^{N} b_{41}^{N} + \eta_{22}^{N} b_{42}^{N} + \eta_{32}^{N} b_{43}^{N} ) + w_{3}^{N} (\eta_{13}^{N} b_{41}^{N} + \eta_{23}^{N} b_{42}^{N} + \eta_{33}^{N} b_{43}^{N} )] \\ \end{aligned} $$
$$ \begin{gathered} = \frac{1}{3}[0.3\{ 1 \times (0.3,0.2,0.5) + \frac{19}{{150}} \times (0.7,0.2,0.1) + \frac{17}{{150}} \times (0.4,0.2,0.4)\} \hfill \\ + 0.2\{ \frac{19}{{150}} \times (0.3,0.2,0.5) + 1 \times (0.7,0.2,0.1) + \frac{19}{{75}} \times (0.4,0.2,0.4)\} \hfill \\ + 0.5\{ \frac{17}{{150}} \times (0.3,0.2,0.5) + \frac{19}{{75}} \times (0.7,0.2,0.1) + 1 \times (0.4,0.2,0.4)\} ], \hfill \\ \end{gathered} $$
$$ \begin{gathered} \frac{1}{3}[ - 0.2\{ - 1 \times ( - 0.2, - 0.3, - 0.5) - \frac{7}{{75}} \times ( - 0.1, - 0.3, - 0.6) - \frac{1}{{15}} \hfill \\ \times ( - 0.1, - 0.8, - 0.1)\} \hfill \\ - 0.2\{ - \frac{7}{{75}} \times ( - 0.2, - 0.3, - 0.5) - 1 \times ( - 0.1, - 0.3, - 0.6) - \frac{4}{{15}} \hfill \\ \times ( - 0.1, - 0.8, - 0.1)\} \hfill \\ - 0.6\{ - \frac{1}{{15}} \times ( - 0.2, - 0.3, - 0.5) - \frac{4}{{15}} \times ( - 0.1, - 0.3, - 0.6) - 1 \hfill \\ \times ( - 0.1, - 0.8, - 0.1)\} ] \hfill \\ = (0.262,0.119,0.219, - 0.052, - 0.242, - 0.141). \hfill \\ \end{gathered} $$

Step 3. Calculate the score function for each alternative.

$$ \begin{array}{*{20}l} {S(\tilde{A}_{1} ) = \frac{{\tilde{\mu }_{1}^{P} \, - \,2\tilde{\nu }_{1}^{P} \, - \,\tilde{\iota }_{1}^{P} \, + \,\tilde{\mu }_{1}^{N} \, - \,2\tilde{\nu }_{1}^{N} \, - \,\tilde{\iota }_{1}^{N} }}{2}} \hfill \\ { = \frac{{0.28\, - \,2\, \times \,0.11\, - \,0.09\, - \,0.171\, + \,2\, \times \,0.121\, + \,0.143}}{2}\, = \,0.092,} \hfill \\ \end{array} $$
$$ \begin{array}{*{20}l} {S(\tilde{A}_{2} ) = \frac{{\tilde{\mu }_{2}^{P} \,- \,2\tilde{\nu }_{2}^{P}\, - \,\tilde{\iota }_{2}^{P} \,+\, \tilde{\mu }_{2}^{N} \,-\, 2\tilde{\nu }_{2}^{N} \,-\, \tilde{\iota }_{2}^{N} }}{2}} \hfill \\ { = \frac{0.293\, -\, 2 \times 0.081\,- \,0.069 \,-\, 0.068\, +\, 2 \times 0.059 \,+\, 0.085}{2}\, =\, 0.0985,} \hfill \\ \end{array} $$
$$ \begin{array}{*{20}l} {S(\tilde{A}_{3} ) = \frac{{\tilde{\mu }_{3}^{P}\, -\, 2\tilde{\nu }_{3}^{P} \,-\, \tilde{\iota }_{3}^{P} \,+\, \tilde{\mu }_{3}^{N} \,-\, 2\tilde{\nu }_{3}^{N}\, - \,\tilde{\iota }_{3}^{N} }}{2}} \hfill \\ { = \frac{0.275\, -\, 2 \times 0.128\, -\, 0.101\, -\, 0.205\, +\, 2 \times 0.108 \,+\, 0.068}{2} \,= \,- 0.0015,} \hfill \\ \end{array} $$
$$ \begin{array}{*{20}l} {S(\tilde{A}_{4} ) = \frac{{\tilde{\mu }_{4}^{P}\, -\, 2\tilde{\nu }_{4}^{P} \,- \,\tilde{\iota }_{4}^{P} \,+\, \tilde{\mu }_{4}^{N}\, -\, 2\tilde{\nu }_{4}^{N}\, -\, \tilde{\iota }_{4}^{N} }}{2}} \hfill \\ { \,=\, \frac{0.262\, -\, 2 \times 0.119\, -\, 0.219\, -\, 0.052 \,+\, 2 \times 0.242 \,+\, 0.141}{2}\, = \,0.1895.} \hfill \\ \end{array} $$

Step 4. We rank the alternatives as \(A_{4} > A_{2} > A_{1} > A_{3}\). Hence, \(A_{4}\) is the optimal choice in the decision making problem.

5 Conclusion

In this paper, we discuss the multiple attribute decision making problem in term of the bipolar picture fuzzy graph framework. Two decision making algorithms are raised and an example is presented to show how to implement the algorithm for a specific decision making problem. More about the algorithm and specific application of the decision support system graph model need to be further studied in the future.