Introduction

The structure of deterministic mathematical models for observing and controlling the spread of various human diseases is of public health interest in the light of the fact that the mathematics helps to formulate effective mechanisms for controlling their spread. Since the first compartmental model is given by Kermack and McKendrick (1927), various mathematical models involving some complex assumptions (Gumel et al. 2006; Korobeinikov and Maini 2005; Kumar and Nilam 2018, 2019a; b, 2019; Dubey et al. 2013, 2015; Cui et al. 2017; Xiao and Ruan 2007; Li and Zhang 2017; Huang et al. 2010; Goel and Nilam 2019; Hattaf and Yousfi 2009; Hattaf et al. 2013; Zhou and Fan 2012; Dubey et al. 2016; Naresh et al. 2009; Xu and Ma 2009; Wang and Ruan 2004; Wang 2002; Li Michael et al. 1999; Zhang and Suo 2010) have been proposed and considered, for instance, SIR, SIS, SEIR and SEIRS models. In recent times, considerable attention has been paid to study the dynamics of epidemic models with epidemiologically meaningful time delays. In the context of disease transmission, delays can be caused by a variety of factors. The most well-known reasons for a delay are (1) the latency of the infection in a vector and (2) the latency of the infection in an infected host (Huang et al. 2010; Li and Liu 2014). In these cases, some time should elapse before the level of infection in the infected host or the vector reaches a sufficiently high level to transmit the infection further.

It is well known that disease transmission progress plays a vital role in epidemic dynamics; that is, applying different incidence rates can potentially change the behaviors of the system. In many epidemic models, numerous incidence functions with or without delay are widely used in different epidemiological backgrounds (Li and Liu 2014). The incidence rate can also be modeled by many other kinds of more general functions. It is interesting whether the functional form of the incidence rate can change the epidemic dynamics or not. Liu et al. (1986) suggested a nonlinear saturated incidence function \( \beta SI^{l} /\left( {1 + \alpha I^{h} } \right) \) to model the impact of behavioral changes to certain communicable diseases, where \( \beta SI^{l} \) describes the infection force of the disease and \( 1/\left( {1 + \alpha I^{h} } \right) \) measures the inhibition effect from the behavioral change of the susceptible people when the number of infectious people increases; \( l, h \) and \( \beta \) are all positive constants, and \( \alpha \) is a nonnegative constant. The case \( l = h = 1 \), i.e., the function \( \beta SI/\left( {1 + \alpha I} \right) \), was used by Capasso and Serio (1978) to represent a “protection measure” in modeling the cholera epidemics in Bari in 1973.

The resources of the health system available to the public determine how well the diseases are controlled. Particularly, the capacity of the hospital setting and the effectiveness and efficiency of treatment may influence the recovery rate (Cui et al. 2017). In this manner, consideration of the treatment rate is very important. For this, numerous authors (Kumar and Nilam 2018, 2019a, b; Kumar et al. 2019; Dubey et al. 2013, 2015) have suggested various treatment rates such as Monod–Haldane functional type and Holling type I and II. To contribute to the study of saturated treatment, we incorporate the Holling type III (Dubey et al. 2013, 2016) treatment rate, which characterizes the case in which removal rate initially is rapid with increment in infectives, and afterward, it develops gradually, finally settling to a saturated value. Any subsequent expansion in infectives will not influence the recovery/removal rate. This case relates to a known disease which has re-emerged and has available treatment methods.

In this article, we propose and analyze a mathematical susceptible—infected—recovered model to gain a better understanding of transmission and subsequent control of the spread of infectious/communicable disease via a combination of nonlinear saturated incidence and Holling type III treatment rates. We incorporate time delay in incidence rate as the incubation period of the disease. We discuss the positivity and boundedness of the model solution. Further, we find the equilibrium points of the model and discuss the local and global stability of the equilibria. The stability of equilibria is discussed in terms of the basic reproduction number (van den Driessche and Watmough 2002), Routh–Hurwitz criterion and Lyapunov functional. Moreover, bifurcation analysis and an undelayed system are also discussed. Our goal is to study the effect of nonlinear incidence along with time delay and Holling type III treatment, on the transmission dynamics of the infectious disease in the human population.

The remaining part of the manuscript is organized as follows: In “The mathematical model and its basic properties” section, the mathematical model is presented together with its basic properties as positivity and boundedness of the solutions. In “Equilibria and their stability analysis” section, a rigorous analysis of the model is provided including the existence and local stability analysis of model equilibria. The “Global stability” section analyzes the global stability of the equilibrium points. The stability of the undelayed system is presented in “Undelayed system” section. Finally, a discussion is presented in “Discussion” section.

The mathematical model and its basic properties

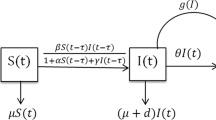
In this section, we present a deterministic epidemic model to prevent an outbreak of an epidemic. We assume that the human population under consideration is \( N\left( t \right) \). We divide \( N\left( t \right) \) into three isolated compartments or classes \( X\left( t \right), Y\left( t \right) \) and \( Z\left( t \right) \). Here, \( X\left( t \right) \) represents the susceptible population, \( Y\left( t \right) \) represents the compartment of infectious individuals, and recovered individuals are represented by \( Z\left( t \right) \). The useful postulates for the model formulation are as follows.

Postulates

  1. (A1)

    The nonlinear incidence rate is given by the function \( F\left( Y \right) \).

  2. (A2)

    It is supposed that all the newborns are susceptible.

  3. (A3)

    The force of infection at any time \( t \) is given by \( \alpha X\left( t \right)F\left( {Y\left( {t - \tau } \right)} \right) \) (Kumar and Nilam 2018; Naresh et al. 2009), because those infected at the time \( \left( {t - \tau } \right) \) become infectious \( \tau \) time later.

  4. (A4)

    The total population is supposed to be large enough to be adequately described by a deterministic model and is divided into compartments (or classes) based on the disease status.

The susceptible population is generated via recruitment by birth at a constant rate \( A \). The natural death rate is supposed to be the same for all the individuals and is represented by \( \mu \). The contact capable of leading the infection in the human population is assumed as a rate \( \alpha \) (transmission rate of infection). The protection measures (psychological or inhibitory effect) are considered at a rate \( \beta \). The infected people also die due to disease-related death at a rate \( \sigma \) (disease–induced mortality). The rate of cure of infection is \( \omega \), and limitation rate in the treatment of infected is \( \varphi \). The rate of recovery from infection is \( \theta \). These assumptions lead to the following nonlinear system of the delay differential equations to describe the changes in \( X\left( t \right) \), \( Y\left( t \right) \) and \( Z\left( t \right) \) with respect to time \( t \):

$$ \begin{aligned} \frac{{{\text{d}}X\left( t \right)}}{{{\text{d}}t}} & = A - \mu X\left( t \right) - \frac{{\alpha X\left( t \right)Y\left( {t - \tau } \right)}}{{1 + \beta Y\left( {t - \tau } \right)}}, \\ \frac{{{\text{d}}Y\left( t \right)}}{{{\text{d}}t}} & = \frac{{\alpha X\left( t \right)Y\left( {t - \tau } \right)}}{{1 + \beta Y\left( {t - \tau } \right)}} - \left( {\mu + \sigma + \theta } \right)Y\left( t \right) - \frac{{\omega Y^{2} \left( t \right)}}{{1 + \varphi Y^{2} \left( t \right)}}, \\ \frac{{{\text{d}}Z\left( t \right)}}{{{\text{d}}t}} & = \frac{{\omega Y^{2} \left( t \right)}}{{1 + \varphi Y^{2} \left( t \right)}} + \theta Y\left( t \right) - \mu Z\left( t \right). \\ \end{aligned} $$
(1)

Here, time lag \( \tau > 0 \) represents the incubation period of the disease, defined as a fixed time during which the infectious agents develop in the vector, and it is only after that time that the infected vector can infect a susceptible individual.

For biological reasons, the initial conditions are nonnegative continuous functions as

$$ X\left( \rho \right) = x\left( \rho \right); \quad Y\left( \rho \right) = y\left( \rho \right); \quad Z\left( \rho \right) = z\left( \rho \right), $$
(2)

where \( H\left( \rho \right) = \left( {x,y,z} \right)^{\text{T}} \in C, \) are functions such that \( x,y,z \ge 0, \left( { - \tau \le \rho \le 0} \right) \). \( C \) denotes the Banach space \( C\left( {\left[ { - \tau ,0} \right],{\mathbb{R}}_{ + }^{3} } \right) \) of continuous functions mapping the interval \( \left[ { - \tau ,0} \right] \) into \( {\mathbb{R}}_{ + }^{3} \) with the supremum norm

$$ H = \mathop {\sup }\limits_{{\rho \in \left[ { - \tau ,0} \right]}} \left| {H\left( \rho \right)} \right|, $$

where \( \left| \cdot \right| \) is any norm in \( {\mathbb{R}}_{ + }^{3} . \)

The fundamental theory of functional differential equations (Hale and Verduyn Lunel 1993) implies for any initial conditions (2), system (1) has a unique solution \( \left( {X\left( t \right),Y\left( t \right),Z\left( t \right)} \right) \). The non-negativity and boundedness of the solution with a positive initial value (2) is guaranteed by the following theorem:

Theorem 1

All solutions of model (1) starting in\( {\mathbb{R}}_{ + }^{3} \)are bounded and enter the set\( \varGamma = \left\{ {\left( {X, Y, Z} \right) \in {\mathbb{R}}_{ + }^{3} : X\left( t \right) + Y\left( t \right) + Z\left( t \right) = N\left( t \right) \le \frac{A}{\mu }} \right\} \).

Proof

We assume that the model-dependent variables and parameters are nonnegative. Continuity of the right-hand side of system (1) and its derivative imply that the model is well posed for \( N\left( t \right) > 0 \). The invariant region for the existence of the solutions can be obtained as given below:

$$ \frac{{{\text{d}}\left[ {X\left( t \right) + Y\left( t \right) + Z\left( t \right)} \right]}}{{{\text{d}}t}} = \frac{{{\text{d}}N\left( t \right)}}{{{\text{d}}t}} \le A - \mu N\left( t \right) $$
(3)
$$ \Rightarrow \quad 0 < \lim \inf \;N\left( t \right) \le \lim \sup \;N\left( t \right) \le \frac{A}{\mu } \left( {{\text{as}}\; t \to \infty } \right). $$
(4)

Since \( N\left( t \right) > 0 \) on \( \left[ { - \tau , 0} \right] \) by assumption \( N\left( t \right) > 0 \) for all \( t \ge 0 \). Therefore, from (3) above, \( N\left( t \right) \) cannot blow up to infinity in finite time. The model system is dissipative (solutions are bounded), and therefore, the solution exists globally for all \( t > 0 \) in the invariant and compact set \( \varGamma = \left\{ {\left( {X, Y, Z} \right) \in {\mathbb{R}}_{ + }^{3} : X\left( t \right) + Y\left( t \right) + Z\left( t \right) = N\left( t \right) \le \frac{A}{\mu }} \right\} \). As \( N \to 0, X\left( t \right), Y\left( t \right) \) and \( Z\left( t \right) \) also tend to zero, each of these terms tends to zero as \( N\left( t \right) \) does. It is therefore natural to interpret these terms as zero when \( N\left( t \right) = 0 \).

Remark

In the region \( \varGamma \), the elementary results, for example local existence, uniqueness and continuity of solutions, are valid for model (1). Therefore, there exists a unique solution \( \left( {X\left( t \right), Y\left( t \right), Z\left( t \right)} \right) \) of model (1) starting in the interior of \( \varGamma \) that exists on a maximal interval \( \left[ {0,\infty } \right) \) if solutions remain bounded (Naresh et al. 2009).

Since the first two equations of model (1) are independent of \( R\left( t \right), \) it is convenient to study the first two equations of system (1) for theoretical analysis. The reduced model is as follows:

$$ \frac{{{\text{d}}X\left( t \right)}}{{{\text{d}}t}} = A - \mu X\left( t \right) - \frac{{\alpha X\left( t \right)Y\left( {t - \tau } \right)}}{{1 + \beta Y\left( {t - \tau } \right)}}, $$
$$ \frac{{{\text{d}}Y\left( t \right)}}{{{\text{d}}t}} = \frac{{\alpha X\left( t \right)Y\left( {t - \tau } \right)}}{{1 + \beta Y\left( {t - \tau } \right)}} - \left( {\mu + \sigma + \theta } \right)Y\left( t \right) - \frac{{\omega Y^{2} \left( t \right)}}{{1 + \varphi Y^{2} \left( t \right)}}. $$
(5)

The initial conditions are

$$ X\left( \rho \right) = x\left( \rho \right); \quad Y\left( \rho \right) = y\left( \rho \right) $$
(6)

Theorem 2

All state variables\( \left( {X\left( t \right), Y\left( t \right)} \right) \)of the reduced model (5) with the initial condition (6) are nonnegative.

Proof

First we show that \( X\left( t \right) \) is nonnegative for all \( t \ge 0 \). On the contrary, it is assumed that there exist \( t_{1} > 0 \) be the first time such that \( X\left( {t_{1} } \right) = 0 \), and then by the first equation of system (5), we have \( X^{\prime}\left( {t_{1} } \right) = A > 0 \), and hence, \( X\left( t \right) < 0 \) for \( t \in \left( {t_{1} - \varepsilon , t_{1} } \right) \), where \( \varepsilon > 0 \) is sufficiently small. This contradicts \( X\left( t \right) > 0 \) for \( t \in \left[ {0, t_{1} } \right) \). It follows that \( X\left( t \right) > 0 \) for \( t > 0 \). Now, we prove that positivity of solution \( Y\left( t \right) \). Integrating the second equation of system (5) from 0 to \( t \) for \( 0 < t \le \tau \), by applying the variation of constant formula and the step-by-step integration method, we obtain:

$$ Y\left( t \right) = Y\left( 0 \right){\text{e}}^{{ - \left( {\mu + \sigma + \theta } \right)t}} \cdot {\text{e}}^{{\mathop \smallint \limits_{0}^{t} F\left( {X\left( \delta \right), Y\left( {\delta - \tau } \right), Y\left( \delta \right)} \right) {\text{d}}\delta }} $$

where \( F\left( {X\left( \delta \right), Y\left( {\delta - \tau } \right), Y\left( \delta \right)} \right) = \left( {\frac{{\alpha X\left( \delta \right)Y\left( {\delta - \tau } \right)}}{{\left( {1 + \beta Y\left( {\delta - \tau } \right)} \right)Y\left( \delta \right)}} - \frac{\omega Y\left( \delta \right)}{{\varphi Y^{2} \left( \delta \right) + 1}}} \right). \)

It is easy to see that \( Y\left( t \right) > 0 \) for all \( 0 \le t \le \tau \). Integrating the second equation of system (5) from \( \tau \) to \( t \) for \( \tau < t \le 2\tau \) gives

$$ Y\left( t \right) = Y\left( \tau \right){\text{e}}^{{ - \left( {\mu + \sigma + \theta } \right)t}} \cdot {\text{e}}^{{\mathop \smallint \limits_{\tau }^{t} F\left( {X\left( \delta \right), Y\left( {\delta - \tau } \right), Y\left( \delta \right)} \right) {\text{d}}\delta }} $$

Note that \( Y\left( t \right) > 0 \) for all \( \tau \le t \le 2\tau \), and this procedure can easily carry on. It follows that for all \( t > 0 \), we have \( Y\left( t \right) > 0 \). This completes the proof.

Equilibria and their stability analysis

In this section, we analyze the equilibrium points of system (5). The equilibrium solutions of a time-delayed system are equivalent to the corresponding system with zero delays (Kumar and Nilam 2018). There are only two types of equilibria for our model, namely

  1. 1.

    \( Q = \left( {\frac{A}{\mu },0} \right) \), disease- or infection-free equilibrium.

  2. 2.

    \( Q^{*} = \left( {X^{*} ,Y^{*} } \right) \), endemic or positive equilibrium.

Infection-free steady state

In this subsection, we analyze system (5) by finding its equilibria and their stability analysis. The steady state of system (5) satisfies the following system of equations:

$$ A - \mu X\left( t \right) - \frac{\alpha X\left( t \right)Y\left( t \right)}{1 + \beta Y\left( t \right)} = 0 $$
(7)
$$ \frac{\alpha X\left( t \right)Y\left( t \right)}{1 + \beta Y\left( t \right)} - \left( {\mu + \sigma + \theta } \right)Y\left( t \right) - \frac{{\omega Y^{2} \left( t \right)}}{{1 + \varphi Y^{2} \left( t \right)}} = 0. $$
(8)

Systems (7)–(8) has the infection-free equilibrium \( Q = \left( {\frac{A}{\mu },0} \right) \), that is, there is no infection present in the community and all people are susceptible. The characteristic equation (the corresponding matrix \( \left( { J_{1} } \right) \) is given in “Appendix”) of system (5) at Q is given by the following equation:

$$ \left( {\mu + \lambda } \right)\left( {\lambda - \frac{\alpha A}{\mu } {\text{e}}^{ - \lambda \tau } + \left( {\mu + \sigma + \theta } \right)} \right) = 0 $$
(9)

The term \( \frac{\alpha A}{{\mu \left( {\mu + \sigma + \theta } \right)}} e^{ - \lambda \tau } \) at \( \tau = 0 \) is known as basic reproduction number denoted as \( R_{0} \). The threshold parameter \( R_{0} \) is helpful in describing the spread of an infectious disease. Thus, \( R_{0} \) for the model system (5) is obtained as

$$ R_{0} = \frac{\alpha A}{{\mu \left( {\mu + \sigma + \theta } \right)}}. $$

Analysis for \( R_{0} \ne 1 \)

One of the roots of (9) is given by \( \lambda_{1} = - \mu \), and the other roots can be obtained from

$$ \frac{\alpha A}{\mu } {\text{e}}^{ - \lambda \tau } - \left( {\mu + \sigma + \theta } \right) - \lambda = 0 $$
(10)

Suppose that

$$ G\left( \lambda \right) = \lambda - \frac{\alpha A}{\mu } {\text{e}}^{ - \lambda \tau } + \left( {\mu + \sigma + \theta } \right). $$
(11)

If \( R_{0} > 1 \), it is readily seen that for \( \lambda \) real,

$$ \begin{aligned}& G\left( 0 \right) = \left( {\mu + \sigma + \theta } \right) - \frac{\alpha A}{\mu } = \left( {\mu + \sigma + \theta } \right)\left( {1 - R_{0} } \right),\quad \\& \mathop {\lim }\limits_{\lambda \to + \infty } G\left( \lambda \right) = + \infty . \end{aligned} $$

Hence, \( G\left( \lambda \right) = 0 \) has a positive real root if \( R_{0} > 1. \)

If \( R_{0} < 1, \) we assume that \( \text{Re} \; \lambda \ge 0. \)

We see that

$$ \begin{aligned} \text{Re} \;\lambda &= \frac{\alpha A}{\mu }{\text{e}}^{{ - \text{Re} \; \lambda \tau }} \cos \text{Im} \lambda \tau \\&\quad- \left( {\mu + \sigma + \theta } \right) < \left( {\mu + \sigma + \theta } \right)\left( {R_{0} - 1} \right) < 0, \end{aligned} $$

a contradiction to our assumption. Hence, if \( R_{0} < 1 \) then the characteristic root \( \lambda \) of (10) has a negative real part.

Thus, the following theorem is proposed:

Theorem 3

The infection-free steady state\( Q \)is locally asymptotically stable (LAS) when\( R_{0} < 1 \)and unstable when\( R_{0} > 1 \)for\( \tau > 0 \).

Analysis at \( R_{0} = 1 \)

If \( R_{0} = 1 \), then \( \lambda = 0 \) is a simple characteristic root of (9). Let \( \lambda = a + ib \) be any of the other solutions, then (10) changes into:

$$ a + ib + \mu + \sigma + \theta - \frac{\alpha A}{\mu }{\text{e}}^{{ - \left( {a + ib} \right)\tau }} = 0 $$
(12)

By using Euler’s formula and by separating real and imaginary parts, we can write

$$ a + \mu + \sigma + \theta = \frac{\alpha A}{\mu } \cos b\tau {\text{e}}^{ - a\tau } ,\quad b = - \frac{\alpha A}{\mu }\sin b\tau {\text{e}}^{ - a\tau } $$
(13)

Observing that \( R_{0} = 1 \) implies \( \frac{\alpha A}{\mu } = \left( {\mu + \sigma + \theta } \right) \). Moreover, if there exists a root satisfying both (13), then it also satisfies the equation obtained by squaring and adding them member to member,

$$ \left( {a + \mu + \sigma + \theta } \right)^{2} + b^{2} = \left( {\mu + \sigma + \theta } \right)^{2} {\text{e}}^{ - 2a\tau } . $$
(14)

For (14) to be verified, we must have \( a \le 0 \). Thus, we propose the following theorem:

Theorem 4

The infection-free steady state\( Q \)of system (5) is linearly neutrally stable if\( R_{0} = 1 \)for\( \tau > 0 \).

Endemic steady state

To establish the existence of an endemic equilibrium \( Q^{*} \left( {X^{*} ,Y^{* } } \right) \), the right-hand side of system (5) is equated to zero. Thus, the solution of following a set of algebraic equations gives the endemic equilibrium point \( Q^{*} \left( {X^{*} ,Y^{*} } \right) \) for the proposed model system:

$$ \begin{aligned}& A - \mu X^{*} - \frac{{\alpha X^{*} Y^{*} }}{{1 + \beta Y^{*} }} = 0,\quad \\&\frac{{\alpha X^{*} Y^{*} }}{{1 + \beta Y^{*} }} - \left( {\mu + \sigma + \theta } \right)Y^{*} - \frac{{\omega Y^{*2} }}{{1 + \varphi Y^{*2} }} = 0. \end{aligned} $$
(15)

The solution of (15) gives the following:

  1. 1.

    \( X^{*} = \frac{{A\left( {1 + \beta Y^{*} } \right)}}{{\mu + \left( {\mu \beta + \alpha } \right)Y^{*} }}, \)

  2. 2.

    \( Y^{*} \).

Here, \( Y^{*} \) is given by the following cubic equation:

$$ P\left( {Y^{*} } \right) = K_{0} + K_{1} Y^{*} + K_{2} Y^{*2} + K_{3} Y^{*3} = 0 $$
(16)

where

$$ \begin{aligned} K_{0} & = A\alpha - \theta \mu - \mu^{2} - \mu \sigma = \mu \left( {\mu + \sigma + \theta } \right)\left( {R_{0} - 1} \right), \\ K_{1} & = - \left( {\alpha + \beta \mu } \right)\left( {\theta + \mu + \sigma } \right) - \mu \omega , \\ K_{2} & = \mu \left( {\theta + \mu + \sigma } \right)\varphi \left( {R_{0} - 1} \right) - \left( {\alpha + \beta \mu } \right)\omega , \\ K_{3} & = - \left( {\alpha + \beta \mu } \right)\left( {\theta + \mu + \sigma } \right)\varphi . \\ \end{aligned} $$

Next, we propose the following result for the existence of endemic equilibrium:

Theorem 5

If \( R_{0} > 1 \) , then there are either one or three positive endemic equilibria, and if all equilibria are simple roots and if \( R_{0} \le 1 \) then no positive endemic equilibria exist.

Proof

It is evident from the expressions of \( K_{1} , K_{2} , K_{3} \) and \( K_{4} \) that \( K_{3} \) is always negative. Suppose \( R_{0} > 1 (K_{0} > 0) \). The leading coefficient \( K_{3} \) is negative. Hence, \( \mathop { {\text{lim}}}\limits_{{Y^{*} \to \infty }} P\left( {Y^{*} } \right) = - \infty \). Also, note that \( P\left( 0 \right) > 0 \) when \( R_{0} > 1 \). \( P\left( {Y^{*} } \right) \) is a continuous function of \( Y^{*} \), and by applying fundamental theorem of algebra, it is evident that (16) can have at most three real roots. By a geometric argument, it is readily seen that there is either one or three positive endemic equilibria, if all equilibria are simple roots. However, when \( R_{0} < 1 \), the coefficients \( K_{0} , K_{1} , K_{2} \) and \( K_{3} \) all are negative, and then by a fundamental theorem of algebra, we know that (16) cannot have any positive real root, and when \( R_{0} = 1 \), the coefficients \( K_{0} \) is zero and other coefficients \( K_{1} , K_{2} \) and \( K_{3} \) all are negative, and then by a fundamental theorem of algebra, we know that this polynomial cannot have any positive real root.

Stability analysis of endemic or positive equilibria

To investigate the local stability of system (5) at endemic equilibrium \( \left( {Q^{*} } \right) \), we linearize system (5) at \( Q^{*} \) and obtained the characteristic equation (the corresponding matrix \( ( J_{2} ) \) is given in “Appendix”) which is as given below:

$$ \begin{aligned} & \lambda^{2} + M_{1} \lambda + N_{1} + \left( {M_{2} \lambda + N_{2} } \right)e^{ - \lambda \tau } = 0 \\ & M_{1} = \frac{{\left( {1 + Y^{*} \beta } \right)\left( {\theta + 2\mu + \sigma + Y^{*3} \left( {\alpha + \beta \left( {\theta + 2\mu + \sigma } \right)} \right)\varphi^{2} + Y^{*} \left( {\alpha + \beta \left( {\theta + 2\mu + \sigma } \right) + 2\left( {\theta \varphi + 2\mu \varphi + \sigma \varphi + \omega } \right)} \right)} \right)}}{{\left( {1 + Y^{*} \beta } \right)^{2} \left( {1 + Y^{*} \varphi } \right)^{2} }} \\ & \quad + \frac{{\left( {1 + Y^{*} \beta } \right)Y^{*2} \left( {2\alpha \varphi + \left( {\theta + 2\mu + \sigma } \right)\varphi^{2} + 2\beta \left( {\theta \varphi + 2\mu \varphi + \sigma \varphi + \omega } \right)} \right)}}{{\left( {1 + Y^{*} \beta } \right)^{2} \left( {1 + Y^{*} \varphi } \right)^{2} }}, \\ & M_{2} = \frac{{ - X^{*} \alpha }}{{\left( {1 + Y^{*} \beta } \right)^{2} }}, \\ & N_{1} = \frac{{\left( {1 + Y^{*} \beta } \right)\left( {\mu + Y^{*} \left( {\alpha + \beta \mu } \right)} \right)\left( {\theta + \mu + \sigma } \right)}}{{\left( {1 + Y^{*} \beta } \right)^{2} }}, \\ & N_{2} = \frac{{ - X^{*} \alpha \mu }}{{\left( {1 + Y^{*} \beta } \right)^{2} }}. \\ \end{aligned} $$
(17)

Theorem 5

For \( \tau > 0 \) , system ( 5 ) at \( Q^{*} \) is locally asymptotically stable if \( M_{1}^{2} - 2N_{1} - M_{2}^{2} > 0 \) and \( N_{1}^{2} - N_{2}^{2} > 0 \) are satisfied simultaneously.

Proof

At endemic equilibrium \( Q^{*} \), the characteristic equation of the system for \( \tau > 0 \) is given by (17):

$$ \lambda^{2} + M_{1} \lambda + N_{1} + \left( {M_{2} \lambda + N_{2} } \right)e^{ - \lambda \tau } = 0. $$

For \( \tau > 0 \), by corollary 2.4 in Ruan and Wei (2003), it follows that a characteristic root of (17) must cross the imaginary axis for the occurrence of instability for a specific value of the delay \( \tau \). Accordingly, we assume that \( \lambda = i\omega , \omega > 0 \) is the root of the characteristic (17). Putting \( \lambda = i\omega \) in (17) gives the following:

$$ \begin{aligned} & - \omega^{2} + N_{1} + M_{2} \omega \sin \omega \tau + N_{2} \cos \omega \tau\\&\quad + i \left( {M_{2} \omega \cos \omega \tau - N_{2} \sin \omega \tau + M_{1} \omega } \right) = 0 \end{aligned} $$
(18)

Using Euler’s formula and separating the real and imaginary part of (18), we get

$$ M_{2} \omega \sin \omega \tau + N_{2} \cos \omega \tau = \omega^{2} - N_{1} $$
(19)
$$ M_{2} \omega \cos \omega \tau - N_{2} \sin \omega \tau = - M_{1} \omega $$
(20)

Squaring and adding both sides of Eqs. (19) and (20) yields

$$ \omega^{4} + \left( {M_{1}^{2} - 2N_{1} - M_{2}^{2} } \right)\omega^{2} + \left( {N_{1}^{2} - N_{2}^{2} } \right) = 0 $$
(21)

Setting \( \omega^{2} = Z_{1} \), (21) becomes

$$ Z_{1}^{2} + MZ_{1} + T = 0. $$
(22)

Here, \( M = \left( {M_{1}^{2} - 2N_{1} - M_{2}^{2} } \right) \) and \( T = \left( {N_{1}^{2} - N_{2}^{2} } \right) \).

Clearly, if \( M = \left( {M_{1}^{2} - 2N_{1} - M_{2}^{2} } \right) > 0 \) and \( T = \left( {N_{1}^{2} - N_{2}^{2} } \right) > 0 \) are satisfied simultaneously, and then by Routh–Hurwitz Criterion (22) will always have roots with the negative real part. It contradicts our assumption for instability that \( \lambda = i\omega \) is a root of (17). Hence, \( {\text{Q}}^{ *} \) is locally asymptotically stable for \( \tau > 0 \).

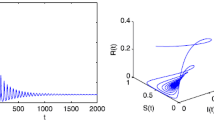
Hopf bifurcation analysis

In this section, we discuss the Hopf bifurcation of system (5).

If \( T = \left( {N_{1}^{2} - N_{2}^{2} } \right) \) in (22) is negative, then there is unique positive \( \omega_{0} \) satisfying (22), i.e., there is a single pair of purely imaginary roots \( \pm i\omega_{0} \) to (22).

From Eqs. (19) and (20), \( \tau_{n} \) corresponding to \( \omega_{0} \) can be obtained as

$$ \tau_{n} = \frac{1}{{\omega_{0} }} \arccos \left( {\frac{{\left( {N_{2} - M_{1} M_{2} } \right)\omega_{0}^{2} - N_{1} N_{2} }}{{M_{2}^{2} \omega_{0}^{2} + N_{2}^{2} }}} \right) + \frac{2n\pi }{{\omega_{0} }},\quad n = 0, 1, 2, \ldots . $$
(23)

Endemic equilibrium \( Q^{*} \) is stable for \( \tau < \tau_{0} \) if transversality condition holds true, i.e., if \( \left. {\frac{{{\text{d}} }}{{{\text{d}}\tau }}\left( {\text{Re} \left( \lambda \right)} \right)} \right|_{{\lambda = i\omega_{0} }} > 0 \).

Differentiating (17) with respect to \( \tau \), we get

$$ \begin{aligned} & \left( {2\lambda + M_{1} + M_{2} {\text{e}}^{ - \lambda \tau } - \left( {M_{2} \lambda + N_{2} } \right)\tau {\text{e}}^{ - \lambda \tau } } \right)\frac{{{\text{d}}\lambda }}{{{\text{d}}\tau }} = \lambda \left( {M_{2} \lambda + N_{2} } \right){\text{e}}^{ - \lambda \tau } \\ & \left( {\frac{{{\text{d}}\lambda }}{{{\text{d}}\tau }}} \right)^{ - 1} = \frac{{\left( {2\lambda + M_{1} + M_{2} e^{ - \lambda \tau } - \left( {M_{2} \lambda + N_{2} } \right)\tau {\text{e}}^{ - \lambda \tau } } \right)}}{{\lambda \left( {M_{2} \lambda + N_{2} } \right){\text{e}}^{ - \lambda \tau } }} = \frac{{\left( {2\lambda + M_{1} } \right)}}{{\lambda \left( {M_{2} \lambda + N_{2} } \right){\text{e}}^{ - \lambda \tau } }} + \frac{{M_{2} }}{{\lambda \left( {M_{2} \lambda + N_{2} } \right)}} - \frac{\tau }{\lambda } \\ & \left( {\frac{{{\text{d}}\lambda }}{{{\text{d}}\tau }}} \right)^{ - 1} = \frac{{\left( {2\lambda + M_{1} } \right)}}{{ - \lambda \left( {\lambda^{2} + M_{1} \lambda + N_{1} } \right)}} + \frac{{M_{2} }}{{\lambda \left( {M_{2} \lambda + N_{2} } \right)}} - \frac{\tau }{\lambda } \\ & \left. {\frac{{{\text{d}} }}{{{\text{d}}\tau }}\left( {\text{Re} \left( \lambda \right)} \right)^{ - 1} } \right|_{{\lambda = i\omega_{0} }} = \left. {\text{Re} \left( {\frac{{{\text{d}}\lambda }}{{{\text{d}}\tau }}} \right)^{ - 1} } \right|_{{\lambda = i\omega_{0} }} \\ & = \text{Re} \left( {\frac{{\left( {2i\omega_{0} + M_{1} } \right)}}{{ - i\omega_{0} \left( { - \omega_{0}^{2} + iM_{1} \omega_{0} + N_{1} } \right)}} + \frac{{M_{2} }}{{i\omega_{0} \left( {iM_{2} \omega_{0} + N_{2} } \right)}} - \frac{\tau }{{i\omega_{0} }} } \right) \\ & = \text{Re} \left( {\frac{1}{{\omega_{0} }}\left( {\frac{{\left( {2i\omega_{0} + M_{1} } \right)}}{{\left( {\omega_{0}^{2} - N_{1} } \right)i + M_{1} \omega_{0} )}} + \frac{{M_{2} }}{{\left( { - M_{2} \omega_{0} + iN_{2} } \right)}} + i\tau } \right)} \right) \\ & = \frac{1}{{\omega_{0} }}\left( {\frac{{2\omega_{0} \left( {\omega_{0}^{2} - N_{1} } \right) + M_{1}^{2} \omega_{0} }}{{\left( {\omega_{0}^{2} - N_{1} } \right)^{2} + \left( {M_{1} \omega_{0} } \right)^{2} }} - \frac{{M_{2}^{2} \omega_{0} }}{{\left( {M_{2} \omega_{0} } \right)^{2} + N_{2}^{2} }} } \right) \\ \end{aligned} $$
(24)

\( = \frac{{2\omega_{0}^{2} + \left( {M_{1}^{2} - 2N_{1} - M_{2}^{2} } \right)}}{{\left( {M_{2} \omega_{0} } \right)^{2} + N_{2}^{2} }} \) [since, from Eqs. (19), (20), \( \left( {\omega_{0}^{2} - N_{1} } \right)^{2} + \left( {M_{1} \omega_{0} } \right)^{2} = \left( {M_{2} \omega_{0} } \right)^{2} + N_{2}^{2} \)].

Under the condition \( M_{1}^{2} - 2N_{1} - M_{2}^{2} > 0 \), we have \( \left. {\frac{{{\text{d}} }}{{{\text{d}}\tau }}\left( {\text{Re} \left( \lambda \right)} \right)} \right|_{{\lambda = i\omega_{0} }} > 0 \).

Thus, the transversality condition holds and Hopf bifurcation occurs at \( \omega = \omega_{0} , \tau = \tau_{0} \).

By summarizing the above analysis, we arrive at the following theorem.

Theorem 6

The endemic equilibrium (EE) of system (5) is locally asymptotically stable for\( \tau \in \left[ {0, \tau_{0} } \right) \), and it exhibits Hopf bifurcation at\( \tau = \tau_{0} \).

Global stability

We suppose that

$$ H\left( {X\left( t \right)} \right) = \alpha X\left( t \right),\quad F\left( {Y\left( t \right)} \right) = \frac{Y\left( t \right)}{1 + \beta Y\left( t \right)}. $$

To prove our results, we need the following assumptions:

  1. (H1)

    \( H\left( 0 \right) = F\left( 0 \right) = 0; H^{\prime}\left( X \right) > 0, \) for all \( X,Y > 0 \).

  2. (H2)

    \( F^{\prime}\left( Y \right) > 0; \frac{{\partial^{2} F\left( Y \right)}}{{\partial Y^{2} }} \le 0, \) for all \( X,Y > 0 \).

  3. (H3)

    \( \frac{F\left( Y \right)}{{F\left( {Y^{*} } \right)}} \le 1; \frac{{\left( {\mu + \sigma + \theta } \right)Y + \frac{{\omega Y^{2} }}{{1 + \varphi Y^{2} }}}}{{H\left( {X^{*} } \right)F\left( Y \right)}} \ge 1 \) or \( \frac{F\left( Y \right)}{{F\left( {Y^{*} } \right)}} \ge 1; \frac{{\left( {\mu + \sigma + \theta } \right)Y + \frac{{\omega Y^{2} }}{{1 + \varphi Y^{2} }}}}{{H\left( {X^{*} } \right)F\left( Y \right)}} \le 1 \) for all \( X,Y > 0 \).

Theorem 7

Suppose that assumptions (H1–H3) are satisfied.

  1. 1.

    If\( R_{0} > 1, \)the endemic equilibrium\( Q^{*} \left( {X^{*} , Y^{*} } \right) \)is globally asymptotically stable (GAS) for any\( \tau \ge 0 \).

  2. 2.

    If\( R_{0} \le 1, \)the infection-free equilibrium\( Q\left( {X_{0} ,0} \right) = Q\left( {\frac{A}{\mu },0} \right) \)is globally asymptotically stable (GAS) for any\( \tau \ge 0 \).

Proof

(1) Let us consider any solution \( \left( {X\left( t \right),Y\left( t \right)} \right) \) of system (5) with the initial conditions. For any \( \tau \ge 0, \) we define the function \( U_{1} \left( t \right) \) as follows:

$$ U_{1} \left( t \right) = X\left( t \right) - \mathop \smallint \limits_{{X^{*} }}^{X\left( t \right)} \frac{{H\left( {X^{*} } \right)}}{H\left( \eta \right)}{\text{d}}\eta + Y\left( t \right) - \mathop \smallint \limits_{{Y^{*} }}^{Y\left( t \right)} \frac{{F\left( {Y^{*} } \right)}}{F\left( \eta \right)}{\text{d}}\eta . $$

Korobeinikov and Maini (2005) showed that \( Q^{*} \) is the only internal stationary point and the minimum point of \( U_{1} \left( t \right) \to \infty \) at the boundary of the positive quadrant. Therefore, \( Q^{*} \) is the global minimum point, and the function is bounded from below.

Let

$$ U_{2} = \mathop \smallint \limits_{0}^{\tau } \left[ {\frac{{F\left( {Y\left( {t - \xi } \right)} \right)}}{{F\left( {Y^{*} } \right)}} - 1 - \ln \frac{{F\left( {Y\left( {t - \xi } \right)} \right)}}{{F\left( {Y^{*} } \right)}}} \right]{\text{d}}\xi . $$

It easy to see that \( U_{2} \ge 0 \) and \( U_{2} = 0 \) if and only if \( Y\left( {t - \xi } \right) = Y^{*} \) for all \( \xi \in \left[ {0,\tau } \right] \). For any positive \( Y\left( {t - \xi } \right) \) for \( \xi \) in \( \left[ {0,\tau } \right] \), \( U_{2} \) will be finite and can be differentiated. Then, the derivative of \( U_{2} \) satisfies

$$ \begin{aligned} \frac{{{\text{d}}U_{2} }}{{{\text{d}}t}} & = \frac{\text{d}}{{{\text{d}}t}}\mathop \smallint \limits_{0}^{\tau } \left[ {\frac{{F\left( {Y\left( {t - \xi } \right)} \right)}}{{F\left( {Y^{*} } \right)}} - 1 - \ln \frac{{F\left( {Y\left( {t - \xi } \right)} \right)}}{{F\left( {Y^{*} } \right)}}} \right]{\text{d}}\xi \\ & = \mathop \smallint \limits_{0}^{\tau } \frac{\text{d}}{{{\text{d}}t}}\left[ {\frac{{F\left( {Y\left( {t - \xi } \right)} \right)}}{{F\left( {Y^{*} } \right)}} - 1 - \ln \frac{{F\left( {Y\left( {t - \xi } \right)} \right)}}{{F\left( {Y^{*} } \right)}}} \right]{\text{d}}\xi \\ & = - \mathop \smallint \limits_{0}^{\tau } \frac{\text{d}}{{{\text{d}}\xi }}\left[ {\frac{{F\left( {Y\left( {t - \xi } \right)} \right)}}{{F\left( {Y^{*} } \right)}} - 1 - \ln \frac{{F\left( {Y\left( {t - \xi } \right)} \right)}}{{F\left( {Y^{*} } \right)}}} \right]{\text{d}}\xi \\ & = - \left[ {\frac{{F\left( {Y\left( {t - \xi } \right)} \right)}}{{F\left( {Y^{*} } \right)}} - 1 - \ln \frac{{F\left( {Y\left( {t - \xi } \right)} \right)}}{{F\left( {Y^{*} } \right)}}} \right]_{\xi = 0}^{\tau } \\ & = - \frac{{F\left( {Y\left( {t - \tau } \right)} \right)}}{{F\left( {Y^{*} } \right)}} + \frac{{F\left( {Y\left( t \right)} \right)}}{{F\left( {Y^{*} } \right)}} + \ln \frac{{F\left( {Y\left( {t - \tau } \right)} \right)}}{F\left( Y \right)}. \\ \end{aligned} $$

Now, we study the behavior of Lyapunov functional

$$ V_{1} = U_{1} \left( t \right) + \left( {\mu + \sigma + \theta + \frac{{\omega Y^{*} }}{{1 + \varphi Y^{*2} }}} \right)Y^{*} U_{2} $$

The derivative of \( V_{1} \) along the solution of (5) is given by:

$$ \begin{aligned} \frac{{{\text{d}}V_{1} }}{{{\text{d}}t}} & = \left( {1 - \frac{{H\left( {X^{*} } \right)}}{H\left( X \right)}} \right)\dot{X}\left( t \right) + \left( {1 - \frac{{F\left( {Y^{*} } \right)}}{F\left( Y \right)}} \right)\dot{Y}\left( t \right)\\&\quad + \left( {\mu + \sigma + \theta + \frac{{\omega Y^{*} }}{{1 + \varphi Y^{*2} }}} \right)Y^{*} \frac{{{\text{d}}U_{2} }}{{{\text{d}}t}} \\ & = \left( {1 - \frac{{H\left( {X^{*} } \right)}}{H\left( X \right)}} \right)\left( {\mu X^{*} + H\left( {X^{*} } \right)F\left( {Y^{*} } \right)}\right.\\&\quad\left.{ - \mu X - H\left( X \right)F\left( {Y\left( {t - \tau } \right)} \right)} \right) + \left( {1 - \frac{{F\left( {Y^{*} } \right)}}{F\left( Y \right)}} \right)\\&\quad\times\left( {H\left( X \right)F\left( {Y\left( {t - \tau } \right)} \right) - \left( {\mu + \sigma + \theta } \right)Y - \frac{{\omega Y^{2} }}{{1 + \varphi Y^{2} }}} \right) \\ & \quad - \left( {\mu + \sigma + \theta + \frac{{\omega Y^{*} }}{{1 + \varphi Y^{*2} }}} \right)Y^{*}\\&\quad\times \left( {\frac{{F\left( {Y\left( {t - \tau } \right)} \right)}}{{F\left( {Y^{*} } \right)}} - \frac{F\left( Y \right)}{{F\left( {Y^{*} } \right)}} - \ln \frac{{F\left( {Y\left( {t - \tau } \right)} \right)}}{F\left( Y \right)}} \right). \\ \end{aligned} $$

By noting that

$$ \ln \frac{{F\left( {Y\left( {t - \tau } \right)} \right)}}{F\left( Y \right)} = \ln \frac{{H\left( {X^{*} } \right)}}{H\left( X \right)} + \ln \frac{{H\left( X \right)F\left( {Y\left( {t - \tau } \right)} \right)}}{{H\left( {X^{*} } \right)F\left( Y \right)}}, $$

and

$$ \left( {\mu + \sigma + \theta + \frac{{\omega Y^{*} }}{{1 + \varphi Y^{*2} }}} \right)Y^{*} = H\left( {X^{*} } \right)F\left( {Y^{*} } \right), $$

it is easy to see that

$$ \begin{aligned} \frac{{{\text{d}}V_{1} }}{{{\text{d}}t}} & = \frac{\mu }{H\left( X \right)}\left( {H\left( X \right) - H\left( {X^{*} } \right)} \right)\left( {X^{*} - X} \right) + H\left( {X^{*} } \right)F\left( {Y^{*} } \right)\\&\quad\times\left( {1 - \frac{{H\left( {X^{*} } \right)}}{H\left( X \right)} + \ln \frac{{H\left( {X^{*} } \right)}}{H\left( X \right)}} \right) + H\left( {X^{*} } \right)F\left( {Y^{*} } \right)\\&\quad\times\left( {1 + { \ln }\frac{{H\left( X \right)F\left( {Y\left( {t - \tau } \right)} \right)}}{{H\left( {X^{*} } \right)F\left( Y \right)}} - \frac{{H\left( X \right)F\left( {Y\left( {t - \tau } \right)} \right)}}{{H\left( {X^{*} } \right)F\left( Y \right)}}} \right) \\ & \quad + H\left( {X^{*} } \right)F\left( {Y^{*} } \right)\left( {\left( {\frac{F\left( Y \right)}{{F\left( {Y^{*} } \right)}} - 1} \right)}\right.\\&\quad\times\left.{\left( {1 - \frac{{\left( {\mu + \sigma + \theta } \right)Y + \frac{{\omega Y^{2} }}{{1 + \varphi Y^{2} }}}}{{H\left( {X^{*} } \right)F\left( Y \right)}}} \right)} \right). \\ \end{aligned} $$

Here,

$$ \begin{aligned} & 1 - \frac{{H\left( {X^{*} } \right)}}{H\left( X \right)} + \ln \frac{{H\left( {X^{*} } \right)}}{H\left( X \right)} \le 0;\;{\text{for}}\;{\text{all}}\;X > 0,\;{\text{and}}\;\\&1 + { \ln }\frac{{H\left( X \right)F\left( {Y\left( {t - \tau } \right)} \right)}}{{H\left( {X^{*} } \right)F\left( Y \right)}} \\ & \quad - \frac{{H\left( X \right)F\left( {Y\left( {t - \tau } \right)} \right)}}{{H\left( {X^{*} } \right)F\left( Y \right)}} \le 0;\;{\text{for}}\;{\text{all}}\;Y\left( {t - \tau } \right) > 0,\quad X > 0. \\ \end{aligned} $$
(25)

For monotonically increasing function \( H\left( X \right),H\left( X \right) \ge H\left( {X^{*} } \right) \) holds when \( X \ge X^{*} \), and hence, the following inequalities hold:

$$ \left( {X^{*} - X} \right)\left( {H\left( X \right) - H\left( {X^{*} } \right)} \right) \le 0. $$
(26)

Hence, by condition (H3) and inequalities (25)–(26), all the conditions of corollary 5.2 of Kuang (1993) hold true. Hence, \( Q^{*} \) is globally asymptotically stable for any \( \tau \ge 0 \) when \( R_{0} > 1. \)

(2) We consider the Lyapunov functional

$$ V_{2} = X\left( t \right) - \mathop \smallint \limits_{{X_{0} }}^{X\left( t \right)} \frac{{H\left( {X_{0} } \right)}}{H\left( \eta \right)}{\text{d}}\eta + Y\left( t \right) + H\left( {X_{0} } \right)\mathop \smallint \limits_{0}^{\tau } F\left( {Y\left( {t - \xi } \right)} \right){\text{d}}\xi . $$
(27)

Let

$$ U_{3} = \mathop \smallint \limits_{0}^{\tau } F\left( {Y\left( {t - \xi } \right)} \right){\text{d}}\xi . $$

The derivative of \( U_{3} \) is

$$ \begin{aligned} \frac{{{\text{d}}U_{3} }}{{{\text{d}}t}}& = \mathop \smallint \limits_{0}^{\tau } \frac{\text{d}}{{{\text{d}}t}}F\left( {Y\left( {t - \xi } \right)} \right){\text{d}}\xi = - \mathop \smallint \limits_{0}^{\tau } \frac{\text{d}}{{{\text{d}}\xi }}F\left( {Y\left( {t - \xi } \right)} \right){\text{d}}\xi\\& = - F\left( {Y\left( {t - \tau } \right)} \right) + F\left( {Y\left( t \right)} \right). \end{aligned} $$

Hence, we obtain

$$ \begin{aligned} \frac{{{\text{d}}V_{2} }}{{{\text{d}}t}} & = \left( {1 - \frac{{H\left( {X_{0} } \right)}}{H\left( X \right)}} \right)\dot{X}\left( t \right) + \dot{Y}\left( t \right) + H\left( {X_{0} } \right)\frac{{{\text{d}}U_{3} }}{{{\text{d}}t}} \\ & = \left( {1 - \frac{{H\left( {X_{0} } \right)}}{H\left( X \right)}} \right)\left( {\mu X^{*} - \mu X - H\left( X \right)F\left( {Y\left( {t - \tau } \right)} \right)} \right)\\&\quad + \left( {H\left( X \right)F\left( {Y\left( {t - \tau } \right)} \right) - \left( {\mu + \sigma + \theta } \right)Y - \frac{{\omega Y^{2} }}{{1 + \varphi Y^{2} }}} \right) \\ & \quad - H\left( {X_{0} } \right)F\left( {Y\left( {t - \tau } \right)} \right) + H\left( {X_{0} } \right)F\left( {Y\left( t \right)} \right) \\ & = - \frac{\mu }{H\left( X \right)}\left( {X - X_{0} } \right)\left( {H\left( X \right) - H\left( {X_{0} } \right)} \right) - \frac{{\omega Y^{2} }}{{1 + \varphi Y^{2} }} \\&\quad+ \left( {\mu + \sigma + \theta } \right)\left( {\frac{{H\left( {X_{0} } \right)F\left( {Y\left( t \right)} \right)}}{{\left( {\mu + \sigma + \theta } \right)}} - Y} \right). \\ \end{aligned} $$

It holds that \( \mathop {\lim }\limits_{t \to \infty } \frac{{{\text{d}}V_{2} }}{{{\text{d}}t}} = 0 \), which yields \( \mathop {\lim }\limits_{t \to \infty } X\left( t \right) = X_{0} \) and \( \mathop {\lim }\limits_{t \to \infty } Y\left( t \right) = 0. \)

Now,

$$ \left( {X - X_{0} } \right)\left( {H\left( X \right) - H\left( {X_{0} } \right)} \right) \ge 0, $$
(28)

and the condition (H2) ensures that \( F\left( Y \right) \le \frac{\partial F\left( 0 \right)}{\partial Y}Y \) for all \( Y > 0. \) Hence,

$$ \frac{{H\left( {X_{0} } \right)F\left( {Y\left( t \right)} \right)}}{{\left( {\mu + \sigma + \theta } \right)}} - Y \le \left( {\frac{{H\left( {X_{0} } \right)\frac{\partial F\left( 0 \right)}{\partial Y}}}{{\left( {\mu + \sigma + \theta } \right)}} - 1} \right)Y = \left( {R_{0} - 1} \right)Y. $$
(29)

Therefore, \( R_{0} < 1 \) ensures that \( \frac{{{\text{d}}V_{2} }}{{{\text{d}}t}} \le 0 \) for all \( X\left( t \right),Y\left( t \right) \ge 0 \). Hence, again from corollary 5.2 of Kuang (1993), we have that \( Q \) is stable.

Furthermore, also for \( R_{0} = 1,\frac{{{\text{d}}V_{2} }}{{{\text{d}}t}} = 0 \) implies that \( X\left( t \right) = X_{0} \). Hence, it can be shown that \( Q\left( {X_{0} ,0} \right) \) is the largest invariant set in \( \left\{ {\left. {\left( {X\left( t \right),Y\left( t \right)} \right) } \right| \dot{V}_{2} = 0} \right\} \). With the help of the classical Lyapunov–LaSalle invariance principle (Hale and Verduyn Lunel 1993; Sastry 1999), \( Q \) is globally stable.

This completes the proof of Theorem 7.

Undelayed system

In this section, we consider the case of instantaneous transmission of primary infection. We perform a qualitative analysis of system (5) without delay, i.e., we set τ = 0. This analysis has interest in itself and will also allow getting some information on the stability of coexistence equilibrium in the case with delay.

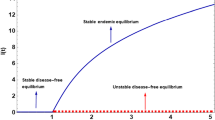
It is useful to investigate the stability properties of system (5), without delay, near the criticality (that is, at Q and R0 = 1). To this aim, we use the bifurcation theory approach developed in Buonomo and Cerasuolo (2015), which is based on the center manifold theory (Sastry 1999). In particular, we are interested to assess if there is a stable coexistence equilibrium bifurcation form Q, and Q changes from being stable to unstable. This behavior is called forward bifurcation (Buonomo and Cerasuolo 2015).

Now, for the undelayed system, we propose the following result:

Theorem 8

When τ = 0, system (5) exhibits a forward bifurcation at Q and R0 = 1.

Proof

Clearly, from the expression of R0 it can be seen that R0 is directly related to α. Subsequently, we choose α as the bifurcation parameter. Moreover, R0 = 0 implies that \( \alpha = \alpha^{*} = \frac{\mu (\mu + \sigma + \theta )}{A} \). Since the linearization technique is not applicable to check the stability behavior at \( R_{0} = 1 \), so we use center manifold theory (Sastry 1999). For this, we redefined \( X = x_{1} \; {\text{and}}\;Y = x_{2} \), and then system (5) takes the form

$$ \begin{aligned} \frac{{{\text{d}}x_{1} }}{{{\text{d}}t}} & = A - \mu x_{1} - \frac{{\alpha x_{1} x_{2} \left( t \right)}}{{1 + \beta x_{2} \left( t \right)}} \equiv f_{1} , \\ \frac{{{\text{d}}x_{2} }}{{{\text{d}}t}} & = \frac{{\alpha x_{1} x_{2} \left( t \right)}}{{1 + \beta x_{2} \left( t \right)}} - \left( {\mu + \sigma + \theta } \right)x_{2} - \frac{{\omega x_{2}^{2} }}{{1 + \varphi x_{2}^{2} }} \equiv f_{2} . \\ \end{aligned} $$
(30)

The Jacobian matrix \( J^{\prime} \) of the model system (30) evaluated at \( R_{0} = 1 \) and \( \alpha = \alpha^{*} \) around the disease-free equilibrium is

$$ J^{\prime} = \left[ {\begin{array}{*{20}c} { - \mu } & { - \frac{{\alpha^{*} A}}{\mu }} \\ 0 & 0 \\ \end{array} } \right]. $$

\( J^{\prime} \) has a simple zero eigenvalue while the other eigenvalue is negative. The right eigenvector \( w = \left[ {w_{1} , w_{2} } \right]^{\text{T}} \) of \( J^{\prime} \) corresponding to zero eigenvalue can be obtained as given below:

$$ w_{1} = - \frac{{\alpha^{*} A}}{{\mu^{2} }}, \quad w_{2} = 1 $$

Similarly, the left eigenvector \( u = \left[ {u_{1} , u_{2} } \right] \) of \( J^{\prime} \) corresponding to zero eigenvalue is obtained as \( \left[ {0, 1} \right] \). The nonzero partial derivatives associated with the functions \( f_{1} \) and \( f_{2} \) evaluated at \( R_{0} = 1 \) and \( \alpha = \alpha^{*} \) are

$$ \begin{aligned}& \left( {\frac{{\partial^{2} f_{2} }}{{\partial x_{1} \partial x_{2} }}} \right)_{Q} = \left( {\frac{{\partial^{2} f_{2} }}{{\partial x_{2} \partial x_{1} }}} \right)_{Q} = \alpha^{*} , \quad \\&\left( {\frac{{\partial^{2} f_{2} }}{{\partial x_{2}^{2} }}} \right)_{Q} = - \frac{{2\beta \alpha^{*} A}}{\mu } - 2\omega \; {\text{and}}\;\left( {\frac{{\partial^{2} f_{2} }}{{\partial x_{2} \partial \alpha^{*} }}} \right)_{Q} = \frac{A}{\mu }. \end{aligned} $$

Using Theorem 4.1 given in Castillo-Chavez and Song (2004), the coefficients \( a_{1} \;{\text{and}}\; b_{1} \) can be computed as

$$ \begin{aligned} a_{1} & = \mathop \sum \limits_{k,i,j = 1}^{2} u_{k} w_{i} w_{j} \left( {\frac{{\partial^{2} f_{k} }}{{\partial x_{i} \partial x_{j} }}} \right)_{Q} \\ & = u_{2} \left( {2w_{1} w_{2} \alpha^{*} - w_{2}^{2} \left( {\frac{{2\beta \alpha^{*} A}}{\mu } + 2\omega } \right)} \right) \\ & = - \left( {2\frac{{\alpha^{*} A}}{{\mu^{2} }}\alpha^{*} + \frac{{2\beta \alpha^{*} A}}{\mu } + 2\omega } \right) < 0 \\ \end{aligned} $$

and

$$ \begin{aligned} b_{1} & = \mathop \sum \limits_{k,i = 1}^{2} u_{k} w_{i} \left( {\frac{{\partial^{2} f_{k} }}{{\partial x_{i} \partial \beta^{*} }}} \right)_{Q} \\ & = u_{2} \left( {w_{2} \frac{A}{\mu }} \right) \\ & = \frac{A}{\mu } > 0. \\ \end{aligned} $$

From the expressions of \( a_{1} \) and \( b_{1} \), it is evident that \( a_{1} < 0 \) and \( b_{1} > 0 \). Therefore, from Theorem 4.1 of Castillo-Chavez and Song (2004) bifurcation is forward. This completes the proof.

Theorem 9

For \( \tau = 0 \) , system ( 5 ) at \( Q^{*} \) is locally asymptotically stable if \( M_{1} + M_{2} > 0 \) and \( N_{1} + N_{2} > 0 \) are satisfied simultaneously.

Proof

At endemic equilibrium \( Q^{*} \), the characteristic equation of system (5) is obtaining by putting \( \tau = 0 \) in (17) as given below:

$$ \lambda^{2} + M_{1} \lambda + N_{1} + \left( {M_{2} \lambda + N_{2} } \right) = 0 $$
(31)

Clearly, if \( M_{1} + M_{2} > 0 \) and \( N_{1} + N_{2} > 0 \) are satisfied simultaneously, and then by Routh–Hurwitz Criterion (31) will always have roots with the negative real part, and hence, system (5) at \( Q^{*} \) for \( \tau = 0 \) is locally asymptotically stable.

Discussion

In this study, we have proposed and analyzed a novel SIR epidemic model along with nonlinear incidence rate, time delay (describing the incubation period) and Holling type III treatment rate. The analysis of the model has been discussed in terms of a threshold parameter \( R_{0} \). The mathematical analysis has shown that DFE is locally asymptotically stable when \( R_{0} < 1 \) and unstable when \( R_{0} > 1 \) for time delay \( \tau > 0 \) which describes that disease can be eliminated from the community when \( R_{0} < 1 \) and it will persist when \( R_{0} > 1 \). Further, we have shown that the DFE at \( R_{0} = 1 \) is linearly neutrally stable for time delay \( \tau > 0 \) which reveals that disease may persist at a very low level in society and exhibits a forward bifurcation for the time delay \( \tau = 0 \), i.e., there is a stable coexistence equilibrium \( Q^{*} \) bifurcating from \( Q \), and \( Q \) changes from being stable to unstable. We have shown that EE is locally asymptotically stable under the conditions stated in Theorems 5 and 9 for \( \tau > 0 \) and \( \tau = 0 \), respectively. Furthermore, conditions for Hopf bifurcation have also been discussed. Moreover, it has also shown that both DFE and EE are globally asymptotically stable when \( R_{0} \le 1 \) and \( R_{0} > 1 \) respectively.