A mathematical and numerical study of a SIR epidemic model with time delay, nonlinear incidence and treatment rates

Abstract

A novel nonlinear time-delayed susceptible–infected–recovered epidemic model with Beddington–DeAngelis-type incidence rate and saturated functional-type treatment rate is proposed and analyzed mathematically and numerically to control the spread of epidemic in the society. Analytical study of the model shows that it has two equilibrium points: disease-free equilibrium (DFE) and endemic equilibrium (EE). The stability of the model at DFE is discussed with the help of basic reproduction number, denoted by ${R_0}$, and it is shown that if the basic reproduction number ${R_0}$ is less than one, the DFE is locally asymptotically stable and unstable if ${R_0}$ is greater than one. The stability of the model at DFE for ${R_0}=1$ is analyzed using center manifold theory and Castillo-Chavez and Song theorem which reveals a forward bifurcation. We also derived the conditions for the stability and occurrence of Hopf bifurcation of the model at endemic equilibrium. Further, to illustrate the analytical results, the model is simulated numerically.

Introduction

Mathematical analysis and modeling of infectious diseases play a crucial role in studying a wide range of infectious diseases to better understand the transmission dynamics and have the capacity to influence expectations and to decide and assess control strategies. Elementary descriptions of infectious diseases have been considered mainly by three epidemiological classes which measure the susceptible portion of population, the infected and the removed (recovered) ones. Authors around the world have proposed different kinds of epidemic models such as susceptible–infected (SI) (Mukherjee 1996), susceptible–infected–susceptible (SIS) (Hethcote and van den Driessche 1995), susceptible–infected–recovered (SIR) (Kumar and Nilam 2018a), susceptible–infected–recovered–susceptible (SIRS) (Mena-Lorca and Hethcote 1992), susceptible–exposure–infected–recovered (SEIR) (Dubey et al. 2013; Tipsri and Chinviriyasit 2014), susceptible–Vaccinated–exposure–infected–recovered (SVEIR) (Gumel et al. 2007) and many more, to understand the dynamics of disease transmission. In the mathematical epidemiological literature, several authors have studied the epidemiological models with latent or incubation period, because many diseases have a latent or incubation period, during which the susceptible individual becomes infected but is not yet infectious. Such latency in disease transmission can be modeled by a delay differential equation. Delay differential equations (DDE) have been a very successful tool to capture the effect of varying infectious period in a range of SIR, SIS, SIRS and other epidemic models. Hethcote and van den Driessche (1995) have studied an SIS epidemic model with constant time delay, which accounts for duration of infectiousness. Also, Song and Cheng (2005) have studied the impact of time delay on the stability of the positive equilibrium, as a resultant of which conditions have been stated for the asymptotical stability of the endemic equilibrium for all delays. Xu and Ma (2009b), Hattaf et al. (2013), Kumar and Nilam (2018a, b) considered the effect of time delay on SIRS and SIR models, respectively, and provided the conditions for the stability of their proposed models.

The incidence rate of a disease is the number of new cases per unit time and plays a crucial role in the study of transmission of disease dynamics. Several authors suggested different types of incidence rate. Firstly, the bilinear incidence rate $\beta$SI (Kermack and McKendrick 1927; Bailey 1975; Anderson and May 1992; Brauer and Castillo-Chavez 2001; Zhang and Suo 2010) is based on the law of mass action, which describes the situation that if the number of susceptibles increases, the number of individuals who become infected per unit of time increases, which is not realistic. In reality, however, by the impact of media, open mindfulness or individual experience, people apply careful steps that decrease the contact number or the transmission potential. Since nonlinearity in the incidence rates has been seen in disease transmission dynamics, it has been proposed that the standard bilinear incidence rate shall be modified into a nonlinear incidence rate by numerous authors (Capasso and Serio 1978; Korobeinikov 2007). Several authors such as Anderson and May (1978), Wei and Chen (2008), Zhang et al. (2008), Li et al. (2009), Li and Muldowney (1995), Korobeinikov and Maini (2005), Xu and Ma (2009b), Capasso and Serio (1978) suggested different types of nonlinear incidence rates, and they incorporated nonlinear-type incidence rate in their model and studied the disease dynamics. Beddington (1975) and DeAngelis et al. (1975) independently introduced nonlinear incidence rate known as Beddington–DeAngelis-type incidence rate. Later, some authors (Kaddar 2010; Elaiw and Azoz 2013; Dubey et al. 2015) used this incidence rate in epidemiological models. To contribute to the nonlinear dynamics of infectious disease, in the present study we introduce the incidence rate as Beddington–DeAngelis type. Since nonlinear-type incidence rate alone cannot determine the actual transmission of the disease dynamics completely, for a more realistic model, inclusion of time delay must be considered. Therefore, in the present study we are incorporating the effect of time lag into Beddington DeAngelis functional-type incidence rate and investigating its impact on the disease dynamics.

It is well known that to prevent and control the spread of epidemics, the treatment rate has played a substantial role. In the classical epidemic model, treatment rate was considered to be either constant (Wang and Ruan 2004) or proportional to number of infected individuals (Wang 2006). This type of treatment rate is suitable in the case when the number of infectives is small and treatment resources are sufficient and unsuitable when the number of the infectives is large and treatment resources are limited. To control the disease, most researchers focus on a nonlinear-type treatment rate. Dubey et al. (2013, 2015, 2016) introduced the nonlinear treatment rate as Holling type II, Holling type III and Holling type IV in their model and proposed nonlinear dynamics to control the epidemic. Holling type III defines the condition in which removal rate initially becomes quick with increment in infectives and after that it develops gradually and lastly settles down to maximum saturated value. After this any increase in infectives won’t influence the removal rate (Dubey et al. 2013). Motivated by these work, in the present study we take the nonlinear treatment rate as saturated treatment rate functional type of the form

$$\begin{aligned} g(I)= \frac{aI^2}{bI^2+cI+1} \quad ({\text{where}} \,\, I \ge 0,\,\, a,b >0 \,\, \text{and}\,\,c\ge 0) \end{aligned}$$

In the present study our aim is to understand and predict actual transmission of the infectious diseases and investigate the effect of treatment rate to provide effective control strategy that can hasten the dying out of disease. Therefore, motivated by the work of (Dubey et al. 2013, 2015, 2016) we consider a susceptible–infected–recovered (SIR) epidemic model setting with a nonlinear Beddington–DeAngelis functional-type incidence rate that includes awareness/inhibitions behavior by susceptibles and infectives with the inclusion of time lag (describing the latent period). We also consider nonlinear saturated treatment rate to provide a control strategy of the infectious diseases and show that if this behavioral response is delayed, then this simple looking system can exhibit interesting dynamics. For the dynamics of the model, we discuss the existence and stability behavior of model for equilibriums. The existence of a Hopf bifurcation is also discussed.

The rest of the paper is organized as follows: SIR model for disease dynamics and the basic mathematical properties of the model are studied in "Mathematical framework" section. In "Equilibrium and stability analysis" section, the basic reproduction number is derived, and we study the qualitative behavior of the model via stability at the equilibrium points and Hopf bifurcation when time delay is considered as the bifurcation parameter. Furthermore, in "Numerical simulation" section, numerical simulations are presented using MATHEMATICA 11, and lastly, we present our conclusion in "Conclusion" section.

Mathematical framework

In this section we present our mathematical model which is described by delay differential equation constructed from the interaction among the compartments: susceptible, infective and recovered for the model equation.

The basic model equations

We consider that in the region under consideration, the total population is N(t) at time t. The total population N(t) is divided into three subclasses: the susceptible class S(t), the infective I(t) and the recovered individuals R(t). Susceptible class S(t) consists of those individuals who are healthy but can contract the disease. The infective class I(t) is the class of individuals who have contracted the disease and are now infectious and can transmit the disease to others. R(t) represents the number of individuals who are recovered from the diseases with partial immunity or treatment. The conceptual description of the model is represented by a block diagram (Fig. 1).

Fig. 1

Transfer diagram for the delayed SIR model with the susceptible class S(t), the infective class I(t) and the recover class R(t)

The model we present in this paper is defined by the following system of nonlinear delay differential equations:

$$\begin{aligned} \frac{{\mathrm{d}S}}{{\mathrm{d}t}}&= \pi - \mu S - \frac{{\beta S(t - \tau )I(t - \tau )}}{{1 + \alpha S(t - \tau ) + \gamma I(t - \tau )}}, \\ \frac{{\mathrm{d}I}}{{\mathrm{d}t}}&= \frac{{\beta S(t - \tau )I(t - \tau )}}{{1 + \alpha S(t - \tau ) + \gamma I(t - \tau )}} - (\mu + d + \theta )I - \frac{{aI^2}}{{{bI^2} +cI + 1}}, \\ \frac{{\mathrm{d}R}}{{\mathrm{d}t}}&= \theta I + \frac{{aI^2}}{{{bI^2} +cI + 1}} - \mu R. \end{aligned}$$

(1)

where ${\tau > 0}$ represents the time delay describing the latent period of the disease.

The initial conditions $\phi = ({\phi _1},{\phi _2},{\phi _3})$ of (1) are defined in the Banach space

$$\begin{aligned} {C_ + } = \left\{ \phi \in C\left( [ - \tau ,0],R_ + ^3\right) :{\phi _1}(\Omega ) = S(\Omega ),\quad {\phi _2}(\Omega ) = I(\Omega ),\quad {\phi _3}(\Omega ) = R(\Omega )\right\} , \end{aligned}$$

where $R_ + ^3 = \{ (S,I,R) \in {R^3}:S \ge 0,I \ge 0,R \ge 0\}$. Biologically, we assume that ${\phi _i} > 0\quad (i = 1,2,3)$.

In the above model (1), we consider the total population N(t) at time t, with immigration of susceptible population with a constant rate $\pi$. The parameters $\mu$, d and $\theta$ represent the natural death rate, disease-induced death rate and recovery rate, respectively. In epidemiological models, by modifying the incidence rate (the number of individuals who become infected per unit of time), behavioral changes during an epidemic can be seen to shape the dynamics very differently from the kind predicted by simple models. Therefore, in the present model (1), we have taken the incidence rate as Beddington–DeAngelis type with delay:

$$\begin{aligned} f(S,I)= \frac{{\beta S(t - \tau )I(t - \tau )}}{{1 + \alpha S(t - \tau ) + \gamma I(t - \tau )}} \end{aligned}$$

Here, $\beta$ is the effective contact rate (or transmission rate) of susceptibles with infectives, $\alpha$ is a measure of inhibition effect, such as preventive measures taken by susceptible individuals, and $\gamma$ is a measure of inhibition effect such as treatment with respect to infectives. The incidence function f includes some special cases. For instance, if we set $\alpha = 0, \gamma = 0$, then the incidence rate is bilinear (Gumel et al. 2007) and if $\alpha = 0$ the incidence rate, describing saturated effects of the prevalence of infectious diseases, is used in McCluskey (2010) and Xu and Ma (2009a). The term $g(I)=\frac{{aI^2}}{{{bI^2} +cI + 1}}$ in model (1) is the saturated treatment rate, where $a > 0$ represents the treatment rate of infected individuals (cure rate), $b > 0$ is the limitation rate in treatment availability, and $c \ge 0$ is the saturation constant in absence of inhibitory effect.

Basic properties of the model

The equations of the model (1) monitor populations. From the proposition 2.1 in Hattaf et al. (2013) and proposition 2.3. in Yang and Sun (2015), it can be shown that all state variables of the model (1) are nonnegative. That is, $(S,I,R) \in {R^3_+}$. Also, for ecological reasons, we supposed that all parameters $\pi$, $\mu$, $\beta$, $\alpha$, $\gamma$, d, $\theta$, a, b are positive and c is nonnegative.

Since $N(t)=S(t)+I(t)+R(t)$, the governing equations of model (1) can be rewritten as,

$$\begin{aligned} \frac{\mathrm{d}N}{\mathrm{d}t}&= \pi -\mu N -dI \end{aligned}$$

(2)

$$\begin{aligned}&\le \pi -\mu N \end{aligned}$$

(3)

Lemma 1

All solutions of the model (1) starting in$R_+^3$are bounded and eventually enter a compact attracting set

$$\begin{aligned} \Phi =\left\{ \left( S,I,R\right) \in R^3_+: S(t)+I(t)+R(t)=N(t) \le \frac{\pi }{\mu } \right\} . \end{aligned}$$

Proof

Continuity of the right-hand side of the model (1) and its derivative assure the well-posedness of the model for $N(t) > 0$. The invariant region for the existence of the solutions can be determined as given below:

$$\begin{aligned} 0< \liminf \limits _{t\rightarrow \infty } N(t) \le \limsup \limits _{t\rightarrow \infty } N(t) \le \frac{\pi }{\mu } \end{aligned}$$

Since $N(t) > 0$ on $[-\tau , 0]$ by assumption, $N(t) > 0$ for all $t\ge 0$. Therefore, with the help of Eq. (3), it can be seen that for any finite time t, N(t) cannot blow up to infinity. The model system is dissipative (solutions are bounded), and consequently, the solution exists globally for all $t > 0$ in the invariant and compact set

$$\begin{aligned} \Phi =\left\{ \left( S,I,R\right) \in R^3_+: S(t)+I(t)+R(t)=N(t) \le \frac{\pi }{\mu } \right\} , \end{aligned}$$

As N(t) approaches zero, S(t), I(t), and R(t) also approach zero. Thus, each of these terms tends toward zero as N(t) does. Thus, it is reasonable to interpret these terms as zero when $N(t) = 0$. $\square$

Remark 1

In this region $\Phi$, basic results such as usual local existence, uniqueness and continuation of solutions are valid for model (1). Hence, there exists a unique solution (S(t), I(t), R(t)) of model (1) starting in the interior of $\Phi$ that exists on a maximal interval $[0,\infty )$ if solutions remain bounded (Kuang 1993).

Equilibrium and stability analysis

From the model (1) we infer that since R(t) does not appear in equations for $\frac{{\mathrm{d}S}}{{\mathrm{d}t}}$ and $\frac{{\mathrm{d}I}}{{\mathrm{d}t}}$, it is sufficient to analyze the behaviors of solutions of (1) by the following system of DDEs:

$$\begin{aligned} \frac{{\mathrm{d}S}}{{\mathrm{d}t}}&= \pi - \mu S - \frac{{\beta S(t - \tau )I(t - \tau )}}{{1 + \alpha S(t - \tau ) + \gamma I(t - \tau )}} \\ \frac{{\mathrm{d}I}}{{\mathrm{d}t}}&= \frac{{\beta S(t - \tau )I(t - \tau )}}{{1 + \alpha S(t - \tau ) + \gamma I(t - \tau )}} - (\mu + d + \theta )I \\&\quad - \frac{{aI^2}}{{{bI^2} +cI + 1}} \end{aligned}$$

(4)

with initial conditions $\phi = ({\phi _1},{\phi _2})$ of (4) defined in the Banach space

$$\begin{aligned} {C_ + } = \left\{ \phi \in C\left( [ - \tau ,0],R_ + ^2\right) :{\phi _1}(\Omega ) = S(\Omega ),{\phi _2}(\Omega ) = I(\Omega )\right\} , \end{aligned}$$

where $R_ + ^2 = \{ (S,I) \in {R^2}:S \ge 0,I \ge 0\}$,${\phi _i} > 0\quad (i = 1,2)$.

Now, we analyze the equilibrium points of the system (4). There are only two types of physically, and in addition biologically, relevant equilibria, namely

• 1. ${E_0}\left( {S_0},0 \right)$ = ${E_0}\left( \frac{\pi }{\mu },0 \right)$, disease-free equilibrium (DFE).

• 2. ${E_{\mathrm{e}}}({S^*},{I^*})$, positive or endemic equilibrium (EE)

where $S^*$ and $I^*$ are given in Section 3.2.

Disease-free equilibrium and its stability

System (4) has always a disease-free equilibrium point of the form ${E_0}\left( \frac{\pi }{\mu },0 \right)$ (that is, there is no infection present in the community and all individuals are susceptible) which is obtained by setting right-hand sides of the system (4) to zero. The characteristic equation of the linearization of model (4) near the disease-free equilibrium ${E_0}\left( \frac{ \pi }{\mu },0 \right)$ is given by

$$\begin{aligned} \left( \mu + \lambda \right) \left( {\frac{{\beta \pi {e^{ - \lambda \tau }}}}{{\mu + \alpha \pi }} - (\mu + d + \theta ) - \lambda } \right) = 0 \end{aligned}$$

(5)

One of the roots of Eq. (5) is given by ${\lambda _1} = - \mu$ and other root can be obtained from

$$\begin{aligned} {\frac{{\beta \pi {e^{ - \lambda \tau }}}}{{\mu + \alpha \pi }} - (\mu + d + \theta ) - \lambda }= 0 \end{aligned}$$

The term $\frac{{\beta \pi }}{{(\mu + \alpha \pi )\left( {\mu + d + \theta } \right) }}{e^{ - \lambda \tau }}$ at $\tau = 0$ is termed as basic reproduction number. In epidemiological research, the basic reproduction number, denoted by ${R_0}$, is defined as the average number of secondary infections caused by a single infected agent, during his/her entire infectious period, in a completely susceptible population (Van den Driessche and Watmough 2002). Thus, basic reproduction number for our model is given by

$$\begin{aligned} {R_0} = \frac{{\beta \pi }}{{(\mu + \alpha \pi )\left( {\mu + d + \theta } \right) }}. \end{aligned}$$

Analysis for ${{\varvec{R}}_0} \ne 1$

Clearly, Eq. (5) has one negative root ${\lambda _1} = - \mu$ and other root is obtained by the equation

$$\begin{aligned} \lambda + \mu + d + \theta - \frac{{\beta \pi }}{{(\mu + \alpha \pi )}}{e^{ - \lambda \tau }} = 0 \end{aligned}$$

Let

$$\begin{aligned} f(\lambda )&= \lambda + \mu + d + \theta - \frac{{\beta \pi }}{{(\mu + \alpha \pi )}}{e^{ - \lambda \tau }} \\&=\lambda +\left( \mu + d + \theta \right) \left( 1-R_0 {e^{ - \lambda \tau }} \right) \end{aligned}$$

If ${R_0} > 1$, it is readily seen that for real $\lambda$,

$$\begin{aligned} f(0) =\lambda +\left( \mu + d + \theta \right) \left( 1-R_0 \right) < 0, \,\,\,\,\mathop {\lim }\limits _{\lambda \rightarrow \infty } f(\lambda ) = + \infty \end{aligned}$$

Hence,$f(\lambda ) = 0$ and $f'(\lambda )>0$, so $f(\lambda ) = 0$ has a unique positive real root if $R{}_0 > 1$.

If $R{}_0 < 1$, we assume that $Re\lambda \ge 0$.

We notice that

$$\begin{aligned} {Re} \lambda&= \frac{{\beta \pi {e^{ - ({Re} \lambda )\tau }}\cos (Im\lambda )\tau }}{{(\mu + \alpha \pi )}} - \left( {\mu + d + \theta } \right) \\&< \frac{{\beta \pi }}{{(\mu + \alpha \pi )}} - \left( {\mu + d + \theta } \right) < 0 \end{aligned}$$

which contradicts our assumption. Therefore, if $R{}_0 < 1$ then $\lambda$ will be a root of Eq. (5) with negative real part. The result can be written in form of the theorem which is given below:

Theorem 1

The disease-free equilibrium${E_0}$is locally asymptotically stable if${{R} _0} < 1$and unstable if${{R} _0} > 1$.

Analysis at $R_0 = 1$

In this section, we analyze the behavior of system (4) when the basic reproduction number ${{R} _0}$ is equal to one. We observe that the Jacobian matrix of system (4) evaluated at ${{R} _0} = 1$ and bifurcation parameter $\beta = {\beta ^*} = \frac{{\left( {\mu + \alpha \pi } \right) \left( {\mu + d + \theta } \right) }}{\pi }$ has a simple zero eigenvalue and another eigenvalue with negative real part. Since linearization is not suitable to analyze the stability behavior of equilibrium points at ${R_0 = 1}$, center manifold theory (Sastry 1999) is used. Following assumptions are made to apply center manifold theory to system (4): let $S = {x_1}$ and $I={x_2}$, then the system (4) can be written as

$$\begin{aligned} {\frac{{\mathrm{d}{x_1}}}{{\mathrm{d}t}}}&= \pi - \mu {x_1} - \frac{{\beta {x_1}(t - \tau ){x_2}(t - \tau )}}{{1 + \alpha {x_1}(t - \tau ) + \gamma {x_2}(t - \tau )}} \equiv f_1 \\ {\frac{{\mathrm{d}{x_2}}}{{\mathrm{d}t}}}&= \frac{{\beta {x_1}(t - \tau ){x_2}(t - \tau )}}{{1 + \alpha {x_1}(t - \tau ) + \gamma {x_2}(t - \tau )}} - (\mu + d + \theta ){x_2} \\&\quad - \frac{{a{x_2^2}}}{{{x_2}^2 + b{x_2} + c}}\equiv f_2 \end{aligned}$$

(6)

Let J denotes the Jacobian matrix evaluated at ${R_0 = 1}$, and $\beta = {\beta ^*}$ then

$$\begin{aligned} J = \left[ {\begin{array}{ccc} { - \mu }&{}&{}{ - \frac{{{\beta ^* \pi } }}{{(\mu + \alpha \pi )}}}\\ 0&{}&{}0 \end{array}} \right] \end{aligned}$$

Let $w = \left[ {{w_1}}\,\,\,{{w_2}} \right]$ and $u = {\left[ {{u_1}}\,\,\,{{u_2}} \right] ^T}$ be the left and right nullvectors of J corresponding to the zero eigenvalue. Then we have

$$\begin{aligned} {w_1} = 0,\quad {w_2} = 1\quad \hbox {and} \quad {u_1} = - \frac{{{\beta ^* \pi } }}{{\mu (\mu + \alpha \pi )}},\quad {u_2} = 1 \end{aligned}$$

The nonzero partial derivatives associated with the functions $f_1$ and $f_2$ of the system (6) evaluated at ${R_0 = 1}$ and $\beta = {\beta ^*}$ are

$$\begin{aligned}&{\left( {\frac{{{\partial ^2}{f_2}}}{{\partial x_2^2}}} \right) _{{E_0}}}=-2a-\frac{2 \pi \mu \beta \gamma }{\left( \mu +\alpha \pi \right) ^2} ,\quad {\left( {\frac{{{\partial ^2}{f_2}}}{{\partial {x_1}\partial {x_2}}}} \right) _{{E_0}}}= {\left( {\frac{{{\partial ^2}{f_2}}}{{\partial {x_2}\partial {x_1}}}} \right) _{{E_0}}} = -\frac{\pi \alpha \beta \mu }{(\mu +\alpha \pi )^2}+\frac{\beta \mu }{\mu +\alpha \pi }\quad \text{and}\\&{\left( {\frac{{{\partial ^2}{f_2}}}{{\partial {x_2}\partial {\beta ^*}}}} \right) _{{E_0}}} = \frac{\pi }{\mu +\alpha \pi }. \end{aligned}$$

Then from Theorem 4.1 of Castillo-Chavez and Song (2004), the bifurcation constants $a_1$ and $b_1$ are calculated as follows:

$$\begin{aligned} {a_1}= & {} {\sum \limits _{k,i,j = 1}^2 {{w_k}{u_i}{u_j}\left( {\frac{{{\partial ^2}{f_k}}}{{\partial {x_i}\partial {x_j}}}} \right) } _{{E_0}}}\\= & {} -\frac{2\beta ^*\pi }{\left( \mu +\alpha \pi \right) }\left[ -\frac{\pi \alpha \beta ^* }{\left( \mu +\alpha \pi \right) ^2}+\frac{\beta ^*}{\mu +\alpha \pi }\right] -2a-\frac{2\mu \pi \beta ^* \gamma }{\left( \mu +\alpha \mu \right) ^2}\\= & {} -\frac{2\beta ^*\pi \mu }{\mu +\alpha \pi }\left( \frac{\beta ^*+\pi (\mu +\alpha \pi )}{\left( \mu +\alpha \pi \right) ^2}\right) -2a\\< & {} 0 \quad \text{(as all parameters are positive)}. \end{aligned}$$

and

$$\begin{aligned} {b_1} = {\sum \limits _{k,i = 1}^2 {{w_k}{u_i}\left( {\frac{{{\partial ^2}{f_k}}}{{\partial {x_i}\partial {\beta ^*}}}} \right) } _{{E_0}}} = {w_2}{u_2}{\left( {\frac{{{\partial ^2}{f_2}}}{{\partial {x_2}\partial {\beta ^*}}}} \right) _{{E_0}}} = \frac{\pi }{\mu +\alpha \pi } > 0. \end{aligned}$$

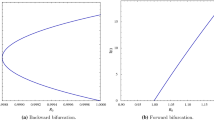
Sign of $a_1$ determines the nature of the bifurcation at $R_0=1$. The local analysis of the center manifold yields a parameter, $a_1$, whose sign indicates the existence and stability of a branch of endemic equilibria near the threshold $R_0 = 1$. If $a_1$ is negative, then a branch of super-threshold endemic equilibria exists, and the bifurcation is supercritical. This case is frequently alluded to as a forward bifurcation.

Thus, with the help of Theorem 4.1(iv) of Castillo-Chavez and Song (2004), the following theorem is being concluded:

Theorem 2

The disease-free equilibrium (DFE) is locally asymptotically stable if$R_0$is slightly less than one and if$R_0$is slightly greater than one then the DFE is unstable and there is a locally asymptotically stable positive equilibrium near the DFE. Hence the model system (4) exhibits forward bifurcation at${R_0 = 1}$.

The bifurcation from the disease-free equilibrium at $R_0=1$ is forward which can be observed from Fig. 2.

Fig. 2

Figure of I(t) versus $R_0$. The parameter values are listed in Table 1

Endemic equilibrium and its stability

In this section we investigate the stability of the system (4) at the endemic equilibrium ${E_{\mathrm{e}}}({S^*},{I^*})$.

Equating the second equation of the system (4) to zero, we get:

$$\begin{aligned} \frac{{\beta {S^*}{I^*}}}{{1 + \alpha {S^*} + \gamma {I^{*}}}} - (\mu + d + \theta ){I^*} - \frac{{a{I^{*2}}}}{{{bI^{*2}} + c{I^*} + 1}} = 0 \end{aligned}$$

(7)

After solving the above Eq. (7), we get ${S^*}$ in terms of ${I^*}$ as follows:

$$\begin{aligned} {S^*} = \frac{{(1 + \gamma {I^*})(p({bI^{*2}} + c{I^*} + 1) + aI^*)}}{(\beta - p\alpha ){\left( bI^{*2}+1\right) }+I^*\left( c\left( \beta -p\alpha \right) -a\alpha \right) } \end{aligned}$$

(8)

where

$$\begin{aligned} p = \mu + d + \theta \end{aligned}$$

${S^*} > 0$ if

$$\begin{aligned} c(\beta - p\alpha ) - \alpha a > 0 \end{aligned}$$

(9)

This condition also implies that

$$\begin{aligned} \beta - p \alpha > 0. \end{aligned}$$

(10)

Now adding first and second equations of the system (4) and equate it to zero, we get :

$$\begin{aligned} \pi -\mu S^*-(\mu +d+ \theta )I^*-\frac{aI^{*2}}{bI^{*2}+cI*+1}=0 \end{aligned}$$

(11)

Substituting the value of ${S^*}$ from Eq. (8) into Eq. (11), we get the following equation in ${I^*}$ :

$$\begin{aligned} {A_0} + {A_1}{I^*} + {A_2}{I^{*2}} + {A_3}{I^{*3}} + {A_4}{I^{*4}} + {A_5}{I^{*5}} = 0 \end{aligned}$$

(12)

where

$$\begin{aligned} A_0&= p \left( \mu +\pi \alpha \right) \left( 1-R_0\right) ,\\ A_1&= a\left( \mu +\pi \alpha \right) +\left( \beta -p\alpha \right) \left( p-2c\pi \right) +p\mu \left( 2c+\gamma \right) ,\\ A_2&= ac\left( \mu +\pi \alpha \right) +2pc\left( \beta -p\alpha +\gamma \mu \right) +p\mu \left( 2b+c^2\right) \\&\quad +a\left( \beta +\gamma \mu \right) -\left( 2\alpha p a+\pi \left( 2b+c^2\right) \left( \beta -p\alpha \right) \right) ,\\ A_3&=ab\left( \mu +\pi \alpha \right) +pc^2\gamma \mu +2bp\mu \left( c+\gamma \right) \\&\quad +\left( \beta -p\alpha \right) \left( c\left( a+pc\right) +2b\left( p-c\pi \right) \right) -a^2\alpha -ac\left( p\alpha -\gamma \mu \right) ,\\ A_4&=ab\left( \beta -2p\alpha +\gamma \mu \right) +b\left( \beta -p\alpha \right) \left( 2pc-b\pi \right) \\&\quad +bp\mu \left( b+2c\gamma \right) ,\\ A_5&=pb^2(\beta -\alpha p +\gamma \mu ). \end{aligned}$$

With the help of Descartes’ rule of signs (Wang 2004), Eq. (12) has a unique positive real root ${I^*}$ if any one of the following holds:

$$\begin{aligned}&\hbox {(i)} \,\,\,A_5>0,\quad A_4<0,\quad A_3<0,\quad A_2<0,\quad A_1<0 \quad \text{and}\quad A_0<0. \\&\hbox {(ii)} \,\,\,A_5>0,\quad A_4>0,\quad A_3<0,\quad A_2<0,\quad A_1<0 \quad \text{and}\quad A_0<0. \\&\hbox {(iii)} \,\,\,A_5>0,\quad A_4>0,\quad A_3>0,\quad A_2<0,\quad A_1<0 \quad \text{and}\quad A_0<0. \\&\hbox {(iv)}\,\,\, A_5>0,\quad A_4>0,\quad A_3>0,\quad A_2>0,\quad A_1<0 \quad \text{and}\quad A_0<0. \\&\hbox {(v)} \,\,\,A_5>0,\quad A_4>0,\quad A_3>0,\quad A_2>0,\quad A_1>0 \quad \text{and}\quad A_0<0. \end{aligned}$$

(13)

After determining the value of ${I^*}$, we can determine the value of ${S^*}$ from Eq. (8). This implies that there exists a unique positive endemic equilibrium ${E_{\mathrm{e}}}({S^*},{I^*})$ if one of the conditions (13) hold.

If conditions (13) are not satisfied, then we obtain the following result:

Proposition 1

If$R_0>1$, then there is either a unique or three or five positive endemic equilibria, if all equilibria are simple roots.

Proof

Suppose $R_0>1$. From Eq. (12) we have fifth degree polynomial in $I^*$:

$$\begin{aligned} F(I^*)= {A_0} + {A_1}{I^*} + {A_2}{I^{*2}} + {A_3}{I^{*3}} + {A_4}{I^{*4}} + {A_5}{I^{*5}}. \end{aligned}$$

Leading coefficient of $I^*$ is $A_5=pb^2(\beta -\alpha p +\gamma \mu )>0$. Hence

$$\begin{aligned} \lim _{I^* \rightarrow \infty }F(I^*)=+\infty . \end{aligned}$$

Also note that $F(0)=A_0$ and $A_0<0$ if $R_0>1$. $F(I^*)$ is a continuous function on $I^*$ and by fundamental theorem of algebra, we know that this polynomial can have at most five real roots. $\square$

We now analyze the local stability of endemic equilibrium ${E_{\mathrm{e}}}$ as follows:

The characteristic equation of the system (4) evaluated at ${E_{\mathrm{e}}}$ is a second-degree transcendental equation:

$$\begin{aligned} {\lambda ^2} + {p_0}\lambda + {q_0} + ({p_1}\lambda + {q_1}){e^{ - \lambda \tau }} = 0 \end{aligned}$$

(14)

where

$$\begin{aligned} {p_0}= & {} 2\mu + d + \theta + \frac{acI^{*2}+2aI^*}{bI^{*2}+cI^*+1},\\ {q_0}= & {} \mu \left( \mu + d + \theta + \frac{acI^{*2}+2aI^*}{bI^{*2}+cI^*+1}\right) ,\\ {p_1}= & {} \frac{\beta }{{(1 + \alpha {S^*} + \gamma {I^*})}^2} \left( I^*\left( 1+\gamma I^*\right) -S^*\left( 1+\alpha S^*\right) \right) ,\\ {q_1}= & {} - \frac{{\mu \beta {S^*}(1 + \alpha {S^*})}}{{{{(1 + \alpha {S^*} + \gamma {I^*})}^2}}} + \frac{{\beta {I^*}(1 + \gamma {I^*})}}{{{{(1 + \alpha {S^*} + \gamma {I^*})}^2}}}\left( \mu + d + \theta +\frac{acI^{*2}+2aI^*}{bI^{*2}+cI^*+1}\right) . \end{aligned}$$

Theorem 3

At${\tau =0}$, ${E_{\mathrm{e}}}$is locally asymptotically stable if$\frac{S^*}{I^*}\le \frac{1+\gamma I^*}{1+\alpha S^*}$is satisfied.

Proof

The characteristic equation for the endemic equilibrium $E_{\mathrm{e}}$ at $\tau =0$ is given by

$$\begin{aligned} {\lambda ^2} + {p_0}\lambda + {q_0} + ({p_1}\lambda + {q_1}) = 0. \end{aligned}$$

It is easy to verify that if $\frac{{ac - a{I^{*2}}}}{{{{\left( {{I^{*2}} + b{I^*} + c} \right) }^2}}} \ge \frac{{\beta {S^*}(1 + \alpha {S^*})}}{{{{(1 + \alpha {S^*} + \gamma {I^*})}^2}}}$ is satisfied, then

$$\begin{aligned} {p_0} + {p_1}&= 2\mu + d + \theta + \frac{acI^{*2}+2aI^*}{\left( bI^{*2}+cI^*+1\right) ^2}\\&\quad +\frac{\beta }{\left( 1+\alpha S^*+\gamma I^*\right) ^2}\left( I^*\left( 1+\gamma I^*\right) -S^*\left( 1+\alpha S^*\right) \right)> 0,\\ {q_0} + {q_1}&= \mu \left( \mu + d + \theta \right) +\frac{aI^*\left( 2+cI^*\right) }{\left( bI^{*2}+cI^*+1\right) ^2}\\&\quad \left( \mu +\frac{\beta I^*\left( 1+\gamma I^*\right) }{\left( 1+\alpha S^*+\gamma I^*\right) ^2}\right) +\frac{\beta }{\left( 1+\alpha S^*+\gamma I^*\right) ^2}\\&\left( \left( d+\theta \right) I^*\left( 1+\gamma I^*\right) +\mu \left( I^*\left( 1+\gamma I^*\right) -S^*\left( 1+\alpha S^*\right) \right) \right) > 0. \end{aligned}$$

Hence, by Routh–Hurwitz criterion, it is concluded that the endemic equilibrium $E_{\mathrm{e}}$ of the system (4) is locally asymptotically stable when $\tau =0$. $\square$

Theorem 4

For$\tau > 0, E_{\mathrm{e}}$is locally asymptotically stable if the conditions $\mu \left( 1+\alpha S^*+\gamma I^*\right) ^2 \ge \beta I^* \left( 1+\gamma I^*\right)$and$2(\mu +d+\theta )I^*(1+\gamma I^*) \ge \mu S^*\left( 1+\alpha S^*\right)$are satisfied simultaneously.

Proof

The characteristic equation for $\tau > 0$ evaluated at $E_{\mathrm{e}}$ is given by Eq. (14) which is

$$\begin{aligned} {\lambda ^2} + {p_0}\lambda + {q_0} + ({p_1}\lambda + {q_1}){e^{ - \lambda \tau }} = 0. \end{aligned}$$

For $\tau > 0$, by applying theorem 2.4 in Ruan and Wei (2003), it follows that the characteristic root of (14) must pass through the imaginary axis for the occurrence of instability for fixed value of time delay $\tau$. Assume that $\lambda = i\eta ,\eta > 0$ is the root of the characteristic Eq. (14).

Substituting $\lambda = i\eta$ in Eq. (14), we obtain

$$\begin{aligned} \left( - {\eta ^2} + {q_0} + {p_1}\eta \sin \eta \tau + {q_1}\cos \eta \tau \right) + i\left( {p_0}\eta + {p_1}\eta \cos \eta \tau - {q_1}\sin \eta \tau \right) \end{aligned}$$

(15)

After separation of real and imaginary parts of Eq. (15), we get

$$\begin{aligned} {p_1}\eta \sin \eta \tau + {q_1}\cos \eta \tau&= {\eta ^2} - {q_0} , \end{aligned}$$

(16)

$$\begin{aligned} {p_1}\eta \cos \eta \tau - {q_1}\sin \eta \tau&= - \eta {p_0}. \end{aligned}$$

(17)

Eliminating $\tau$ by squaring and adding equations (16) and (17), we obtain a biquadratic polynomial in $\eta$ as

$$\begin{aligned} {\eta ^4} + \left( p_0^2 - 2{q_0} - p_1^2\right) {\eta ^2} + \left( q_0^2 - q_1^2\right) = 0. \end{aligned}$$

(18)

Letting $\eta ^2=x$, Eq. (18) becomes:

$$\begin{aligned} {x^2} + Ax + B = 0 \end{aligned}$$

(19)

where

$$\begin{aligned} A&= p_0^2 - 2{q_0} - p_1^2, \quad B = q_0^2 - q_1^2.\\ A&= \left( 2\mu +d+\theta +\frac{acI^{*2}+2aI^*}{bI^{*2}+cI^*+1}\right) ^2-2\mu \left( \mu +d+\theta +\frac{acI^{*2}+2aI^*}{bI^{*2}+cI^*+1}\right) \\&\quad - \frac{{\beta }^2}{\left( 1+\alpha S^*+\gamma I^*\right) ^4}\left( I^*\left( 1+\gamma I^*\right) -S^*\left( 1+\alpha S^*\right) \right) ^2\\&= \left( \mu +d+\theta \right) ^2+2\left( \mu +d+\theta \right) \frac{acI^{*2}+2aI^*}{bI^{*2}+cI^*+1}+\left( \frac{acI^{*2}+2aI^*}{bI^{*2}+cI^*+1}\right) ^2+\mu ^2\\&\quad -\left( \frac{\beta }{(1+\alpha S^*+\gamma I^*)^2}\left( I^*(1+\gamma I^*)-S^*(1+\alpha S^*)\right) \right) ^2,\\ B&= q_0^2 - q_1^2\\&=\left( \mu \left( \mu + d + \theta + \frac{acI^{*2}+2aI^*}{bI^{*2}+cI^*+1}\right) \right) ^2\\&\quad -\left( - \frac{{\mu \beta {S^*}(1 + \alpha {S^*})}}{{{{(1 + \alpha {S^*} + \gamma {I^*})}^2}}} + \frac{{\beta {I^*}(1 + \gamma {I^*})}}{{{{(1 + \alpha {S^*} + \gamma {I^*})}^2}}}\left( \mu + d + \theta +\frac{acI^{*2}+2aI^*}{bI^{*2}+cI^*+1}\right) \right) ^2\\&=\left( \mu +d+\theta +\frac{acI^{*2}+2aI^*}{bI^{*2}+cI^*+1}\right) ^2 \left( \mu ^2-\frac{\beta ^2I^{*2}\left( 1+\gamma I^*\right) ^2}{\left( 1+\alpha S^*+\gamma I^*\right) ^4}\right) \\&\quad + \frac{2\mu \beta ^2 S^*(1+\alpha S^*)I^*(1+\gamma I^*)(acI^{*2}+2aI^*)}{\left( 1+\alpha S^*+\gamma I^*\right) ^4(bI^{*2}+cI^*+1)}\\&\quad + \frac{\mu \beta ^2 S^*(1+\alpha S^*)}{(1+\alpha S^*+\gamma I^*)^4}\left( 2(\mu +d+\theta )I^*(1+\gamma I^*)-\mu S^*(1+\alpha S^*)\right) .\\ \end{aligned}$$

$A>0$ if and only if $\mu \left( 1+\alpha S^*+\gamma I^*\right) ^2 \ge \beta \left( I^*\left( 1+\gamma I^*\right) -S^*\left( 1+\alpha S^*\right) \right)$ and $B>0$ if and only if both the conditions $\mu \left( 1+\alpha S^*+\gamma I^*\right) ^2 \ge \beta I^* \left( 1+\gamma I^*\right)$ and $2(\mu +d+\theta )I^*(1+\gamma I^*) \ge \mu S^*\left( 1+\alpha S^*\right)$ are satisfied simultaneously.

Note that $\mu \left( 1+\alpha S^*+\gamma I^*\right) ^2 \ge \beta I^* \left( 1+\gamma I^*\right)$ implies that:

$$\begin{aligned} \mu \left( 1+\alpha S^*+\gamma I^*\right) ^2 \ge \beta \left( I^*\left( 1+\gamma I^*\right) -S^*\left( 1+\alpha S^*\right) \right) . \end{aligned}$$

According to Routh–Hurwitz criterion, a contradiction arises with the assumption of instability i.e $\lambda = i \eta$. Thus, it can be concluded that the endemic equilibrium $E_{\mathrm{e}}$ of the system (4) is locally asymptotically stable for $\tau >0$. $\square$

Hopf bifurcation analysis

If $B = q_0^2 - q_1^2$ in Eq. (19) is negative, then there is a unique positive $\eta _0$ satisfying Eq. (19), i.e., there is single pair of purely imaginary roots $\pm i\eta _0$ to Eq. (14).

From Eqs. (16) and (17), $\tau _n$ corresponding to $\eta _0$ can be obtained as

$$\begin{aligned} \tau _n=\frac{1}{\eta _0}\arccos \left( \frac{\eta _0^2(q_1-p_0p_1)-q_0q_1}{p_1^2\eta _0^2+q_1^2}\right) +\frac{2n\pi }{\eta _0} , \quad n=0,1,2\ldots \end{aligned}$$

(20)

Endemic equilibrium $E_{\mathrm{e}}$ is stable for $\tau <\tau _0$ if transversality condition holds, i.e., $\left.\frac{\mathrm{d}}{\mathrm{d}t}\left( {Re} \lambda \right) \right|_{\lambda =i\eta _0}\ne 0.$

Differentiating Eq. (14) with respect to $\tau$, we get

$$\begin{aligned}&\left( 2\lambda +p_0+p_1 e^{-\lambda \tau }-(p_1 \lambda +q_1)\tau e^{-\lambda \tau } \right) \frac{\mathrm{d} \lambda }{\mathrm{d} \tau }=\lambda (p_1 \lambda +q_1)e^{-\lambda \tau } \\&\left[ \frac{\mathrm{d} \lambda }{\mathrm{d} \tau }\right] ^{-1} = \frac{ 2\lambda +p_0+p_1 e^{-\lambda \tau }-(p_1 \lambda +q_1)\tau e^{-\lambda \tau }}{\lambda (p_1 \lambda +q_1)e^{-\lambda \tau }} \\&\quad =\frac{2\lambda +p_0}{\lambda (p_1 \lambda +q_1)e^{-\lambda \tau }}+\frac{p_1}{\lambda (p_1 \lambda +q_1)}-\frac{\tau }{\lambda } \\&\quad =\frac{2\lambda +p_0}{-\lambda (\lambda ^2+p_0\lambda +q_0)}+\frac{p_1}{\lambda (p_1 \lambda +q_1)}-\frac{\tau }{\lambda }. \end{aligned}$$

(21)

$$\begin{aligned}&\left.\frac{\mathrm{d}}{\mathrm{d} \tau }\left( {Re} \lambda \right) \right|_{\lambda =i\eta _0}= \left.{Re}\left(\frac{\mathrm{d} \lambda }{\mathrm{d} \tau }\right) ^{-1} \right|_{\lambda =i\eta _0} \\&\quad ={Re}\left( \frac{2i \eta _0+p_0}{-i \eta _0 (-\eta _0^2+ip_0 \eta _0+q_0)}+\frac{p_1}{-p_1 {\eta _0}^2+i q_1 \eta _0}+\frac{i \tau }{\eta _0} \right) \\&\quad =\frac{1}{\eta _0}\left( \frac{2\eta _0(\eta _0^2-q_0)+p_0^2 \eta _0}{(p_0\eta _0)^2+(\eta _0^2-q_0)^2} -\frac{p_1^2\eta _0}{(p_1\eta _0)^2+q_1^2}\right) \\&\quad = \frac{2(\eta _0^2-q_0)+p_0^2 }{(p_0\eta _0)^2+(\eta _0^2-q_0)^2} -\frac{p_1^2}{(p_1\eta _0)^2+q_1^2}. \end{aligned}$$

(22)

Now, on squaring and adding Eqs. (16) and (17), we get

$$\begin{aligned} (p_1\eta _0)^2+q_1^2=(p_0\eta _0)^2+(\eta _0^2-q_0)^2 \end{aligned}$$

so that Eq. (22) can be written as

$$\begin{aligned} \left.\frac{\mathrm{d}}{\mathrm{d} \tau }\left( {Re} \lambda \right) \right|_{\lambda =i\eta _0}&=\frac{2\eta _0^2+(p_0^2-2q_0-p_1^2)}{p_1^2\eta _0^2+q_1^2}. \end{aligned}$$

(23)

Under the condition $A = p_0^2-2q_0-p_1^2 > 0$, it can be seen that

$$\begin{aligned} \left.\frac{\mathrm{d}}{\mathrm{d} \tau }\left( {Re} \lambda \right) \right|_{\lambda =i\eta _0}>0. \end{aligned}$$

Therefore, the transversality condition holds and Hopf bifurcation occurs at $\eta =\eta _0$, $\tau =\tau _0$.

Summarizing the above analysis, we arrive at the following theorem:

Theorem 5

If condition$q_0^2 - q_1^2 <0$holds, the endemic equilibrium$E_{\mathrm{e}}$of the system (4) is asymptotically stable for$\tau \in [0,\tau _0)$and it undergoes Hopf bifurcation at$\tau =\tau _0$.

Numerical simulation

Since it is important to analyze the dynamical behavior of the model, in this section, the system (4) is integrated numerically using the set of tested parameters given in Table 1.

Table 1 List of parameters

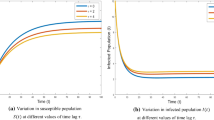
The computer simulations are performed for S and I for various values of $\tau$. The trajectory of S and I with initial conditions $S(0)=33$, $I(0)=5$ approaches the endemic equilibrium as shown in Fig. 3.

Fig. 3

Susceptible and infected population for various values of $\tau$

Figure 3 shows the effect of time delay on susceptible population and infective population, respectively, with respect to time for the set of parameters given in Table 1 for different values of time delay $\tau$. It is shown that as the time delay $\tau$ increases, the number of susceptible starts decreasing and number of infectives starts growing. Due to interplay between the number of infectives and susceptibles, infectives settle to its steady state but never approaches to zero, which shows that system approaches endemic equilibrium $E_{\mathrm{e}} (9.8292,18.4177)$.

Fig. 4

Behavior of infected population for various values of $\beta$ at $\tau = 1$ day

Figure 4 shows the influence of transmission rate $\beta$ on infected population for $\tau = 1$ day. It is true that the higher the effective contact rate, the higher will be the possibility of spreading the disease. In Fig. 4 we note that when the effective contact rate $\beta$ is high, then more people will be infected, and when the effective contact rate $\beta$ is low, then fewer people are infected.

Fig. 5

Infectives I(t) versus treatment rate a

Figure 5 depicts the behavior of infected population I(t) with respect to cure rate a. From this figure, it can be seen that infected population is decreasing with the increment in treatment rate a.

Fig. 6

Effects of measure of inhibitions

Figure 6 shows the effect of measure of inhibitions taken by susceptible and infectives respectively. These figures show that when the inhibition is less, then more number of people are getting infected, and when inhibition is more, then fewer people are getting infected.

Fig. 7

Infected population with and without saturated treatment rate at $\tau = 1$ day

Figure 7 shows the effect of saturated treatment rate on the infected individuals for the time lag $\tau = 1$ day. The treatment is an imperative strategy to diminish the spread of diseases. This figure shows that saturated treatment rate is diminishing the infection.

Fig. 8

Behavior of susceptible and infected population for the time lag $\tau =12$ days

In Fig. 8a, a plot is drawn for infected and susceptible population versus time t for time lag $\tau =12$ days. Figure 8b shows the phase plot between susceptible S(t) and infected I(t) population which shows the limit cycle for time lag $\tau =12$ days. Using parameter values given in Table 1, it clear from Fig. 8a, b that endemic equilibrium $E_{\mathrm{e}} = (9.8292,18.4177)$ is the unique endemic equilibrium. According to the algorithm given in Eq. (20) and Theorem 5, we can compute $\tau _0=12.5801$, $p_0^2-2q_0-p_1^2= 0.0109139>0$ and $q_0^2-q_1^2= -0.000150942<0$. Clearly, from Fig. 8 it can be seen that when $\tau =12< \tau _0=12.5801$, then the endemic equilibrium is asymptotically stable.

Conclusion

In conclusion, this paper has, as the fundamental objective, the formulation of a nonlinear SIR mathematical model to study the role of Beddington–DeAngelis-type nonlinear incidence rate, by incorporating a delay time to analyze the equilibrium points and their stability and saturated treatment rate-type nonlinear treatment rate. It is assumed that there is a time lag due to latency period of pathogens, i.e., the development of an infection from the time the pathogen enters the body until symptoms first appear. The model exhibits two equilibria; the disease-free and endemic equilibrium. The local stability of the disease-free equilibrium is determined by the basic reproduction number $R_0$. The disease-free equilibrium has been shown to be stable for $R_0 < 1$, i.e., disease dies out for $R_0 < 1$ and for $R_0 > 1$, it becomes unstable and the endemic equilibrium exists. We also discuss the stability of disease-free equilibrium at $R_0 = 1$ using center manifold theory. We observed that at $R_0 = 1$, model exhibits forward bifurcation and changes its stability as $R_0$ crosses one. The stability analysis demonstrates that endemic equilibrium is locally asymptotically stable under certain conditions for the time lag $\tau \ge 0$ as stated in Theorems 3 and 4. Further, system (4) has been simulated numerically for the effect of time delay $\tau$ and showed that as delay increases, infected population also increases. Furthermore, we simulated the model numerically to see the effects of transmission rate, measure of inhibition and treatment rate. From the graphs, it is depicted that the infection can be eradicated from the society if the treatment given to the population is managed according to saturated treatment rate. Also, analytical and numerical results showed that oscillatory behavior of the infected population will also occur, indicating the existence of a Hopf bifurcation.