1 Introduction

The widespread and frequent occurrence of many communicable diseases represents a major problem for healthcare workers and policymakers worldwide. Controlling infectious diseases has become an increasingly complex issue in recent years. To control or remove a disease, complete understanding of the dynamics of its progression is required. Based on the observed characteristics of infectious diseases, epidemiologists [1,2,3,4,5,6,7,8,9,10,11,12,13] have attempted to construct mathematical models that make it possible to understand various aspects of many diseases and suggest methods for their control. A crucial issue in the study of the spread of an infectious disease is how it is transmitted. In epidemiology, the transmission of an infectious disease is determined by the incidence rate, defined as the average number of new cases of a disease per unit time. The incidence rate therefore plays a key role in study of the qualitative description of the transmission dynamics of infectious diseases. In 1927, Kermack and McKendrick [14] proposed that the dynamics of an infectious disease could be described using a bilinear incidence rate \(\beta SI\) of infection. However, this bilinear-type incidence rate is based on the law of mass action, which is unreasonable for large populations. Indeed, one can infer from the term \(\beta SI\) that, if the number of susceptible individuals increases, the number of individuals who become infected per unit time also increases, which is not realistic. There is therefore a need to modify the classical linear incidence rate in order to study the dynamics of infection among a large population. Many researchers [2,3,4,5, 7, 10, 11, 15,16,17,18] have proposed transmission laws that include nonlinearity, such as the Holling type II functional, Crowley–Martin functional, Beddington–DeAngelis functional, etc., to study the dynamics of infectious diseases. The general incidence rate

$$\begin{aligned} g(I)S=\frac{kI^{p}S}{1+\alpha I^{q}}, \end{aligned}$$

was suggested by Liu et al. [19] and used by numerous authors in their models (see, for example, [9, 15, 20,21,22]). If the function g(I) is nonmonotonic, that is, g(I) is increasing when I is small but decreasing when I is large, it can be used to interpret the “psychological” effect, i.e., that the force of infection may reduce as the number of infected individuals increases becomes large, because in this situation the number of contacts per unit time may tend to reduce; For example, the epidemic outbreak of severe acute respiratory syndrome (SARS) showed such psychological effects on the general public; aggressive measures and policies, such as border screening, mask wearing, quarantine, isolation, etc., have been proven to be very effective [23] in reducing the infective rate at the late stage of the SARS outbreak, even when the number of infected individuals was increasing.

The above-mentioned phenomenon can be modeled by using the nonlinear Monod–Haldane incidence rate:

$$\begin{aligned} f\left( S,\,I \right) =g(I)S=\frac{kIS}{1+\alpha I^{2}},\,\mathrm {where}\,k,\,\alpha >0, \end{aligned}$$

where kI measures the force of infection of the disease and \(1/(1+\alpha I^{2})\) describes the psychological effect from the behavioral change of susceptible individuals when the number of infected individuals is very large.

Delay differential equations allow the inclusion of past actions into mathematical models, thus making the model closer to the real-world phenomenon [24]. For most communicable diseases, there is an interval between infection and the occurrence of symptoms (the incubation period), during which the infectious agent is multiplying or developing. Some persons who are infected may never develop manifestations of the disease, even though they may be capable of transmitting it (inapparent infection). Measles, for example, has a predictable incubation period (10–14 days) and limited duration of infectivity for a given patient (4–7 days). In addition, it is highly infectious (nearly every susceptible person who comes into contact with an infectious person will become infected), and nearly everyone who is infected develops the clinical illness. Incorporation of the incubation time during which the infectious agent develops makes the model more realistic, as pointed out by various studies and observations [25]. To achieve a higher level of realism in epidemic models, we consider a simplified Monod–Haldane incidence rate with the inclusion of time delay (representing the incubation period), having the form

$$\begin{aligned} f\left( S(t),I(t-\tau ) \right) =\frac{\beta S(t)I(t-\tau )}{1+\alpha I^{2}(t-\tau )},\,\mathrm {where\,}\beta ,\alpha >0, \end{aligned}$$

where \(\beta I\) measures the force of infection of the disease and \(1/(1+\alpha I^{2})\) describes the psychological or inhibitory effect from the behavioral change of the susceptible individuals when the number of infected individuals is very large. This has great significance, because the number of effective contacts between infected and susceptible individuals decreases at high levels, because of either isolation of infected individuals or security measures taken by susceptible individuals.

It is well known that a proper and timely treatment methodology can substantially reduce the effect of disease on society. In classical epidemic models, the treatment rate of infected individuals is assumed to be either constant or proportional to the number of infected individuals. However, it is known that there are limited treatment resources available in the community [2]. In the absence of effective therapeutic treatments and vaccines, epidemic control strategies are based on taking appropriate preventive measures. In 2004, Wang and Ruan [26] considered a susceptible–infectious–recovered (SIR) epidemic model with a constant treatment rate (i.e., recovery of the infected subpopulation per unit time). They carried out stability analysis and showed that this model exhibits various bifurcations. Furthermore, in 2012, Zhou and Fan [8] modified the treatment rate to Holling type II:

$$\begin{aligned} T(I)=\frac{aI}{1+bI}\,,\,I\ge 0,\,a>0,\,b>0. \end{aligned}$$

They showed that, on varying the amount of medical resources and their supply efficiency, the target model admits both backward and Hopf bifurcation. Dubey et al. [5] also used a Holling type II treatment rate to study the SIR model. Furthermore, for better understanding of the dynamics of infectious disease, in 2013, Dubey et al. [4] modified the treatment rate to a Holling type III functional for use in a susceptible–exposed–infectious–recovered (SEIR) model to understand the treatment of a disease which has reemerged and has available treatment modalities, having the following form:

$$\begin{aligned} T(I)=\frac{aI^{2}}{1+bI^{2}}\,,\,I\ge 0,\,a>0,\,b>0. \end{aligned}$$

The present study is motivated by the important works of Xu and Ma [11], Hattaf et al. [7], Dubey et al. [4], and Xiao et al. [23]. Xu and Ma proposed a delayed SIRS model for epidemics, Hattaf et al. proposed a SIR model with delay in the general incidence rate, Dubey et al. [4] proposed the dynamics for a SEIR model with different types of treatment rate, such as Holling type III and IV, and also discussed the stability behavior of their model. This paper aims to describe a novel dynamics of infectious diseases to address a more realistic situation for disease control. We discuss herein the stability of the proposed model at equilibrium points based on the basic reproduction number \({\,R}_{0}\), center manifold theory, and Routh–Hurwitz criterion.

The remainder of this manuscript is organized as follows: A time-delayed SIR epidemic model with a simplified Monod–Haldane incidence rate function and Holling type III treatment rate function is proposed in Sect. 2. The positivity and boundedness of the solutions are discussed in Sect. 3. Stability analysis of the model at equilibrium points is discussed in Sect. 4. The Hopf bifurcation of the model at endemic equilibrium is discussed in Sect. 5. The global stability of equilibria is discussed in Sect. 6. Furthermore, numerical simulations carried out using MATLAB 2012b and MATHEMATICA 11 are presented in Sect. 7. Finally, a discussion and conclusions are presented in Sect. 8.

2 Mathematical framework

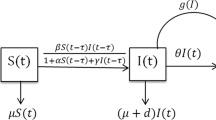
Mathematical models help to study the transmission dynamics and spread of infectious diseases, to recognize the factors governing the transmission process in order to improve effective control strategies and evaluate the efficacy of surveillance strategies and possible interventions. Therefore, in this section, we propose a mathematical SIR epidemic model including time delay, nonlinear incidence rate, and nonlinear treatment rate. It is supposed that the treatment rate is proportional to the number of patients as long as this number remains below a certain limit, and becomes steady when the number of patients surpasses this limit. For this, we consider a Holling type III treatment rate. We consider the total population N(t) at time t, with immigration of susceptible individuals at a constant rate A. Furthermore, it is assumed that the total population N(t) is divided into three disjoint subclasses of individuals, namely susceptible individuals S(t), infective individuals I(t), and recovered individuals R(t). It is assumed that the disease can be spread by direct contact between susceptible and infective individuals only. Let \(\mu \) be the natural death rate of the population, d be the disease-induced death rate, and \(\delta \) the recovery rate of infected individuals.

The dynamics of the model is given by the following system of nonlinear delay differential equations:

$$\begin{aligned} \frac{\mathrm {d}S(t)}{\mathrm {d}t}= & {} A-\mu S(t)-\frac{\beta S(t)I(t-\tau )}{1+\alpha I^{2}(t-\tau )}, \end{aligned}$$
(1)
$$\begin{aligned} \frac{\mathrm {d}I(t)}{\mathrm {d}t}= & {} \frac{\beta S(t)I(t-\tau )}{1+\alpha I^{2}(t-\tau )}-\left( \mu +d+\delta \right) I(t)-\frac{aI^{2}(t)}{1+bI^{2}(t)}, \end{aligned}$$
(2)
$$\begin{aligned} \frac{\mathrm {d}R(t)}{\mathrm {d}t}= & {} \frac{aI^{2}(t)}{1+bI^{2}(t)}+\delta I(t)-\mu R(t), \end{aligned}$$
(3)

where the time lag \(\tau >0\) represents the incubation period of the disease, defined as a fixed time during which the infectious agent develops in the vector; only after this time can the infected vector infect a susceptible individual.

Let \(C=C\left( \left[ -\tau ,0 \right] , {\mathbb {R}}^{3} \right) \) denote the Banach space of continuous functions, mapping the interval \(\left[ -\tau ,0 \right] \) to \({\mathbb {R}}^{3}\) with the topology of uniform convergence. It is well known from the fundamental theory of functional differential equations [3, 7, 11, 27] that the model described by Equations (1)–(3) admits a unique solution \(\left( S(t),\,I(t),\,R(t) \right) \) with initial data \(\left( S_{0},\,I_{0},\,R_{0}\,\right) \in C\). For biological reasons, the initial conditions of the model described by Equations (1)–(3) are nonnegative continuous functions

$$\begin{aligned} S_{0}\left( \varphi \right) \ge 0,\,I_{0}\left( \varphi \right) \ge 0,\,R_{0}\left( \varphi \right) \ge 0,\,\,\varphi \in \left[ -\tau ,0 \right] . \end{aligned}$$
(4)

In the model described by Equations (1)–(3), the derivative \(\,\frac{\mathrm {d}\,}{\mathrm {d}t}\) represents the rate of change in the corresponding compartment or class. The term \(\,\frac{\beta S(t)I(t-\tau )}{1+\alpha I^{2}(t-\tau )}\) in the model represents the nonlinear Monod–Haldane functional-type incidence rate with time lag \(\tau \), where \(\beta \) is the transmission rate of infection and \(\alpha \) measures the inhibitory or psychological effects exhibited by infected individuals. This nonlinear functional response was suggested by Sokol and Howell [28] to model prey–predator dynamics. The Monod–Haldane incidence rate is of nonmonotone type, which can be used to interpret the “psychological” effects [29]. In this incidence rate, for a very large number of infectious individuals, the force for infection may decrease as the number of infectious individuals increases, because in the presence of a large number of infectious individuals, the population may tend to reduce the number of contacts per unit time [23]. The term \(\,\frac{aI^{2}(t)}{1+bI^{2}(t)}\) in the model represents the Holling type III treatment rate, where a and b are both nonnegative constants. The constants a and b are the cure rate of infected individuals and the limitation rate of treatment availability, respectively. The Holling type III treatment rate defines the condition in which the removal rate grows very fast initially with an increase in infective individuals, then slowly, finally settling down to a maximum saturated value. After this, any increase in the infective individuals will not affect the removal rate [4].

The first two equations of Equations (1)–(3) do not depend on the third equation; therefore, it is sufficient to consider the following reduced system for study:

$$\begin{aligned} \frac{\mathrm {d}S(t)}{\mathrm {d}t}= & {} A-\mu S(t)-\frac{\beta S(t)I(t-\tau )}{1+\alpha I^{2}(t-\tau )}, \end{aligned}$$
(5)
$$\begin{aligned} \frac{\mathrm {d}I(t)}{\mathrm {d}t}= & {} \frac{\beta S(t)I(t-\tau )}{1+\alpha I^{2}(t-\tau )}-\left( \mu +d+\delta \right) I(t)-\frac{aI^{2}(t)}{1+bI^{2}(t)}, \end{aligned}$$
(6)

with the initial conditions defined in the Banach space \(C=C\left( \left[ -\tau ,0 \right] ,\, {\mathbb {R}}^{2} \right) \) of continuous functions mapping the interval \(\left[ -\tau ,0 \right] \) to \({\mathbb {R}}^{2}\) with the topology of uniform convergence:

$$\begin{aligned} S_{0}\left( \varphi \right) \ge 0,\,I_{0}\left( \varphi \right) \ge 0,\,\,\,\varphi \in \left[ -\tau ,0 \right] . \end{aligned}$$
(7)

3 Positivity and boundedness of the solutions

In the model, for ecological reasons, it is assumed that all the parameters \(A,\mu ,\beta ,d,\delta ,a,\alpha , \mathrm {\,and}\,b\) are positive. Since the system of Equations (5)–(6) monitors the population, it is important to show that all state variables with nonnegative initial data will remain nonnegative and bounded for all time. Thus, we prove the following theorem:

Theorem 1

All state variables of the system of Equations (5)–(6), subject to the condition (7) remain nonnegative and bounded for all \(t\ge 0\).

Proof

First we show that S(t) is positive for all \(\,t\ge 0\). On the contrary, it is assumed that there exists a first time (\(t_{1}>0\)) such that \(\,S\left( t_{1} \right) =0\); then, by Eq. (5), we have \(\,S{'}\left( t_{1} \right) =A>0\), and hence \(S(t)<0\) for \(\,t\in (t_{1}-\theta ,\,t_{1})\), where \(\theta >0\) is sufficiently small. This contradicts \(S(t)>0\) for \(\,t\in [0,\,t_{1})\). It follows that \(S(t)>0\) for \(\,t>0\). Now, we prove that \(\,I(t)\) is positive. By applying the variation of constant formula and the step-by-step integration method [3], on integrating Eq. (6) of the model from 0 to t for \(\,0<t\le \tau \), we obtain

$$\begin{aligned} I(t)=I(0)\mathrm {e}^{-(\mu +d+\delta )t}\times \mathrm {e}^{\int _0^t {f(S\left( {\varepsilon -\uptau } \right) \mathrm {,\,\,I}\left( {\varepsilon -\uptau } \right) ,\,I(\varepsilon ))} \,\mathrm {d}\varepsilon }, \end{aligned}$$

where

$$\begin{aligned} f\left( S\left( {\varepsilon -\uptau } \right) \mathrm {,\,\,I}\left( {\varepsilon -\uptau } \right) ,\,I\left( \varepsilon \right) \right) =\left( \frac{\mathrm {\upbeta S(\varepsilon -\uptau )I}\left( {\varepsilon -\uptau } \right) }{\mathrm {(1+\upalpha }\mathrm {I}^{2}\left( {\varepsilon -\uptau } \right) )I(\varepsilon )}-\frac{\mathrm {a\,}I(\varepsilon )}{\mathrm {1+b}\mathrm {I}^{\mathrm {2}}\mathrm {(\varepsilon )}} \right) . \end{aligned}$$

It is easy to see that \(I(t)>0\) for all \(\,0\le t\le \tau \). Now, integrating Eq. (6) of the model from \(\tau \) to t for \(\tau <t\le 2\tau \) gives

$$\begin{aligned} I(t)=I(\tau )\mathrm {e}^{-(\mu +d+\delta )t}\times \mathrm {e}^{\int _\tau ^t {f(S\left( {\varepsilon -\uptau } \right) \mathrm {,\,\,I}\left( {\varepsilon -\uptau } \right) ,\,I(\varepsilon ))} \,\mathrm {d}\varepsilon }. \end{aligned}$$

Note that \(I(t)>0\) for all \(\tau \le t\le 2\tau \), and likewise, it can be proved that I(t) is positive for all \(2\tau \le t\le 3\tau \). This process holds for all values of \(t>0\). Hence, it implies that, for all \(\,t>0\), we have \(\,I(t)>0\).

Next, we prove the boundedness of the solutions of the model for all \(t\ge 0\).

For boundedness of the solution, we define

$$\begin{aligned} N(t)=S(t)+I(t). \end{aligned}$$

By the nonnegativity of the solution, it follows that

$$\begin{aligned} \frac{\mathrm {d}N(t)}{\mathrm {d}t}=A-\mu N(t)-dI(t)\le A-\mu N(t). \end{aligned}$$

This implies that N(t) is bounded, and so are S(t) and I(t). This completes the proof of the theorem. \(\square \)

4 Equilibria and stability analysis

Since stability analysis can provide a sense of the behavior of a solution, it can predict the long-term behavior of the model solutions. Therefore, in this section, we find the equilibria and investigate the stability of the system of Equations (5)–(6). The model system of Equations (5)–(6) has two equilibria, which are obtained from the system of equations by setting the right-hand-side terms to zero. The equilibrium points are as follows:

  1. (i)

    Disease-free equilibrium (DFE) \(Q\left( \frac{A}{\mu },\,0 \right) \)

  2. (ii)

    Endemic equilibrium (EE) \(Q^{*}(S^{*},\,I^{*})\)

where \(S^{*}\) and \(I^{*}\) are given in Sect. 4.2(A).

4.1 Stability of disease-free equilibrium (DFE)

In this subsection, we investigate the stability of the disease-free equilibrium using the basic reproduction number \(R_{0}\). The basic reproduction number \(R_{0}\) is defined as “the expected number of secondary cases produced, in a completely susceptible population, by a typical infective individual” [30]. For the stability of the DFE first, we determine the basic reproduction number \(R_{0}\) as given below:

4.1.1 Computation of basic reproduction number \(R_0\)

The corresponding characteristic equation of the system of Equations (5)–(6) at Q is given by

$$\begin{aligned} \left( \mu +\lambda \right) \left( \frac{\beta A}{\mu }\,\mathrm {e}^{-\lambda \tau }-\mu -d-\delta -a-\lambda \right) =0. \end{aligned}$$
(8)

One root of equations (8) is given by \(\lambda _{1}=-\mu \), and other roots are solutions to the equation

$$\begin{aligned} \left( \frac{\beta A}{\mu }\,\mathrm {e}^{-\lambda \tau }-\mu -d-\delta -a-\lambda \right) =0. \end{aligned}$$

The term \(\frac{\beta A}{\mu (\mu +d+\delta +a)}\mathrm {e}^{-\lambda \tau }\) at \(\tau =0\) is defined as the basic reproduction number, denoted by \({\,R}_{0}\); i.e., the basic reproduction number for our model is

$$\begin{aligned} R_{0}=\frac{\beta A}{\mu (\mu +d+\delta +a)}\,. \end{aligned}$$

4.1.2 Analysis at \(R_0\ne 1\)

Clearly, Eq. (8) has a negative real root \(\lambda _{1}=-\mu \), and other roots can be obtained by solving the equation

$$\begin{aligned} \lambda +\mu +d+\delta +a-\frac{\beta A}{\mu }\,\mathrm {e}^{-\lambda \tau }=0. \end{aligned}$$

Let

$$\begin{aligned} f\left( \lambda \right) =\lambda +\mu +d+\delta +a-\frac{\beta A}{\mu }\,\mathrm {e}^{-\lambda \tau }. \end{aligned}$$

If \(R_{0}>1\), it can be seen that, for real \(\lambda \),

$$\begin{aligned} f\left( 0 \right) =\left( \mu +d+\delta +a \right) \left( 1-\frac{\beta A}{\mu \left( \mu +d+\delta +a \right) } \right) <0,\,\lim _{\lambda \rightarrow +\infty }{f\left( \lambda \right) =+\infty }. \end{aligned}$$

Hence, if \(R_{0}>1\), there exists at least one positive root of the equation \(f\left( \lambda \right) =0\).

If \({\,R}_{0}<1\), we assume that \(\mathrm {Re}\,(\lambda )\ge 0\).

We notice that

$$\begin{aligned} \mathrm {Re}\,(\lambda )&=\frac{\beta A}{\mu }\,\mathrm {e}^{-\mathrm {Re}(\,\lambda \,\tau )}\cos {(\mathrm {Im}\,(\lambda \,\tau ))}-\left( \mu +d+\delta +a \right)<\left( \,\frac{\beta A}{\mu (\mu +d+\delta +a)}\,-1 \right) (\mu +d+\delta +a)<0. \end{aligned}$$

This contradicts our assumption that \(\mathrm {Re}\,\left( \lambda \right) \ge 0\). Hence, if \({\,R}_{0}<1\), then \(\lambda \) is a root of Eq. (8) with negative real part. Hence, we state the following theorem:

Theorem 2

The disease-free equilibrium \(Q\left( \frac{A}{\mu },\,0 \right) \) of the system of Equations (5)–(6) is locally asymptotically stable if \({\,R}_{0}<1\) and unstable if \(R_{0}>1\).

4.1.3 Analysis at \(R_0=1\)

We notice that the system of Equations (5)–(6) evaluated at \({\,R}_{0}=1\) with bifurcation parameter \({\beta =\beta }^{*}=\frac{\mu (\mu +d+\delta +a)}{A}\) has a zero eigenvalue and another eigenvalue that is negative. Since it is not possible to analyze the stability behavior of DFE Q at \({\,R}_{0}=1\) using linearization, we use center manifold theory [2, 3, 31]. For this, we redefine \(S=y_{1}\,\mathrm {and}\,I=y_{2}\), then the system of Equations (5)–(6) can be rewritten as

$$\begin{aligned} \frac{\mathrm {d}y_{1}(t)}{\mathrm {d}t}= & {} A-\mu y_{1}(t)-\frac{\beta y_{1}(t)y_{2}\left( t-\tau \right) }{1+\alpha y_{2}^{2}(t-\tau )}\mathrm {\,\equiv }\,G_{1}, \end{aligned}$$
(9)
$$\begin{aligned} \frac{\mathrm {d}y_{2}(t)}{\mathrm {d}t}= & {} \frac{\beta y_{1}(t)y_{2}\left( t-\tau \right) }{1+\alpha y_{2}^{2}(t-\tau )}-\left( \mu +d+\delta \right) y_{2}(t)-\frac{ay_{2}^{2}(t)}{1+by_{2}^{2}(t)}\equiv G_{2}. \end{aligned}$$
(10)

Let \({\,J}^{*}\) be the Jacobian matrix at \({\,R}_{0}=1\) and bifurcation parameter \({\beta =\beta }^{*}\). Then

$$\begin{aligned} J^{*}\mathbf {=}\left[ {\begin{array}{cc} -\mu &{} -\frac{\beta ^{*}A}{\mu }\\ 0 &{} 0\\ \end{array} } \right] . \end{aligned}$$

Let \(u=[u_{1},\,u_{2}\,]\) and \(w={[w_{1},\,w_{2}\,]}^{T}\) denote the left eigenvector and right eigenvector of the Jacobian matrix \({\,J}^{*}\) corresponding to the zero eigenvalue. Then we have

$$\begin{aligned} u_{1}=0,\,u_{2}=1\,\mathrm {and}\, w_{1}=-\frac{\beta ^{*}A}{\mu ^{2}},\,w_{2}=1. \end{aligned}$$

The nonzero partial derivatives associated with the functions \(G_{1}\) and \(G_{2}\) of the system of Equations (9)–(10) evaluated at \({\,R}_{0}=1\) and \({\beta =\beta }^{*}\) are

$$\begin{aligned} \left( \frac{\partial ^{2}G_{2}}{\partial y_{1}\partial y_{2}} \right) _{Q}=\left( \frac{\partial ^{2}G_{2}}{\partial y_{2}\partial y_{1}} \right) _{Q}=\beta ^{*} \quad \hbox {and} \quad \left( \frac{\partial ^{2}G_{2}}{\partial y_{2}\partial \beta ^{*}} \right) _{Q}=\frac{A}{\mu }. \end{aligned}$$

Using Theorem 4.1 of Castillo Chavez and Song [32], we obtain the bifurcation constants \(B_{1}\) and \({\,B}_{2}\) as

$$\begin{aligned} B_{1}=\sum \limits _{k,i,j=1}^2 {u_{k}w_{i}w_{j}} \left( \frac{\partial ^{2}G_{k}}{\partial y_{i}\partial y_{j}} \right) _{Q}=u_{2}\left( 2w_{1}w_{2}{\,\beta }^{*} \right) =-2\frac{{\,\beta }^{{*}^{2}}A}{\mu ^{2}}<0, \end{aligned}$$

and

$$\begin{aligned} B_{2}=\sum \limits _{k,i=1}^2 {u_{k}w_{i}} \left( \frac{\partial ^{2}G_{k}}{\partial y_{i}\partial \beta ^{*}} \right) _{Q}=u_{2}\left( w_{2}\frac{A}{\mu } \right) =\frac{A}{\mu }>0. \end{aligned}$$

Thus, from Theorem 4.1(iv) of Castillo Chavez and Song [32], we state the following theorem:

Theorem 3

DFE \(Q\left( \frac{A}{\mu },\,0 \right) \) changes its stability from stable to unstable at \({\,R}_{0}=1\), and there exists a positive equilibrium as \({\,R}_{0}\) crosses 1. Hence, the system of Equations (9)–(10) undergoes a transcritical bifurcation at \({\,R}_{0}=1\).

4.2 Stability of endemic equilibrium (EE)

In this section, we examine the behavior of the system near the endemic equilibrium. For this, we investigate the stability of the endemic equilibrium (EE) point.

4.2.1 Existence of endemic equilibrium points

To find the condition for the existence of the endemic equilibrium \(Q^{*}\left( S^{*},I^{*} \right) \), the system of Equations (5)–(6) is rearranged to get \(S^{*}\) and \(I^{*}\), yielding

$$\begin{aligned} \left( S^{*},I^{*} \right) =\left( \frac{\left( \left( \mu +d+\delta \right) \left( 1+bI^{*} \right) +aI^{*} \right) \left( 1+\alpha I^{{*}^{2}} \right) }{\beta \left( 1+bI^{*} \right) }\mathrm {\,,\,}I^{*} \right) , \end{aligned}$$

where \(I^{*}\) is given by the equation

$$\begin{aligned} {K_{1}I^{{*}^{4}}+K}_{2}I^{{*}^{3}}+K_{3}I^{{*}^{2}}+K_{4}I^{*}+K_{5}=0 \end{aligned}$$
(11)

with

$$\begin{aligned} K_{1}= & {} \mu \alpha b(\mu +d+\delta ),\\ K_{\mathrm {2}}= & {} b\beta \left( \mu \mathrm {+}d\mathrm {+}\delta \right) \mathrm {-}a\mu \alpha ,\\ K_{\mathrm {3}}= & {} \mu \left( \alpha \mathrm {+}b \right) \left( \mu \mathrm {+}d\mathrm {+}\delta \right) \mathrm {-(}a\mathrm {+}A\mathrm {)}\beta ,\\ K_{\mathrm {4}}= & {} \beta \left( \mu \mathrm {+}d\mathrm {+}\delta \right) \mathrm {-}a\mu ,\\ K_{\mathrm {5}}= & {} \mu \left( \mu \mathrm {+}d\mathrm {+}\delta \right) \mathrm {-}\beta A. \end{aligned}$$

Applying Descartes’ rule of signs [33], there exists a unique positive real root \(I^{*}\) of the biquadratic equation (11) if any one of the following holds true:

  1. (i)

    \(K_{1}>0,K_{2}>0,K_{3}>0,\,K_{4}>0,\) and \(K_{5}<0\),

  2. (ii)

    \(K_{1}>0,K_{2}>0,K_{3}>0,\,K_{4}<0,\) and \(K_{5}<0\),

  3. (iii)

    \(K_{1}>0,K_{2}>0,K_{3}<0,\,K_{4}<0,\) and \(K_{5}<0\),

  4. (iv)

    \(K_{1}>0,K_{2}<0,K_{3}<0,\,K_{4}<0,\) and \(K_{5}<0\).

Once we get the value of \(I^{*}\), we can obtain the value of \(S^{*}\) as well. Thus, this implies that the system of Equations (5)–(6) admits a unique endemic equilibrium \(Q^{*}(S^{*}\mathrm {\,,}I^{*}\mathrm {\,})\) if one of the above condition holds true.

4.2.2 Stability analysis of endemic equilibrium (EE)

To investigate the local stability of endemic equilibrium\({\,Q}^{*}\), we linearize this system of Equations (5)–(6) at \(Q^{*}\mathrm {\,}\)and obtain the characteristic equation, which is a second-degree transcendental equation as given below:

$$\begin{aligned} \lambda ^{2}+M_{0}\lambda +N_{0}+\left( M_{1}\lambda +N_{1} \right) \mathrm {e}^{-\lambda \tau }=0, \end{aligned}$$
(12)

where

$$\begin{aligned} M_{0}= & {} \left( 2\mu +d+\delta \right) +\frac{a}{{(1+bI^{{*}^{2}})}^{2}}+\frac{\beta I^{*}}{(1+\alpha I^{{*}^{2}})},\\ N_{0}= & {} \left( \mu +\frac{\beta I^{*}}{(1+\alpha I^{{*}^{2}})} \right) \left( \left( \mu +d+\delta \right) +\frac{a}{\left( 1+bI^{{*}^{2}} \right) ^{2}} \right) ,\\ M_{1}= & {} -\frac{\beta S^{*}(1-\alpha I^{{*}^{2}})}{{(1+\alpha I^{{*}^{2}})}^{2}}, \\ N_{1}= & {} -\frac{\beta {\mu S}^{*}(1-\alpha I^{{*}^{2}})}{{(1+\alpha I^{{*}^{2}})}^{2}}. \end{aligned}$$

Theorem 4

For \(\tau =0\), endemic equilibrium \(Q^{*}\) of the system of Equations (5)–(6) is locally asymptotically stable if \({\,M}_{0}+M_{1}>0\) and \(N_{0}+N_{1}>0\) are satisfied simultaneously.

Proof

At endemic equilibrium \(Q^{*}\), the characteristic equation of the system for \(\tau =0\) is obtained by putting \(\tau =0\) in Eq. (12), as given below:

$$\begin{aligned}&\lambda ^{2}+M_{0}\lambda +N_{0}+\left( M_{1}\lambda +N_{1} \right) =0 \Rightarrow \lambda ^{2}+\left( M_{0}+M_{1} \right) \lambda +(N_{0}+N_{1})=0. \end{aligned}$$
(13)

Clearly, if \(M_{0}\mathrm {+}M_{1}\mathrm {>}\) and \(N_{0}\mathrm {+}N_{1}\mathrm {>}0\) are satisfied simultaneously, then by the Routh–Hurwitz criterion, Eq. (13) will always have roots with negative real part, hence the system of Equations (5)–(6) at \(\mathrm {Q}^{\mathrm {*}}\) for \(\mathrm {\uptau =0}\) is locally asymptotically stable. This completes the proof. \(\square \)

Theorem 5

For \(\tau >0\), endemic equilibrium \(Q^{*}\) of the system of Equations (5)–(6) is locally asymptotically stable if \(M_{0}^{2}-2N_{0}-M_{1}^{2}>0\) and \(N_{0}^{2}-N_{1}^{2}>0\) are satisfied simultaneously.

Proof

At endemic equilibrium \(Q^{*}\), the characteristic equation of the system for \(\tau >0\) is given by Eq. (12):

$$\begin{aligned} \lambda ^{2}+M_{0}\lambda +N_{0}+\left( M_{1}\lambda +N_{1} \right) \mathrm {e}^{-\lambda \tau }=0. \end{aligned}$$

For\(\mathrm {\,\,}\tau >0\), corollary 2.4 from Ruan and Wei [34] ensures that, if the endemic equilibrium \(Q^{*}\) is unstable for a particular value of the delay parameter, then roots of the characteristic equation (12) must intersect the imaginary axis. Thus, to prove the stability of the system of Equations (5)–(6), we use the contradictory assumption; i.e., we assume that \(\lambda =\mathrm {i}\omega ,\,\omega >0\) is the root of Eq. (12). Putting \(\mathrm {\,\,}\lambda =\mathrm {i}\omega \) into Eq. (12) yields

$$\begin{aligned} -\omega ^{2}+N_{0}+M_{1}\omega \,\sin \left( \omega \tau \right) +N_{1}\cos \left( \omega \tau \right) +\mathrm {i}\,\left( M_{1}\omega \,\cos \left( \omega \tau \right) -N_{1}\,\sin \left( \omega \tau \right) +\,M_{0}\omega \right) =0. \end{aligned}$$
(14)

By using Euler’s formula and by separating the real and imaginary parts of Eq. (14), we get

$$\begin{aligned}&M_{1}\omega \,\sin {(\omega \tau )}+N_{1}\,\cos {(\omega \tau )}=\omega ^{2}-N_{0}, \end{aligned}$$
(15)
$$\begin{aligned}&M_{1}\omega \cos {(\omega \tau )}-N_{1}\,\sin \left( \omega \tau \right) ={-M}_{0}\omega . \end{aligned}$$
(16)

Squaring and adding both sides of Equations (15) and (16) yields

$$\begin{aligned} \omega ^{4}+\left( M_{0}^{2}-2N_{0}-M_{1}^{2} \right) \omega ^{2}+\left( N_{0}^{2}-N_{1}^{2} \right) =0. \end{aligned}$$
(17)

Letting\({\,\omega }^{2}=Z_{1}\), Eq. (19) becomes

$$\begin{aligned} Z_{1}^{2}+MZ_{1}+T=0, \end{aligned}$$
(18)

where \(M=\left( M_{0}^{2}-2N_{0}-M_{1}^{2} \right) \) and \(T=\left( N_{0}^{2}-N_{1}^{2} \right) \).

Clearly, if \(M=\left( M_{0}^{2}-2N_{0}-M_{1}^{2} \right) \mathrm {\,}>0\) and \(T=\left( N_{0}^{2}-N_{1}^{2} \right) \mathrm {>}0\) are satisfied simultaneously, then by the Routh–Hurwitz criterion, Eq. (18) will always have roots with negative real part. This contradicts our assumption for instability that \(\lambda =\mathrm {i}\omega \) is a root of Eq. (12). Hence, the endemic equilibrium \(\mathrm {Q}^{\mathrm {*}}\) of the system of Equations (5)–(6) is locally asymptotically stable for\(\mathrm {\,}\tau >0\). This completes the proof. \(\square \)

5 Hopf bifurcation analysis

In this section, we discuss the Hopf bifurcation of the system of Equations (5)–(6).

If \(T=\left( N_{0}^{2}-N_{1}^{2} \right) \) in Eq. (18) is negative, then there is a unique positive \(\omega _{0}\) satisfying Eq. (18); i.e., there is a single pair of purely imaginary roots \(\pm \mathrm {i}\omega _{0}\) to Eq. (2).

From Equations (15) and (16), the \(\tau _{n}\) corresponding to \(\omega _{0}\) can be obtained as

$$\begin{aligned} \tau _{n}=\frac{1}{\omega _{0}}\,\mathrm {arccos} \left( \frac{\left( N_{1}-M_{0}M_{1} \right) \omega _{0}^{2}-N_{0}N_{1}}{M_{1}^{2}\omega _{0}^{2}+N_{1}^{2}} \right) +\frac{2n\pi }{\omega _{0}},\,\,n=0,\,1,\,2,\,\ldots \,. \end{aligned}$$
(19)

The endemic equilibrium \(Q^{*}\) is stable for \(\tau <\tau _{0}\) if the transversality condition holds true, i.e., if \(\,\left. \frac{\mathrm {d}\,}{\mathrm {d}t}(\mathrm {Re}\,(\lambda )) \right| _{\lambda =\mathrm {i}\omega _{0}}>0\).

Differentiating Eq. (12) with respect to \(\tau \), using the chain rule as \(\lambda \) is a function of \(\tau \), yields

$$\begin{aligned} \left( 2\lambda +M_{0}+M_{1}\mathrm {e}^{-\lambda \tau }-\left( M_{1}\lambda +N_{1} \right) \tau \mathrm {e}^{-\lambda \tau } \right) \frac{\mathrm {d}\lambda }{\mathrm {d}\tau }=\lambda (M_{1}\lambda +N_{1})\mathrm {e}^{-\lambda \tau }. \end{aligned}$$
(20)
$$\begin{aligned} \left( \frac{\mathrm {d}\lambda }{\mathrm {d}\tau } \right) ^{-1}&=\frac{\left( 2\lambda +M_{0}+M_{1}\mathrm {e}^{-\lambda \tau }-\left( M_{1}\lambda +N_{1} \right) \tau \mathrm {e}^{-\lambda \tau } \right) }{\lambda (M_{1}\lambda +N_{1})\mathrm {e}^{-\lambda \tau }}\\&=\frac{(2\lambda +M_{0})}{\lambda (M_{1}\lambda +N_{1})\mathrm {e}^{-\lambda \tau }}+\frac{M_{1}}{\lambda (M_{1}\lambda +N_{1})}-\frac{\tau }{\lambda }. \end{aligned}$$
$$\begin{aligned}&\left( \frac{\mathrm {d}\lambda }{\mathrm {d}\tau } \right) ^{-1}=\frac{(2\lambda +M_{0})}{-\lambda (\lambda ^{2}+M_{0}\lambda +N_{0})}+\frac{M_{1}}{\lambda (M_{1}\lambda +N_{1})}-\frac{\tau }{\lambda }.\\&\left. \frac{\mathrm {d}\,}{\mathrm {d}\tau }(\mathrm {Re}\,(\lambda )) \right| _{\lambda =\mathrm {i}\omega _{0}}=\left. \mathrm {Re}\left( \frac{\mathrm {d}\lambda }{\mathrm {d}\tau } \right) ^{-1} \right| _{\lambda =\mathrm {i}\omega _{0}}\\&\quad =\mathrm {Re}\left( \frac{(2\mathrm {i}\omega _{0}+M_{0})}{-\mathrm {i}\omega _{0}(-\omega _{0}^{2}+{\mathrm {i}M}_{0}\omega _{0}+N_{0})}+\frac{M_{1}}{\mathrm {i}\omega _{0}({\mathrm {i}M}_{1}\omega _{0}+N_{1})}-\frac{\tau }{\mathrm {i}\omega _{0}}\mathrm {\,} \right) \\&\quad =\mathrm {Re}\left( \frac{1}{\omega _{0}}\left( \frac{(2\mathrm {i}\omega _{0}+M_{0})}{\left( \omega _{0}^{2}-N_{0} \right) \mathrm {i}+M_{0}\omega _{0})}+\frac{M_{1}}{({-M}_{1}\omega _{0}+\mathrm {i}N_{1})}+\mathrm {i}\tau \mathrm {\,} \right) \right) \\&\quad =\frac{1}{\omega _{0}}\left( \frac{2\omega _{0}\left( \omega _{0}^{2}-N_{0} \right) +M_{0}^{2}\omega _{0}}{\left( \omega _{0}^{2}-N_{0} \right) ^{2}+{(M_{0}\omega _{0})}^{2}}-\frac{M_{1}^{2}\omega _{0}}{{(M_{1}\omega _{0})}^{2}+N_{1}^{2}}\mathrm {\,} \right) \\&\quad =\frac{2\omega _{0}^{2}+(M_{0}^{2}-2N_{0}-M_{1}^{2})}{{(M_{1}\omega _{0})}^{2}+N_{1}^{2}}. \end{aligned}$$

\(\big (\text {Since, from Equations }(15)\, \text {and}\, (16),\big ( \omega _{0}^{2}-N_{0} \big )^{2}+\big ( M_{0}\omega _{0} \big )^{2}=\left( M_{1}\omega _{0} \right) ^{2}+N_{1}^{2}.\big )\)

Under the condition \(M_{0}^{2}-2N_{0}-M_{1}^{2}>0\), we have \(\,\left. \frac{\mathrm {d}\,}{\mathrm {d}\tau }(\mathrm {Re}\,(\lambda )) \right| _{\lambda =\mathrm {i}\omega _{0}}>0\).

Thus, this proves that the transversality condition holds true and hence Hopf bifurcation occurs at \(\omega =\omega _{0},\,\tau =\tau _{0}\). Summarizing the above analysis, we arrive at the following theorem:

Theorem 6

The endemic equilibrium (EE) of the system of Equations (5)–(6) is asymptotically stable for \(\tau \in [0,\,\tau _{0})\), and it undergoes a Hopf bifurcation at \(\tau =\tau _{0}\).

6 Global stability

In this section, we discuss the global stability analysis of equilibrium points. For this, we state the results in the form of theorems and prove them.

We see that \(Y\left( S(t),\,I(t) \right) =\frac{\beta S(t)I(t)}{1+\alpha I^{2}(t)}\) and \(H\left( I(t) \right) =\frac{aI^{2}(t)}{1+bI^{2}(t)}\) are always positive, continuously differentiable, and monotonically increasing for all \(S>0\) and \(I>0\); That is, they satisfy the following conditions:

H1 :

\(Y\left( S(t),\,I(t) \right)>0,\,Y^{'}_{S}\left( S,\,I \right)>0,\,Y^{'}_{I}\left( S,\,I \right) >0\) for \(S>0\) and \(I>0\).

H2 :

\(Y\left( S,0 \right) =Y\left( 0,I \right) =0,\,Y^{'}_{S}\left( S,\,0 \right)>0,\,Y^{'}_{I}\left( S,\,0 \right) >0\) for \(S>0\) and \(I>0\).

H3 :

\(H\left( 0 \right) =0,\,H^{'}(I)>0\) for \(I>0\).

These properties will be used to prove the global stability of equilibria.

6.1 Global stability of disease-free equilibrium (DFE)

In this subsection, we show the global stability of DFE of the system of Equations (5)–(6). For this, we suppose the following conditions:

H4 :

\(\varphi \left( S,I \right) =\frac{Y\left( S,I \right) }{I}\) is a bounded and monotone decreasing function of \(I>0\), for any fixed \(S\ge 0\), and \(K\left( S \right) ={\varphi \left( S,I \right) }\) is continuous on \(S\ge 0\) and a monotone increasing function of \(S\ge 0\).

H5 :

\(h'(0)\le \frac{H(I)}{I}\) with respect to \(I>0 \quad \left( \mathrm {where\,}h(I)=\frac{aI}{1+bI^{2}} \right) \).

For the global stability of DFE, we prove the following theorem:

Theorem 7

The DFE \(Q\left( \frac{A}{\mu },0 \right) \) of the system of Equations (5)–(6) is globally asymptotically stable if and only if \({\,R}_{0}\le 1\).

Proof

To prove this theorem, consider the following Lyapunov function:

$$\begin{aligned} W(t)=W_{1}(t)+W_{2}(t)+I(t), \end{aligned}$$

where

$$\begin{aligned} W_{1}(t)=\int _{S_{0}=\frac{A}{\mu }}^{S(t)} {\left( 1-\frac{K\left( S_{0} \right) }{K(s)} \right) \mathrm {d}s}\quad \text {and}\quad W_{2}(t)=\int _{t-\tau }^t {Y\left( s\left( u+\tau \right) ,\,I\left( u \right) \right) \frac{K\left( S_{0} \right) }{K(S(u+\tau ))}\mathrm {d}u}. \end{aligned}$$

The derivative of \({\,W}_{1}(t)\) is

$$\begin{aligned} \frac{\mathrm {d}W_{1}(t)}{\mathrm {d}t}&=\left( 1-\frac{K\left( S_{0} \right) }{K(S(t))} \right) \left( A-\mu S(t)-Y(S(t),\,I(t-\tau )) \right) \\&=-\left( 1-\frac{K\left( S_{0} \right) }{K\left( S(t) \right) } \right) Y\left( S(t),\,I\left( t-\tau \right) \right) -\mu (S(t)-S_{0})\left( 1-\frac{K\left( S_{0} \right) }{K\left( S(t) \right) } \right) . \end{aligned}$$

The derivative of \({\,W}_{2}(t)\) is

$$\begin{aligned} \frac{\mathrm {d}W_{2}(t)}{\mathrm {d}t}=Y\left( S\left( t+\tau \right) ,\,I(t) \right) \left( \frac{K\left( S_{0} \right) }{K\left( S\left( t+\tau \right) \right) } \right) -Y\left( S(t),\,I\left( t-\tau \right) \right) \frac{K\left( S_{0} \right) }{K\left( S(t) \right) }. \end{aligned}$$

Hence, we obtain

$$\begin{aligned} \frac{\mathrm {d}W(t)}{\mathrm {d}t}&=-\left( 1-\frac{K\left( S_{0} \right) }{K\left( S(t) \right) } \right) Y\left( S(t),\,I\left( t-\tau \right) \right) -\mu \left( S(t)-S_{0} \right) \left( 1-\frac{K\left( S_{0} \right) }{K\left( S(t) \right) } \right) \\&\quad + Y\left( S\left( t+\tau \right) ,\,I(t) \right) \left( \frac{K\left( S_{0} \right) }{K\left( S\left( t+\tau \right) \right) } \right) -Y\left( S(t),\,I\left( t-\tau \right) \right) \frac{K\left( S_{0} \right) }{K\left( S(t) \right) }\\&\quad +\,Y\left( S(t),\,I\left( t-\tau \right) \right) -\left( \mu +d+\delta \right) I(t)-\frac{aI^{2}(t)}{1+bI^{2}(t)}\\&=-\mu \left( S(t)-S_{0} \right) \left( 1-\frac{K\left( S_{0} \right) }{K\left( S(t) \right) } \right) +Y\left( S\left( t+\tau \right) ,\,I(t) \right) \left( \frac{K\left( S_{0} \right) }{K\left( S\left( t+\tau \right) \right) } \right) \\&\quad -\left( \mu +d+\delta +\frac{aI}{1+bI^{2}} \right) I(t). \end{aligned}$$

Here, by conditions (H1–H2), we obtain that

$$\begin{aligned} -\mu \left( S(t)-S_{0} \right) \left( 1-\frac{K\left( S_{0} \right) }{K\left( S(t) \right) } \right) \le 0, \end{aligned}$$

with equality if and only if \(S(t)=S_{0}\). From the conditions (H4–H5), it follows that

$$\begin{aligned}&Y\left( S\left( t+\tau \right) ,\,I(t) \right) \left( \frac{K\left( S_{0} \right) }{K\left( S\left( t+\tau \right) \right) } \right) -\left( \mu +d+\delta +\frac{aI}{1+bI^{2}} \right) I(t)\\&\quad \le \left( \frac{Y\left( S\left( t+\tau \right) ,\,I(t) \right) }{\left( \mu +d+\delta +h^{'}\left( 0 \right) \right) I(t)}\left( \frac{K\left( S_{0} \right) }{K\left( S\left( t+\tau \right) \right) } \right) -1 \right) \left( \mu +d+\delta +h^{'}\left( 0 \right) \right) I(t)\\&\quad \le \left( \frac{K\left( S\left( t+\tau \right) \right) }{\left( \mu +d+\delta +h^{'}\left( 0 \right) \right) }\times \frac{K\left( S_{0} \right) }{K\left( S\left( t+\tau \right) \right) }-1 \right) \left( \mu +d+\delta +h^{'}\left( 0 \right) \right) I(t)\\&\quad =\left( \frac{K\left( S_{0} \right) }{\left( \mu +d+\delta +h^{'}\left( 0 \right) \right) }-1 \right) \left( \mu +d+\delta +h^{'}\left( 0 \right) \right) I(t)\\&\quad =\left( R_{0}-1 \right) \left( \mu +d+\delta +h^{'}\left( 0 \right) \right) I(t). \end{aligned}$$

Therefore, \(R_{0}\le 1\) ensures that \(\frac{\mathrm {d}W(t)}{\mathrm {d}t}\le 0\) for all \(t>0\), where \(\frac{\mathrm {d}W(t)}{\mathrm {d}t}=0\) holds if \(S(t)=S_{0}\). Hence, it immediately follows from the system of Equations (5) – (6) that DFE Q is the largest invariant set in \(\{(S(t),\,I(t))\in {\mathbb {R}}_{+0}^{2}\left| \frac{\mathrm {d}W(t)}{\mathrm {d}t}=0 \right. \}\). From the Lyapunov–LaSalle asymptotic stability theorem [27], we obtain that DFE Q is globally asymptotically stable. This completes the proof. \(\square \)

6.2 Global stability of endemic equilibrium (EE)

In this subsection, we discuss the global stability of endemic equilibrium \(Q^{*}(S^{*},\,I^{*})\) of the system of Equations (5)–(6) using the Lyapunov direct method. For this, we propose the following hypotheses:

H6 :

\(\frac{I(t)}{I^{*}}\le \frac{Y\left( S(t),\,I\left( t-\tau \right) \right) }{Y\left( S(t),\,I^{*} \right) }\) for \(I\in \left( 0,\,I^{*} \right) ,\frac{Y\left( S(t),\,I\left( t-\tau \right) \right) }{Y\left( S(t),\,I^{*} \right) }\le \frac{I(t)}{I^{*}}\) for \(I\ge I^{*}\).

H7 :

\(\frac{H\left( I(t) \right) }{H(I^{*})}\le \frac{I(t)}{I^{*}}\) for \(I\in \left( 0,\,I^{*} \right) ,\frac{H\left( I(t) \right) }{H(I^{*})}\ge \frac{I(t)}{I^{*}}\) for \(I\ge I^{*}\).

Theorem 8

Suppose that conditions (H1)–(H3) and (H6)–(H7) are satisfied. Then the endemic equilibrium \(Q^{*}(S^{*},\,I^{*})\) of the system of Equations (5)–(6) is globally asymptotically stable if \(\,R_{0}>1\).

Proof

Consider the following Lyapunov functional:

$$\begin{aligned} X(t)=X_{1}(t)+X_{1}(t), \end{aligned}$$

where

$$\begin{aligned} X_{1}(t)&=S(t)-S^{*}-\int _{S^{*}}^{S(t)} {\frac{Y\left( S^{*},\,I^{*} \right) }{Y\left( u,\,I^{*} \right) }\mathrm {d}u} +I(t)-I^{*}-I^{*}\log _{\mathrm {e}}{\frac{I(t)}{I^{*}}-}\int _{t-\tau }^t {Y\left( S\left( u+\tau \right) ,\,I\left( u \right) \right) \mathrm {d}u},\\ X_{2}(t)&=Y\left( S^{*},\,I^{*} \right) \int _{t-\tau }^t \left( \frac{Y\left( S\left( u+\tau \right) ,\,I\left( u \right) \right) }{Y\left( S^{*},\,I^{*} \right) }-1-\log _{\mathrm {e}}\frac{Y\left( S\left( u+\tau \right) ,\,I\left( u \right) \right) }{Y\left( S^{*},\,\,I^{*} \right) } \right) \mathrm {d}u. \end{aligned}$$

\(X(t)=X_{1}(t)+X_{1}(t)\) is defined and continuously differentiable for all \(S(t),\,I(t)>0\). And \(X\left( 0 \right) =0\) at \(Q^{*}\left( S^{*},\,I^{*} \right) \). At \(Q^{*}(S^{*},\,I^{*})\),

$$\begin{aligned}&A-\mu S^{*}=Y\left( S^{*},\,I^{*} \right) ,\\&Y\left( S^{*},\,I^{*} \right) =\left( \mu +d+\delta \right) I^{*}+H(I^{*}). \end{aligned}$$

The time derivative of \(X_{1}(t)\) along the solution of the system of Equations (5)–(6) is given by

$$\begin{aligned} \frac{\mathrm {d}X_{1}(t)}{\mathrm {d}t}&=S{'}(t)-\frac{Y\left( S^{*},\,I^{*} \right) }{Y\left( S(t),\,I^{*} \right) }S{'}(t)+I^{'}(t)-\frac{I^{*}}{I(t)}I^{'}(t)-Y(S(t+\tau ),\,I(t))+Y(S(t),\,I(t-\tau ))\\&=\left( 1-\frac{Y\left( S^{*},\,I^{*} \right) }{Y\left( S(t),\,I^{*} \right) } \right) \left( \mu S^{*}-\mu S(t)+Y\left( S^{*},\,I^{*} \right) -Y((S(t),\,I(t-\tau )) \right) \\&\quad +\left( 1-\frac{I^{*}}{I(t)} \right) \left( Y\left( S(t),\,I\left( t-\tau \right) \right) -Y\left( S^{*},\,I^{*} \right) \frac{I(t)}{I^{*}}+H\left( I^{*} \right) \frac{I(t)}{I^{*}}-H\left( I(t) \right) \right) \\&\quad -\,Y(S(t+\tau ),\,I(t))+Y(S(t),\,I(t-\tau ))\\&=\mu S^{*}\left( 1-\frac{Y\left( S^{*},\,I^{*} \right) }{Y\left( S(t),\,I^{*} \right) } \right) \left( 1-\frac{S(t)}{S^{*}} \right) +Y\left( S^{*},\,I^{*} \right) \\&\quad \left( 1-\frac{Y\left( S^{*},\,I^{*} \right) }{Y\left( S(t),\,I^{*} \right) }+\frac{Y\left( S(t),\,I\left( t-\tau \right) \right) }{Y\left( S(t),\,I^{*} \right) } \right) \\&\quad +\,Y\left( S^{*},\,I^{*} \right) \left( 1-\frac{I(t)}{I^{*}}-\frac{Y\left( S(t),\,I\left( t-\tau \right) \right) }{Y\left( S(t),\,I^{*} \right) }\frac{I^{*}}{I(t)} \right) \\&\quad + H\left( I^{*}\right) \left( \frac{I(t)}{I^{*}}-1+\frac{H\left( I(t) \right) }{H\left( I^{*} \right) }-\frac{H\left( I(t) \right) }{H\left( I^{*} \right) }\frac{I^{*}}{I(t)} \right) \\&\quad -\,Y(S(t+\tau ),\,I(t))+Y(S(t),\,I(t-\tau )). \end{aligned}$$

Further,

$$\begin{aligned} \frac{\mathrm {d}X_{2}(t)}{\mathrm {d}t}&=Y\left( S^{*},\,I^{*} \right) \left( \frac{Y\left( S\left( t+\tau \right) ,\,I(t) \right) }{Y\left( S^{*},\,I^{*} \right) }-1-\log _{\mathrm {e}}\frac{Y\left( S\left( t+\tau \right) ,\,I(t) \right) }{Y\left( S^{*},\,I^{*} \right) }\right. \\&\quad \left. -\frac{Y\left( S(t),\,I\left( t-\tau \right) \right) }{Y\left( S^{*},\,I^{*} \right) }+1+\log _{\mathrm {e}}\frac{Y\left( S(t),\,I\left( t-\tau \right) \right) }{Y\left( S^{*},\,I^{*} \right) } \right) \\&=Y\left( S\left( t+\tau \right) ,\,I(t) \right) -Y\left( S(t),\,I\left( t-\tau \right) \right) +Y\left( S^{*},\,I^{*} \right) \log _{e}\frac{Y\left( S(t),\,I\left( t-\tau \right) \right) }{Y\left( S\left( t+\tau \right) ,\,I(t) \right) }. \end{aligned}$$

Then, we have

$$\begin{aligned} \frac{\mathrm {d}X(t)}{\mathrm {d}t}&=\mu S^{*}\left( 1-\frac{Y\left( S^{*},\,I^{*} \right) }{Y\left( S(t),\,I^{*} \right) } \right) \left( 1-\frac{S(t)}{S^{*}} \right) +Y\left( S^{*},\,I^{*} \right) \left( 1-\frac{Y\left( S^{*},\,I^{*} \right) }{Y\left( S(t),\,I^{*} \right) }+\frac{Y\left( S(t),\,I\left( t-\tau \right) \right) }{Y\left( S(t),\,I^{*} \right) } \right) \\&\quad +\,Y\left( S^{*},\,I^{*} \right) \left( 1-\frac{I(t)}{I^{*}}-\frac{Y\left( S(t),\,I\left( t-\tau \right) \right) }{Y\left( S(t),\,I^{*} \right) }\frac{I^{*}}{I(t)} \right) \\&\quad +H\left( I^{*} \right) \left( \frac{I(t)}{I^{*}}-1+\frac{H\left( I(t) \right) }{H\left( I^{*} \right) }-\frac{H\left( I(t) \right) }{H\left( I^{*} \right) }\frac{I^{*}}{I(t)} \right) \\&\quad -\,Y\left( S\left( t+\tau \right) ,\,I(t) \right) +Y\left( S(t),\,I\left( t-\tau \right) \right) +Y\left( S\left( t+\tau \right) ,\,I(t) \right) \\&\quad -\,Y\left( S(t),\,I\left( t-\tau \right) \right) +Y\left( S^{*},\,I^{*} \right) \log _{e}\frac{Y\left( S(t),\,I\left( t-\tau \right) \right) }{Y\left( S\left( t+\tau \right) ,\,I(t) \right) }\\&=\mu S^{*}\left( 1-\frac{Y\left( S^{*},\,I^{*} \right) }{Y\left( S(t),\,I^{*} \right) } \right) \left( 1-\frac{S(t)}{S^{*}} \right) +Y\left( S^{*},\,I^{*} \right) \left( 1-\frac{Y\left( S^{*},\,I^{*} \right) }{Y\left( S(t),\,I^{*} \right) }+\log _{\mathrm {e}}\frac{Y\left( S^{*},\,I^{*} \right) }{Y\left( S(t),\,I^{*} \right) } \right) \\&\quad +\,Y\left( S^{*},\,I^{*} \right) \left( 1-\frac{Y\left( S(t),\,I\left( t-\tau \right) \right) }{Y\left( S(t),\,I^{*} \right) }\frac{I^{*}}{I(t)}+\log _{\mathrm {e}}{\frac{Y\left( S(t),\,I\left( t-\tau \right) \right) }{Y\left( S(t),\,I^{*} \right) }\frac{I^{*}}{I(t)}} \right) \\&\quad +\,Y\left( S^{*},\,I^{*} \right) \left( 1-\frac{I(t)}{I^{*}}\frac{Y\left( S(t),\,I^{*} \right) }{Y\left( S(t),\,I\left( t-\tau \right) \right) }+\log _{e}{\frac{I(t)}{I^{*}}\frac{Y\left( S(t),\,I^{*} \right) }{Y\left( S(t),\,I\left( t-\tau \right) \right) }} \right) \\&\quad +\,Y\left( S^{*},\,I^{*} \right) \left( \frac{I(t)}{I^{*}}-\frac{Y\left( S(t),\,I\left( t-\tau \right) \right) }{Y\left( S(t),\,I^{*} \right) } \right) \left( \frac{Y\left( S(t),\,I^{*} \right) }{Y\left( S(t),\,I\left( t-\tau \right) \right) }-1 \right) \\&\quad +\,H(I^{*})\left( \frac{H\left( I(t) \right) }{H(I^{*})}-\frac{I(t)}{I^{*}} \right) \left( \frac{I^{*}}{I(t)}-1 \right) . \end{aligned}$$

The function \(Y(S,\,I)\) is monotonically increasing for any \(S>0\); hence, the following inequality holds:

$$\begin{aligned} \left( 1-\frac{Y\left( S^{*},\,I^{*} \right) }{Y\left( S(t),\,I^{*} \right) } \right) \left( 1-\frac{S(t)}{S^{*}} \right) \le 0. \end{aligned}$$
(21)

And by the properties of the function \(r\left( x \right) =1-x+\log _{e}x,\,(x>0)\), we note that r(x) has its global maximum \(r\left( 1 \right) =0\). Hence \(r(x)\le 0\) when \(x>0\), and the following inequalities hold true:

$$\begin{aligned}&1-\frac{Y\left( S^{*},\,I^{*} \right) }{Y\left( S(t),\,I^{*} \right) }+\log _{e}\frac{Y\left( S^{*},\,I^{*} \right) }{Y\left( S(t),\,I^{*} \right) }\le 0\mathrm {,} \nonumber \\&1-\frac{Y\left( S(t),\,I\left( t-\tau \right) \right) }{Y\left( S(t),\,I^{*} \right) }\frac{I^{*}}{I(t)} +\log _{\mathrm {e}}{\frac{Y\left( S(t),\,I\left( t-\tau \right) \right) }{Y\left( S(t),\,I^{*} \right) }\frac{I^{*}}{I(t)}}\le 0, \text { and }\nonumber \\&1-\frac{I(t)}{I^{*}}\frac{Y\left( S(t),\,I^{*} \right) }{Y\left( S(t),\,I\left( t-\tau \right) \right) } +\log _{e}{\frac{I(t)}{I^{*}}\frac{Y\left( S(t),\,I^{*} \right) }{Y\left( S(t),\,I\left( t-\tau \right) \right) }}\le 0. \end{aligned}$$
(22)

Further, by conditions (H6)–(H7), the following inequalities apply:

$$\begin{aligned}&\left( \frac{I(t)}{I^{*}}-\frac{Y\left( S(t),\,I\left( t-\tau \right) \right) }{Y\left( S(t),\,I^{*} \right) } \right) \left( \frac{Y\left( S(t),\,I^{*} \right) }{Y\left( S(t),\,I\left( t-\tau \right) \right) }-1 \right) \le 0, \nonumber \\&\left( \frac{H\left( I(t) \right) }{H(I^{*})}-\frac{I(t)}{I^{*}} \right) \left( \frac{I^{*}}{I(t)}-1 \right) \le 0. \end{aligned}$$
(23)

From inequalities (21)–(23), we see that \(\frac{\mathrm {d}X(t)}{\mathrm {d}t}\le 0\) for all \(S(t)\ge 0,I(t)\ge 0\). It is easy to verify that the largest invariant set in \(\{(S(t),\,I(t))\left| \mathrm {\,}\frac{\mathrm {d}X(t)}{\mathrm {d}t}=0 \right. \}\) is the singleton \(\{Q^{*}\}\). By the Lyapunov–LaSalle asymptotic stability theorem [27], endemic equilibrium \(Q^{*}\) is globally asymptotically stable. \(\square \)

7 Numerical simulations

In this section, we present numerical simulations of the system of Equations (5)–(6). All computations are done with the following data (Table 1).

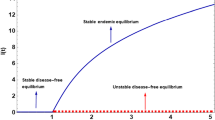
Table 1 Description of parameters for simulation and their values
Full size table

The variation in the susceptible and infected populations with respect to time delay, taking various values of the time lag (\(\tau =0,\,2\), and 4 days) at different initial values is shown in Figs. 1a and 2a and Figs. 1b and 2b, respectively. Clearly, Figs. 1a and 2a show a decrement in the susceptible population, while Figs. 1b and 2b show an increment in the infected population, as the time lag \(\tau \) increases. Thus, the longer the delay, the greater the occurrence of infection in the society, which is biologically true.

Fig. 1
figure 1

a Variation in susceptible population S(t) for different values of time lag \(\tau \). b Variation in infected population I(t) for different values of time lag \(\tau \)

Full size image
Fig. 2
figure 2

a Variation in susceptible population S(t) for different values of time lag \(\tau \). b Variation in infected population I(t) at different values of time lag \(\tau \)

Full size image
Fig. 3
figure 3

Effect of transmission rate \(\beta \) on infected population I(t)

Full size image
Fig. 4
figure 4

Effect of measure of inhibition \(\alpha \) on infected population I(t)

Full size image
Fig. 5
figure 5

Impact of cure rate a on infected population I(t)

Full size image
Fig. 6
figure 6

Variation in infected population with various combinations of incidence and treatment rates for time lag \(\tau =1\)

Full size image
Fig. 7
figure 7

Variation in infected population for various values of limitation rate in treatment availability b

Full size image

The influence of the transmission rate \(\beta \) and inhibitory effect \(\alpha \) on the infected population is simulated in Figs. 3 and 4, respectively. Figure 3 shows that the infected population increases with increase in the transmission rate \(\beta \), while the infected population decreases with increasing value of the inhibitory effect \(\alpha \) in Fig. 4. Based on these figures, it can be concluded that inhibitions must be exercised to control the disease in society. Furthermore, the similarity between Figs. 3 and 4 validates the mathematical structure of the model.

Figure 5 shows the impact of the cure rate on the infected population for various values of the cure rate (\(a=0.02,\,0.04\), and 0.06). The diminution of the infected population with the increment in the cure rate a can be seen from this graph, then the infected population settles down to its steady state. Also, it is readily seen from this graph that, when there is low treatment availability, infection occurs at a higher rate.

Figure 6 presents the variation in the population of infected individuals in the presence of inhibitory effects and a Holling type III treatment rate, in the absence of the inhibitory effect and in the presence of a Holling type III treatment rate, in the presence of the inhibitory effect and in the absence of the Holling type III treatment rate, and in the absence of the inhibitory effect and Holling type III treatment rate. This figure shows how the combination of Monod–Haldane incidence (presence of inhibitory effects) and Holling type III treatment rates helps control the spread of an infectious disease effectively. From this graph, it can be seen that, when infected individuals are treated at a Holling type III rate, the number of infected individuals sharply decreases initially, and thereafter begins to decrease gradually before reaching a steady state.

Figure 7 shows the infected population at increased values of limitation rate in treatment availability. It can be observed from this figure that, the higher the limitation in treatment availability, the greater the infection will be.

To illustrate the Hopf bifurcation numerically, the oscillatory and periodic behavior of the infected population is drawn in Figs. 8, 9 and 10. For this, we take the following data [10]:

$$\begin{aligned} A= & {} 5\,\mathrm{person}\,(day)^{-1},\,\mu =0.05\,(day)^{-1},\,\beta =0.54\,(\mathrm{person})^{-1}\,(day)^{-1},\,\alpha =1.2\,(\mathrm{person})^{-1}\,(day)^{-1},\\ d= & {} 0.001\,{(day)}^{-1},\,\delta =0.002\,{(day)}^{-1},a=0.1\,{\mathrm{(person)}}^{-1}\,{(day)}^{-1},\,b=0.0387\,{\mathrm{(person)}}^{-1}\,{(day)}^{-1}. \end{aligned}$$
Fig. 8
figure 8

Oscillatory behavior of infected population for \(\tau =9\) days

Full size image
Fig. 9
figure 9

Oscillatory behavior of infected population for \(\tau =11\) days

Full size image
Fig. 10
figure 10

Periodic behavior of infected population for \(\tau =13.5\) days

Full size image

Figures 8 and 9 show damped oscillations for the delay of \(\tau =9\) and \(\tau =11\) days, indicating that the inherent dynamics contains a strong oscillatory component, but the amplitude of these fluctuations declines over time as the system equilibrates. This shows how the fraction of infective individuals oscillates with decreasing amplitude as it settles towards the equilibrium, whereas Fig. 10 shows the periodic solution of the infected population with respect to time for a time delay of \(\tau =13.5\) days, which confirms the occurrence of Hopf bifurcation.

8 Discussion and conclusions

We propose and analyze a time-delayed SIR epidemic model with a novel combination of nonlinear incidence and treatment rates to study the transmission dynamics of an infectious disease. The nonlinear incidence rate is taken as Monod–Haldane functional type to interpret the inhibitory effect on the population with a time delay representing the incubation period of the disease, while the treatment rate is taken as a Holling type III functional to capture the limitation in treatment of infected individuals. The mathematical study of the model shows that it has two equilibrium points, namely disease-free equilibrium (DFE) and endemic equilibrium (EE). The stability of equilibria is discussed based on the threshold parameter \(R_{0}\), revealing that the DFE is locally asymptotically stable when the basic reproduction number \(R_{0}\) is less than unity but unstable when \(R_{0}\) is greater than unity, implying that the disease can be eradicated from society if the basic reproduction number is less than unity but will persist if the basic reproduction number is more than unity. Furthermore, the results show that the model undergoes a transcritical bifurcation at DFE based on center manifold theory, when the basic reproduction number equals unity. We also discuss the stability of the model at EE; the results show that EE is locally asymptotically stable for time lag \(\tau \ge 0\) under the conditions stated in Theorem 4 and 5, respectively. We show that the model undergoes a Hopf bifurcation at endemic equilibrium under the condition stated in Theorem 6. Furthermore, the results show that DFE is globally asymptotically stable when \(R_{0}\le 1\) and EE is globally asymptotically stable when \(R_{0}>1\) under the conditions (H4–H5) and (H6–H7), respectively. We also simulate the model numerically to support our theoretical findings and plot graphs for time delay, transmission rate, a measure of inhibition, and treatment rate. From these graphs, it is observed that, the longer the delay, the greater the infection (Figs. 1, 2), and that Holling type III treatment may play a crucial role in controlling the infection (Fig. 6). The effect of inhibitory measures and the transmission rate of the disease on the infected population is shown in Figs. 3 and 4, respectively, from which it is evident that the infected population increases with increasing value of the transmission rate, but decreases with increasing inhibitory measures. This implies that, the greater the inhibitory effects, the lesser will be the infection. With the help of figures, we also show the oscillatory and periodic behavior of the infection in the population (Figs. 8, 9 and 10), revealing the occurrence of Hopf bifurcation and also confirming the appearance of the periodic solution.

The numerical results validate our theoretical findings, demonstrating that the delay parameter, inhibitory effects, cure rate, and limitation in treatment availability have significant impacts on transmission during the epidemic. When using this novel combination (Monod–Haldane incidence rate and Holling type III treatment rate), the infected population decreases at a very high rate in a short time (Fig. 6). Hence, this study provides a possible mechanism to control the impact of a disease on society in the presence of limitation of available treatment methods and inhibitory effects during an epidemic.